Intelligent Soft Sensor for Spindle Convective Heat Transfer Coefficient Under Varying Operating Conditions Using Improved Grey Wolf Optimization Algorithm
Abstract
1. Introduction
2. Spindle CHTC Problem Description
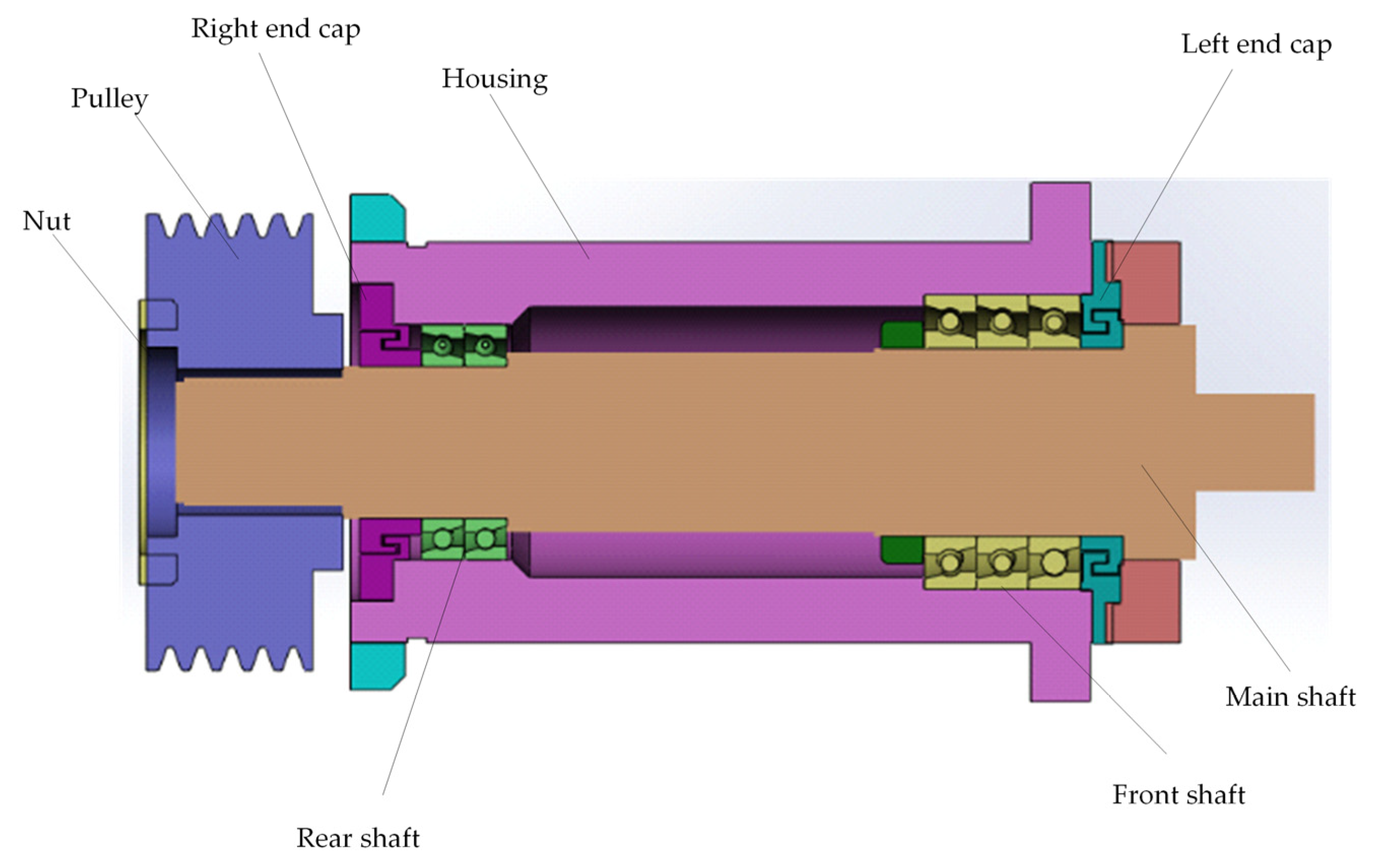
2.1. Mechanical Spindle Structure
- Complexity of CHTC’s physical characteristics: The value of CHTC is influenced not only by inherent factors such as the surface roughness and thermal conductivity of the spindle material but also by factors such as the fluid flow state, temperature distribution, and heat transfer conditions at the contact surface. These variables are interrelated, making the calculation and measurement of CHTC extremely complex. As a result, it is difficult to obtain accurate values through traditional direct measurement methods.
- Limitations of measurement methods: Traditional methods for measuring CHTC typically rely on devices like heat flux sensors or infrared thermometers. However, these methods mainly depend on indirect measurements of surface temperature or heat flow and cannot directly capture the heat exchange process between the spindle and its surrounding medium. Moreover, the complex surface shape of the spindle, combined with the constantly changing fluid flow conditions during high-speed operation, limits the accuracy and applicability of traditional methods. They often fail to reflect the actual heat exchange efficiency under working conditions.
- Dynamics and variability of operating conditions: The operating conditions of the spindle vary significantly across different machining tasks, including factors such as speed, load, and environmental temperature. These fluctuations lead to dynamic changes in the fluid state, heat transfer mode, and the CHTC. As a result, traditional static measurement methods struggle to track and capture these changes in real-time, causing delays and inaccuracies in CHTC measurements.
- Challenges in high-temperature and high-flow environments: During high-speed operation, heat exchange between the spindle surface and the fluid occurs in a high-temperature, high-flow environment. This makes it difficult for traditional measurement methods, such as direct placement of thermocouples or heat flux sensors, to accurately capture the CHTC. Furthermore, these methods may damage the equipment or interfere with the spindle’s operation. Therefore, accurately measuring the CHTC under these extreme conditions remains a significant technical challenge.
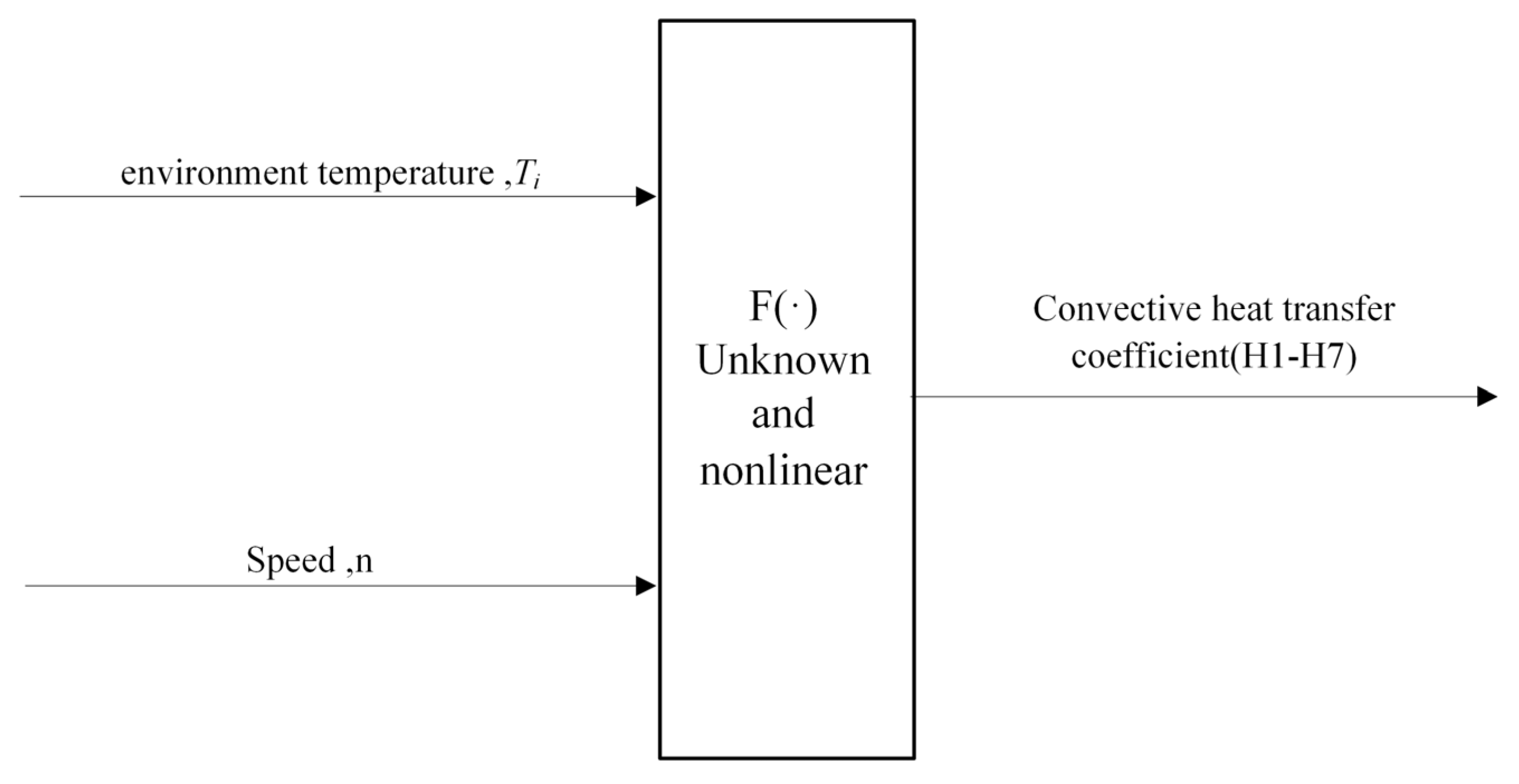
2.2. Analysis of Factors Affecting the CHTC
- Convection heat transfer coefficient H1 at the rear shaft pulley and environment air: This region is an exposed external part of the spindle shaft, directly contacting environment air. It is significantly influenced by airflow and environmental temperature; thus, analyzing its heat transfer characteristics is essential.
- Convection heat transfer coefficient H2 at the right end face of the rear bearing and the air gap: This interface connects the spindle interior to the external environment. Frictional heat from the bearing is dissipated here, exchanging heat with air via the air gap. Understanding heat transfer at this location is critical for evaluating bearing heat dissipation performance.
- Convection heat transfer coefficient H3 at the intermediate bearing and the air gap: The intermediate bearing is a critical spindle component. Subject to frictional heat and rotational speed, heat transfer between the bearing and the surrounding air gap is vital for overall spindle thermal management.
- Convection heat transfer coefficient H4 at the left end face of the rear bearing and the air gap: This end face also participates in heat exchange, conducting heat to the air through the air gap. It influences the spindle’s thermal distribution and stability. Analysis here further clarifies the heat dissipation capacity from the bearing heat source.
- Convection heat transfer coefficient H5 at the front shaft shoulder and environment air: Contacting environment air, the front shaft shoulder represents another key heat dissipation zone. Particularly during high-speed operation, its heat transfer characteristics play a pivotal role in spindle temperature control.
- Convection heat transfer coefficient H6 at the housing and the air gap: The spindle housing is isolated from direct environmental air contact. The presence of the air gap necessitates a focused analysis of heat transfer characteristics at this interface. Heat exchange efficiency between the housing and air gap is crucial for the spindle’s overall thermal performance.
- Convection heat transfer coefficient H7 at the housing and environment air: Direct contact between the housing and environment air affects the spindle’s heat exchange efficiency, especially under elevated temperatures. Heat transfer characteristics here are essential for maintaining operational stability and extending service life.
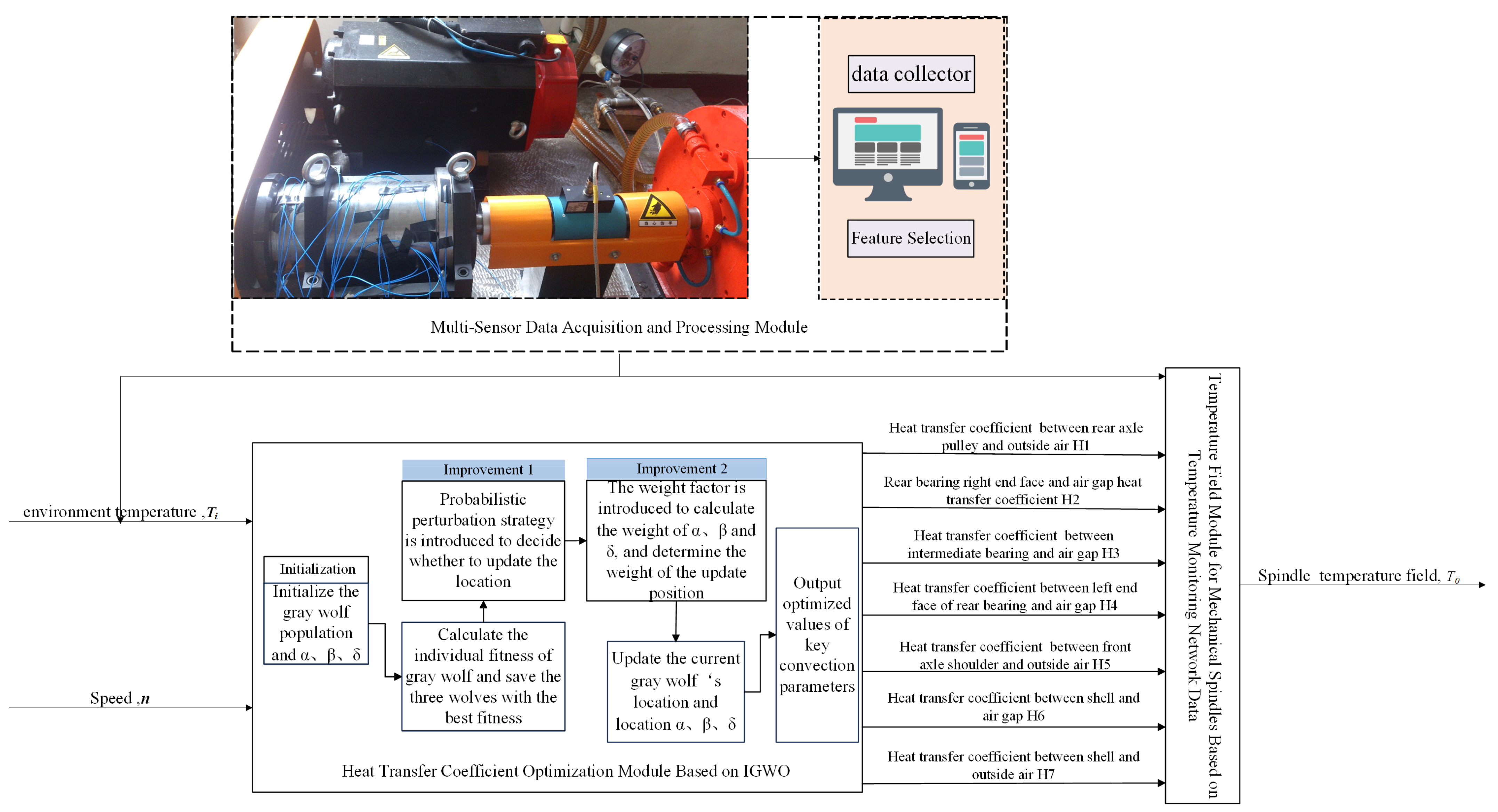
3. Intelligent Soft Sensor for Spindle CHTC Under Varying Operating Conditions Using IGWO
3.1. Soft Sensor Modeling Strategy
3.2. Soft Sensor Algorithm
3.2.1. Improved Grey Wolf Optimizer
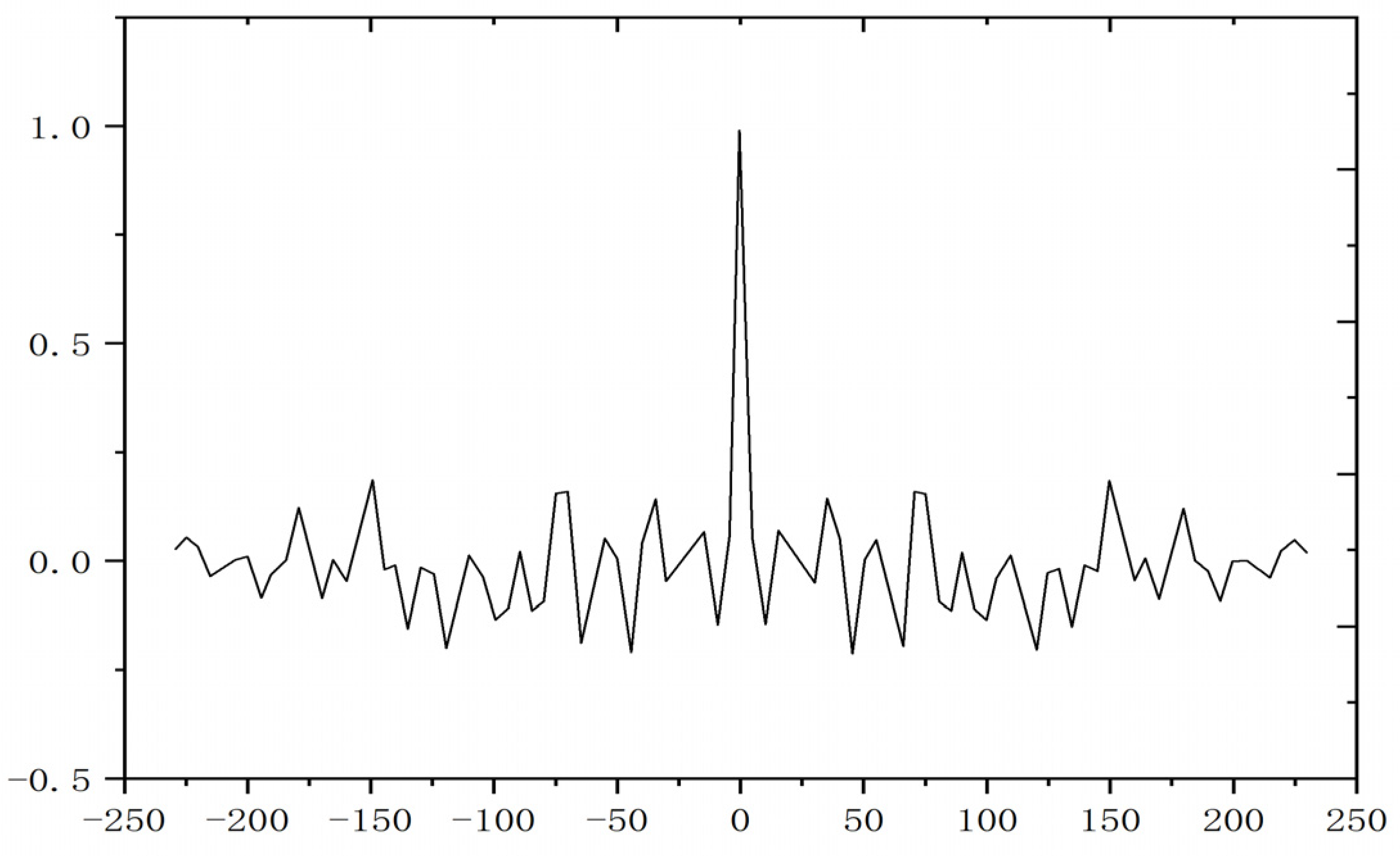
3.2.2. Validation of Effectiveness for the IGWO
3.2.3. Optimization of CHTC Based on Improved Grey Wolf Algorithm
- (1)
- Initialization: At the start of the search, each gray wolf represents a candidate CHTC solution. The initial positions of the wolf population, denoted as X(0) (i = 1, 2, …, N), are determined. The time step is set to t = 0.
- (2)
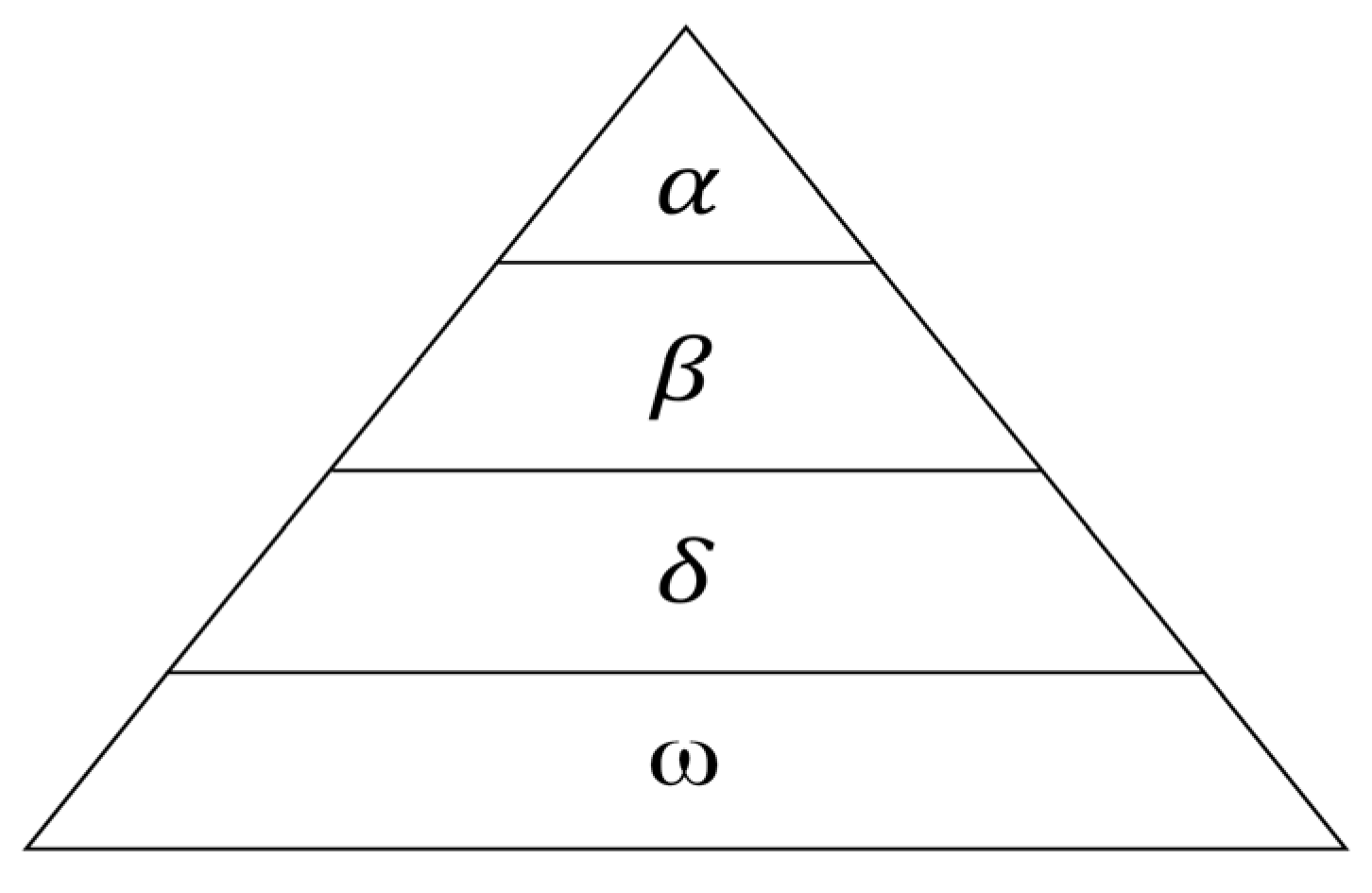
- Fitness Evaluation and Ranking: The fitness of all gray wolves (CHTC values) is evaluated. Subsequently, these values are sorted in ascending order. The three wolves with the highest fitness (representing the best CHTC values) are identified as α, β, and δ. Their position coordinates are recorded as Xα(t), Xβ (t), and Xδ(t), respectively.
- (3)
- Position Update: For each CHTC value (gray wolf), the coefficient vectors A and C are first calculated using Equations (17) and (18). Then, Equations (19)–(22) are applied to determine the new position X(t + 1) of the wolf at the next time step t + 1.
- (4)
- Termination and Update Check: The algorithm terminates if a stopping criterion is met (reaching the maximum iteration count or desired accuracy). In this case, Xα (t) is output as the global optimal solution. Otherwise, t is incremented (t = t + 1), and the process returns to Step (2). Additionally, if a specific CHTC value fails to update after k consecutive iterations, it is discarded as having converged to a local optimum.
3.3. Implementation Procedures for CHTC Soft Sensor
4. Experimental Studies
4.1. Experimental Platform and Data Description
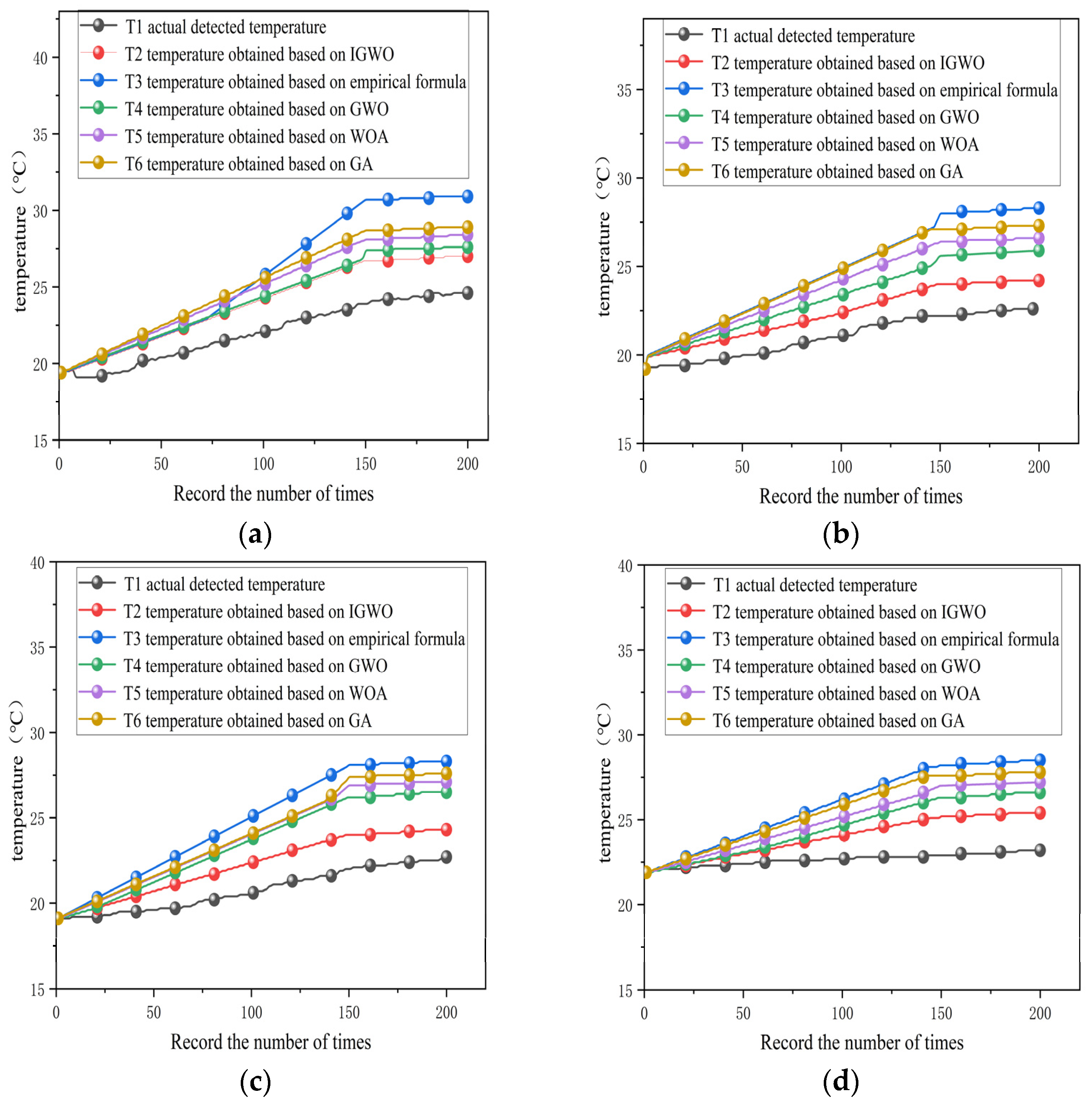
4.2. Validation of the Effectiveness of the Improved Grey Wolf Algorithm Under Variable Operating Conditions
5. Conclusions
- A soft-sensor method based on an intelligent optimization algorithm: This approach enables accurate dynamic identification of spindle CHTC through the optimization algorithm, overcoming limitations of conventional methods under variable operating conditions.
- Innovative adaptive weight adjustment and dynamic disturbance strategies: These mechanisms enhance the algorithm’s global search ability and convergence speed, allowing the model to respond to spindle variations under complex conditions and further improving the prediction accuracy of the CHTC.
- A potential technical pathway for thermal error compensation: By supporting accurate spindle CHTC estimation, this study offers a transferable framework that may facilitate thermal error compensation in CNC machine tools, showing promise for engineering applications.
- Collaborative field validation with manufacturing enterprises: Continuous 24 h production data should be collected from industrial CNC machine tools to assess the method’s performance under actual disturbances.
- Development of a hybrid anti-disturbance system: This system would combine sensor-level calibration (to reduce drift) and algorithm-level denoising techniques, such as integrating wavelet transforms into IGWO, to enhance the method’s resistance to interference.
- Cross-process validation: Testing should be carried out in various machining scenarios, including milling, turning, and grinding, to ensure the method’s generalizability across diverse CNC machining applications.
- Further optimization of the algorithm: To improve real-time performance and convergence speed, adaptive optimization strategies that respond to dynamic changes can be introduced, thereby strengthening the model’s robustness under extreme working conditions.
- Data processing and fusion methods: By refining data preprocessing techniques and algorithmic design, the model’s adaptability to varying working conditions can be improved, along with its ability to identify diverse heat exchange phenomena.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Variable | Variable Name |
| H1 | Heat transfer coefficient between the rear axle pulley and the outside air |
| H2 | Rear bearing right end face and air gap heat transfer coefficient |
| H3 | Heat transfer coefficient between the intermediate bearing and the air gap |
| H4 | Heat transfer coefficient between the left end face of the rear bearing and the air gap |
| H5 | Heat transfer coefficient between the front axle shoulder and the outside air |
| H6 | Heat transfer coefficient between the shell and the air gap |
| H7 | Heat transfer coefficient between the shell and the outside air |
| H | Heat Transfer Coefficient |
| λ | Thermal Conductivity of Air |
| Nu | Nusselt Number |
| l | Characteristic Length |
| ΔT | The temperature difference between the spindle surface and the air |
| Re | Reynolds Number |
| n | speed |
| r | Bearing Radius |
| d | Bearing Diameter |
| v | linear velocity |
| μ | Kinematic Viscosity of Air |
| Pr | Prandtl Number |
| Ti | environment temperature |
| T0 | Transient temperature field of the spindle |
| α,β,δ,ω | The level of wolf packs |
| A | Coefficient Vector A |
| C | Coefficient Vector C |
| D0 | The distance measurement between the individual gray wolf and its prey is based on the coefficient C. |
| r1 | random vector r1 |
| r2 | random vector r2 |
| ωi | weight factors |
| Xp(t) | Indicate the location of the prey |
| X(t) | The position of the gray wolf individual at the t-th generation |
| P | Disturbance probability |
| G | The dimension of the optimization problem |
| k | number of iterations |
| a | Control parameters |
| M | An individual, after a disturbance |
| lb | Lower bound of the individual gray wolf’s position |
| ub | Upper bound of an individual gray wolf’s position |
| r3 | random vector r3 |
| Ω | spatial function |
| Ts | Actual measured temperature |
| Ty | Temperature obtained from finite element simulation |
| fi | objective function |
| fiti | Fitness function |
| Tx(t) | Instantaneous values of each node on the main axis |
| E | Heat Capacity Matrix |
| K | Thermal Conductivity Matrix |
| Z | Temperature load matrix |
| Node temperature array | |
| ∆t | Time step |
| Derivative array of node temperature with respect to time |
References
- Cao, H.; Zhang, X.; Chen, X. The Concept and Progress of Intelligent Spindles: A Review. Int. J. Mach. Tools Manuf. 2017, 112, 21–52. [Google Scholar] [CrossRef]
- Yu, X.; Shao, M.; Yang, X.; Lin, Y.; Lan, Z.; Li, L.; Li, E.; Dai, R.; Jia, W.; Wang, J.; et al. Advances in the Investigation of Thermal Characteristics of Hydrostatic Bearing Spindle: An Overview. J. Therm. Anal. Calorim. 2025, 150, 3139–3171. [Google Scholar] [CrossRef]
- Li, K.; Zhang, Y.; He, Q. A Review of Research on Thermal Characteristics and Cooling Strategies of High-Speed Motorized Spindles. J. Therm. Anal. Calorim. 2024, 149, 5883–5902. [Google Scholar] [CrossRef]
- Dai, Y.; Li, W.; Qu, H.; Pang, J.; Li, Y. Study on Parameters of T-Type Cooling System for Motorized Spindle Based on Thermal Characteristics. Int. J. Adv. Manuf. Technol. 2024, 131, 5265–5276. [Google Scholar] [CrossRef]
- Kaulagi, M.N.; Sonawane, H.A. Thermal Network-Based Compensation Model for a Vertical Machining Center Subjected to Ambient Temperature Fluctuations. Int. J. Adv. Manuf. Technol. 2023, 124, 3973–3994. [Google Scholar] [CrossRef]
- Ma, C.; Yang, L.; Li, M.; He, J.; Hua, C.; Wang, L.; Li, G.; Liu, J.; Yang, J.; Liu, K.; et al. Closed-Loop Two-Phase Pulsating Heat Pipe towards Heat Export and Thermal Error Control for Spindle-Bearing System of Large-Size Vertical Machining Center. Appl. Therm. Eng. 2025, 269, 125993. [Google Scholar] [CrossRef]
- Dai, Y.; Wang, J.; Li, Z.; Wang, G.; Yin, X.; Yu, X.; Sun, Y. Thermal Performance Analysis and Experimental Study of High-Speed Motorized Spindle Based on the Gradient Descent Method. Case Stud. Therm. Eng. 2021, 26, 101056. [Google Scholar] [CrossRef]
- Lin, X.; Deng, X.; Zheng, J.; Yao, X.; Shen, H. Thermal Characteristics of Spindle System Based on the Comprehensive Effect of Multiple Nonlinear Time-Varying Factors. Processes 2024, 12, 423. [Google Scholar] [CrossRef]
- Zhou, W.; Ma, C.; Yang, L.; Luo, F.; Liu, J. Regulation of Thermo-Fluid-Solid Coupling Characteristics in High-Speed Spindle-Bearing System for Boring Machine Tool Based on Sintered-Core Heat Pipes. Int. Commun. Heat Mass Transf. 2024, 157, 107717. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, J.; Tong, Q.; An, G.; Liu, R.; Zhang, Y.; Yan, H. Study on the Thermal Performance and Temperature Distribution of Ball Bearings in the Traction Motor of a High-Speed EMU. Appl. Sci. 2020, 10, 4373. [Google Scholar] [CrossRef]
- Shen, Z.; Du, X.; Li, H.; Cao, W.; Cui, Y. Research on Accurate Modeling of Hydrostatic Motorized Spindle Based on Response Surface Optimization Algorithm. J. Mech. Strength 2022, 44, 1179–1185. [Google Scholar] [CrossRef]
- Zhang, L.; Li, C.; Wu, Y.; Zhang, K.; Shi, H. Hybrid Prediction Model of the Temperature Field of a Motorized Spindle. Appl. Sci. 2017, 7, 1091. [Google Scholar] [CrossRef]
- Zhang, Z.; Feng, S.; Ding, Y.; Mei, X.; Tao, Z. Thermal Error Modeling of Spindle and Dynamic Machining Accuracy Reliability Analysis of CNC Machine Tools Based on IA and LHSMC. Eksploat. Niezawodn. Maint. Reliab. 2022, 24, 100–113. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Wang, Z. Analysis of Thermal Characteristics of Machine Tool Spindle Based on Lion Swarm Optimization Algorithm. J. Mech. Strength 2024, 46, 708–716. [Google Scholar] [CrossRef]
- Zhang, L.; Gong, W.; Zhang, K.; Wu, Y.; An, D.; Shi, H.; Shi, Q. Thermal Deformation Prediction of High-Speed Motorized Spindle Based on Biogeography Optimization Algorithm. Int. J. Adv. Manuf. Technol. 2018, 97, 3141–3151. [Google Scholar] [CrossRef]
- Zhang, L.; Bao, R. Prediction of Temperature Field in the Whole Process of Instantaneous and Steady State of High-Speed Motorized Spindle. Int. J. Adv. Manuf. Technol. 2024, 131, 4021–4034. [Google Scholar] [CrossRef]
- Li, Y.; Yu, M.; Bai, Y.; Hou, Z.; Zhang, H.; Wu, W. A Heat Dissipation Enhancing Method for the High-Speed Spindle Based on Heat Conductive Paths. Adv. Mech. Eng. 2023, 15, 16878132231167676. [Google Scholar] [CrossRef]
- Yang, J.; Wang, M.; Wang, C.; Li, F.; Hui, Y.; Liu, S.; Zhang, Z.; Lei, M.; Zhu, J. Mechanism, Calculation Method, and Analytical Modeling of Spindle Thermal Characteristics Considering Radiation Heat Transfer. CIRP J. Manuf. Sci. Technol. 2025, 61, 175–200. [Google Scholar] [CrossRef]
- Li, Z.; Du, J.; Zhu, W.; Wang, B.; Wang, Q.; Sun, B. Regression Predictive Modeling of High-Speed Motorized Spindle Using POA-LSTM. Case Stud. Therm. Eng. 2024, 54, 104053. [Google Scholar] [CrossRef]
- Xiang, S.; Yang, J.; Zhang, Y. Modeling Method for Spindle Thermal Error Based on MechanismAnalysis and Thermal Basic Characteristics Tests. J. Mech. Eng. 2014, 50, 144–152. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, K.; Hao, Y.; Yao, Y. Short-Term Wind Power Prediction Using a Novel Model Based on Butterfly Optimization Algorithm-Variational Mode Decomposition-Long Short-Term Memory. Appl. Energy 2024, 366, 123313. [Google Scholar] [CrossRef]
- Chai, X.; Wu, Z.; Li, W.; Fan, H.; Sun, X.; Xu, J. Image Segmentation Based on the Optimized K-Means Algorithm with the Improved Hybrid Grey Wolf Optimization: Application in Ore Particle Size Detection. Sensors 2025, 25, 2785. [Google Scholar] [CrossRef] [PubMed]
- Arularasan, A.N.; Ganeshkumar, P.; Alkhatib, M.; Albalawi, T. Harmonized Integration of GWO and J-SLnO for Optimized Asset Management and Predictive Maintenance in Industry 4.0. Sensors 2025, 25, 2896. [Google Scholar] [CrossRef]
- Xue, Y.; Ni, D.; Lu, Q.; Wang, Y. Path Planning of Mobile Robot Based on PGWO Algorithm. Control Decis. 2025, 40, 1395–1401. [Google Scholar] [CrossRef]
- Chen, D.; Liu, J.; Li, T.; He, J.; Chen, Y.; Zhu, W. Research on Mobile Robot Path Planning Based on MSIAR-GWO Algorithm. Sensors 2025, 25, 892. [Google Scholar] [CrossRef]
- Narasimhan, G.; Victor, A. Grey Wolf Optimized Stacked Ensemble Machine Learning Based Model for Enhanced Efficiency and Reliability of Predicting Early Heart Disease. Automatika 2024, 65, 749–762. [Google Scholar] [CrossRef]
- Pian, J.; Liu, M.; Liu, J.; Zhang, L.; Zhang, K. The Bee Colony Algorithm Calculation Method of the Convective Heat Transfer Coefficient in the Spindle. Control Eng. China 2018, 25, 1578–1584. [Google Scholar] [CrossRef]
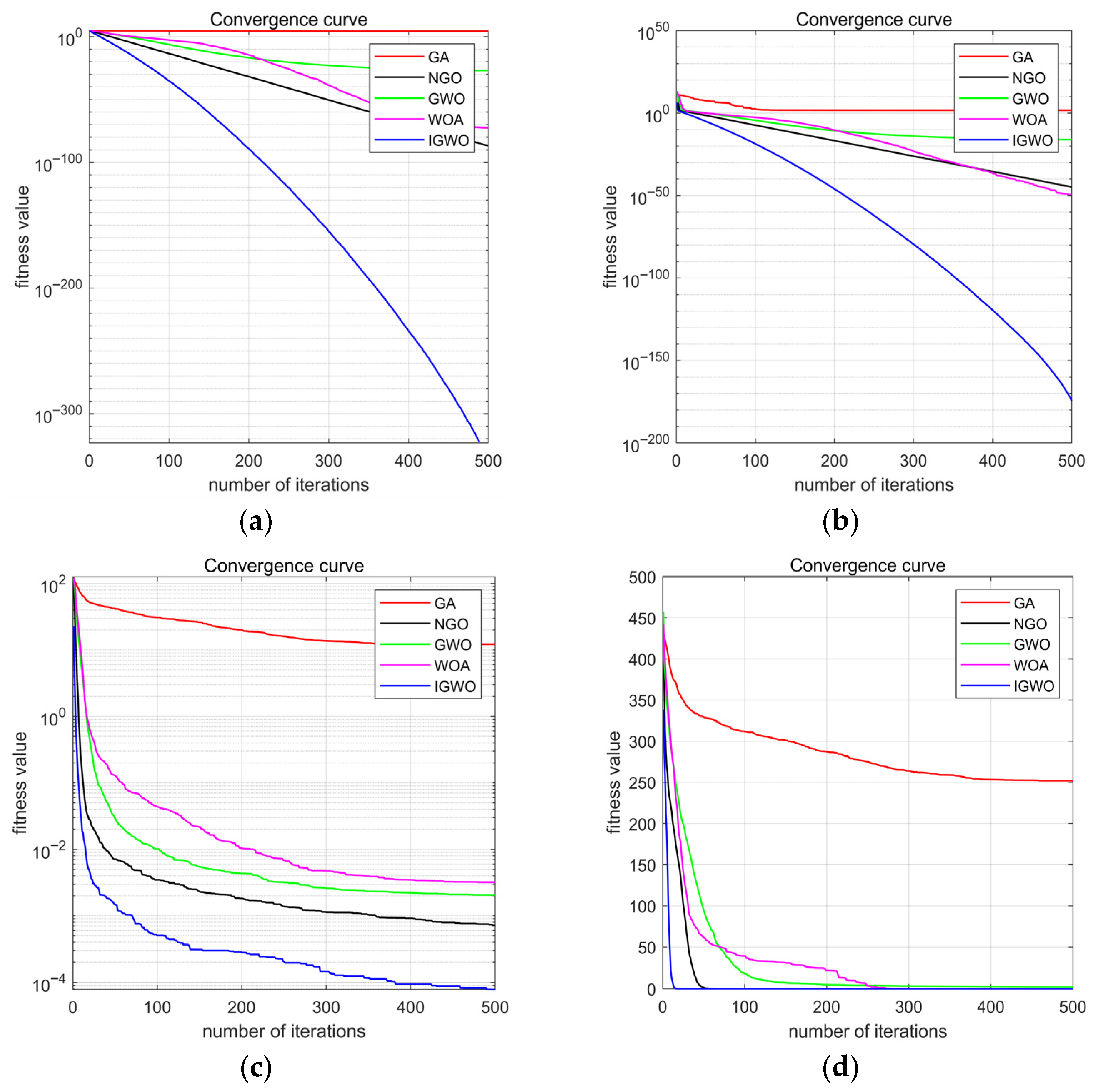



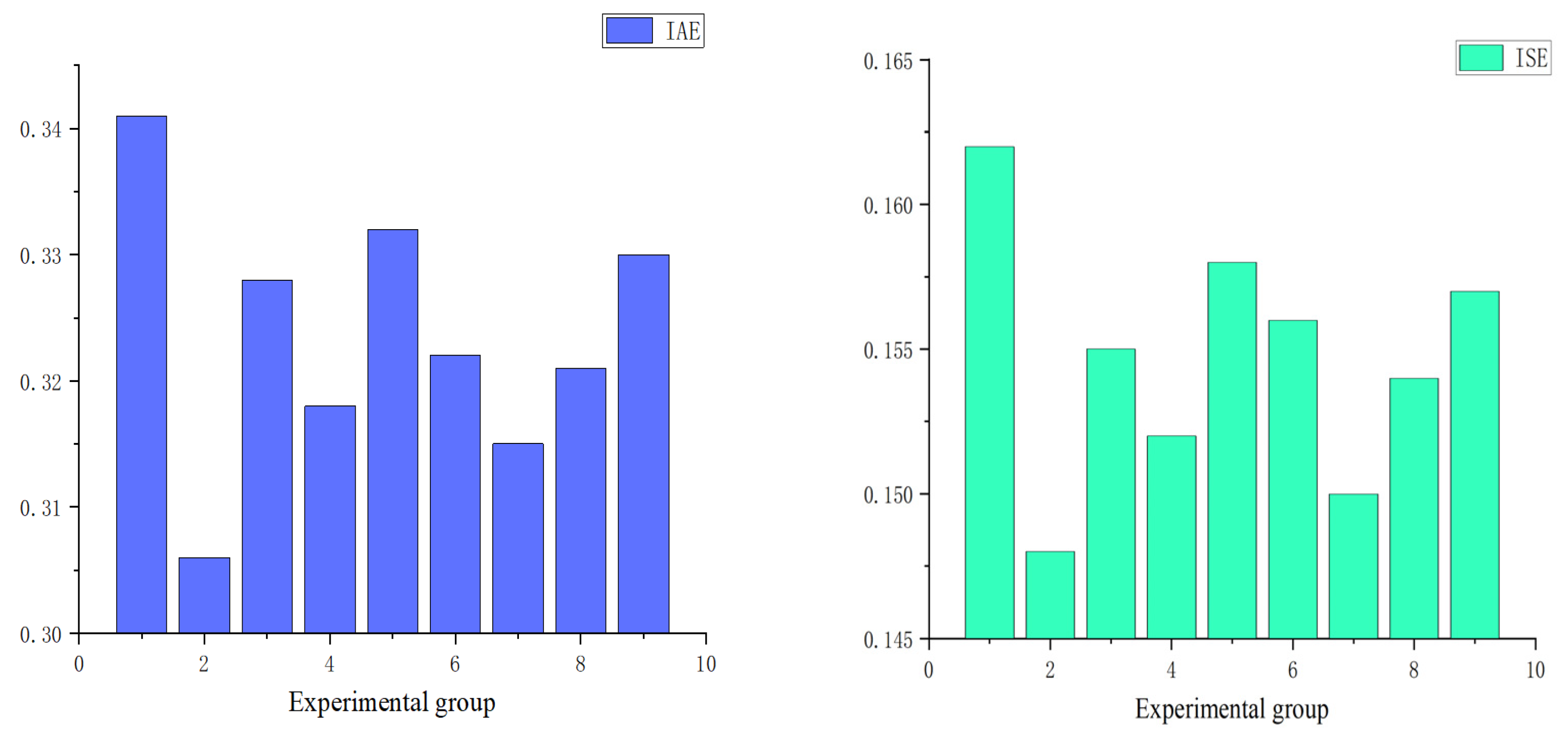
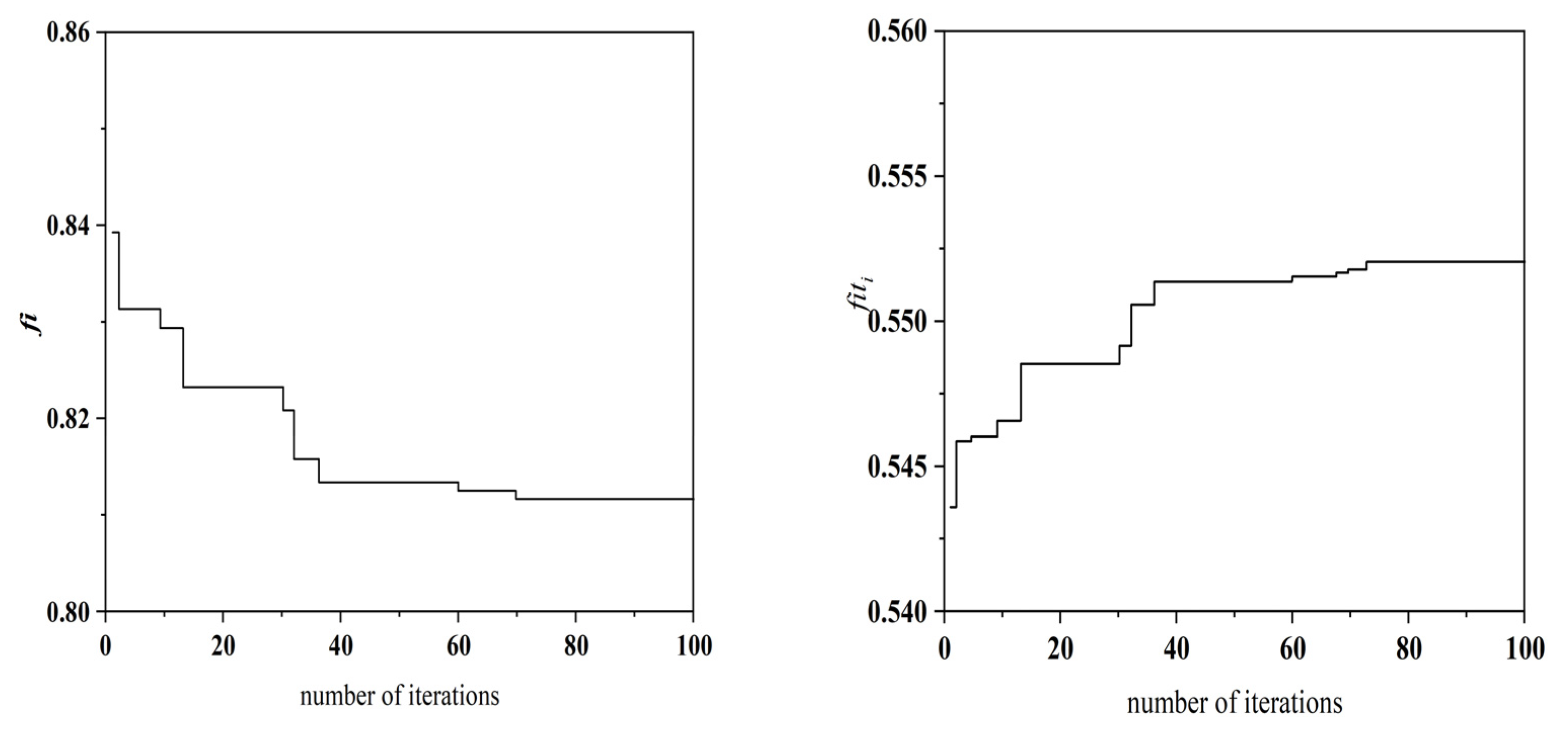


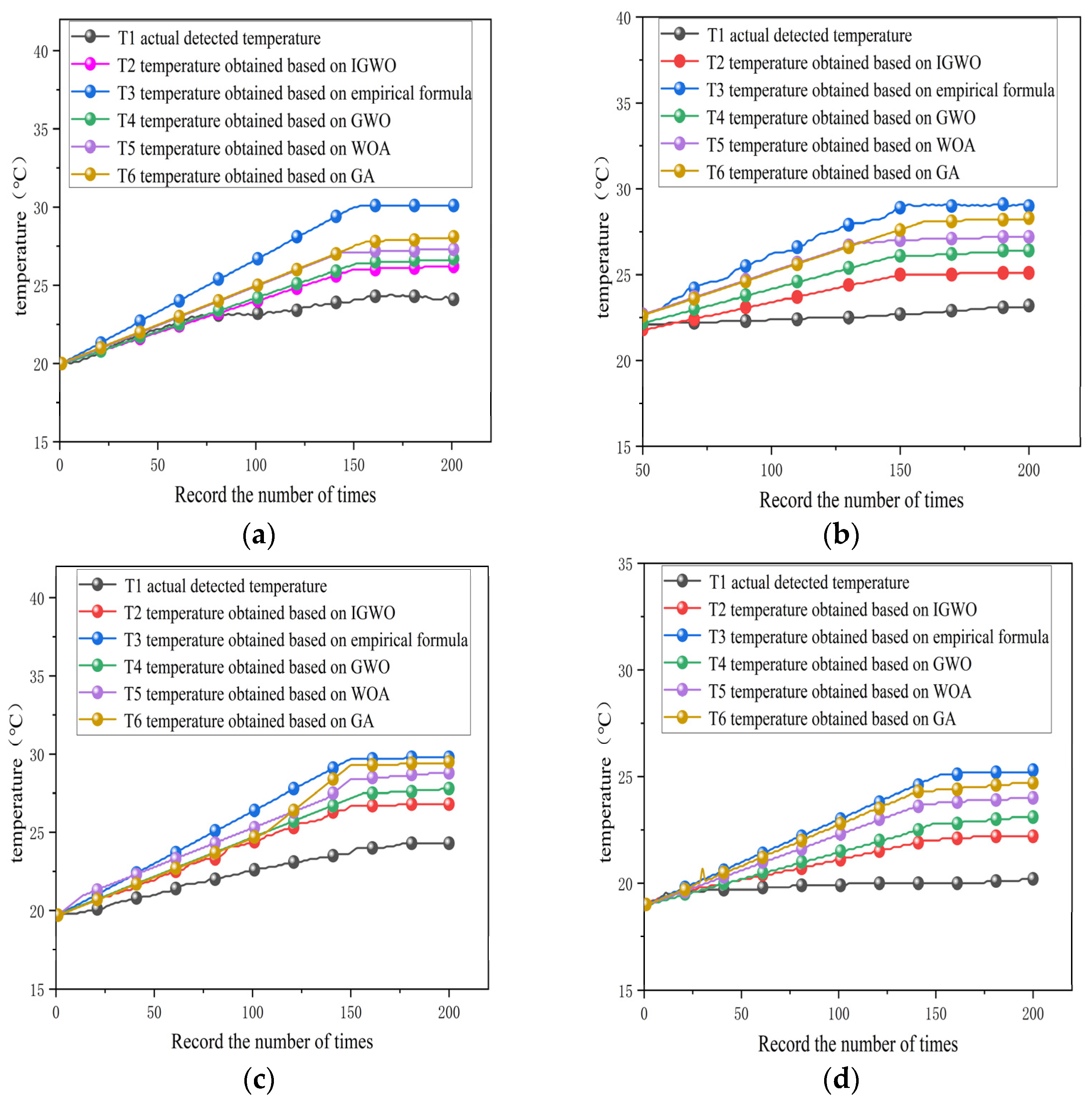
| Test Function | Dimension | Search Scope | Search Scope |
|---|---|---|---|
| 30 | [−100,100] | 0 | |
| 30 | [−10,10] | 0 | |
| 30 | [−1.28,1.28] | 0 | |
| 30 | [−5.12,5.12] | 0 |
| Hunting Behavior of Grey Wolves | CHTC |
|---|---|
| Wolves | Feasible solution for CHTC |
| The position of the wolf pack | Location of CHTC (H1–H7) |
| The three leading wolves in the wolf pack | The fitness value of CHTC |
| The process of searching, surrounding, and attacking prey | The process of solving problems |
| The position of the alpha wolf | The optimal solution to the problem |
| Experiment | D | k | Starting from a | Termination of a |
|---|---|---|---|---|
| 1 | 7 | 50 | 1.8 | 0.01 |
| 2 | 7 | 100 | 2.0 | 0.001 |
| 3 | 7 | 150 | 2.2 | 0.0001 |
| 4 | 14 | 50 | 2.0 | 0.0001 |
| 5 | 14 | 100 | 2.2 | 0.01 |
| 6 | 14 | 150 | 1.8 | 0.001 |
| 7 | 28 | 50 | 2.2 | 0.001 |
| 8 | 28 | 100 | 1.8 | 0.0001 |
| 9 | 28 | 150 | 2.0 | 0.01 |
| Location of CHTC | CHTC Value |
|---|---|
| H1 | 88.21 |
| H2 | 46.32 |
| H3 | 68.49 |
| H4 | 46.72 |
| H5 | 52.13 |
| H6 | 70.23 |
| H7 | 16.54 |
| Test Points | ME (°C) | MAE (°C) | MSE (°C) |
|---|---|---|---|
| 1 | 2.01 | 1.11 | 0.43 |
| 3 | 2.50 | 1.54 | 0.69 |
| 5 | 2.22 | 1.25 | 0.58 |
| 7 | 2.10 | 1.10 | 0.53 |
| Test Points | ME (°C) | MAE (°C) | MSE (°C) |
|---|---|---|---|
| 1 | 2.41 | 1.41 | 0.57 |
| 3 | 3.20 | 1.68 | 0.79 |
| 5 | 3.53 | 1.46 | 0.66 |
| 7 | 2.95 | 1.53 | 0.51 |
| Test Points | ME (°C) | MAE (°C) | MSE (°C) |
|---|---|---|---|
| 1 | 3.25 | 1.83 | 0.74 |
| 3 | 4.05 | 2.07 | 0.92 |
| 5 | 4.57 | 1.89 | 0.71 |
| 7 | 3.28 | 1.91 | 0.69 |
| Test Points | ME (°C) | MAE (°C) | MSE (°C) |
|---|---|---|---|
| 1 | 3.83 | 2.53 | 1.13 |
| 3 | 5.16 | 2.62 | 1.36 |
| 5 | 5.24 | 2.26 | 1.25 |
| 7 | 4.57 | 2.15 | 1.32 |
| Test Points | ME (°C) | MAE (°C) | MSE (°C) |
|---|---|---|---|
| 1 | 6.10 | 3.30 | 1.66 |
| 3 | 6.21 | 3.36 | 1.72 |
| 5 | 5.53 | 2.68 | 1.39 |
| 7 | 5.21 | 2.50 | 1.53 |
| Location of CHTC | CHTC Value |
|---|---|
| H1 | 79.75 |
| H2 | 46.25 |
| H3 | 61.89 |
| H4 | 45.31 |
| H5 | 46.20 |
| H6 | 68.23 |
| H7 | 11.12 |
| Test Points | ME (°C) | MAE (°C) | MSE (°C) |
|---|---|---|---|
| 1 | 2.43 | 1.21 | 0.45 |
| 3 | 2.18 | 1.43 | 0.61 |
| 5 | 2.39 | 1.29 | 0.59 |
| 7 | 2.22 | 1.16 | 0.49 |
| Test Points | ME (°C) | MAE (°C) | MSE (°C) |
|---|---|---|---|
| 1 | 3.12 | 1.56 | 0.62 |
| 3 | 3.45 | 1.72 | 0.86 |
| 5 | 4.01 | 1.53 | 0.73 |
| 7 | 3.49 | 1.67 | 0.59 |
| Test Points | ME (°C) | MAE (°C) | MSE (°C) |
|---|---|---|---|
| 1 | 3.83 | 1.87 | 0.76 |
| 3 | 4.08 | 2.09 | 0.94 |
| 5 | 4.63 | 1.91 | 0.72 |
| 7 | 4.07 | 2.01 | 0.73 |
| Test Points | ME (°C) | MAE (°C) | MSE (°C) |
|---|---|---|---|
| 1 | 4.37 | 2.72 | 1.26 |
| 3 | 4.71 | 2.42 | 1.19 |
| 5 | 4.92 | 2.04 | 1.21 |
| 7 | 4.68 | 2.17 | 1.30 |
| Test Points | ME (°C) | MAE (°C) | MSE (°C) |
|---|---|---|---|
| 1 | 6.33 | 3.32 | 1.69 |
| 3 | 5.71 | 3.16 | 1.70 |
| 5 | 5.24 | 2.57 | 1.41 |
| 7 | 5.36 | 2.53 | 1.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pian, J.; Li, G. Intelligent Soft Sensor for Spindle Convective Heat Transfer Coefficient Under Varying Operating Conditions Using Improved Grey Wolf Optimization Algorithm. Sensors 2025, 25, 5806. https://doi.org/10.3390/s25185806
Pian J, Li G. Intelligent Soft Sensor for Spindle Convective Heat Transfer Coefficient Under Varying Operating Conditions Using Improved Grey Wolf Optimization Algorithm. Sensors. 2025; 25(18):5806. https://doi.org/10.3390/s25185806
Chicago/Turabian StylePian, Jinxiang, and Gen Li. 2025. "Intelligent Soft Sensor for Spindle Convective Heat Transfer Coefficient Under Varying Operating Conditions Using Improved Grey Wolf Optimization Algorithm" Sensors 25, no. 18: 5806. https://doi.org/10.3390/s25185806
APA StylePian, J., & Li, G. (2025). Intelligent Soft Sensor for Spindle Convective Heat Transfer Coefficient Under Varying Operating Conditions Using Improved Grey Wolf Optimization Algorithm. Sensors, 25(18), 5806. https://doi.org/10.3390/s25185806






