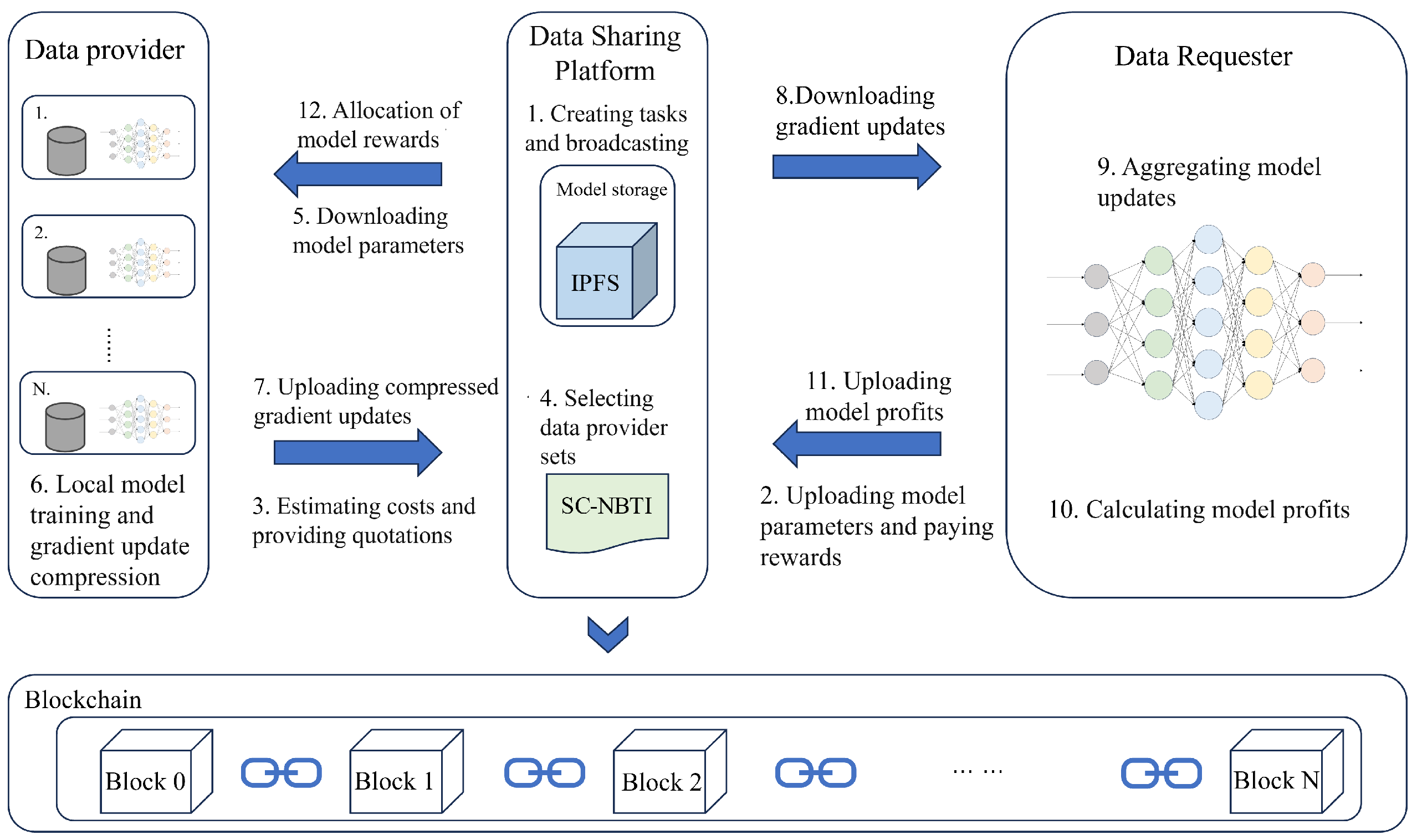
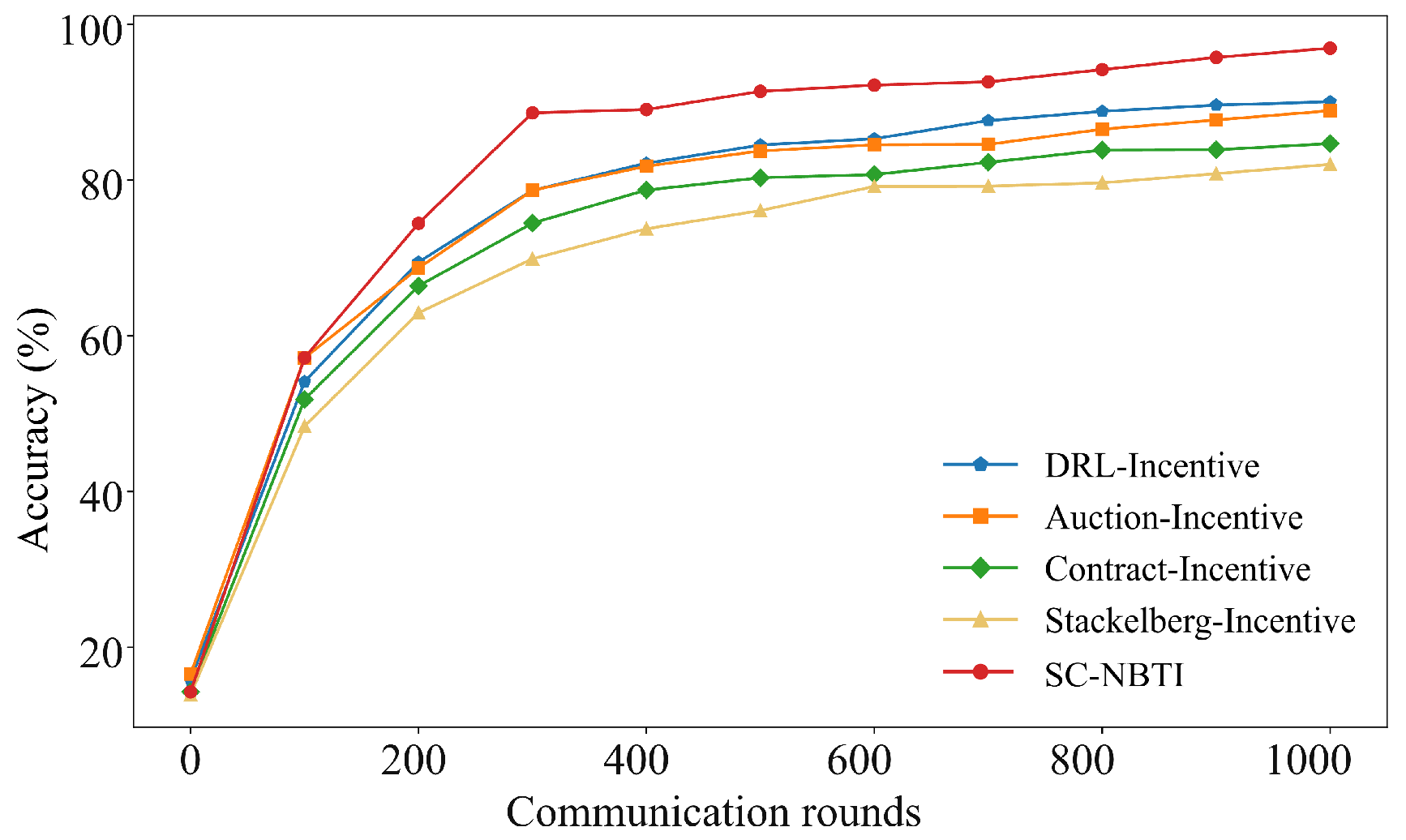
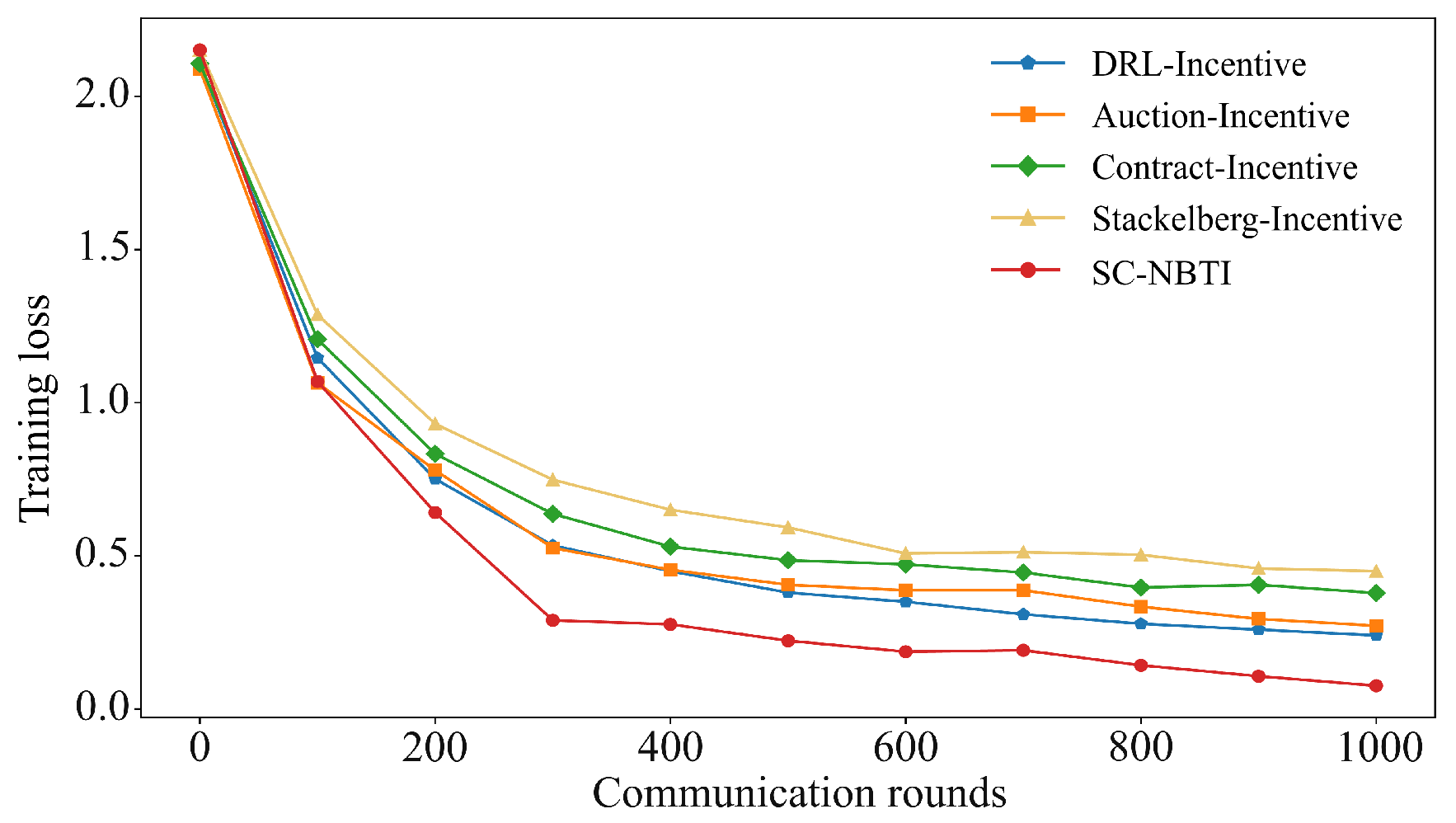
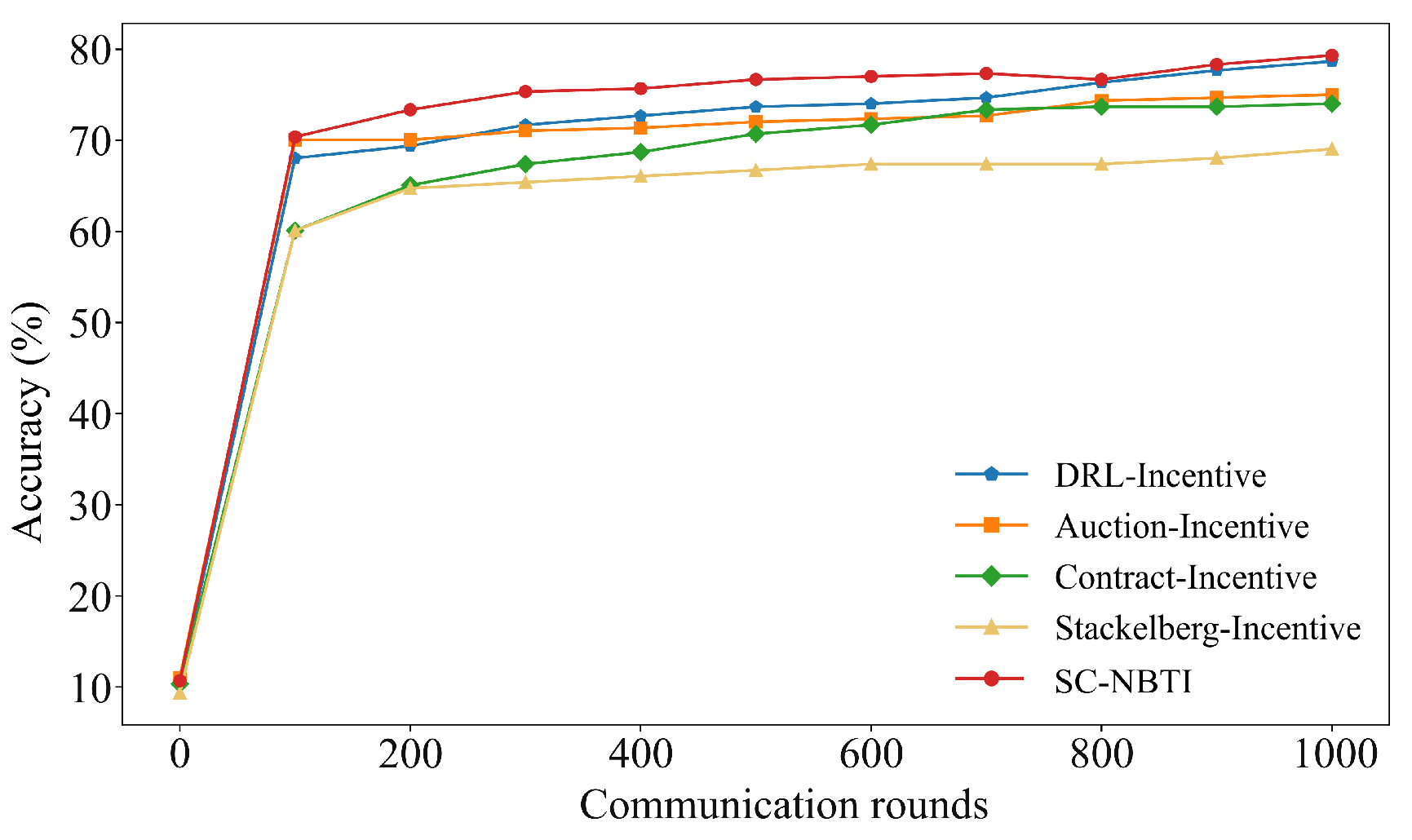
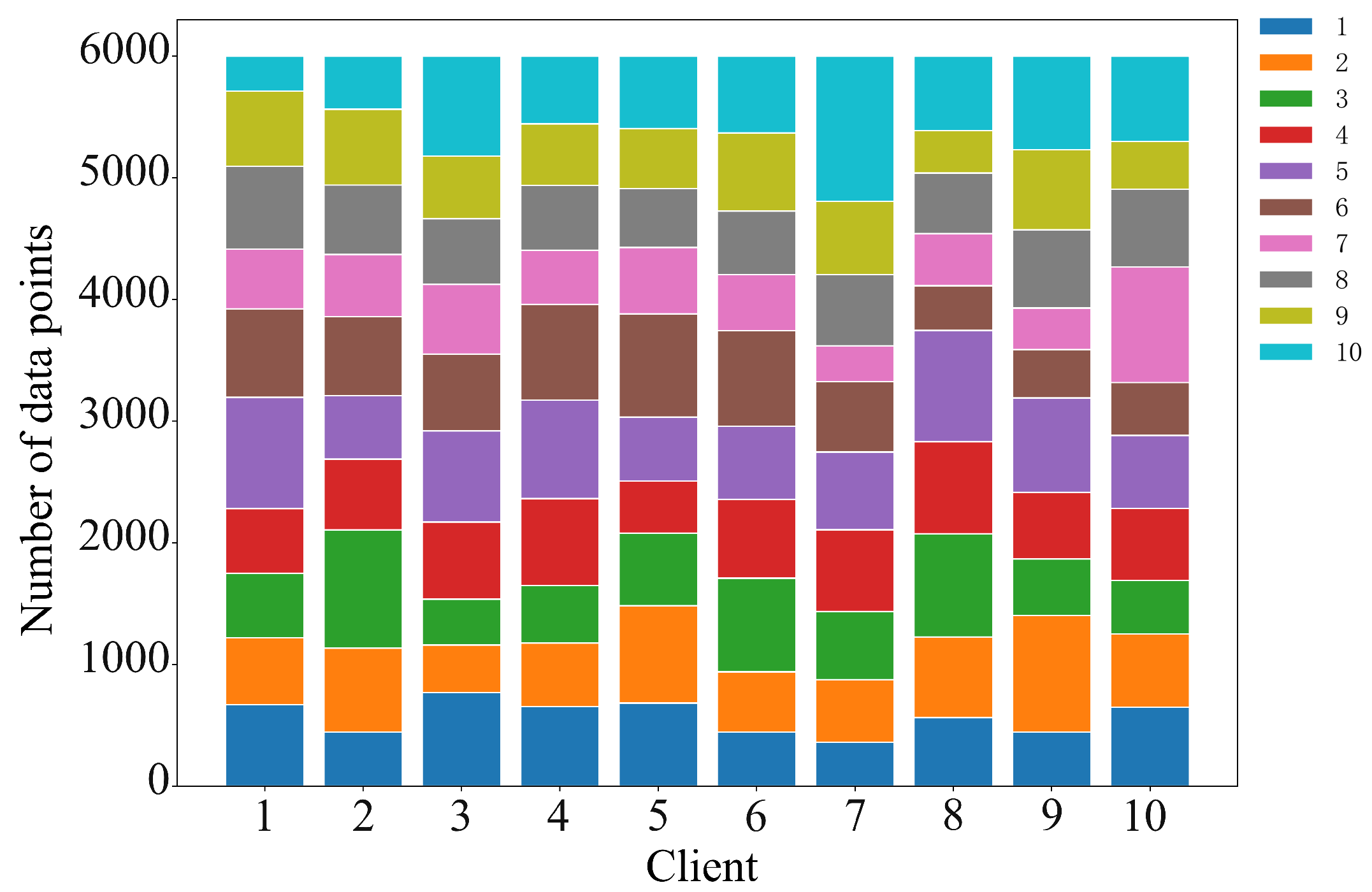
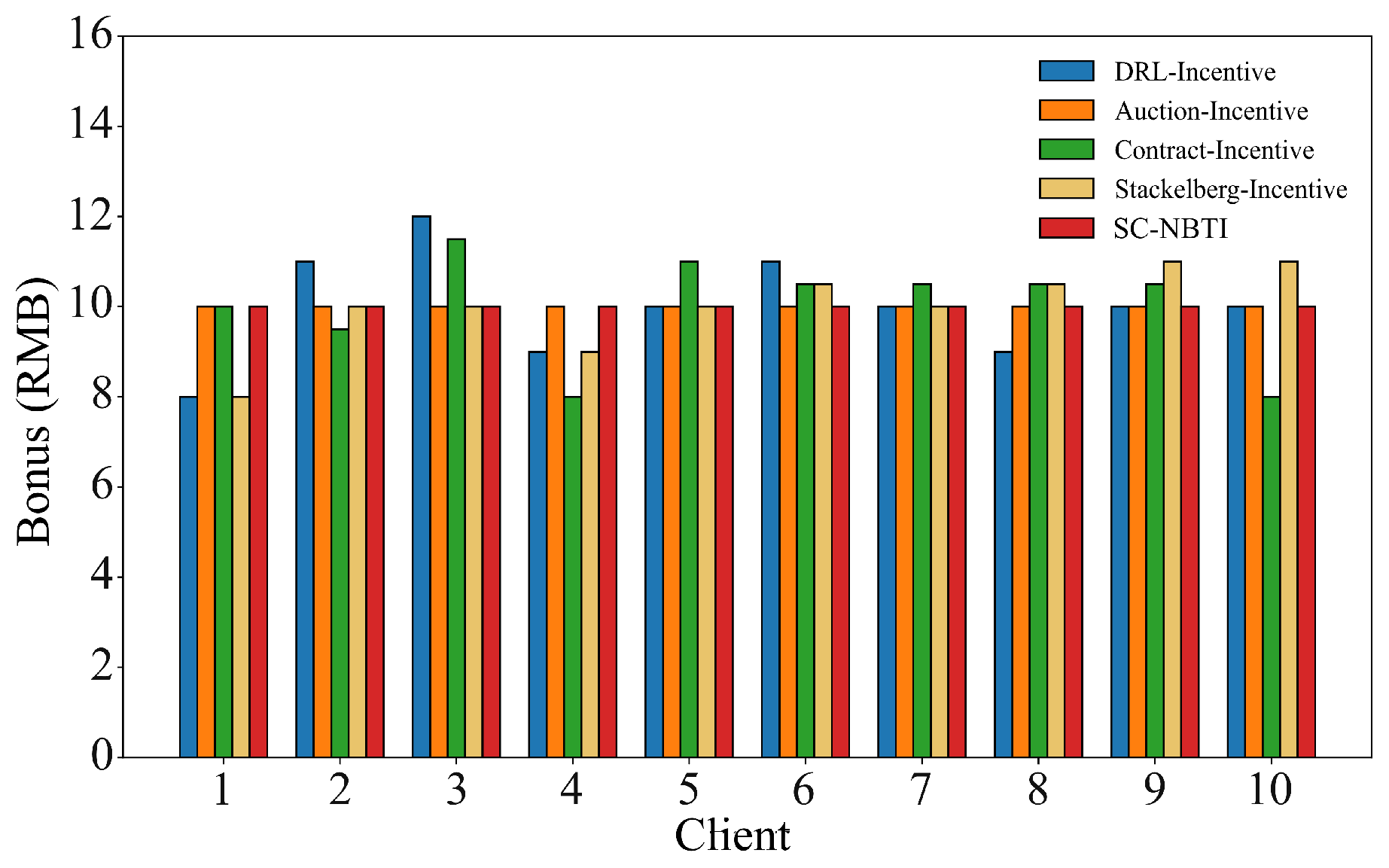
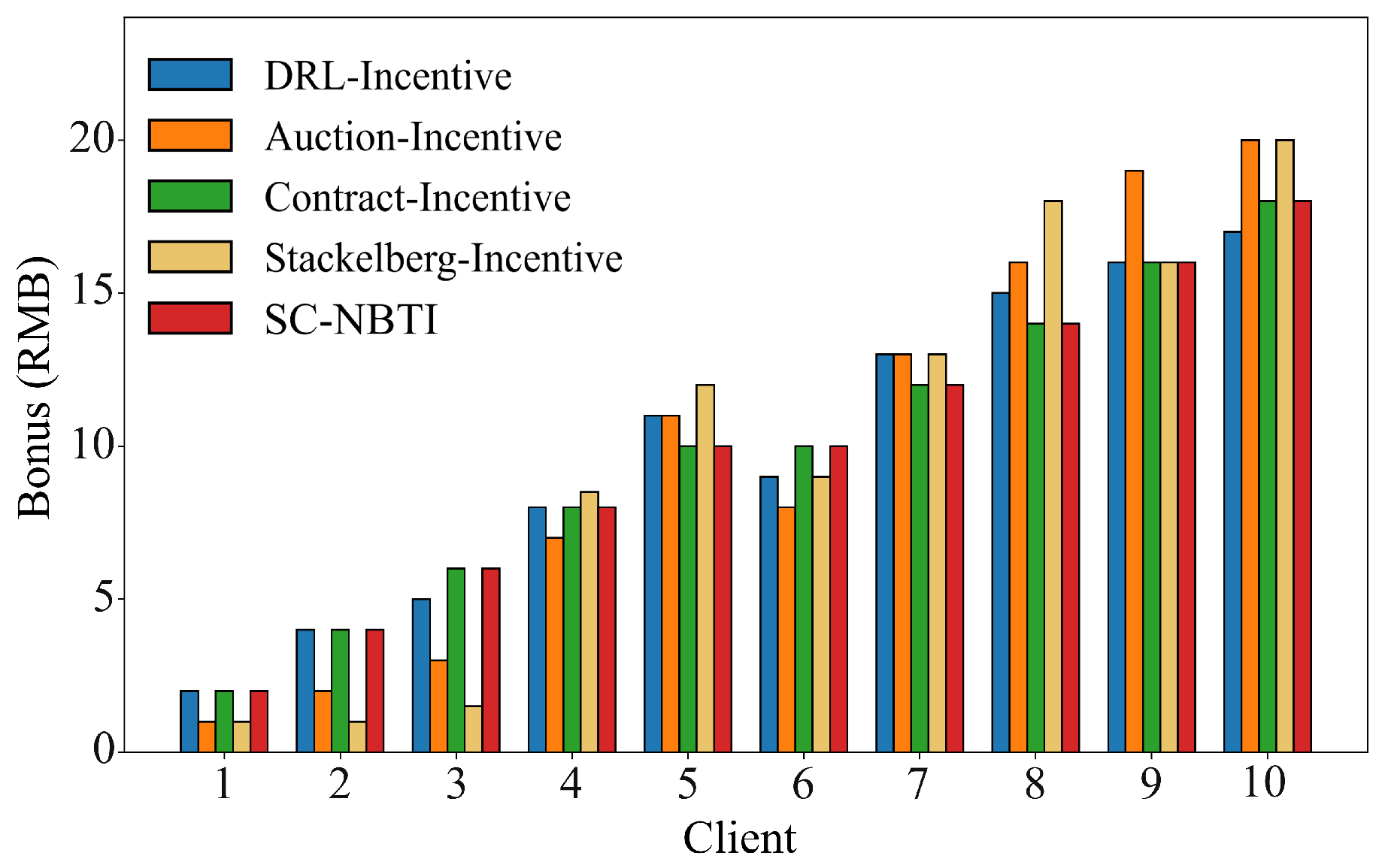
In the above scenario, we construct a cooperative game model for participants in federated learning based on Nash bargaining theory. Nash bargaining aims to maximize the joint surplus by multiplying each participant’s utility gain relative to their disagreement outcome. In the context of federated learning, this means determining a reward allocation scheme that enables the data requester to train a better global model while ensuring that data providers receive higher rewards. In the following, we model each party involved in federated learning to formulate the corresponding optimization problem and design the incentive mechanism we proposed.
3.3.1. Revenue Modeling for Data Providers
If data provider m decides to participate in round t of federated learning, then from the perspective of m, their utility is the reward obtained from participating in this round. Clearly, . At the same time, the provider incurs a cost , where denotes the computation cost and denotes the communication cost.
We define a binary variable
to indicate whether data provider
m participates in round
t of federated learning: if they participate, then
; otherwise,
. For any client
m in round
t, the utility can be expressed as the difference between the reward and incurred cost, as shown in Equation (
3).
Here, is the decision made by data provider m, while is determined by the data requester R. The possible combinations of these decisions by R and data provider m can be interpreted as whether an agreement is reached for m to participate in the federated task in this round. Once decisions are made, the provider’s utility can be computed accordingly.
The total cost of a client can be explicitly modeled as a function of its dataset size
[
26]. Specifically, the cost consists of three parts: (i) data cost
, where
is the unit data processing cost; (ii) computation cost
, where
M is the model dimension,
and
are the numbers of local and global iterations, and
is the unit computation cost; and (iii) communication cost
, which depends on bandwidth, channel gain, and rate constraints but is independent of
. Therefore, the total cost is as shown in Equation (
4).
This affine form shows that costs grow linearly with dataset size, which plays a key role in ensuring truthfulness in our mechanism.
If data provider
m decides to participate in the federated learning task for round
t, they will sparsify their local gradient update according to the method in
Section 3.2, upload it to the shared data system, and wait for the aggregated gradient to be used in reward calculation.
3.3.2. Revenue Modeling for Data Requesters
When data requester
R engages in bargaining with multiple data providers
during round
t of a federated learning task, it must first determine which type of bargaining protocol to adopt. Existing one-to-many bargaining protocols include sequential bargaining [
27] and parallel bargaining [
19]. In sequential bargaining, the requester negotiates with each data provider in a predetermined order, which in the worst case requires time complexity of
[
28], making it impractical in real-world data-sharing scenarios.
Therefore, this paper adopts a **parallel bargaining framework for incentive mechanism design. Inspired by the study by Tang [
28], we define the utility of the data requester in round
t as the global model’s accuracy improvement function [
29,
30,
31].
As mentioned above, when data requester
R receives gradient updates from data providers
m containing
non-zero elements, the total number of received sparse gradient parameters
increases, leading to an increase in the model’s overall accuracy
[
29,
30,
31].
If no gradient is received (i.e., zero parameters), the model’s accuracy remains
. Hence, the accuracy gain during this round of bargaining is defined in Equation (
5).
Here, is the amplification coefficient that reflects the data requester’s sensitivity to accuracy improvements.
For data requester R, the incurred cost includes both communication cost and payment cost. It is assumed here that the data requester has sufficient communication resources and bears a fixed communication cost to communicate with the data providers. Therefore, the total communication cost for the data requester is . For each data provider m, the requester provides a reward for participating in round t of federated learning. Obviously, if , then , meaning the requester does not pay providers who do not participate.
For simplicity, we define the participation vector
and the payment vector
. Based on these definitions, the requester’s revenue is given by Equation (
6).
For any data provider , if they do not participate in the current round (i.e., ), they will receive no reward (i.e., ) and incur no cost (i.e., ). In this case, their utility is zero (i.e., ). Similarly, if no data provider participates in this round, the data requester’s utility is also evidently zero (i.e., ). Therefore, the worst-case utility in this bargaining process is 0.
If provider
does not participate (
), then
,
, and revenue
. If no providers participate, requester revenue
is the worst case. After agreeing on
and
, the requester and providers’ revenues are
and
. By Nash bargaining, the negotiation solves the optimization in Equation (
7), equivalently transformed to convex form in Equation (
8) via log transform under the same constraints.
The objective in Equation (
8) maximizes the joint surplus of the requester and providers above their disagreement points (here
and
), which is the classical Nash bargaining criterion (log-sum form after a log transform). In Equation (
8), (i) the budget/value constraint ensures that the total payment to providers does not exceed the requester’s available benefit
, (ii) the provider cost constraints
guarantee individual rationality (no provider is paid below its incurred cost), and (iii) the non-negativity conditions ensure all parties obtain non-negative utility. Together, these conditions make the outcome both fair and feasible: improving one party’s utility cannot occur at the complete expense of another, and the surplus is split in a way that balances all sides.
Unfortunately, this is a typical Mixed Integer Convex Programming (MICP) problem, which is a classical NP-hard problem. It is difficult to find a globally optimal solution and also challenging to design an algorithm with theoretical approximation guarantees. This difficulty arises because the global utility function and communication costs are determined only after the decisions are made. To address this issue, we propose a heuristic algorithm that derives an approximate Nash bargaining solution within polynomial time complexity. The proposed algorithm is based on the following two key processes: client selection and bonus payment.
3.3.3. Client Selection Strategy
We adopt a non-uniform probabilistic sampling distribution to design the client selection strategy. The proposed strategy is based on the practical observation that the more parameters the data requester receives, the greater the potential utility gain—i.e., the probability that
increases is higher [
29,
30,
31]. Since
is a non-decreasing function of
, this method assigns a non-zero probability to each data provider
m based on the size of their local dataset using the Softmax function, thereby enabling the mechanism to better adapt to non-IID data scenarios [
32] and ensuring the global model’s convergence [
32]. The probability that data provider
m is selected in the
t-th round of federated learning is calculated as shown in Equation (
9).
As provider
m increases reported cost
, their selection probability decreases, while underbidding lowers rewards, incentivizing truthful reporting. Since costs correlate with dataset size
[
26], misreporting data size has similar effects, encouraging truthfulness.
Although Equation (
9) suggests that a client might increase its reported
to gain a higher selection probability, the affine cost function above guarantees that such misreporting cannot improve net utility. If a client is already selected truthfully, exaggerating
does not change the allocation or payment but increases the incurred cost
, reducing utility. If a client is not selected truthfully, inflating
may cross the selection threshold, but the payment is determined by the critical type (threshold), not by the inflated report. Since the cost strictly increases with
, the utility under misreporting cannot exceed that under truthful reporting. Therefore, under monotone allocation and threshold-based payments, truth telling is a dominant strategy, and our client selection strategy satisfies the truthfulness property.
Based on this, we design a probabilistic client selection: At round
t, set all
. If providers
, select all; else, compute selection probabilities via Equation (
9), and randomly sample
B clients to form set
S. Return participation vector
. Algorithm 1 runs in
time.
3.3.4. Bonus Payment Strategy
For simplicity, we define
as the data requester’s net benefit in round
t and
as provider
m’s incurred cost. Substituting these into Equation (
8), we derive the equivalent optimization in Equation (
10) and, by reorganizing the constraints, express the problem equivalently as Equation (
11).
Given the convex nature of Equation (
11), we apply the Karush–Kuhn–Tucker (KKT) conditions to characterize its optimal solution. By introducing Lagrange multipliers
and
to constrain
and
, we derive the KKT conditions as in Equation (
12). Solving them yields the closed-form solution in Equation (
13), from which the optimal payment
for selected providers can be computed (Equation (
14)).
From these conditions, the complementary slackness relations imply that the optimal solution must satisfy
for each selected provider and that the total payment cannot exceed the requester’s budget or task value. Rearranging the first-order condition in Equation (
12) yields a system of linear equations in the payment variables, where each
depends on the requester’s budget
A, minimum cost
, and the payments of other selected providers. Solving this system leads to the recursive form shown in Equation (
13).
Finally, under the mild symmetry assumption that all selected providers are treated homogeneously in equilibrium, the surplus can be evenly divided among the
providers plus the requester. This simplification yields the closed-form expression in Equation (
14), where each selected provider receives a payment proportional to its minimum cost and the requester’s budget. This step makes explicit the assumption of symmetric equilibrium and explains the transition from Equation (
13) to Equation (
14).
Equation (
14) distributes the cooperative surplus between the requester and the
selected providers in a Nash-consistent manner: each provider’s payment increases with its minimum cost
(ensuring individual rationality), while the requester’s share is implicitly reflected through the denominator
. This is a differentiated allocation (not an equal split) in general; it reduces to equal sharing only under symmetry.
The overall social welfare generated by federated learning is shared between the requester and the providers, ensuring aligned interests and encouraging cooperation. As in
Section 3.3.3, our incentive mechanism prevents cost or data misreporting and stops the requester from undervaluing benefits to cut costs. Providers can verify accuracy gains locally each round, ensuring transparency. As discussed in
Section 3.4, smart contracts provide an additional layer of assurance. The full process is detailed in Algorithm 2.
| Algorithm 2 Incentive mechanism. |
- Input:
- Output:
Global model - 1:
Initialization: global model , initial accuracy - 2:
for to T do - 3:
- 4:
Select data providers for round t based on budget - 5:
Send the latest global model to each data provider in - 6:
Each data provider trains a local model and obtains local gradient - 7:
Each data provider sparsifies using Equation ( 2) and uploads it - 8:
- 9:
- 10:
Compute the payment amount for each data provider in the current round according to Equation ( 14) - 11:
end for - 12:
return
|