High Bandwidth Control of a Piezo-Actuated Nanopositioning System Based on a Discrete-Time High-Order Dual-Loop Framework
Abstract
1. Introduction
2. Problem Formulation
2.1. Conventional Dual-Loop Control Framework
2.2. Problem Description
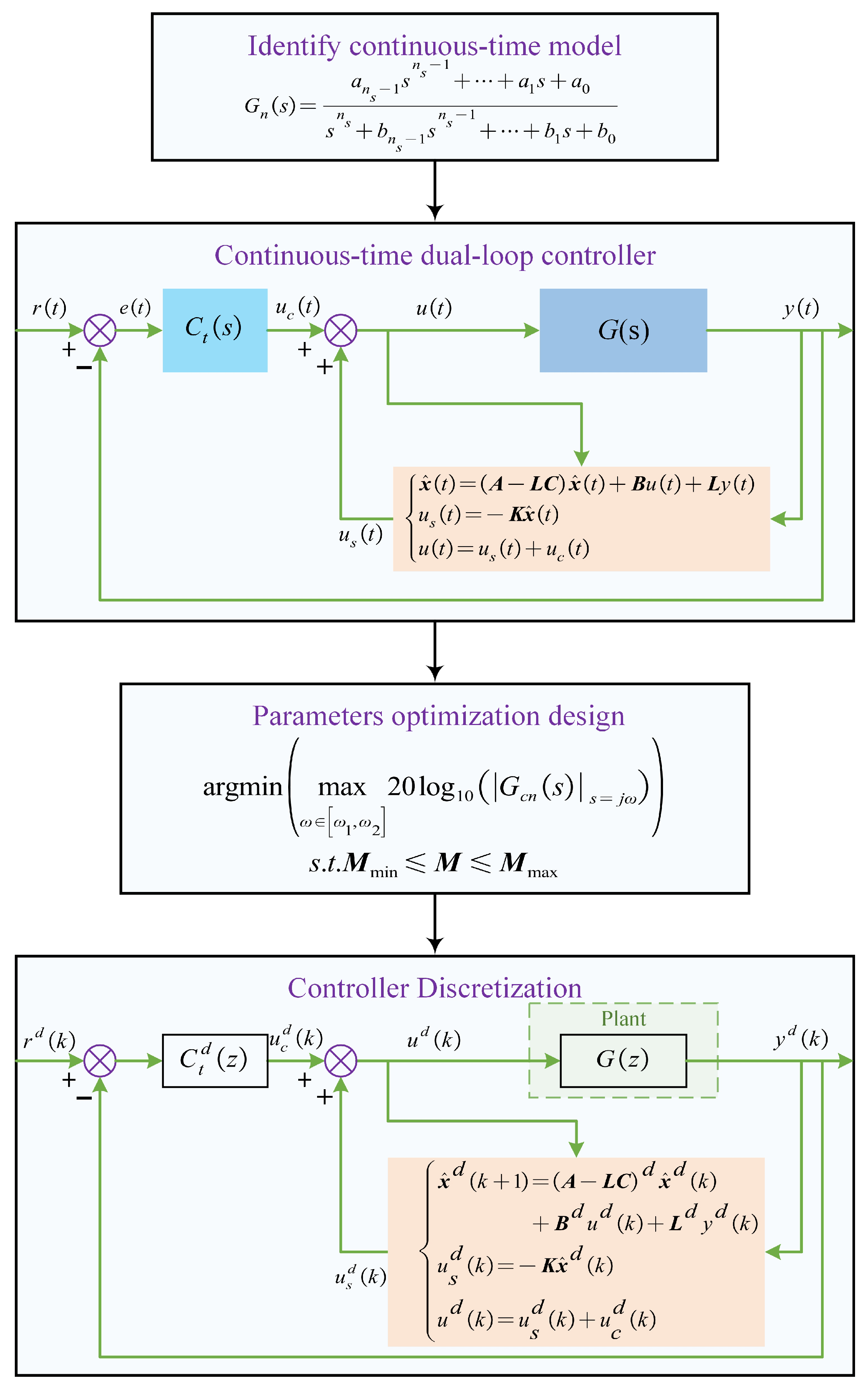
3. Developed Dual-Loop Control Framework
3.1. Controller Structure
3.2. Parameter Design
3.3. Stability Analysis
4. Experimental Validation
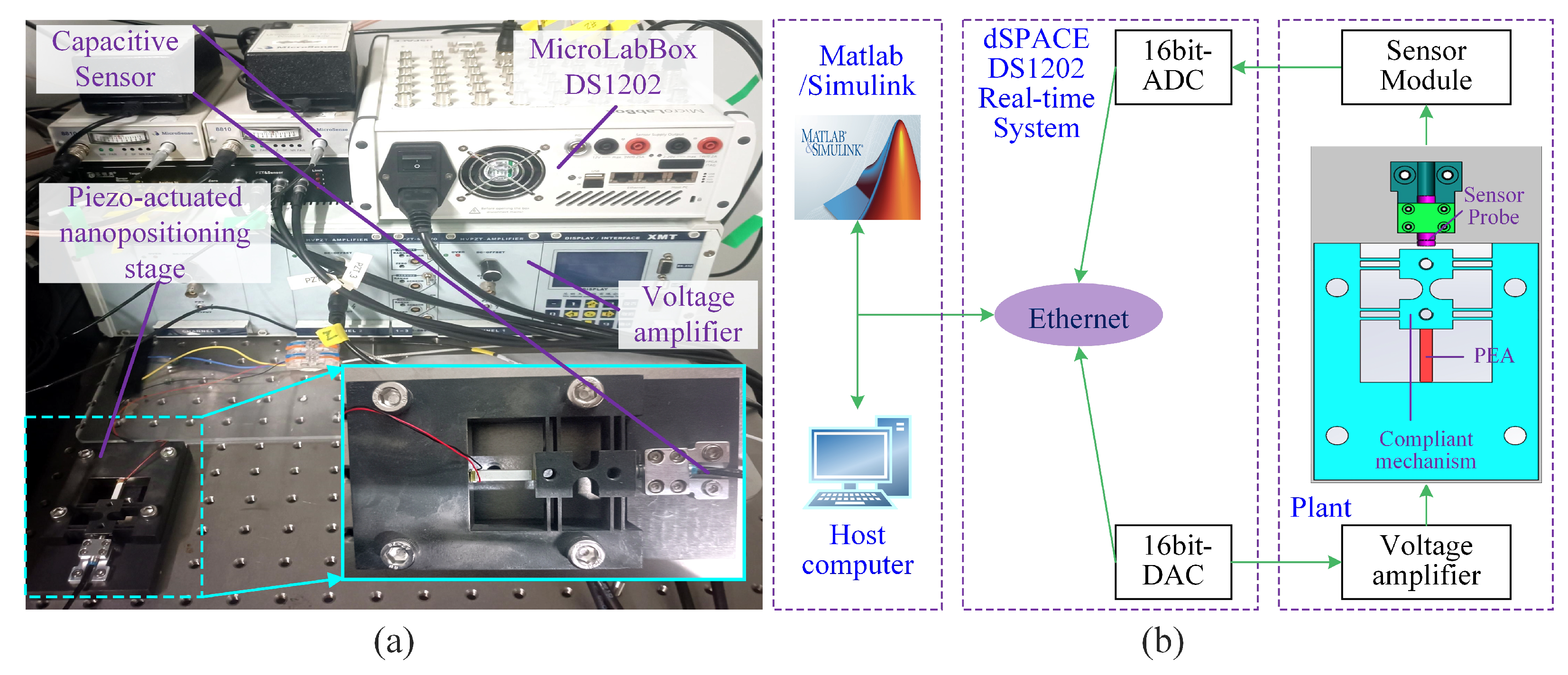
4.1. Experimental Setup
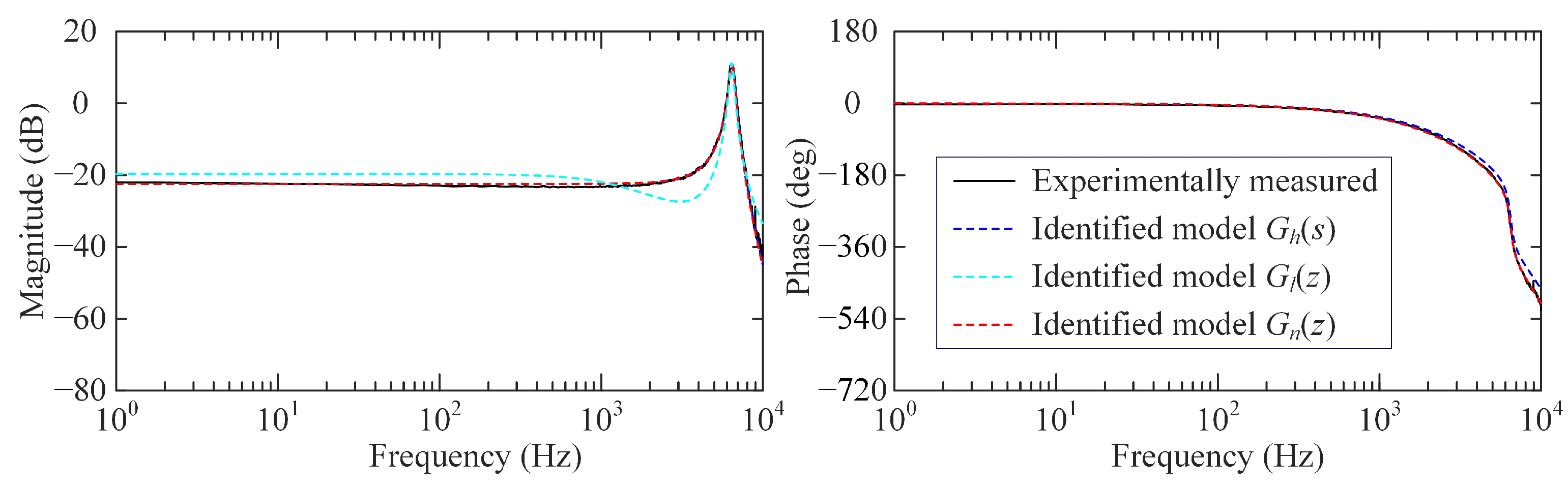
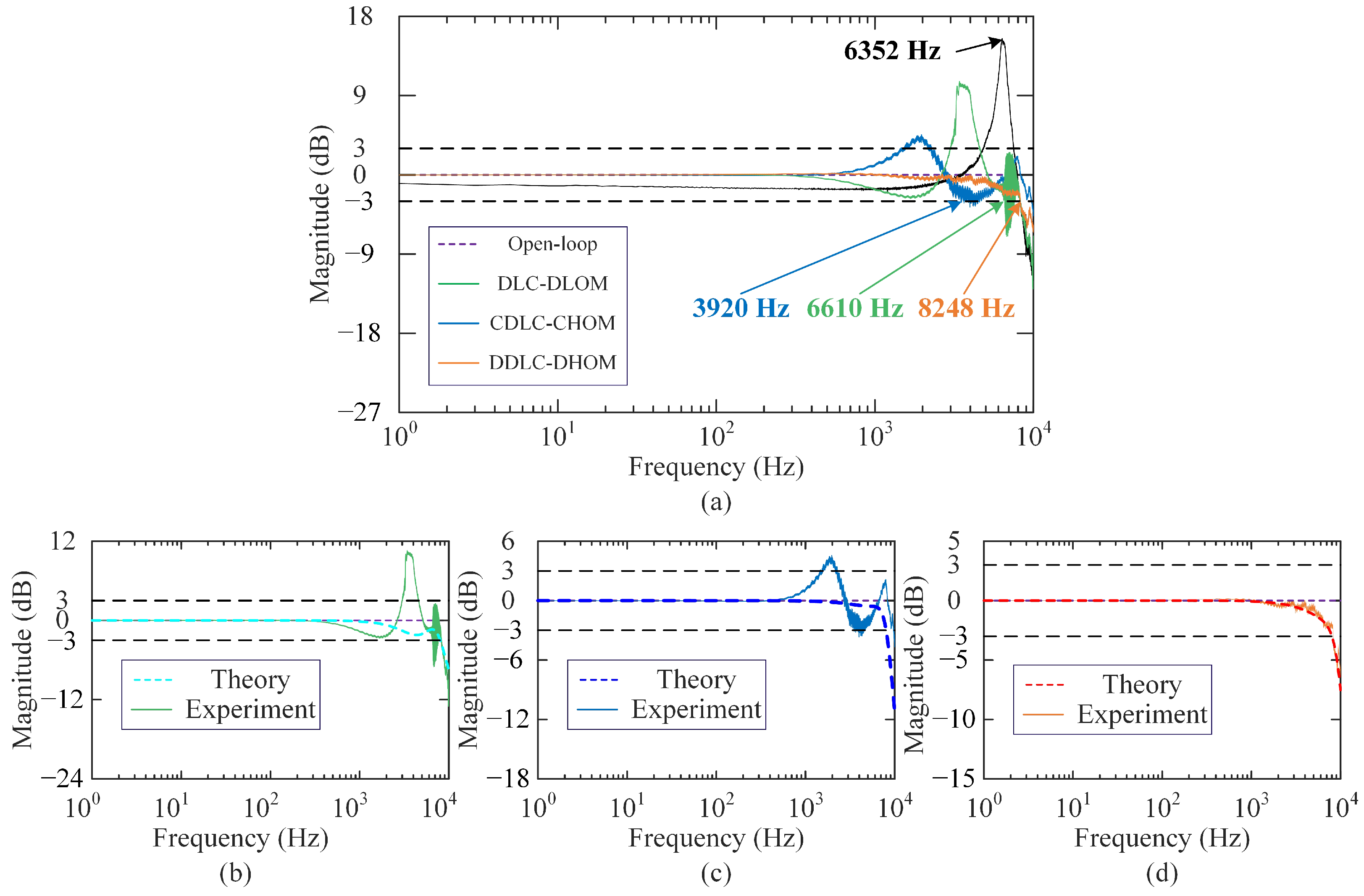
4.2. System Identification
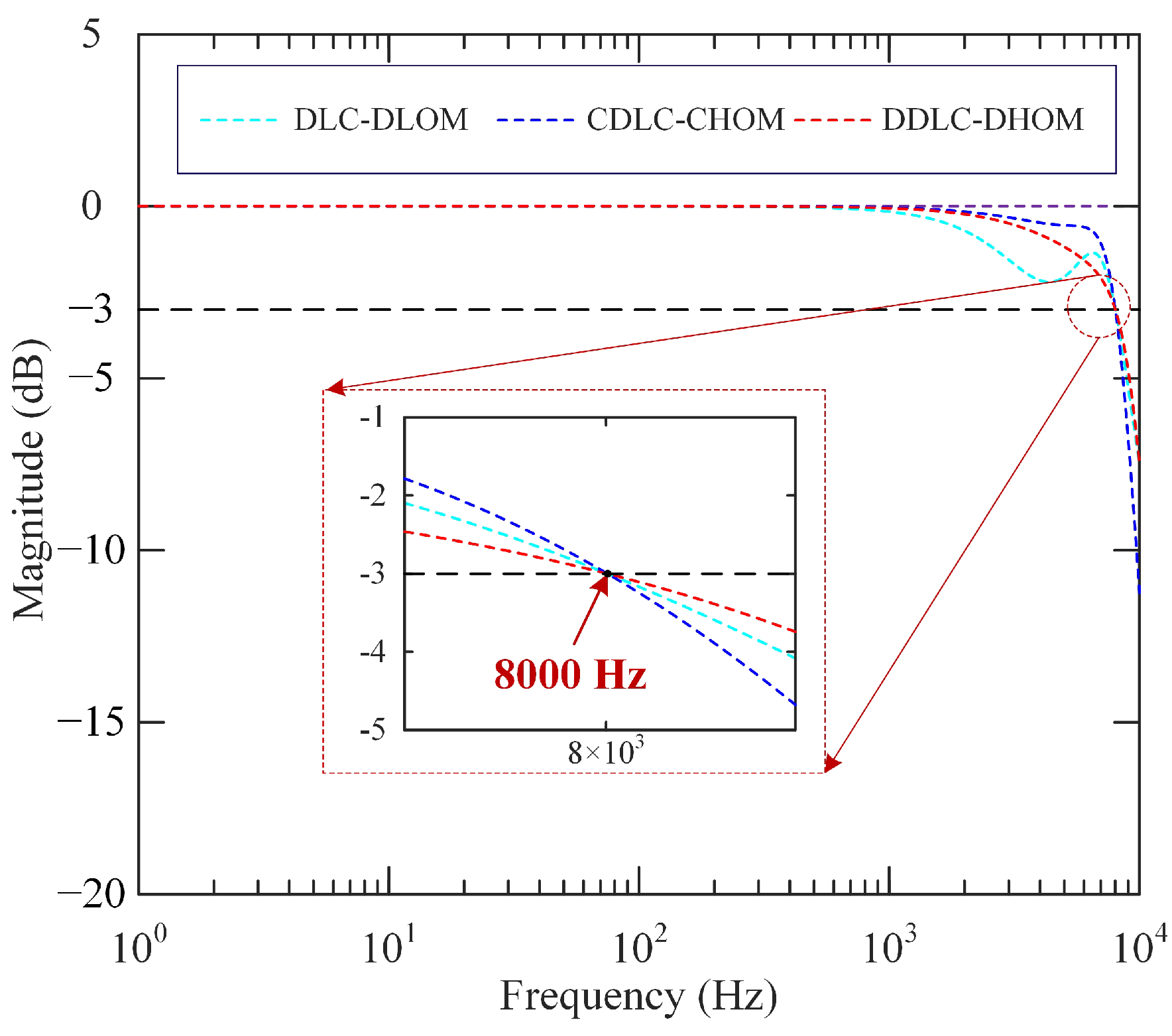
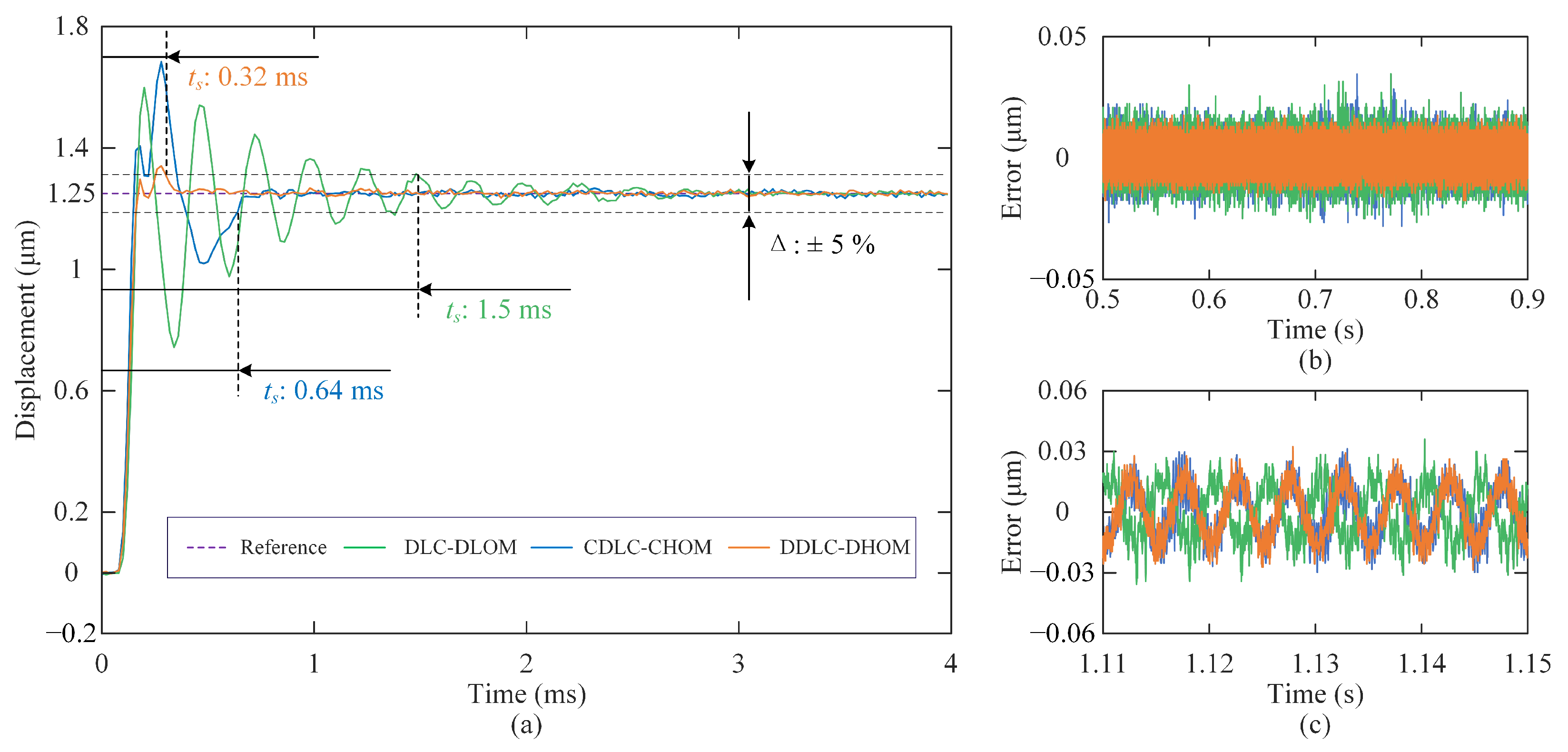
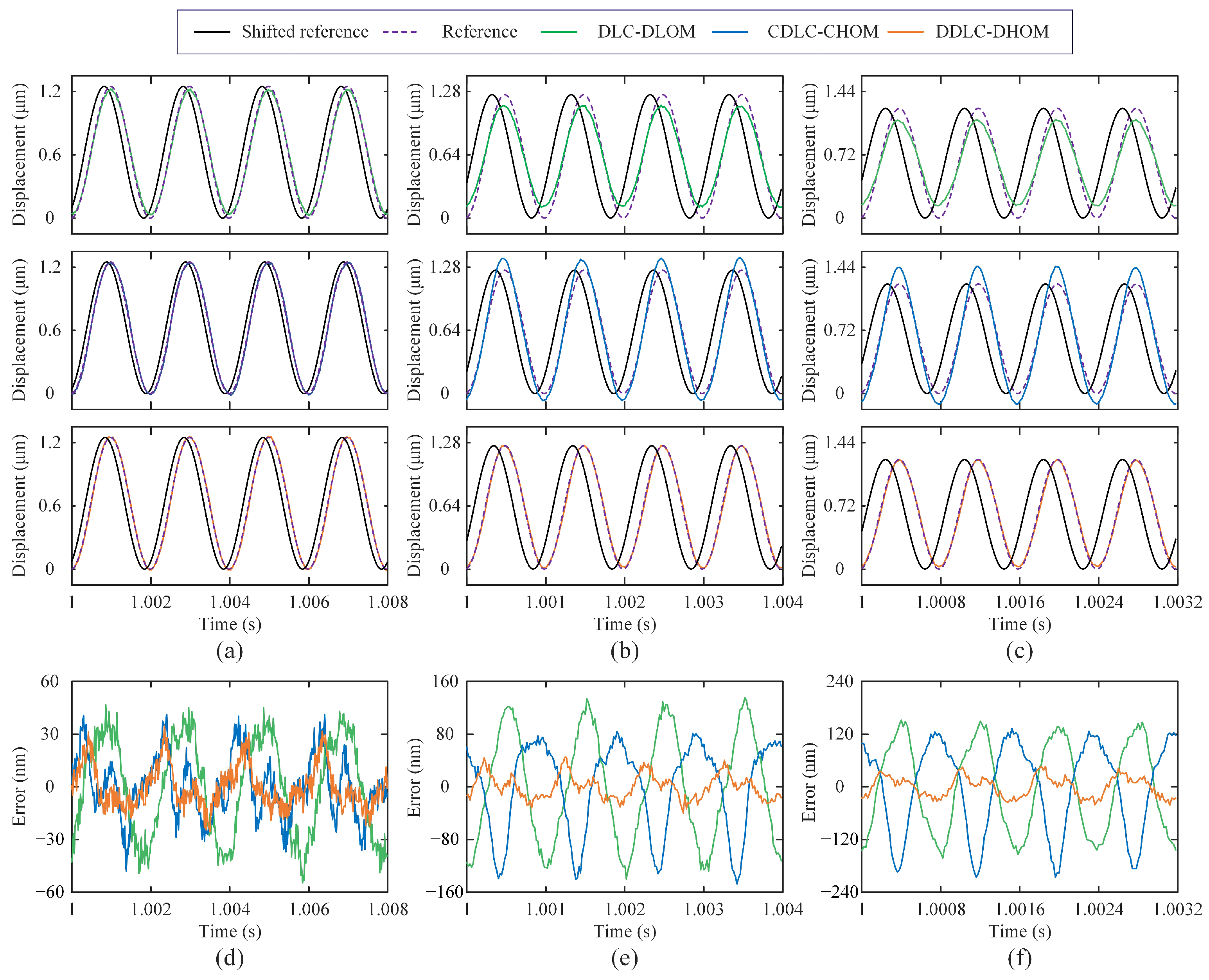
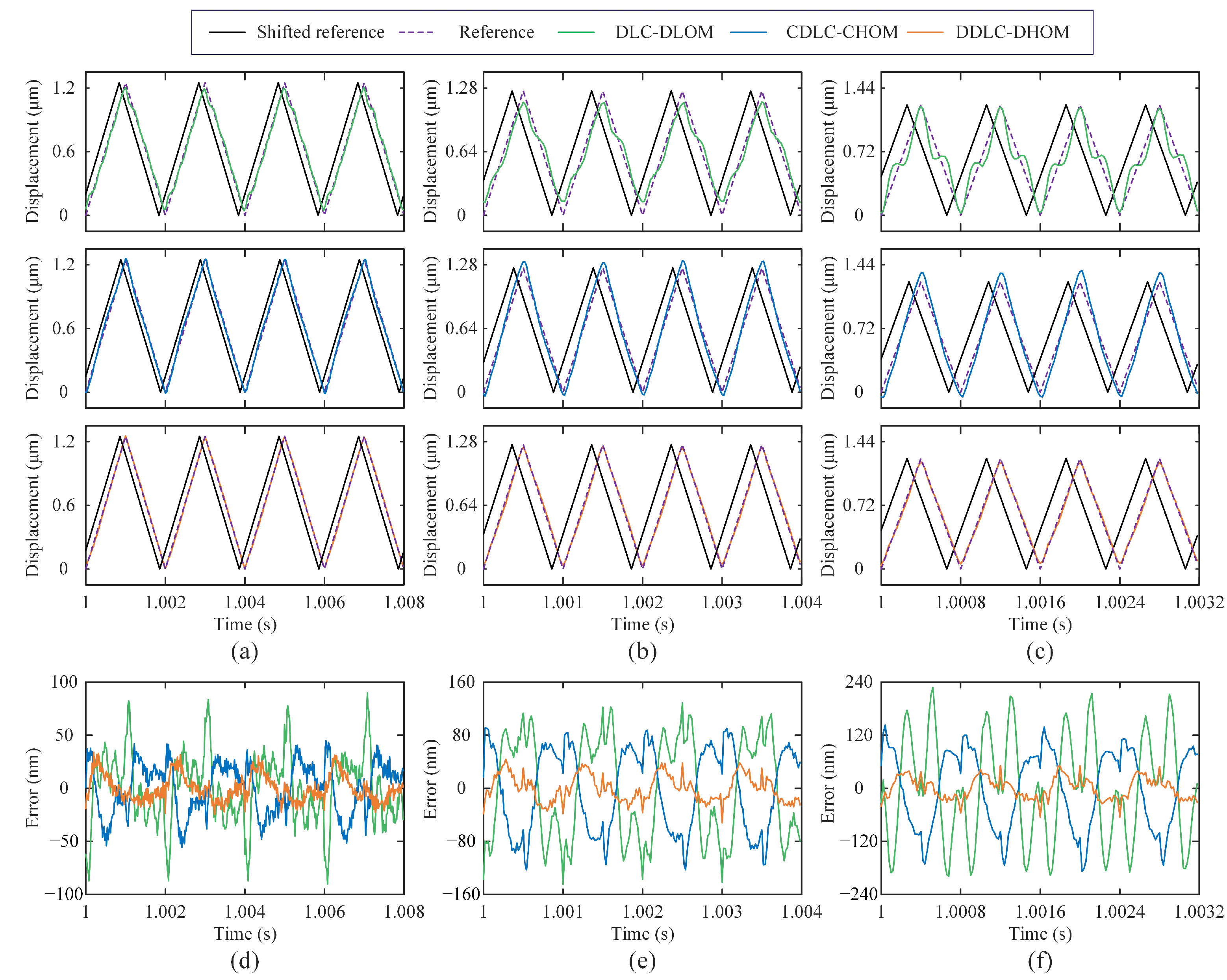
4.3. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AFM | Atomic force microscope |
| PPF | Positive position feedback |
| PVPF | Positive velocity and position feedback |
| IRC | Integral resonant control |
| PAVPF | Positive acceleration, velocity, and position feedback |
| ZOH | Zero-order holder |
| DDLC-DHOM | Developed Dual-loop control framework based on the discrete-time high-order model |
| DLC-DLOM | Dual-loop control framework based on the discrete-time low-order model |
| CDLC-CHOM | Conventional Dual-loop control framework based on the continuous-time high-order model |
| DAC | Digital-to-analog |
| ADC | Analog-to-digital |
| SW | Sinusoidal wave |
| TW | Triangular wave |
References
- Guo, D.J.; Nagel, W.S.; Clayton, G.M.; Leang, K.K. Spatial-Temporal Trajectory Redesign for Dual-Stage Nanopositioning Systems With Application in AFM. IEEE/ASME Trans. Mechatron. 2020, 25, 558–569. [Google Scholar] [CrossRef]
- Wang, R.X.; Zhang, X.M.; Zhu, B.L.; Li, H.; Zhong, X.N.; Xu, N. A Topology-Optimized Compliant Microgripper With Replaceable Modular Tools for Cross-Scale Microassembly. IEEE/ASME Trans. Mechatron. 2024, 29, 2067–2078. [Google Scholar] [CrossRef]
- Zhong, J.P.; Nishida, R.; Shinshi, T. Design and precision tracking control of a high-bandwidth fast steering mirror for laser beam machining. Precis. Eng. 2022, 73, 128–139. [Google Scholar] [CrossRef]
- Croft, D.; Shed, G.; Devasia, S. Creep, Hysteresis, and Vibration Compensation for Piezoactuators: Atomic Force Microscopy Application. J. Dyn. Sys. Meas. Control 2001, 123, 35–43. [Google Scholar] [CrossRef]
- Liu, L.; Tan, K.K.; Teo, C.S.; Chen, S.L.; Lee, T.H. Development of an Approach Toward Comprehensive Identification of Hysteretic Dynamics in Piezoelectric Actuators. IEEE Trans. Contr. Syst. Technol. 2013, 21, 1834–1845. [Google Scholar] [CrossRef]
- Yang, H.G.; Zhu, W. High-bandwidth open-loop motion control of a piezo-positioning mechanism based on a composite electromechanical dynamic model. Smart Mater. Struct. 2020, 29, 107001. [Google Scholar] [CrossRef]
- Gu, G.Y.; Zhu, L.M. Motion control of piezoceramic actuators with creep, hysteresis and vibration compensation. Sensor Actuators A-Phys. 2013, 197, 76–87. [Google Scholar] [CrossRef]
- Yang, M.J.; Gu, G.Y.; Zhu, L.M. High-bandwidth tracking control of piezo-actuated nanopositioning stages using closed-loop input shaper. Mechatronics 2014, 24, 724–733. [Google Scholar] [CrossRef]
- Wang, G.; Chen, G.Q.; Bai, F.Z. High-speed and precision control of a piezoelectric positioner with hysteresis, resonance and disturbance compensation. Microsyst. Technol. 2016, 22, 2499–2509. [Google Scholar] [CrossRef]
- Yu, L.H.; Zhang, X.M.; Lai, J.H.; Fatikow, S.; Zhong, X.N.; Xu, N. Tracking control of a piezo-actuated compliant mechanism based on an improved Bouc–Wen hysteresis model with variable parameters. AIP Adv. 2023, 13, 055129. [Google Scholar] [CrossRef]
- Altaher, M.; Russell, D.; Aphale, S.S. A dual-loop tracking control approach to precise nanopositioning. J. Vib. Control 2019, 25, 666–674. [Google Scholar] [CrossRef]
- Ling, J.; Rakotondrabe, M.; Feng, Z.; Ming, M.; Xiao, X.H. A Robust Resonant Controller for High-Speed Scanning of Nanopositioners: Design and Implementation. IEEE Trans. Contr. Syst. Technol. 2020, 28, 1116–1123. [Google Scholar] [CrossRef]
- Yong, Y.K.; Ahmed, B.; Moheimani, S.O.R. Atomic force microscopy with a 12-electrode piezoelectric tube scanner. Rev. Sci. Instrum. 2010, 81, 033701. [Google Scholar] [CrossRef]
- Bhikkaji, B.; Ratnam, M.; Fleming, A.J.; Moheimani, S.O.R. High-Performance Control of Piezoelectric Tube Scanners. IEEE Trans. Contr. Syst. Technol. 2007, 29, 2067–2078. [Google Scholar] [CrossRef]
- Bhikkaji, B.; Moheimani, S.O.R. Integral Resonant Control of a Piezoelectric Tube Actuator for Fast Nanoscale Positioning. IEEE Trans. Contr. Syst. Technol. 2008, 13, 530–537. [Google Scholar] [CrossRef]
- Li, L.L.; Li, C.X.; Gu, G.Y.; Li, H.; Zhu, L.M. Positive acceleration, velocity and position feedback based damping control approach for piezo-actuated nanopositioning stages. Mechatronics 2017, 47, 97–104. [Google Scholar] [CrossRef]
- Tao, T.D.; Li, L.L.; Li, H.X.; Li, H.; Zhong, X.N.; Xu, N. High-Bandwidth Tracking Control of Piezoactuated Nanopositioning Stages via Active Modal Control. IEEE Trans. Autom. Sci. Eng. 2022, 19, 2998–3006. [Google Scholar] [CrossRef]
- Orszulik, R.R.; Shan, J.J. Output feedback integral control of piezoelectric actuators considering hysteresis. Precis. Eng. 2017, 47, 90–96. [Google Scholar] [CrossRef]
- Leang, K.K.; Devasia, S. Feedback-Linearized Inverse Feedforward for Creep, Hysteresis, and Vibration Compensation in AFM Piezoactuators. IEEE Trans. Contr. Syst. Technol. 2007, 15, 927–935. [Google Scholar] [CrossRef]
- Li, C.X.; Ding, Y.; Gu, G.Y.; Zhu, L.M. Damping Control of Piezo-Actuated Nanopositioning Stages With Recursive Delayed Position Feedback. IEEE/ASME Trans. Mechatron. 2017, 22, 855–864. [Google Scholar] [CrossRef]
- Wang, T.C.; San-Millan, A.; Aphale, S.S. Quantifying the performance enhancement facilitated by fractional-order implementation of classical control strategies for nanopositioning. ISA Trans. 2024, 147, 153–162. [Google Scholar] [CrossRef]
- Russell, D.; Aphale, S.S. Evaluating the performance of robust controllers for a nanopositioning platform under loading. IFAC-PapersOnLine. 2017, 50, 10895–10900. [Google Scholar] [CrossRef]
- Liu, L.; Li, Q.; Yun, H.; Liang, J.; Ma, X.F. Composite modeling and parameter identification of broad bandwidth hysteretic dynamics in piezoelectric fast steering platform. Mech. Syst. Signal Process. 2019, 121, 97–111. [Google Scholar] [CrossRef]
- Yepes, A.J.; Freijedo, F.D.; Doval-Gandoy, J.; Loṕez, Ó.; Malvar, J.; Fernandez-Comesanña, P. Effects of Discretization Methods on the Performance of Resonant Controllers. IEEE Trans. Power Electron. 2010, 25, 1692–1712. [Google Scholar] [CrossRef]
- Malik, F.M.; Malik, M.B. Discretization Error Bounds for Sampled-Data Control of Nonlinear Systems. Arab. J. Sci. Eng. 2013, 38, 3429–3435. [Google Scholar] [CrossRef]
- Stojic, D. Digital Resonant Controller based on Modified Tustin Discretization Method. Adv. Electr. Comput. Eng. 2016, 16, 83–88. [Google Scholar] [CrossRef]
- Russell, D.; Fleming, A.J.; Aphale, S.S. Simultaneous Optimization of Damping and Tracking Controller Parameters Via Selective Pole Placement for Enhanced Positioning Bandwidth of Nanopositioners. J. Dyn. Sys. Meas. Control 2015, 137, 101004. [Google Scholar] [CrossRef]
- Altaher, M.; Aphale, S.S. Enhanced Positioning Bandwidth in Nanopositioners via Strategic Pole Placement of the Tracking Controller. Vibration 2019, 2, 49–63. [Google Scholar] [CrossRef]
- Wang, X.Y.; Li, L.L.; Zhu, Z.W.; Zhu, L.M. Simultaneous damping and tracking control of a normal-stressed electromagnetic actuated nano-positioning stage. Sensor Actuators A-Phys. 2022, 338, 113467. [Google Scholar] [CrossRef]
- Dorf, R.C.; Bishop, R.H. Modern Control Systems, 13th ed.; Pearson: Upper Saddle River, NJ, USA, 2016; pp. 797–800. [Google Scholar]
- Franklin, G.F.; Powell, J.D.; Workman, M.L. Digital Control of Dynamic Systems, 3rd ed.; Ellis-Kagle: Half Moon Bay, CA, USA, 2006; pp. 293–294. [Google Scholar]
- Lewis, F.L.; Vrabie, D.; Syrmos, V.L. Optimal Control, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012; pp. 19–202. [Google Scholar]
- Han, J.Q. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]

| 0.01011 | 0.06889 | 0.09101 | ||
| 2.918 | −1.833 | 0.6346 |
| 5523 | ||||
| Trajectory | Frequency | Index | DLC-DLOM | CDLC-CHOM | DDLC-DHOM |
|---|---|---|---|---|---|
| SW | 10 | / | 6.88 ± 0.29/27.55 ± 2.79 | 7.53 ± 0.18/29.76 ± 2.32 | 5.47 ± 0.06/18.81 ± 1.35 |
| 50 | / | 7.15 ± 0.39/27.37 ± 5.46 | 7.49 ± 0.24/27.38 ± 4.50 | 5.46 ± 0.07/19.03 ± 1.38 | |
| 200 | / | 8.08 ± 0.38/26.46 ± 3.26 | 9.42 ± 0.18/30.55 ± 1.19 | 7.23 ± 0.07/23.16 ± 1.81 | |
| 500 | / | 27.91 ± 0.13/56.72 ± 2.05 | 18.11 ± 0.27/49.38 ± 3.59 | 11.80 ± 0.27/35.21 ± 2.65 | |
| 1000 | / | 82.47 ± 0.14/138.65 ± 1.8 | 70.85 ± 0.46/155.88 ± 8.93 | 18.08 ± 0.26/50.76 ± 3.98 | |
| 1250 | / | 100.27 ± 0.14/160.29 ± 2.62 | 7.6 ± 0.3/215.68 ± 3.49 | 22.98 ± 0.21/55.23 ± 6.77 | |
| TW | 10 | / | 7.22 ± 0.29/28.61 ± 4.99 | 7.56 ± 0.32/29.25 ± 4.51 | 5.32 ± 0.08/18.81 ± 1.65 |
| 50 | / | 7.55 ± 0.45/29.56 ± 6.09 | 8.57 ± 0.32/30.36 ± 5.00 | 5.49 ± 0.07/17.98 ± 1.71 | |
| 200 | / | 11.56 ± 0.39/53.24 ± 3.10 | 24.19 ± 0.29/58.01 ± 4.09 | 7.38 ± 0.09/25.21 ± 1.78 | |
| 500 | / | 32.69 ± 0.26/98.60 ± 4.25 | 11.56 ± 0.39/53.24 ± 3.10 | 12.54 ± 0.13/36.25 ± 1.8 | |
| 1000 | / | 77.33 ± 0.22/142.83 ± 4.23 | 63.99 ± 0.44/127.43 ± 2.77 | 19.65 ± 0.14/53.43 ± 0.79 | |
| 1250 | / | 121.31 ± 0.54/231.87 ± 3.05 | 91.74 ± 0.35/200.01 ± 4.34 | 25.35 ± 0.14/77.70 ± 2.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, L.; Zhang, X.; Fatikow, S. High Bandwidth Control of a Piezo-Actuated Nanopositioning System Based on a Discrete-Time High-Order Dual-Loop Framework. Sensors 2025, 25, 5754. https://doi.org/10.3390/s25185754
Yu L, Zhang X, Fatikow S. High Bandwidth Control of a Piezo-Actuated Nanopositioning System Based on a Discrete-Time High-Order Dual-Loop Framework. Sensors. 2025; 25(18):5754. https://doi.org/10.3390/s25185754
Chicago/Turabian StyleYu, Longhuan, Xianmin Zhang, and Sergej Fatikow. 2025. "High Bandwidth Control of a Piezo-Actuated Nanopositioning System Based on a Discrete-Time High-Order Dual-Loop Framework" Sensors 25, no. 18: 5754. https://doi.org/10.3390/s25185754
APA StyleYu, L., Zhang, X., & Fatikow, S. (2025). High Bandwidth Control of a Piezo-Actuated Nanopositioning System Based on a Discrete-Time High-Order Dual-Loop Framework. Sensors, 25(18), 5754. https://doi.org/10.3390/s25185754








