PMMCT: A Parallel Multimodal CNN-Transformer Model to Detect Slow Eye Movement for Recognizing Driver Sleepiness
Abstract
1. Introduction
- (1)
- We propose a PMMCT model that combines the advantages of convolutional modules and the self-attention mechanism in Transformers, enabling the effective capture of both local and global features of the signals.
- (2)
- We develop an efficient parallel feature extraction and fusion strategy for bimodal signals, which improves detection performance with minimal false positives and false negatives.
- (3)
- We validate that the HEOG+HSUM combination applied to the PMMCT model yields comparable performance to the HEOG + O2 combination, enabling accurate SEM detection with only dual single-channel HEOG electrodes, which enhances practicality in real-world driving scenarios.
- (4)
- We developed SEMData, a publicly available dataset comprising dual single-channel HEOG and single-channel EEG (O2) data from 10 participants during simulated driving to support SEM detection research.
2. Materials
2.1. Experimental Settings
2.2. Data Acquisition
2.3. Data Preprocessing
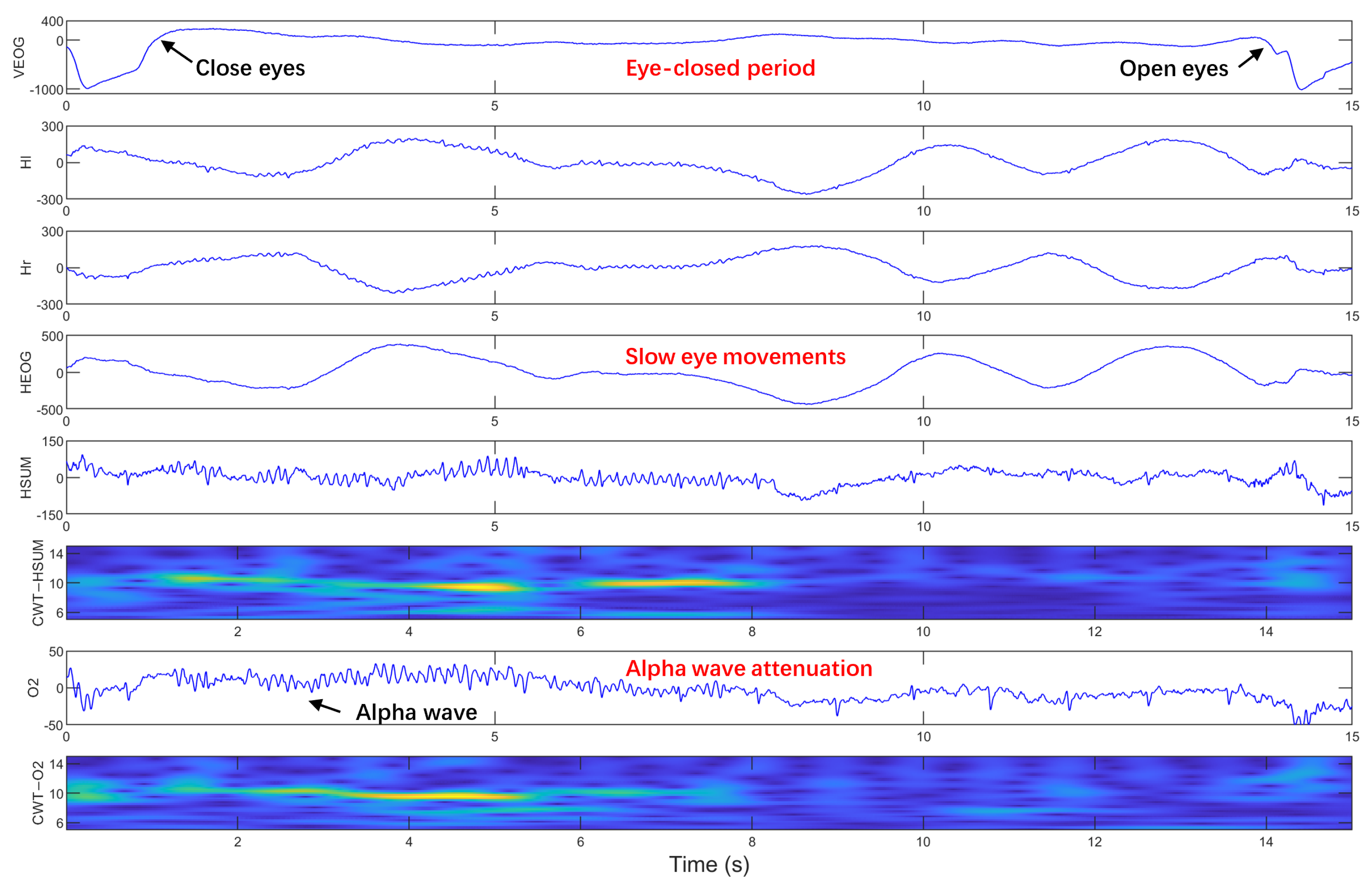
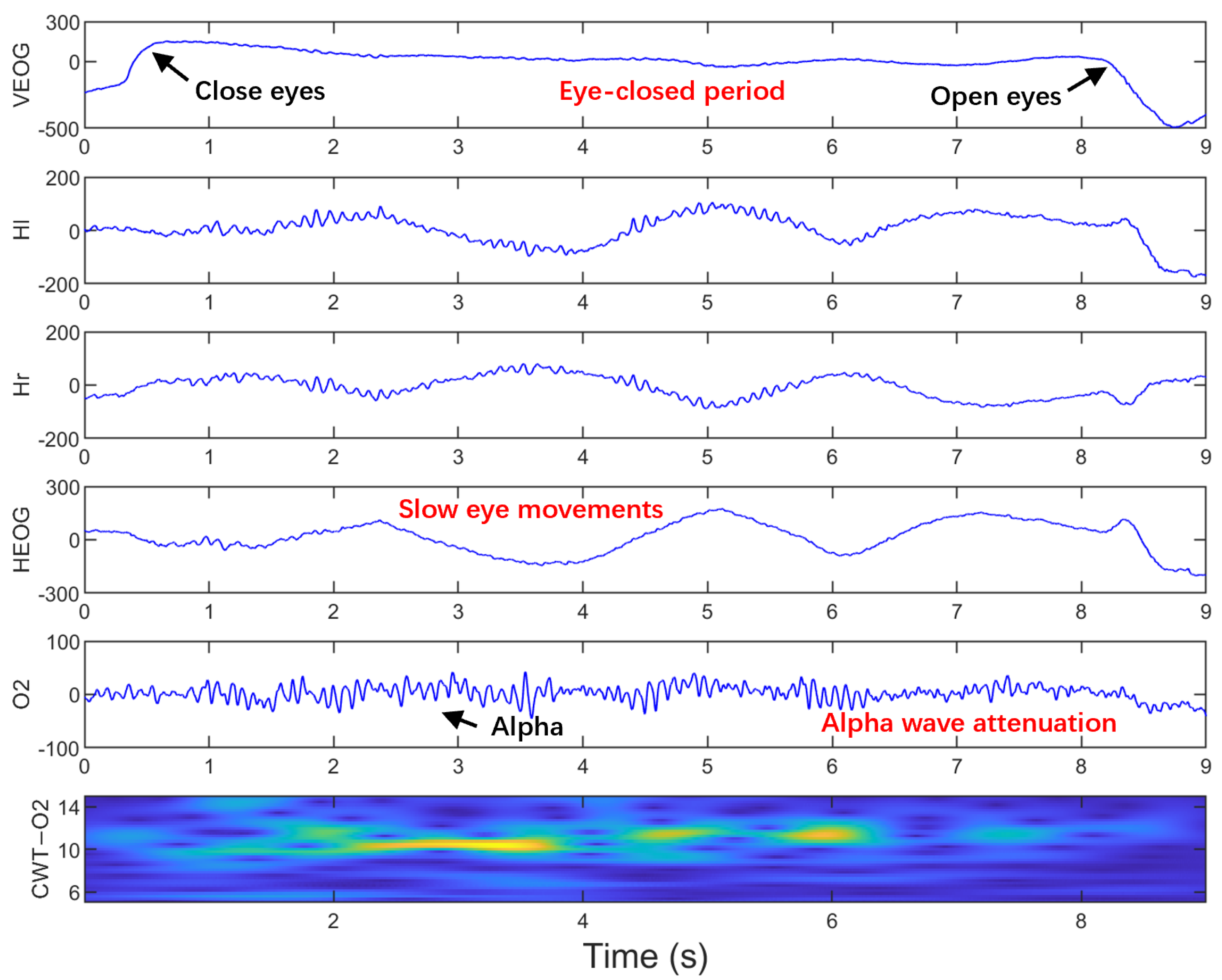
2.4. Visual Labeling of SEMs
3. Methods
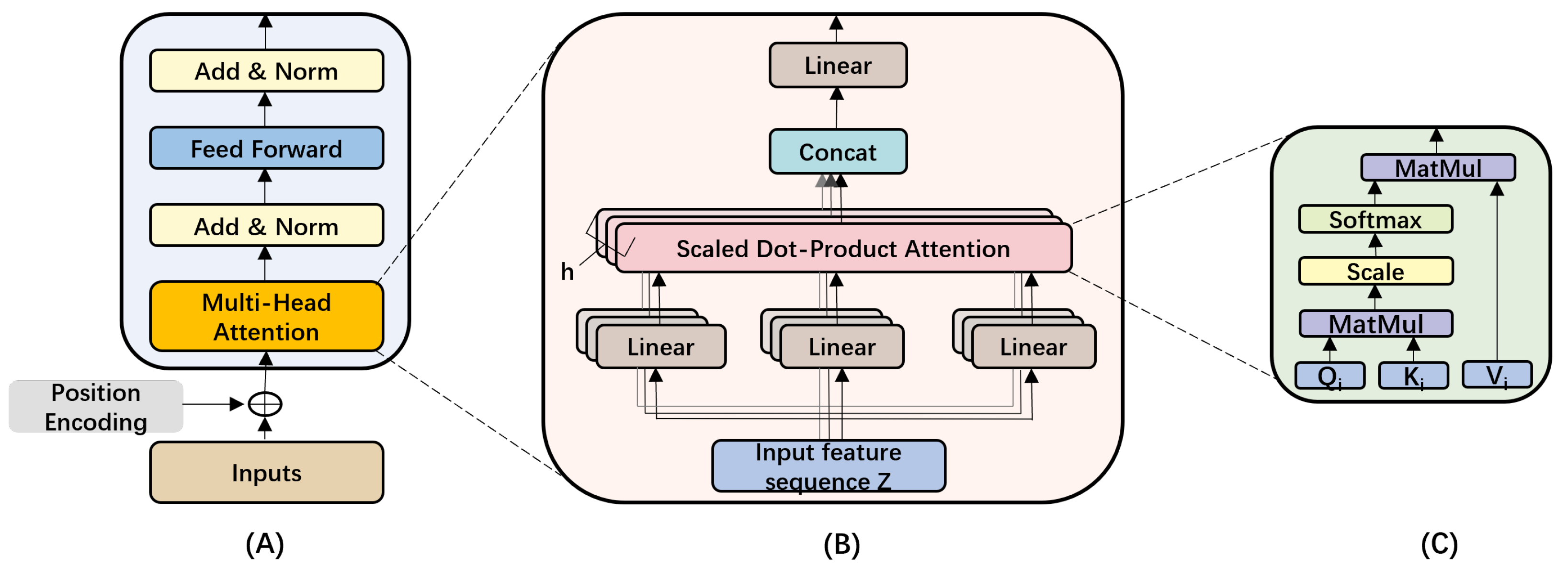
3.1. Feature Extraction
3.1.1. Convolution Module
3.1.2. Transformer Module
3.1.3. Global Average Pooling (GAP)
3.2. Feature Fusion
3.3. Classification
4. Experimental Results
4.1. Data Preparation
4.2. Experimental Setup
4.2.1. Running Environment
4.2.2. Compared Algorithms
4.2.3. Hyperparameters Tuning
4.2.4. Evaluation Metrics
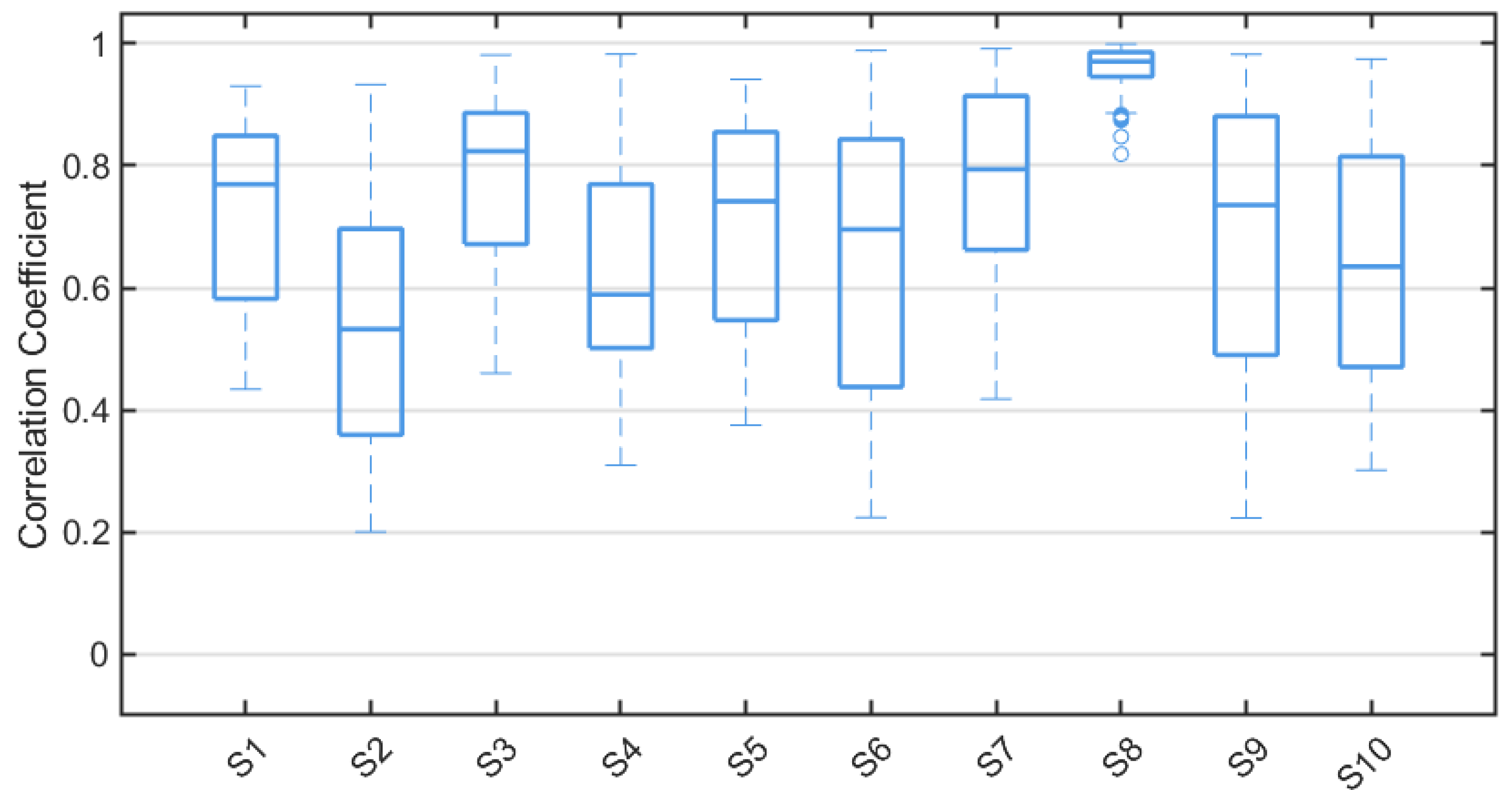
4.3. Cross-Correlation Analysis
4.4. Scoring Performance
4.5. Compared Results
4.6. Modality Analysis
4.7. Parameter Sensitivity Analysis
4.8. Ablation Study
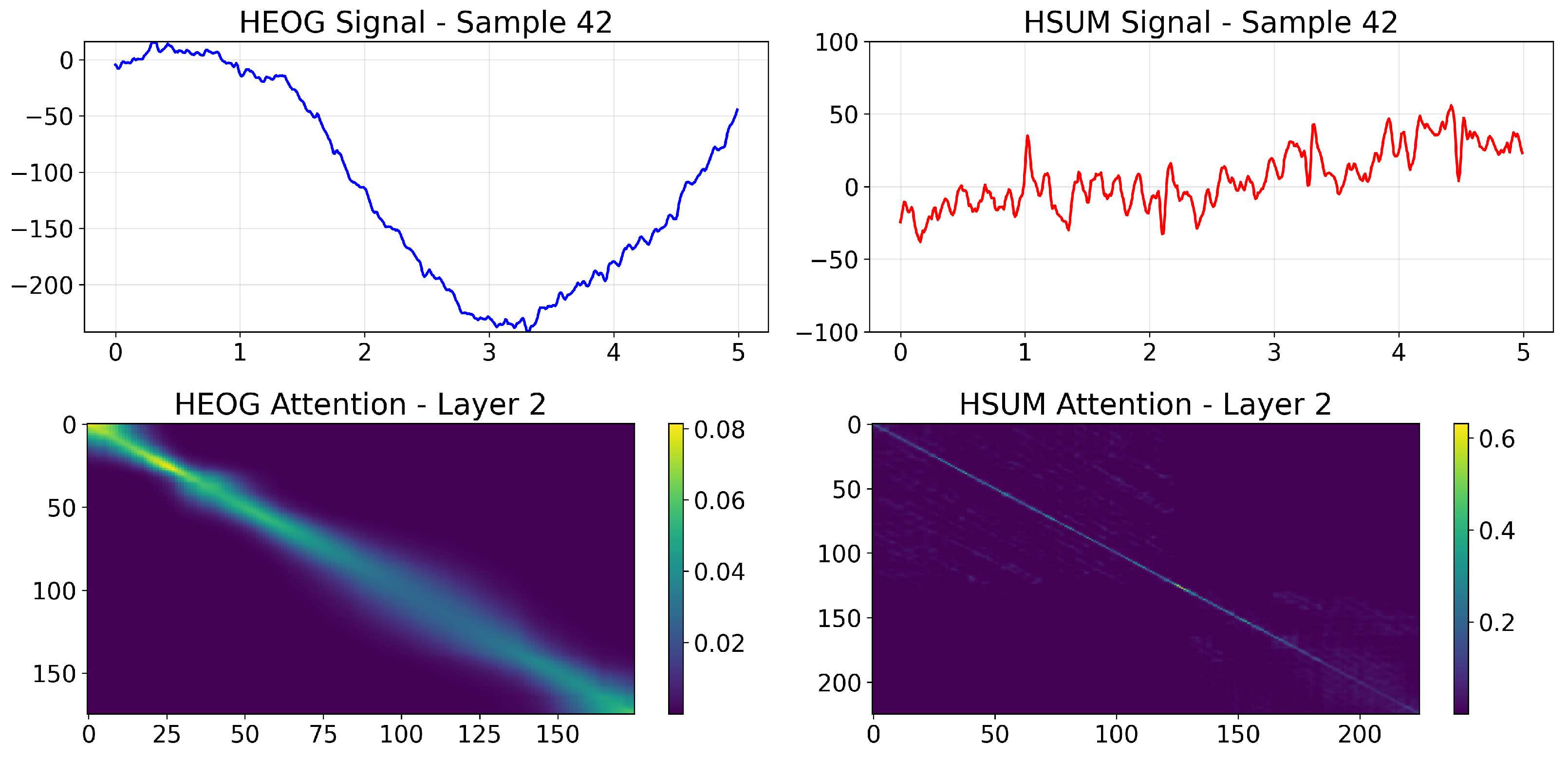
4.9. Interpretability Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, F.; Wang, H.; Zhou, X.; Fu, R. A driving fatigue feature detection method based on multifractal theory. IEEE Sens. J. 2022, 22, 19046–19059. [Google Scholar] [CrossRef]
- Tuncer, T.; Dogan, S.; Subasi, A. EEG-based driving fatigue detection using multilevel feature extraction and iterative hybrid feature selection. Biomed. Signal Process. Control 2021, 68, 102591. [Google Scholar] [CrossRef]
- Marzano, C.; Fratello, F.; Moroni, F.; Pellicciari, M.C.; Curcio, G.; Ferrara, M.; Ferlazzo, F.; De Gennaro, L. Slow eye movements and subjective estimates of sleepiness predict EEG power changes during sleep deprivation. Sleep 2007, 30, 610–616. [Google Scholar] [CrossRef]
- Cataldi, J.; Stephan, A.M.; Marchi, N.A.; Haba-Rubio, J.; Siclari, F. Abnormal timing of slow wave synchronization processes in non-rapid eye movement sleep parasomnias. Sleep 2022, 45, zsac111. [Google Scholar] [CrossRef]
- De Gennaro, L.; Ferrara, M.; Ferlazzo, F.; Bertini, M. Slow eye movements and EEG power spectra during wake-sleep transition. Clin. Neurophysiol. 2000, 111, 2107–2115. [Google Scholar] [CrossRef] [PubMed]
- Ogilvie, R.D. The process of falling asleep. Sleep Med. Rev. 2001, 5, 247–270. [Google Scholar] [CrossRef] [PubMed]
- Silber, M.H.; Ancoli-Israel, S.; Bonnet, M.H.; Chokroverty, S.; Grigg-Damberger, M.M.; Hirshkowitz, M.; Kapen, S.; Keenan, S.A.; Kryger, M.H.; Penzel, T.; et al. The visual scoring of sleep in adults. J. Clin. Sleep Med. 2007, 3, 121–131. [Google Scholar] [CrossRef]
- Arif, S.; Arif, M.; Munawar, S.; Ayaz, Y.; Khan, M.J.; Naseer, N. EEG spectral comparison between occipital and prefrontal cortices for early detection of driver drowsiness. In Proceedings of the 2021 International Conference on Artificial Intelligence and Mechatronics Systems (AIMS), Bandung, Indonesia, 28–30 April 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Pizza, F.; Fabbri, M.; Magosso, E.; Ursino, M.; Provini, F.; Ferri, R.; Montagna, P. Slow eye movements distribution during nocturnal sleep. Clin. Neurophysiol. 2011, 122, 1556–1561. [Google Scholar] [CrossRef]
- Jiao, Y.; Jiang, F. Detecting slow eye movements with bimodal-LSTM for recognizing drivers’ sleep onset period. Biomed. Signal Process. Control 2022, 75, 103608. [Google Scholar] [CrossRef]
- Jiao, Y.; He, X.; Jiao, Z. Detecting slow eye movements using multi-scale one-dimensional convolutional neural network for driver sleepiness detection. J. Neurosci. Methods 2023, 397, 109939. [Google Scholar] [CrossRef]
- Hiroshige, Y. Linear automatic detection of eye movements during the transition between wake and sleep. Psychiatry Clin. Neurosci. 1999, 53, 179–181. [Google Scholar] [CrossRef] [PubMed]
- Magosso, E.; Provini, F.; Montagna, P.; Ursino, M. A wavelet based method for automatic detection of slow eye movements: A pilot study. Med. Eng. Phys. 2006, 28, 860–875. [Google Scholar] [CrossRef]
- Shin, D.U.K.; Sakai, H.; Uchiyama, Y. Slow eye movement detection can prevent sleep-related accidents effectively in a simulated driving task. J. Sleep Res. 2011, 20, 416–424. [Google Scholar] [CrossRef] [PubMed]
- Jiao, Y.; Peng, Y.; Lu, B.L.; Chen, X.; Chen, S.; Wang, C. Recognizing slow eye movement for driver fatigue detection with machine learning approach. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 4035–4041. [Google Scholar] [CrossRef]
- Feng, K.; Qin, H.; Wu, S.; Pan, W.; Liu, G. A sleep apnea detection method based on unsupervised feature learning and single-lead electrocardiogram. IEEE Trans. Instrum. Meas. 2020, 70, 4000912. [Google Scholar] [CrossRef]
- Hu, S.; Cai, W.; Gao, T.; Wang, M. A hybrid transformer model for obstructive sleep apnea detection based on self-attention mechanism using single-lead ECG. IEEE Trans. Instrum. Meas. 2022, 71, 2514011. [Google Scholar] [CrossRef]
- Li, C.; Zhang, Z.; Zhang, X.; Huang, G.; Liu, Y.; Chen, X. EEG-based emotion recognition via transformer neural architecture search. IEEE Trans. Ind. Inform. 2022, 19, 6016–6025. [Google Scholar] [CrossRef]
- Yildirim, O.; Baloglu, U.B.; Acharya, U.R. A deep learning model for automated sleep stages classification using PSG signals. Int. J. Environ. Res. Public Health 2019, 16, 599. [Google Scholar] [CrossRef]
- Song, Y.; Zheng, Q.; Liu, B.; Gao, X. EEG conformer: Convolutional transformer for EEG decoding and visualization. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 31, 710–719. [Google Scholar] [CrossRef]
- Eldele, E.; Chen, Z.; Liu, C.; Wu, M.; Kwoh, C.K.; Li, X.; Guan, C. An attention-based deep learning approach for sleep stage classification with single-channel EEG. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 809–818. [Google Scholar] [CrossRef]
- Yan, R.; Li, F.; Zhou, D.D.; Ristaniemi, T.; Cong, F. Automatic sleep scoring: A deep learning architecture for multi-modality time series. J. Neurosci. Methods 2021, 348, 108971. [Google Scholar] [CrossRef]
- Lee, C.; An, J. LSTM-CNN model of drowsiness detection from multiple consciousness states acquired by EEG. Expert Syst. Appl. 2023, 213, 119032. [Google Scholar] [CrossRef]
- Supratak, A.; Dong, H.; Wu, C.; Guo, Y. DeepSleepNet: A model for automatic sleep stage scoring based on raw single-channel EEG. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 1998–2008. [Google Scholar] [CrossRef]
- Korkalainen, H.; Aakko, J.; Nikkonen, S.; Kainulainen, S.; Leino, A.; Duce, B.; Afara, I.O.; Myllymaa, S.; Töyräs, J.; Leppänen, T. Accurate deep learning-based sleep staging in a clinical population with suspected obstructive sleep apnea. IEEE J. Biomed. Health Inform. 2019, 24, 2073–2081. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. LSTM can solve hard long time lag problems. In Proceedings of the 1996 Neural Information Processing Systems, Denver, CO, USA, 2–5 December 1996; Volume 9. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Li, R.; Hu, M.; Gao, R.; Wang, L.; Suganthan, P.N.; Sourina, O. TFormer: A time–frequency Transformer with batch normalization for driver fatigue recognition. Adv. Eng. Inform. 2024, 62, 102575. [Google Scholar] [CrossRef]
- Dai, Y.; Li, X.; Liang, S.; Wang, L.; Duan, Q.; Yang, H.; Zhang, C.; Chen, X.; Li, L.; Li, X.; et al. Multichannelsleepnet: A transformer-based model for automatic sleep stage classification with psg. IEEE J. Biomed. Health Inform. 2023, 27, 4204–4215. [Google Scholar] [CrossRef] [PubMed]
- Qu, W.; Wang, Z.; Hong, H.; Chi, Z.; Feng, D.D.; Grunstein, R.; Gordon, C. A residual based attention model for EEG based sleep staging. IEEE J. Biomed. Health Inform. 2020, 24, 2833–2843. [Google Scholar] [CrossRef]
- Ding, S.; Yuan, Z.; An, P.; Xue, G.; Sun, W.; Zhao, J. Cascaded convolutional neural network with attention mechanism for mobile eeg-based driver drowsiness detection system. In Proceedings of the 2019 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), San Diego, CA, USA, 18–21 November 2019; pp. 1457–1464. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, S.; Jia, N.; Zhao, L.; Han, C.; Li, L. Integrating visual large language model and reasoning chain for driver behavior analysis and risk assessment. Accid. Anal. Prev. 2024, 198, 107497. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, T.; Huang, Z.; Xing, Y.; Chen, S. Personalizing driver agent using large language models for driving safety and smarter human–machine interactions. IEEE Intell. Transp. Syst. Mag. 2025, 17, 96–111. [Google Scholar] [CrossRef]
- Hu, C.; Li, X. Human-Centric Context and Self-Uncertainty-Driven Multi-Modal Large Language Model for Training-Free Vision-Based Driver State Recognition. IEEE Trans. Intell. Transp. Syst. 2025, 1–11. [Google Scholar] [CrossRef]
- Johns, M.W. A new method for measuring daytime sleepiness: The Epworth sleepiness scale. Sleep 1991, 14, 540–545. [Google Scholar] [CrossRef]
- Rafiee, J.; Rafiee, M.A.; Prause, N.; Schoen, M.P. Wavelet basis functions in biomedical signal processing. Expert Syst. Appl. 2011, 38, 6190–6201. [Google Scholar] [CrossRef]
- Porte, H.S. Slow horizontal eye movement at human sleep onset. J. Sleep Res. 2004, 13, 239–249. [Google Scholar] [CrossRef]
- Jiao, Y.; Lu, B.L. Detecting slow eye movement for recognizing driver’s sleep onset period with EEG features. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 4658–4661. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015. [Google Scholar] [CrossRef]
- Phan, H.; Mikkelsen, K.; Chén, O.Y.; Koch, P.; Mertins, A.; De Vos, M. Sleeptransformer: Automatic sleep staging with interpretability and uncertainty quantification. IEEE Trans. Biomed. Eng. 2022, 69, 2456–2467. [Google Scholar] [CrossRef] [PubMed]
- Ming, Y.; Ma, J.; Yang, X.; Dai, W.; Peng, Y.; Kong, W. AEGIS-Net: Attention-guided multi-level feature aggregation for indoor place recognition. In Proceedings of the ICASSP 2024—2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 4030–4034. [Google Scholar] [CrossRef]
- Lin, M.; Chen, Q.; Yan, S. Network in network. arXiv 2013. [Google Scholar] [CrossRef]
- Buitinck, L.; Louppe, G.; Blondel, M.; Pedregosa, F.; Mueller, A.; Grisel, O.; Niculae, V.; Prettenhofer, P.; Gramfort, A.; Grobler, J.; et al. API design for machine learning software: Experiences from the scikit-learn project. arXiv 2013. [Google Scholar] [CrossRef]
- King, G.; Zeng, L. Logistic regression in rare events data. Political Anal. 2001, 9, 137–163. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014. [Google Scholar] [CrossRef]
- Nogay, H.S.; Adeli, H. Diagnostic of autism spectrum disorder based on structural brain MRI images using, grid search optimization, and convolutional neural networks. Biomed. Signal Process. Control 2023, 79, 104234. [Google Scholar] [CrossRef]
- Wang, H.; Cao, L.; Huang, C.; Jia, J.; Dong, Y.; Fan, C.; de Albuquerque, V.H.C. A novel algorithmic structure of EEG channel attention combined with swin transformer for motor patterns classification. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 3132–3141. [Google Scholar] [CrossRef] [PubMed]


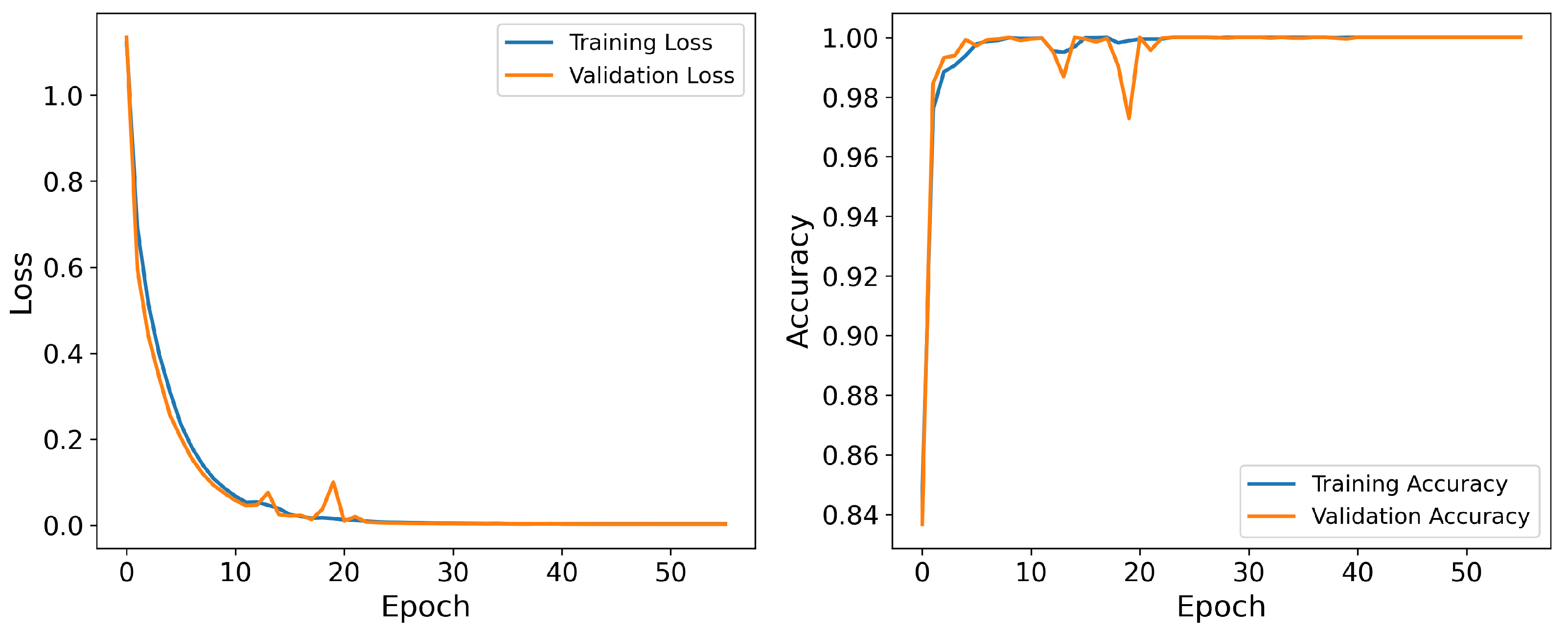
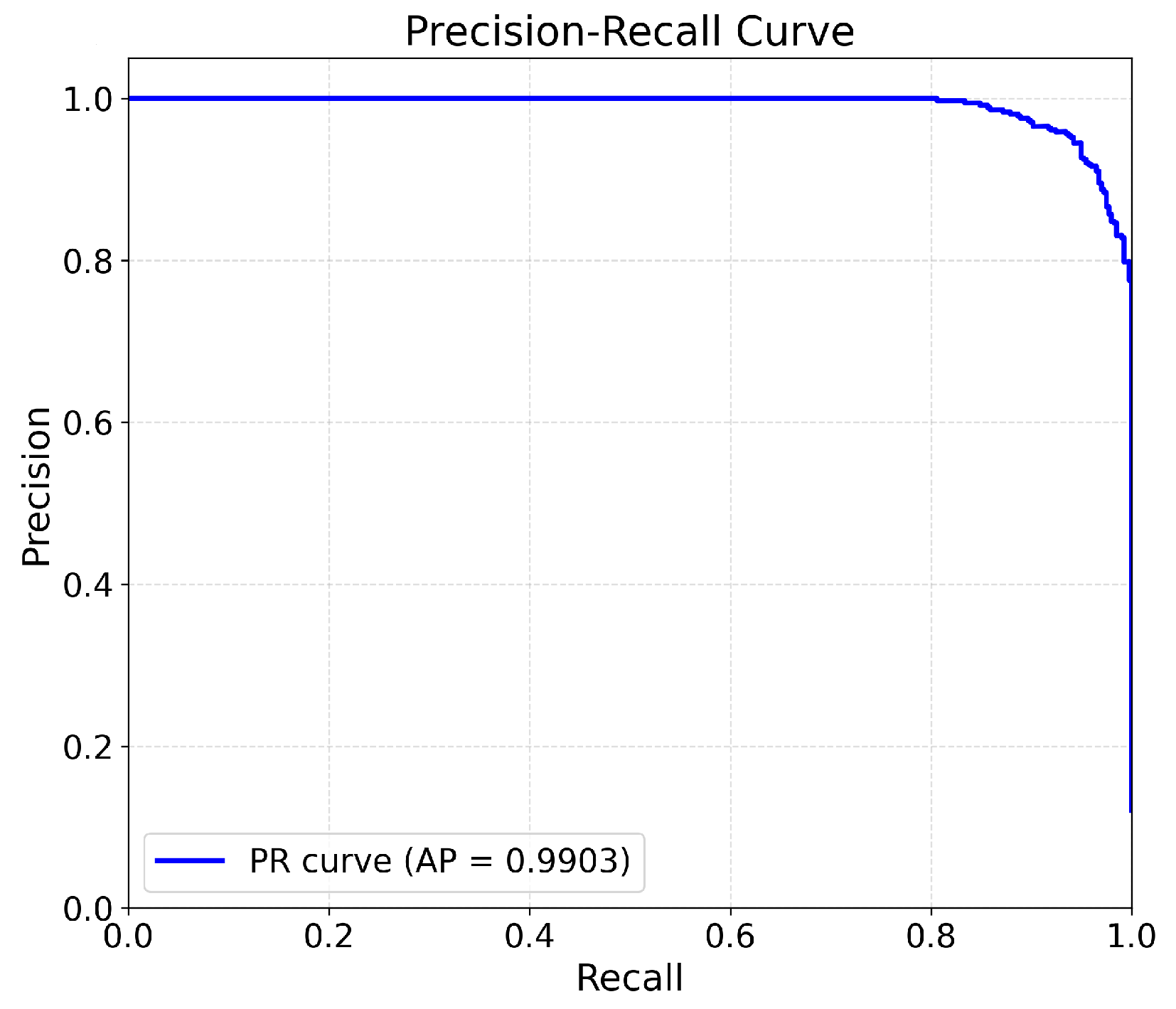

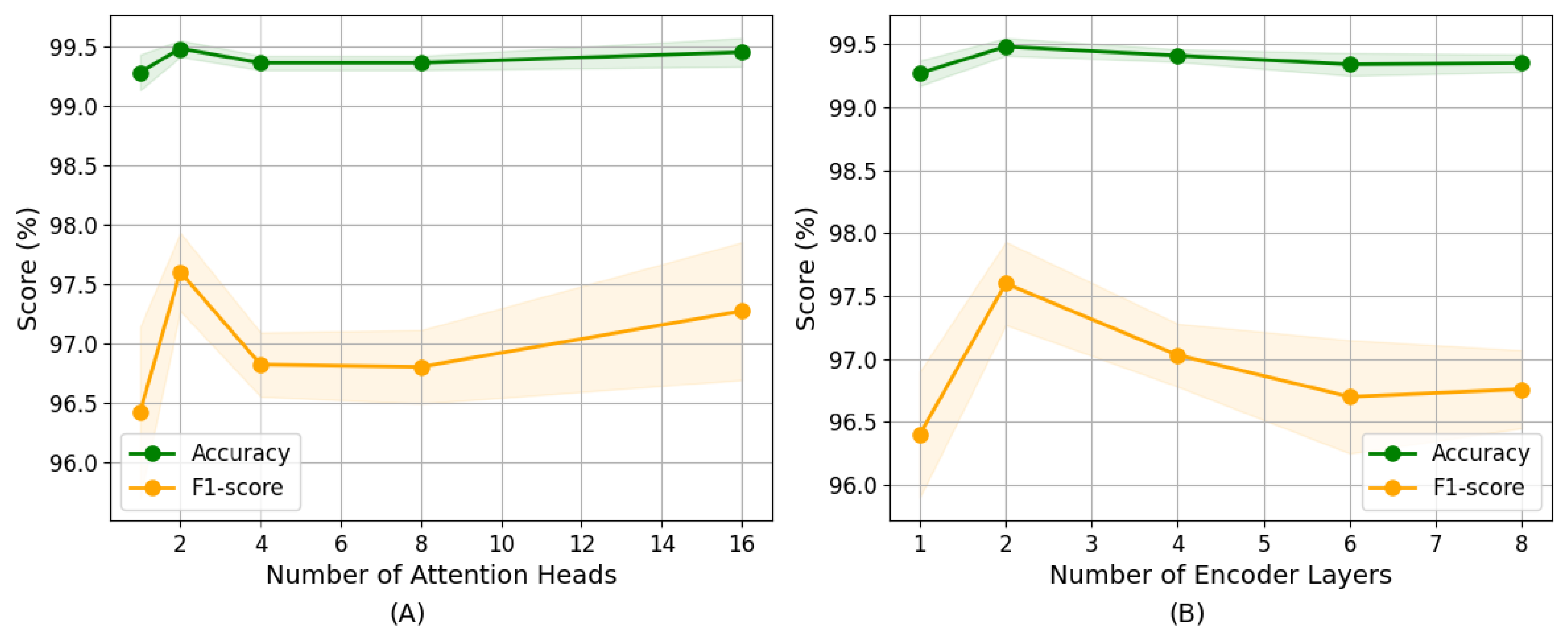
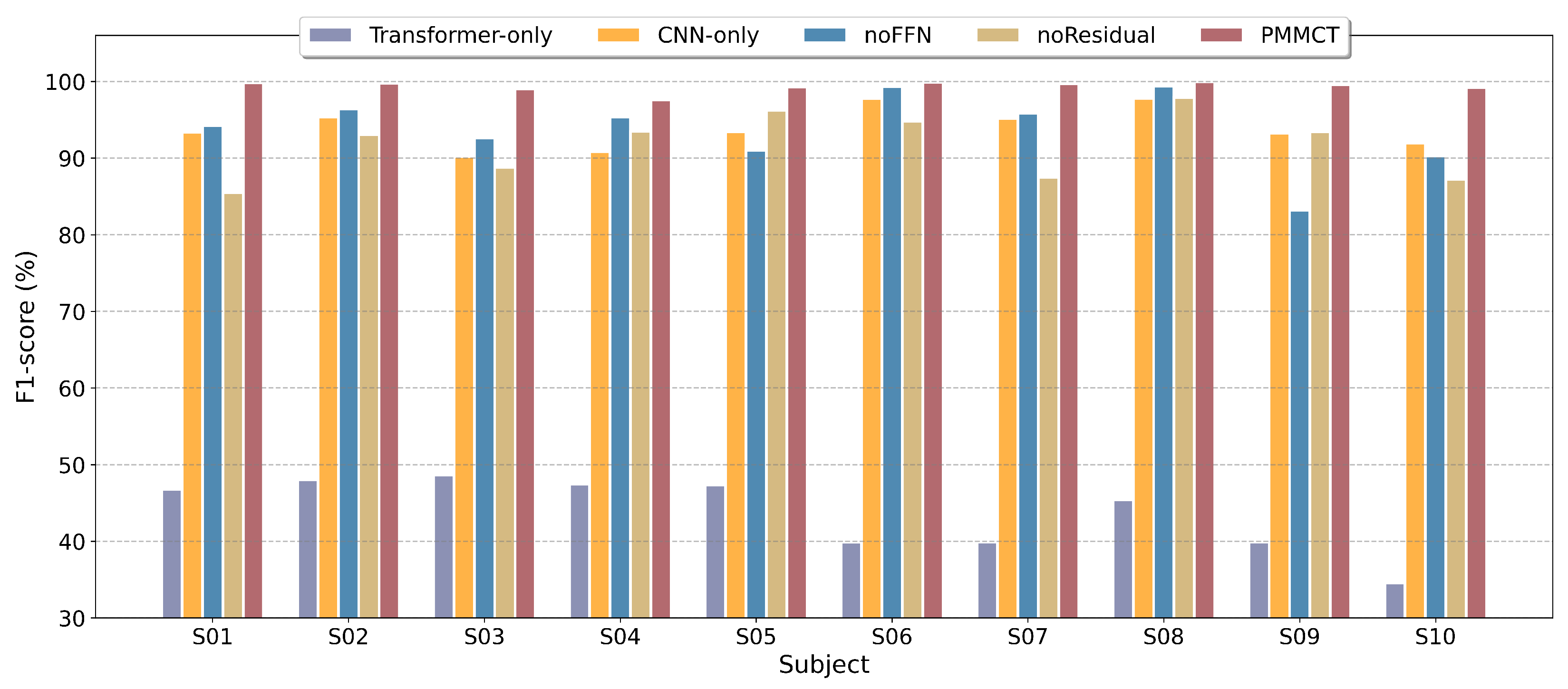


| Subject | Positive Samples | Negative Samples | FP | FN | Precision (%) | Recall (%) | Accuracy (%) | F1-Score (%) |
|---|---|---|---|---|---|---|---|---|
| S01 | 397 | 2891 | 1 | 0 | 99.75 | 100 | 99.97 | 99.87 |
| S02 | 454 | 5627 | 3 | 0 | 99.34 | 100 | 99.95 | 99.67 |
| S03 | 283 | 5252 | 5 | 0 | 99.26 | 100 | 99.91 | 99.12 |
| S04 | 728 | 6747 | 34 | 1 | 95.53 | 99.86 | 99.53 | 97.65 |
| S05 | 396 | 3542 | 4 | 1 | 99.00 | 99.75 | 99.87 | 99.37 |
| S06 | 193 | 2756 | 1 | 2 | 99.48 | 98.96 | 99.90 | 99.22 |
| S07 | 208 | 3901 | 1 | 0 | 99.52 | 100 | 99.98 | 99.76 |
| S08 | 637 | 3158 | 1 | 0 | 99.84 | 100 | 99.97 | 99.92 |
| S09 | 199 | 3739 | 0 | 2 | 100 | 98.99 | 99.95 | 99.49 |
| S10 | 373 | 4554 | 2 | 2 | 99.46 | 99.46 | 99.92 | 99.46 |
| Average | - | - | 5.20 ± 9.71 | 0.80 ± 0.87 | 99.12 ± 1.23 | 99.70 ± 0.40 | 99.89 ± 0.13 | 99.35 ± 0.62 |
| CNN | CNN-LSTM | CNN-LSTM-Attention | PMMCT | |||||
|---|---|---|---|---|---|---|---|---|
| Accuracy (%) | F1-Score (%) | Accuracy (%) | F1-Score (%) | Accuracy (%) | F1-Score (%) | Accuracy (%) | F1-Score (%) | |
| S01 | 95.47 ± 2.03 | 85.36 ± 5.11 | 87.10 ± 3.83 | 66.09 ± 7.06 | 96.87 ± 1.72 | 89.32 ± 4.92 | 98.69 ± 1.01 | 95.31 ± 2.63 |
| S02 | 97.84 ± 2.71 | 91.42 ± 7.09 | 96.25 ± 2.14 | 82.68 ± 6.75 | 98.72 ± 1.51 | 94.11 ± 5.18 | 99.69 ± 0.45 | 98.21 ± 1.78 |
| S03 | 97.69 ± 1.91 | 85.01 ± 6.89 | 94.05 ± 2.57 | 66.73 ± 8.84 | 98.75 ± 1.05 | 90.83 ± 5.58 | 99.56 ± 0.33 | 96.52 ± 2.23 |
| S04 | 96.67 ± 1.44 | 86.41 ± 4.20 | 96.23 ± 1.37 | 84.48 ± 4.22 | 97.85 ± 0.93 | 90.58 ± 3.28 | 98.58 ± 0.59 | 93.45 ± 2.38 |
| S05 | 97.95 ± 1.60 | 91.90 ± 4.68 | 95.17 ± 3.02 | 83.52 ± 7.05 | 98.39 ± 1.27 | 93.37 ± 3.79 | 99.39 ± 0.49 | 97.26 ± 1.86 |
| S06 | 98.31 ± 1.40 | 90.67 ± 6.70 | 96.41 ± 1.99 | 81.64 ± 6.46 | 98.76 ± 1.24 | 92.91 ± 5.49 | 99.26 ± 1.19 | 96.21 ± 3.65 |
| S07 | 99.03 ± 1.71 | 94.67 ± 5.56 | 97.08 ± 2.89 | 84.05 ± 7.20 | 99.11 ± 1.83 | 95.24 ± 5.09 | 99.32 ± 0.90 | 95.25 ± 4.02 |
| S08 | 98.79 ± 0.64 | 96.48 ± 2.31 | 97.25 ± 1.50 | 92.81 ± 3.23 | 99.10 ± 0.82 | 97.54 ± 2.04 | 99.76 ± 0.28 | 99.31 ± 0.75 |
| S09 | 98.01 ± 1.64 | 87.20 ± 6.94 | 96.25 ± 1.78 | 76.50 ± 7.30 | 98.76 ± 1.23 | 91.55 ± 6.09 | 99.46 ± 0.73 | 96.14 ± 3.65 |
| S10 | 98.51 ± 1.85 | 89.43 ± 4.67 | 96.15 ± 2.13 | 85.57 ± 5.45 | 98.93 ± 1.77 | 92.55 ± 3.69 | 99.60 ± 0.59 | 97.50 ± 2.01 |
| CNN | CNN-LSTM | CNN-LSTM-Attention | PMMCT | |
|---|---|---|---|---|
| S01 | [250, 150, 50, 250] | [250, 150, 250, 250, 150] | [50, 250, 50, 150, 50] | [150, 150, 50, 250] |
| S02 | [250, 150, 50, 150] | [50, 150, 50, 250, 50] | [150, 150, 150, 50, 50] | [250, 50, 50, 250] |
| S03 | [150, 250, 50, 250] | [250, 50, 50, 50, 100] | [150, 150, 50, 50, 50] | [50, 250, 150, 250] |
| S04 | [250, 50, 50, 50] | [250, 150, 50, 250, 150] | [250, 50, 50, 50, 150] | [250, 150, 50, 250] |
| S05 | [150, 50, 50, 250] | [50, 250, 50, 250, 50] | [50, 50, 50, 250, 50] | [50, 50, 50, 150] |
| S06 | [50, 250, 50,250] | [150, 150, 50, 50, 50] | [50, 50, 50, 50, 100] | [50, 250, 50, 50] |
| S07 | [50, 250, 50, 50] | [50, 50, 150, 250, 100] | [150, 250, 50, 150, 50] | [250, 150, 50, 150] |
| S08 | [150, 150, 50, 50] | [50, 250, 50, 50, 50] | [50, 50, 50, 50, 100] | [250, 50, 50, 50] |
| S09 | [150, 50, 50, 50] | [150, 50, 50, 50, 50] | [50, 250, 50, 250, 50] | [50, 250, 150, 150] |
| S10 | [50, 150, 50, 250] | [150, 50, 150, 250, 150] | [250, 50, 50, 150, 50] | [150, 150, 50, 250] |
| CNN | CNN-LSTM | CNN-LSTM-Attention | PMMCT | |||||
|---|---|---|---|---|---|---|---|---|
| Accuracy (%) | F1-Score (%) | Accuracy (%) | F1-Score (%) | Accuracy (%) | F1-Score (%) | Accuracy (%) | F1-Score (%) | |
| S01 | 93.73 | 79.32 | 98.21 | 93.03 | 99.45 | 97.76 | 99.97 | 99.87 |
| S02 | 99.77 | 98.48 | 98.64 | 91.62 | 99.82 | 98.80 | 99.95 | 99.67 |
| S03 | 99.78 | 97.90 | 95.95 | 70.13 | 99.73 | 97.39 | 99.91 | 99.12 |
| S04 | 98.98 | 94.97 | 94.57 | 77.86 | 97.86 | 90.10 | 99.53 | 97.65 |
| S05 | 98.81 | 94.38 | 90.15 | 66.32 | 99.80 | 99.00 | 99.87 | 99.37 |
| S06 | 99.73 | 97.97 | 99.80 | 98.47 | 99.83 | 98.72 | 99.90 | 99.22 |
| S07 | 99.03 | 90.57 | 99.22 | 92.59 | 99.34 | 93.91 | 99.98 | 99.76 |
| S08 | 97.47 | 92.30 | 99.47 | 98.45 | 97.84 | 93.93 | 99.97 | 99.92 |
| S09 | 99.52 | 95.44 | 96.72 | 75.43 | 99.34 | 93.50 | 99.95 | 99.49 |
| S10 | 99.63 | 97.35 | 99.63 | 91.25 | 99.53 | 96.94 | 99.92 | 99.46 |
| Average | 98.64 ± 1.77 | 93.87 ± 5.44 | 97.24 ± 2.89 | 85.52 ± 11.30 | 99.25 ± 0.72 | 96.00 ± 2.83 | 99.89 ± 0.13 | 99.35 ± 0.62 |
| Model | Accuracy ± Std (%) | F1-Score ± Std (%) | FP ± Std | FN ± Std |
|---|---|---|---|---|
| Bimodal-LSTM | 97.96 ± 2.68 | 89.78 ± 6.99 | 69.60 ± 21.81 | 9.40 ± 6.80 |
| CNN | 98.64 ± 1.77 | 93.87 ± 5.44 | 43.60 ± 56.26 | 10.00 ± 18.00 |
| CNN-LSTM | 97.24 ± 2.89 | 85.52 ± 11.30 | 138.70 ± 134.24 | 7.80 ± 7.63 |
| CNN-LSTM-Attention | 99.25 ± 0.72 | 96.00 ± 2.83 | 31.60 ± 47.89 | 3.90 ± 3.73 |
| PMMCT | 99.89 ± 0.13 | 99.35 ± 0.62 | 5.20 ± 9.71 | 0.80 ± 0.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, Y.; Zhang, J.; Jiao, Z. PMMCT: A Parallel Multimodal CNN-Transformer Model to Detect Slow Eye Movement for Recognizing Driver Sleepiness. Sensors 2025, 25, 5671. https://doi.org/10.3390/s25185671
Jiao Y, Zhang J, Jiao Z. PMMCT: A Parallel Multimodal CNN-Transformer Model to Detect Slow Eye Movement for Recognizing Driver Sleepiness. Sensors. 2025; 25(18):5671. https://doi.org/10.3390/s25185671
Chicago/Turabian StyleJiao, Yingying, Jiajia Zhang, and Zhuqing Jiao. 2025. "PMMCT: A Parallel Multimodal CNN-Transformer Model to Detect Slow Eye Movement for Recognizing Driver Sleepiness" Sensors 25, no. 18: 5671. https://doi.org/10.3390/s25185671
APA StyleJiao, Y., Zhang, J., & Jiao, Z. (2025). PMMCT: A Parallel Multimodal CNN-Transformer Model to Detect Slow Eye Movement for Recognizing Driver Sleepiness. Sensors, 25(18), 5671. https://doi.org/10.3390/s25185671





