Optimisation of Sensor and Sensor Node Positions for Shape Sensing with a Wireless Sensor Network—A Case Study Using the Modal Method and a Physics-Informed Neural Network
Abstract
1. Introduction
2. State of the Art
2.1. Shape Sensing in Structural Health Monitoring
- 1.
- 2.
- Methods using global or piecewise continuous basis functions to approximate the displacement field, like the modal method (MM), which utilises the connection between modal matrices for strains and displacements from the mode shapes of a part to estimate the displacement field of various forms of structures from strain measurements [16].
- 3.
- 4.
2.1.1. Modal Method
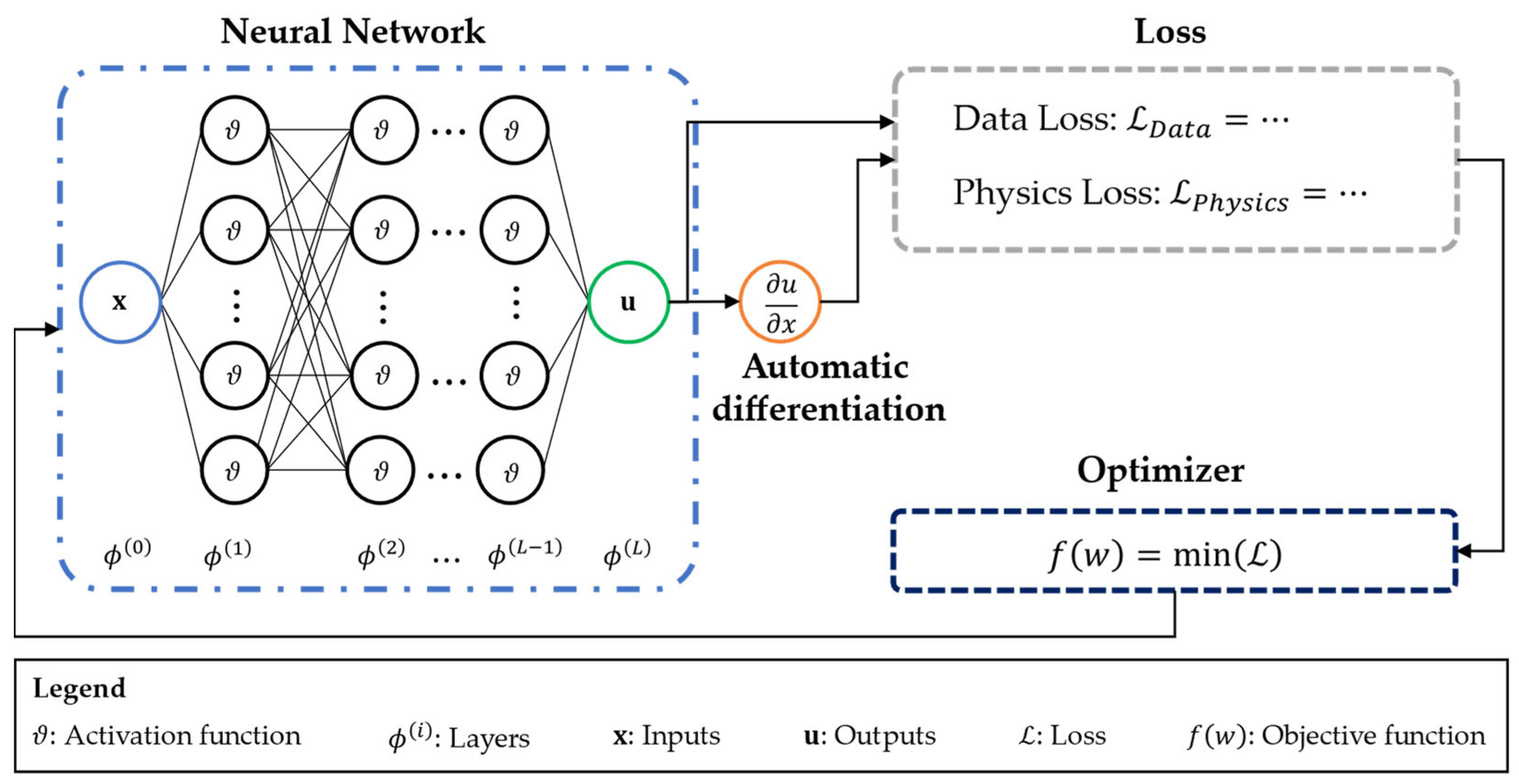
2.1.2. Physics-Informed Neural Networks for Shape Sensing
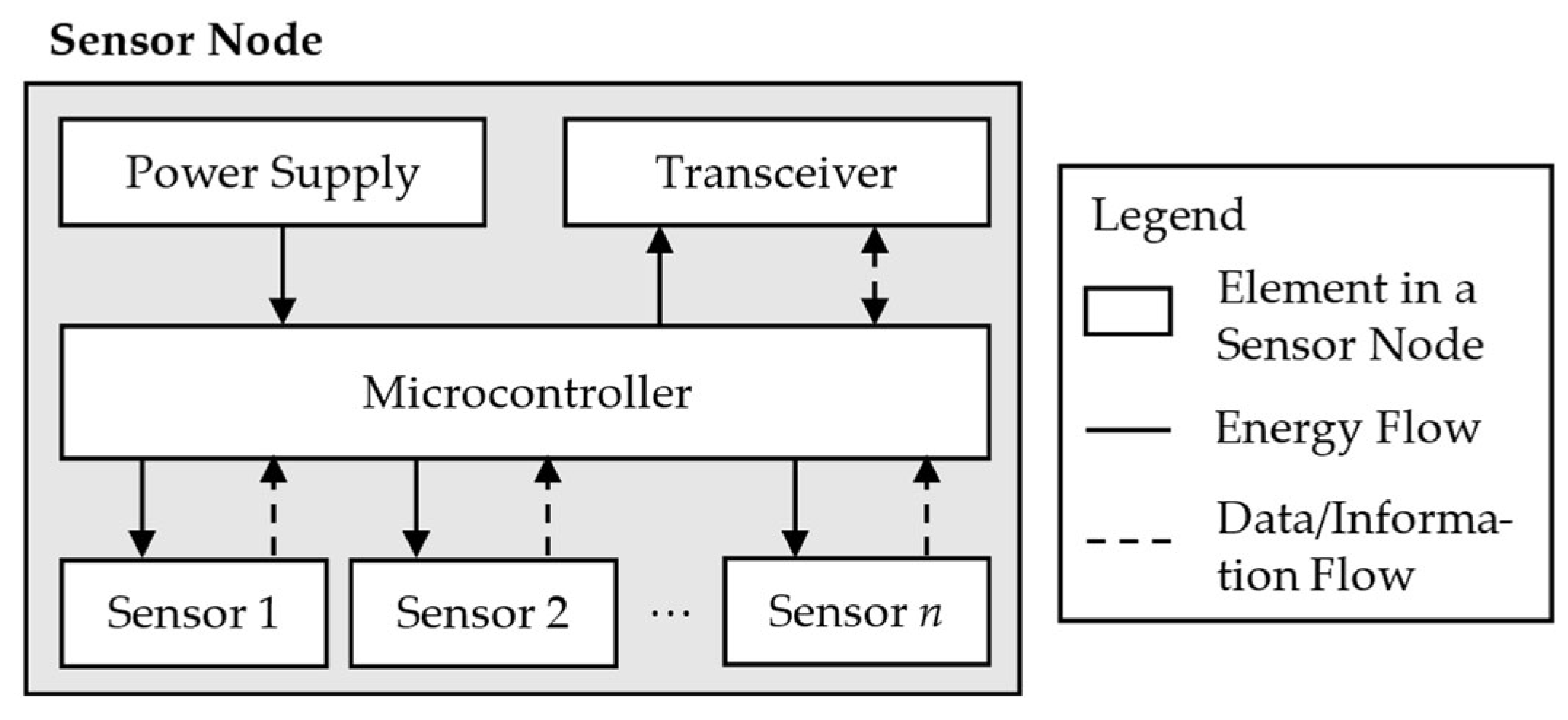
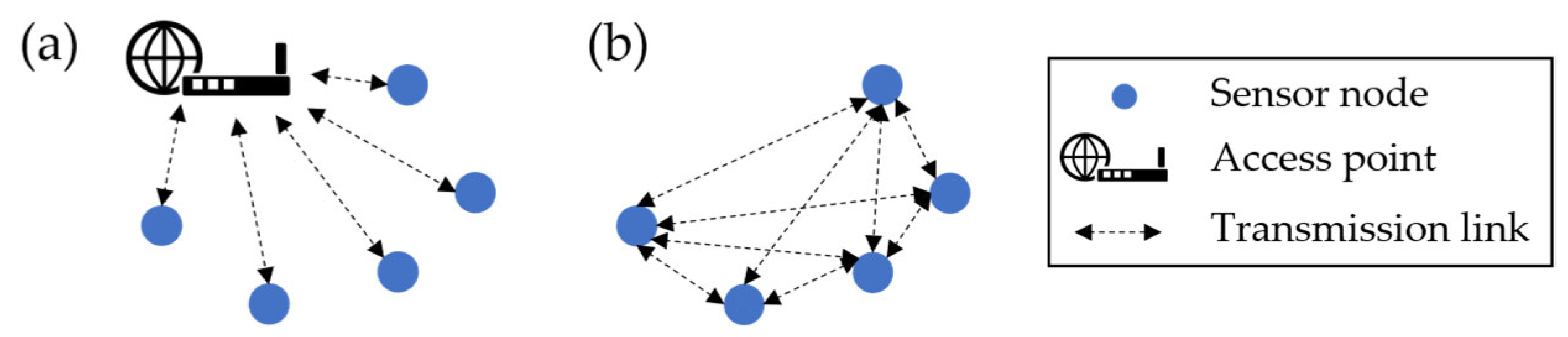
2.2. Wireless Sensor Networks for Monitoring Structural Components
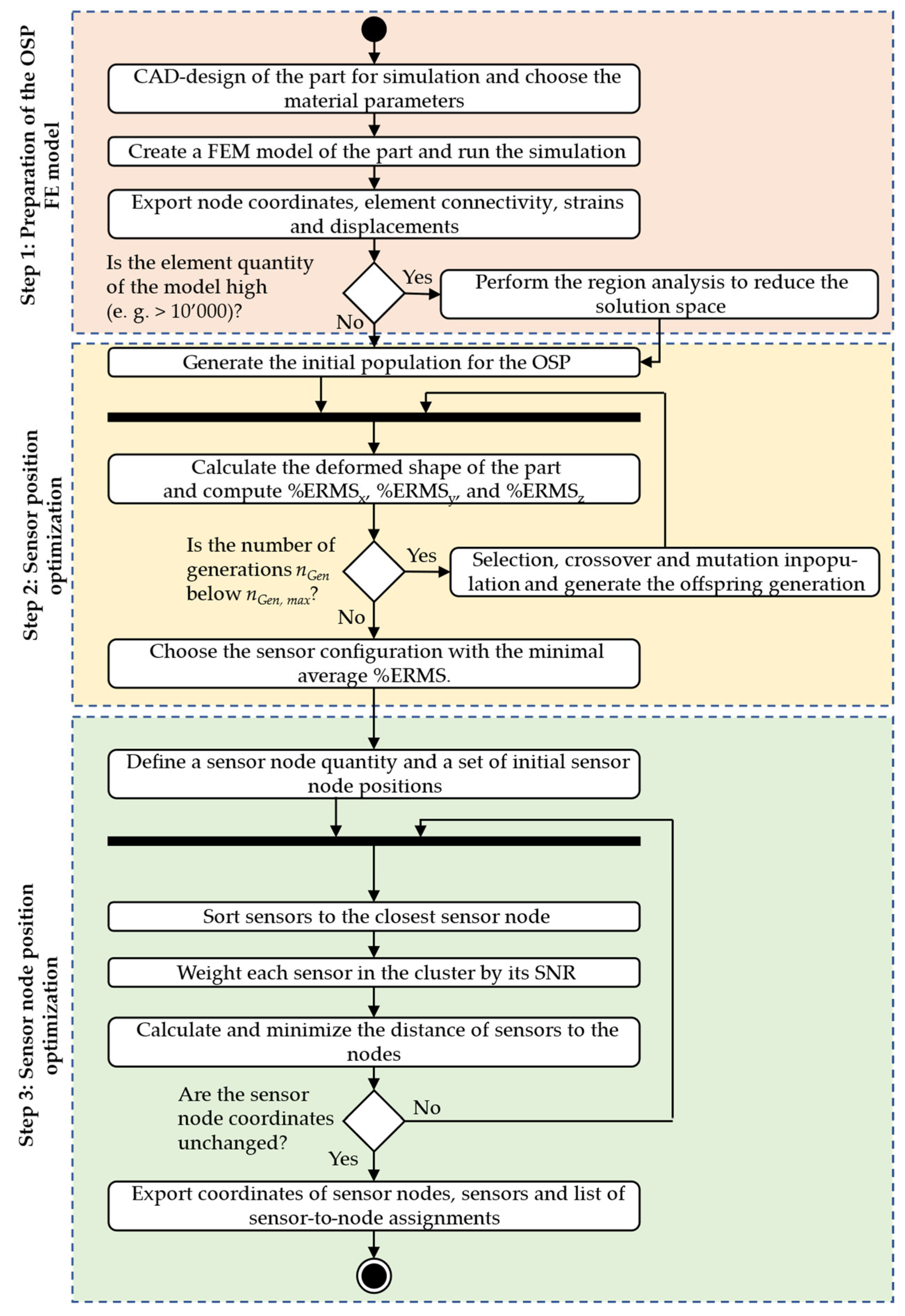
3. Methodology
4. Case Study on the Application
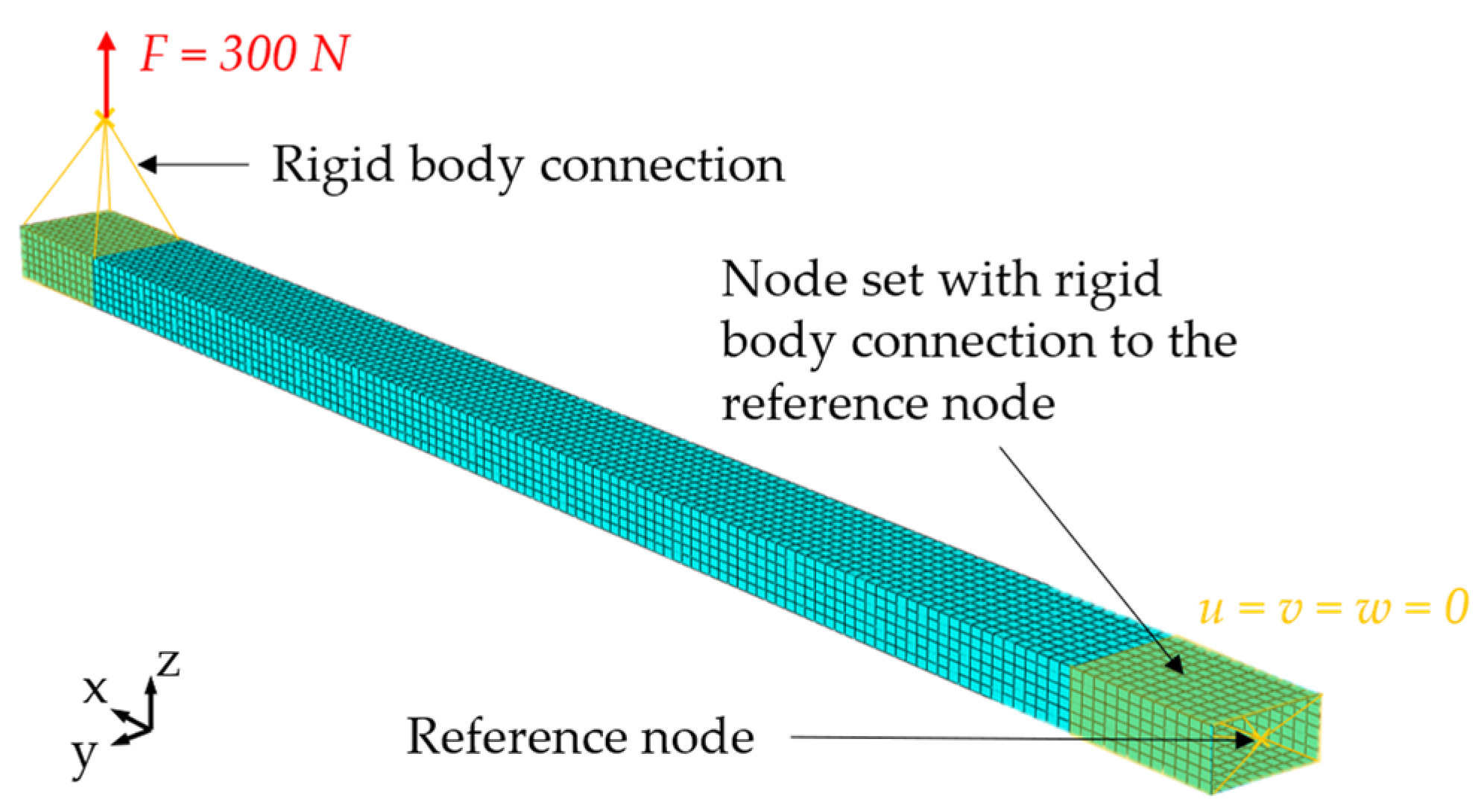
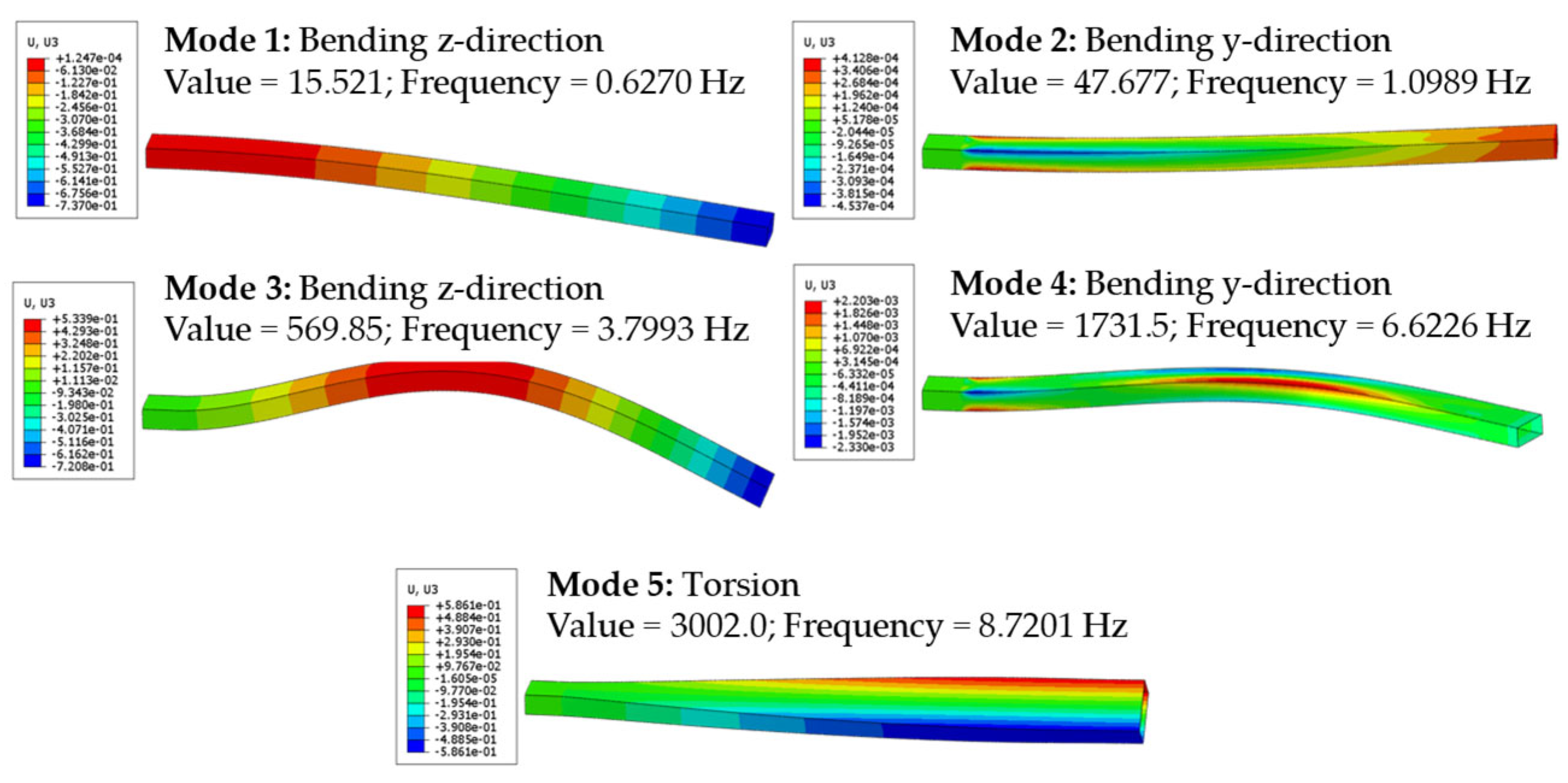
4.1. Demonstration Part, Load Case and Simulation
4.2. Optimisation Results for Sensor and Sensor Node Positions
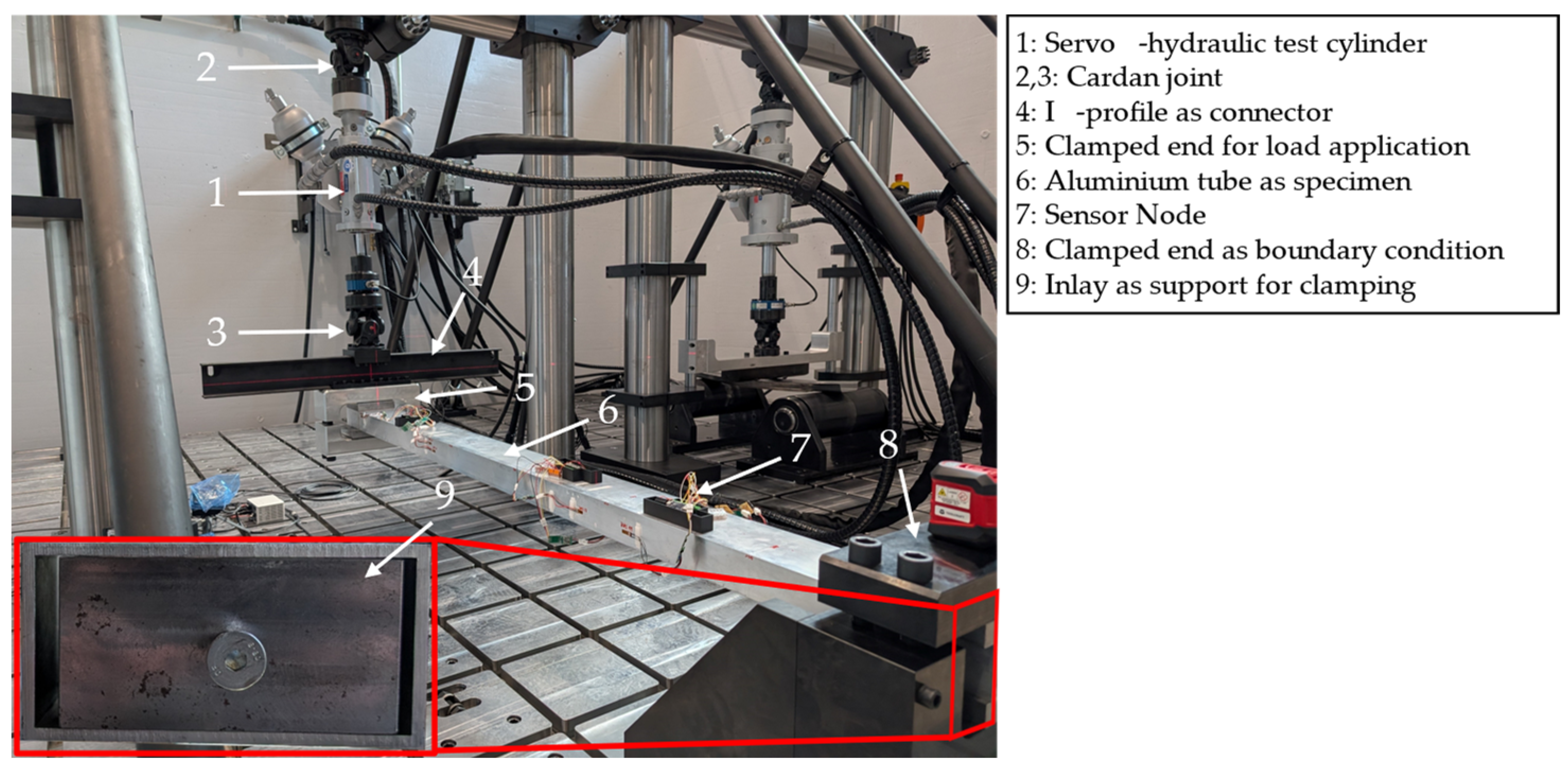
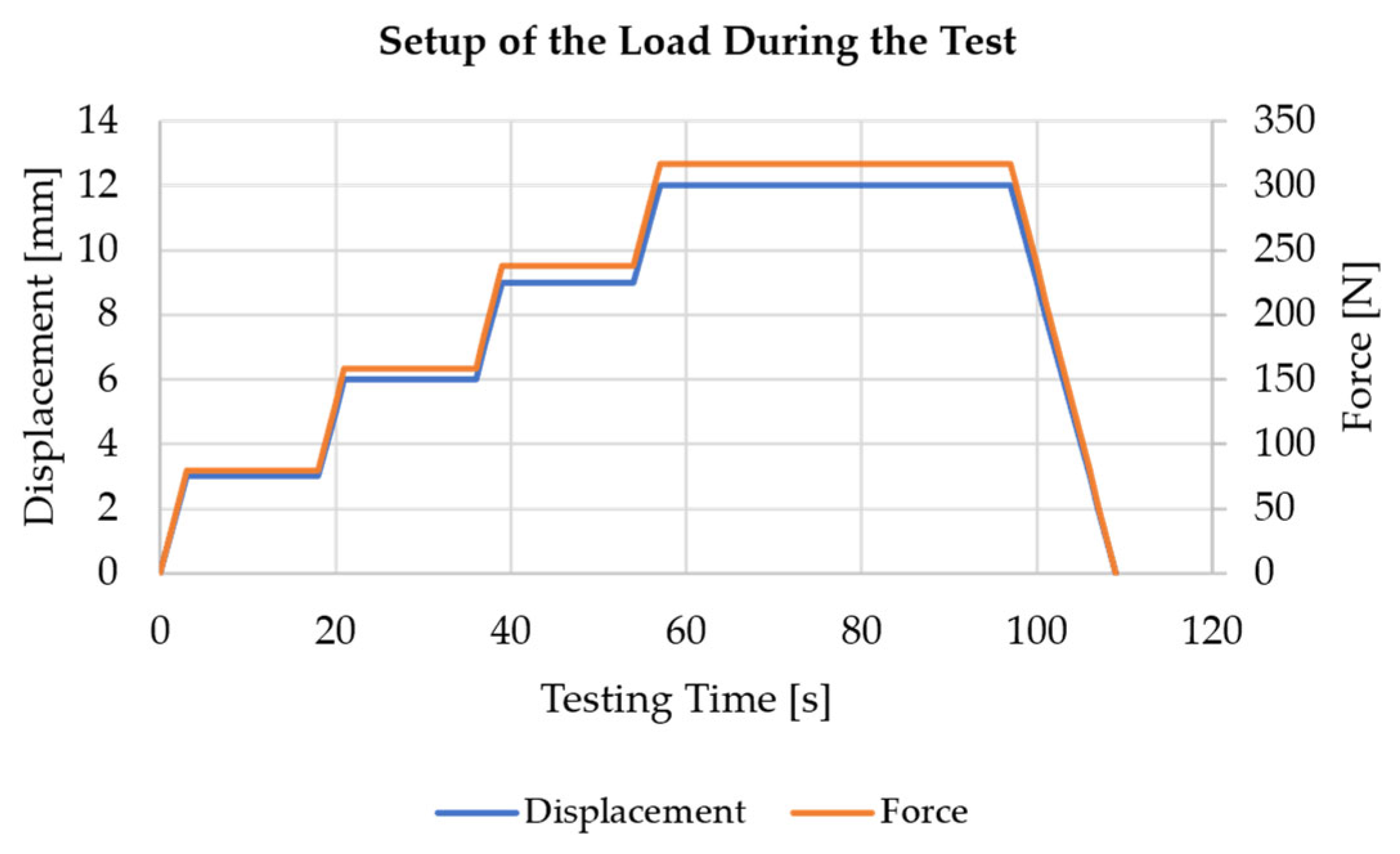
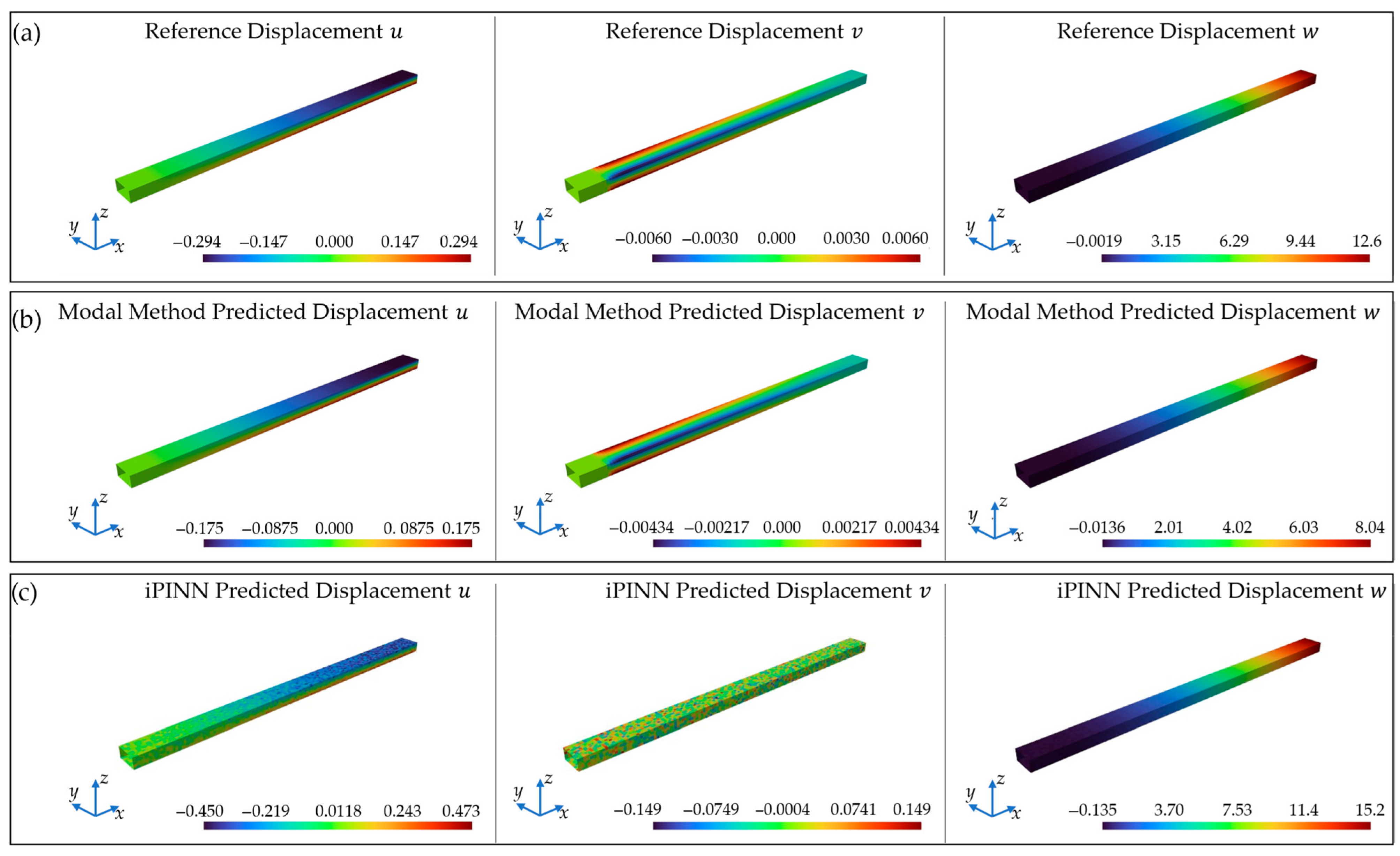
4.3. Application on the Real-World Demonstrator on the Test Bench
5. Discussion
6. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 3D | Three-dimensional |
| aNoise | Noise amplitude |
| ANN | Artificial Neural Network |
| A/D | Analogue/digital |
| CAD | Computer-aided design |
| CFRP | Carbon fiber reinforced plastic |
| E | Young’s modulus |
| Energy contribution of mode i | |
| f | Objective/fitness function |
| F | Force |
| FEM | Finite element method |
| FOS | Fiber optical sensor |
| GUI | Graphical user interface |
| HTML | Hypertext markup language |
| iFEM | Inverse Finite Element Method |
| iPINN | Physics-informed Neural Network for inverse Problems |
| IoT | Internet of Things |
| L | Number of layers |
| Loss during training | |
| M | Number of modes |
| MM | MM |
| n | Maximal number |
| nGen | Number of generations |
| NSGA-II | Non-dominated Sorting Genetic Algorithm II |
| OSP | Optimal Sensor Placement |
| PC | Personal computer |
| PCB | Printed circuit board |
| PINN | Physics-informed Neural Network |
| ReLU | Rectified linear unit function |
| S | Number of strains |
| SHM | Structural health monitoring |
| SNR | Signal-to-noise ratio |
| Modal coordinates | |
| Vector of displacements | |
| Displacement components in x, y, z direction | |
| UML | Unified Modeling Language |
| WLAN | Wireless local area network |
| WSN | Wireless Sensor Network |
| Neural network input | |
| x, y, z | Directions in the three-dimensional coordinate space |
| %ERMS | Percentage root mean square error |
| Vector of measured strains | |
| Strain in x direction | |
| Activation function | |
| Mean value | |
| Poisson ratio | |
| Standard deviation | |
| Displacement modal shape matrix | |
| Strain modal shape matrix | |
| Angular frequency | |
| Loss function |
Appendix A
| Sensor ID | Expected SNR [dB] | Real SNR [dB] |
|---|---|---|
| SG11 | 35.35787 | 55.7515179 |
| SG12 | 28.40767 | 49.1740088 |
| SG13 | 30.55412 | 51.692899 |
| SG14 | 26.90719 | 47.5269178 |
| SG21 | 37.63991 | 58.9215918 |
| SG22 | 21.71773 | 42.4208688 |
| SG23 | 26.14873 | 47.2005006 |
| SG31 | 7.265055 | 27.8748798 |
| SG32 | 20.43918 | 41.5085269 |
| SG33 | 5.75661 | 16.6517324 |
References
- Narayana, K.J.; Gupta Burela, R. A review of recent research on multifunctional composite materials and structures with their applications. Mater. Today Proc. 2018, 5, 5580–5590. [Google Scholar] [CrossRef]
- Gherlone, M.; Cerracchio, P.; Mattone, M. Shape sensing methods: Review and experimental comparison on a wing-shaped plate. Prog. Aerosp. Sci. 2018, 99, 14–26. [Google Scholar] [CrossRef]
- Lachmayer, R.; Mozgova, I.; Reimche, W.; Colditz, F.; Mroz, G.; Gottwald, P. Technical Inheritance: A Concept to Adapt the Evolution of Nature to Product Engineering. Procedia Technol. 2014, 15, 178–187. [Google Scholar] [CrossRef]
- Lachmayer, R.; Mozgova, I.; Scheidel, W. An Approach to Describe Gentelligent Components in their Life Cycle. Procedia Technol. 2016, 26, 199–206. [Google Scholar] [CrossRef]
- Denkena, B.; Dittrich, M.-A.; Stamm, S.; Wichmann, M.; Wilmsmeier, S. Gentelligent processes in biologically inspired manufacturing. CIRP J. Manuf. Sci. Technol. 2021, 32, 1–15. [Google Scholar] [CrossRef]
- Esposito, M.; Gherlone, M. Composite wing box deformed-shape reconstruction based on measured strains: Optimization and comparison of existing approaches. Aerosp. Sci. Technol. 2020, 99, 105758. [Google Scholar] [CrossRef]
- Mieloszyk, M.; Majewska, K.; Ostachowicz, W. Application of embedded fibre Bragg grating sensors for structural health monitoring of complex composite structures for marine applications. Mar. Struct. 2021, 76, 102903. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, X.; Meves, J.; Billings, C.; Liu, Y. 3D Printed and Embedded Strain Sensors in Structural Composites for Loading Monitoring and Damage Diagnostics. J. Compos. Sci. 2023, 7, 437. [Google Scholar] [CrossRef]
- Haentzsche, E.; Mueller, R.; Huebner, M.; Ruder, T.; Unger, R.; Nocke, A.; Cherif, C. Manufacturing technology of integrated textile-based sensor networks for in situ monitoring applications of composite wind turbine blades. Smart Mater. Struct. 2016, 25, 105012. [Google Scholar] [CrossRef]
- Swartz, R.A.; Lynch, J.P.; Zerbst, S.; Sweetman, B.; Rolfes, R. Structural monitoring of wind turbines using wireless sensor networks. Smart Struct. Syst. 2010, 6, 183–196. [Google Scholar] [CrossRef]
- Fu, Z.; Luo, Y.; Gu, C.; Li, F.; Yue, Y. Reliability Analysis of Condition Monitoring Network of Wind Turbine Blade Based on Wireless Sensor Networks. IEEE Trans. Sustain. Energy 2019, 10, 549–557. [Google Scholar] [CrossRef]
- Bashian, A.; Assili, M.; Anvari-Moghaddam, A.; Marouzi, O.R. Co-optimal PMU and communication system placement using hybrid wireless sensors. Sustain. Energy Grids Netw. 2019, 19, 100238. [Google Scholar] [CrossRef]
- Meyer zu Westerhausen, S.; Kyriazis, A.; Hühne, C.; Lachmayer, R. Design methodology for optimal sensor placement for cure monitoring and load detection of sensor-integrated, gentelligent composite parts. Proc. Des. Soc. 2024, 4, 673–682. [Google Scholar] [CrossRef]
- Ko, W.L.; Richards, W.L.; van Tran, T. Displacement Theories for In-Flight Displacement Theories for In-Flight Deformed Shape Predictions of Aerospace Structures; NASA/TP-2007-214612; Armstrong Flight Research Center: Edwards, CA, USA, 2007. [Google Scholar]
- Meyer zu Westerhausen, S.; Kasal, V.; Wurst, J.; Lachmayer, R. Enhancement of accuracy in deformation and load estimation of gentelligent, sensor-integrating components for technical inheritance. Procedia CIRP 2025, 136, 111–116. [Google Scholar] [CrossRef]
- Foss, G.; Haugse, E. Using Modal Test Results to Develop Strain to Displacement Transformations. In Proceedings of the 13th International Modal Analysis Conference, Nashville, TN, USA, 13–16 February 1995. [Google Scholar]
- Bruno, R.; Toomarian, N.; Salama, M. Shape estimation from incomplete measurements: A neural-net approach. Smart Mater. Struct. 1994, 3, 92. [Google Scholar] [CrossRef]
- Altun, O.; Zhang, D.; Siqueira, R.; Wolniak, P.; Mozgova, I.; Lachmayer, R. Identification of dynamic loads on structural compo-nent with artificial neural networks. Procedia Manuf. 2020, 52, 181–186. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Go, M.-S.; Noh, H.-K.; Hyuk Lim, J. Real-time full-field inference of displacement and stress from sparse local measurements using physics-informed neural networks. Mech. Syst. Signal Process. 2025, 224, 112009. [Google Scholar] [CrossRef]
- Tessler, A.; Spangler, J.L. A least-squares variational method for full-field reconstruction of elastic deformations in shear-deformable plates and shells. Comput. Methods Appl. Mech. Eng. 2005, 194, 327–339. [Google Scholar] [CrossRef]
- Kefal, A.; Yildiz, M. Modeling of Sensor Placement Strategy for Shape Sensing and Structural Health Monitoring of a Wing-Shaped Sandwich Panel Using Inverse Finite Element Method. Sensors 2017, 17, 2775. [Google Scholar] [CrossRef]
- Pham, J.; Ghattas, O.; Willcox, K.E. Real-time aerodynamic load estimation for hyperson-ics via strain-based inverse maps. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2024. [Google Scholar]
- Valoriani, F.; Esposito, M.; Gherlone, M. Shape Sensing for an UAV Composite Half-Wing: Numerical Comparison between Modal Method and Ko’s Displacement Theory. Aerospace 2022, 9, 509. [Google Scholar] [CrossRef]
- Esposito, M. A novel shape sensing approach based on the coupling of Modal Virtual Sensor Expansion and iFEM: Numerical and experimental assessment on composite stiffened structures. Comput. Struct. 2024, 305, 107520. [Google Scholar] [CrossRef]
- Esposito, M.; Gherlone, M. Material and strain sensing uncertainties quantification for the shape sensing of a composite wing box. Mech. Syst. Signal Process. 2021, 160, 107875. [Google Scholar] [CrossRef]
- Jiang, X.H.; Wang, X.-J. Unified model modal expansion method for full field reconstruction and inversion under mechanical and thermal loading. Aerosp. Sci. Technol. 2024, 151, 109258. [Google Scholar] [CrossRef]
- Li, L.; Zhong, B.S.; Geng, Z.Y.; Sun, W. Structural Shape Reconstruction of FBG Flexible Plate Using Modal Superposition Method. In Proceedings of the ASME International Design Engi-neering Technical Conferences and Computers and Information in Engineering Conference—2017, Cleveland, OH, USA, 6–9 August 2017; The American Society of Mechanical Engineers: New York, NY, USA, 2017. [Google Scholar]
- Bogert, P.; Haugse, E.; Gehrki, R. Structural Shape Identification from Experimental Strains Using a Modal Transformation Technique. In Proceedings of the 44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Norfolk, VA, USA, 7–10 April 2003. [Google Scholar]
- Drachinsky, A.; Freydin, M.; Raveh, D.E. Large Deformation Shape Sensing Using a Nonlinear Strain To Displacement Method. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA & Virtual, 3–7 January 2022; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2022; p. 01032022, ISBN 978-1-62410-631-6. [Google Scholar] [CrossRef]
- Galfione, A.; Meyer zu Westerhausen, S.; Stauß, T.; Wawer, M.L.; Ameduri, S.; Totaro, G.; Esposito, M.; Lachmayer, R.; Gherlone, M. Methodology for consideration of different load cases in the design of a sensor-integrating, gentelligent antenna. Proc. Des. Soc. 2025, 5, 2401–2410. [Google Scholar] [CrossRef]
- Qiu, Y.; Arunachala, P.K.; Linder, C. SenseNet: A Physics-Informed Deep Learning Model for Shape Sensing. J. Eng. Mech. 2023, 149, 04023002. [Google Scholar] [CrossRef]
- Bai, J.; Jeong, H.; Batuwatta-Gamage, C.P.; Xiao, S.; Wang, Q.; Rathnayaka, C.M.; Alzubaidi, L.; Liu, G.-R.; Gu, Y. An Introduction to Programming Physics-Informed Neural Network-Based Computational Solid Mechanics. Int. J. Comput. Methods 2023, 20, 2350013. [Google Scholar] [CrossRef]
- Wang, C.; Xiao, Q.; Zhou, Z.; Yang, Y.; Kosec, G.; Wang, L.; Abdel Wahab, M. A data-assisted physics-informed neural network (DA-PINN) for fretting fatigue lifetime prediction. Int. J. Mech. Sys Dyn. 2024, 4, 361–373. [Google Scholar] [CrossRef]
- Yang, S.; Kim, H.; Hong, Y.; Yee, K.; Maulik, R.; Kang, N. Data-driven physics-informed neural networks: A digital twin perspective. Comput. Methods Appl. Mech. Eng. 2024, 428, 117075. [Google Scholar] [CrossRef]
- Yan, C.A.; Vescovini, R.; Dozio, L. Analysis of Lightweight Structures Using Physics Informed Neural Networks. In Proceedings of the Aerospace Europe Conference 2021, Warsaw, Poland, 23–26 November 2021. [Google Scholar]
- Xu, C.; Cao, B.T.; Yuan, Y.; Meschke, G. Transfer learning based physics-informed neural networks for solving inverse problems in engineering structures under different loading scenarios. Comput. Methods Appl. Mech. Eng. 2023, 405, 115852. [Google Scholar] [CrossRef]
- Meyer zu Westerhausen, S.; Chandra, S.; Herrmann, K.; Wurst, J.; Lachmayer, R. A Sensitivity Study on a Physics-informed Neural Network for Solving Inverse Problems (iPINN) in Deformation Reconstruction for Structural Health Monitoring. Procedia Computer Sci. 2025, accepted. [Google Scholar]
- Kilic, G.; Unluturk, M.S. Testing of wind turbine towers using wireless sensor network and accelerometer. Renew. Energy 2015, 75, 318–325. [Google Scholar] [CrossRef]
- Wan, J.; Yu, Y.; Wu, Y.; Feng, R.; Yu, N. Hierarchical leak detection and localization method in natural gas pipeline monitoring sensor networks. Sensors 2012, 12, 189–214. [Google Scholar] [CrossRef]
- Meyer zu Westerhausen, S.; Raveendran, G.; Lauth, T.-H.; Meyer, O.; Rosemann, D.; Wawer, M.L.; Stauß, T.; Wurst, J.; Lachmayer, R. Reliability Assessment of Wireless Sensor Networks by Strain-Based Region Analysis for Redundancy Estimation in Measurements on the Example of an Aircraft Wing Box. Sensors 2024, 24, 4107. [Google Scholar] [CrossRef]
- Meyer zu Westerhausen, S.; Haußmann, S.; Stauß, T.; Wawer, M.L.; Wurst, J.; Lachmayer, R. Design of a wireless sensor network for load and deformation reconstruction for technical inheritance of gentelligent structural components. Proc. Des. Soc. 2025, 5, 1235–1244. [Google Scholar] [CrossRef]
- Dâmaso, A.; Rosa, N.; Maciel, P. Integrated Evaluation of Reliability and Power Consumption of Wireless Sensor Networks. Sensors 2017, 17, 2547. [Google Scholar] [CrossRef]
- Pandey, O.J.; Gautam, V.; Jha, S.; Shukla, M.K.; Hegde, R.M. Time Synchronized Node Localization Using Optimal H-Node Allocation in a Small World WSN. IEEE Commun. Lett. 2020, 24, 2579–2583. [Google Scholar] [CrossRef]
- Patel, N.R.; Kumar, S. Wireless Sensor Networks’ Challenges and Future Prospects. In Proceedings of the 2018 International Conference on System Modeling & Advancement in Research Trends (SMART), Moradabad, India, 23–24 November 2018; Dwivedi, R.K., Ed.; IEEE: Piscataway, NJ, USA, 2018; pp. 60–65, ISBN 978-1-5386-6369-1. [Google Scholar] [CrossRef]
- Giancol, G.; Martello, C.; Cuomo, F.; Di Benedetto, M.-G. Radio resource management in infrastructure-based and ad hoc UWB networks. Wirel. Commun. 2005, 5, 581–597. [Google Scholar] [CrossRef]
- Bhuiyan, M.Z.A.; Wang, G.; Wu, J.; Cao, J.; Liu, X.; Wang, T. Dependable Structural Health Monitoring Using Wireless Sensor Networks. IEEE Trans. Dependable Secur. Comput. 2017, 14, 363–376. [Google Scholar] [CrossRef]
- Liu, S.-P.; Shi, B.; Gu, K.; Zhang, C.-C.; He, J.-H.; Wu, J.-H.; Wei, G.-Q. Fiber-optic wireless sensor network using ultra-weak fiber Bragg gratings for vertical subsurface deformation monitoring. Nat. Hazards 2021, 109, 2557–2573. [Google Scholar] [CrossRef]
- Taher, S.A.; Li, J.; Jeong, J.-H.; Laflamme, S.; Jo, H.; Bennett, C.; Collins, W.N.; Downey, A.R.J. Structural Health Monitoring of Fatigue Cracks for Steel Bridges with Wireless Large-Area Strain Sensors. Sensors 2022, 22, 5076. [Google Scholar] [CrossRef]
- Herrasti, Z.; Val, I.; Gabilondo, I.; Berganzo, J.; Arriola, A.; Martínez, F. Wireless sensor nodes for generic signal conditioning: Application to Structural Health Monitoring of wind turbines. Sens. Actuators A Phys. 2016, 247, 604–613. [Google Scholar] [CrossRef]
- Tantele, E.A.; Votsis, R.A.; Onoufriou, T.; Milis, M.; Kareklas, G. Remote monitoring as a tool in condition assessment of a highway bridge. In Fourth International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2016), Paphos, Cyprus, 4 April 2016; Themistocleous, K., Hadjimitsis, D.G., Michaelides, S., Papadavid, G., Eds.; SPIE: Bellingham, WA, USA, 2016; p. 968824. [Google Scholar] [CrossRef]
- Wu, J.; Yuan, S.; Shang, Y.; Wang, Z. Strain distribution monitoring wireless sensor network design and its evaluation research on aircraft wingbox. Int. J. Appl. Electromagn. Mech. 2009, 31, 17–28. [Google Scholar] [CrossRef]
- Wu, J.; Yuan, S.; Zhou, G.; Ji, S.; Wang, Z.; Wang, Y. Design and evaluation of a wireless sensor network based aircraft strength testing system. Sensors 2009, 9, 4195–4210. [Google Scholar] [CrossRef]
- Saleem, M.M.; Jo, H. Multi-objective sensor placement optimization for structural response estimation under spatially varying dynamic loading of bridges. Adv. Struct. Eng. 2021, 24, 2255–2266. [Google Scholar] [CrossRef]
- Ghasemzadeh, M.; Kefal, A. Sensor Placement Optimization for Shape Sensing of Plates and Shells Using Genetic Algorithm and Inverse Finite Element Method. Sensors 2022, 22, 9252. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Computat. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Kuehn, A.A.; Hamburger, M.J. A Heuristic Program for Locating Warehouses. In Mathematical Models in Marketing: A Collection of Abstracts; Funke, U.H., Ed.; Springer: Berlin, Germany, 1976; pp. 406–407. ISBN 978-3-540-07869-2. [Google Scholar] [CrossRef]
- Blank, J. Pymoo: NSGA-II: Non-Dominated Sorting Genetic Algorithm: Version: 0.6.1.5. Available online: https://pymoo.org/algorithms/moo/nsga2.html (accessed on 15 July 2025).
- Li, H. Solving the TSP Problem Based on Improved Genetic Algorithm. Appl. Comput. Eng. 2025, 133, 74–80. [Google Scholar] [CrossRef]
- Meyer zu Westerhausen, S.; Chandra, S. SoerenMeyerzuWesterhausen/iPINN-for-shape-sensing: iPINN for Shape Sensing. Zenodo 2025. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method. for Stochastic Optimization. arXiv 2014. [Google Scholar] [CrossRef]
- Tay, W.-B.; Damodaran, M.; Teh, Z.-D.; Halder, R. Investigation of Applying Physics Informed Neural Networks (PINN) and Variants on 2D Aerodynamics Problems. In Proceedings of the ASME 2020 Fluids Engineering Division Summer Meeting collocated with the ASME 2020 Heat Transfer Summer Conference and the ASME 2020 18th International Conference on Nanochannels, Microchannels, and Minichannels, Virtual, Online, 13–15 July 2020; The American Society of Mechanical Engineers: New York, NY, USA, 2020. ISBN 978-0-7918-8373-0. [Google Scholar] [CrossRef]



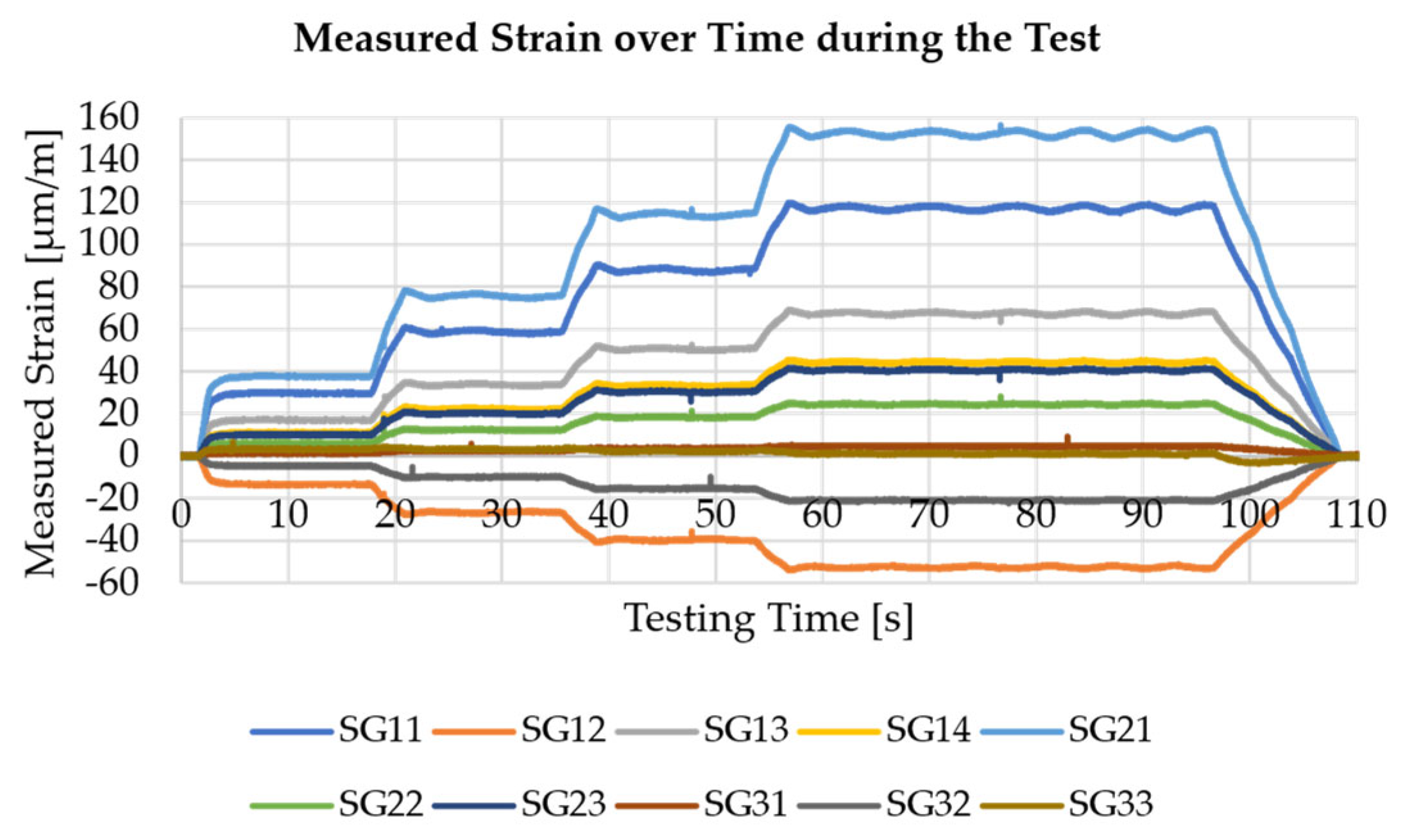
| Sensor ID | Measured Strain [µm/m] | Simulated Strain [µm/m] |
|---|---|---|
| SG11 | 117.19895 | 180.4 |
| SG12 | −52.65185 | −80.5 |
| SG13 | 67.4118 | 102.5 |
| SG14 | 44.29854 | 68.3 |
| SG21 | 152.41414 | 227.9 |
| SG22 | 24.37343 | 37.4 |
| SG23 | 40.59444 | 58.2 |
| SG31 | 4.61618 | 6.3 |
| SG32 | −21.03724 | −55.7 |
| SG33 | 1.03086 | −7.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meyer zu Westerhausen, S.; Hichri, I.; Herrmann, K.; Lachmayer, R. Optimisation of Sensor and Sensor Node Positions for Shape Sensing with a Wireless Sensor Network—A Case Study Using the Modal Method and a Physics-Informed Neural Network. Sensors 2025, 25, 5573. https://doi.org/10.3390/s25175573
Meyer zu Westerhausen S, Hichri I, Herrmann K, Lachmayer R. Optimisation of Sensor and Sensor Node Positions for Shape Sensing with a Wireless Sensor Network—A Case Study Using the Modal Method and a Physics-Informed Neural Network. Sensors. 2025; 25(17):5573. https://doi.org/10.3390/s25175573
Chicago/Turabian StyleMeyer zu Westerhausen, Sören, Imed Hichri, Kevin Herrmann, and Roland Lachmayer. 2025. "Optimisation of Sensor and Sensor Node Positions for Shape Sensing with a Wireless Sensor Network—A Case Study Using the Modal Method and a Physics-Informed Neural Network" Sensors 25, no. 17: 5573. https://doi.org/10.3390/s25175573
APA StyleMeyer zu Westerhausen, S., Hichri, I., Herrmann, K., & Lachmayer, R. (2025). Optimisation of Sensor and Sensor Node Positions for Shape Sensing with a Wireless Sensor Network—A Case Study Using the Modal Method and a Physics-Informed Neural Network. Sensors, 25(17), 5573. https://doi.org/10.3390/s25175573








