Indoor Pedestrian Location via Factor Graph Optimization Based on Sliding Windows
Abstract
1. Introduction
- (1)
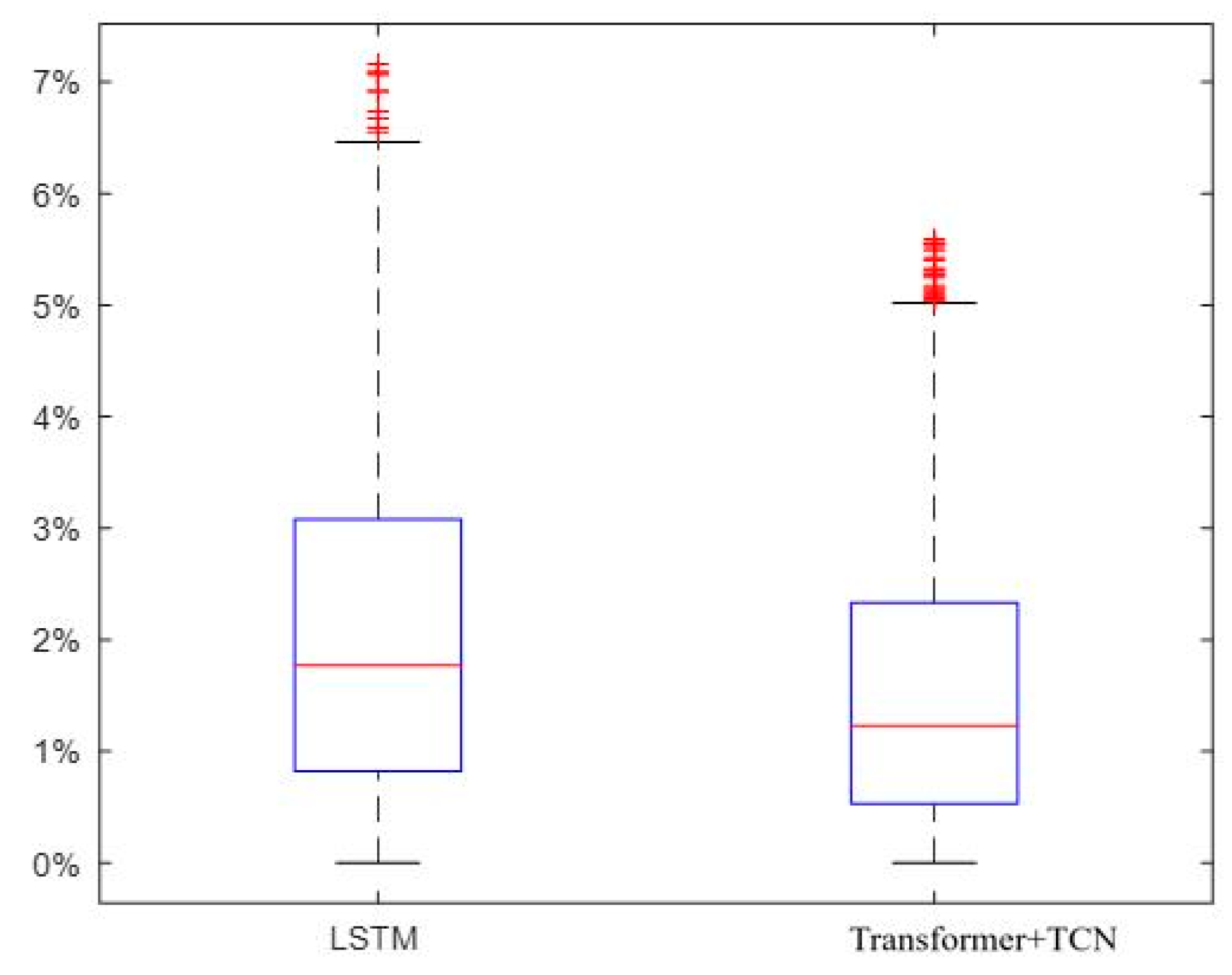
- We propose a lightweight stride length estimation algorithm based on Transformer+TCN and examine the impact of different pedestrian activity differences on stride length estimation accuracy. We train the Transformer+TCN model using IMU data and corresponding movement distance data to learn stride length characteristics from the input data time series. Experimental results show that the step length estimation model error of Transformer+TCN is 1.61%, and the step length estimation accuracy is improved by 24.41%, which can adapt to the different stride length characteristics of different pedestrians and improve the accuracy and robustness of stride length estimation.
- (2)
- We propose a sliding window-based factor graph optimization model (SW-FGO) that integrates information from IMU, PDR, and magnetometer. Experimental results show that compared with the traditional FGO model, the SW-FGO model improves positioning performance by 29.68%.
- (3)
- Since low-cost IMUs have greater zero bias and noise, we are inspired by the IMU/ODO pre-integration algorithm in vehicle-mounted navigation and positioning. In the optimization of smart handheld terminals, we obtain the mileage increment information of the PDR to constrain the IMU relative mileage. Experimental results show that the IMU/PDR pre-integration improves the positioning accuracy by 21.6% compared with the IMU pre-integration.
- (4)
- We collected data from 10 users in four different terminal postures (flat, talking, hand-free, and pocket). Experimental results validated the effectiveness of the proposed Transformer+TCN step-size estimation algorithm and sliding-window-based factor graph optimization model. The experimental results show that the proposed method can effectively improve positioning accuracy.
2. Theory and Methodology
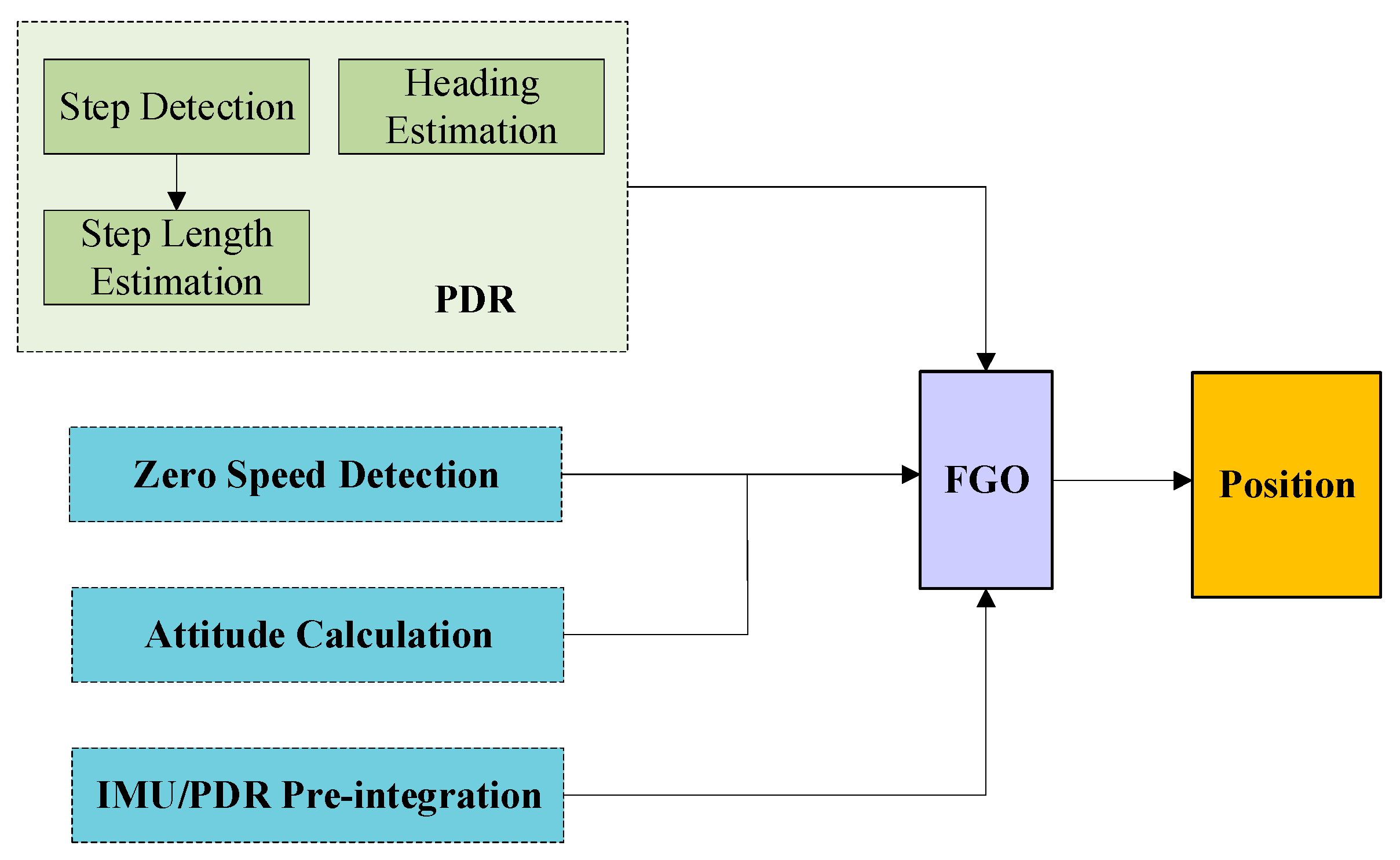
2.1. Overall Architecture
2.2. IMU/PDR Pre-Integration
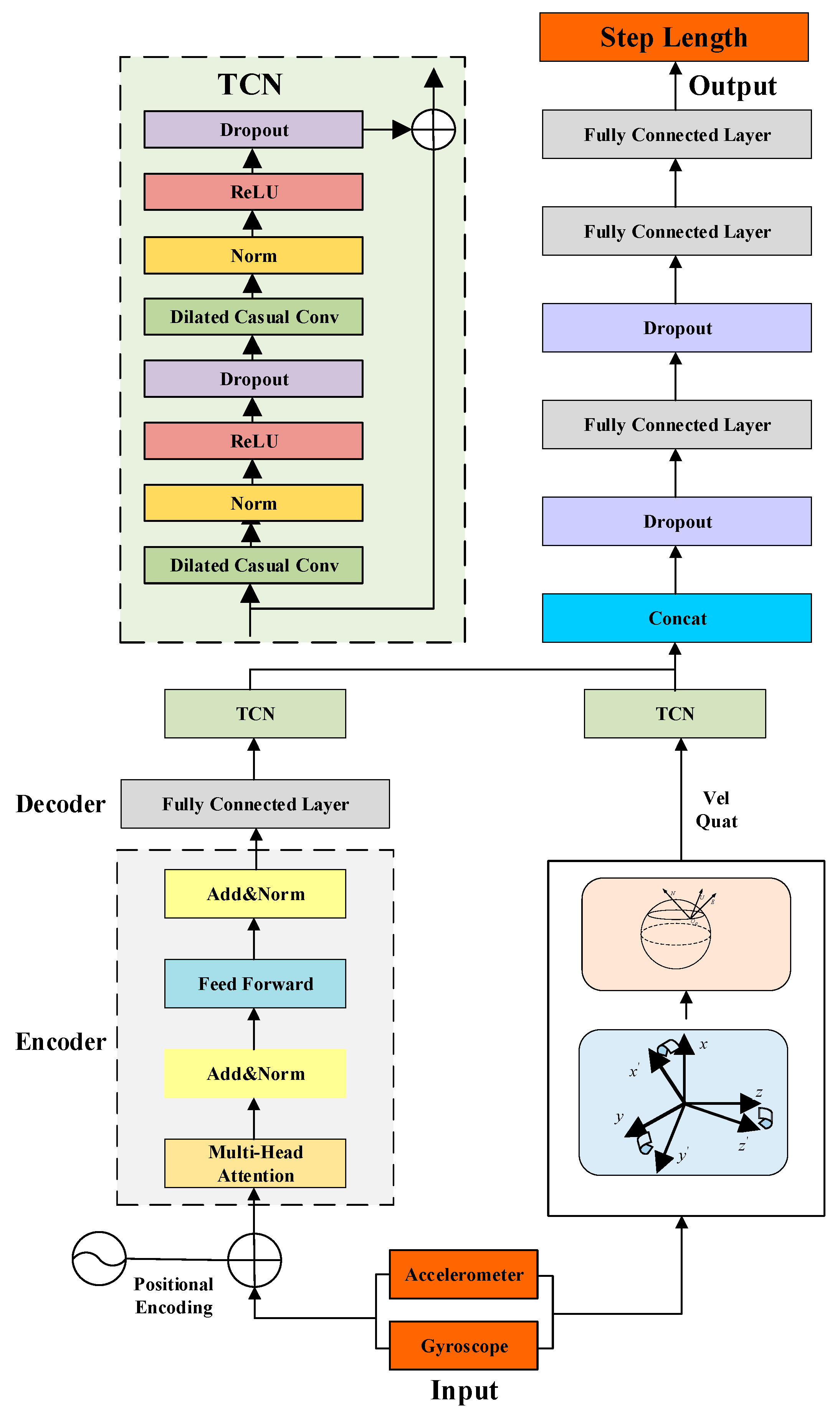
2.3. Step Length Estimation Algorithm Based on Transformer+TCN
2.3.1. Feature Extraction Based on Transformer Architecture
2.3.2. TCN Module
2.4. PDR/IMU/Magnetometer Fusion
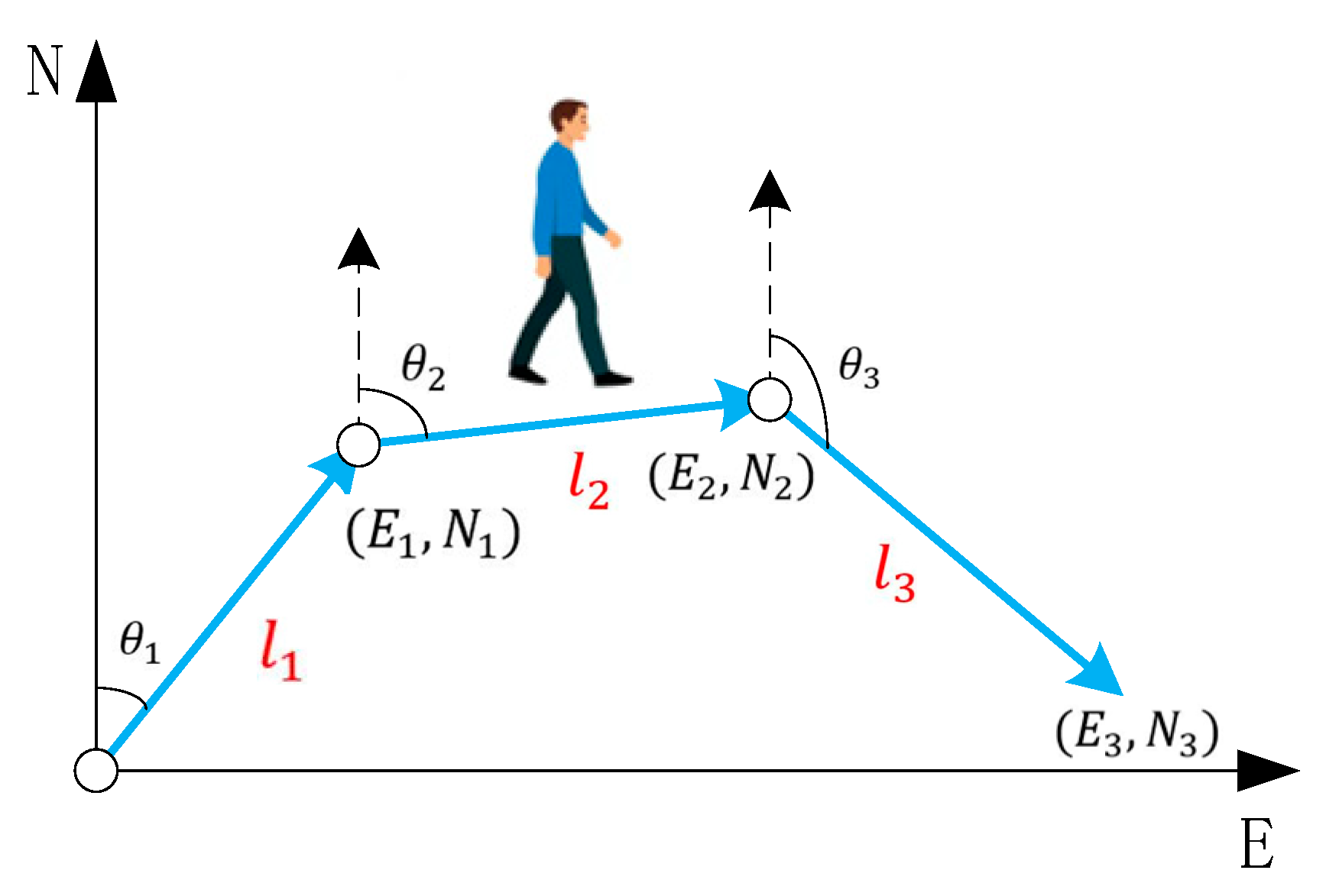
2.4.1. PDR Factor
2.4.2. Attitude Factor
2.4.3. Zero Speed Factor Model
2.4.4. Sliding Windows Marginalization
3. Implementation Details
3.1. Dataset
3.2. Implementation and Training Details
4. Experiments
4.1. Experimental Study on Step Estimation Algorithm Based on Transformer+TCN
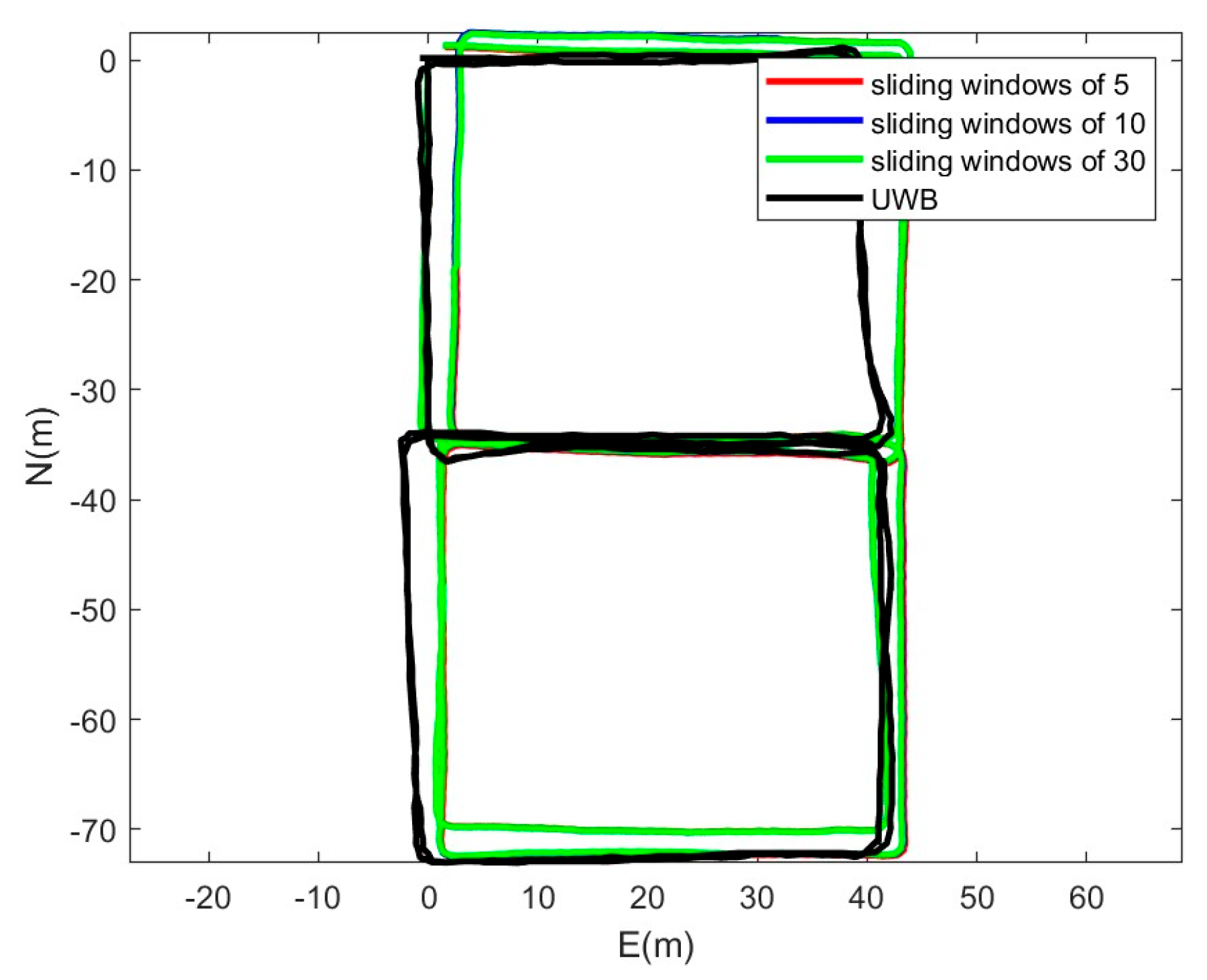
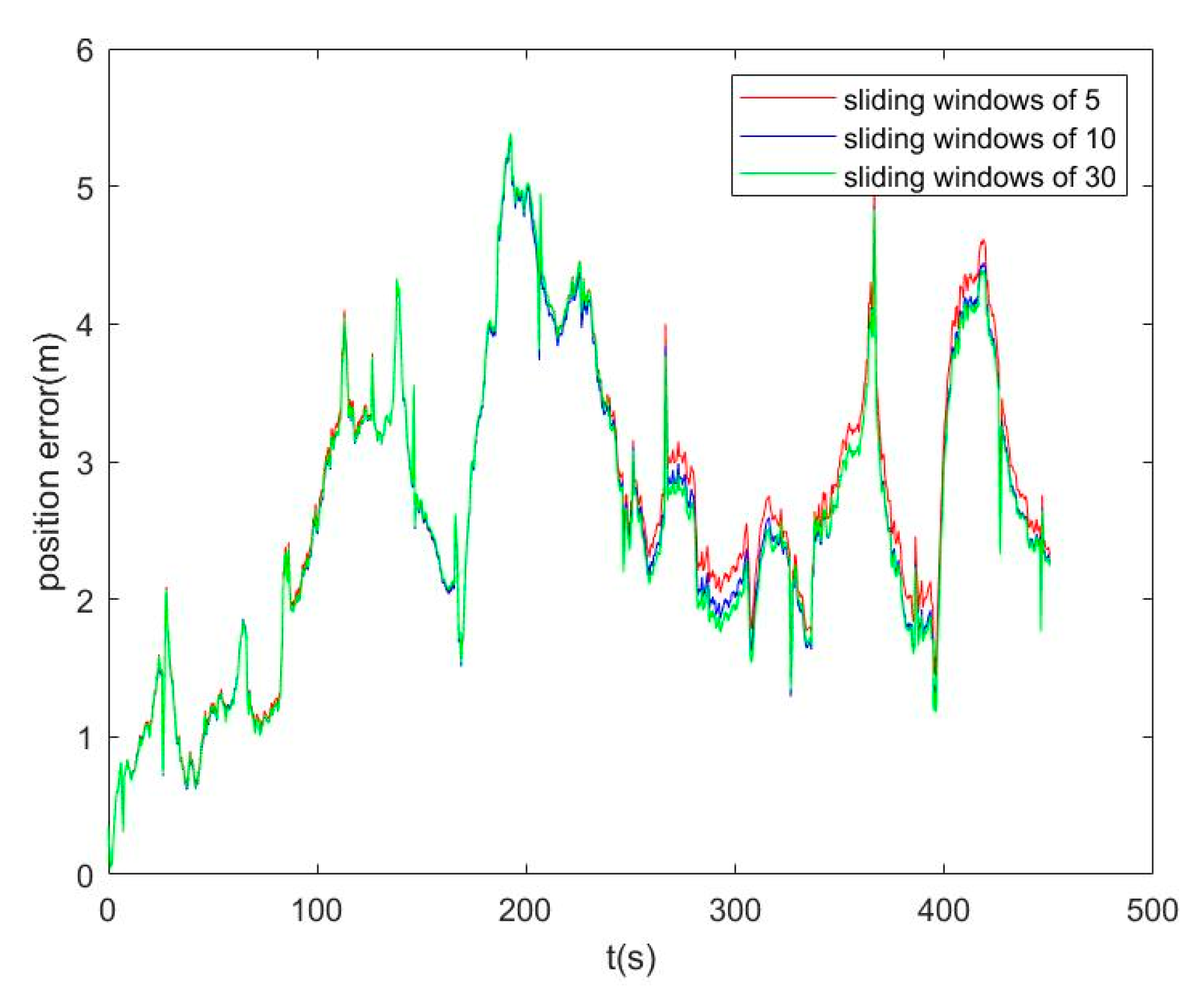
4.2. Sliding Windows Test
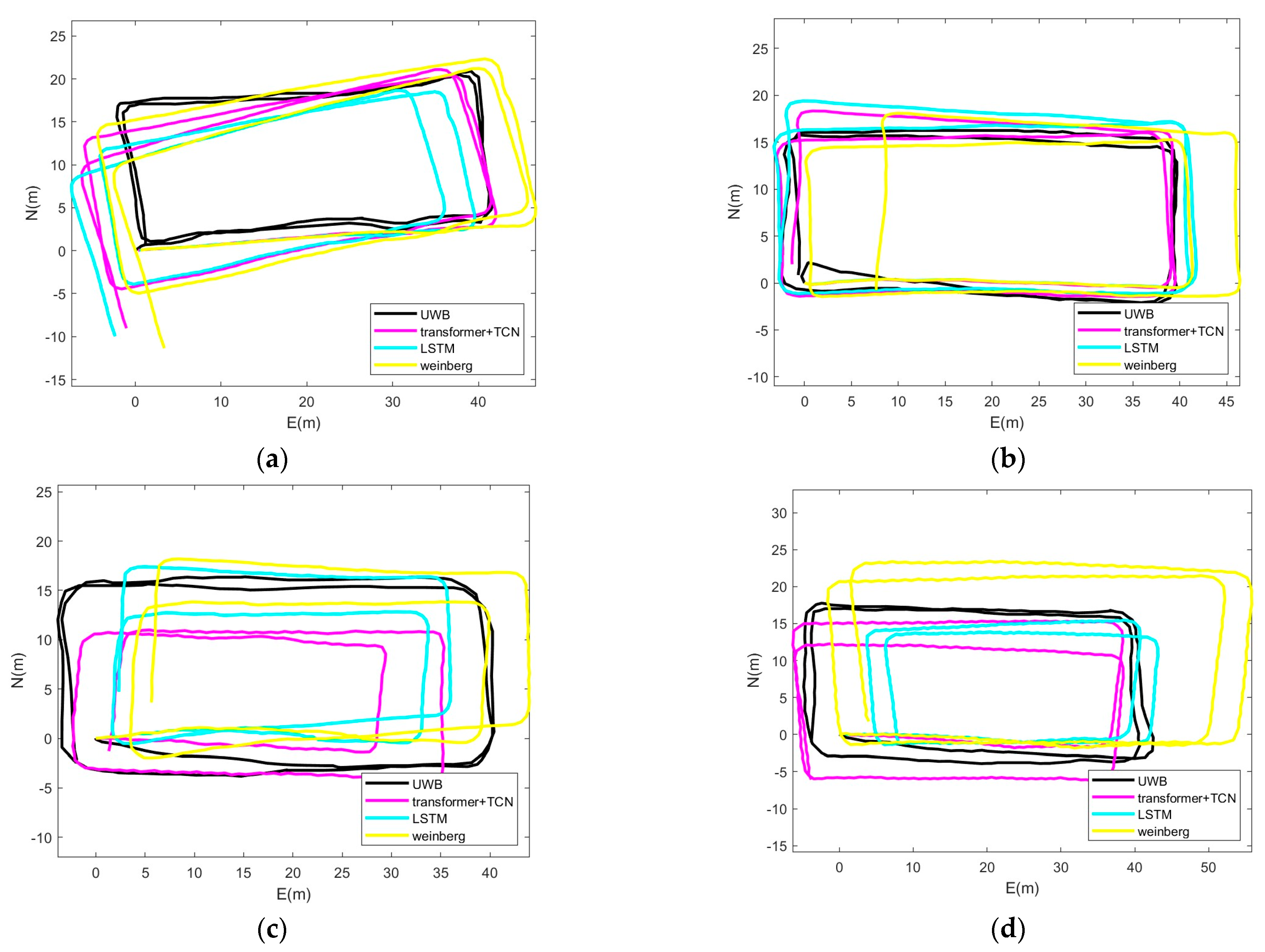
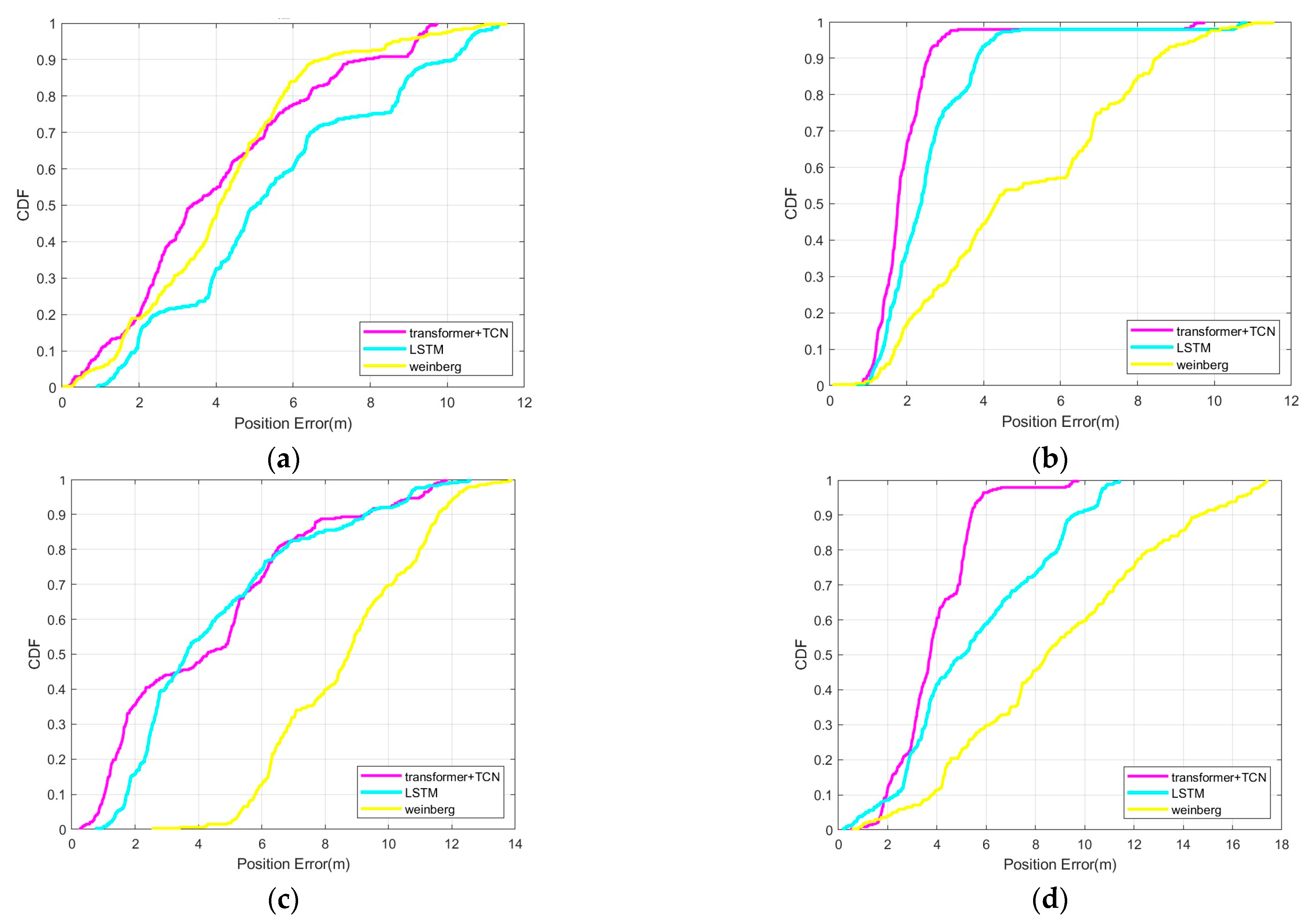
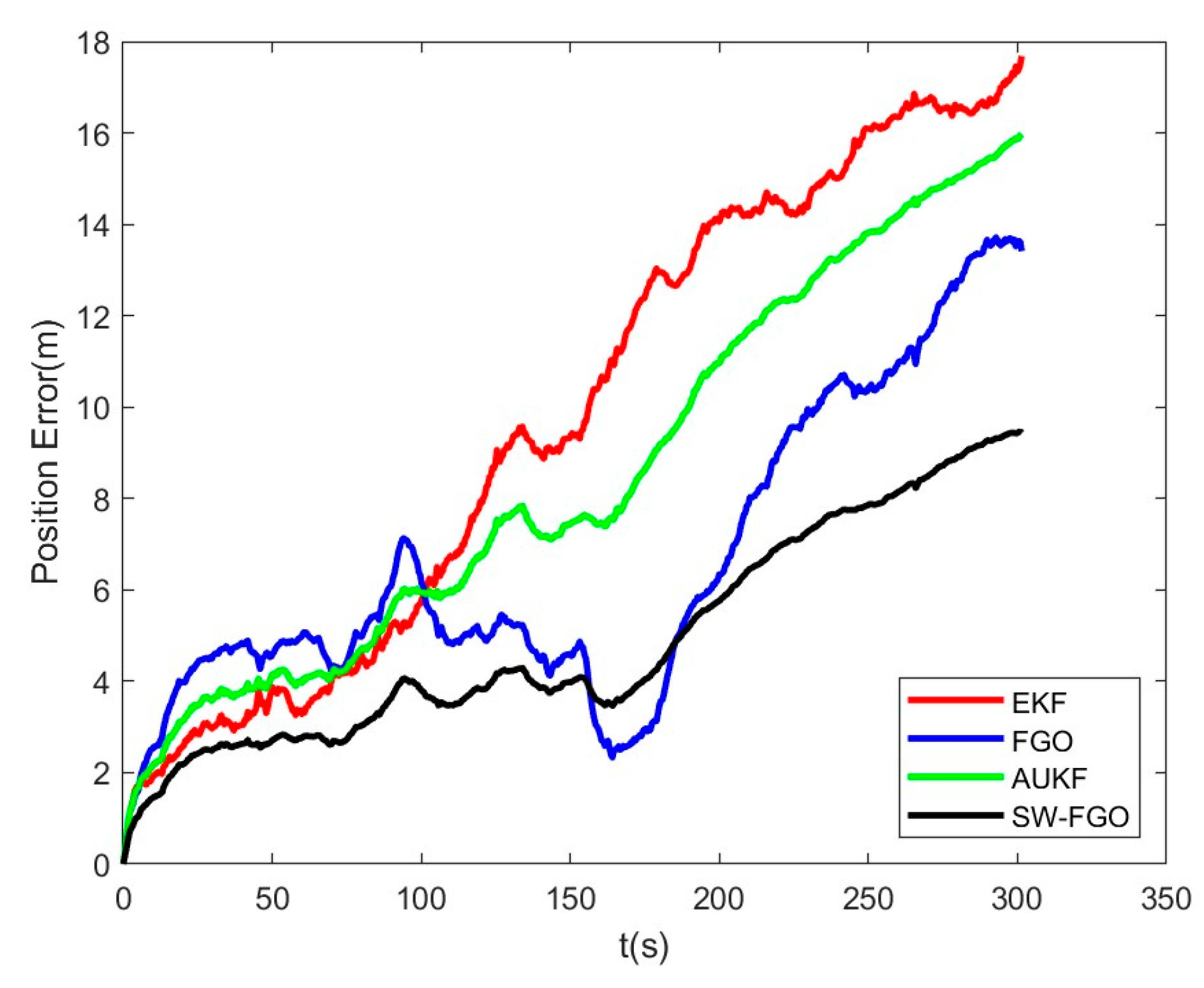
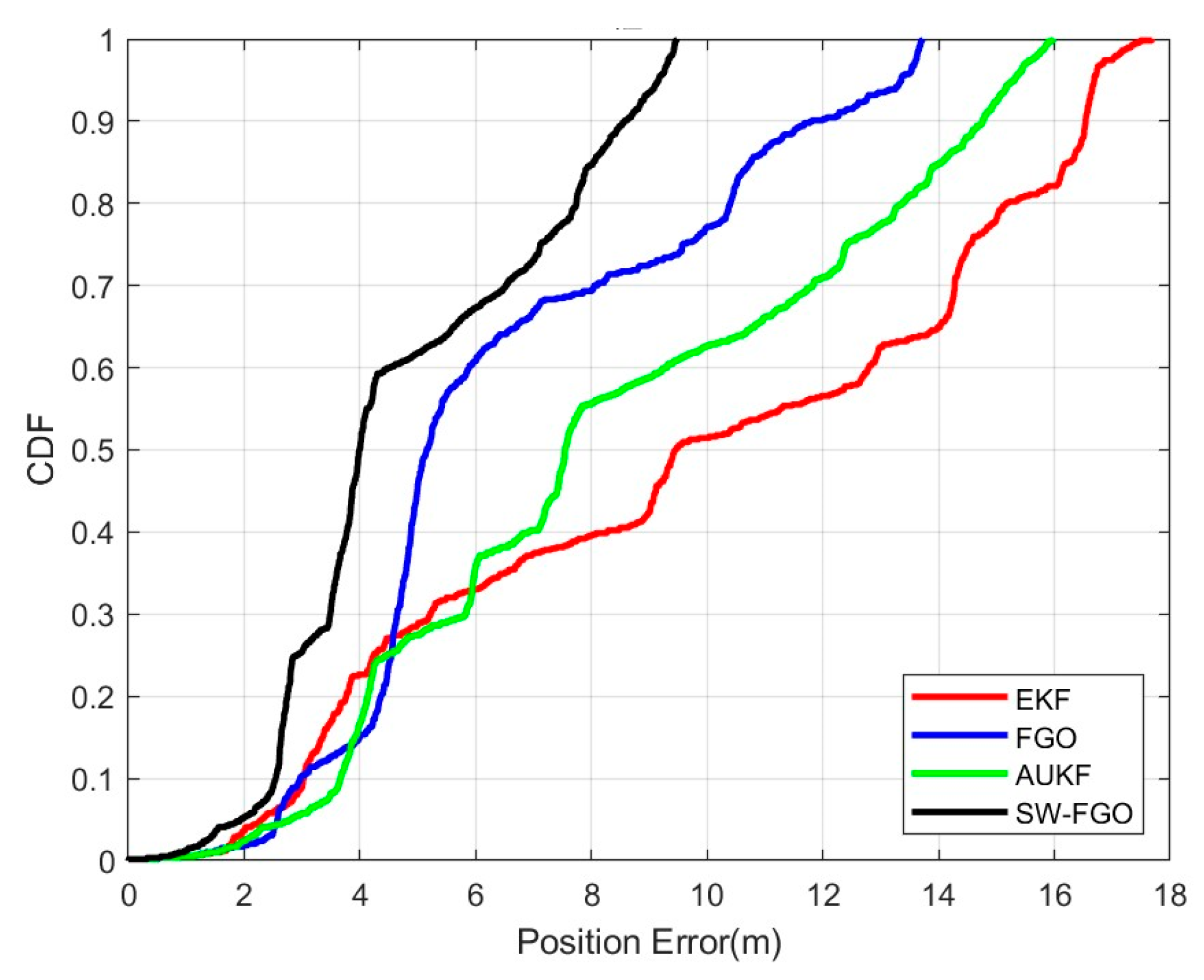
4.3. Positioning Accuracy Test on Fusion Algorithm
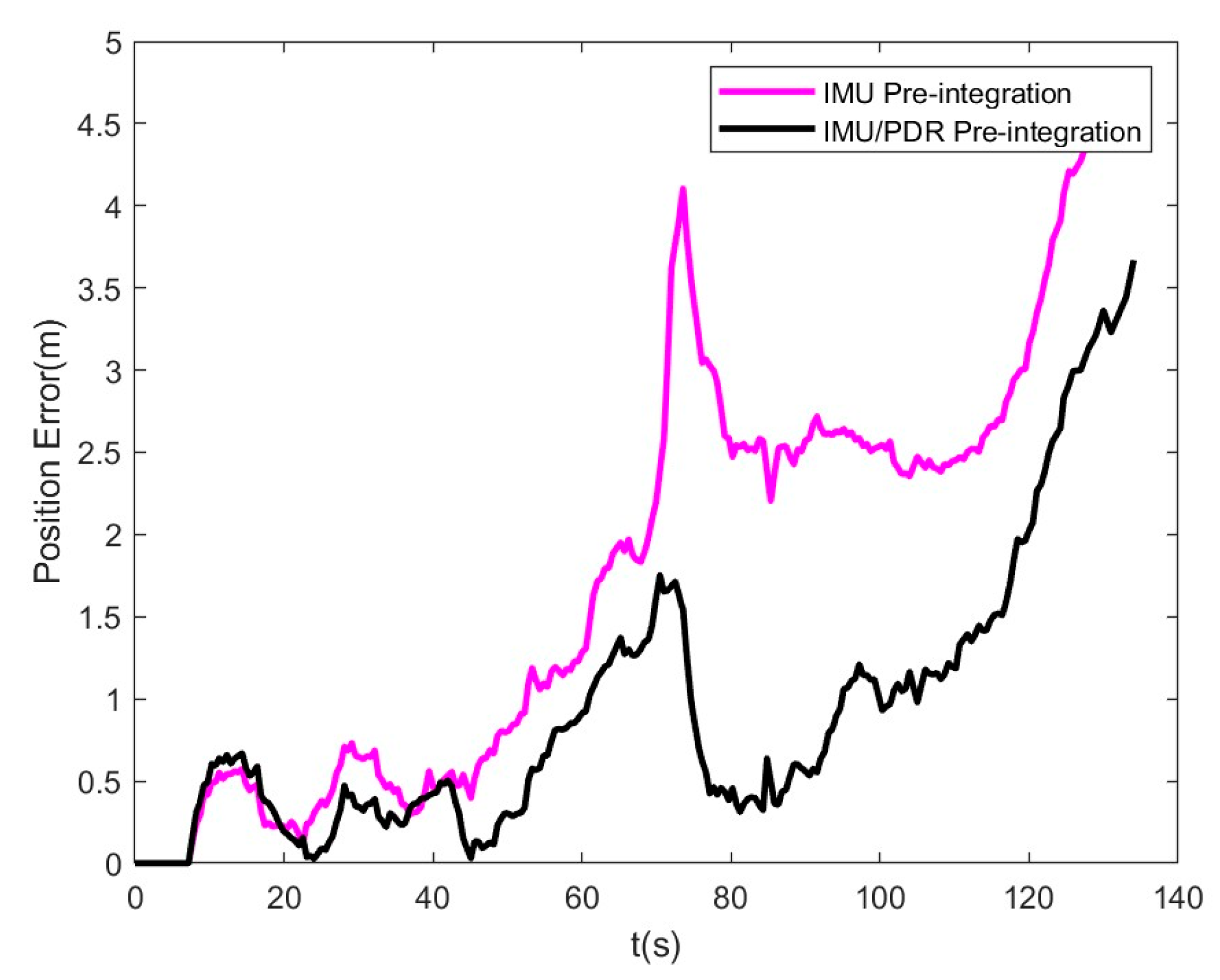
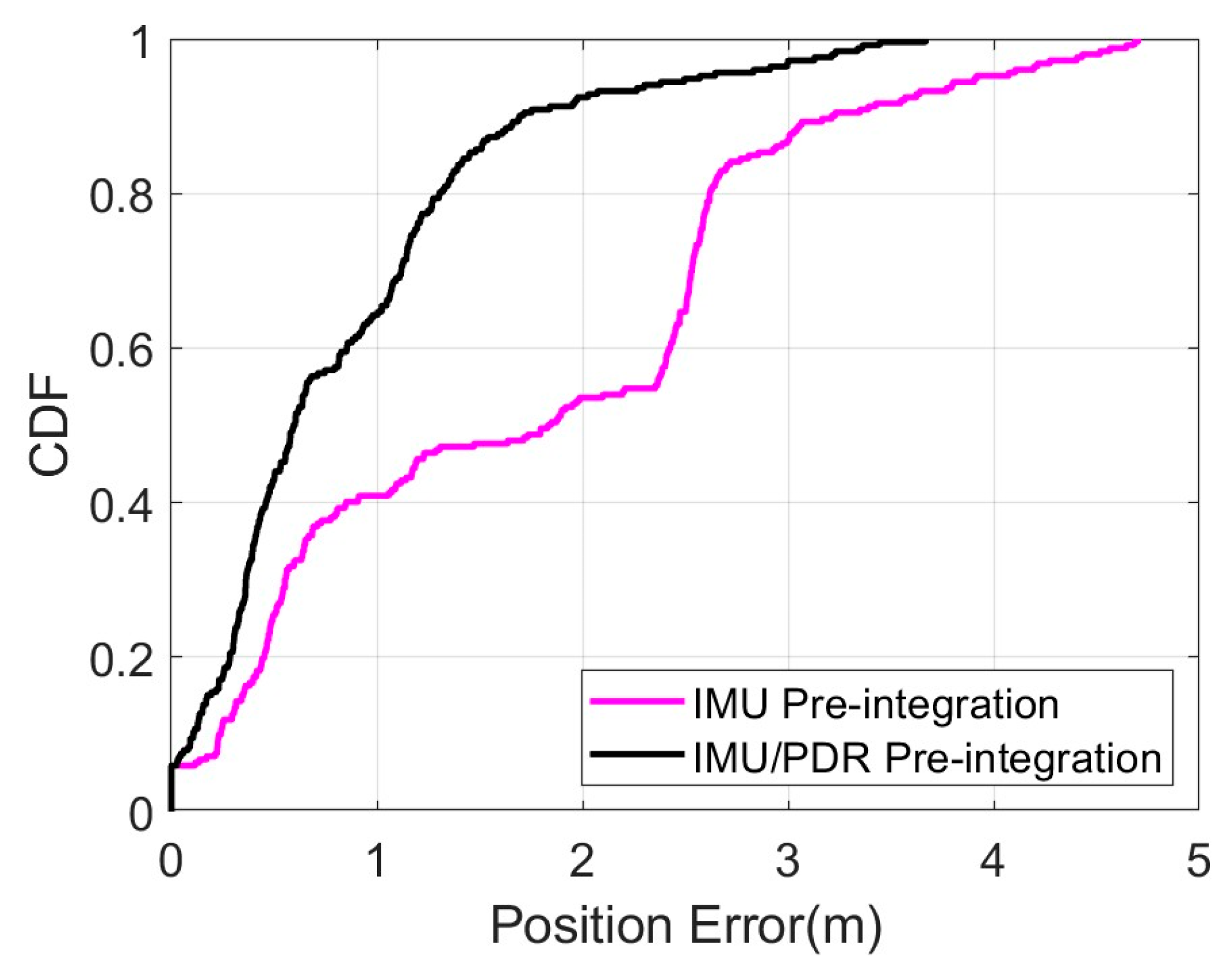
4.4. IMU/PDR Pre-Integration Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, J.; Miao, Y.; Zheng, X. Design and Implementation of Indoor Positioning Performance Test System for IoT Intelligent Com munication Terminal. J. Phys. Conf. Ser. 2021, 1732, 012030. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, R.; Pei, L.; Kröger, T.; Kuusniemi, H.; Liu, J.; Chen, W. Knowledge-based error detection and correction method of a multi-sensor multi-network positioning platform for pedestrian indoor navigation. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Indian Wells, CA, USA, 4–6 May 2010; pp. 873–879. [Google Scholar]
- Fontana, R.J. Recent system applications of short-pulse ultra-wideband (UWB) technology. IEEE Trans. Microw. Theory Tech. 2004, 52, 2087–2104. [Google Scholar] [CrossRef]
- Chen, R.; Li, Z.; Ye, F.; Guo, G.; Xu, S.; Qian, L.; Liu, Z.; Huang, L. Precise indoor positioning based on acoustic ranging in smartphone. IEEE Trans. Instrum. Meas. 2021, 70, 9509512. [Google Scholar] [CrossRef]
- You, Y.; Wu, C. Hybrid indoor positioning system for pedestrians with swinging arms based on smartphone IMU and RSSI of BLE. IEEE Trans. Instrum. Meas. 2021, 70, 9510615. [Google Scholar] [CrossRef]
- Xia, H.; Zuo, J.; Liu, S.; Qiao, Y. Indoor localization on smartphones using built-in sensors and map constraints. IEEE Trans. Instrum. Meas. 2019, 68, 1189–1198. [Google Scholar] [CrossRef]
- Oh, J.; Han, J. Pedestrian travel distance estimation using optical flow and smartphone sensors. IEEE Trans. Instrum. Meas. 2021, 70, 5005908. [Google Scholar] [CrossRef]
- Chen, R.; Chen, W.; Chen, X.; Zhang, X.; Chen, Y. Sensing strides using EMG signal for pedestrian navigation. GPS Solut. 2021, 15, 161–170. [Google Scholar] [CrossRef]
- Soni, R.; Trapasiya, S. A survey of step length estimation models based on inertial sensors for indoor navigation systems. Int. J. Commun. Syst. 2022, 35, e5053. [Google Scholar] [CrossRef]
- Diez, L.E.; Bahillo, A.; Otegui, J.; Otim, T. Step length estimation methods based on inertial sensors: A review. IEEE Sens. J. 2018, 18, 6908–6926. [Google Scholar] [CrossRef]
- Vezocnik, M.; Juric, M.B. Average step length estimation models’ evaluation using inertial sensors: A review. IEEE Sens. J. 2019, 19, 396–403. [Google Scholar] [CrossRef]
- Kone, Y.; Zhu, N.; Renaudin, V. Zero velocity detection without motion pre-classification: Uniform AI model for all pedestrian motions (UMAM). IEEE Sens. J. 2022, 22, 5113–5121. [Google Scholar] [CrossRef]
- Wang, H.; Xue, C.; Wang, Z.; Zhang, L.; Luo, X.; Wang, X. Smartphone-based pedestrian NLOS positioning based on acoustics and IMU parameter estimation. IEEE Sens. J. 2022, 22, 23095–23108. [Google Scholar] [CrossRef]
- Hannink, J.; Kautz, T.; Pasluosta, C.F.; Barth, J.; Schulein, S.; Gassmann, K.-G.; Klucken, J.; Eskofier, B.M. Mobile stride length estimation with deep convolutional neural networks. IEE J. Biomed. Health Inform. 2018, 22, 354–362. [Google Scholar] [CrossRef]
- Wang, Q.; Ye, L.; Luo, H.; Men, A.; Zhao, F.; Huang, Y. Pedestrian stride length estimation based on LSTM and denoising autoencoders. Sensors 2019, 19, 840. [Google Scholar] [CrossRef]
- Sui, J.D.; Chang, T.S. IMU based deep stride length estimation with self-supervised learning. IEEE Sens. J. 2021, 21, 7380–7387. [Google Scholar] [CrossRef]
- Sun, Y.; Mao, S.; Su, Y.; Yang, M. Research on improved PDR algorithm for underground personnel positioning. Ind. Mine Autom. 2021, 47, 43–48. [Google Scholar]
- Wang, Q.; Luo, H.; Ye, L.; Men, A.; Zhao, F.; Huang, Y.; Ou, C. Personalized stride-length estimation based on active online learning. IEEE Internet Things J. 2020, 7, 4885–4897. [Google Scholar] [CrossRef]
- Jin, Y.; Motani, M.; Soh, W.-S.; Zhang, J. Sparse Track: Enhancing indoor pedestrian tracking with sparse infrastructure support. In Proceedings of the 2010 Proceedings IEEE INFOCOM, San Diego, CA, USA, 14–19 March 2010; pp. 1–9. [Google Scholar]
- Coulin, J.; Guillemard, R.; Gay-Bellile, V.; Joly, C.; de La Fortelle, A. Tightly-Coupled Magneto-Visual-Inertial Fusion for Long Term Localization in Indoor Environment. IEEE Robot. Autom. Lett. 2022, 7, 952–959. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Wang, X.; Chang, H.; Tan, Y.; Shen, Z. Factor graph-based PPP-RTK for accurate and robust positioning in urban environments. J. Geod. 2024, 98, 21. [Google Scholar] [CrossRef]
- Hu, G.; Xu, L.; Gao, B.; Chang, L.; Zhong, Y. Robust unscented Kalman filter-based decentralized multisensor information fusion for INS/GNSS/CNS integration in hypersonic vehicle navigation. IEEE Trans. Instrum. Meas. 2023, 72, 8504011. [Google Scholar] [CrossRef]
- Gao, B.; Hu, G.; Zhong, Y.; Zhu, X. Distributed State Fusion Using Sparse-Grid Quadrature Filter with Application to INS/CNS/GNSS Integration. IEEE Sens. J. 2021, 22, 3430–3441. [Google Scholar] [CrossRef]
- Gao, B.; Hu, G.; Gao, S.; Zhong, Y.; Gu, C. Multi-sensor Optimal Data Fusion for INS/GNSS/CNS Integration Based on Unscented Kalman Filter. Int. J. Control Autom. Syst. 2018, 16, 129–140. [Google Scholar] [CrossRef]
- Hu, G.; Gao, S.; Zhong, Y.; Gao, B.; Subic, A. Matrix weighted multisensor data fusion for INS/GNSS/CNS integration. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 230, 1011–1026. [Google Scholar] [CrossRef]
- Gao, S.; Zhong, Y.; Zhang, X.; Shirinzadeh, B. Multi-sensor optimal data fusion for INS/GPS/SAR integrated navigation system. Aerosp. Sci. Technol. 2009, 13, 232–237. [Google Scholar] [CrossRef]
- Lin, Z.; Zhou, H.; Gao, Y. An in-motion alignment method of AUV SINS/DVL navigation system based on FGO. Measurement 2023, 222, 113578. [Google Scholar]
- Wang, Y.; Li, Z.; Gao, J.; Zhao, L. Deep neural network-based WiFi/pedestrian dead reckoning indoor positioning system using adaptive robust factor graph model. IET Radar Sonar Navig. 2020, 14, 36–47. [Google Scholar] [CrossRef]
- Zuo, Z.; Liu, L.; Zhang, L.; Fang, Y. Indoor Positioning Based on Bluetooth Low-Energy Beacons Adopting Graph Optimization. Sensors 2018, 18, 3736. [Google Scholar] [CrossRef]
- Merfels, C.; Stachniss, C. Sensor fusion for self-localization of automated vehicles. PFG–J. Photogramm. Remote Sens. Geoinf. Sci. 2017, 85, 113–126. [Google Scholar]
- Wen, W.; Pfeifer, T.; Bai, X.; Hsu, L. Factor graph optimization for GNSS/INS integration: A comparison with the extended Kalman filter. J. Inst. Navig. 2021, 68, 315–331. [Google Scholar] [CrossRef]
- Qin, T.; Li, P.; Shen, S. Vins-mono: A robust and versatile monocular visual-inertial state estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Mascaro, R.; Teixeira, L.; Hinzmann, T.; Siegwart, R.; Chli, M. Gomsf: Graph-optimization based multi-sensor fusion for robust uav pose estimation. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 1421–1428. [Google Scholar]
- Dong, X.; Hu, G.; Gao, B.; Zhong, Y.; Ruan, W. Windowing-Based Factor Graph Optimization with Anomaly Detection Using Mahalanobis Distance for Underwater INS/DVL/USBL Integration. IEEE Trans. Instrum. Meas. 2024, 73, 8501213. [Google Scholar] [CrossRef]
- Li, Z.; Junna, S.; Liao, W. A robust factor graph framework for navigation on PDR/magnetic field integration. Measurement 2025, 245, 116509. [Google Scholar] [CrossRef]
- Pan, C.; Li, Z.; Zhang, Q.; Soja, B.; Gao, J. Smartphone-based vision/MEMS IMU/GNSS tightly coupled seamless positioning using factor graph optimization. Measurement 2024, 229, 114420. [Google Scholar] [CrossRef]
- Jiang, C.; Chen, Y.; Chen, C.; Jia, J.; Sun, H.; Wang, T.; Hyyppa, J. Smartphone PDR/GNSS Integration via Factor Graph Optimization for Pedestrian Navigation. IEEE Trans. Instrum. Meas. 2022, 71, 8504112. [Google Scholar] [CrossRef]
- Wang, M.; Li, L.; Liu, J.; Chen, R. Neural network aided factor graph optimization for collaborative pedestrian navigation. IEEE Trans. Intell. Transp. Syst. 2023, 25, 303–314. [Google Scholar] [CrossRef]




| Sensor | Parameter | Index |
|---|---|---|
| Accelerometer | Range | ±16 g |
| Bias | 25 mg | |
| Noise | 230 μg/√Hz | |
| Gyroscope | Range | ±2000 |
| Bias | 5 | |
| Noise | 0.015 dps/√Hz | |
| Magnetometer | Range | ±4800 μT |
| Bias | 2000 LSB | |
| UWB | Range | 200 m |
| Positioning error | 30 cm | |
| GNSS | Positioning error | 5 m |
| Number | Gender (M or F) | Height (cm) | Weight (kg) | Age |
|---|---|---|---|---|
| 1 | M | 178 | 85 | 25 |
| 2 | M | 172 | 73 | 26 |
| 3 | M | 173 | 70 | 25 |
| 4 | M | 170 | 71 | 25 |
| 5 | M | 168 | 73 | 25 |
| 6 | F | 160 | 52 | 26 |
| 7 | F | 158 | 49 | 25 |
| 8 | F | 164 | 53 | 25 |
| 9 | F | 162 | 51 | 26 |
| 10 | F | 161 | 50 | 25 |
| Modes | Weinberg | LSTM | Transformer+TCN |
|---|---|---|---|
| flat mode | 4.32% | 4.22% | 3.71% |
| call mode | 4.18% | 1.62% | 1.28% |
| hand-shaking mode | 4.67% | 2.93% | 1.69% |
| pocket mode | 7.81% | 4.84% | 2.80% |
| Sliding Windows | 5 | 10 | 30 |
|---|---|---|---|
| Fusion Time (s) | 0.104 | 0.164 | 0.679 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.; Li, H.; Liu, X.; Chen, S.; Zhu, S. Indoor Pedestrian Location via Factor Graph Optimization Based on Sliding Windows. Sensors 2025, 25, 5545. https://doi.org/10.3390/s25175545
Cheng Y, Li H, Liu X, Chen S, Zhu S. Indoor Pedestrian Location via Factor Graph Optimization Based on Sliding Windows. Sensors. 2025; 25(17):5545. https://doi.org/10.3390/s25175545
Chicago/Turabian StyleCheng, Yu, Haifeng Li, Xixiang Liu, Shuai Chen, and Shouzheng Zhu. 2025. "Indoor Pedestrian Location via Factor Graph Optimization Based on Sliding Windows" Sensors 25, no. 17: 5545. https://doi.org/10.3390/s25175545
APA StyleCheng, Y., Li, H., Liu, X., Chen, S., & Zhu, S. (2025). Indoor Pedestrian Location via Factor Graph Optimization Based on Sliding Windows. Sensors, 25(17), 5545. https://doi.org/10.3390/s25175545





