Performance Analysis of OCDM in ISAC Scenario
Abstract
1. Introduction
- Derivation of the closed-form solution for the BER: A series of closed-form expressions of BER are derived for OCDM and related systems in the linear equalization from the perspective of precoded OFDM system, and the performance gains across these systems are analyzed.
- Derivation of the ambiguity function: The ambiguity functions of the OCDM and OFDM waveforms are derived to preliminarily evaluate their suitability for ISAC applications.
- Analysis of the detection performance of the OCDM waveform: The theoretical expressions for the detection probability of OCDM under a constant false alarm rate (CFAR) criterion using a matched filter (MF) and GLRT detector are formulated, with a corresponding training symbol design proposed.
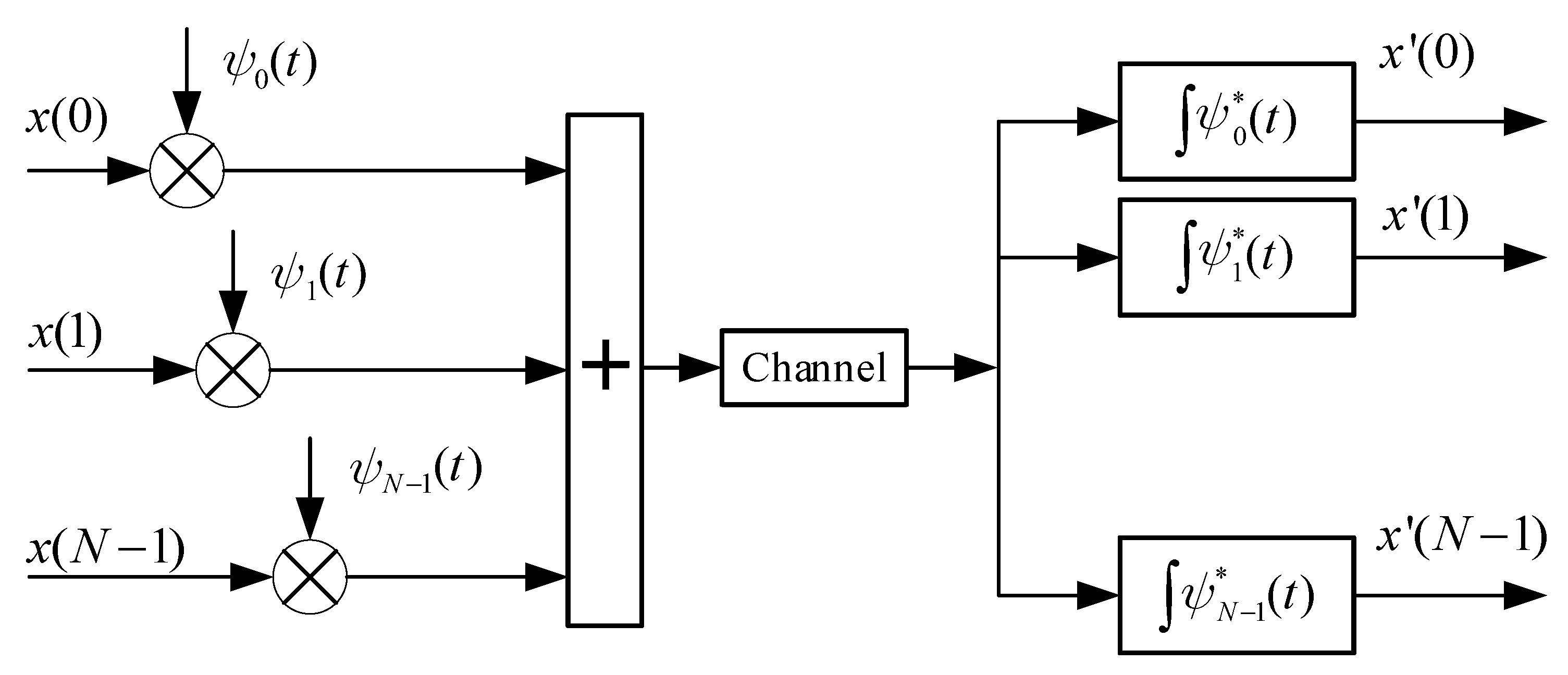
2. OCDM System Model
3. BER Analysis of OCDM with Equalization
3.1. ZF Equalization
3.2. MMSE Equalization
3.3. Multipath Diversity Gain Analysis
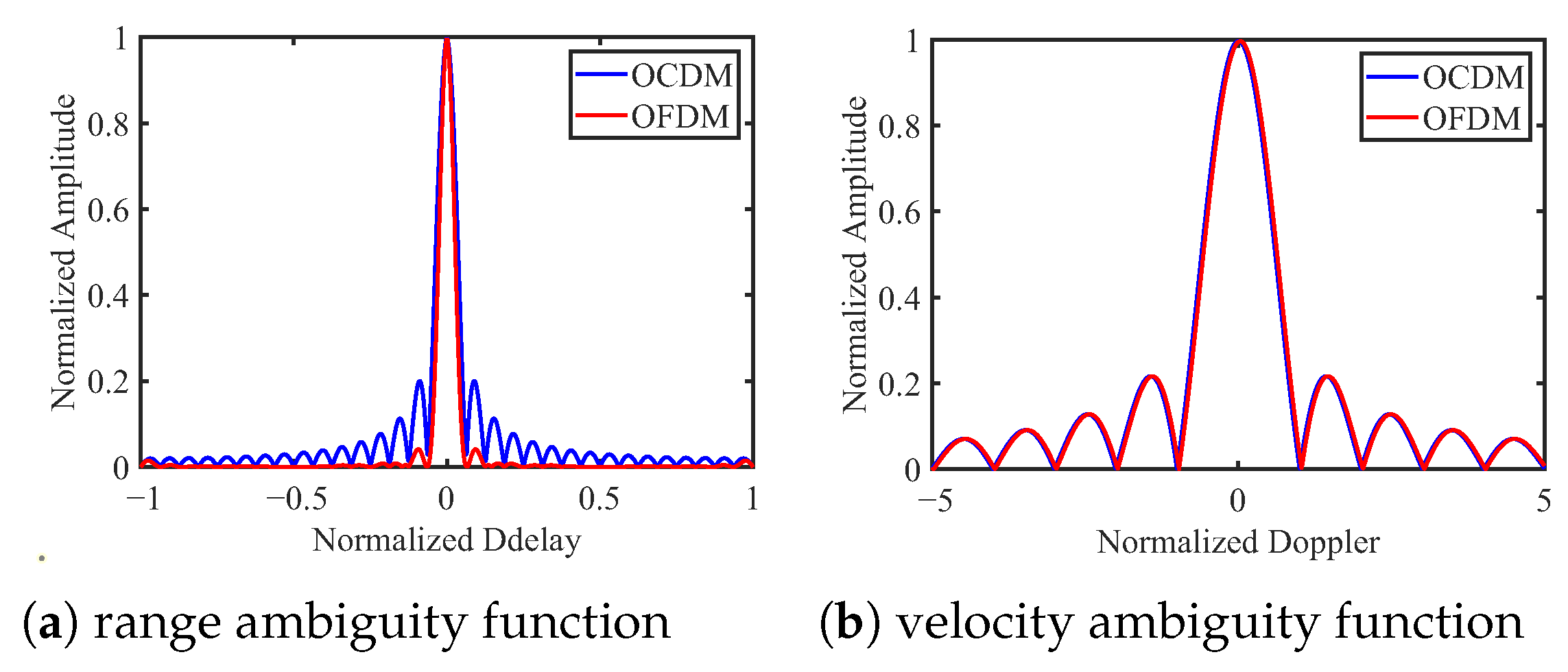
4. Ambiguity Function Characteristic Analysis
4.1. OFDM Ambiguity Function
4.2. OCDM Ambiguity Function
5. OCDM-Based Sensing Detection Performance Analysis
5.1. MF Detector Performance Analysis
5.2. GLRT Detector Performance Analysis
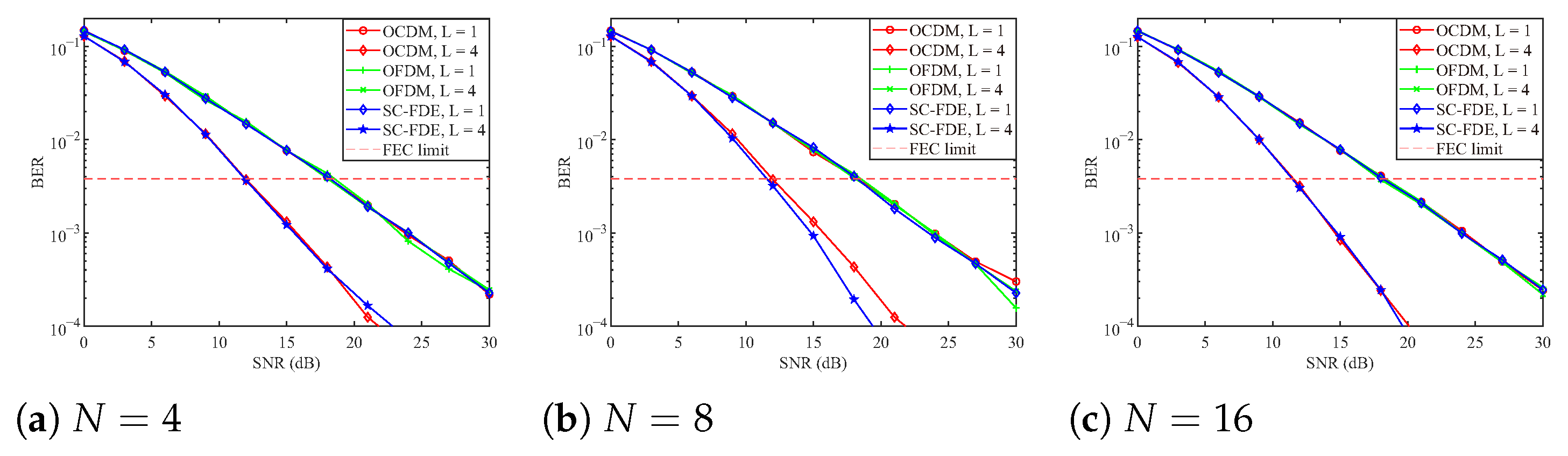
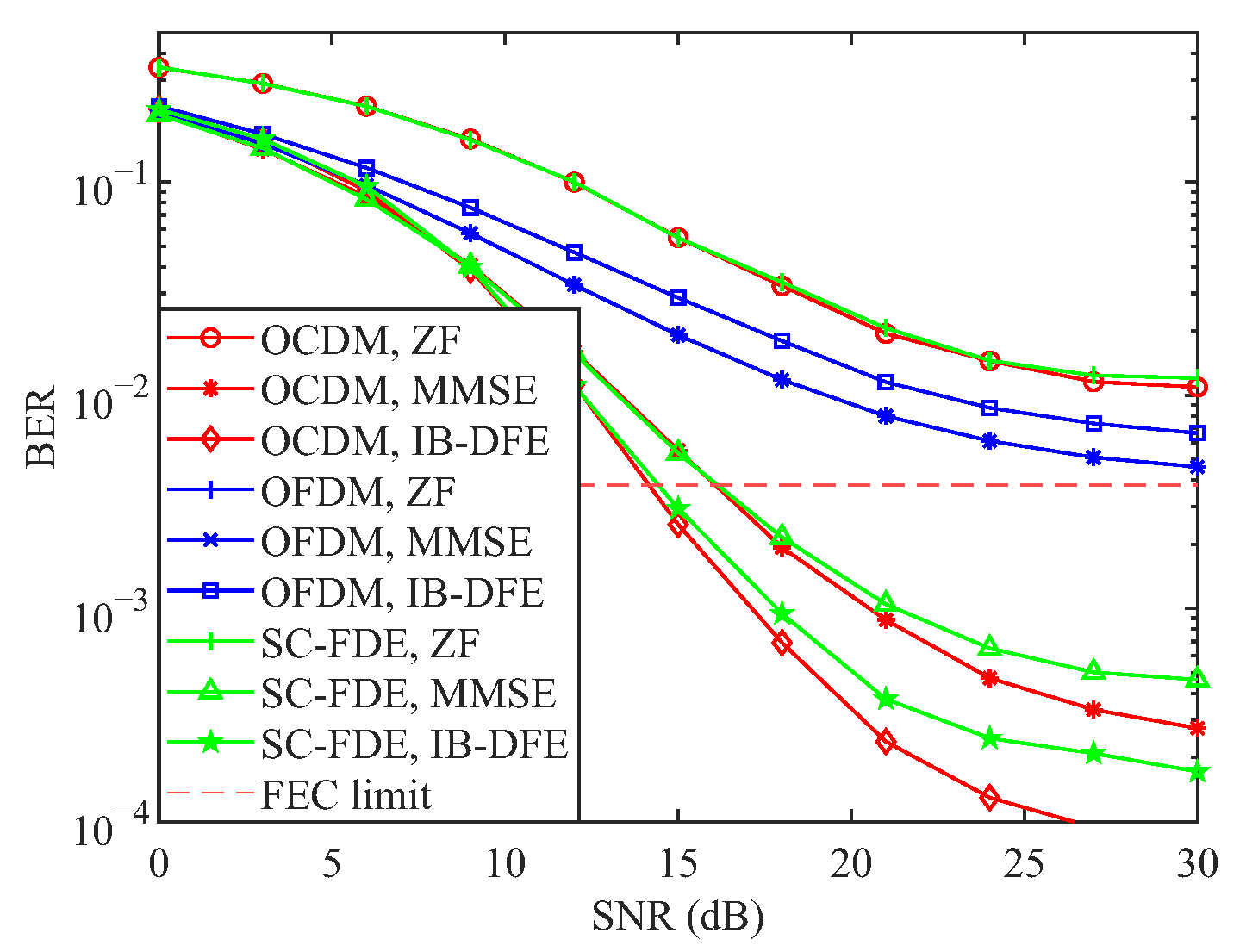
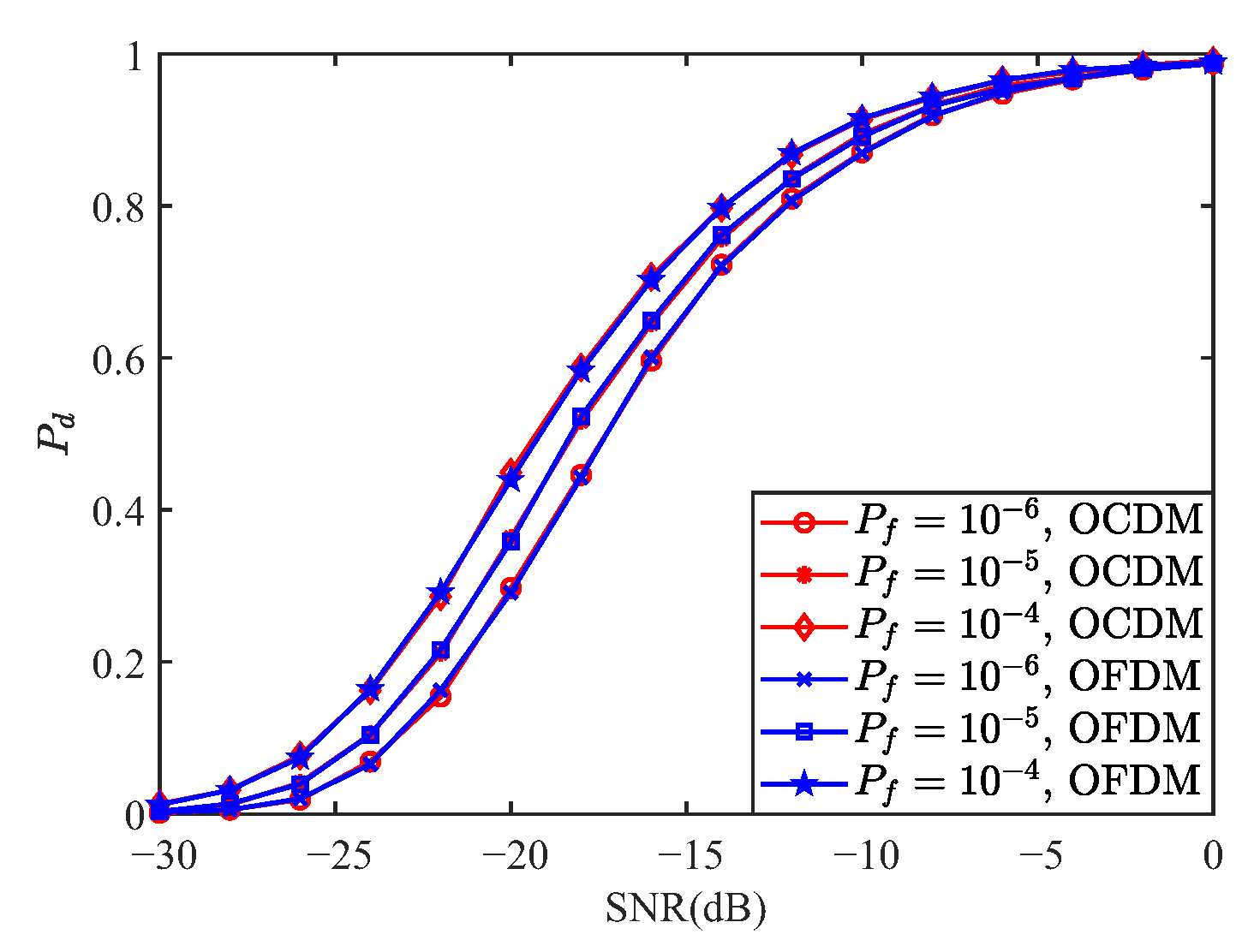
6. Simulation Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Osseiran, A.; Boccardi, F.; Braun, V.; Kusume, K.; Marsch, P.; Maternia, M.; Queseth, O.; Schellmann, M.; Schotten, H.; Taoka, H.; et al. Scenarios for 5G mobile and wireless communications: The vision of the METIS project. IEEE Commun. Mag. 2014, 52, 26–35. [Google Scholar] [CrossRef]
- Xiao, Y.; Ye, Z.; Wu, M.; Li, H.; Xiao, M.; Alouini, M.S.; Al-Hourani, A.; Cioni, S. Space-Air-Ground Integrated Wireless Networks for 6G: Basics, Key Technologies, and Future Trends. IEEE J. Sel. Areas Commun. 2024, 42, 3327–3354. [Google Scholar] [CrossRef]
- Wang, C.X.; You, X.; Gao, X.; Zhu, X.; Li, Z.; Zhang, C.; Wang, H.; Huang, Y.; Chen, Y.; Haas, H.; et al. On the Road to 6G: Visions, Requirements, Key Technologies, and Testbeds. IEEE Commun. Surv. Tutor. 2023, 25, 905–974. [Google Scholar] [CrossRef]
- Ma, T.; Xiao, Y.; Lei, X.; Zhang, L.; Niu, Y.; Karagiannidis, G.K. Reconfigurable Intelligent Surface-Assisted Localization: Technologies, Challenges, and the Road Ahead. IEEE Open J. Commun. Soc. 2023, 4, 1430–1451. [Google Scholar] [CrossRef]
- Ma, T.; Xiao, Y.; Lei, X.; Niu, H.; Xiao, M.; Guan, Y.L.; Yuen, C. Sensing-Resistance-Oriented Design for Privacy-Concerned Secure Transmission in ISAC Scenarios. IEEE Trans. Wirel. Commun. 2025; early access. [Google Scholar] [CrossRef]
- Ma, T.; Xiao, Y.; Lei, X.; Renzo, M.D. Integrated Sensing and Communication With Reconfigurable Intelligent Surfaces. IEEE Trans. Veh. Technol. 2024, 73, 19051–19064. [Google Scholar] [CrossRef]
- Dong, F.; Liu, F.; Cui, Y.; Wang, W.; Han, K.; Wang, Z. Sensing as a Service in 6G Perceptive Networks: A Unified Framework for ISAC Resource Allocation. IEEE Trans. Wirel. Commun. 2023, 22, 3522–3536. [Google Scholar] [CrossRef]
- Wang, J.; Varshney, N.; Gentile, C.; Blandino, S.; Chuang, J.; Golmie, N. Integrated Sensing and Communication: Enabling Techniques, Applications, Tools and Data Sets, Standardization, and Future Directions. IEEE Internet Things J. 2022, 9, 23416–23440. [Google Scholar] [CrossRef] [PubMed]
- Zheng, L.; Lops, M.; Eldar, Y.C.; Wang, X. Radar and Communication Coexistence: An Overview: A Review of Recent Methods. IEEE Signal Process. Mag. 2019, 36, 85–99. [Google Scholar] [CrossRef]
- Chen, X.; Feng, Z.; Wei, Z.; Zhang, P.; Yuan, X. Code-Division OFDM Joint Communication and Sensing System for 6G Machine-Type Communication. IEEE Internet Things J. 2021, 8, 12093–12105. [Google Scholar] [CrossRef]
- Baquero Barneto, C.; Riihonen, T.; Turunen, M.; Anttila, L.; Fleischer, M.; Stadius, K.; Ryynänen, J.; Valkama, M. Full-Duplex OFDM Radar With LTE and 5G NR Waveforms: Challenges, Solutions, and Measurements. IEEE Trans. Microw. Theory Tech. 2019, 67, 4042–4054. [Google Scholar] [CrossRef]
- Shi, C.; Wang, F.; Sellathurai, M.; Zhou, J.; Salous, S. Power Minimization-Based Robust OFDM Radar Waveform Design for Radar and Communication Systems in Coexistence. IEEE Trans. Signal Process. 2018, 66, 1316–1330. [Google Scholar] [CrossRef]
- Dai, Q.; Zeng, Y.; Wang, H.; You, C.; Zhou, C.; Cheng, H.; Xu, X.; Jin, S.; Swindlehurst, A.L.; Eldar, Y.C.; et al. A Tutorial on MIMO-OFDM ISAC: From Far-Field to Near-Field. arXiv 2025, arXiv:2504.19091. [Google Scholar]
- Ouyang, X.; Zhao, J. Orthogonal Chirp Division Multiplexing. IEEE Trans. Commun. 2016, 64, 3946–3957. [Google Scholar] [CrossRef]
- Bomfin, R.; Chafii, M.; Fettweis, G. Performance Assessment of Orthogonal Chirp Division Multiplexing in MIMO Space Time Coding. In Proceedings of the 2019 IEEE 2nd 5G World Forum (5GWF), Dresden, Germany, 30 September–2 October 2019; IEEE: New York, NY, USA, 2019; pp. 220–225. [Google Scholar]
- Omar, M.S.; Ma, X. Designing OCDM-Based Multi-User Transmissions. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; IEEE: New York, NY, USA, 2019; pp. 1–6. [Google Scholar]
- Omar, M.S.; Ma, X. Spectrum Design for Orthogonal Chirp Division Multiplexing Transmissions. IEEE Wirel. Commun. Lett. 2020, 9, 1990–1994. [Google Scholar] [CrossRef]
- Ouyang, X.; Zhao, J. Orthogonal Chirp Division Multiplexing for Coherent Optical Fiber Communications. J. Light. Technol. 2016, 34, 4376–4386. [Google Scholar] [CrossRef]
- Zhu, P.; Xu, X.; Tu, X.; Chen, Y.; Tao, Y. Anti-Multipath Orthogonal Chirp Division Multiplexing for Underwater Acoustic Communication. IEEE Access 2020, 8, 13305–13314. [Google Scholar] [CrossRef]
- de MBA Dib, L.; Colen, G.R.; Filomeno, M.d.L.; Ribeiro, M.V. Orthogonal Chirp Division Multiplexing for Baseband Data Communication Systems. IEEE Syst. J. 2020, 14, 2164–2174. [Google Scholar] [CrossRef]
- Omar, M.S.; Ma, X. Performance Analysis of OCDM for Wireless Communications. IEEE Trans. Wirel. Commun. 2021, 20, 4032–4043. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, Z.; Ma, X.; Liu, L. A Joint Sonar-Communication System Based on Multicarrier Waveforms. IEEE Signal Process. Lett. 2022, 29, 777–781. [Google Scholar] [CrossRef]
- Oliveira, L.G.d.; Alabd, M.B.; Nuss, B.; Zwick, T. An OCDM Radar-Communication System. In Proceedings of the 2020 14th European Conference on Antennas and Propagation (EuCAP), Copenhagen, Denmark, 15–20 March 2020; IEEE: New York, NY, USA, 2020; pp. 1–5. [Google Scholar]
- Giroto de Oliveira, L.; Nuss, B.; Alabd, M.B.; Diewald, A.; Li, Y.; Gehre, L.; Long, X.; Antes, T.; Galinsky, J.; Zwick, T. Discrete-Fresnel Domain Channel Estimation in OCDM-Based Radar Systems. IEEE Trans. Microw. Theory Tech. 2023, 71, 2258–2275. [Google Scholar] [CrossRef]
- de Oliveira, L.G.; Nuss, B.; Alabd, M.B.; Li, Y.; Yu, L.; Zwick, T. MIMO-OCDM-based Joint Radar Sensing and Communication. In Proceedings of the 2021 15th European Conference on Antennas and Propagation (EuCAP), Dusseldorf, Germany, 22–26 March 2021; IEEE: New York, NY, USA, 2021; pp. 1–5. [Google Scholar]
- Miuccio, L.; Panno, D.; Pisacane, P.; Riolo, S. A QoS-aware and channel-aware Radio Resource Management framework for multi-numerology systems. Comput. Commun. 2022, 191, 299–314. [Google Scholar] [CrossRef]
- Beyranvand, H.; Salehi, J.A. Efficient Optical Resource Allocation and QoS Differentiation in Optical Burst Switching Networks Utilizing Hybrid WDM/OCDM. J. Light. Technol. 2012, 30, 2427–2441. [Google Scholar] [CrossRef]
- Lv, X.; Wang, J.; Jiang, Z.; Jiao, W. A novel PAPR reduction method for OCDM-based radar-communication signal. In Proceedings of the 2018 IEEE MTT-S International Microwave Workshop Series on 5G Hardware and System Technologies (IMWS-5G), Dublin, Ireland, 30–31 August 2018; IEEE: New York, NY, USA, 2018; pp. 1–3. [Google Scholar]
- Zhu, P.; Yang, G.; Chen, W.; Xu, X.; Chen, Y. Doppler-Resistant Orthogonal Chirp Division Multiplexing with Multiplex Resampling for Mobile Underwater Acoustic Communication. IEEE Access 2022, 10, 55151–55163. [Google Scholar] [CrossRef]
- Lin, Y.P.; Phoong, S.M. BER minimized OFDM systems with channel independent precoders. IEEE Trans. Signal Process. 2003, 51, 2369–2380. [Google Scholar]
- Liu, Z.; Xin, Y.; Giannakis, G. Linear constellation precoding for OFDM with maximum multipath diversity and coding gains. IEEE Trans. Commun. 2003, 51, 416–427. [Google Scholar] [CrossRef]
- Ghogho, M.; Gil-Jimenez, V.P.; Swami, A. Multipath diversity and coding gains of cyclic-prefixed single carrier systems. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; IEEE: New York, NY, USA, 2009; pp. 2837–2840. [Google Scholar]
- Ng, B.; Lam, C.t.; Falconer, D. Turbo frequency domain equalization for single-carrier broadband wireless systems. IEEE Trans. Wirel. Commun. 2007, 6, 759–767. [Google Scholar] [CrossRef]
- Zhang, J.; Shi, C.; Qiu, X.; Wu, Y. Shaping Radar Ambiguity Function by L-Phase Unimodular Sequence. IEEE Sens. J. 2016, 16, 5648–5659. [Google Scholar] [CrossRef]
- Bayat, S.; Li, Y.; Song, L.; Han, Z. Matching Theory: Applications in wireless communications. IEEE Signal Process. Mag. 2016, 33, 103–122. [Google Scholar] [CrossRef]
- Gu, Y.; Saad, W.; Bennis, M.; Debbah, M.; Han, Z. Matching theory for future wireless networks: Fundamentals and applications. IEEE Commun. Mag. 2015, 53, 52–59. [Google Scholar] [CrossRef]
- Simon, M.K. Sum of Chi-Square Random Variables. In Probability Distributions Involving Gaussian Random Variables; Springer: Boston, MA, USA, 2002; pp. 35–47. [Google Scholar] [CrossRef]
- Liu, F.; Garcia-Rodriguez, A.; Masouros, C.; Geraci, G. Interfering Channel Estimation in Radar-Cellular Coexistence: How Much Information Do We Need? IEEE Trans. Wirel. Commun. 2019, 18, 4238–4253. [Google Scholar] [CrossRef]
- Sedighi, S.; Taherpour, A.; Monfared, S.S. Bayesian generalised likelihood ratio test-based multiple antenna spectrum sensing for cognitive radios. IET Commun. 2013, 7, 2151–2165. [Google Scholar] [CrossRef]
- Xu, L.; Li, J. Iterative Generalized-Likelihood Ratio Test for MIMO Radar. IEEE Trans. Signal Process. 2007, 55, 2375–2385. [Google Scholar] [CrossRef]
- Maya, J.A.; Vega, L.R.; Tonello, A.M. An Asymptotically Equivalent GLRT Test for Distributed Detection in Wireless Sensor Networks. IEEE Trans. Signal Inf. Process. Netw. 2023, 9, 888–900. [Google Scholar] [CrossRef]
- Soltanmohammadi, E.; Orooji, M.; Naraghi-Pour, M. Spectrum Sensing Over MIMO Channels Using Generalized Likelihood Ratio Tests. IEEE Signal Process. Lett. 2013, 20, 439–442. [Google Scholar] [CrossRef]
- Benvenuto, N.; Dinis, R.; Falconer, D.; Tomasin, S. Single Carrier Modulation With Nonlinear Frequency Domain Equalization: An Idea Whose Time Has Come—Again. Proc. IEEE 2010, 98, 69–96. [Google Scholar] [CrossRef]





| 5G | Fifth-Generation |
| 6G | Sixth-Generation |
| BER | Bit Error Rate |
| BPSK | Binary Phase-Shift Keying |
| CFAR | Constant False Alarm Rate |
| CP | Cyclic Prefix |
| DFnT | Discrete Fresnel Transform |
| DFT | Discrete Fourier Transform |
| EVA | Extended Vehicular A |
| FEC | Forward Error Correction |
| FFT | Fast Fourier Transform |
| GLRT | Generalized Likelihood Ratio Test |
| IB-DFE | Iterative Block-Decision Feedback Equalization |
| ICI | Inter-Carrier Interference |
| IDFnT | Inverse Discrete Fresnel Transform |
| IDFT | Inverse Discrete Fourier Transform |
| IoT | Internet of Things |
| IoV | Internet of Vehicles |
| ISAC | Integrated Sensing and Communication |
| LTI | Linear Time-Invariant |
| LTV | Linear Time-Variant |
| MF | Matched Filter |
| MIMO | Multiple Input Multiple Output |
| MLE | Maximum Likelihood Equalization |
| MMSE | Minimum Mean Square Error |
| mMTC | Massive Machine-Type Communication |
| OCDM | Orthogonal Chirp Division Multiplexing |
| OFDM | Orthogonal Frequency Division Multiplexing |
| Probability Density Function | |
| QAM | Quadrature Amplitude Modulation |
| QPSK | Quadrature Phase-Shift Keying |
| SC-FDE | Single-Carrier Frequency-Domain Equalization |
| SNR | Signal-to-Noise Ratio |
| uRLLC | Ultra-Reliable and Low-Latency Communication |
| ZC | Zadoff–Chu |
| ZF | Zero Forcing |
| Methods | OFDM | SC-FDE | OCDM |
|---|---|---|---|
| ZF | |||
| MMSE | |||
| MLE | |||
| IB-DFE |
| Simulation | Simulation Type | |
|---|---|---|
| Parameters | Communication | Sensing |
| Channel Model | EVA, LTV | EVA |
| Frequency of Carrier | 2 GHz | 2 GHz |
| OCDM Symbol Period | 1 s | 1 s |
| OFDM Subcarrier Interval | 1 MHz | 1 MHz |
| Number of Symbols per Subframe | 14 | 14 |
| Number of Subcarriers | 16 | 16 |
| Cyclic Prefix Length | ||
| Multipath | Delay (ns) | Average Path Gain (dB) |
|---|---|---|
| 1 | 0 | 0 |
| 2 | 30 | −1.5 |
| 3 | 150 | −1.4 |
| 4 | 310 | −3.6 |
| 5 | 370 | −0.6 |
| 6 | 710 | −9.1 |
| 7 | 1090 | −7.0 |
| 8 | 1730 | −12.0 |
| 9 | 2510 | −16.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, P.; Li, M.; Zhan, T.; Gong, F.; Xiao, Y.; Lei, X. Performance Analysis of OCDM in ISAC Scenario. Sensors 2025, 25, 5481. https://doi.org/10.3390/s25175481
Xu P, Li M, Zhan T, Gong F, Xiao Y, Lei X. Performance Analysis of OCDM in ISAC Scenario. Sensors. 2025; 25(17):5481. https://doi.org/10.3390/s25175481
Chicago/Turabian StyleXu, Pengfei, Mao Li, Tao Zhan, Fengkui Gong, Yue Xiao, and Xia Lei. 2025. "Performance Analysis of OCDM in ISAC Scenario" Sensors 25, no. 17: 5481. https://doi.org/10.3390/s25175481
APA StyleXu, P., Li, M., Zhan, T., Gong, F., Xiao, Y., & Lei, X. (2025). Performance Analysis of OCDM in ISAC Scenario. Sensors, 25(17), 5481. https://doi.org/10.3390/s25175481





