Super-Resolution Parameter Estimation Using Machine Learning-Assisted Spatial Mode Demultiplexing
Abstract
1. Introduction
2. Methods
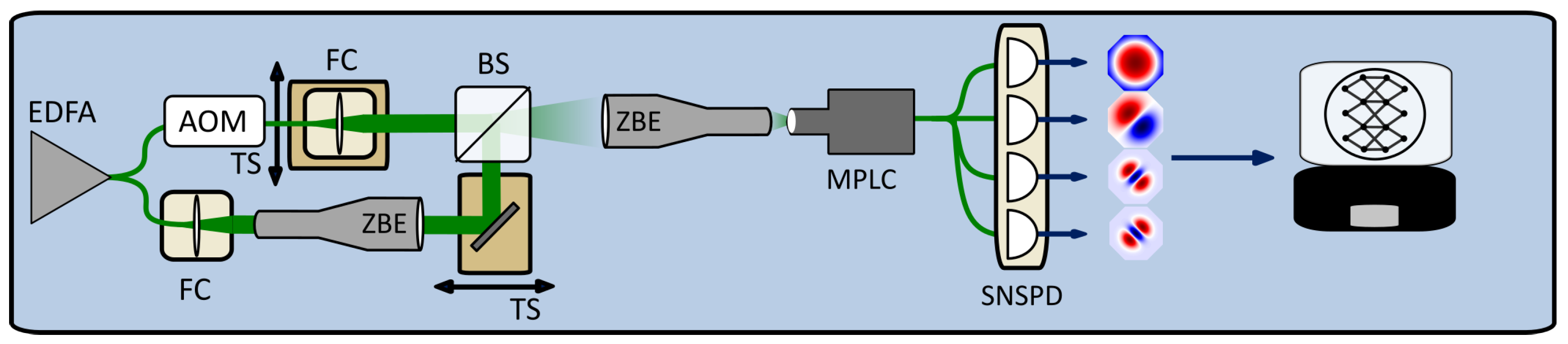
2.1. Optical Setup
2.2. Machine Learning Model
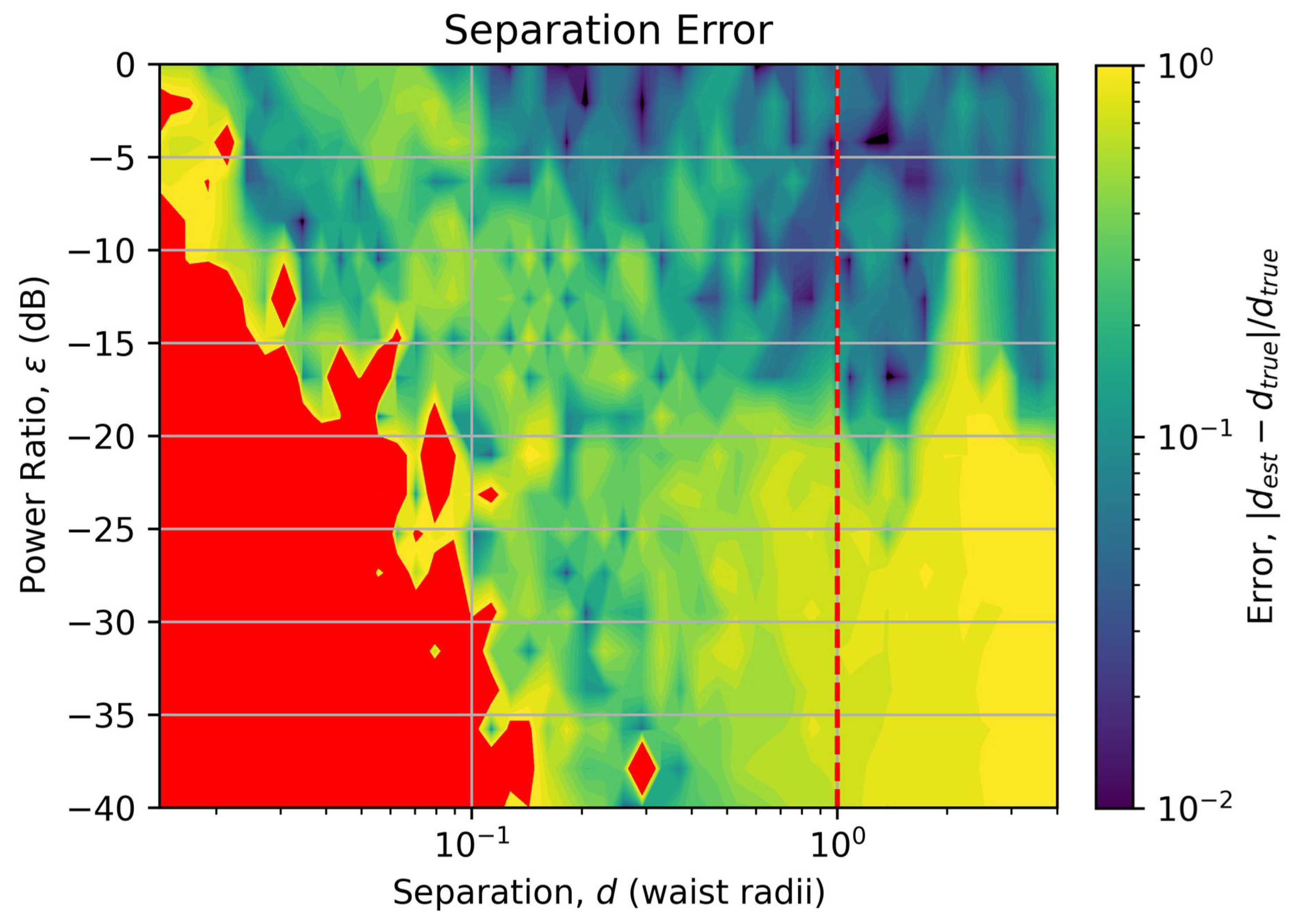
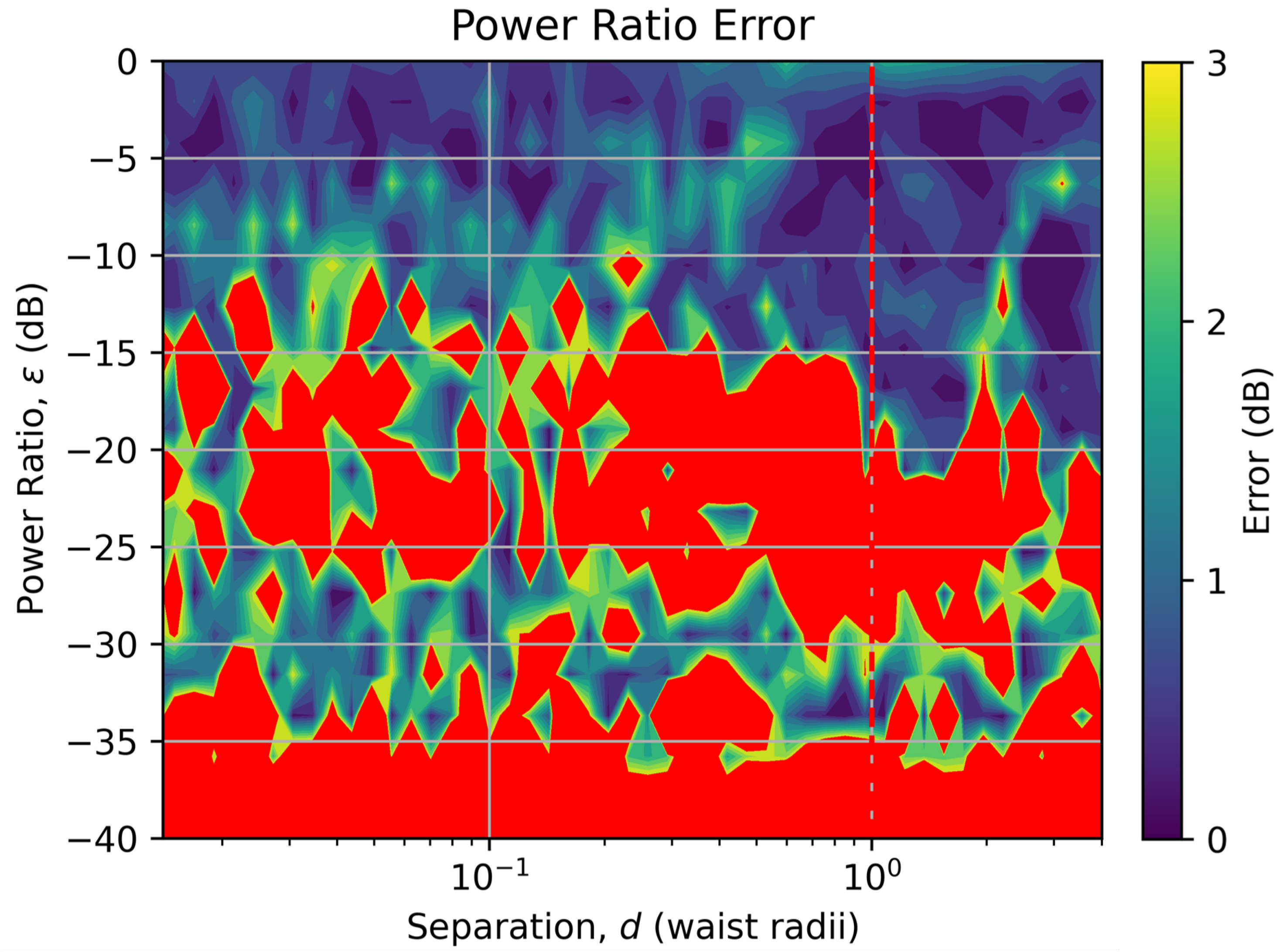
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | artificial neural network |
| AOM | acousto-optic modulator |
| BS | beam-splitter |
| COTS | commercial-off-the-shelf |
| DI | direct imaging |
| EDFA | erbium-doped fiber amplifier |
| FC | fiber collimator |
| FPGA | field programmable gate array |
| GPU | graphics processing unit |
| HG | Hermite Gaissian |
| ITU | International Telecommunications Union |
| ML | machine learning |
| MNIST | modified National Institute of Standards and Technology |
| MPLC | multi-planar light converter |
| OCOM | optical center of mass |
| PSF | point spread function |
| QPD | quadrant photodetector |
| SMF | single-mode fiber |
| SNSPD | superconducting single photon detector |
| SPADE | spatial mode demultiplexing |
| TS | translation stage |
| ZBE | zoom beam expander |
References
- Rayleigh, L. XXXI. Investigations in optics, with special reference to the spectroscope. London Edinburgh Dublin Philos. Mag. J. Sci. 1879, 8, 261–274. [Google Scholar] [CrossRef]
- Abbe, E. Ueber einen neuen Beleuchtungsapparat am Mikroskop. In Archiv für Mikroskopische Anatomie; Forgotten Books: London, UK, 1873. [Google Scholar]
- Sparrow, C.M. On spectroscopic resolving power. Astrophys. J. 1916, 44, 76. [Google Scholar] [CrossRef]
- Padovani, P.; Cirasuolo, M. The Extremely Large Telescope. Contemp. Phys. 2023, 64, 47–64. [Google Scholar] [CrossRef]
- Grainge, K.; Alachkar, B.; Amy, S.; Barbosa, D.; Bommineni, M.; Boven, P.; Braddock, R.; Davis, J.; Diwakar, P.; Francis, V.; et al. Square Kilometre Array: The radio telescope of the XXI century. Astron. Rep. 2017, 61, 288–296. [Google Scholar] [CrossRef]
- Defienne, H.; Bowen, W.P.; Chekhova, M.; Lemos, G.B.; Oron, D.; Ramelow, S.; Treps, N.; Faccio, D. Advances in quantum imaging. Nat. Photonics 2024, 18, 1024–1036. [Google Scholar] [CrossRef]
- Tsang, M.; Nair, R.; Lu, X.M. Quantum theory of superresolution for two incoherent optical point sources. Phys. Rev. X 2016, 6, 031033. [Google Scholar] [CrossRef]
- Tsang, M. Resolving starlight: A quantum perspective. Contemp. Phys. 2019, 60, 279–298. [Google Scholar] [CrossRef]
- Nair, R.; Tsang, M. Far-field superresolution of thermal electromagnetic sources at the quantum limit. Phys. Rev. Lett. 2016, 117, 190801. [Google Scholar] [CrossRef]
- Řehaček, J.; Hradil, Z.; Stoklasa, B.; Paúr, M.; Grover, J.; Krzic, A.; Sánchez-Soto, L. Multiparameter quantum metrology of incoherent point sources: Towards realistic superresolution. Phys. Rev. A 2017, 96, 062107. [Google Scholar] [CrossRef]
- Řeháček, J.; Hradil, Z.; Koutnỳ, D.; Grover, J.; Krzic, A.; Sánchez-Soto, L.L. Optimal measurements for quantum spatial superresolution. Phys. Rev. A 2018, 98, 012103. [Google Scholar] [CrossRef]
- Boucher, P.; Fabre, C.; Labroille, G.; Treps, N. Spatial optical mode demultiplexing as a practical tool for optimal transverse distance estimation. Optica 2020, 7, 1621–1626. [Google Scholar] [CrossRef]
- Tan, X.J.; Qi, L.; Chen, L.; Danner, A.J.; Kanchanawong, P.; Tsang, M. Quantum-inspired superresolution for incoherent imaging. Optica 2023, 10, 1189–1194. [Google Scholar] [CrossRef]
- Rouvière, C.; Barral, D.; Grateau, A.; Karuseichyk, I.; Sorelli, G.; Walschaers, M.; Treps, N. Ultra-sensitive separation estimation of optical sources. Optica 2024, 11, 166–170. [Google Scholar] [CrossRef]
- Santamaria, L.; Pallotti, D.; Siciliani de Cumis, M.; Dequal, D.; Lupo, C. Spatial-mode demultiplexing for enhanced intensity and distance measurement. Opt. Express 2023, 31, 33930–33944. [Google Scholar] [CrossRef] [PubMed]
- Santamaria, L.; Sgobba, F.; Lupo, C. Single-photon sub-Rayleigh precision measurements of a pair of incoherent sources of unequal intensity. Opt. Quantum 2024, 2, 46–56. [Google Scholar] [CrossRef]
- Santamaria, L.; Sgobba, F.; Pallotti, D.; Lupo, C. Single-photon super-resolved spectroscopy from spatial-mode demultiplexing. Photonics Res. 2025, 13, 865–874. [Google Scholar] [CrossRef]
- Tang, Z.S.; Durak, K.; Ling, A. Fault-tolerant and finite-error localization for point emitters within the diffraction limit. Opt. Express 2016, 24, 22004–22012. [Google Scholar] [CrossRef]
- Tham, W.K.; Ferretti, H.; Steinberg, A.M. Beating Rayleigh’s curse by imaging using phase information. Phys. Rev. Lett. 2017, 118, 070801. [Google Scholar] [CrossRef]
- Paúr, M.; Stoklasa, B.; Hradil, Z.; Sánchez-Soto, L.L.; Rehacek, J. Achieving the ultimate optical resolution. Optica 2016, 3, 1144–1147. [Google Scholar] [CrossRef]
- Yang, S.; Su, Y.; Ruan, N.; Wu, Z.; Lin, X. Quantum enhanced long baseline optical interferometers with noiseless linear amplification and displacement operation. In Proceedings of the Quantum and Nonlinear Optics IV, Beijing, China, 12–14 October 2016; Volume 10029, pp. 32–38. [Google Scholar]
- Xie, Y.; Liu, H.; Sun, H.; Liu, K.; Gao, J. Far-field superresolution of thermal sources by double homodyne or double array homodyne detection. Opt. Express 2024, 32, 19495–19507. [Google Scholar] [CrossRef]
- Wallis, J.S.; Gozzard, D.R.; Frost, A.M.; Collier, J.J.; Maron, N.; Dix-Matthews, B.P. Spatial mode demultiplexing for super-resolved source parameter estimation. Opt. Express 2025, 33, 34651–34662. [Google Scholar] [CrossRef]
- Labroille, G.; Denolle, B.; Jian, P.; Genevaux, P.; Treps, N.; Morizur, J.F. Efficient and mode selective spatial mode multiplexer based on multi-plane light conversion. Opt. Express 2014, 22, 15599–15607. [Google Scholar] [CrossRef]
- Fontaine, N.K.; Ryf, R.; Chen, H.; Neilson, D.; Carpenter, J. Design of high order mode-multiplexers using multiplane light conversion. In Proceedings of the 2017 European Conference on Optical Communication (ECOC), Gothenburg, Sweden, 17–21 September 2017; pp. 1–3. [Google Scholar]
- Lin, X.; Rivenson, Y.; Yardimci, N.T.; Veli, M.; Luo, Y.; Jarrahi, M.; Ozcan, A. All-optical machine learning using diffractive deep neural networks. Science 2018, 361, 1004–1008. [Google Scholar] [CrossRef]
- Zhou, T.; Lin, X.; Wu, J.; Chen, Y.; Xie, H.; Li, Y.; Fan, J.; Wu, H.; Fang, L.; Dai, Q. Large-scale neuromorphic optoelectronic computing with a reconfigurable diffractive processing unit. Nat. Photonics 2021, 15, 367–373. [Google Scholar] [CrossRef]
- Sorelli, G.; Gessner, M.; Walschaers, M.; Treps, N. Moment-based superresolution: Formalism and applications. Phys. Rev. A 2021, 104, 033515. [Google Scholar] [CrossRef]
- Matlin, E.F.; Zipp, L.J. Imaging arbitrary incoherent source distributions with near quantum-limited resolution. Sci. Rep. 2022, 12, 2810. [Google Scholar] [CrossRef]
- Pushkina, A.; Maltese, G.; Costa-Filho, J.; Patel, P.; Lvovsky, A. Superresolution linear optical imaging in the far field. Phys. Rev. Lett. 2021, 127, 253602. [Google Scholar] [CrossRef]
- Frank, J.; Duplinskiy, A.; Bearne, K.; Lvovsky, A. Passive superresolution imaging of incoherent objects. Optica 2023, 10, 1147–1152. [Google Scholar] [CrossRef]
- Buonaiuto, G.; Lupo, C. Machine learning with sub-diffraction resolution in the photon-counting regime. Quantum Mach. Intell. 2025, 7, 1–12. [Google Scholar] [CrossRef]
- Sajia, A.; Benzimoun, B.; Khatiwada, P.; Zhao, G.; Qian, X.F. Breaking the Diffraction Barrier for Passive Sources: Parameter-Decoupled Superresolution Assisted by Physics-Informed Machine Learning. arXiv 2025, arXiv:2504.14156. [Google Scholar]
- Fontaine, N.K.; Ryf, R.; Chen, H.; Neilson, D.T.; Kim, K.; Carpenter, J. Multi-plane light conversion of high spatial mode count. In Proceedings of the Laser Beam Shaping XVIII, San Diego, CA, USA, 20–21 August 2018; Volume 10744, pp. 120–125. [Google Scholar]
- Grace, M.R.; Dutton, Z.; Ashok, A.; Guha, S. Approaching quantum-limited imaging resolution without prior knowledge of the object location. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2020, 37, 1288–1299. [Google Scholar] [CrossRef] [PubMed]
- Grace, M.R.; Guha, S. Identifying objects at the quantum limit for superresolution imaging. Phys. Rev. Lett. 2022, 129, 180502. [Google Scholar] [CrossRef] [PubMed]
- LiquidInstruments. Moku Neural Network. 2024. Available online: https://liquidinstruments.com/neural-network/ (accessed on 12 May 2025).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: http://tensorflow.org (accessed on 12 May 2025).
- Kasper, M.; Beuzit, J.L.; Verinaud, C.; Gratton, R.G.; Kerber, F.; Yaitskova, N.; Boccaletti, A.; Thatte, N.; Schmid, H.M.; Keller, C.; et al. EPICS: Direct imaging of exoplanets with the E-ELT. In Proceedings of the Ground-Based and Airborne Instrumentation for Astronomy III, San Diego, CA, USA, 27 June–2 July 2010; Volume 7735, pp. 948–956. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gozzard, D.R.; Wallis, J.S.; Frost, A.M.; Collier, J.J.; Maron, N.; Dix-Matthews, B.P.; Vinsen, K. Super-Resolution Parameter Estimation Using Machine Learning-Assisted Spatial Mode Demultiplexing. Sensors 2025, 25, 5395. https://doi.org/10.3390/s25175395
Gozzard DR, Wallis JS, Frost AM, Collier JJ, Maron N, Dix-Matthews BP, Vinsen K. Super-Resolution Parameter Estimation Using Machine Learning-Assisted Spatial Mode Demultiplexing. Sensors. 2025; 25(17):5395. https://doi.org/10.3390/s25175395
Chicago/Turabian StyleGozzard, David R., John S. Wallis, Alex M. Frost, Joshua J. Collier, Nicolas Maron, Benjamin P. Dix-Matthews, and Kevin Vinsen. 2025. "Super-Resolution Parameter Estimation Using Machine Learning-Assisted Spatial Mode Demultiplexing" Sensors 25, no. 17: 5395. https://doi.org/10.3390/s25175395
APA StyleGozzard, D. R., Wallis, J. S., Frost, A. M., Collier, J. J., Maron, N., Dix-Matthews, B. P., & Vinsen, K. (2025). Super-Resolution Parameter Estimation Using Machine Learning-Assisted Spatial Mode Demultiplexing. Sensors, 25(17), 5395. https://doi.org/10.3390/s25175395





