Efficient Navigable Area Computation for Underground Autonomous Vehicles via Ground Feature and Boundary Processing
Abstract
1. Introduction
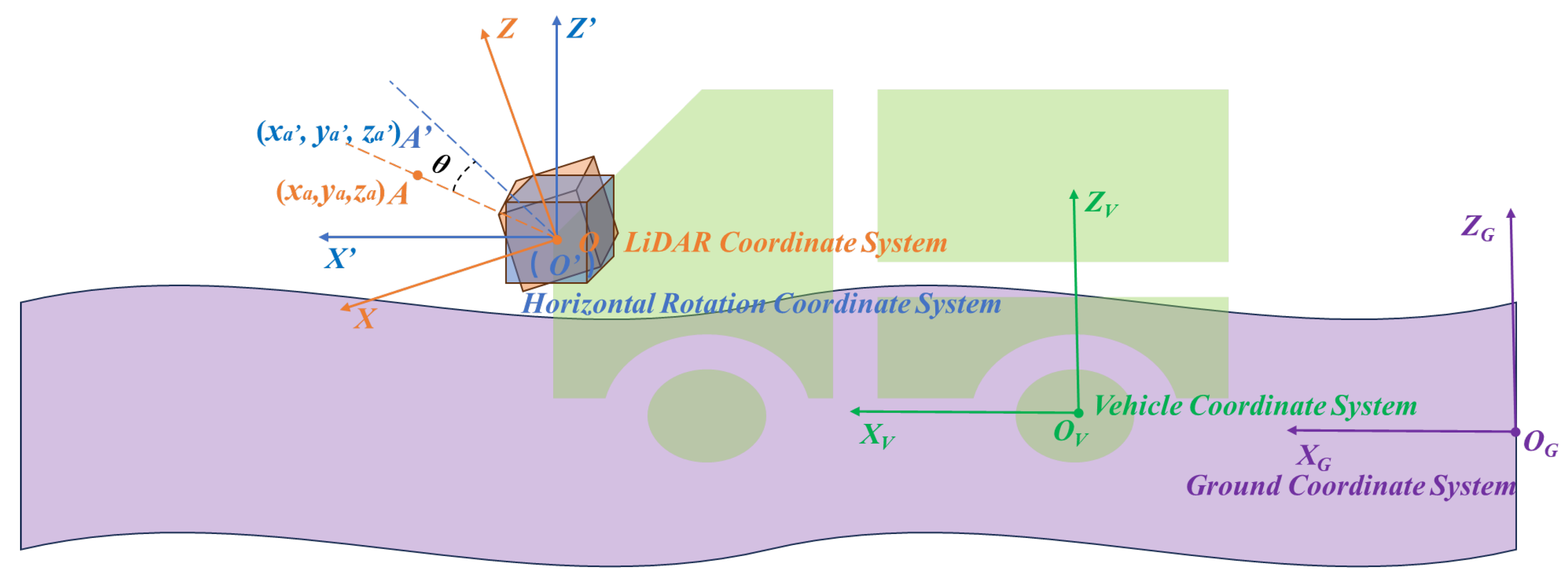
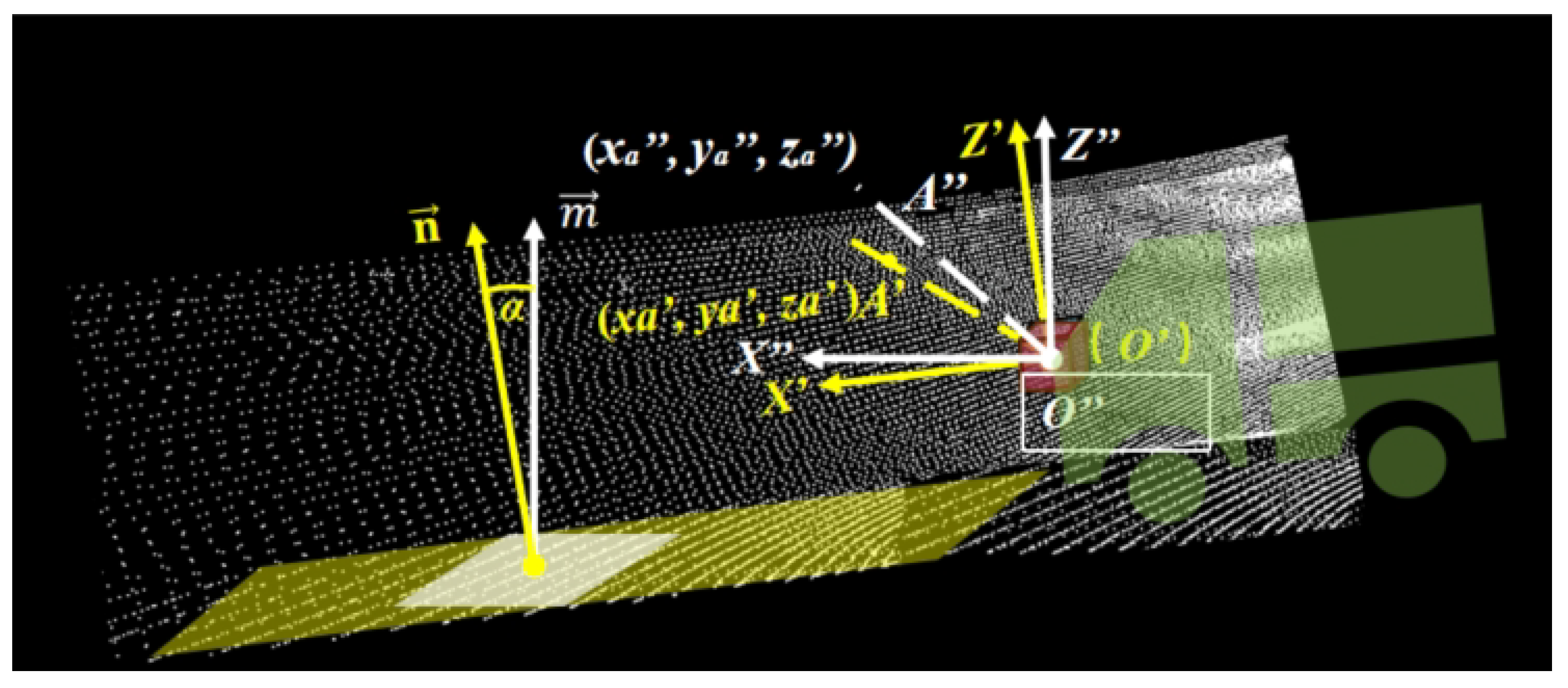
- A rapid ground orientation extraction method is developed to enable efficient initialization of spatial relationships between LiDAR data and tunnel terrain, laying a foundational coordinate reference for subsequent processing;
- A real-time coordinate correction framework is proposed, which achieves alignment between the LiDAR coordinate system and the ground plane through a two-stage mechanism of pre-calibration and dynamic feedback adjustment;
- An adaptive boundary completion algorithm is designed to address boundary discontinuities in complex scenarios, ensuring topological integrity of extracted boundaries;
- A method for continuously extracting boundaries over duration is proposed. By fusing temporal context information, the continuity of boundary detection is maintained in a dynamic environment.
2. Related Work
2.1. Image-Based Road Boundary Detection
2.2. LiDAR-Based Road Boundary Detection
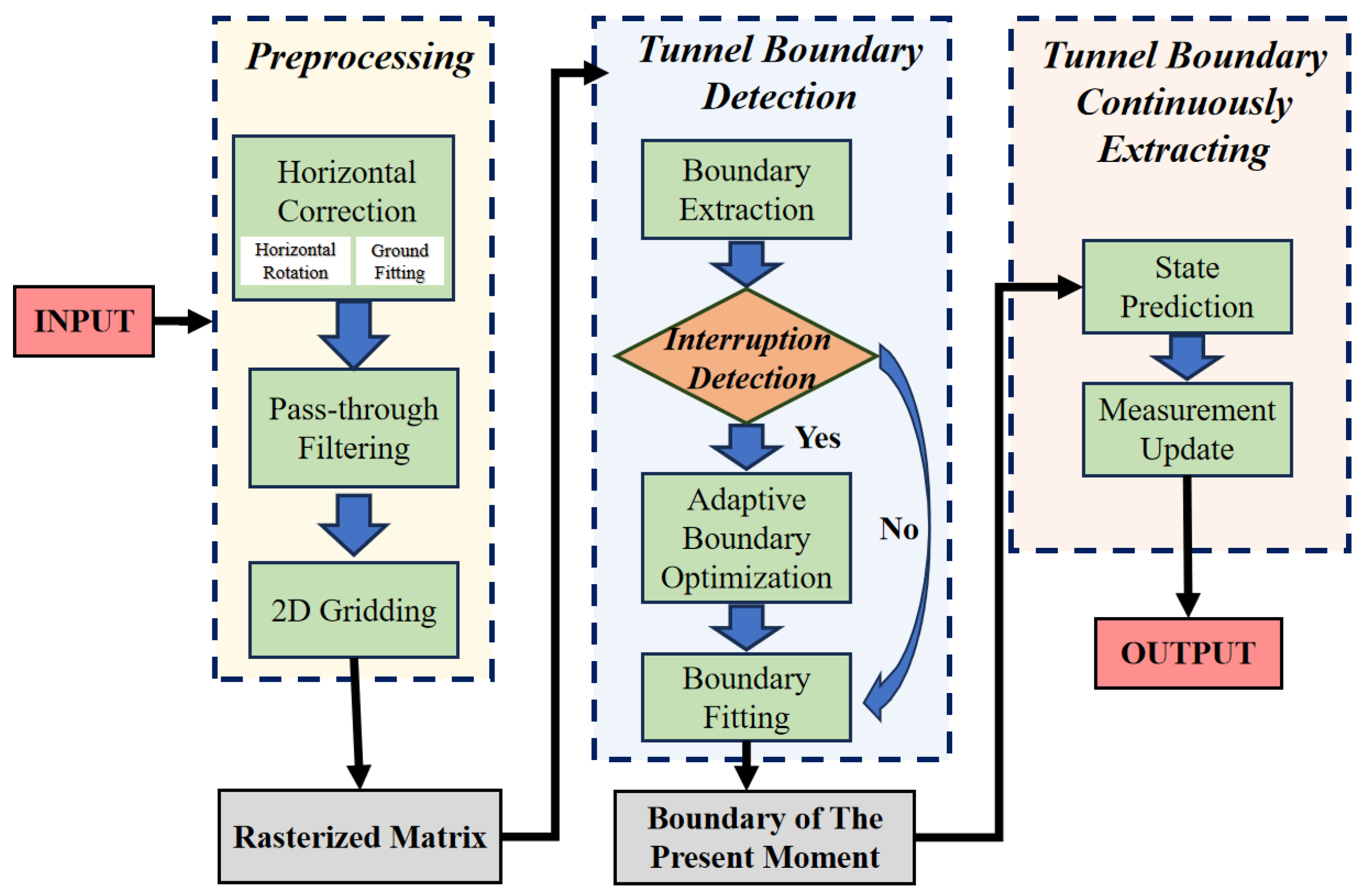
3. Methods
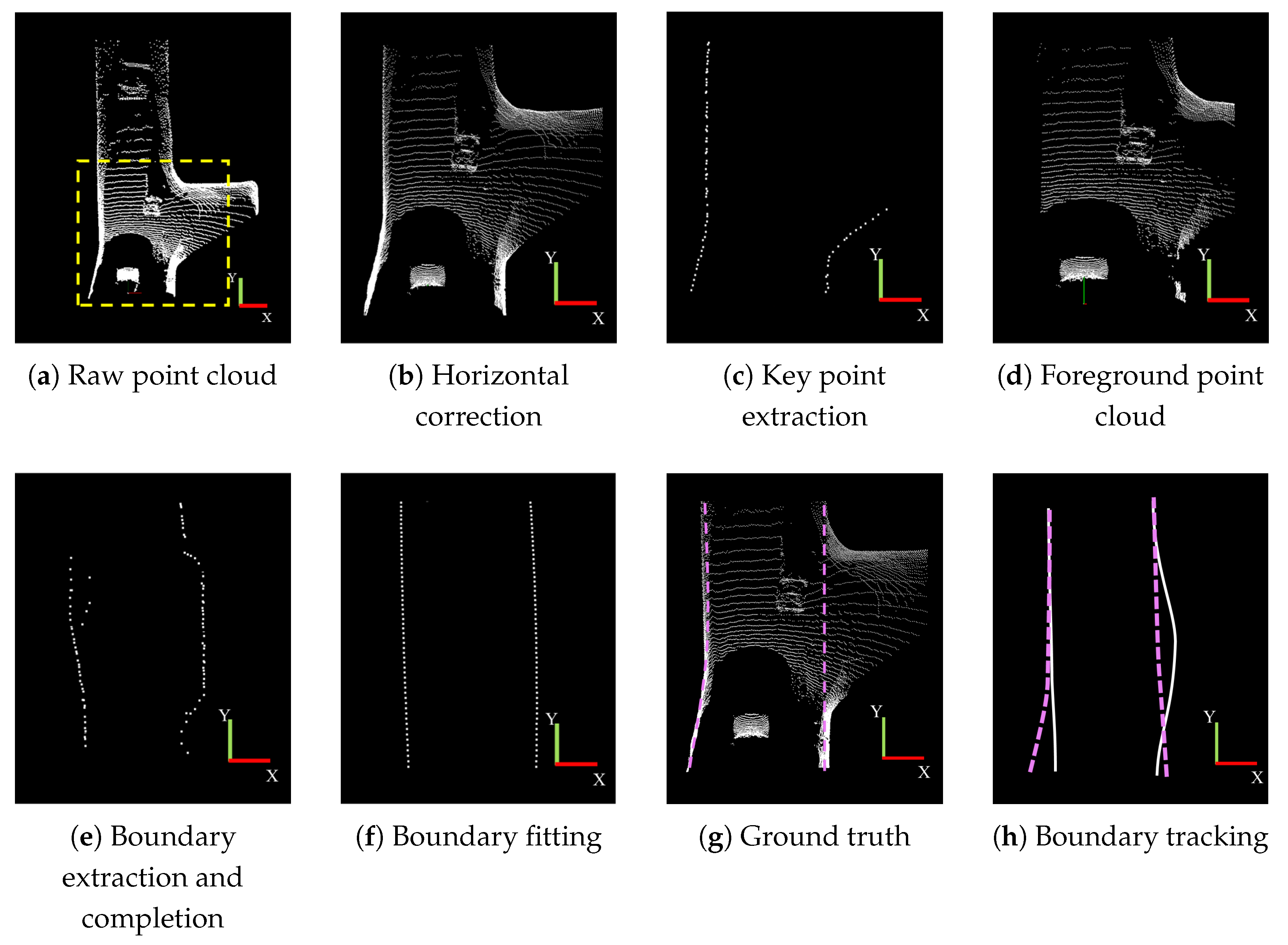
3.1. Preprocessing Module
3.1.1. Horizontal Correction
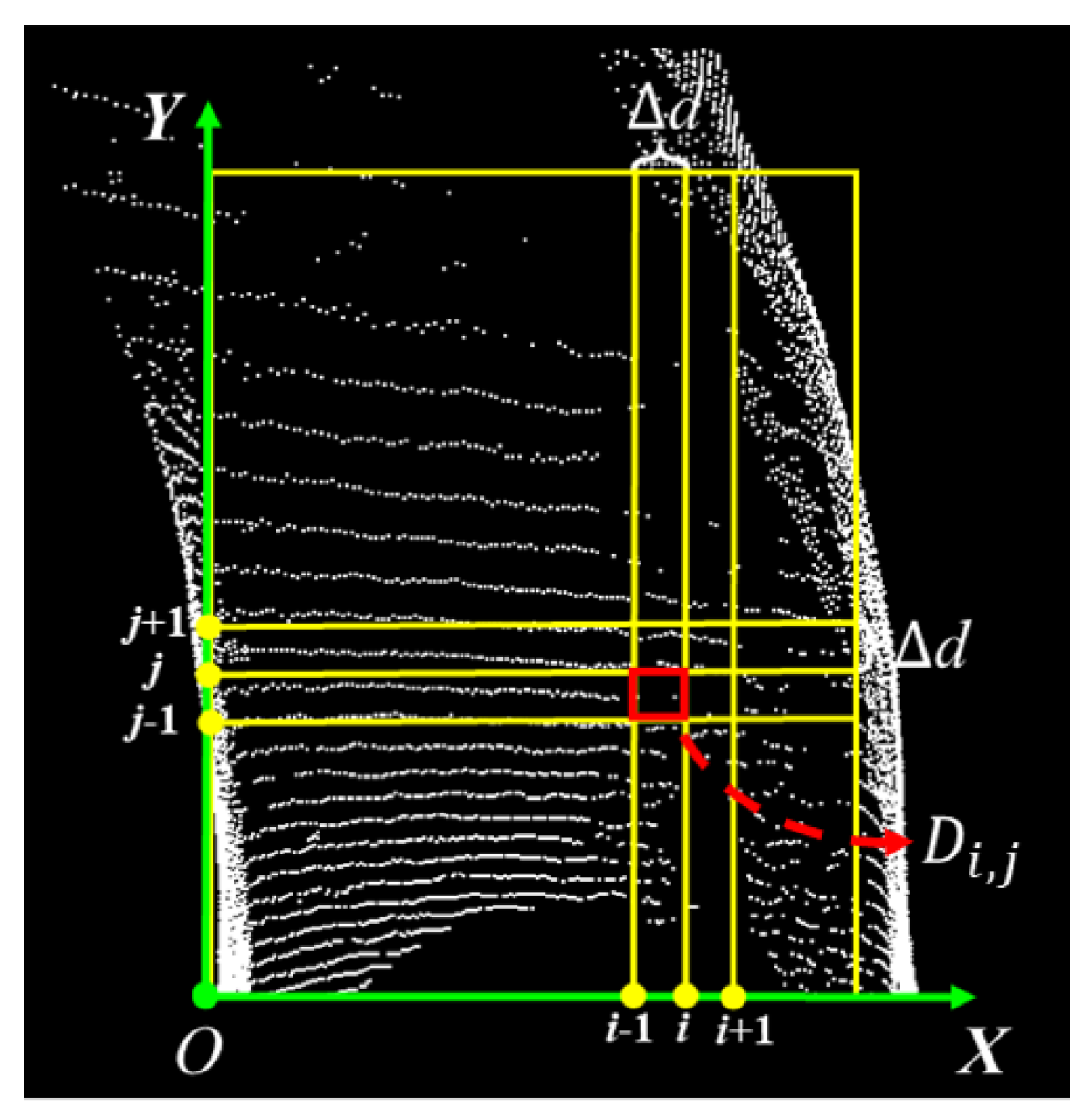
3.1.2. Two-Dimensional Gridding
3.2. Tunnel Boundary Detection
3.2.1. Boundary Extraction
- Initialize the left and right boundary point clouds as L and R.
- Traverse each row of , and initialize the minimum and maximum X coordinates , and their indices.
- Traverse each column within the row to find the points corresponding to the minimum and maximum X coordinates in the non-empty cells. After finding the points, compare them with and , then update , and their indices accordingly.
- Store the leftmost point into the left boundary point cloud L and the rightmost point into the right boundary point cloud R.
- Finally, after traversing all rows, the left boundary point cloud set and the right boundary point cloud set can be obtained, where , , ,…, are the 1st, 2nd, 3rd,..., wth clusters of the left boundary, and , , ,…, are the 1st, 2nd, 3rd,..., vth clusters of the right boundary.
- For each point , where L is the left boundary point cloud set, find the K nearest neighbor points of P.
- Calculate the average distance and standard deviation from P to these K points.
- Determine if the distance from P to the K points is greater than . If not, it is not considered an outlier.
- Check if the difference between the X coordinate of P and the last point in the point cloud L is less than 1. If yes, it is not an aberrant point.
- Add points P that are determined to be neither outliers nor aberrant points to the output point cloud , which is the left boundary point cloud set after removing outliers. Similarly, obtain the right boundary point cloud set after removing outliers.
3.2.2. Adaptive Boundary Optimization
- Perform 2D rasterization on the coordinates of each point in the left boundary point cloud and store them in ; then, perform 2D rasterization on the coordinates of each point in the right boundary point cloud and store them in .
- Traverse each point in the input point cloud, calculate and using Equations (8) and (9), where is the mapped position of from the 3D point cloud onto the grid map, and is the mapped position of from the 3D point cloud onto the grid map. If the conditions of Equations (10) and (11) are met, add the point to the output point cloud.
- Taking the case of a right boundary interruption as an example, select appropriate parameters for boundary fitting on the right boundary extracted in Section 3.2.1 (the specific fitting process will be detailed in Section 3.2.3), resulting in a preliminary fitted right boundary.
- In , for the ith point, connect the (i − 1)th point with the (i + 1)th point, and shift the point along a direction perpendicular to this line by a distance equal to the width of the roadway.
- Add the preliminarily fitted right boundary and the shifted together to form the final right boundary. If the left boundary is interrupted, the same approach is used for completion.
3.2.3. Boundary Fitting
3.3. Continuously Extracting Tunnel Boundaries
4. Experiments
4.1. Experimental Platform Description
4.2. Data Source and Evaluation Metrics
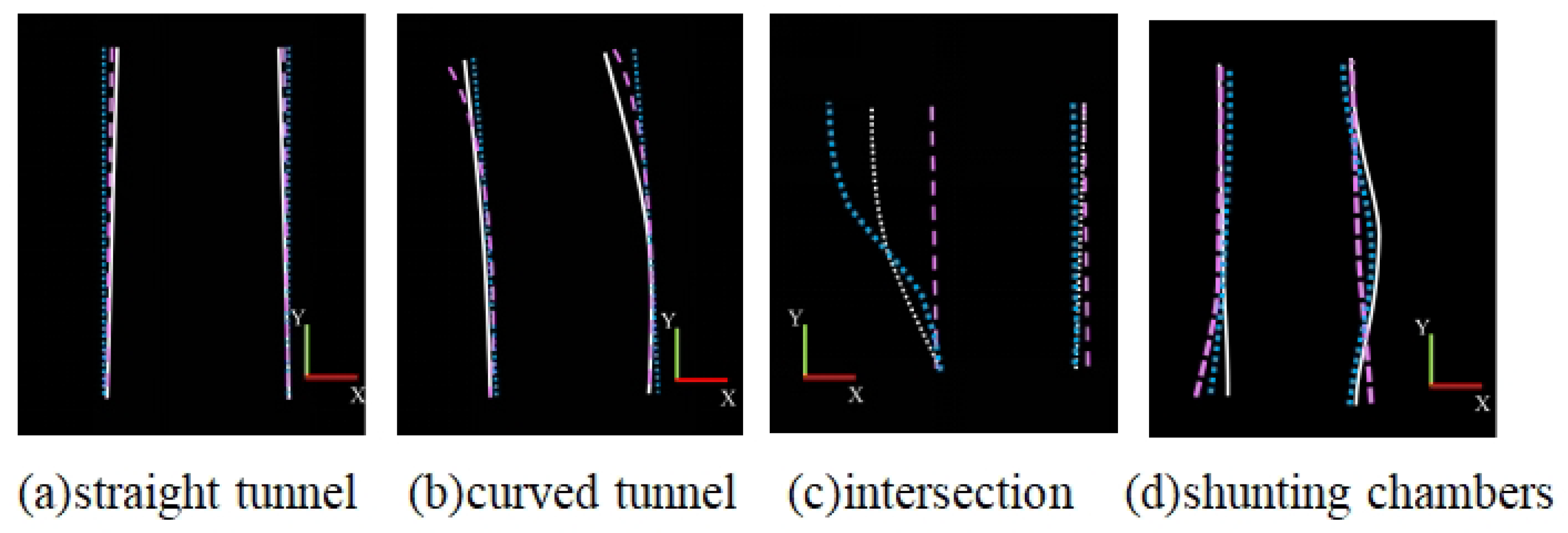
4.3. Underground Tunnel Boundary Detection Results
4.4. Comparative Experiments and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiong, Y.; Zhang, X.; Gao, X.; Qu, Q.; Duan, C.; Wang, R.; Liu, J.; Li, J. Cooperative Camera-LiDAR Extrinsic Calibration for Vehicle-Infrastructure Systems in Urban Intersections. IEEE Internet Things J. 2025, 1. [Google Scholar] [CrossRef]
- Xiong, Y.; Zhang, X.; Gao, W.; Wang, Y.; Liu, J.; Qu, Q.; Guo, S.; Shen, Y.; Li, J. GF-SLAM: A Novel Hybrid Localization Method Incorporating Global and Arc Features. IEEE Trans. Autom. Sci. Eng. 2025, 22, 6653–6663. [Google Scholar] [CrossRef]
- Bar Hillel, A.; Lerner, R.; Levi, D.; Raz, G. Recent progress in road and lane detection: A survey. Mach. Vis. Appl. 2014, 25, 727–745. [Google Scholar] [CrossRef]
- Lan, M.; Zhang, Y.; Zhang, L.; Du, B. Global context based automatic road segmentation via dilated convolutional neural network. Inf. Sci. 2020, 535, 156–171. [Google Scholar] [CrossRef]
- Wang, S.; Nguyen, C.; Liu, J.; Zhang, K.; Luo, W.; Zhang, Y.; Muthu, S.; Maken, F.A.; Li, H. Homography Guided Temporal Fusion for Road Line and Marking Segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 1075–1085. [Google Scholar]
- Li, X.; Zhang, G.; Cui, H.; Hou, S.; Wang, S.; Li, X.; Chen, Y.; Li, Z.; Zhang, L. MCANet: A joint semantic segmentation framework of optical and SAR images for land use classification. Int. J. Appl. Earth Obs. Geoinf. 2022, 106, 102638. [Google Scholar] [CrossRef]
- Mei, J.; Li, R.J.; Gao, W.; Cheng, M.M. CoANet: Connectivity attention network for road extraction from satellite imagery. IEEE Trans. Image Process. 2021, 30, 8540–8552. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Li, D.; Long, Q.; Zhao, Z.; Gao, X.; Chen, J.; Yang, K. Real-time semantic segmentation for underground mine tunnel. Eng. Appl. Artif. Intell. 2024, 133, 108269. [Google Scholar] [CrossRef]
- Kim, H.; Choi, Y. Location estimation of autonomous driving robot and 3D tunnel mapping in underground mines using pattern matched LiDAR sequential images. Int. J. Min. Sci. Technol. 2021, 31, 779–788. [Google Scholar] [CrossRef]
- Kang, J.; Chen, N.; Li, M.; Mao, S.; Zhang, H.; Fan, Y.; Liu, H. A Point Cloud Segmentation Method for Dim and Cluttered Underground Tunnel Scenes Based on the Segment Anything Model. Remote Sens. 2023, 16, 97. [Google Scholar] [CrossRef]
- Li, J.; Liu, C. Research on Unstructured Road Boundary Detection. In Proceedings of the 2021 IEEE International Conference on Unmanned Systems (ICUS), Beijing, China, 15–17 October 2021; pp. 614–617. [Google Scholar]
- Mi, X.; Yang, B.; Dong, Z.; Chen, C.; Gu, J. Automated 3D road boundary extraction and vectorization using MLS point clouds. IEEE Trans. Intell. Transp. Syst. 2021, 23, 5287–5297. [Google Scholar] [CrossRef]
- Yu, B.; Zhang, H.; Li, W.; Qian, C.; Li, B.; Wu, C. Ego-lane index estimation based on lane-level map and LiDAR road boundary detection. Sensors 2021, 21, 7118. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Ai, Y.; Tian, B. Real-time mine road boundary detection and tracking for autonomous truck. Sensors 2020, 20, 1121. [Google Scholar] [CrossRef] [PubMed]
- Maddiralla, V.; Subramanian, S. Effective lane detection on complex roads with convolutional attention mechanism in autonomous vehicles. Sci. Rep. 2024, 14, 19193. [Google Scholar] [CrossRef] [PubMed]
- Swain, S.; Tripathy, A.K. Real-time lane detection for autonomous vehicles using YOLOV5 Segmentation Model. Int. J. Sustain. Eng. 2024, 17, 718–728. [Google Scholar] [CrossRef]
- Zou, Q.; Jiang, H.; Dai, Q.; Yue, Y.; Chen, L.; Wang, Q. Robust lane detection from continuous driving scenes using deep neural networks. IEEE Trans. Veh. Technol. 2019, 69, 41–54. [Google Scholar] [CrossRef]
- Huang, T.; Wang, Z.; Dai, X.; Huang, D.; Su, H. Unstructured lane identification based on hough transform and improved region growing. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 7612–7617. [Google Scholar]
- Han, J.; Kim, D.; Lee, M.; Sunwoo, M. Enhanced road boundary and obstacle detection using a downward-looking LIDAR sensor. IEEE Trans. Veh. Technol. 2012, 61, 971–985. [Google Scholar] [CrossRef]
- Wijesoma, W.S.; Kodagoda, K.S.; Balasuriya, A.P. Road-boundary detection and tracking using ladar sensing. IEEE Trans. Robot. Autom. 2004, 20, 456–464. [Google Scholar] [CrossRef]
- Liu, Z.; Yu, S.; Zheng, N. A co-point mapping-based approach to drivable area detection for self-driving cars. Engineering 2018, 4, 479–490. [Google Scholar] [CrossRef]
- Rato, D.; Santos, V. LIDAR based detection of road boundaries using the density of accumulated point clouds and their gradients. Robot. Auton. Syst. 2021, 138, 103714. [Google Scholar] [CrossRef]
- Jiang, W.; Zhou, S.; Wang, Q.; Chen, W.; Chen, J. Research on Curb Detection and Tracking Method Based on Adaptive Multi-Feature Fusion. Automot. Eng. 2021, 43, 1762–1770. [Google Scholar]









| Filter Field | Filter Range | Inverted |
|---|---|---|
| -axis | (0, 20) | No |
| -axis | (−2, 2) | No |
| Category | Details |
|---|---|
| Operating System | Ubuntu 20.04 LTS |
| CPU | 8-core Arm®Cortex®-A78AE v8.2 |
| 64-bit CPU 2MB L2 + 4MB L3 | |
| GPU | NVIDIA (Santa Clara, CA, USA) Ampere architecture with |
| 1792 NVIDIA CUDA®cores and 56 tensor cores | |
| Memory | 32GB 256-bit LPDDR5 204.8 GB/s |
| CUDA Version | CUDA 11.3 |
| cuDNN Version | cuDNN 8.6 |
| Python Version | Python 3.9 |
| Development Environment | PyCharm 2023.3 |
| Other Libraries | NumPy 1.26.4, OpenCV 3.4.9.31, PyTorch 2.3.1 |
| Scenarios | Precision | Recall | F1-Score | MSE | Time (ms) |
|---|---|---|---|---|---|
| Straight road | 97.5% | 96.9% | 97.2% | 0.015 | 29 |
| Curved road | 93.2% | 91.0% | 92.1% | 0.062 | 30 |
| Intersection | 85.0% | 81.8% | 83.0% | 0.18 | 45 |
| Shunting chambers | 88.3% | 85.11% | 86.7% | 0.12 | 45 |
| Methods | Precision | Average Time per Frame (ms) | |||
|---|---|---|---|---|---|
| Straight Tunnel | Curved Tunnel | Intersection | Shunting Chambers | ||
| Proposed method | 97.5% | 93.2% | 85.0% | 88.3% | 35 ms |
| Comparison method | 92.0% | 83.6% | 72.3% | 72.8% | 39 ms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, M.; Du, Y.; Zhang, X.; Ma, Z.; Wang, Z. Efficient Navigable Area Computation for Underground Autonomous Vehicles via Ground Feature and Boundary Processing. Sensors 2025, 25, 5355. https://doi.org/10.3390/s25175355
Yu M, Du Y, Zhang X, Ma Z, Wang Z. Efficient Navigable Area Computation for Underground Autonomous Vehicles via Ground Feature and Boundary Processing. Sensors. 2025; 25(17):5355. https://doi.org/10.3390/s25175355
Chicago/Turabian StyleYu, Miao, Yibo Du, Xi Zhang, Ziyan Ma, and Zhifeng Wang. 2025. "Efficient Navigable Area Computation for Underground Autonomous Vehicles via Ground Feature and Boundary Processing" Sensors 25, no. 17: 5355. https://doi.org/10.3390/s25175355
APA StyleYu, M., Du, Y., Zhang, X., Ma, Z., & Wang, Z. (2025). Efficient Navigable Area Computation for Underground Autonomous Vehicles via Ground Feature and Boundary Processing. Sensors, 25(17), 5355. https://doi.org/10.3390/s25175355





