Neural Network Method of Analysing Sensor Data to Prevent Illegal Cyberattacks
Abstract
1. Introduction and Related Works
- The lack of unified datasets for evaluating the comparative effectiveness complicates the optimal architecture choice.
- Many studies do not take into account the real transmission delays and end-device resource limitations.
- Neural network solution interpretability. Security operators often require explanations of why a particular point was marked as abnormal.
- Without the deep models’ “black box”, practical implementation in industrial systems is complex.
2. Materials and Methods
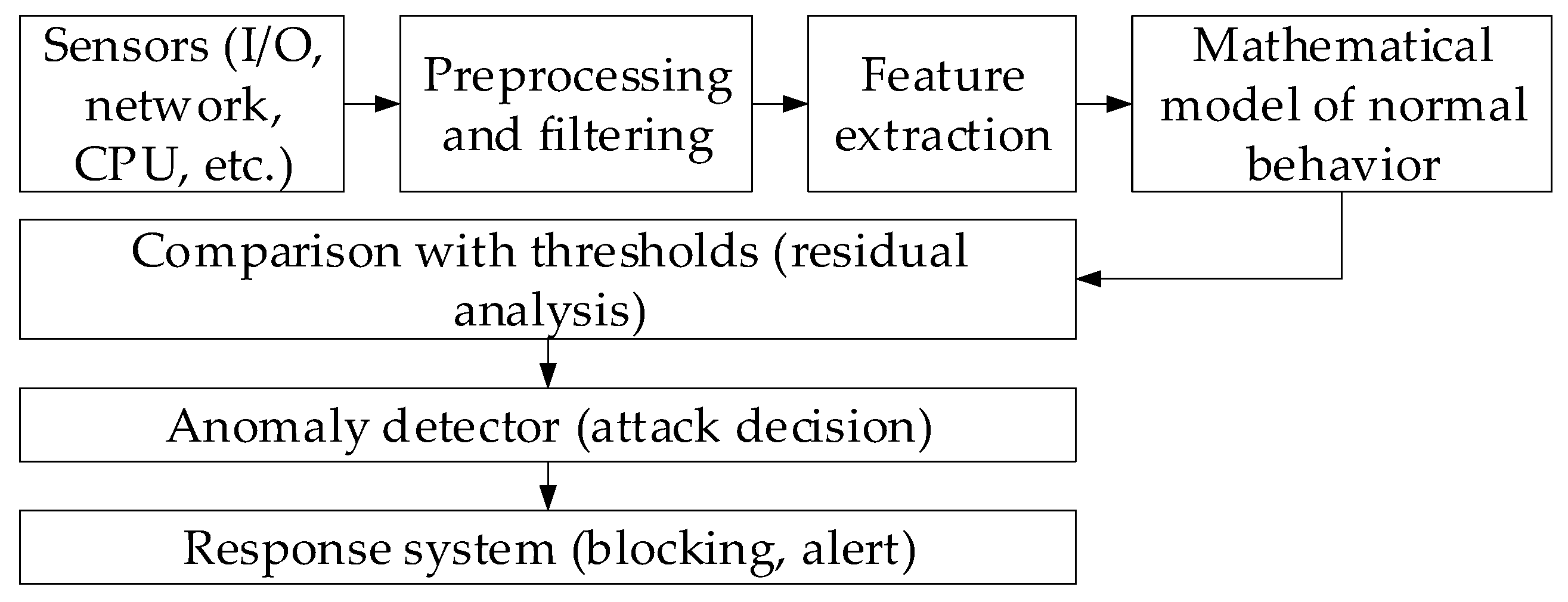
2.1. Theoretical Foundations of Sensory Data Analysis for Cyberattack Prevention
- Step 1. The dk statistic expectation growth.
- Step 2. Markov estimate of the time to reach the level.
- Step 3. The average E[T] estimation.
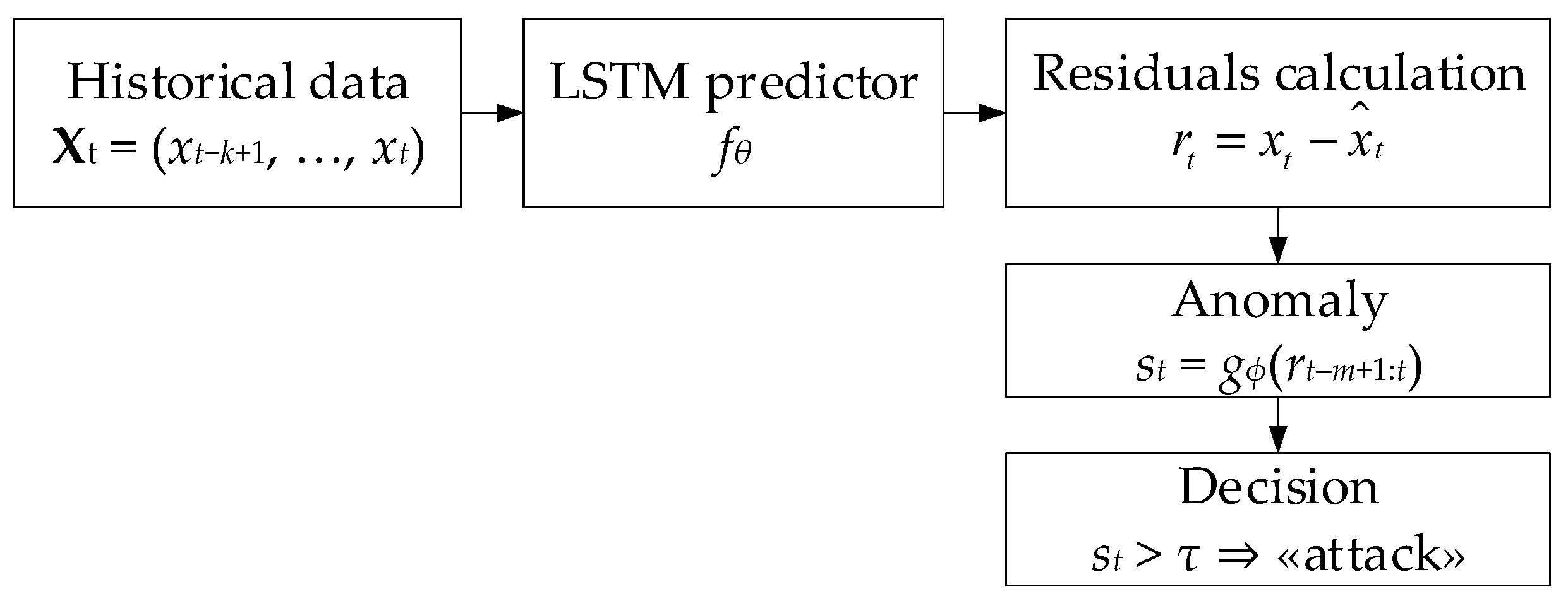
2.2. Development of a Neural Network Method for Analysing Sensory Data to Prevent Cyberattacks
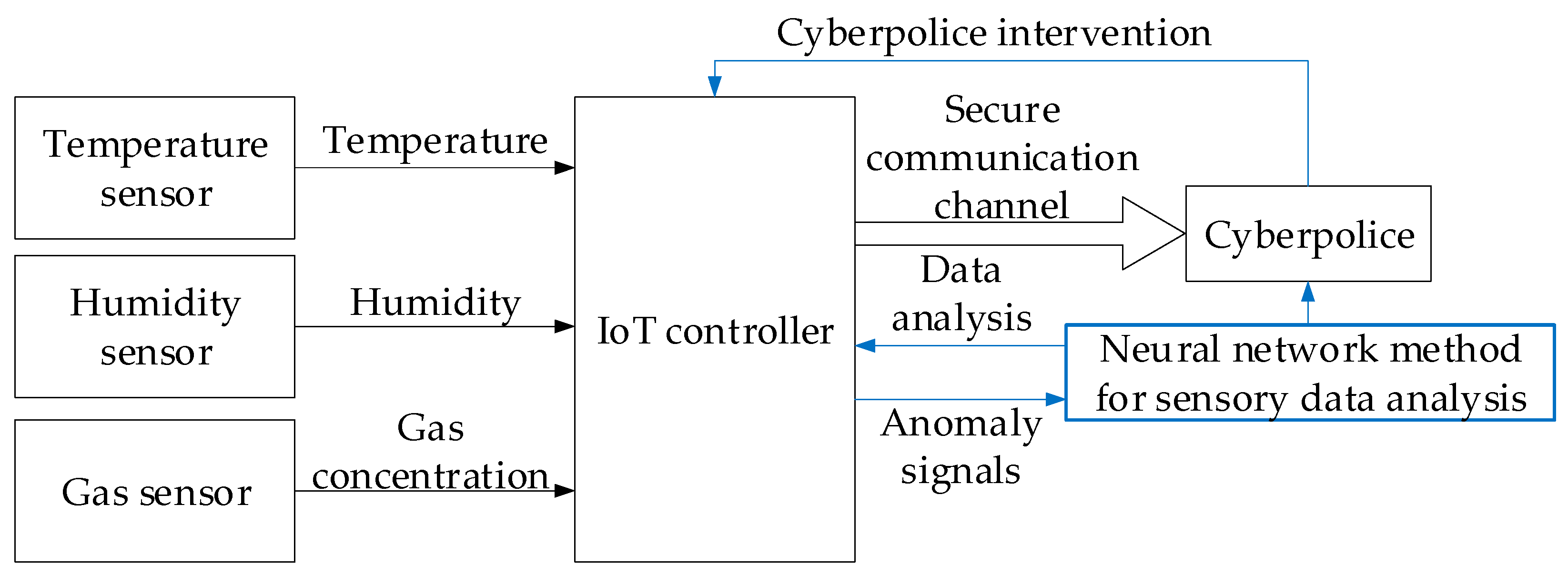
3. Case Study
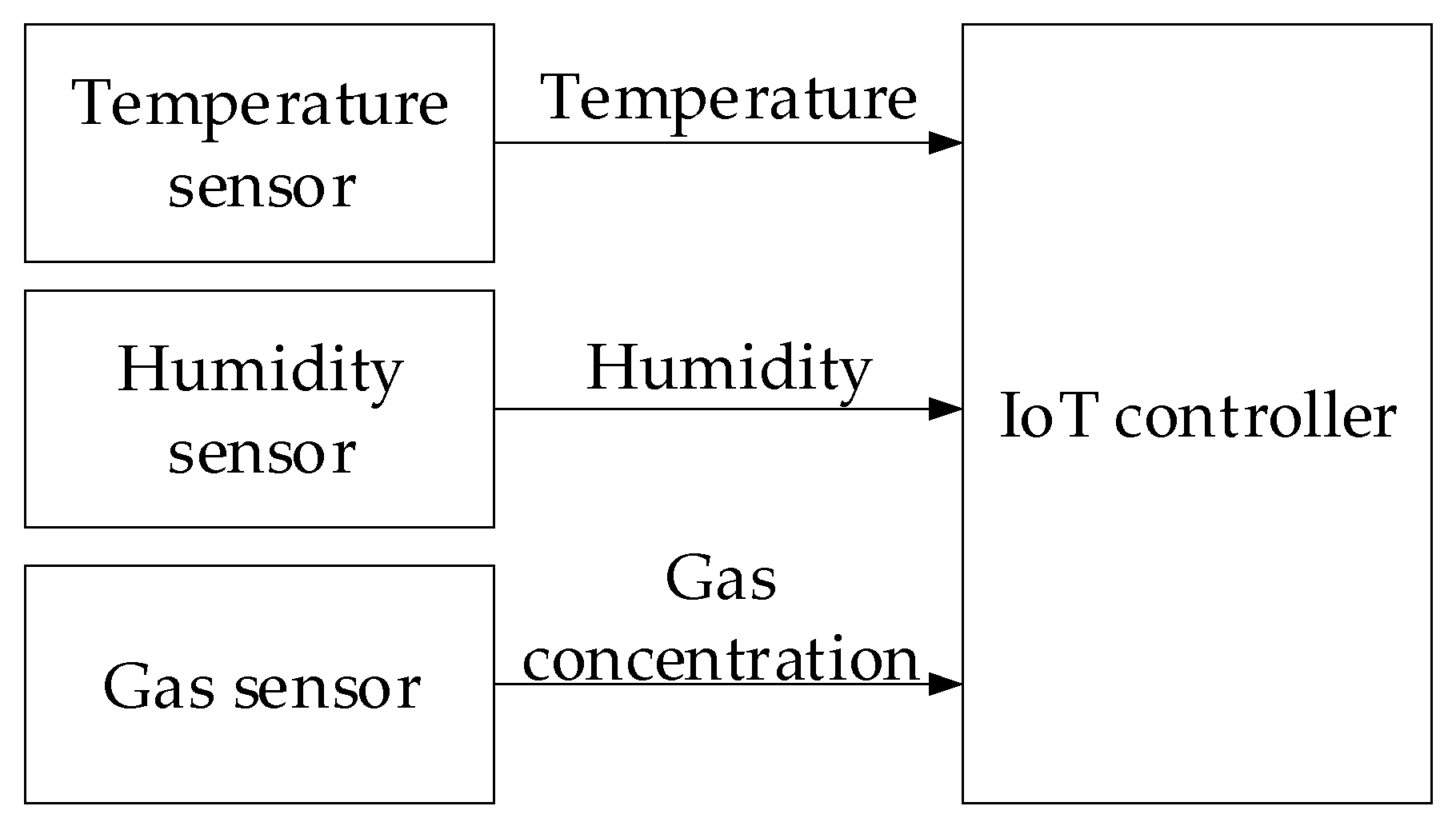
3.1. Description of the Research Object and Experimental Setup
- The temperature sensor measures room temperature.
- The humidity sensor measures air humidity.
- The gas sensor measures gas concentrations, such as CO2 or volatile organic compounds.
- Spoofing, in which an attacker sends fake numeric values, such as an elevated temperature, to cause an emergency shutdown of the equipment.
- A man-in-the-middle (MITM) attack, which allows the information being transmitted to be intercepted and modified.
- A replay attack, in which old but correct data is transmitted to hide current conditions, and a denial of service (DoS), which disrupts data transmission and paralyses the system.
- The input sensor data are first normalised in the preprocessing block (tanh transformation taking into account pre-calculated μ and σ);
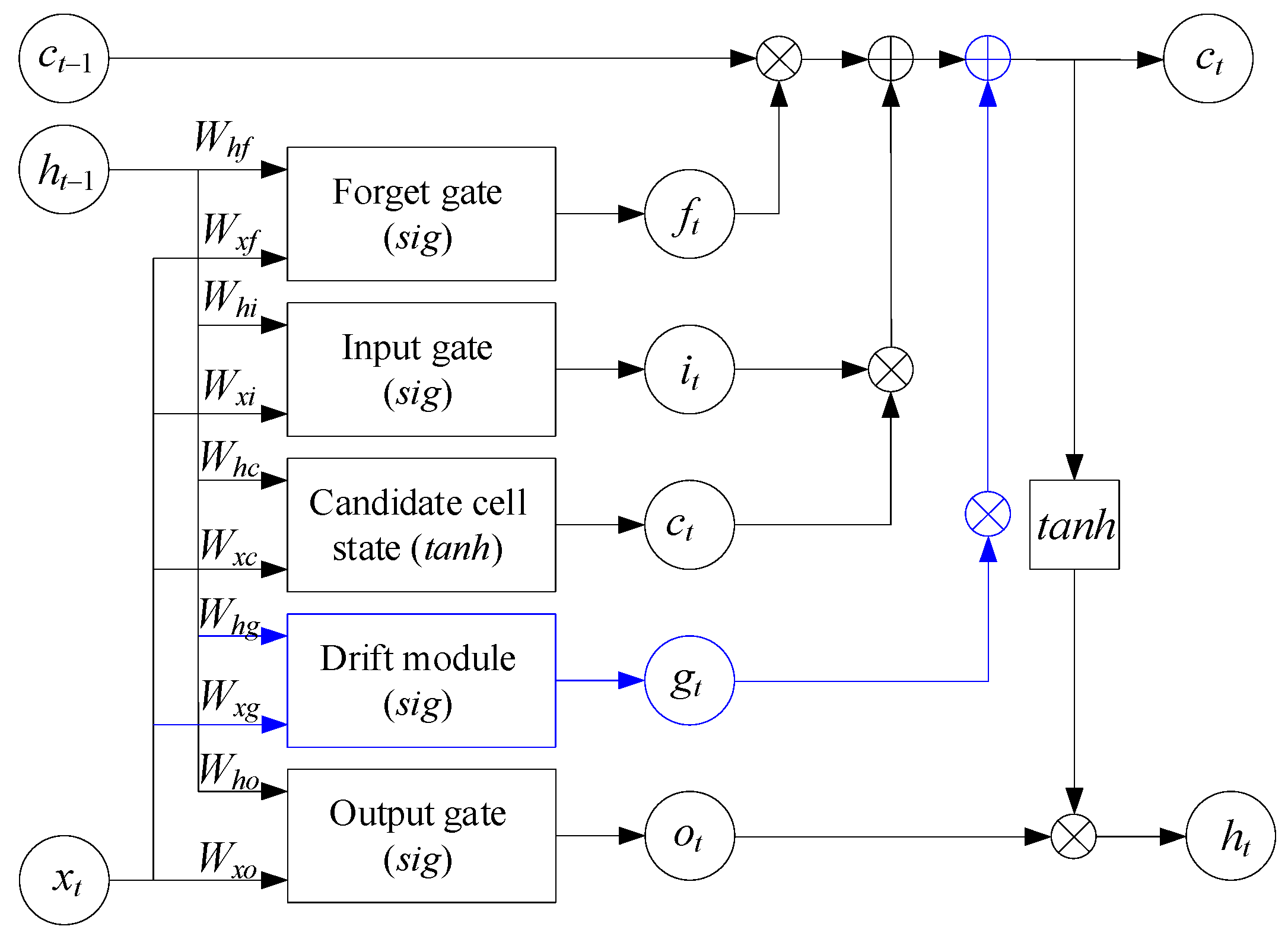
- The sliding-window buffer cumulative block forms a vector for the LSTM predictor (MATLAB function) from the previous k − 1 sample, which, based on the states h(t − 1), c(t − 1), and the model equations, produces a predict and updated states;
- The Residual Computation block calculates the residual and “whitens” it by multiplying by ;
- The Residual Window Buffer accumulates last m vectors rwhitened to form the matrix Rt;
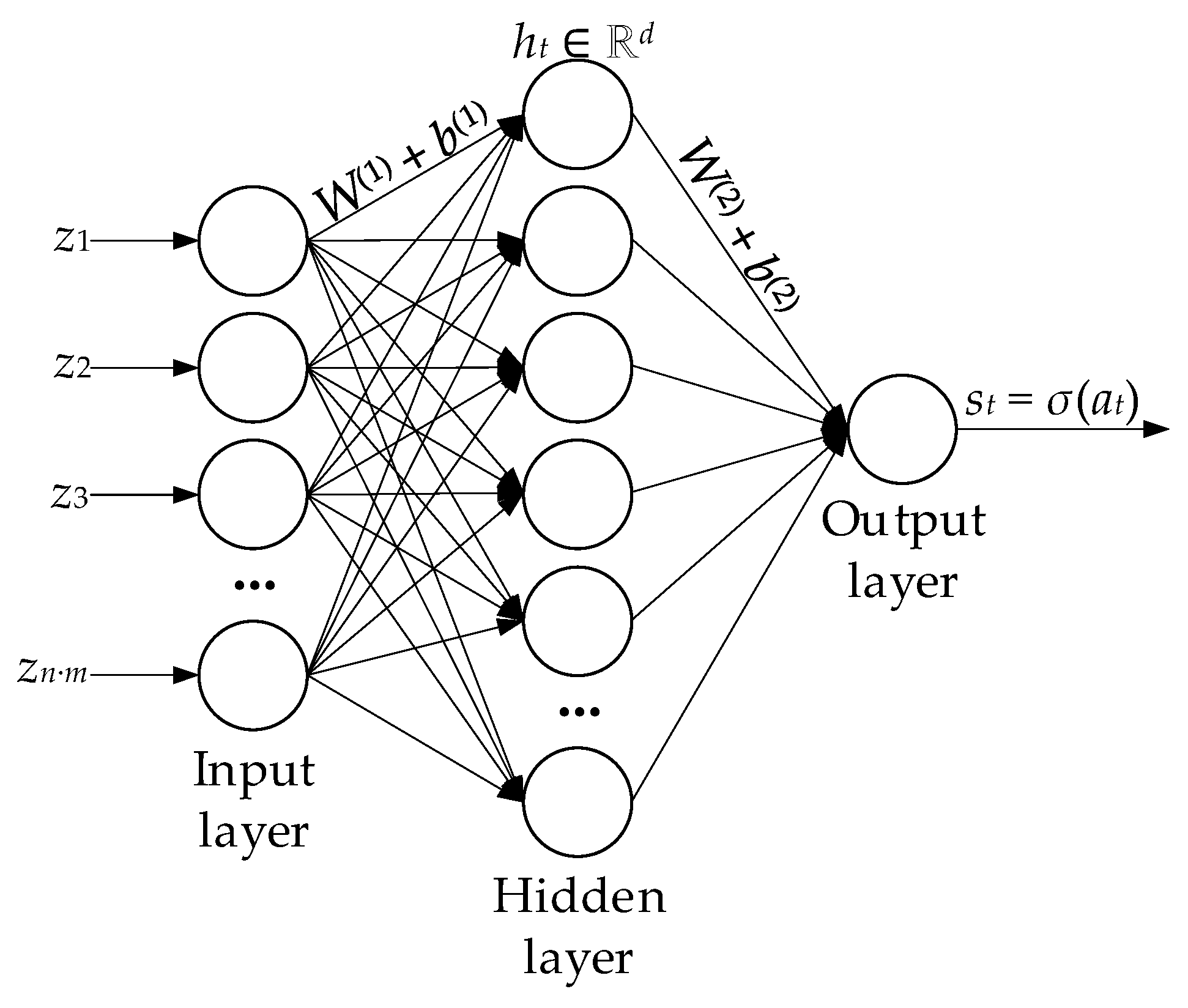
- In the MATLAB Function subsystem, Anomaly Classifier, based on MLP (two linear operations with SmoothReLU and sigmoid), anomaly probability estimate s(t) is produced for vector z = reshape(Rt), which is compared with threshold τ in the Threshold Decision (Compare to Constant block) and generates a Boolean alarm signal.
- The first LSTM layer contains 128 hidden elements, with tanh activation, output mode “sequence,” and a dropout of 0.2;
- The second contains 64 hidden elements, the output mode is “last,” and dropout is 0.1. The second LSTM layer output is passed to the Fully Connected block (10 neurons, softmax) and then to the Classification Output block, which forms a probabilistic vector class label (norm, spoofing, replay, or DoS).
3.2. Analysis and Preprocessing of the Training Dataset
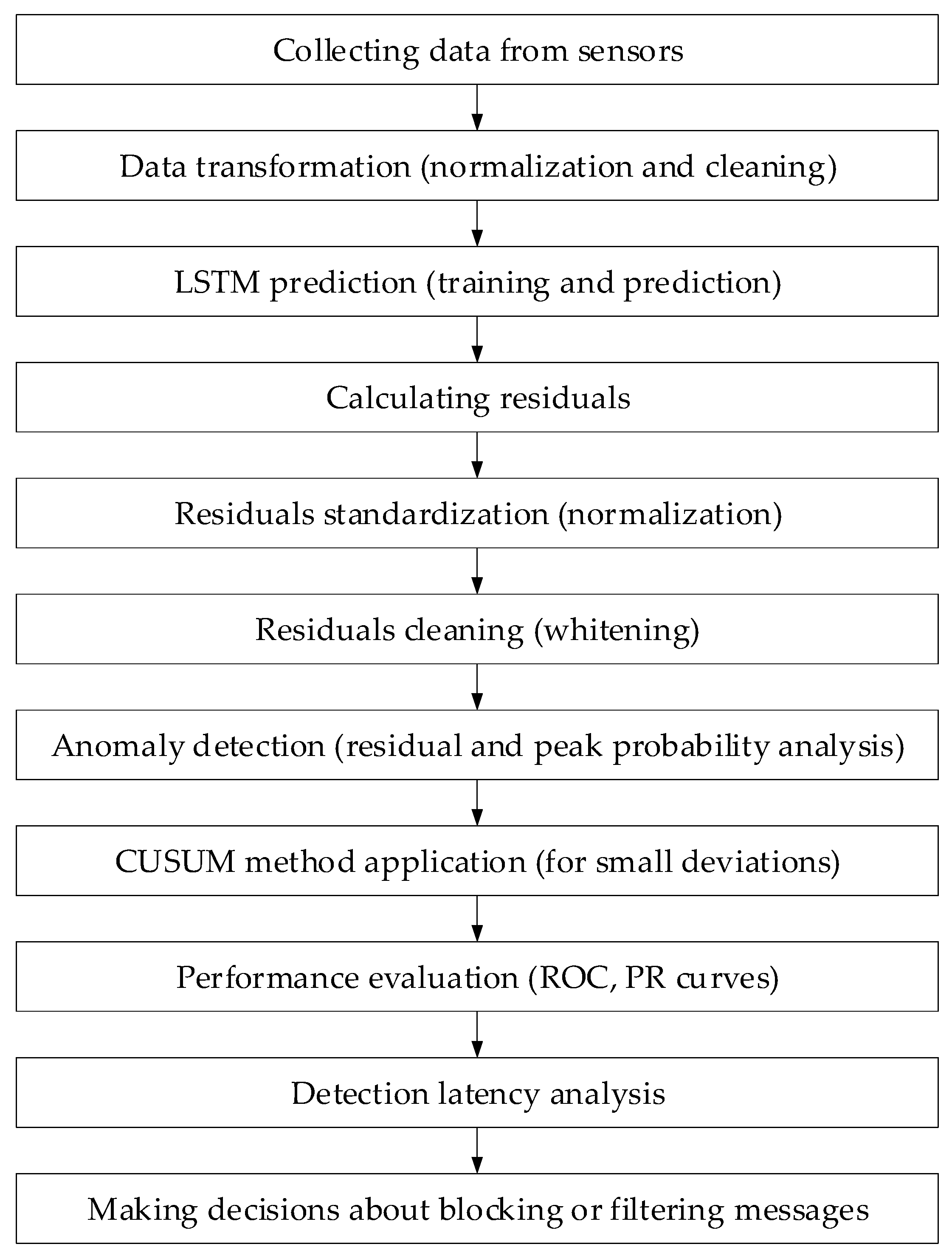
3.3. Results of Testing a Neural Network Method for Analysing Sensory Data to Prevent Cyberattacks
3.3.1. Test Results
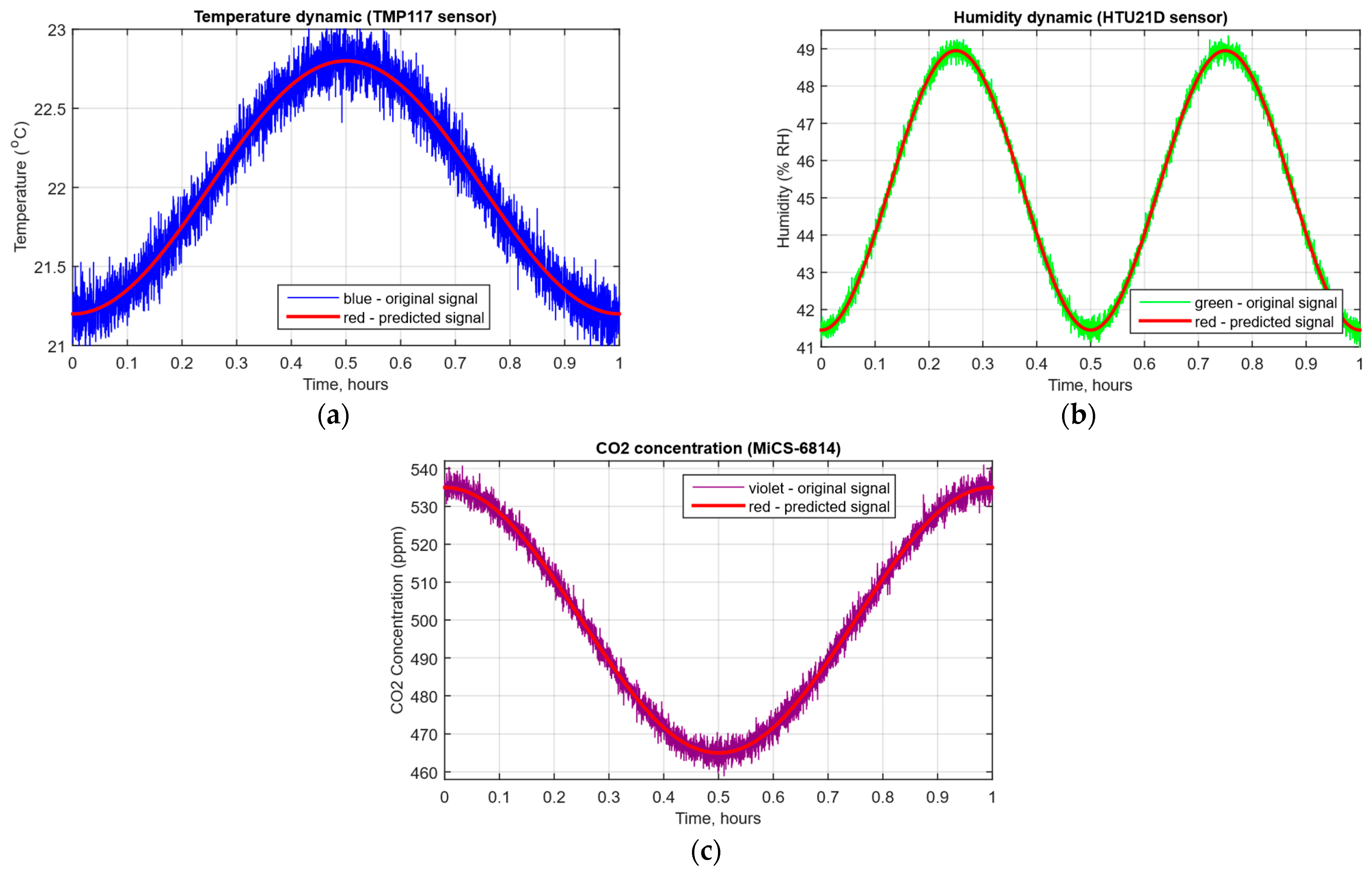
- The original signal and prediction time series (Figure 12), which are the xt and superposition for each sensor, determine the prediction quality of the LSTM predictor.
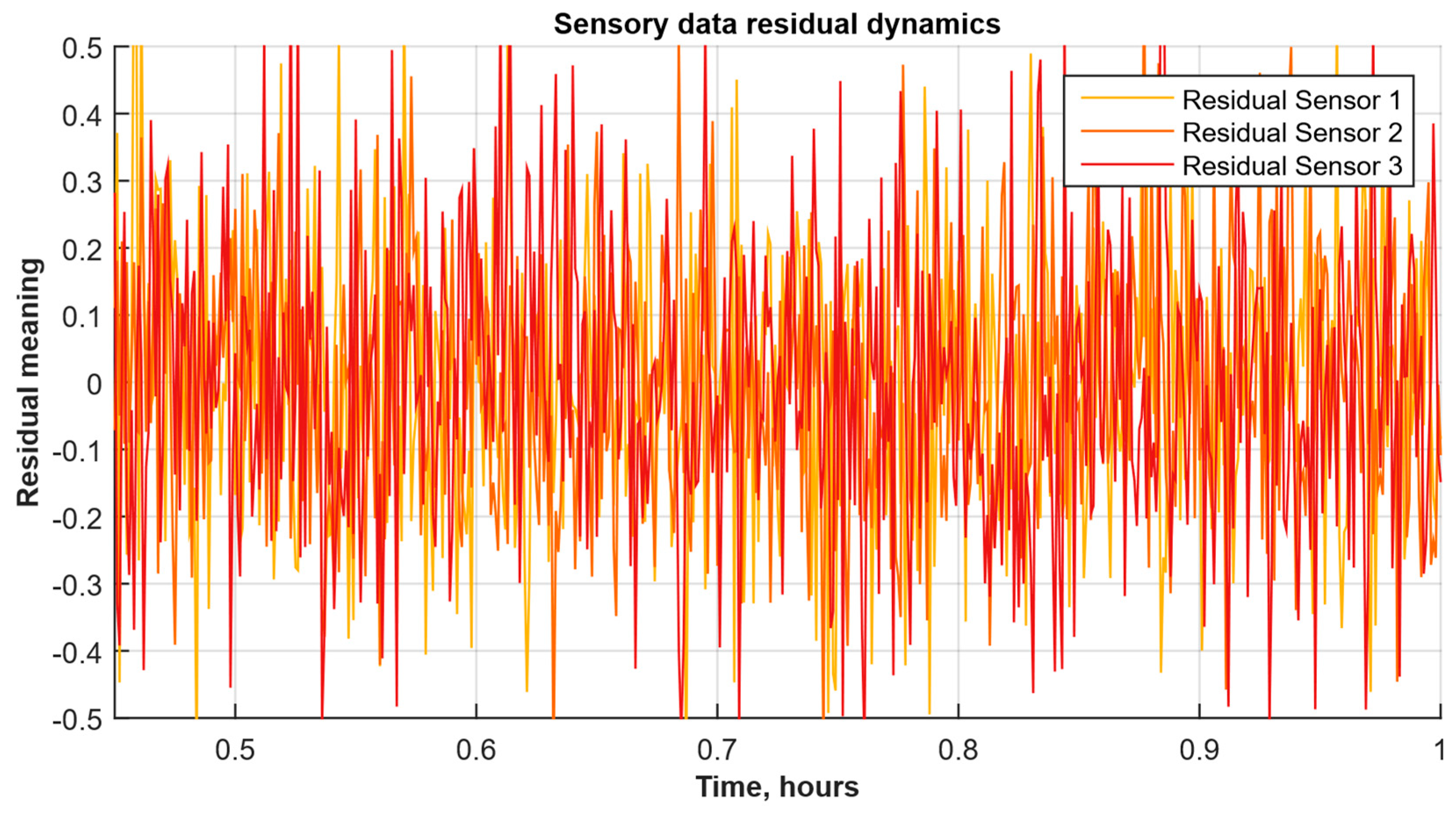
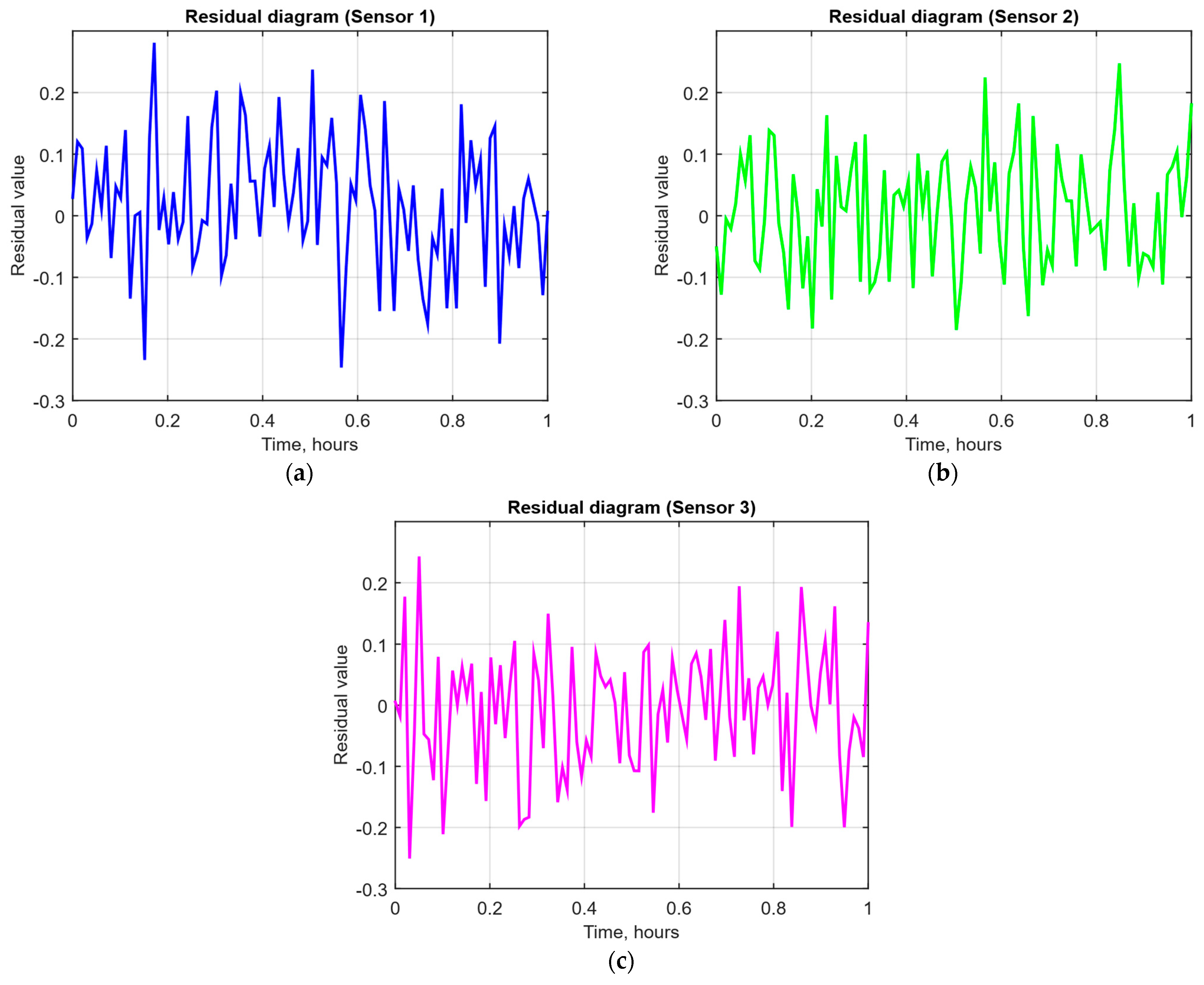
- Residual diagrams (Figure 13) reflecting the noise component and identified outliers.
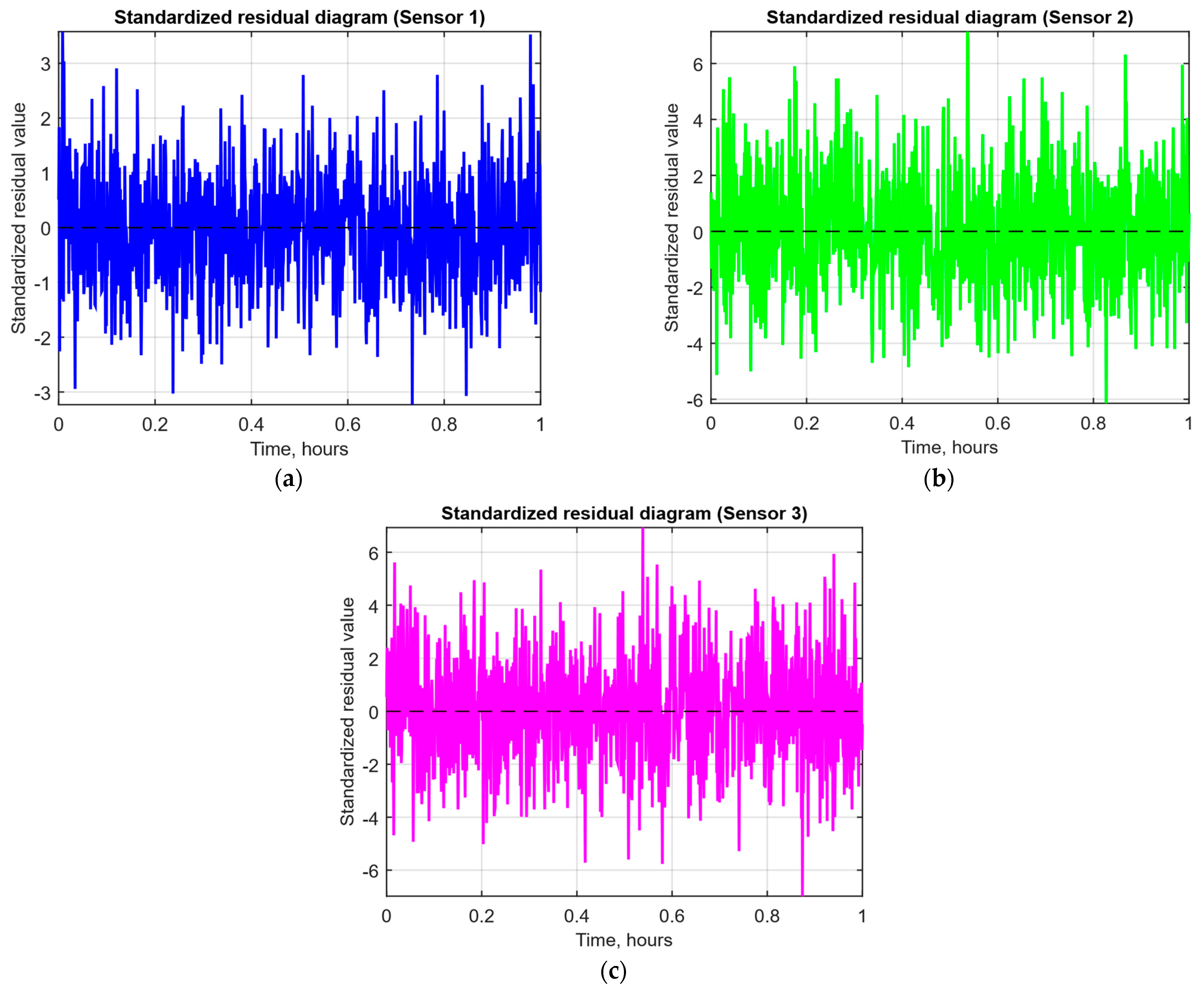
- Standardised residual diagrams (Figure 14), similar to residual diagrams but normalised to zero mean and unit variance, are used to assess the distribution normality.
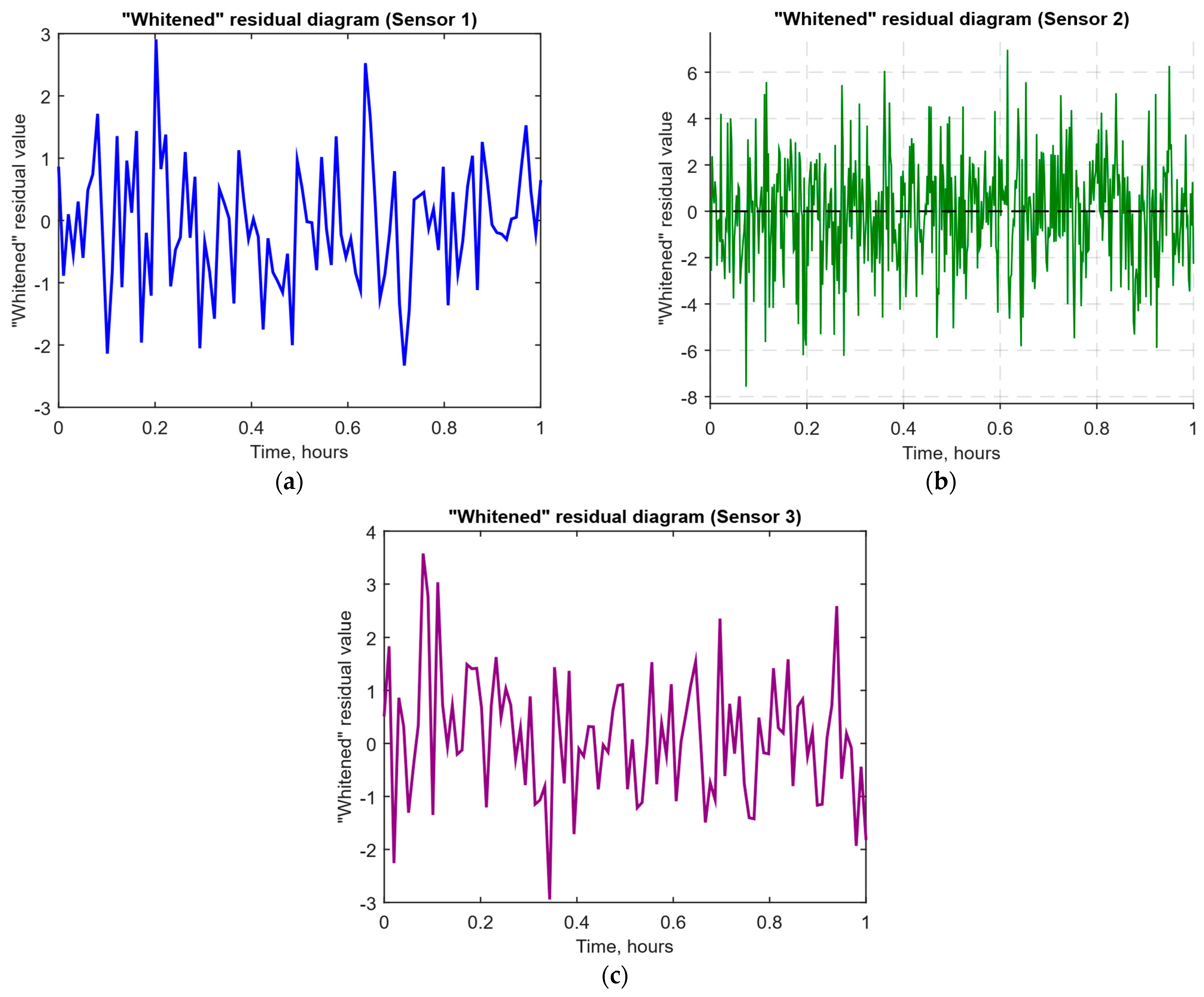
- The “whitened” residuals diagrams (Figure 15), representing correlated channels, are transformed into independent ones, which is convenient for clustering anomalies.
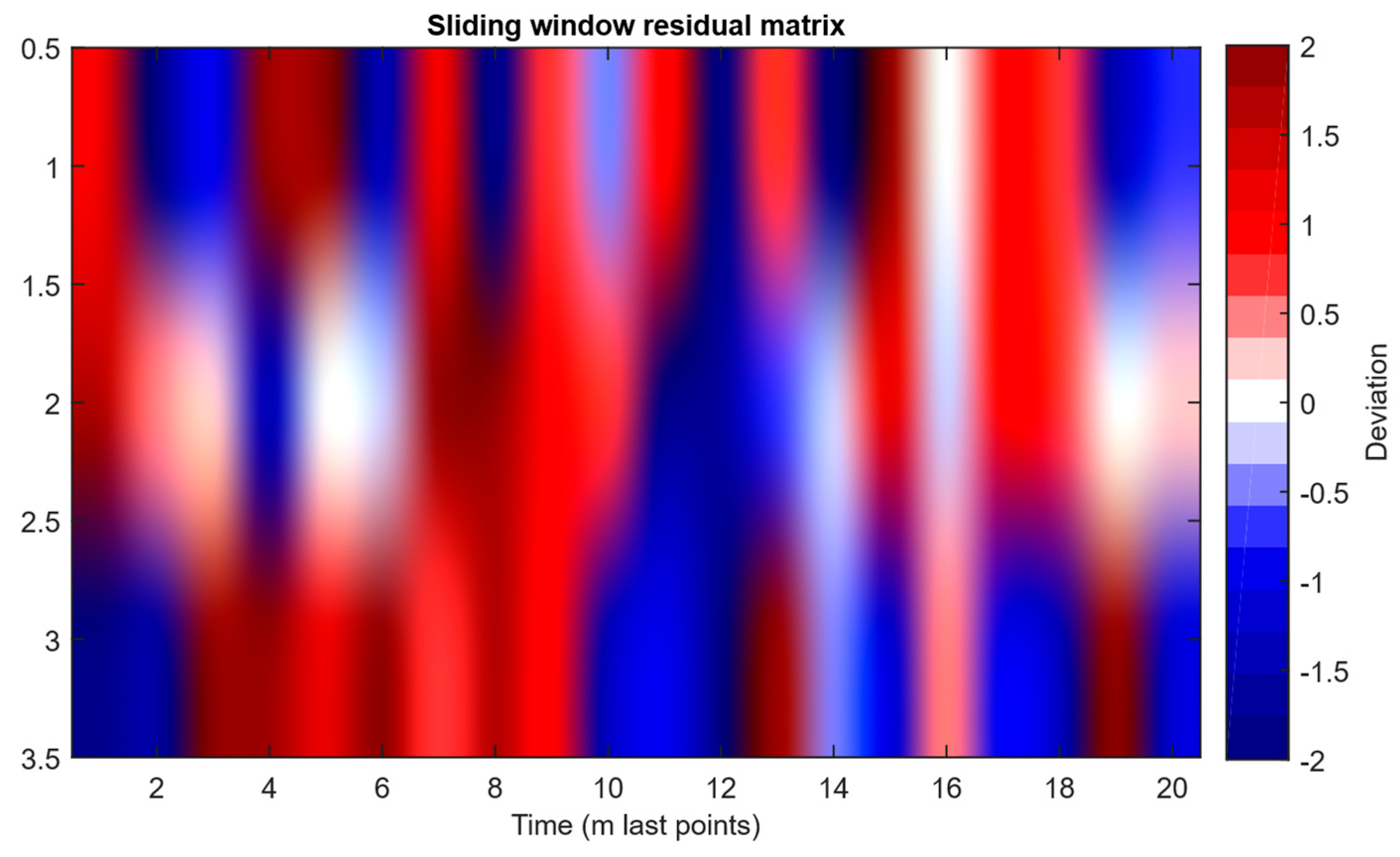
- The residuals matrix in a sliding window (Figure 16) of the array Rt ∈ ℝn×m allows for local deviation pattern analysis.
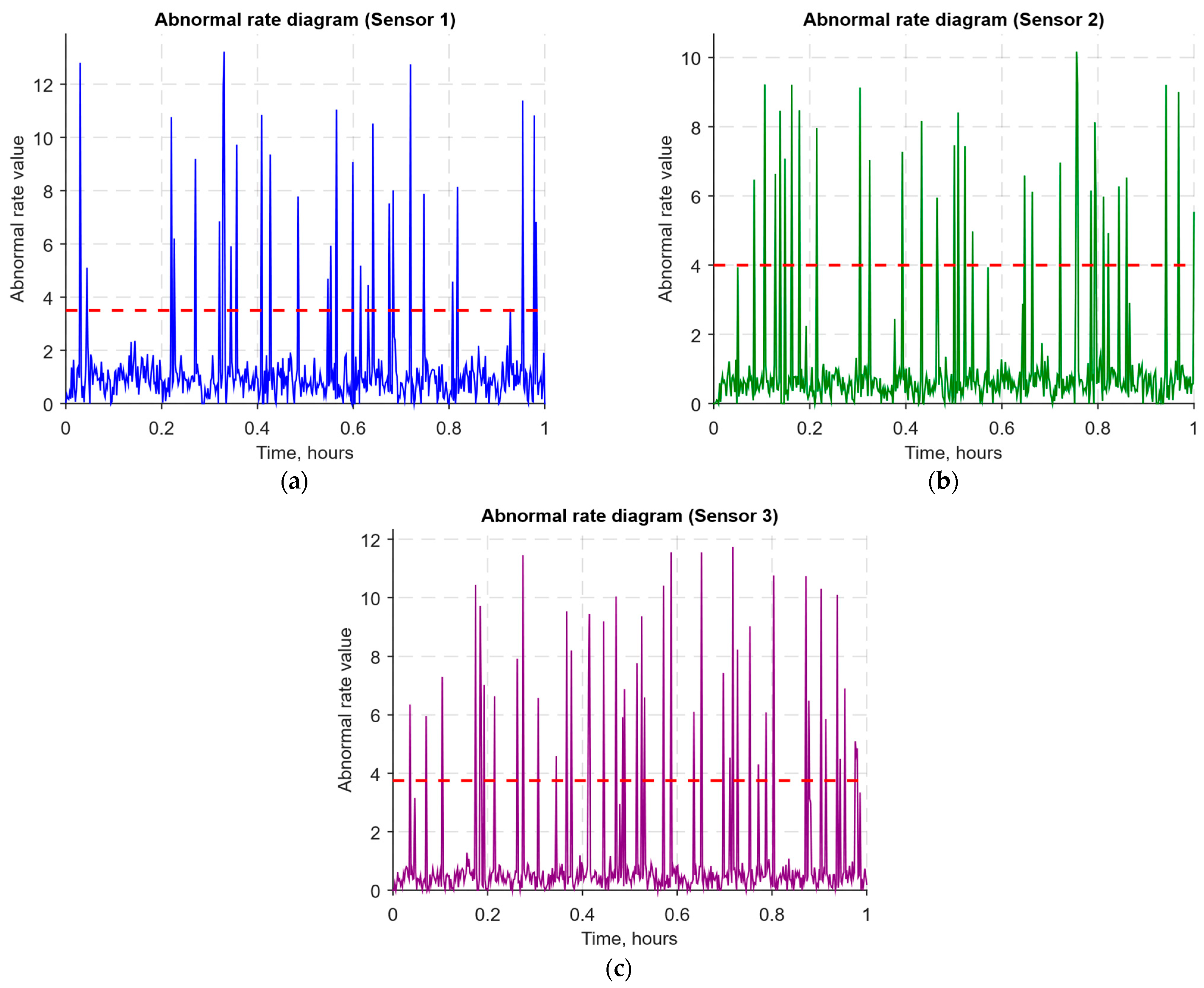
- The abnormal rate st over time diagram (Figure 17) allows you to track changes in the attack probability and the sharp peak locations.
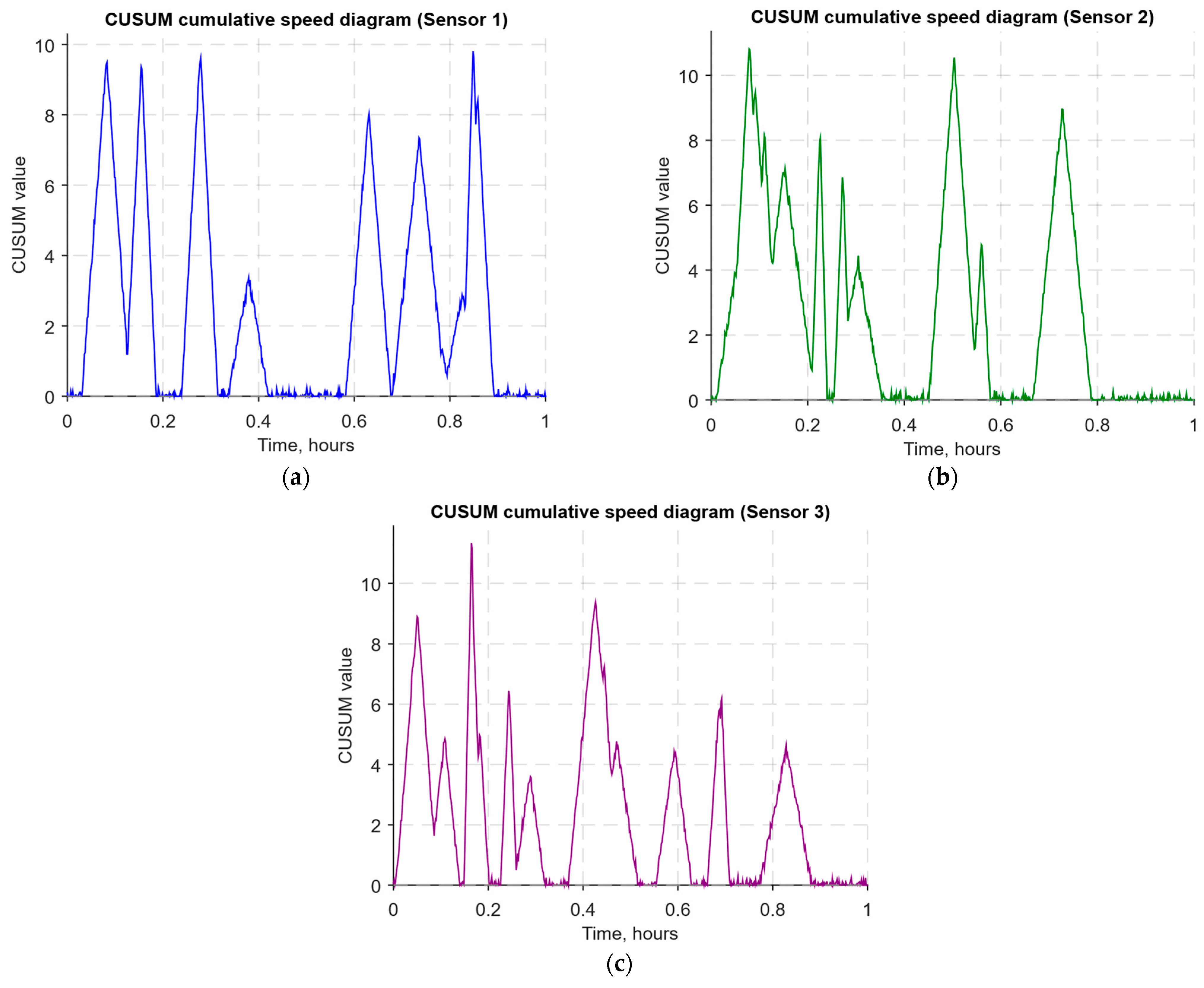
- The cumulative summation CUSUM diagram (Figure 18) provides a curve St = max(0, St−1 + st − ν) for early response to protracted minor anomalies.
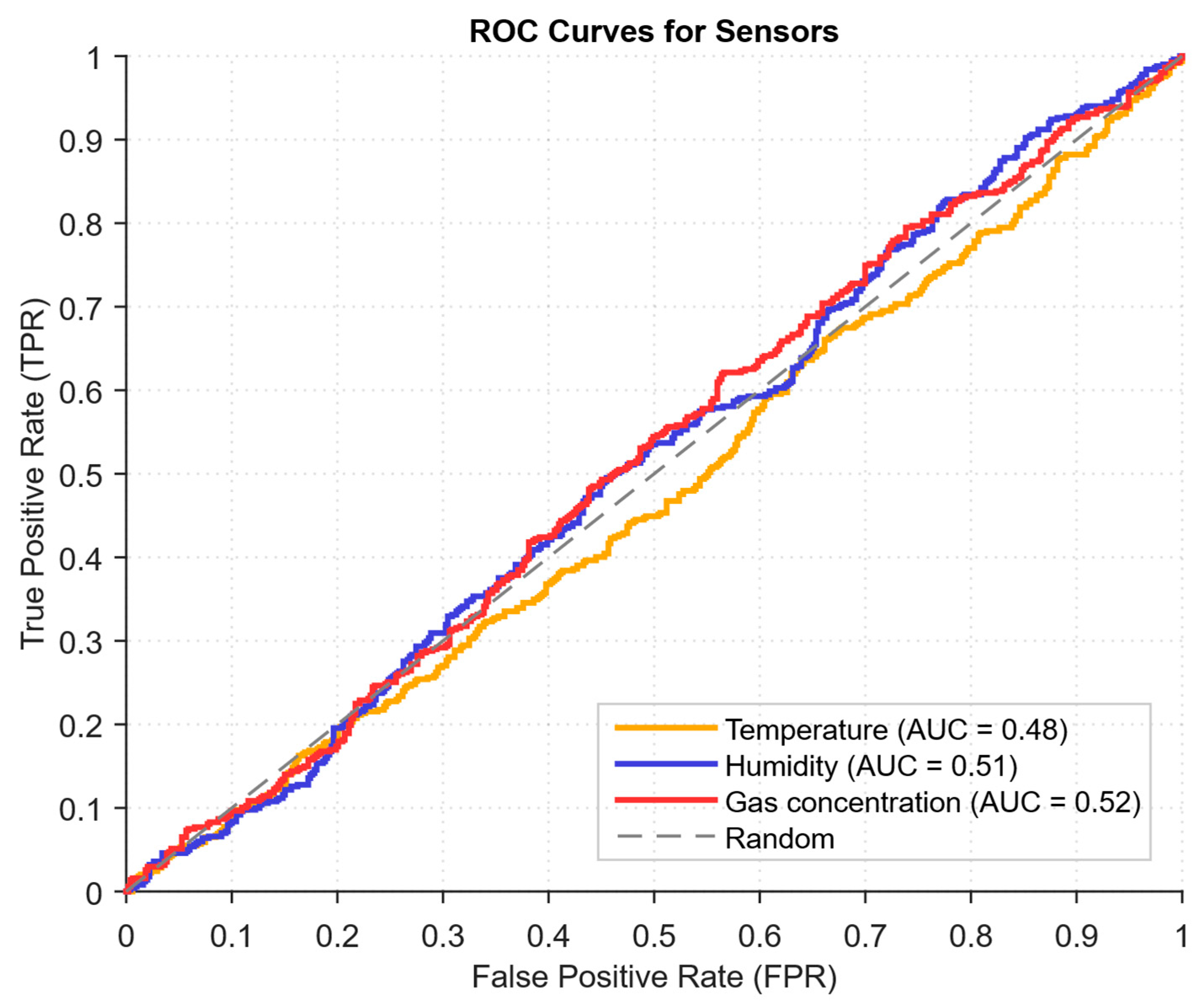
- The ROC curve (Figure 19), which represents the TPR(τ) on FPR(τ) dependence for different thresholds τ, illustrates the “sensitivity–false alarms” trade-off.
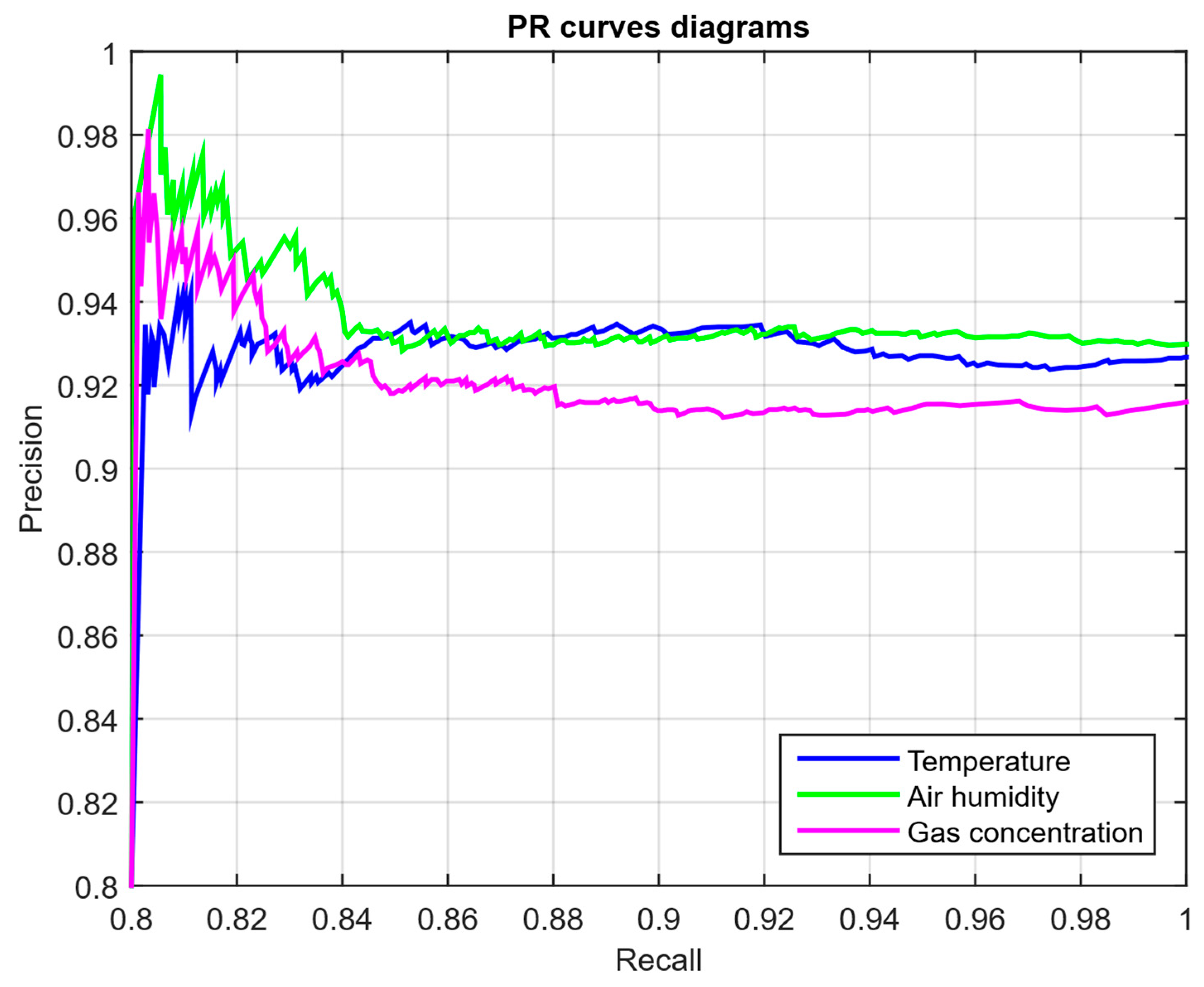
- The PR curve (Figure 20), which represents the precision on recall dependence with varying τ, is more informative for rare attacks.
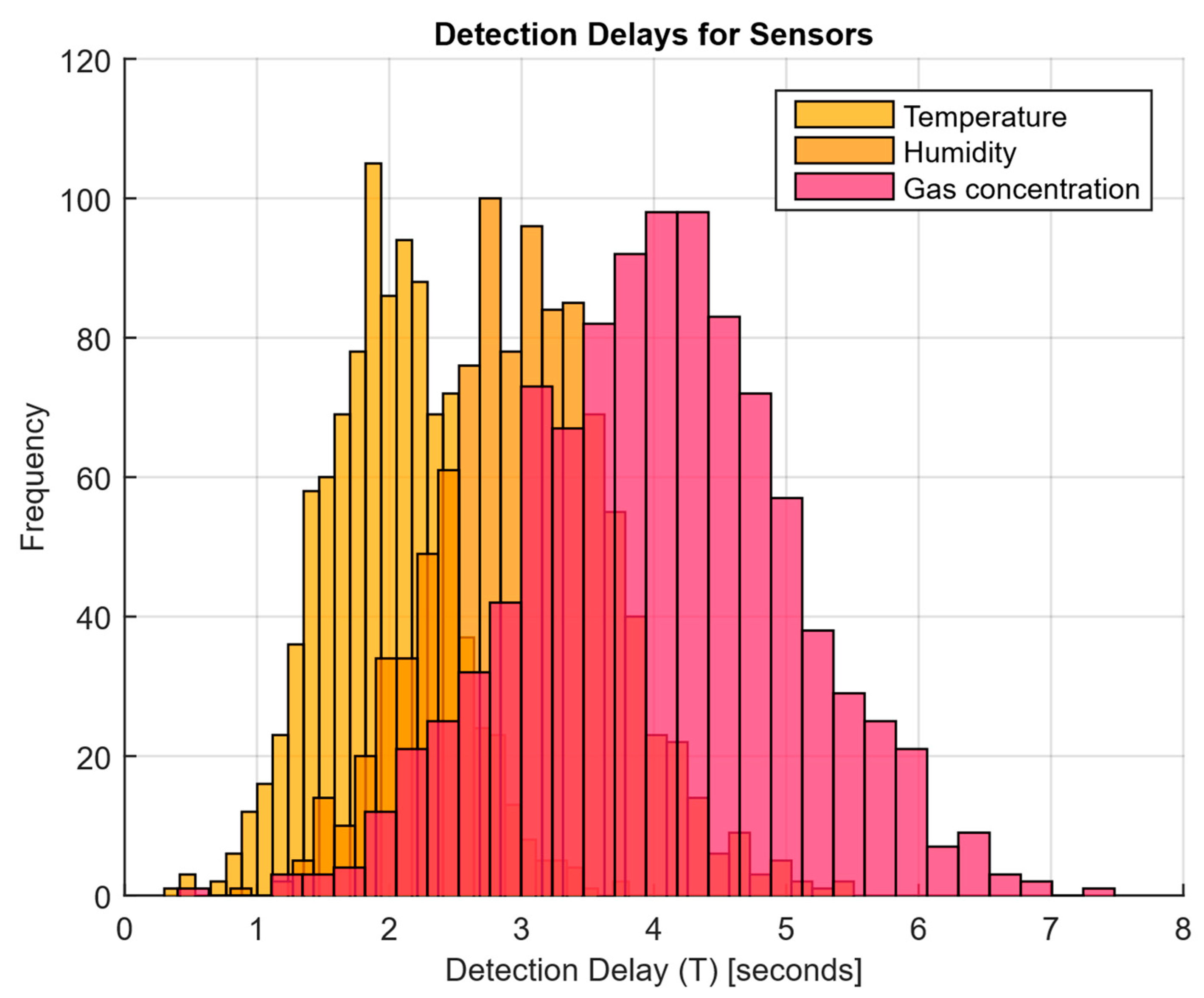
- The detection delays histogram (Figure 21), which represents the times T distribution from the attack’s actual start to the moment the detector is triggered, in order to estimate the reaction speed.
3.3.2. Implementation for Practical Activities of Cyber Police
3.4. Evaluation of the Effectiveness of the Neural Network Method for Analysing Sensory Data to Prevent Cyberattacks
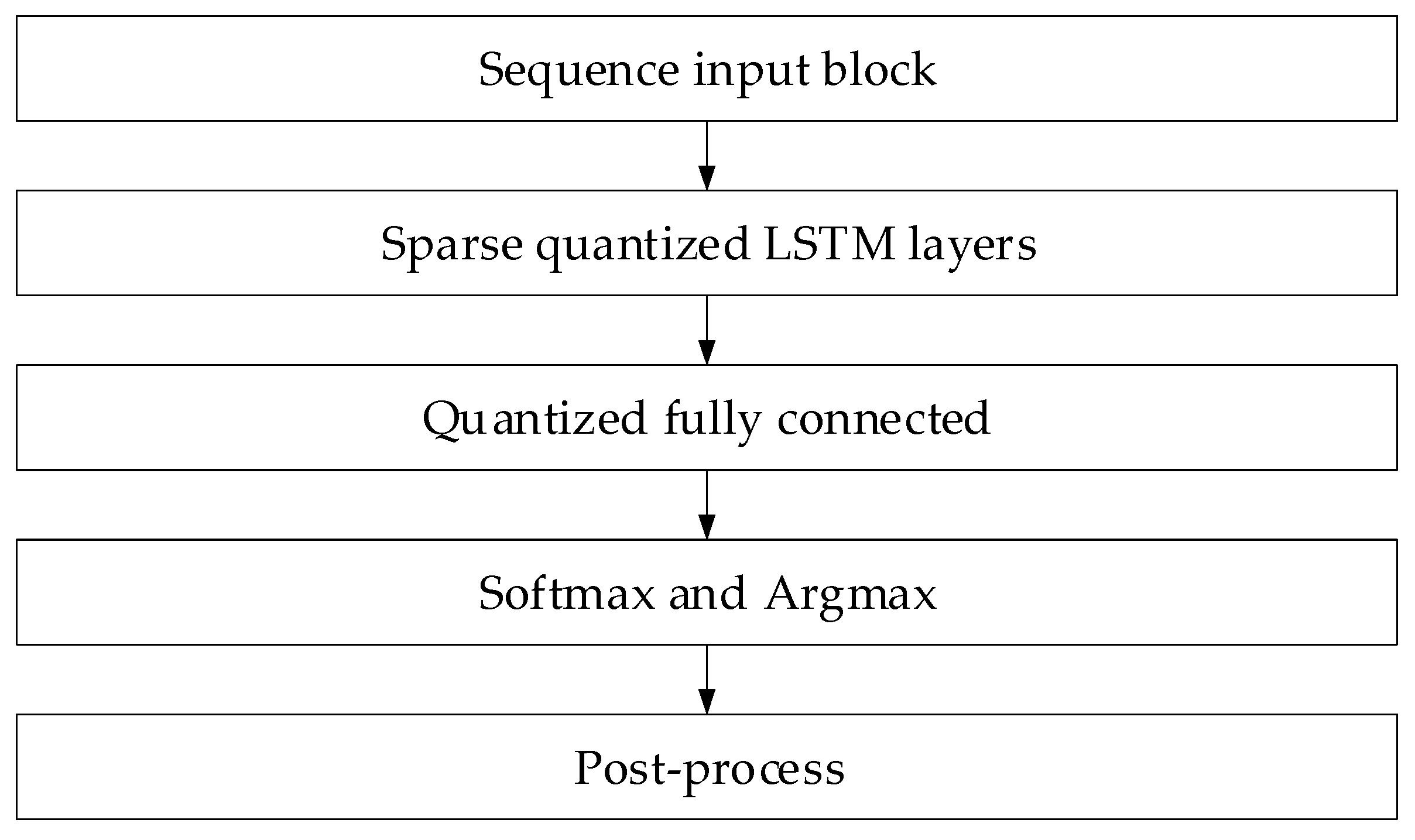
3.5. Development of an Optimisation Method for Low-Power Embedded Devices
4. Discussion
- The technique requires a large amount of “clean data” without attacks to train the LSTM model, which may be a problem in real-world conditions, where data with cyberattack labels may be limited or unavailable for training.
- Determining the optimal threshold for classifying anomalies depends on the chosen level. It requires additional settings and adaptation depending on the particular practical application specifics.
- Despite the method’s effectiveness, it requires significant computing resources to process large amounts of data in real time. It is a limitation for computing devices with limited computing power and energy consumption.
- Like many other neural network-based methods, the proposed approach suffers from the “black box” problem, which may make it difficult to explain to the operator why a particular result was classified as anomalous, which is vital for real-world exploitation in the cybersecurity field.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Song, W.; Zhu, X.; Ren, S.; Tan, W.; Peng, Y. A Hybrid Blockchain and Machine Learning Approach for Intrusion Detection System in Industrial Internet of Things. Alex. Eng. J. 2025, 127, 619–627. [Google Scholar] [CrossRef]
- Abidi, H.; Sidhom, L.; Bollen, M.; Chihi, I. Adaptive Software Sensor for Intelligent Control in Photovoltaic System Optimization. Int. J. Electr. Power Energy Syst. 2025, 170, 110921. [Google Scholar] [CrossRef]
- Yang, C.; Wang, J.; Liu, Y.; Ding, Y.; Liu, Z.; Wang, S. A Lightweight Decentralized Federated Learning Framework for the Industrial Internet of Things. Ad Hoc Netw. 2025, 178, 103962. [Google Scholar] [CrossRef]
- Afrin, S.; Rafa, S.J.; Kabir, M.; Farah, T.; Alam, M.S.B.; Lameesa, A.; Ahmed, S.F.; Gandomi, A.H. Industrial Internet of Things: Implementations, Challenges, and Potential Solutions across Various Industries. Comput. Ind. 2025, 170, 104317. [Google Scholar] [CrossRef]
- Mengash, H.A.; Mahgoub, H.; Alshuhail, A.; Darem, A.A.; Majdoubi, J.; Yafoz, A.; Alsini, R.; Alghushairy, O. Agricultural Consumer Internet of Things Devices: Methods for Optimizing Data Aggregation. Alex. Eng. J. 2025, 125, 692–699. [Google Scholar] [CrossRef]
- Liu, X. Research on Consumers’ Personal Information Security and Perception Based on Digital Twins and Internet of Things. Sustain. Energy Technol. Assess. 2022, 53, 102706. [Google Scholar] [CrossRef]
- Baláž, M.; Kováčiková, K.; Novák, A.; Vaculík, J. The Application of Internet of Things in Air Transport. Transp. Res. Procedia 2023, 75, 60–67. [Google Scholar] [CrossRef]
- Yin, Y.; Wang, H.; Deng, X. Real-Time Logistics Transport Emission Monitoring-Integrating Artificial Intelligence and Internet of Things. Transp. Res. Part D Transp. Environ. 2024, 136, 104426. [Google Scholar] [CrossRef]
- Rey, A.; Panetti, E.; Maglio, R.; Ferretti, M. Determinants in Adopting the Internet of Things in the Transport and Logistics Industry. J. Bus. Res. 2021, 131, 584–590. [Google Scholar] [CrossRef]
- Knieps, G. Internet of Things, Critical Infrastructures, and the Governance of Cybersecurity in 5G Network Slicing. Telecommun. Policy 2024, 48, 102867. [Google Scholar] [CrossRef]
- Bisikalo, O.; Danylchuk, O.; Kovtun, V.; Kovtun, O.; Nikitenko, O.; Vysotska, V. Modeling of Operation of Information System for Critical Use in the Conditions of Influence of a Complex Certain Negative Factor. Int. J. Control Autom. Syst. 2022, 20, 1904–1913. [Google Scholar] [CrossRef]
- Bisikalo, O.; Kovtun, O.; Kovtun, V.; Vysotska, V. Research of pareto-optimal schemes of control of availability of the information system for critical use. CEUR Workshop Proc. 2020, 2623, 174–193. Available online: https://ceur-ws.org/Vol-2623/paper17.pdf (accessed on 29 May 2025).
- Wang, Q.; Mu, Z. Risk Monitoring Model of Intelligent Agriculture Internet of Things Based on Big Data. Sustain. Energy Technol. Assess. 2022, 53, 102654. [Google Scholar] [CrossRef]
- Lan, Y.; Li, L.; Peng, H. A Verifiable Efficient Federated Learning Method Based on Adaptive Boltzmann Selection for Data Processing in the Internet of Things. J. Syst. Archit. 2025, 168, 103523. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, F.; Hu, H.; Liao, L.; Wang, D.; Fan, L. User Security Authentication Protocol in Multi Gateway Scenarios of the Internet of Things. Ad Hoc Netw. 2024, 156, 103427. [Google Scholar] [CrossRef]
- Abdullah, M. IoT-CDS: Internet of Things Cyberattack Detecting System Based on Deep Learning Models. Comput. Mater. Contin. 2024, 81, 4265–4283. [Google Scholar] [CrossRef]
- Alanazi, M.; Aljuhani, A. Anomaly Detection for Internet of Things Cyberattacks. Comput. Mater. Contin. 2022, 72, 261–279. [Google Scholar] [CrossRef]
- Mohamed, H.; Koroniotis, N.; Schiliro, F.; Moustafa, N. IoT-CAD: A Comprehensive Digital Forensics Dataset for AI-Based Cyberattack Attribution Detection Methods in IoT Environments. Ad Hoc Netw. 2025, 174, 103840. [Google Scholar] [CrossRef]
- Kishor, G.; Mugada, K.K.; Mahto, R.P. Sensor-Integrated Data Acquisition and Machine Learning Implementation for Process Control and Defect Detection in Wire Arc-Based Metal Additive Manufacturing. Precis. Eng. 2025, 95, 163–187. [Google Scholar] [CrossRef]
- Xue, D.; El-Farra, N.H. Optimal Sensor and Actuator Scheduling in Sampled-Data Control of Spatially Distributed Processes. IFAC-Pap. 2018, 51, 327–332. [Google Scholar] [CrossRef]
- Fang, W.; Shao, Y.; Love, P.E.D.; Hartmann, T.; Liu, W. Detecting Anomalies and De-Noising Monitoring Data from Sensors: A Smart Data Approach. Adv. Eng. Inform. 2023, 55, 101870. [Google Scholar] [CrossRef]
- Messina, D.; Durand, H. Lyapunov-Based Cyberattack Detection for Distinguishing Between Sensor and Actuator Attacks. IFAC-Pap. 2024, 58, 604–609. [Google Scholar] [CrossRef]
- Awad, A.H.; Alsabaan, M.; Ibrahem, M.I.; Saraya, M.S.; Elksasy, M.S.M.; Ali-Eldin, A.M.T.; Abdelsalam, M.M. Low-Cost IoT-Based Sensors Dashboard for Monitoring the State of Health of Mobile Harbor Cranes: Hardware and Software Description. Heliyon 2024, 10, e40239. [Google Scholar] [CrossRef] [PubMed]
- Golovko, V.; Egor, M.; Brich, A.; Sachenko, A. A Shallow Convolutional Neural Network for Accurate Handwritten Digits Classification. Commun. Comput. Inf. Sci. 2017, 673, 77–85. [Google Scholar] [CrossRef]
- Bodyanskiy, Y.; Deineko, A.; Skorik, V.; Brodetskyi, F. Deep Neural Network with Adaptive Parametric Rectified Linear Units and Its Fast Learning. Int. J. Comput. 2022, 21, 11–18. [Google Scholar] [CrossRef]
- Sun, L.; Sun, Y. Photovoltaic Power Forecasting Based on Artificial Neural Network and Ultraviolet Index. Int. J. Comput. 2022, 21, 153–158. [Google Scholar] [CrossRef]
- Vladov, S.; Shmelov, Y.; Petchenko, M. A Neuro-Fuzzy Expert System for the Control and Diagnostics of Helicopters Aircraft Engines Technical State. CEUR Workshop Proc. 2021, 3013, 40–52. Available online: https://ceur-ws.org/Vol-3013/20210040.pdf (accessed on 8 June 2025).
- Turchenko, V.; Kochan, V.; Sachenko, A. Estimation of Computational Complexity of Sensor Accuracy Improvement Algorithm Based on Neural Networks. Lect. Notes Comput. Sci. 2001, 2130, 743–748. [Google Scholar] [CrossRef]
- Hamolia, V.; Melnyk, V.; Zhezhnych, P.; Shilinh, A. Intrusion detection in computer networks using latent space representation and machine learning. Int. J. Comput. 2020, 19, 442–448. [Google Scholar] [CrossRef]
- Tian, J.; Mercier, P.; Paolini, C. Ultra Low-Power, Wearable, Accelerated Shallow-Learning Fall Detection for Elderly at-Risk Persons. Smart Health 2024, 33, 100498. [Google Scholar] [CrossRef]
- Jokic, A.; Zivkovic, M.; Jovanovic, L.; Mravik, M.; Sarac, M.; Simic, V.; Khan, M.A.; Bacanin, N. A Convolutional Neural Network-Enhanced Attack Detection Framework with Explainable Artificial Intelligence for Internet of Things-Based Metaverse Security. Eng. Appl. Artif. Intell. 2025, 144, 111358. [Google Scholar] [CrossRef]
- Vijayalakshmi, P.; Karthika, D. Hybrid Dual-Channel Convolution Neural Network (DCCNN) with Spider Monkey Optimization (SMO) for Cyber Security Threats Detection in Internet of Things. Meas. Sens. 2023, 27, 100783. [Google Scholar] [CrossRef]
- Balingbing, C.B.; Kirchner, S.; Siebald, H.; Kaufmann, H.-H.; Gummert, M.; Van Hung, N.; Hensel, O. Application of a Multi-Layer Convolutional Neural Network Model to Classify Major Insect Pests in Stored Rice Detected by an Acoustic Device. Comput. Electron. Agric. 2024, 225, 109297. [Google Scholar] [CrossRef]
- Zarzycki, K.; Chaber, P.; Cabaj, K.; Ławryńczuk, M.; Marusak, P.; Nebeluk, R.; Plamowski, S.; Wojtulewicz, A. Forgery Cyber-Attack Supported by LSTM Neural Network: An Experimental Case Study. Sensors 2023, 23, 6778. [Google Scholar] [CrossRef]
- Gupta, B.B.; Chui, K.T.; Gaurav, A.; Arya, V.; Chaurasia, P. A Novel Hybrid Convolutional Neural Network- and Gated Recurrent Unit-Based Paradigm for IoT Network Traffic Attack Detection in Smart Cities. Sensors 2023, 23, 8686. [Google Scholar] [CrossRef]
- Vladov, S.; Vysotska, V.; Sokurenko, V.; Muzychuk, O.; Nazarkevych, M.; Lytvyn, V. Neural Network System for Predicting Anomalous Data in Applied Sensor Systems. Appl. Syst. Innov. 2024, 7, 88. [Google Scholar] [CrossRef]
- Yu, X.; Meng, W.; Liu, Y.; Zhou, F. TridentShell: An Enhanced Covert and Scalable Backdoor Injection Attack on Web Applications. J. Netw. Comput. Appl. 2024, 223, 103823. [Google Scholar] [CrossRef]
- Vladov, S.; Yakovliev, R.; Vysotska, V.; Nazarkevych, M.; Lytvyn, V. The Method of Restoring Lost Information from Sensors Based on Auto-Associative Neural Networks. Appl. Syst. Innov. 2024, 7, 53. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, G.; Chen, Y.; Yang, W.; Wang, G. Inter-Layer Explainable Variational Autoencoder Model for Multivariate Time Series Anomaly Detection. Eng. Appl. Artif. Intell. 2025, 159, 111585. [Google Scholar] [CrossRef]
- Lu, R.; Zheng, D.; Yang, Q.; Cao, W.; Zhu, C. Anomaly Detection for Non-Stationary Rotating Machinery Based on Signal Transform and Memory-Guided Multi-Scale Feature Reconstruction. Eng. Appl. Artif. Intell. 2025, 154, 110824. [Google Scholar] [CrossRef]
- Omatu, S. Classification of Mixed Odors Using A Layered Neural Network. Int. J. Comput. 2017, 16, 41–48. [Google Scholar] [CrossRef]
- Lynnyk, R.; Vysotska, V.; Matseliukh, Y.; Burov, Y.; Demkiv, L.; Zaverbnyj, A.; Sachenko, A.; Shylinska, I.; Yevseyeva, I.; Bihun, O. DDOS Attacks Analysis Based on Machine Learning in Challenges of Global Changes. CEUR Workshop Proc. 2020, 2631, 159–171. Available online: https://ceur-ws.org/Vol-2631/paper12.pdf (accessed on 16 June 2025).
- Striuk, O.; Kondratenko, Y. Generative Adversarial Neural Networks and Deep Learning: Successful Cases and Advanced Approaches. Int. J. Comput. 2021, 20, 339–349. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Y.; Bai, N.; Yu, Q.; Wang, Q. Class-Imbalanced Time Series Anomaly Detection Method Based on Cost-Sensitive Hybrid Network. Expert Syst. Appl. 2024, 238, 122192. [Google Scholar] [CrossRef]
- Mahdi, Z.; Abdalhussien, N.; Mahmood, N.; Zaki, R. Detection of Real-Time Distributed Denial-of-Service (DDoS) Attacks on Internet of Things (IoT) Networks Using Machine Learning Algorithms. Comput. Mater. Contin. 2024, 80, 2139–2159. [Google Scholar] [CrossRef]
- Munir, M.; Siddiqui, S.A.; Chattha, M.A.; Dengel, A.; Ahmed, S. FuseAD: Unsupervised Anomaly Detection in Streaming Sensors Data by Fusing Statistical and Deep Learning Models. Sensors 2019, 19, 2451. [Google Scholar] [CrossRef]
- Xu, C.; Zhu, P.; Wang, J.; Fortino, G. Improving the Local Diagnostic Explanations of Diabetes Mellitus with the Ensemble of Label Noise Filters. Inf. Fusion 2025, 117, 102928. [Google Scholar] [CrossRef]
- Shen, F.; Zheng, J.; Ye, L.; Ma, X. LSTM Soft Sensor Development of Batch Processes with Multivariate Trajectory-Based Ensemble Just-in-Time Learning. IEEE Access 2020, 8, 73855–73864. [Google Scholar] [CrossRef]
- Zhu, P.; Zhang, H.; Shi, Y.; Xie, W.; Pang, M.; Shi, Y. A Novel Discrete Conformable Fractional Grey System Model for Forecasting Carbon Dioxide Emissions. Environ. Dev. Sustain. 2024, 27, 13581–13609. [Google Scholar] [CrossRef]
- Amin, R.; Gantassi, R.; Ahmed, N.; Hassan Alshehri, A.; Alsubaei, F.S.; Frnda, J. A Hybrid Approach for Adversarial Attack Detection Based on Sentiment Analysis Model Using Machine Learning. Eng. Sci. Technol. Int. J. 2024, 58, 101829. [Google Scholar] [CrossRef]
- Sheikh, A.M.; Islam, M.R.; Habaebi, M.H.; Zabidi, S.A.; Bin Najeeb, A.R.; Kabbani, A. A Survey on Edge Computing (EC) Security Challenges: Classification, Threats, and Mitigation Strategies. Future Internet 2025, 17, 175. [Google Scholar] [CrossRef]
- Cho, C.; Kim, C.; Sull, S. PIABC: Point Spread Function Interpolative Aberration Correction. Sensors 2025, 25, 3773. [Google Scholar] [CrossRef]
- Connolly, G.; Sachenko, A.; Markowsky, G. Distributed Traceroute Approach to Geographically Loocating IP Devices. In Proceedings of the Second IEEE International Workshop on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications, Lviv, Ukraine, 8–10 September 2003; pp. 128–131. [Google Scholar] [CrossRef]
- Vladov, S.; Muzychuk, O.; Vysotska, V.; Yurko, A.; Uhryn, D. Modified Kalman Filter with Chebyshev Points Based on a Recurrent Neural Network for Automatic Control System Measuring Channels Diagnosing and Parring off Failures. Int. J. Image Graph. Signal Process. 2024, 16, 36–61. [Google Scholar] [CrossRef]
- Sachenko, A.; Kochan, V.; Turchenko, V. Intelligent Distributed Sensor Network. In Proceedings of the IMTC/98 Conference Proceedings. IEEE Instrumentation and Measurement Technology Conference. Where Instrumentation is Going (Cat. No.98CH36222), St. Paul, MN, USA, 18–21 May 1998; Volume 1, pp. 60–66. [Google Scholar] [CrossRef]
- Vitulyova, Y.; Babenko, T.; Kolesnikova, K.; Kiktev, N.; Abramkina, O. A Hybrid Approach Using Graph Neural Networks and LSTM for Attack Vector Reconstruction. Computers 2025, 14, 301. [Google Scholar] [CrossRef]
- Vladov, S.; Shmelov, Y.; Yakovliev, R. Modified Helicopters Turboshaft Engines Neural Network On-board Automatic Control System Using the Adaptive Control Method. CEUR Workshop Proc. 2022, 3309, 205–224. Available online: https://ceur-ws.org/Vol-3309/paper15.pdf (accessed on 29 June 2025).
- Morales, M.D.; Antelis, J.M.; Moreno, C.; Nesterov, A.I. Deep Learning for Gravitational-Wave Data Analysis: A Resampling White-Box Approach. Sensors 2021, 21, 3174. [Google Scholar] [CrossRef] [PubMed]
- Park, H.; Lee, K. Adaptive Natural Gradient Method for Learning of Stochastic Neural Networks in Mini-Batch Mode. Appl. Sci. 2019, 9, 4568. [Google Scholar] [CrossRef]
- Todo, H.; Chen, T.; Ye, J.; Li, B.; Todo, Y.; Tang, Z. Single-Layer Perceptron Artificial Visual System for Orientation Detection. Front. Neurosci. 2023, 17, 1229275. [Google Scholar] [CrossRef]
- Jeong, S.; Lee, J. Soft-Output Detector Using Multi-Layer Perceptron for Bit-Patterned Media Recording. Appl. Sci. 2022, 12, 620. [Google Scholar] [CrossRef]
- Vladov, S.; Scislo, L.; Sokurenko, V.; Muzychuk, O.; Vysotska, V.; Osadchy, S.; Sachenko, A. Neural Network Signal Integration from Thermogas-Dynamic Parameter Sensors for Helicopters Turboshaft Engines at Flight Operation Conditions. Sensors 2024, 24, 4246. [Google Scholar] [CrossRef]
- Vladov, S.; Sachenko, A.; Sokurenko, V.; Muzychuk, O.; Vysotska, V. Helicopters Turboshaft Engines Neural Network Modeling under Sensor Failure. J. Sens. Actuator Netw. 2024, 13, 66. [Google Scholar] [CrossRef]
- Biçer, C.; Bakouch, H.S.; Biçer, H.D.; Alomair, G.; Hussain, T.; Almohisen, A. Unit Maxwell-Boltzmann Distribution and Its Application to Concentrations Pollutant Data. Axioms 2024, 13, 226. [Google Scholar] [CrossRef]
- Nazarkevych, M.; Kowalska-Styczen, A.; Lytvyn, V. Research of Facial Recognition Systems and Criteria for Identification. In Proceedings of the IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications, IDAACS, Dortmund, Germany, 7–9 September 2023; pp. 555–558. [Google Scholar] [CrossRef]
- Vlasenko, D.; Inkarbaieva, O.; Peretiatko, M.; Kovalchuk, D.; Sereda, O. Helicopter Radio System for Low Altitudes and Flight Speed Measuring with Pulsed Ultra-Wideband Stochastic Sounding Signals and Artificial Intelligence Elements. Radioelectron. Comput. Syst. 2023, 3, 48–59. [Google Scholar] [CrossRef]
- Marakhimov, A.R.; Khudaybergenov, K.K. Approach to the synthesis of neural network structure during classification. Int. J. Comput. 2020, 19, 20–26. [Google Scholar] [CrossRef]
- Bodyanskiy, Y.; Shafronenko, A.; Pliss, I. Clusterization of Vector and Matrix Data Arrays Using the Combined Evolutionary Method of Fish Schools. Syst. Res. Inf. Technol. 2022, 4, 79–87. [Google Scholar] [CrossRef]
- Dyvak, M.; Manzhula, V.; Melnyk, A.; Rusyn, B.; Spivak, I. Modeling the Efficiency of Biogas Plants by Using an Interval Data Analysis Method. Energies 2024, 17, 3537. [Google Scholar] [CrossRef]
- Lopes, J.F.; Barbon Junior, S.; de Melo, L.F. Online Meta-Recommendation of CUSUM Hyperparameters for Enhanced Drift Detection. Sensors 2025, 25, 2787. [Google Scholar] [CrossRef]
- Riad, K. Robust Access Control for Secure IoT Outsourcing with Leakage Resilience. Sensors 2025, 25, 625. [Google Scholar] [CrossRef]
- Pieniazek, J. Thermocouple Sensor Response in Hot Airstream. Sensors 2025, 25, 4634. [Google Scholar] [CrossRef]
- He, Y.; Yang, F.; Wei, P.; Lv, Z.; Zhang, Y. A Novel Adaptive Flexible Capacitive Sensor for Accurate Intravenous Fluid Monitoring in Clinical Settings. Sensors 2025, 25, 4524. [Google Scholar] [CrossRef]
- Ali, M.; Ahmad, I.; Geun, I.; Hamza, S.A.; Ijaz, U.; Jang, Y.; Koo, J.; Kim, Y.-G.; Kim, H.-D. A Comprehensive Review of Advanced Sensor Technologies for Fire Detection with a Focus on Gasistor-Based Sensors. Chemosensors 2025, 13, 230. [Google Scholar] [CrossRef]
- Gao, G.F.; Oh, C.; Saksena, G.; Deng, D.; Westlake, L.C.; Hill, B.A.; Reich, M.; Schumacher, S.E.; Berger, A.C.; Carter, S.L.; et al. Tangent Normalization for Somatic Copy-Number Inference in Cancer Genome Analysis. Bioinformatics 2022, 38, 4677–4686. [Google Scholar] [CrossRef]
- Gao, X.; Yao, X.; Chen, B.; Zhang, H. SBCS-Net: Sparse Bayesian and Deep Learning Framework for Compressed Sensing in Sensor Networks. Sensors 2025, 25, 4559. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, M.; Wang, P.; Liu, B.; Tian, R. The Levene Test Based-Leakage Assessment. Integration 2022, 87, 182–193. [Google Scholar] [CrossRef]
- Zhang, G.; Christensen, R.; Pesko, J. Parametric Boostrap and Objective Bayesian Testing for Heteroscedastic One-Way ANOVA. Stat. Probab. Lett. 2021, 174, 109095. [Google Scholar] [CrossRef]
- Lytvyn, V.; Dudyk, D.; Peleshchak, I.; Peleshchak, R.; Pukach, P. Influence of the Number of Neighbours on the Clustering Metric by Oscillatory Chaotic Neural Network with Dipole Synaptic Connections. CEUR Workshop Proc. 2024, 3664, 24–34. Available online: https://ceur-ws.org/Vol-3664/paper3.pdf (accessed on 8 July 2025).
- Hu, Z.; Kashyap, E.; Tyshchenko, O.K. GEOCLUS: A Fuzzy-Based Learning Algorithm for Clustering Expression Datasets. Lect. Notes Data Eng. Commun. Technol. 2022, 134, 337–349. [Google Scholar] [CrossRef]
- Cai, H.; Xie, Z.; Ma, Y.; Xiang, L. A 209 Ps Shutter-Time CMOS Image Sensor for Ultra-Fast Diagnosis. Sensors 2025, 25, 3835. [Google Scholar] [CrossRef]
- Ablamskyi, S.; Tchobo, D.L.R.; Romaniuk, V.; Šimić, G.; Ilchyshyn, N. Assessing the Responsibilities of the International Criminal Court in the Investigation of War Crimes in Ukraine. Novum Jus 2023, 17, 353–374. [Google Scholar] [CrossRef]
- Ablamskyi, S.; Nenia, O.; Drozd, V.; Havryliuk, L. Substantial Violation of Human Rights and Freedoms as a Prerequisite for Inadmissibility of Evidence. Justicia 2021, 26, 47–56. [Google Scholar] [CrossRef]
- Kovtun, V.; Izonin, I.; Gregus, M. Model of Functioning of the Centralized Wireless Information Ecosystem Focused on Multimedia Streaming. Egypt. Inform. J. 2022, 23, 89–96. [Google Scholar] [CrossRef]



| Neural Network Method | Sensor Type | Kye Results | Limitations | References |
|---|---|---|---|---|
| CNN | Vibration, acoustic | 95% anomaly detection accuracy | High computational load | [32,33] |
| LSTM | Temperature, pressure | AUC ROC = 0.97 | Labelled data for a large amount | [34] |
| Variable autoencoder (VAE) | IoT flows (multiple data) | FP reduction by 30% | Difficulty in selecting threshold values | [38,39,40,41] |
| GNN | Distributed network | Anomaly source localisation to a node ±1 m | Unaccounted impact of delays | [42] |
| Hybrid autoencoder and GCN | Multi-sensor (4 or more sensors) | TPR = 93%, average latency < 50 ms | Lack of explanation of the model for the operator | [43,44,45] |
| Hybrid approaches (FuseAD, ensembles, JIT, DCFGM) | Streaming sensory data, medical data, batch processes, and environmental data | High accuracy of anomaly detection; improved local diagnostic interpretation; adaptive soft sensors; accurate CO2 emission forecasting | They require fine-tuning and markup, are rarely tested during conceptual drift, have high computational requirements, and have low interpretability. | [46,47,48,49] |
| Predicted Attack | Predicted Normal | |
|---|---|---|
| Actual Attack | TP | FN |
| Actual Normal | FP | TN |
| Stage Number | Stage Name | Stage Description |
|---|---|---|
| 1 | Pre-training phase | Clean data without attacks is collected, on which the LSTM fθ basis is trained, minimising Lpred. |
| 2 | Attack generation | The vector u0 is modelled using the SDE model (different intensities and directions). |
| 3 | Classifier training | The residuals from the predictor are used to train an MLP detector to recognise “attacks”. |
| 4 | Online stage | For each new measurement xt, a prediction is made, the remainder is calculated, matrix Rt is formed, and the scalar rate st is calculated. If st > τ, then the response system is launched. |
| Time, Hours | Sensor 1 (Temperature) | Sensor 2 (Air Humidity) | Sensor 3 (CO2 Concentration) |
|---|---|---|---|
| 0.500000 | 0.103013 | 0.889087 | 0.489480 |
| 0.501002 | 0.130157 | 1.023572 | 0.282682 |
| 0.502004 | 0.047899 | 1.030167 | 0.306659 |
| 0.503006 | 0.069855 | 0.772710 | 0.222945 |
| 0.504008 | 0.054991 | 1.003269 | 0.412067 |
| … | … | … | … |
| Time, Hours | Residual Sensor 1 (Temperature) | Residual Sensor 2 (Air Humidity) | Residual Sensor 3 (CO2 Concentration) |
|---|---|---|---|
| 0.500000 | 0.000000 | 0.000000 | 0.000000 |
| 0.501002 | −0.033446 | 0.107082 | −0.017275 |
| 0.502004 | 0.067837 | 0.084994 | 0.070574 |
| 0.503006 | 0.039845 | −0.006814 | 0.033270 |
| 0.504008 | −0.031736 | −0.125322 | 0.054965 |
| … | … | … | … |
| Sensor | σ2 | σ | W | F | Title 6 | Title 7 | |
|---|---|---|---|---|---|---|---|
| Sensor 1 | ≈0 | 1.002 | 1.0009995 | 0.979 | 2.72 × 10−8 | True | False |
| Sensor 2 | 0 | 1.002 | 1.0009995 | 0.707 | 6.22 × 10−6 | True | False |
| Sensor 3 | ≈0 | 1.002 | 1.0009995 | 0.148 | 0.1068 | True | True |
| Number | Name | Description |
|---|---|---|
| 1 | Attack modelling | An adaptive noise vector ua(t) was added to each channel, generated as a Gaussian process, with mean zero and variance σ2 varying from the original signal range of 0.1 to 0.5; the attacked fragments duration was fixed randomly in the 30...120 s range, which ensures a total norm attack ratio of ≈85%: 15%. Attack scenarios included spoofing (smooth drift shift), replay (previous segments repeat), and DoS (fixed signal erasure). |
| 2 | Balancing classes | To compensate for the imbalance, attacks of rare combinations on adjacent channels were additionally synthesised, bringing the “attack type” final proportion classes to 1…5% for each subtype and 10…15% in total. |
| 3 | Annotation and partitioning | Each timestamp was assigned a “norm” or “attack” label, and the data was then randomly split into training (67%) and validation (33%) sets without overlapping fragments. |
| Cyberattack Type | Cyberattack Subtype | Description | Parameters |
|---|---|---|---|
| Spoofing attacks | Constant Substitution | A fixed error Δ0, equal to the normal signal amplitude 20…50% is added to each time sample. | Intensity: Δ0 or α as the normalised amplitude proportion. |
| Incremental Drift | The signal shifts linearly: u(t) = unorm(t) + α · t, where α is set in the (0.01…0.05) · Amax range, where Amax is the normalised amplitude. | Fragment duration is 30…120 s. | |
| Random Spikes | Time intervals of 1…5 s duration with peak emissions up to (0.8…1.0) · Amax, repeating with a frequency of 60…120 s. | Spikes frequency (for Random Spikes) is 0.5…1 time per minute. | |
| Replay attacks | Full Replay | Replacing the current 50… 100 s long window with a pre-recorded “clean” segment. | Segment duration is 25…100 s. |
| Segmented Replay | Repeat only the signal part (e.g., the first 25 s out of 50 s) while preserving the rest of the data. | Interval between playbacks is 100…300 s. | |
| DoS attacks | Blackout | The signal is replaced by a zero level or a constant of 0 ± 1% of Amax for 10…30 s. | Block duration is 10…60 s, where the noise intensity σ2 is the normal signal variance fraction. |
| High-Frequency Noise | Adding white noise with variance σ2 = 0.5 ⋅ Var(unorm) on the 20… 60-s intervals. | The interval between DoS episodes is 200…400 s. |
| Method | Precision | Recall | F1 Score | AUC | Training Time, s |
|---|---|---|---|---|---|
| Developed method | 0.92 | 0.89 | 0.90 | 0.94 | 15 |
| IForest | 0.87 | 0.85 | 0.86 | 0.90 | 5 |
| SVM | 0.89 | 0.87 | 0.88 | 0.91 | 25 |
| K-means | 0.80 | 0.75 | 0.77 | 0.83 | 10 |
| VAE | 0.85 | 0.83 | 0.84 | 0.88 | 20 |
| CNN with MLP | 0.90 | 0.88 | 0.89 | 0.92 | 30 |
| Method | Precision | Recall | F1 Score | AUC | Training Time, s |
|---|---|---|---|---|---|
| LSTM (proposed) | 0.92 | 0.89 | 0.90 | 0.94 | 25 |
| GRU | 0.88 | 0.85 | 0.86 | 0.91 | 20 |
| CNN | 0.85 | 0.83 | 0.84 | 0.89 | 30 |
| MLP | 0.82 | 0.80 | 0.81 | 0.85 | 15 |
| Method | Precision | Recall | F1 Score | AUC | Training Time, s |
|---|---|---|---|---|---|
| Modified LSTM | 0.92 | 0.89 | 0.90 | 0.94 | 25 |
| Traditional LSTM | 0.88 | 0.85 | 0.86 | 0.91 | 22 |
| Adaptive LSTM | 0.90 | 0.87 | 0.88 | 0.92 | 28 |
| Residual LSTM | 0.89 | 0.86 | 0.87 | 0.90 | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vladov, S.; Jotsov, V.; Sachenko, A.; Prokudin, O.; Ostapiuk, A.; Vysotska, V. Neural Network Method of Analysing Sensor Data to Prevent Illegal Cyberattacks. Sensors 2025, 25, 5235. https://doi.org/10.3390/s25175235
Vladov S, Jotsov V, Sachenko A, Prokudin O, Ostapiuk A, Vysotska V. Neural Network Method of Analysing Sensor Data to Prevent Illegal Cyberattacks. Sensors. 2025; 25(17):5235. https://doi.org/10.3390/s25175235
Chicago/Turabian StyleVladov, Serhii, Vladimir Jotsov, Anatoliy Sachenko, Oleksandr Prokudin, Andrii Ostapiuk, and Victoria Vysotska. 2025. "Neural Network Method of Analysing Sensor Data to Prevent Illegal Cyberattacks" Sensors 25, no. 17: 5235. https://doi.org/10.3390/s25175235
APA StyleVladov, S., Jotsov, V., Sachenko, A., Prokudin, O., Ostapiuk, A., & Vysotska, V. (2025). Neural Network Method of Analysing Sensor Data to Prevent Illegal Cyberattacks. Sensors, 25(17), 5235. https://doi.org/10.3390/s25175235









