Sensor-Driven RSSI Prediction via Adaptive Machine Learning and Environmental Sensing
Abstract
1. Introduction
2. Literature Review
3. Methodology Overview
3.1. Experimental Framework
3.1.1. Hardware Description
3.1.2. Dataset Description
3.2. Baseline Model
3.3. Proposed Model
3.3.1. Model Selection
3.3.2. Model Setup
3.4. Evaluation Metrics
3.4.1. Percentage of Variance
3.4.2. Root Mean Squared Error
3.4.3. Mean Absolute Percentage Error
4. Results and Evaluation
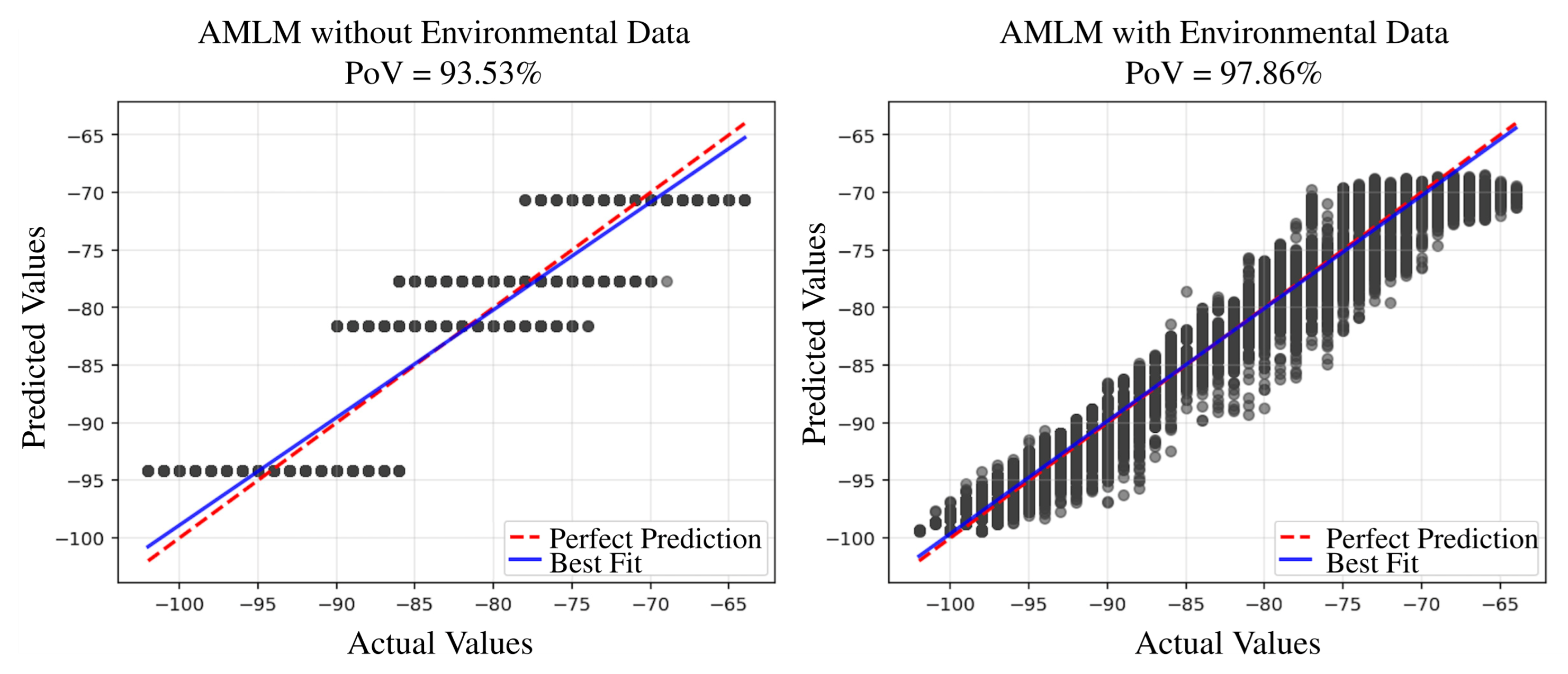
4.1. Performance Analysis of the Proposed Model
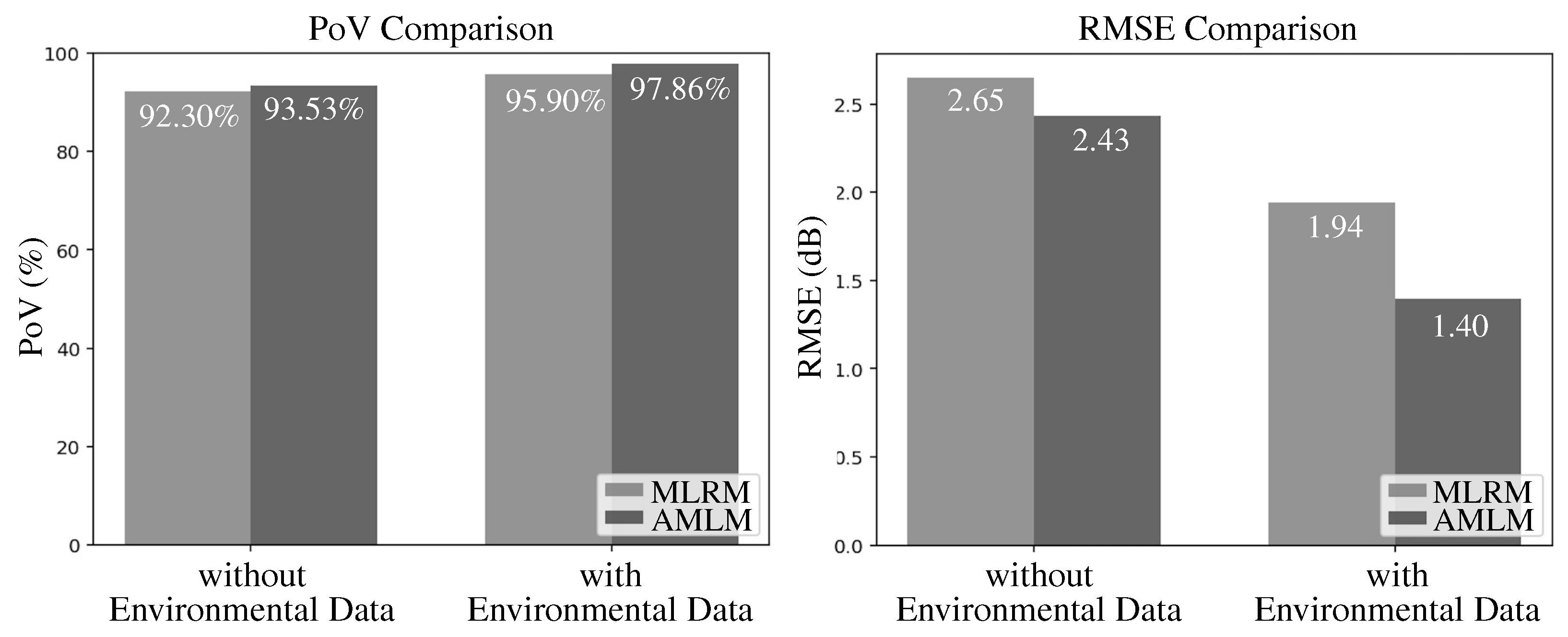
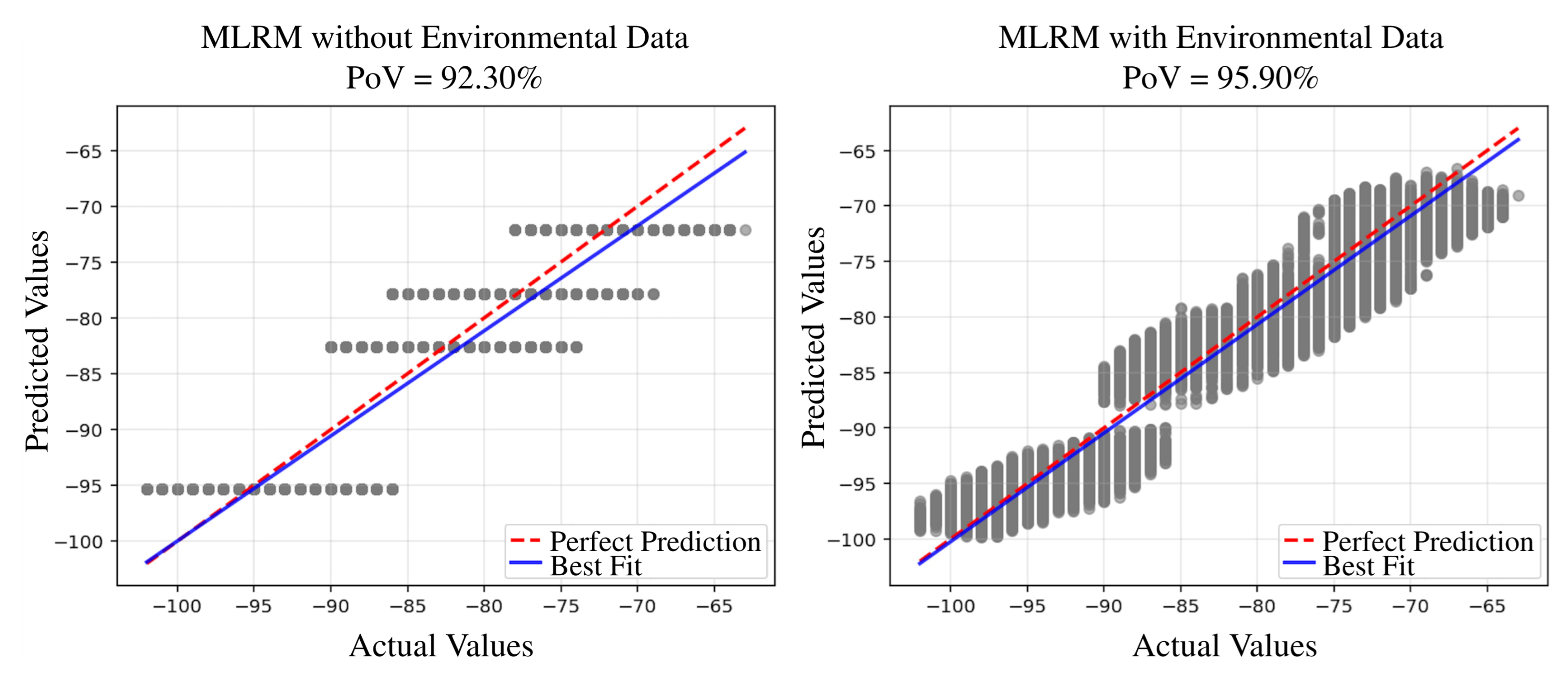
4.1.1. Percentage of Variance Analysis
4.1.2. Root Mean Square Error Analysis
4.1.3. Execution Time
4.2. Evaluation Relative to the Baseline Model
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aiboud, Y.; Elhassani, I.; Griguer, H. RSSI optimization method for indoor positioning systems. In Proceedings of the International Conference on Wireless Networks and Mobile Communications (WINCOM), Rabat, Morocco, 1–4 November 2017; pp. 246–248. [Google Scholar]
- Raj, N.; Wang, X. IndoorRSSINet—Deep learning based 2D RSSI map prediction for indoor environments with application to wireless localization. In Proceedings of the 15th International Conference on COMmunication Systems & NETworkS (COMSNETS), Bangalore, India, 3–8 January 2023; pp. 609–616. [Google Scholar]
- Bashyam, S.L.R.; Chandra, J.; Devi, S.R. An Efficient Node to Node Coverage and Connectivity with RSSI Using Grey-Wolf Prediction Optimization Algorithm in Remote Low Accessibility Area. In Proceedings of the 2nd International Conference on Vision Towards Emerging Trends in Communication and Networking Technologies (ViTECoN), Vellore, India, 5–6 May 2023; pp. 1–6. [Google Scholar]
- Li, M.; de Oliveira, T.E.A. EP-FPG applied to RSSI-Based Wireless Indoor Localization. In Proceedings of the IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), London, ON, Canada, 30 August–2 September 2020; pp. 1–6. [Google Scholar]
- Ogawa, Y.; Umehira, M.; Wang, X. Kriging-based RSSI Prediction for Cell Coverage Discovery using Spectrum Database in 5G Multi-band Cellular Networks. In Proceedings of the 17th International Symposium on Communications and Information Technologies (ISCIT), Perth, WA, Australia, 11–13 December 2017; pp. 1–6. [Google Scholar]
- Apavatjrut, A.; Boonyasiwapong, E. Indoor WIFI localization on embedded systems. In Information Science and Applications; Springer: Berlin/Heidelberg, Germany, 2015; Volume 339, ISBN 978-3-662-46577-6. [Google Scholar]
- Daiya, V.; Ebenezer, J.; Murty, S.A.V.S.; Raj, B. Experimental Analysis of RSSI for Distance and Position Estimation. In Proceedings of the International Conference on Recent Trends in Information Technology (ICRTIT), Chennai, India, 3–5 June 2011; pp. 1093–1098. [Google Scholar]
- González-Palacio, M.; Tobón-Vallejo, D.; Sepúlveda-Cano, L.M.; Rúa, S.; Pau, G.; Le, L.B. LoRaWAN Path Loss Measurements in an Urban Scenario including Environmental Effects. Data 2023, 8, 4. [Google Scholar] [CrossRef]
- Molisch, A.F. Wireless Communications; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Rademacher, M.; Linka, H.; Horstmann, T.; Henze, M. Path Loss in Urban LoRa Networks: A Large-Scale Measurement Study. In Proceedings of the 2021 IEEE 94th Vehicular Technology Conference (VTC2021-Fall), Norman, OK, USA, 27–30 September 2021; pp. 1–6. [Google Scholar]
- Kabiri, M.; Cimarelli, C.; Bavle, H.; Sanchez-Lopez, J.L.; Voos, H. A Review of Radio Frequency Based Localisation for Aerial and Ground Robots with 5G Future Perspectives. Sensors 2023, 23, 188. [Google Scholar] [CrossRef] [PubMed]
- Raj, N. Indoor RSSI Prediction using Machine Learning for Wireless Networks. In Proceedings of the International Conference on COMmunication Systems & NETworkS (COMSNETS), Bangalore, India, 5–9 January 2021; pp. 372–374. [Google Scholar]
- Callebaut, G.; Perre, L.V. Characterization of LoRa Point-to-Point Path Loss: Measurement Campaigns and Modeling Considering Censored Data. IEEE Internet Things J. 2020, 7, 1910–1918. [Google Scholar] [CrossRef]
- Chall, R.E.; Lahoud, S.; Helou, M.E. LoRaWAN Network: Radio Propagation Models and Performance Evaluation in Various Environments in Lebanon. IEEE Internet Things J. 2019, 6, 2366–2378. [Google Scholar] [CrossRef]
- Alobaidy, A.A.H.; Mandeep, J.S.; Behjati, M.; Nordin, R.; Abdullah, N.F. Wireless Transmissions, Propagation and Channel Modeling for IoT Technologies: Applications and Challenges. IEEE Access 2021, 10, 24095–24131. [Google Scholar] [CrossRef]
- Obeidat, H.; Shuaieb, W.; Obeidat, O.; Abd-Alhameed, R. A Review of Indoor Localization Techniques and Wireless Technologies. Wirel. Pers. Commun. 2021, 119, 289–327. [Google Scholar] [CrossRef]
- Seybold, J.S. Introduction to RF Propagation; John Wiley & Sons: Hoboken, NJ, USA, 2005; p. 143. ISBN 0-471-65596-1. [Google Scholar]
- Quispetupa, D.A.; Fernandez, J.P.; Tacas, R.Q. An experimental evaluation of RSSI-LoRa in an olive tree plantations. In Proceedings of the IEEE Engineering International Research Conference (EIRCON), Lima, Peru, 26–28 October 2022; pp. 1–4. [Google Scholar]
- Barbosa, B.S.d.S.; Cruz, H.A.O.; Macedo, A.S.; Cardoso, C.M.M.; Fernandes, F.C.; Eras, L.E.C.; Araújo, J.P.L.d.; Calvacante, G.P.S.; Barros, F.J.B. Application of Artificial Neural Networks for Prediction of Received Signal Strength Indication and Signal-to-Noise Ratio in Amazonian Wooded Environments. Sensors 2024, 24, 2542. [Google Scholar] [CrossRef] [PubMed]
- Hata, M. Empirical Formula for Propagation Loss in Land Mobile Radio Services. IEEE Trans. Veh. Technol. 1980, 29, 317–325. [Google Scholar] [CrossRef]
- Sousa, M.; Alves, A.; Vieira, P.; Queluz, M.P.; Rodrigues, A. Analysis and Optimization of 5G Coverage Predictions Using a Beamforming Antenna Model and Real Drive Test Measurements. IEEE Access 2021, 9, 101787–101808. [Google Scholar] [CrossRef]
- Jo, H.-S.; Park, C.; Lee, E.; Choi, H.K.; Park, J. Path Loss Prediction Based on Machine Learning Techniques: Principal Component Analysis, Artificial Neural Network, and Gaussian Process. Sensors 2020, 20, 1927. [Google Scholar] [CrossRef] [PubMed]
- Moraitis, N.; Tsipi, L.; Gkioni, D.V.A.; Louvros, S. Performance evaluation of machine learning methods for path loss prediction in rural environment at 3.7 GHz. Wirel. Netw. 2021, 27, 4169–4188. [Google Scholar] [CrossRef]
- He, R.; Gong, Y.; Bai, W.; Li, Y.; Wang, X. Random Forests Based Path Loss Prediction in Mobile Communication Systems. In Proceedings of the 2020 IEEE 6th International Conference on Computer and Communications (ICCC), Chengdu, China, 11–14 December 2020; pp. 1246–1250. [Google Scholar]
- Fauzi, M.F.A.; Nordin, R.; Abdullah, N.F.; Alobaidy, H.A.H. Mobile Network Coverage Prediction Based on Supervised Machine Learning Algorithms. IEEE Access 2022, 10, 55782–55793. [Google Scholar] [CrossRef]
- Goldoni, E.; Savazzi, P.; Favalli, L.; Vizziello, A. Correlation between weather and signal strength in LoRaWAN networks: An extensive dataset. Comput. Netw. 2022, 202, 108627. [Google Scholar] [CrossRef]
- Arif, S.; Khan, M.A.; Rehman, S.U. A Lightweight Received Signal Strength Indicator Estimation Model for Low-Power Internet of Things Devices in Constrained Indoor Networks. Appl. Sci. 2025, 15, 3535. [Google Scholar] [CrossRef]
- Freedman, D.A. Statistical Models: Theory and Practice; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Quinlan, J.R. Induction of Decision Trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased Boosting with Categorical Features. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 6639–6649. [Google Scholar]
- Turney, S. Coefficient of Determination (R2)|Calculation & Interpretation. Scribbr. 2022. Available online: https://www.scribbr.com/statistics/coefficient-of-determination (accessed on 1 July 2024).
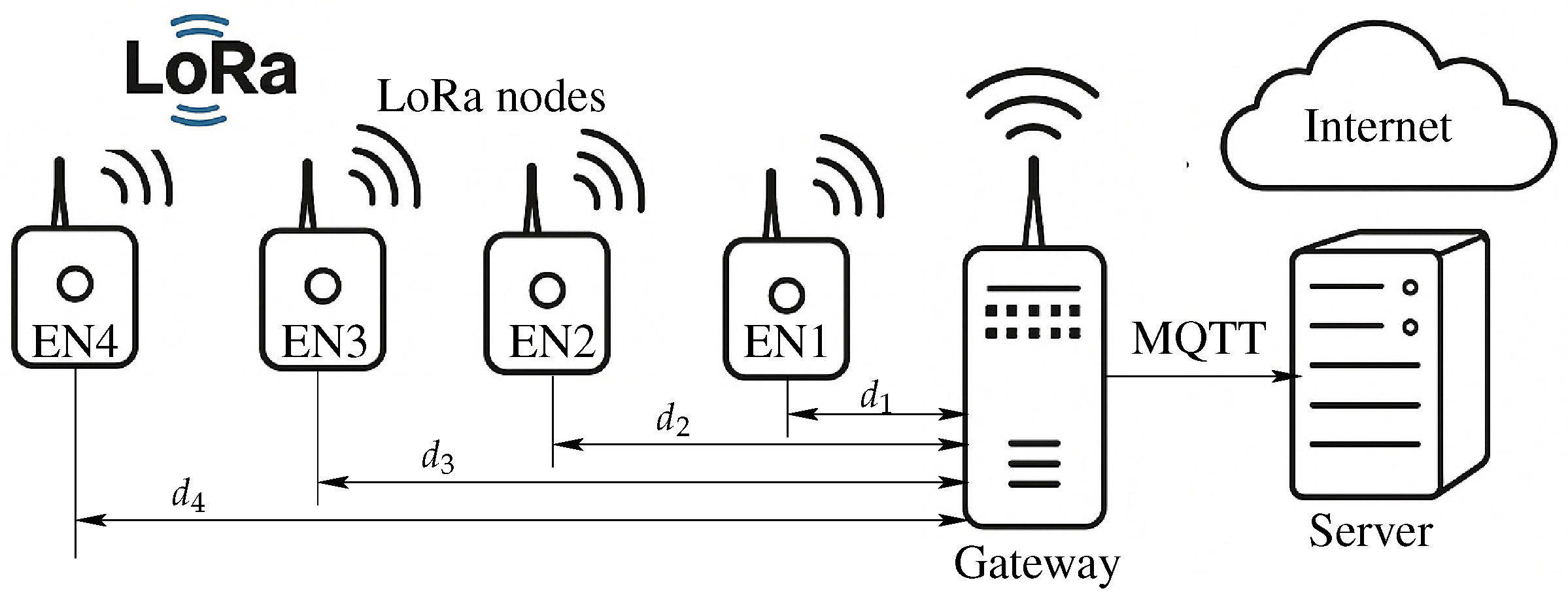
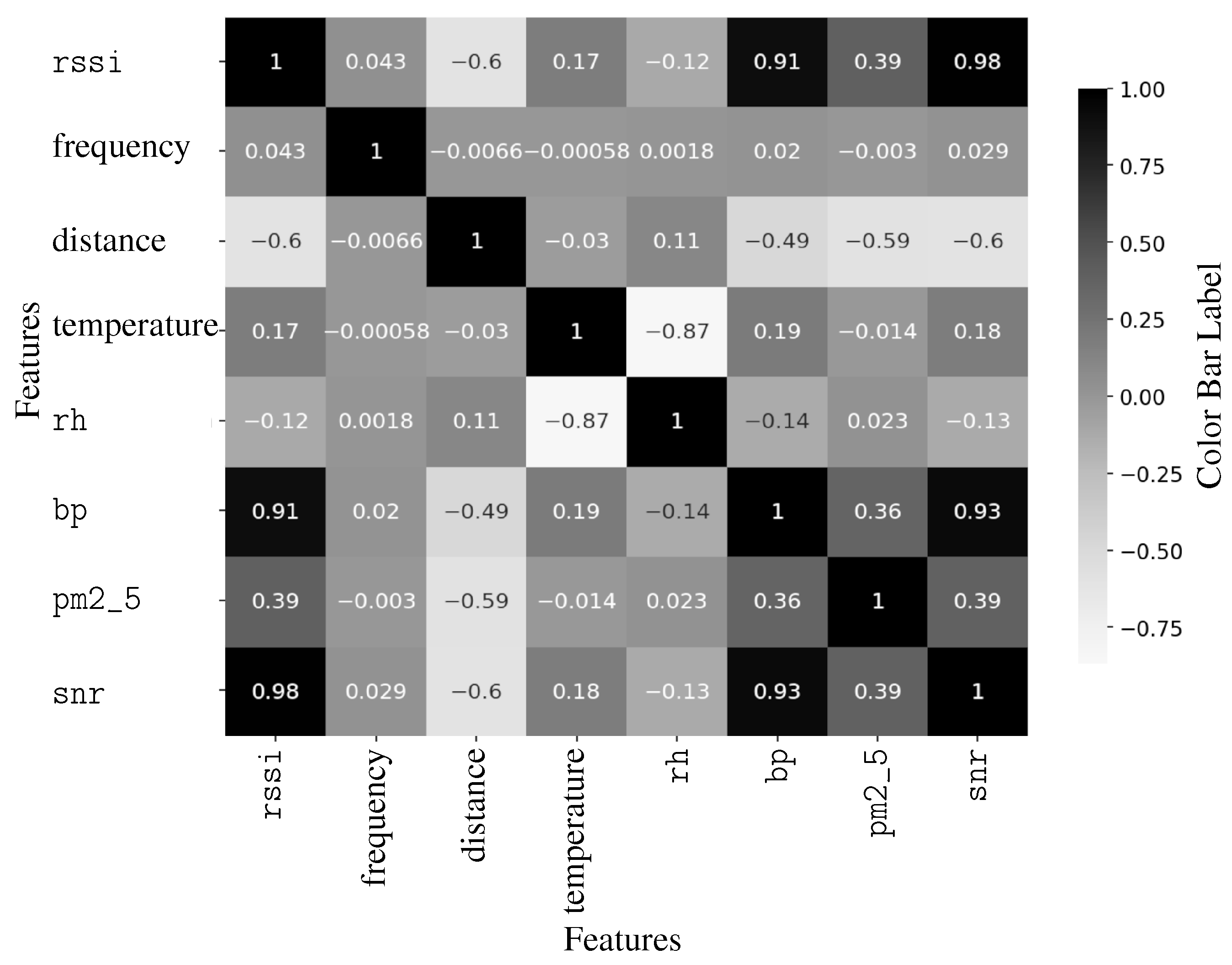
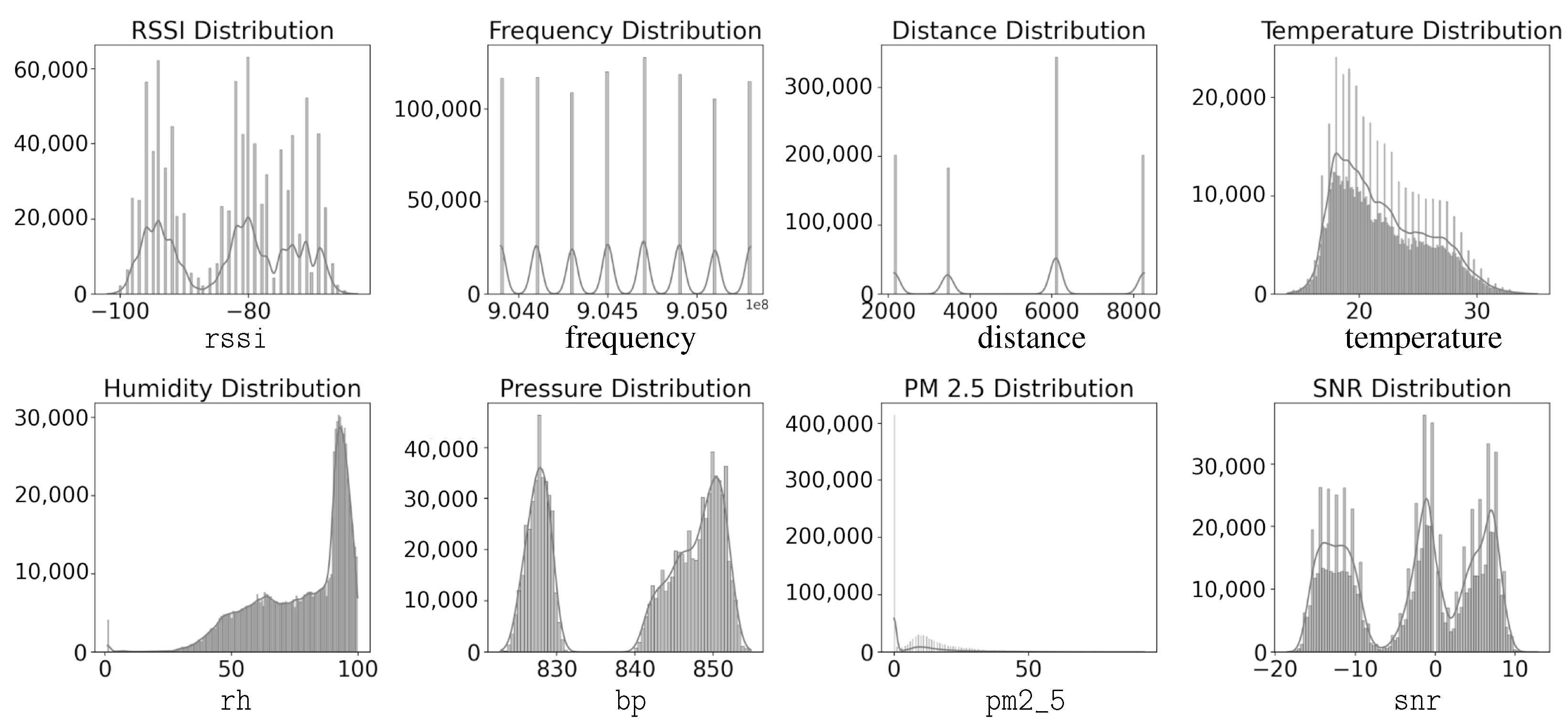

| Column Name | Description |
|---|---|
| index | Sequential number identifying the corresponding observation. |
| timestamp | Date and time of the observation in the format of yyyy-mm-dd hh:mm:ss. |
| device_id | Identifier of the LoRa node defined as EN1, EN2, EN3, or EN4. |
| distance (d) | Distance between the corresponding LoRa node and the gateway in meters. |
| ht | Antenna height of the transmitter (LoRa node) in meters. |
| hr | Antenna height of the receiver (gateway) in meters. |
| ptx | Transmitted radiated power in dBm (fixed at 20 dBm). |
| ltx | Loss associated with cables and connectors at the transmitter in dB. |
| gtx | Antenna gain of the transmitter (LoRa node) in dBi. |
| lrx | Loss associated with cables and connectors at the receiver (gateway) in dB (measured as 4.25 dB). |
| grx | Antenna gain of the receiver (gateway) measured as 4.161 dBi. |
| frequency (f) | Carrier frequency in Hz, operating in the US 902–928 MHz ISM band. |
| frame_length | Number of bytes in the current transmission payload. |
| temperature (T) | Temperature in °C. |
| rh | Relative humidity in %. |
| bp | Barometric pressure in hPa. |
| pm2_5 | Particulate matter (PM2.5) in μg/m3. |
| rssi | The Received Signal Strength Indicator measured at the gateway in dBm. |
| snr | The signal-to-noise ratio in dB. |
| toa | Time on air in seconds. |
| experimental_pl | Experimental path loss in dB, calculated as ptx + gtx + grx - lrx - rssi. |
| energy | Energy consumed during the current transmission in Joules. |
| esp | Effective signal power of the current transmission in dBm. |
| pn | Noise power in dBm. |
| Predictor | Variable | Value | Unit |
|---|---|---|---|
| Intercept | − | dB | |
| Path loss exponent | - | ||
| Temperature | dB/°C | ||
| Relative humidity | dB/% | ||
| Barometric pressure | dB/hPa | ||
| PM2.5 | dB/μg/m3 | ||
| SNR | − | dB/dB |
| Technique | Library |
|---|---|
| LR | sklearn.linear_model.LinearRegression() |
| DT | sklearn.tree.DecisionTreeRegressor() |
| RF | sklearn.ensemble.RandomForestRegressor() |
| GB | sklearn.ensemble.GradientBoostingRegressor() |
| XGB | xgboost.XGBRegressor() |
| CB | catboost.CatBoostRegressor() |
| Feature Selection | LR | DT | RF | GB | XGB | CB |
|---|---|---|---|---|---|---|
| d | 36.48 | 93.53 | 93.53 | 93.53 | 93.53 | 93.53 |
| f | 0.19 | 0.56 | 0.56 | 0.56 | 0.56 | 0.56 |
| d, f | 36.64 | 93.78 | 93.78 | 93.80 | 93.81 | 93.81 |
| d, f, T | 38.92 | 93.94 | 93.95 | 94.06 | 94.12 | 94.07 |
| d, f, rh | 36.97 | 94.00 | 94.01 | 94.12 | 94.19 | 94.15 |
| d, f, bp | 86.35 | 93.82 | 93.82 | 93.91 | 93.95 | 93.93 |
| d, f, pm2_5 | 36.79 | 94.50 | 94.51 | 94.58 | 94.63 | 94.61 |
| d, f, T, rh, bp, pm2_5 | 86.62 | 94.80 | 94.82 | 95.16 | 95.69 | 95.38 |
| d, f, snr, T, rh, bp, pm2_5 | 96.88 | 97.54 | 97.58 | 97.79 | 97.86 | 97.79 |
| Feature Selection | LR | DT | RF | GB | XGB | CB |
|---|---|---|---|---|---|---|
| d | 7.61 | 2.43 | 2.43 | 2.43 | 2.43 | 2.43 |
| f | 9.55 | 9.53 | 9.53 | 9.53 | 9.53 | 9.53 |
| d, f | 7.61 | 2.38 | 2.38 | 2.38 | 2.38 | 2.38 |
| d, f | 7.61 | 2.38 | 2.38 | 2.38 | 2.38 | 2.38 |
| d, f, T | 7.47 | 2.35 | 2.35 | 2.33 | 2.32 | 2.33 |
| d, f, rh | 7.59 | 2.34 | 2.34 | 2.32 | 2.30 | 2.31 |
| d, f, bp | 3.53 | 2.38 | 2.38 | 2.36 | 2.35 | 2.35 |
| d, f, pm2_5 | 7.60 | 2.24 | 2.24 | 2.22 | 2.21 | 2.22 |
| d, fT, rh, bar, pm2_5 | 3.49 | 2.18 | 2.17 | 2.10 | 1.98 | 2.05 |
| d, f, T, rh, bp, pm2_5 | 3.49 | 2.18 | 2.17 | 2.10 | 1.98 | 2.05 |
| d, f, snr, T, rh, bp, pm2_5 | 1.69 | 1.50 | 1.49 | 1.42 | 1.40 | 1.42 |
| Feature Selection | LR | DT | RF | GB | XGB | CB |
|---|---|---|---|---|---|---|
| d | 0.02 | 0.03 | 4.72 | 5.48 | 0.87 | 3.46 |
| f | 0.02 | 0.07 | 9.58 | 8.80 | 1.23 | 3.58 |
| d, f | 0.04 | 0.15 | 15.46 | 16.75 | 2.91 | 4.61 |
| d, f, T | 0.05 | 0.32 | 27.18 | 28.89 | 1.67 | 4.87 |
| d, f, rh | 0.05 | 0.39 | 30.58 | 31.02 | 1.69 | 4.84 |
| d, f, bp | 0.05 | 0.31 | 26.66 | 28.38 | 1.55 | 5.00 |
| d, f, pm2_5 | 0.05 | 0.26 | 22.86 | 24.99 | 1.64 | 5.26 |
| d, f, T, rh, bp, pm2_5 | 0.11 | 0.82 | 58.69 | 63.21 | 2.67 | 5.65 |
| d, f, snr, T, rh, bp, pm2_5 | 0.14 | 0.96 | 68.25 | 74.20 | 1.90 | 6.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Apavatjrut, A. Sensor-Driven RSSI Prediction via Adaptive Machine Learning and Environmental Sensing. Sensors 2025, 25, 5199. https://doi.org/10.3390/s25165199
Apavatjrut A. Sensor-Driven RSSI Prediction via Adaptive Machine Learning and Environmental Sensing. Sensors. 2025; 25(16):5199. https://doi.org/10.3390/s25165199
Chicago/Turabian StyleApavatjrut, Anya. 2025. "Sensor-Driven RSSI Prediction via Adaptive Machine Learning and Environmental Sensing" Sensors 25, no. 16: 5199. https://doi.org/10.3390/s25165199
APA StyleApavatjrut, A. (2025). Sensor-Driven RSSI Prediction via Adaptive Machine Learning and Environmental Sensing. Sensors, 25(16), 5199. https://doi.org/10.3390/s25165199








