Improved WOA-DBSCAN Online Clustering Algorithm for Radar Signal Data Streams
Abstract
1. Introduction
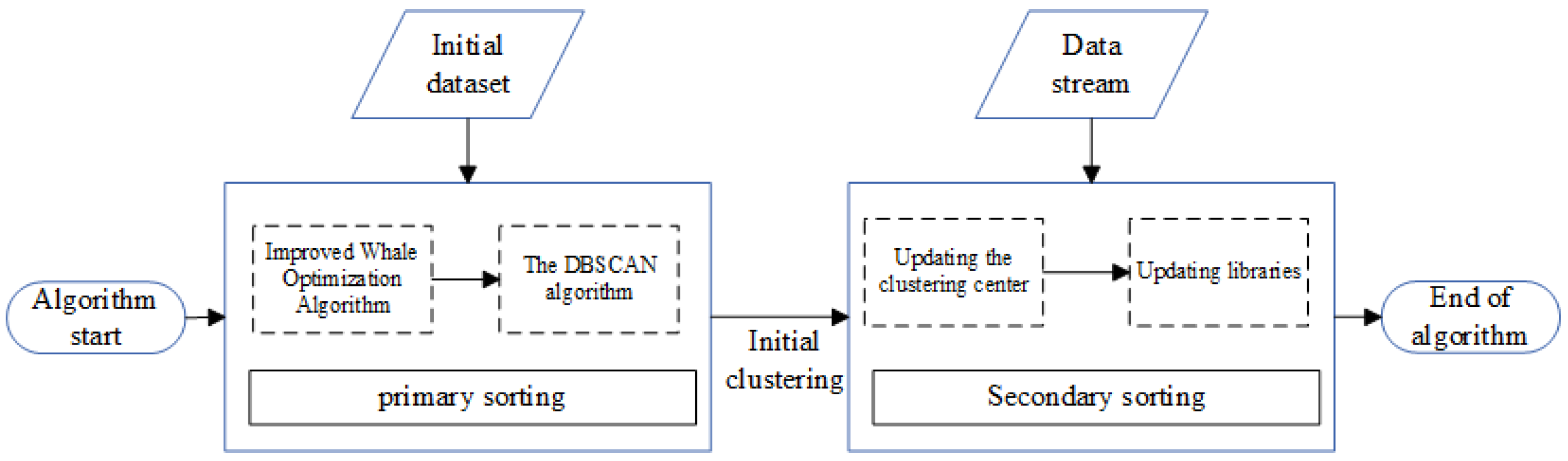
2. Improvement of WOA-DBSCAN Online Clustering Algorithm
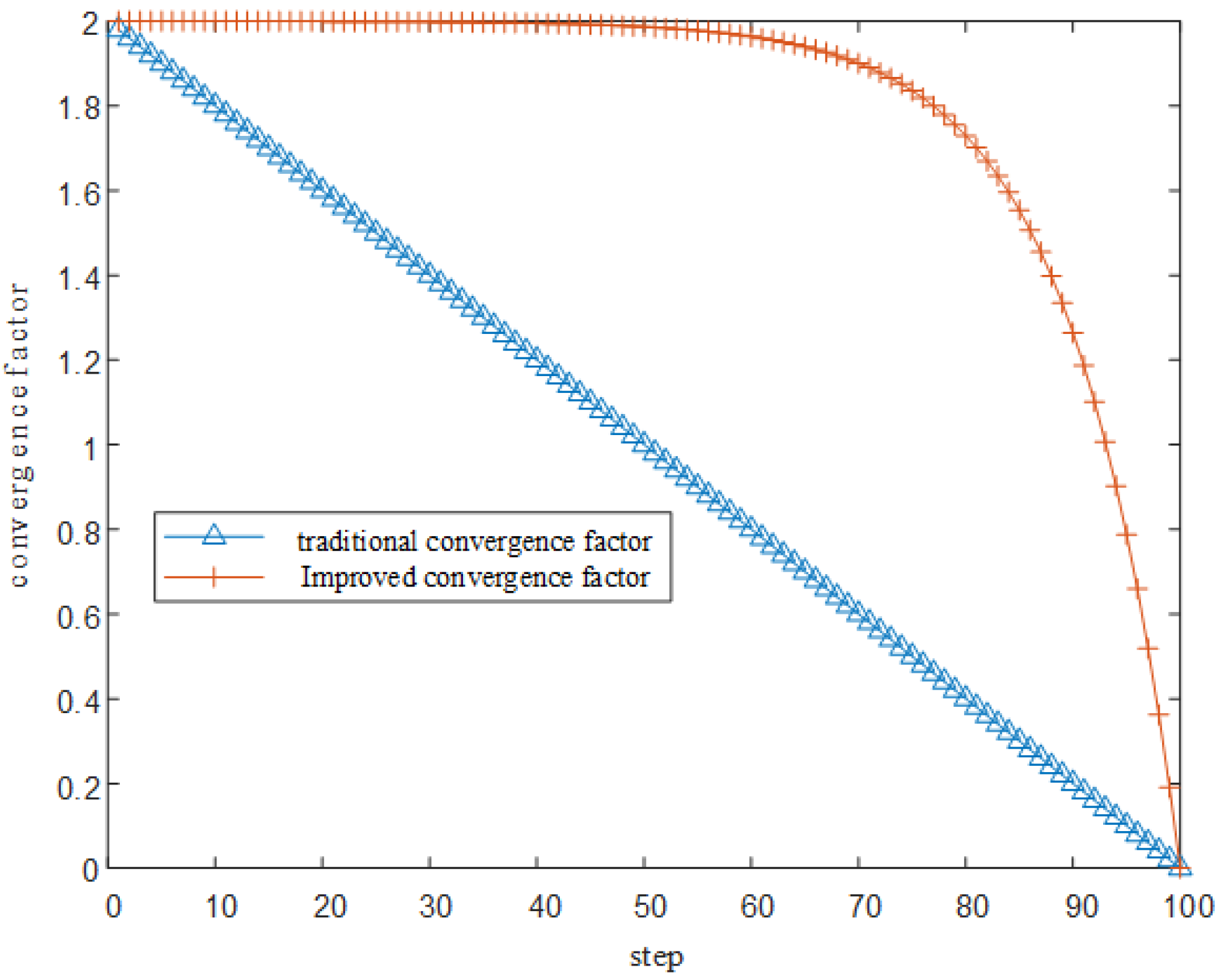
2.1. Parameter Selection Based on the Improved Whale Optimization Algorithm
| Algorithm 1: Improved whale optimization algorithm |
| Input: the whale population (i = 1, 2,…,n), Number of iterations T; |
| Fitness calculation rules S(); |
| 1: z = find(max(F())); |
| 2: =; |
| 3: t = 1; |
| 4: While(t < T) |
| 5: for each search agent; |
| 6: Generate A, C, and a based on position, randomly generate parameters 1 and p; |
| 7: if1(p < 0.5); |
| 8: if2(|A| < 1); |
| 9: ; 10: else; |
| 11: |
| 12: end if2; |
| 13: else; |
| 14: |
| 15: end if1 |
| 16: end for |
| 17: Update when optimal solution ; |
| 18: t = t + 1; |
| 19: end while |
| Output |
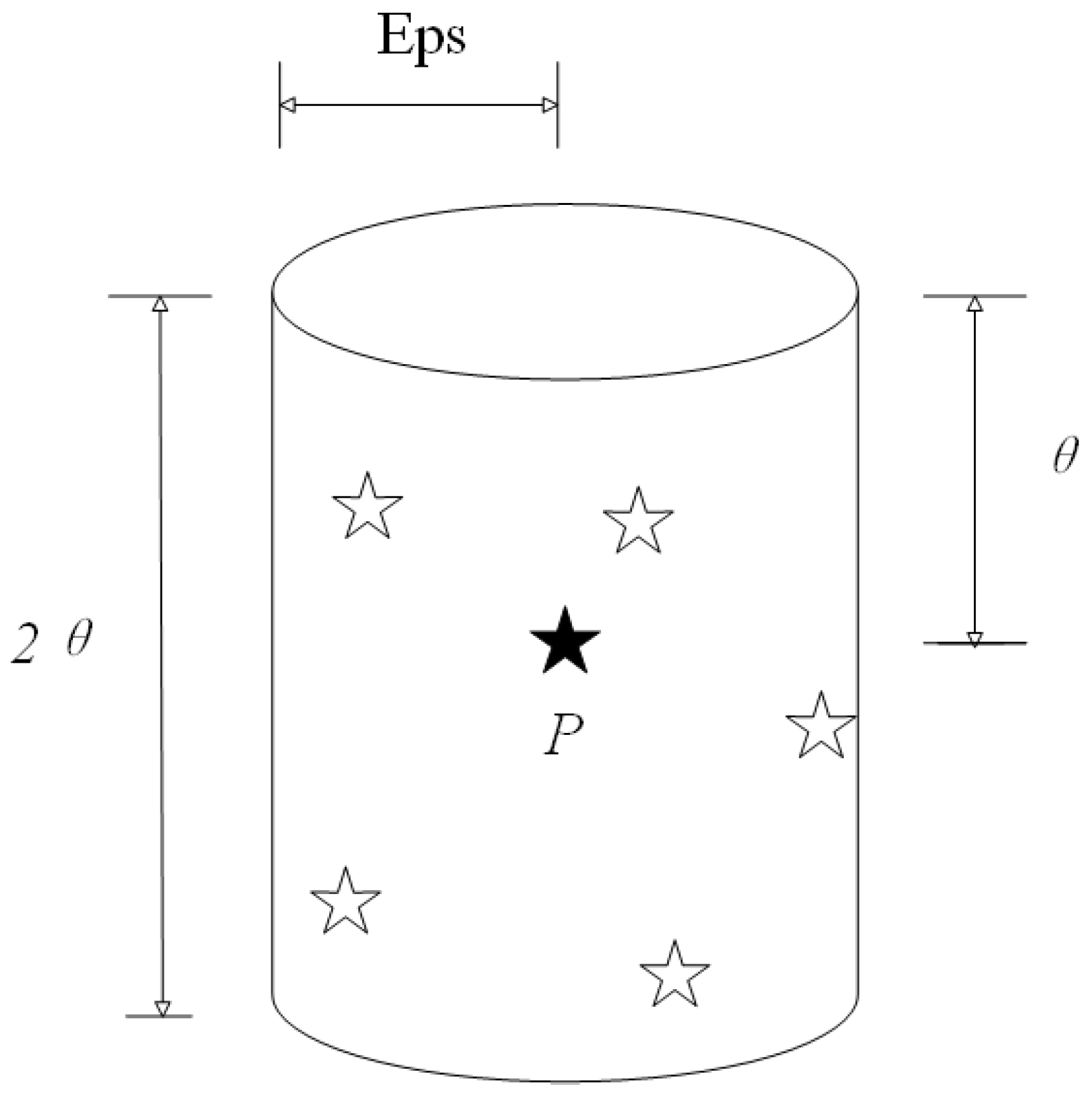
2.2. Signal-Level Binning Based on the IGWOA-DBSCAN Clustering Algorithm
2.3. Secondary Sorting Algorithm for Data Stream Signals
3. Results
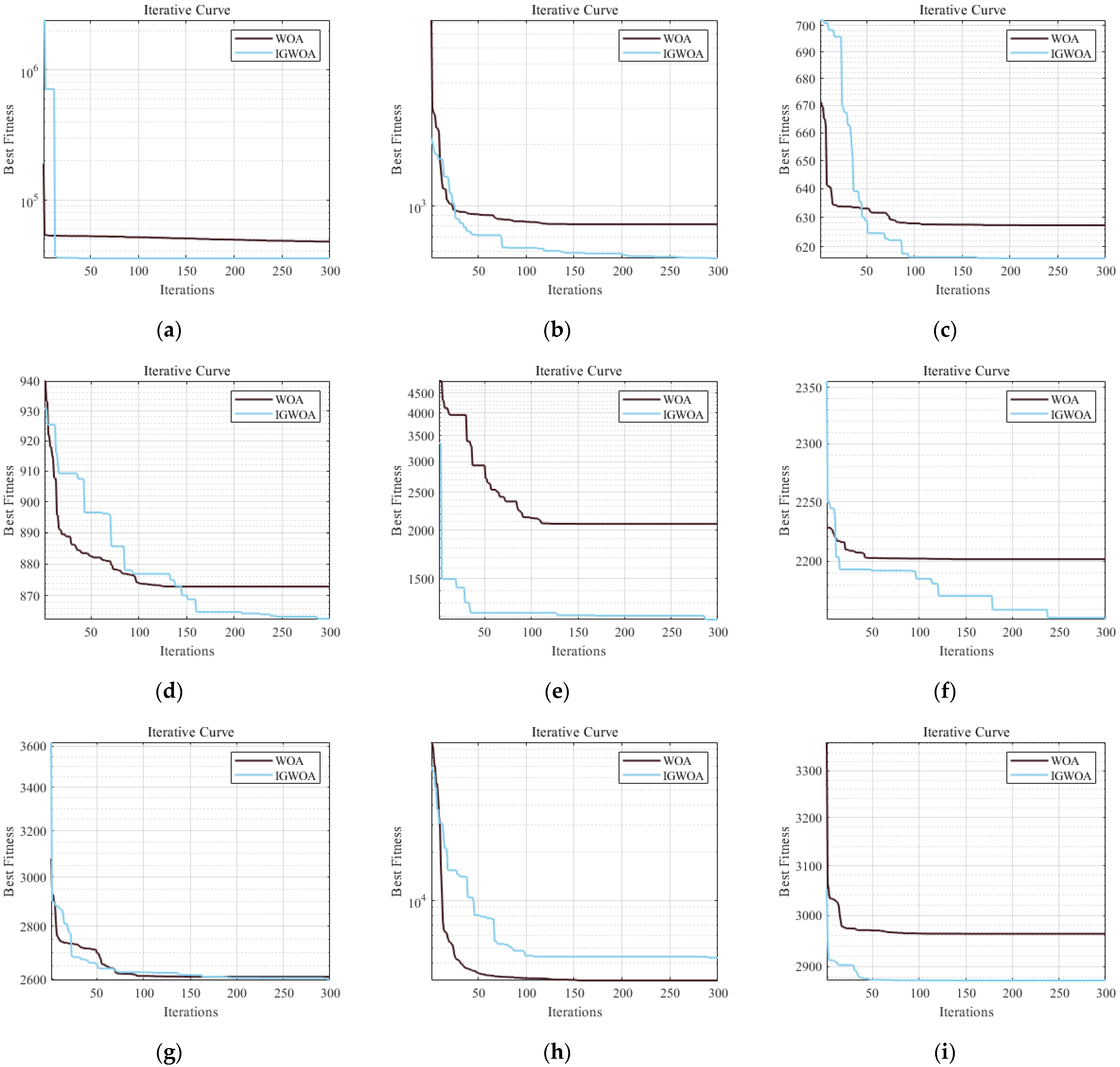
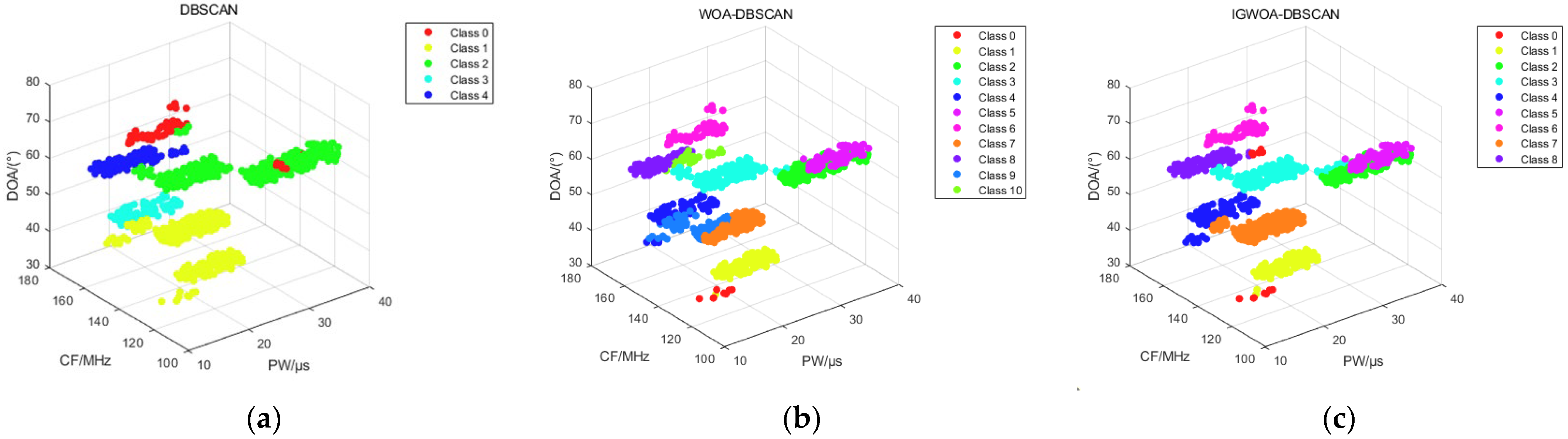
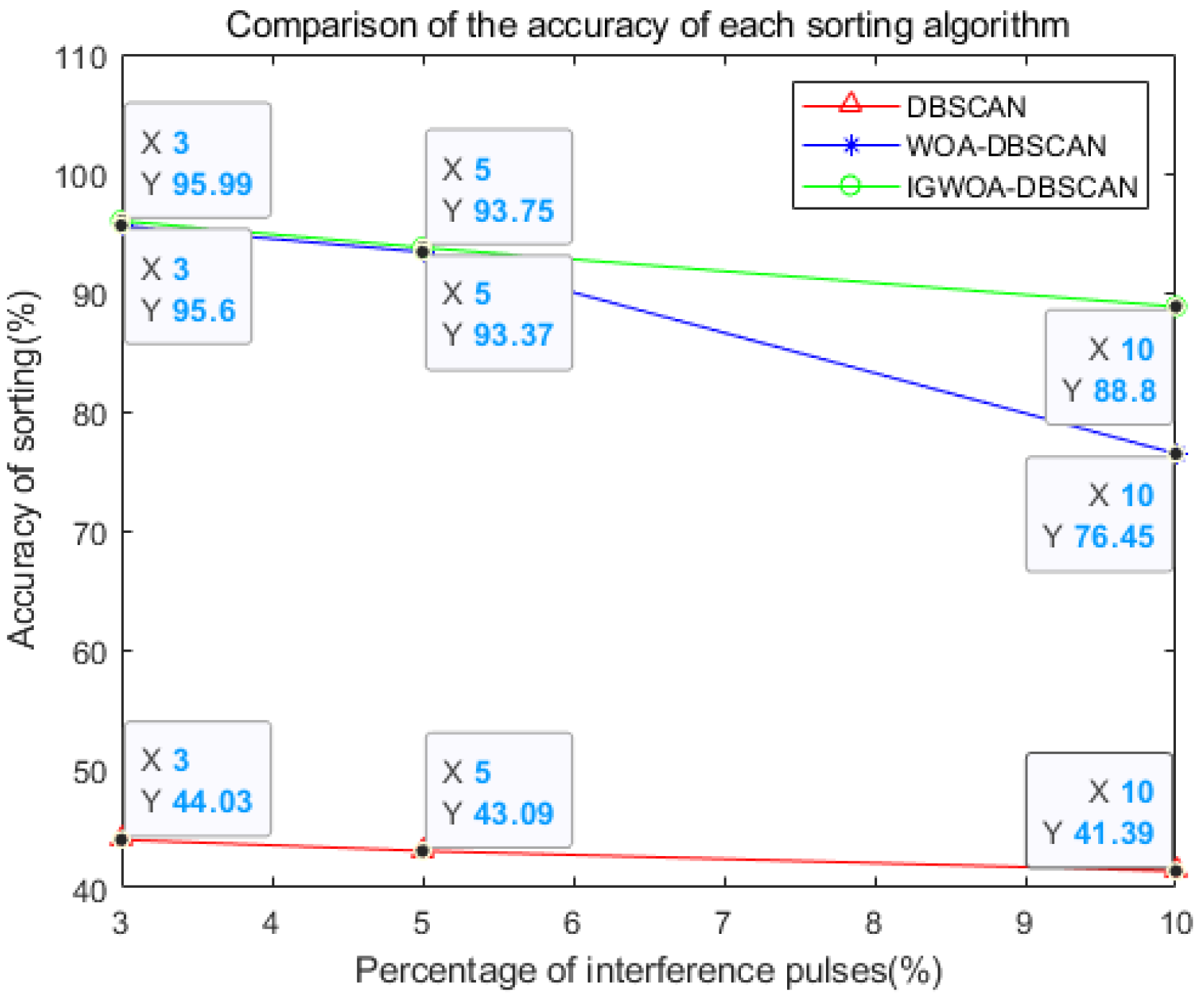
3.1. Verification of the Effectiveness of the First-Level Sorting Algorithm
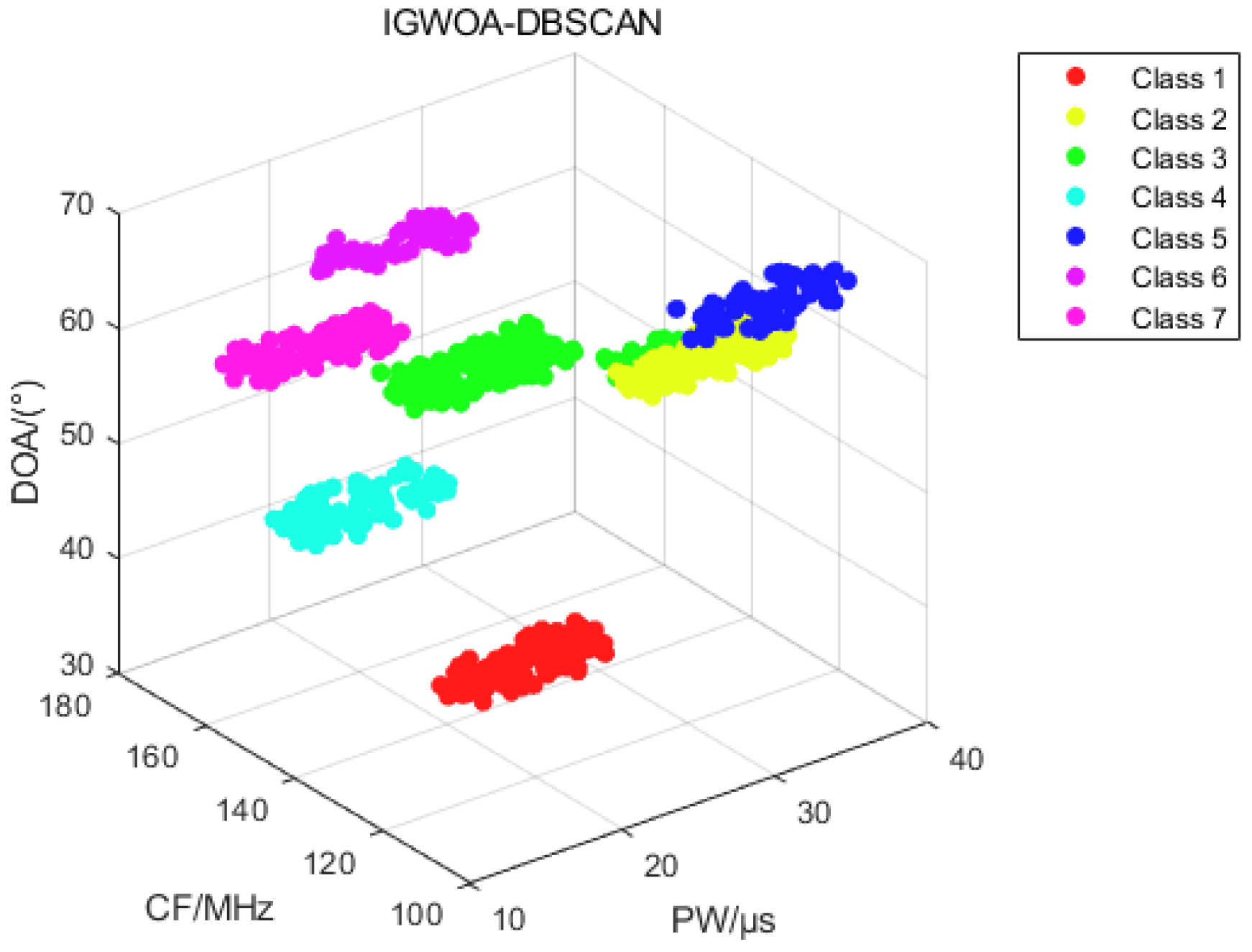
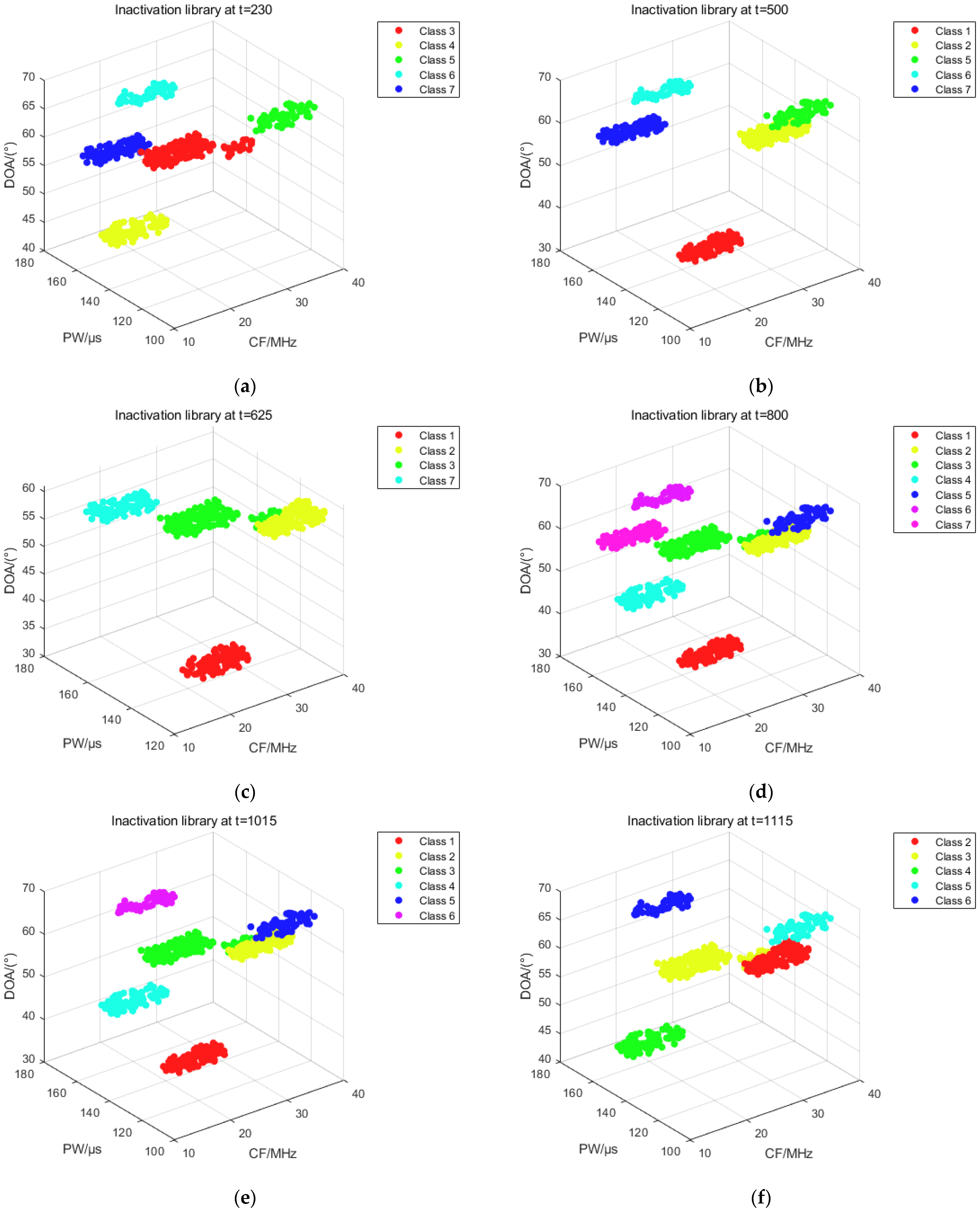
3.2. Validating the Effectiveness of the Secondary Sorting Algorithm
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DBSCAN | Density-based spatial clustering of applications with noise |
| WOA | Whale optimization algorithm |
| IGWOA | Improved golden sine whale optimization algorithm |
References
- Zhu, J.; Song, Y.; Jiang, N.; Xie, Z.; Fan, C.; Huang, X. Enhanced Doppler Resolution and Sidelobe Suppression Performance for Golay Complementary Waveforms. Remote Sens. 2023, 15, 2452. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y.; Sun, S. A radar signal sorting algorithm based on PRI. In Proceedings of the 2019 19th International Symposium on Communications and Information Technologies (ISCIT), Ho Chi Minh, Vietnam, 25–27 September 2019; pp. 144–149. [Google Scholar]
- Ahmed, M.; Seraj, R.; Islam, S.M.S. The k-means Algorithm: A Comprehensive Survey and Performance Evaluation. Electronics 2020, 9, 1295. [Google Scholar] [CrossRef]
- Ikotun, A.M.; Ezugwu, A.E.; Abualigah, L.; Abuhaija, B.; Heming, J. K-means clustering algorithms: A comprehensive review, variants analysis, and advances in the era of big data. Inf. Sci. 2023, 622, 178–210. [Google Scholar] [CrossRef]
- İhsanoğlu, A.; Zaval, M. Statistically Improving K-means Clustering Performance. In Proceedings of the 2024 32nd Signal Processing and Communications Applications Conference (SIU), Mersin, Turkey, 15–18 May 2024; pp. 1–4. [Google Scholar]
- Rodriguez, M.Z.; Comin, C.H.; Casanova, D.; Bruno, O.M.; Amancio, D.R.; Costa, L.d.F.; Rodrigues, F.A. Clustering algorithms: A comparative approach. PLoS ONE 2019, 14, e0210236. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the kdd, Portland, OR, USA, 2–4 August 1996; Volume 96, pp. 226–231. [Google Scholar]
- Su, X.; Zhang, D.; Ye, F. Radar signal sorting method based on hierarchical clustering and spectral adaptation. Syst. Eng. Electron. 2025, 47, 101–108. (In Chinese) [Google Scholar]
- Luo, J.; Li, X.; Li, J.; Xue, Q.; Yang, F.; Zhang, W. Radiation signal sorting method based on PDW multi-feature fusion. Syst. Eng. Electron. 2024, 46, 80–87. (In Chinese) [Google Scholar]
- Wu, J. Research on Radar Signal Sorting Method Based on Machine Learning. Master’s Thesis, Heilongjiang University, Harbin, China, 2024. [Google Scholar] [CrossRef]
- Wang, C.; Ling, Q.; Yan, W. A Radar Emitter Classification Method Based on Fusion of Inter-Pulse Featuresand Intra-Pulse Features. J. Nav. Aviat. Univ. 2025, 40, 278–284. (In Chinese) [Google Scholar]
- Rad, M.H.; Abdolrazzagh-Nezhad, M. A new hybridization of DBSCAN and fuzzy earthworm optimization algorithm for data cube clustering. Soft Comput. 2020, 24, 15529–15549. [Google Scholar] [CrossRef]
- An, X.; Wang, Z.; Wang, D.; Liu, S.; Jin, C.; Xu, X.; Cao, J. STRP-DBSCAN: A Parallel DBSCAN Algorithm Based on Spatial-Temporal Random Partitioning for Clustering Trajectory Data. Appl. Sci. 2023, 13, 11122. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, S. WOA-DBSCAN: Application of Whale Optimization Algorithm in DBSCAN Parameter Adaption. IEEE Access 2023, 11, 91861–91878. [Google Scholar] [CrossRef]
- Sui, J.; Liu, Z.; Li, X. Online Radar Emitter Deinterleaving; Tsinghua University Press: Beijing, China, 2022. (In Chinese) [Google Scholar]
- Zhang, X.; Furtlehner, C.; Germain-Renaud, C.; Sebag, M. Data Stream Clustering With Affinity Propagation. IEEE Trans. Knowl. Data Eng. 2014, 26, 1644–1656. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Zamani, H.; Varzaneh, Z.A.; Mirjalili, S. A Systematic Review of the Whale Optimization Algorithm: Theoretical Foundation, Improvements, and Hybridizations. Arch. Comput. Method Eng. 2023, 30, 4113–4159. [Google Scholar] [CrossRef] [PubMed]
- Kaur, G.; Arora, S. Chaotic whale optimization algorithm. J. Comput. Des. Eng. 2018, 5, 275–284. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Xiao, Z.; Liu, S. Study on Elite Opposition-Based Golden-Sine Whale OptimizationAlgorithm and its Application of Project Optimization. Acta Electron. Sin. 2019, 47, 2177–2186. (In Chinese) [Google Scholar]
- Dai, M.; Tang, D.; Giret, A.; Salido, M.A. Multi-objective optimization for energy-efficient flexible job shop scheduling problem with transportation constraints. Robot. Comput.-Integr. Manuf. 2019, 59, 143–157. [Google Scholar] [CrossRef]
- Zhu, Q.; Tang, X.; Liu, Z. Revised DBSCAN Clustering Algorithm Based on Dual Grid. In Proceedings of the 32nd 2020 Chinese Control and Decision Conference (CCDC 2020), Hefei, China, 22–24 August 2020; IEEE: New York, NY, USA, 2020; pp. 3461–3466. [Google Scholar]
- Hahsler, M.; Piekenbrock, M.; Doran, D. dbscan: Fast Density-Based Clustering with R. J. Stat. Softw. 2019, 91, 1–30. [Google Scholar] [CrossRef]
- Xie, J.; Gao, H.; Xie, W.; Liu, X.; Grant, P.W. Robust clustering by detecting density peaks and assigning points based on fuzzy weighted K-nearest neighbors. Inf. Sci. 2016, 354, 19–40. [Google Scholar] [CrossRef]
- Katebi, M.; RezaKhani, A.; Joudaki, S.; Shiri, M.E. RAPSAMS: Robust affinity propagation clustering on static android malware stream. Concurr. Comput.-Pract. Exp. 2022, 34, e6980. [Google Scholar] [CrossRef]
- Ahmed, R.; Dalkilic, G.; Erten, Y. DGStream: High quality and efficiency stream clustering algorithm. Expert Syst. Appl. 2020, 141, 112947. [Google Scholar] [CrossRef]
- Wan, L.; Ng, W.K.; Dang, X.H.; Yu, P.S.; Zhang, K. Density-Based Clustering of Data Streams at Multiple Resolutions. ACM Trans. Knowl. Discov. Data 2009, 3, 14. [Google Scholar] [CrossRef]
- Li, S.; Yang, S.; Deng, Z.; Si, W. Cooperative Signal Sorting Method Based on Multi-station TDOA andAdaptive Stream Clustering. J. Signal Process. 2024, 40, 682–694. [Google Scholar] [CrossRef]
- Liu, L.; Wang, L.; Li, P.; Chen, T. Radar signal sorting algorithm for DSets-DBSCAN withoutparameter clustering. J. Natl. Univ. Def. Technol. 2022, 44, 158–163. (In Chinese) [Google Scholar]
- Lu, X. PDW Datasets; Science Data Bank: Beijing, China, 2024. [Google Scholar] [CrossRef]







| Radar Catalogs | CF/MHz | s | DOA (°) | Pulse Number |
|---|---|---|---|---|
| Radar 1 | 97–103 | 41–43 | 5–7 | 200 |
| Radar 2 | 147–153 | 36–38 | 9–11 | 200 |
| Radar 3 | 177–183 | 41–43 | 4–6 | 200 |
| Radar 4 | 197–203 | 34–37 | 8–10 | 200 |
| Radar 5 | 297–303 | 36–38 | 15–17 | 200 |
| Radar Catalogs | CF/MHz | s | DOA (°) | Pulse Number |
|---|---|---|---|---|
| Radar 1 | 135–145 | 20–30 | 32–34 | 100 |
| Radar 2 | 120–130 | 27–37 | 59–61 | 170 |
| Radar 3 | 135–145 | 17–27 | 59–61 | 150 |
| Radar 4 | 165–175 | 18–28 | 40–42 | 90 |
| Radar 5 | 105–115 | 27–37 | 67–69 | 60 |
| Radar 6 | 150–160 | 15–25 | 67–69 | 45 |
| Radar 7 | 145–155 | 20–30 | 40–42 | 300 |
| Radar 8 | 165–175 | 15–25 | 55–57 | 100 |
| Performance Evaluation | DBSCAN | WOA-DBSCAN | IGWOA-DBSCAN |
|---|---|---|---|
| Accuracy rate | 40.1% | 60% | 97.8% |
| Representative Moments | Number of Effective Library Pulses | Number of Pulses in the Inactivation Library | Number of Pulses in the Outlier Library |
|---|---|---|---|
| 230 | 230 | 468 | 0 |
| 500 | 230 | 722 | 0 |
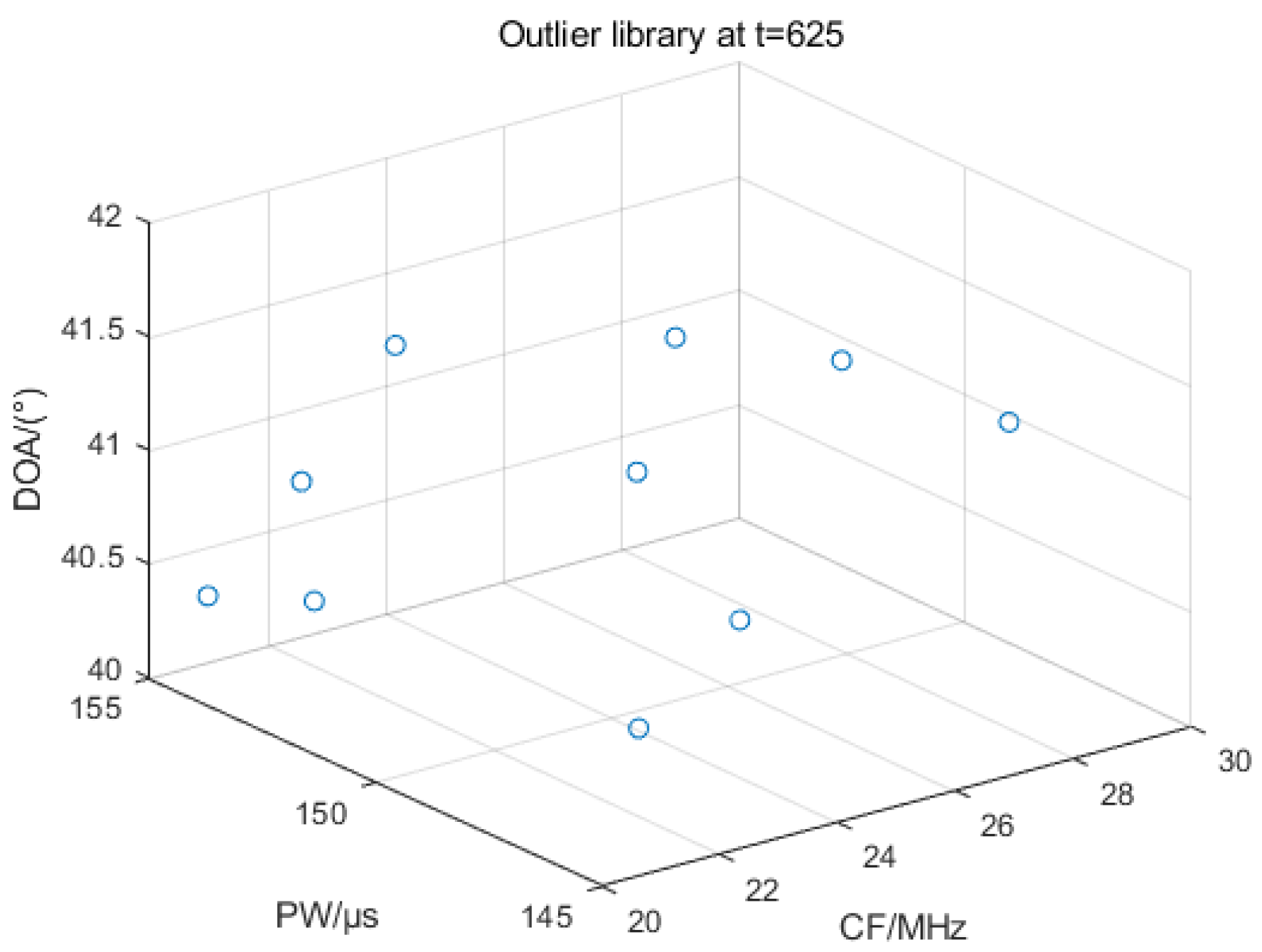
| 625 | 195 | 940 | 10 |
| 800 | 185 | 1330 | 0 |
| 1015 | 400 | 1230 | 0 |
| 1115 | 300 | 1330 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, H.; Lu, C.; Cui, Y. Improved WOA-DBSCAN Online Clustering Algorithm for Radar Signal Data Streams. Sensors 2025, 25, 5184. https://doi.org/10.3390/s25165184
Wan H, Lu C, Cui Y. Improved WOA-DBSCAN Online Clustering Algorithm for Radar Signal Data Streams. Sensors. 2025; 25(16):5184. https://doi.org/10.3390/s25165184
Chicago/Turabian StyleWan, Haidong, Cheng Lu, and Yongpeng Cui. 2025. "Improved WOA-DBSCAN Online Clustering Algorithm for Radar Signal Data Streams" Sensors 25, no. 16: 5184. https://doi.org/10.3390/s25165184
APA StyleWan, H., Lu, C., & Cui, Y. (2025). Improved WOA-DBSCAN Online Clustering Algorithm for Radar Signal Data Streams. Sensors, 25(16), 5184. https://doi.org/10.3390/s25165184






