A Shared Control Approach to Robot-Assisted Cataract Surgery Training for Novice Surgeons
Abstract
1. Introduction
2. State of the Art and Research Gap
2.1. Teleoperation and Shared Control Medical Assistance Systems
2.2. Cataract Surgery Training and Safety Systems
2.3. Research Gap
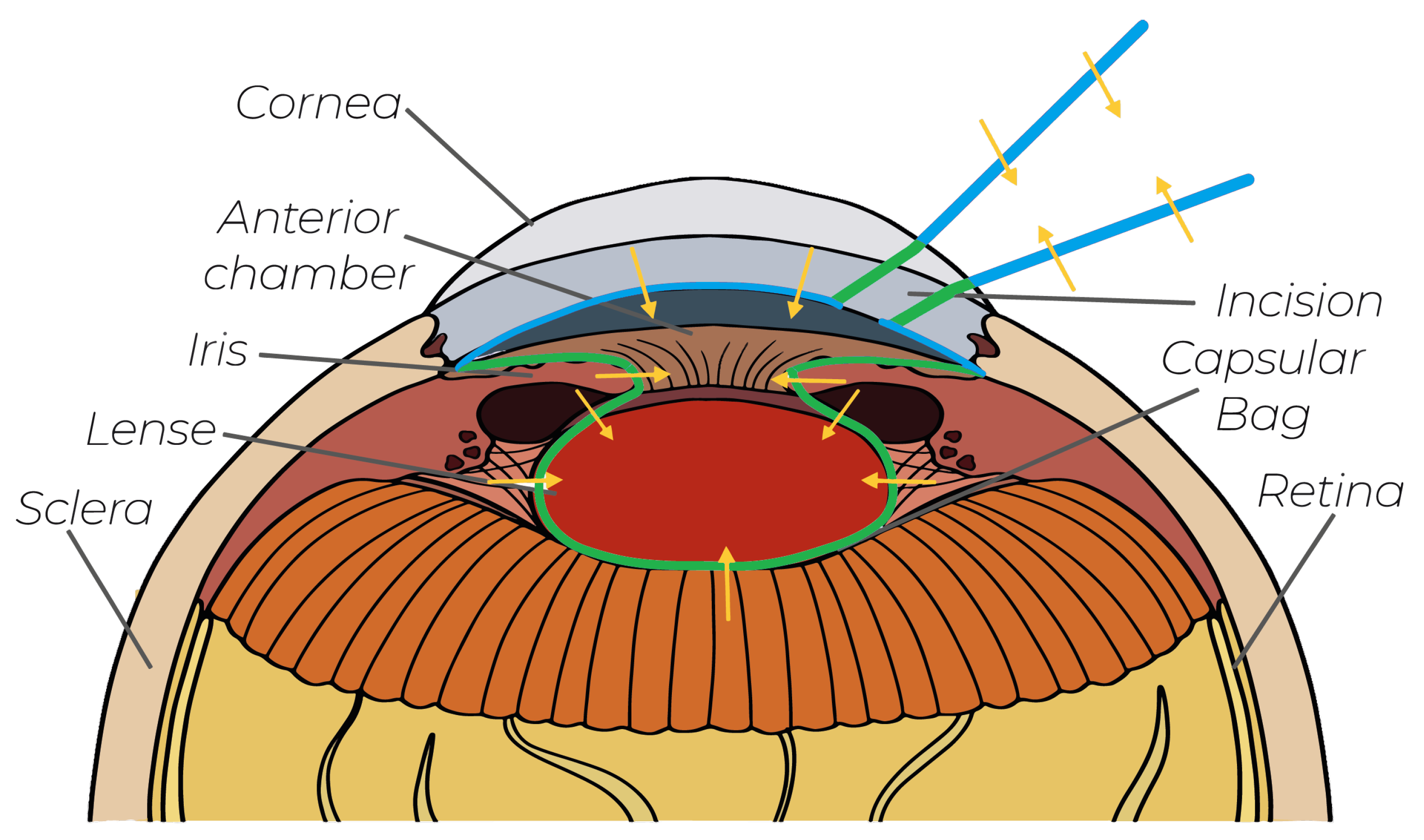
- Guidance to Incisions: This paper uses virtual-fixture-based shared control to generate FF for the guidance of surgeons along a predefined axis to the incision point. The novel guidance concept incorporates an efficient geometrical representation of the virtual fixtures, which can be directly taken from the soft tissue geometry, making our concept generalizable.
- Protection of the Posterior Corneal Surface: The posterior corneal surface is fragile, and therefore it must not be touched during manipulation inside the anterior chamber. A semisphere-shaped virtual fixture is used to generate FF toward the center of the anterior chamber, guiding the operating tool away from the cornea.
| Work | Positioning Support for Incision | Protection of Incision | Protection of Posterior Cornea | Protection of Iris | Guidance for Capsulorhexis | Protecting Capsular Bag |
|---|---|---|---|---|---|---|
| [9] | ✗ | ✓ | ✗ | ✓ back side | ✗ | ✓ |
| [38] | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ |
| [37] | ✗ | ✗ | ✗ | ✓ inner side | ✓ | ✗ |
| [39] | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ |
3. System Overview
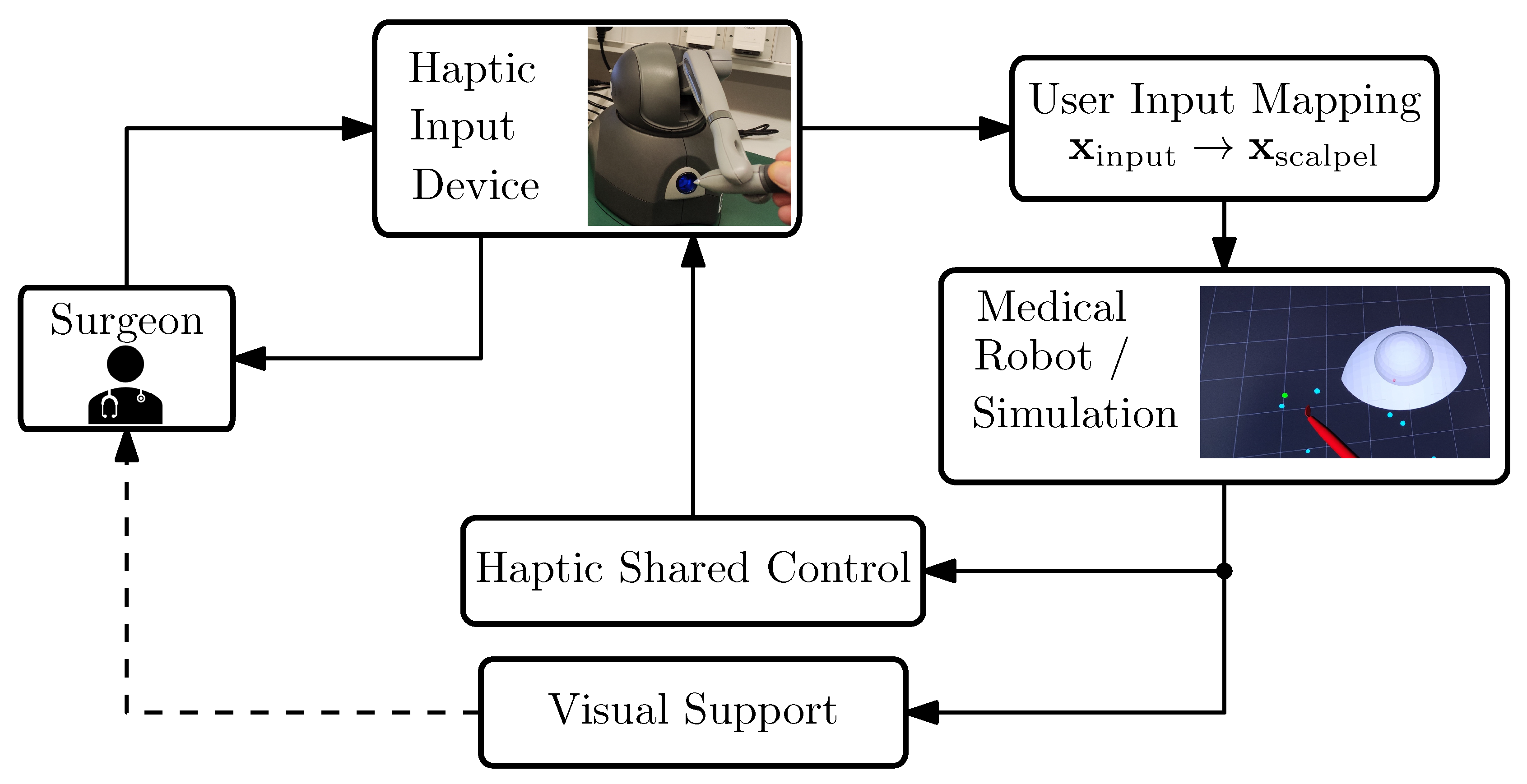
3.1. Technical System
- A haptic input device, a 3D Systems Touch (in the literature, this device is also referred to as the master robot, haptic input device, etc. For brevity, in this work, we will refer to it simply as the input device. More information can be found on the manufacturer’s website and in e.g., [40]).
- Mapping of the user inputs to the medical robot’s motion.
- Simulation of the scalpel’s motion. In our framework, we used SOFA for soft tissue interaction while we employed RViz for rapid deployment in situations that did not demand detailed modeling of tissue–scalpel interactions.
- Haptic shared control function. In general, this function can be virtual-fixture-based, model-based, or model-free. In this work, we propose a virtual-fixture-based haptic support.
- Visual clues for the guidance. It has been shown that visual cues can be helpful for training inexperienced surgeons; therefore, our setup includes visual guidance as well; see [41].
3.2. Technical Requirements
- It must be safe at any time to release the input device. When operators relax their grasp, no dangerous motion should result from the generated FF.
- The system should have a modular architecture. Different types of virtual fixtures should have the same interfaces to be easily exchangeable. This is necessary for the generalization of the shared control concept for various applications.
- The system should have a low latency. The time delay between measuring a new pose and setting the corresponding force field should not be perceptible by the user. The latency of the system needs to be tested.
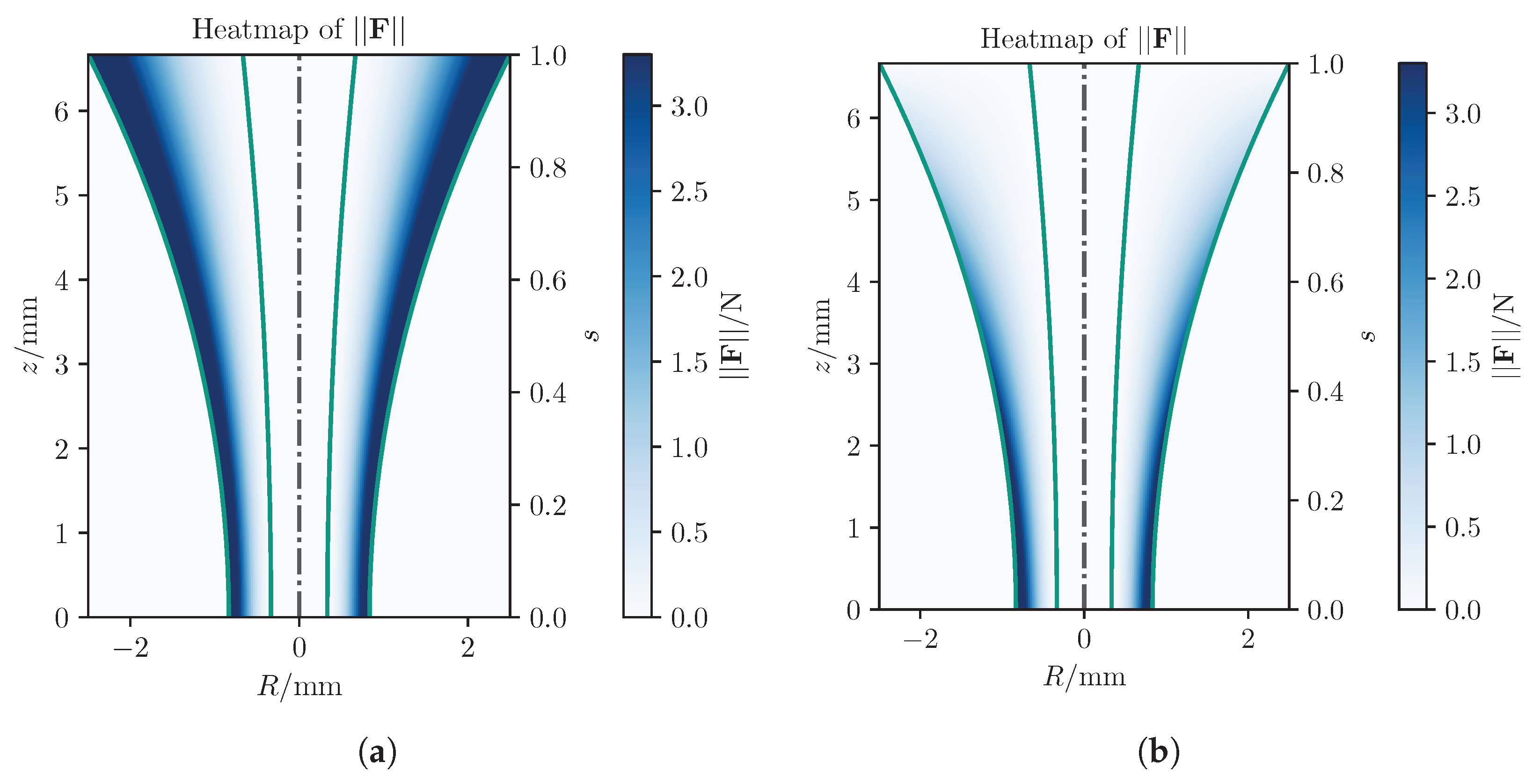
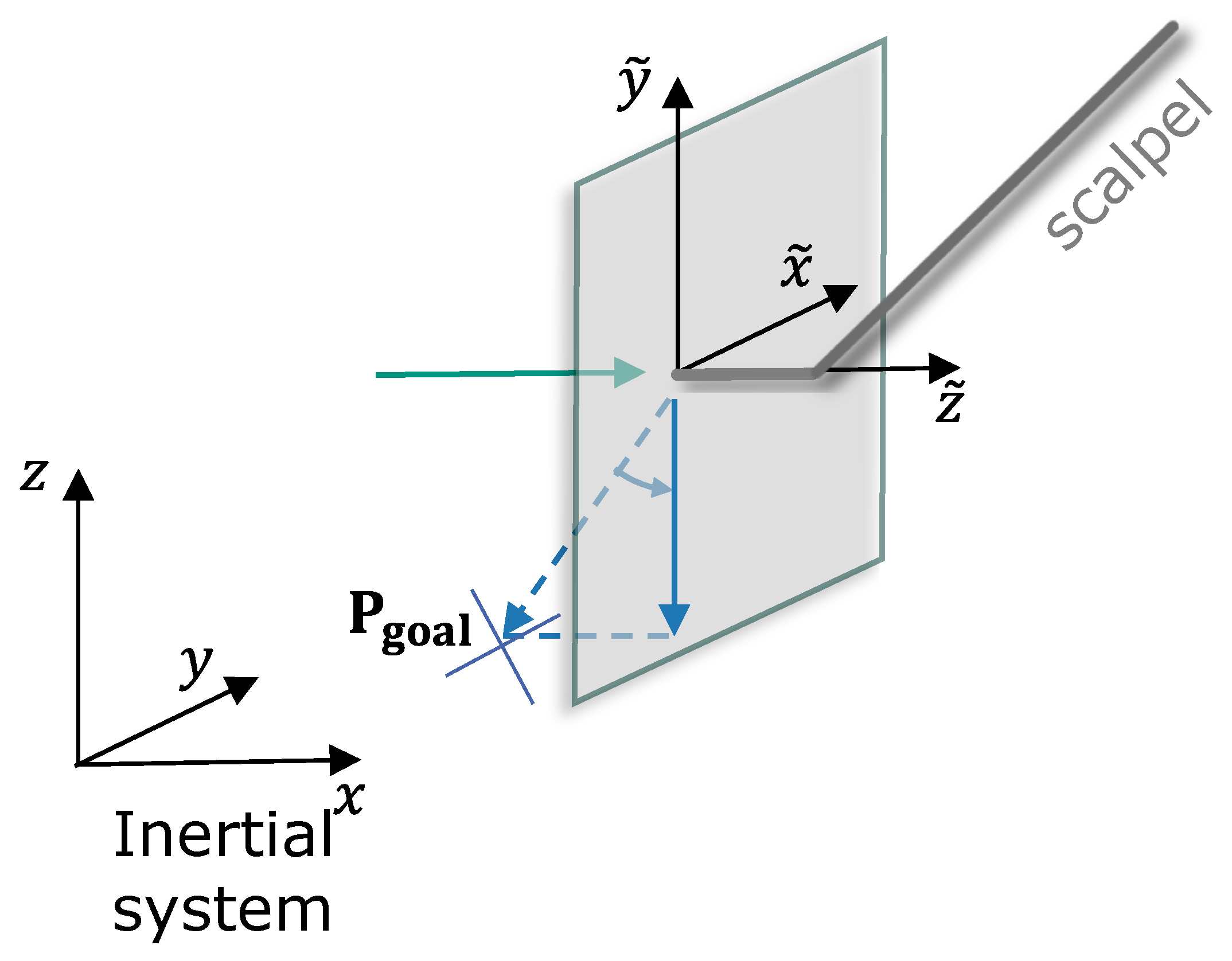
4. The Virtual-Fixture-Based Shared Control Guidance
- Two points and define the start and end of the rotational symmetric volume’s symmetry axis. The axis is parameterized with , so that at point A and at point B (see Figure 3).
- The inner and outer radius being given as functions of s.
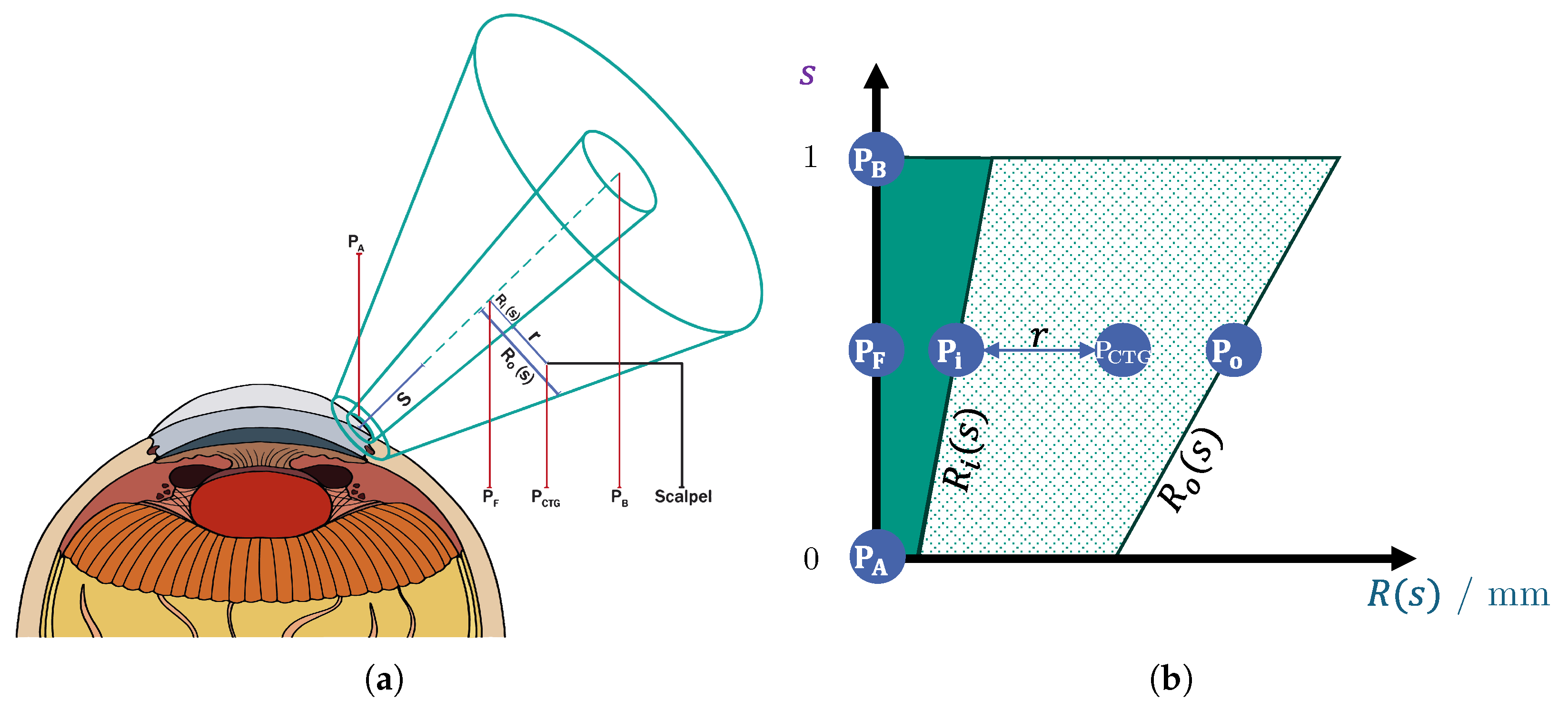
4.1. Goal Point and Gain Adaption
- In the hollow middle cylinder, there is no FF, since here, the surgeon moves the tool into the right direction. Thus, this hollow-formed fixture definition helps to maintain a more intuitive motion.
- The inner radius is defined as the goal point, , along which the tool is attracted.
- The outer radius defines the attraction zone, where the tool is pulled toward .
4.2. Force Feedback Generation
4.2.1. Proportional Feedback Generation
4.2.2. Relative Distance Feedback Generation
4.2.3. Anisotropic Velocity Damping and Integral Feedback Generation
4.2.4. Lateral Filtering of the Feedback Generation
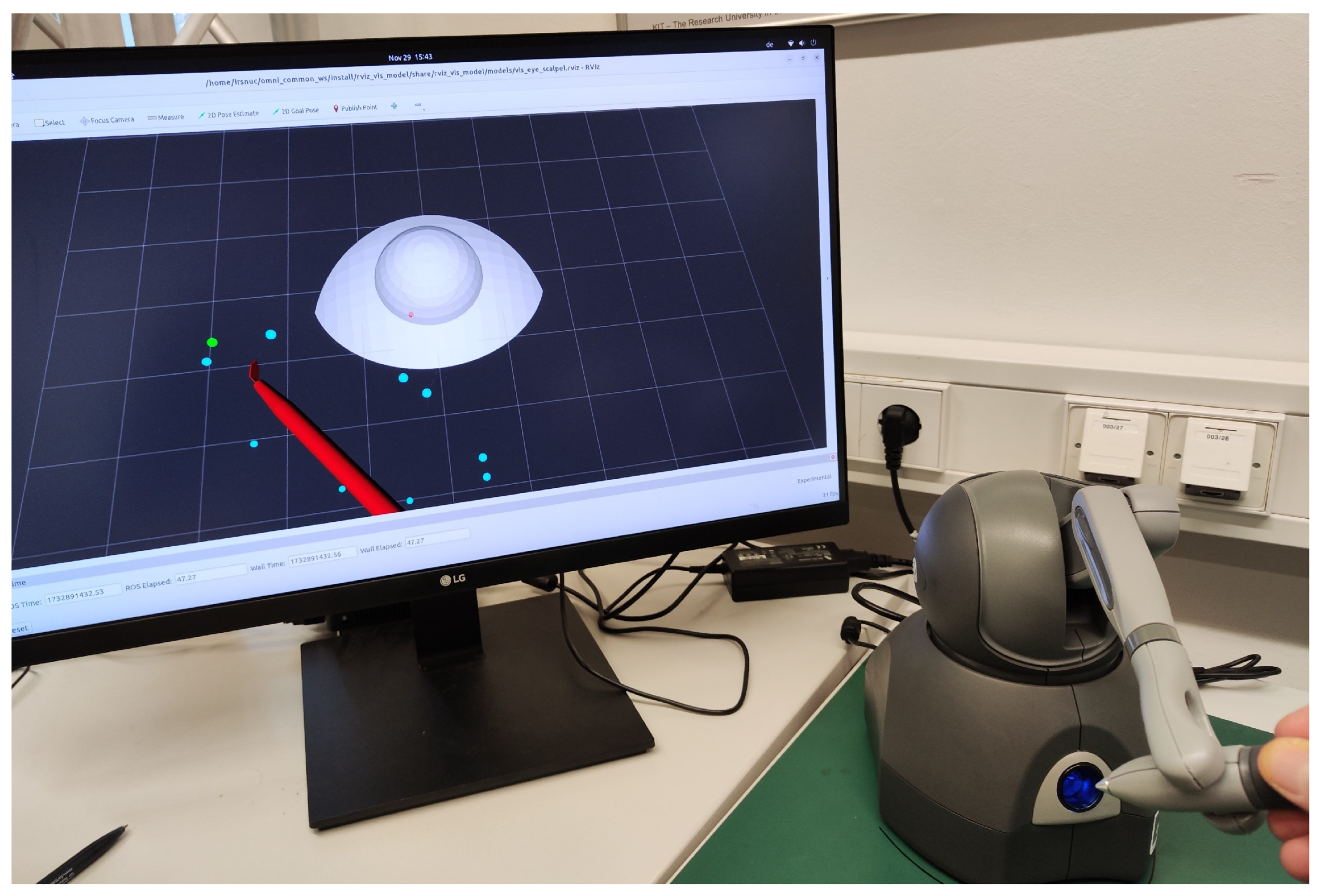
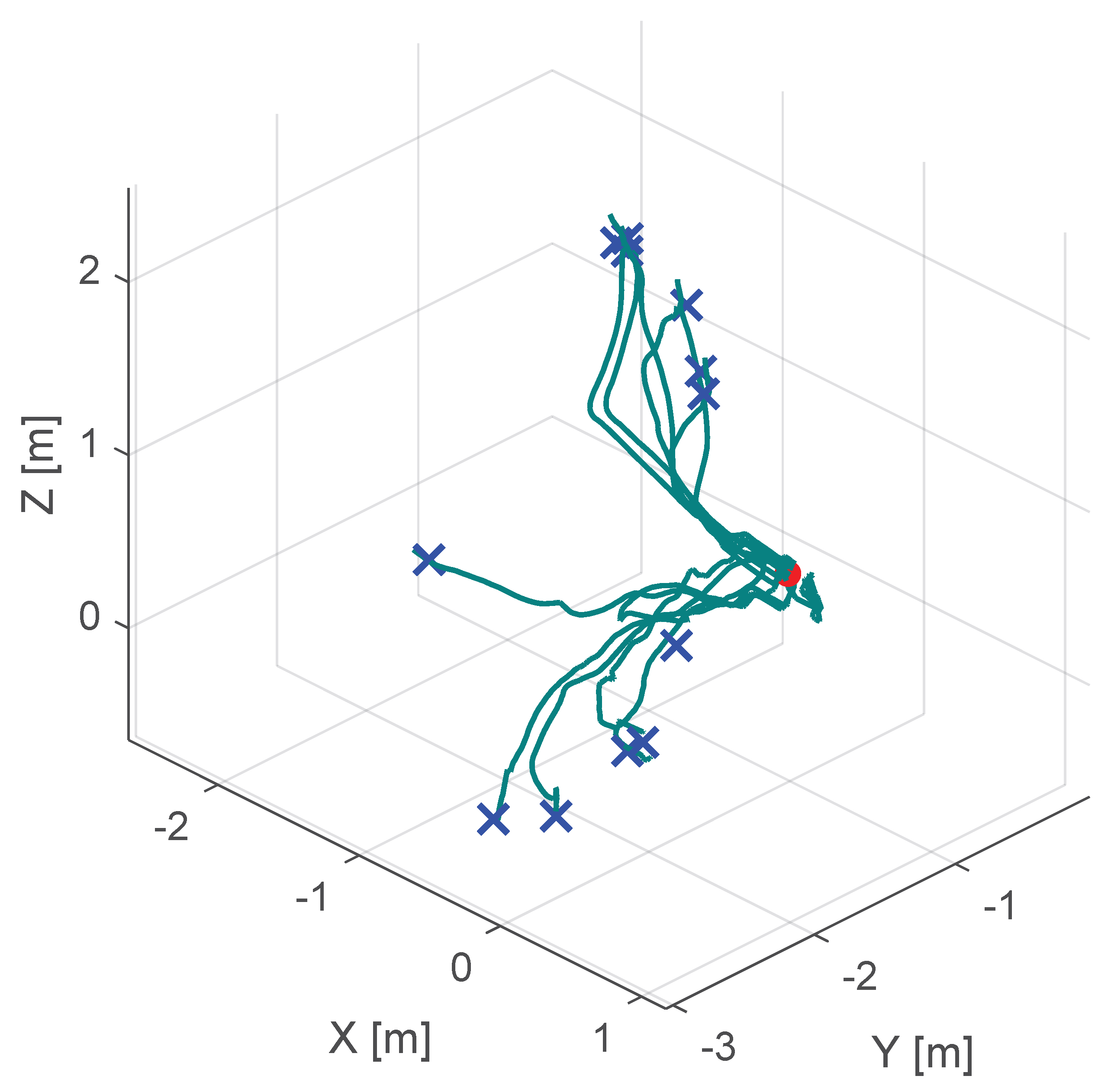
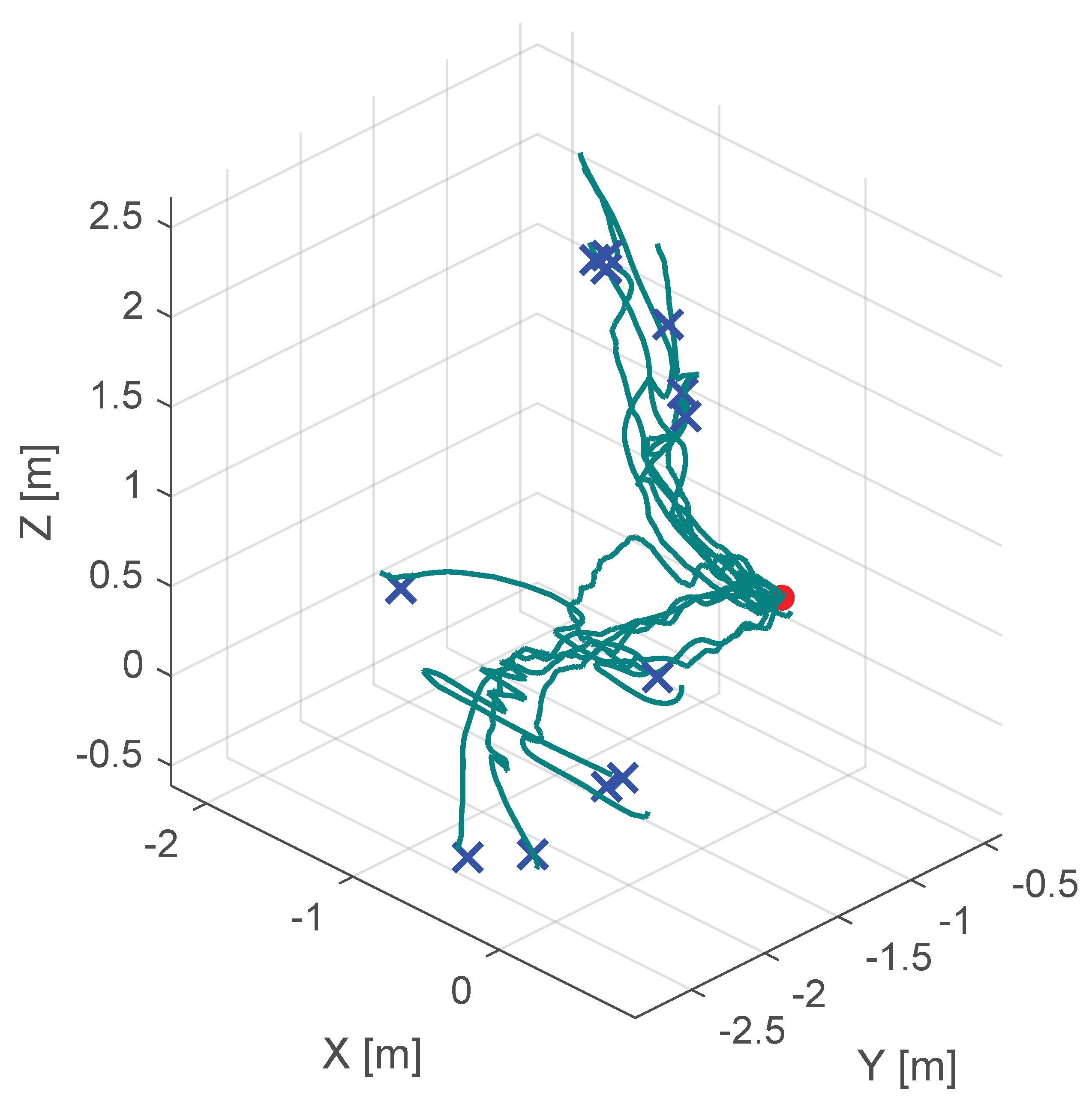
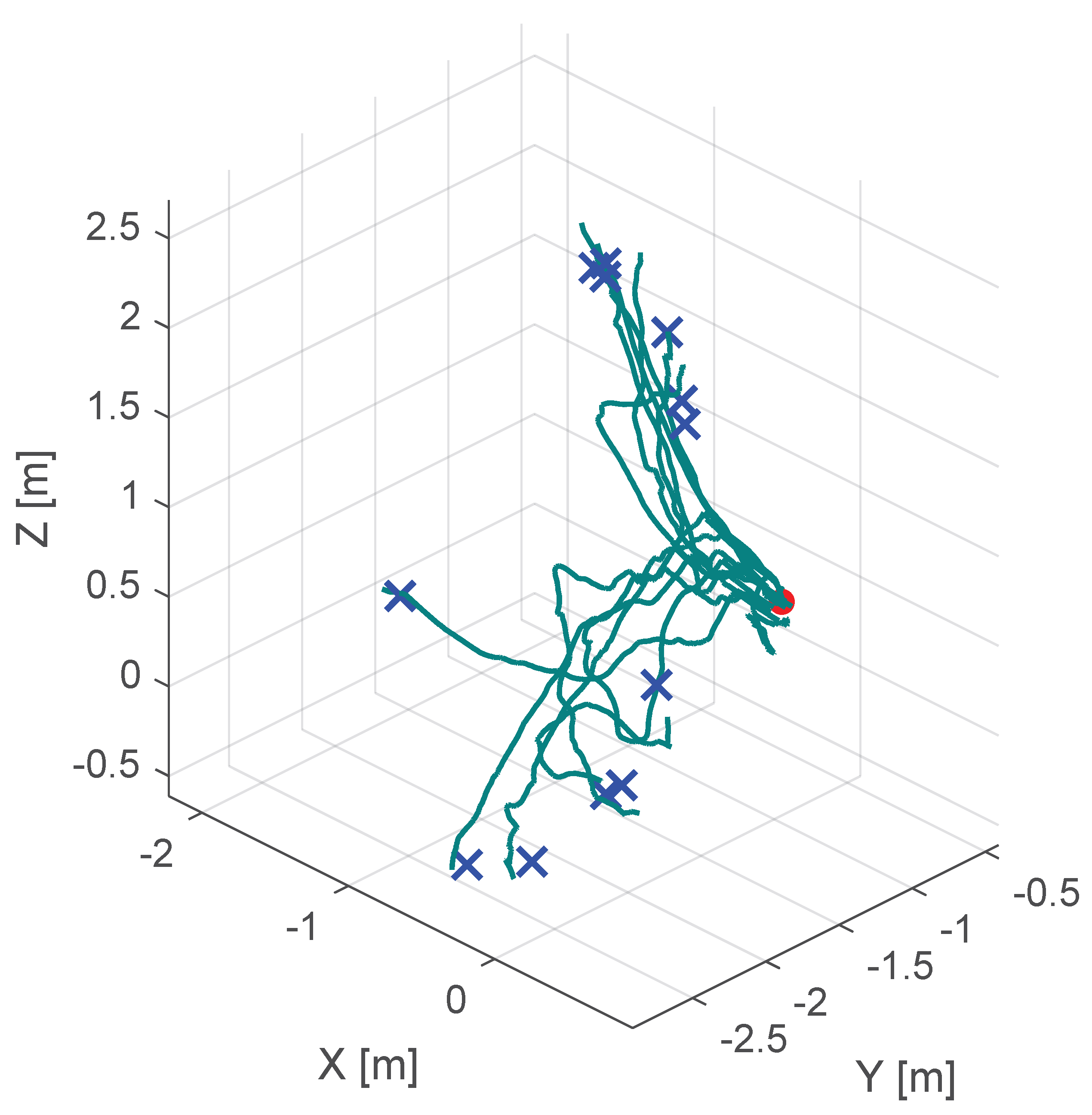
5. Initial Validation
Validation Setup
- 1
- Average completion time:where incisions. This metric evaluates the participant’s speed in completing the task.
- 2
- Time spent near to the incision point (critical proximity region):This metric assesses performance during the most critical phase regarding patient safety.
- 3
- Average positional error within the critical proximity region:where and define a safety-critical proximity.
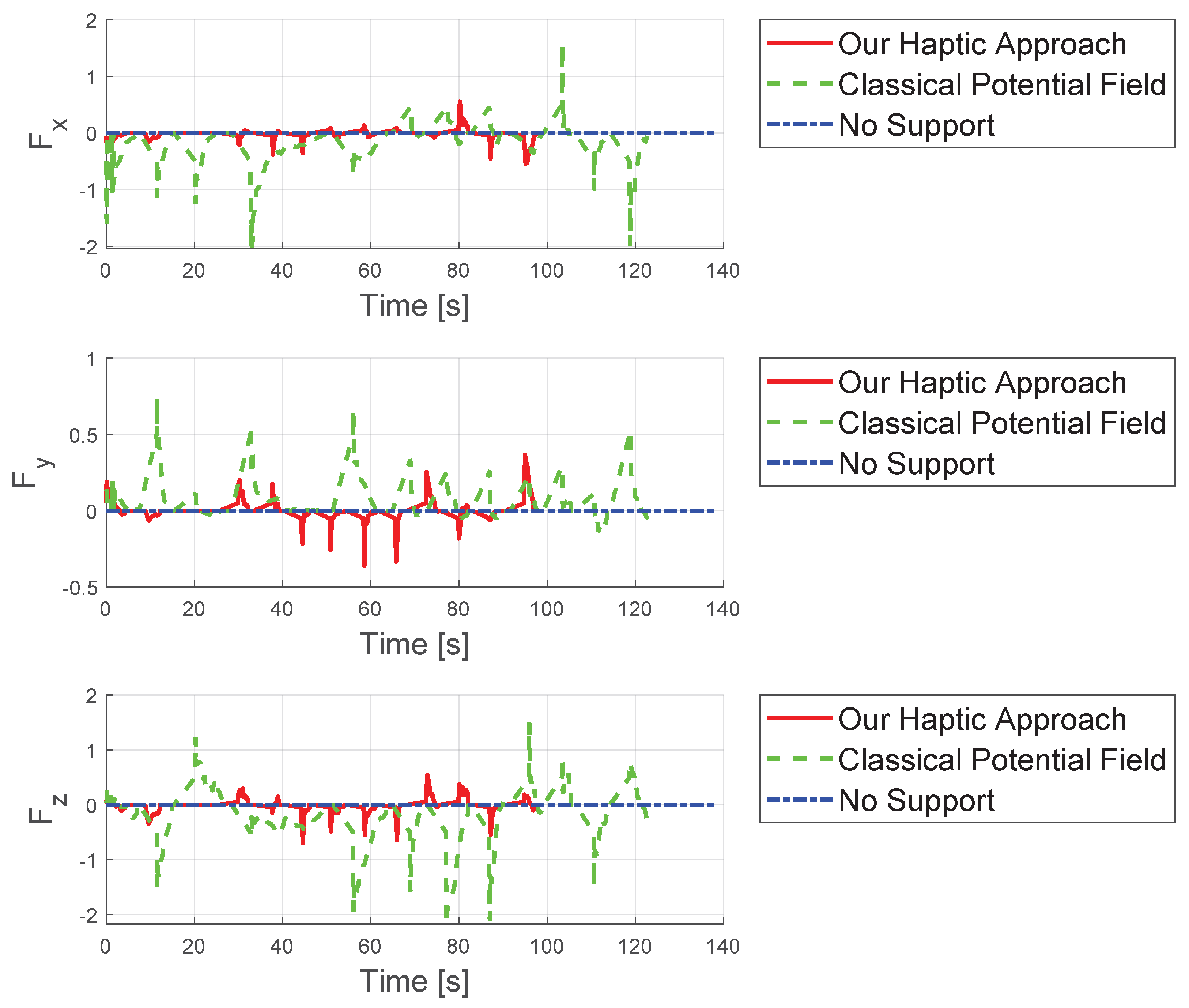
6. Results and Discussions of the Initial Experiment
6.1. Results
6.2. Limitation of the Current Experimental Setup
7. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
Abbreviations
| FF | Force Feedback |
| FDA | Food and Drug Administration |
| EMA | European Medicines Agency |
| CTG | Constrained Tool Geometry |
References
- Chen, J.Y.C.; Flemisch, F.O.; Lyons, J.B.; Neerincx, M.A. Guest Editorial: Agent and System Transparency. IEEE Trans. Hum.-Mach. Syst. 2020, 50, 189–193. [Google Scholar] [CrossRef]
- Guo, X.; McFall, F.; Jiang, P.; Liu, J.; Lepora, N.; Zhang, D. A Lightweight and Affordable Wearable Haptic Controller for Robot-Assisted Microsurgery. Sensors 2024, 24, 2676. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.N. Online Learning Human Behavior for a Class of Human-in-the-Loop Systems via Adaptive Inverse Optimal Control. IEEE Trans. Hum.-Mach. Syst. 2022, 52, 1004–1014. [Google Scholar] [CrossRef]
- Varga, B. Toward Adaptive Cooperation: Model-Based Shared Control Using LQ-Differential Games. Acta Polytech. Hung. 2024, 21, 439–456. [Google Scholar] [CrossRef]
- Wang, T.; Li, H.; Pu, T.; Yang, L. Microsurgery Robots: Applications, Design, and Development. Sensors 2023, 23, 8503. [Google Scholar] [CrossRef] [PubMed]
- Christou, A.S.; Amalou, A.; Lee, H.; Rivera, J.; Li, R.; Kassin, M.T.; Varble, N.; Tse, Z.T.H.; Xu, S.; Wood, B.J. Image-Guided Robotics for Standardized and Automated Biopsy and Ablation. Semin. Interv. Radiol. 2021, 38, 565–575. [Google Scholar] [CrossRef]
- Muñoz, V.F. Sensors Technology for Medical Robotics. Sensors 2022, 22, 9290. [Google Scholar] [CrossRef]
- Lee, A.; Baker, T.S.; Bederson, J.B.; Rapoport, B.I. Levels of Autonomy in FDA-cleared Surgical Robots: A Systematic Review. Npj Digit. Med. 2024, 7, 103. [Google Scholar] [CrossRef]
- Yang, Y.; Jiang, Z.; Yang, Y.; Qi, X.; Hu, Y.; Du, J.; Han, B.; Liu, G. Safety Control Method of Robot-Assisted Cataract Surgery with Virtual Fixture and Virtual Force Feedback. J. Intell. Robot. Syst. Theory Appl. 2020, 97, 17–32. [Google Scholar] [CrossRef]
- Gerber, M.J.; Pettenkofer, M.; Hubschman, J.P. Advanced robotic surgical systems in ophthalmology. Eye 2020, 34, 1554–1562. [Google Scholar] [CrossRef]
- Shajari, M.; Priglinger, S.; Kohnen, T.; Kreutzer, T.C.; Mayer, W.J. Katarakt- und Linsenchirurgie; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Rossi, T.; Romano, M.R.; Iannetta, D.; Romano, V.; Gualdi, L.; D’Agostino, I.; Ripandelli, G. Cataract surgery practice patterns worldwide: A survey. BMJ Open Ophthalmol. 2021, 6, e000464. [Google Scholar] [CrossRef]
- Dormegny, L.; Lansingh, V.C.; Lejay, A.; Chakfe, N.; Yaici, R.; Sauer, A.; Gaucher, D.; Henderson, B.A.; Thomsen, A.S.S.; Bourcier, T. Virtual Reality Simulation and Real-Life Training Programs for Cataract Surgery: A Scoping Review of the Literature. BMC Med. Educ. 2024, 24, 1245. [Google Scholar] [CrossRef]
- Hutter, D.E.; Wingsted, L.; Cejvanovic, S.; Jacobsen, M.F.; Ochoa, L.; González Daher, K.P.; La Cour, M.; Konge, L.; Thomsen, A.S.S. A Validated Test Has Been Developed for Assessment of Manual Small Incision Cataract Surgery Skills Using Virtual Reality Simulation. Sci. Rep. 2023, 13, 10655. [Google Scholar] [CrossRef]
- Varga, B.; Flemisch, F.; Hohmann, S. Human in the Loop. Automatisierungstechnik 2024, 72, 1109–1111. [Google Scholar] [CrossRef]
- Koyama, Y.; Marinho, M.M.; Mitsuishi, M.; Harada, K. Autonomous Coordinated Control of the Light Guide for Positioning in Vitreoretinal Surgery. IEEE Trans. Med. Robot. Bionics 2022, 4, 156–171. [Google Scholar] [CrossRef]
- Rosen, J.; Hannaford, B.; Satava, R.M. (Eds.) Surgical Robotics: Systems Applications and Visions; Springer: Boston, MA, USA, 2011. [Google Scholar] [CrossRef]
- Abedin-Nasab, M.H. (Ed.) Handbook of Robotic and Image-Guided Surgery; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Intuitive Surgical Operations, Inc. Da Vinci 5 Has Force Feedback Surgeons Can Now Feel Instrument Force to Aid in Gentler Surgery; Intuitive Surgical Operations, Inc.: Sunnyvale, CA, USA, 2024. [Google Scholar]
- Intuitive. Da Vinci 5 Has Force Feedback, 2024. Available online: https://www.intuitive.com/en-us/about-us/newsroom/Force%20Feedback (accessed on 19 June 2025).
- Patel, R.V.; Atashzar, S.F.; Tavakoli, M. Haptic Feedback and Force-Based Teleoperation in Surgical Robotics. Proc. IEEE 2022, 110, 1012–1027. [Google Scholar] [CrossRef]
- Haidegger, T. Autonomy for Surgical Robots: Concepts and Paradigms. IEEE Trans. Med. Robot. Bionics 2019, 1, 65–76. [Google Scholar] [CrossRef]
- Flemisch, F.; Abbink, D.; Itoh, M.; Pacaux-Lemoine, M.P.; Weßel, G. Shared Control Is the Sharp End of Cooperation: Towards a Common Framework of Joint Action, Shared Control and Human Machine Cooperation. IFAC-PapersOnLine 2016, 49, 72–77. [Google Scholar] [CrossRef]
- Duan, X.; Tian, H.; Li, C.; Han, Z.; Cui, T.; Shi, Q.; Wen, H.; Wang, J. Virtual-Fixture Based Drilling Control for Robot-Assisted Craniotomy: Learning From Demonstration. IEEE Robot. Autom. Lett. 2021, 6, 2327–2334. [Google Scholar] [CrossRef]
- Tian, H.; Duan, X.; Han, Z.; Cui, T.; He, R.; Wen, H.; Li, C. Virtual-Fixtures Based Shared Control Method for Curve-Cutting With a Reciprocating Saw in Robot-Assisted Osteotomy. IEEE Trans. Automat. Sci. Eng. 2024, 21, 1899–1910. [Google Scholar] [CrossRef]
- Shi, Y.; Zhu, P.; Wang, T.; Mai, H.; Yeh, X.; Yang, L.; Wang, J. Dynamic Virtual Fixture Generation Based on Intra-Operative 3D Image Feedback in Robot-Assisted Minimally Invasive Thoracic Surgery. Sensors 2024, 24, 492. [Google Scholar] [CrossRef]
- Marinho, M.M.; Ishida, H.; Harada, K.; Deie, K.; Mitsuishi, M. Virtual Fixture Assistance for Suturing in Robot-Aided Pediatric Endoscopic Surgery. IEEE Robot. Autom. Lett. 2020, 5, 524–531. [Google Scholar] [CrossRef]
- Hu, Z.J.; Wang, Z.; Huang, Y.; Sena, A.; Rodriguez Y Baena, F.; Burdet, E. Towards Human-Robot Collaborative Surgery: Trajectory and Strategy Learning in Bimanual Peg Transfer. IEEE Robot. Autom. Lett. 2023, 8, 4553–4560. [Google Scholar] [CrossRef]
- Kong, C.F.; Lee, B.W.; George, A.; Ling, M.L.; Jain, N.S.; Francis, I.C. Cataract Surgery Operating Times: Relevance to Surgical and Visual Outcomes. J. Cataract Refract. Surg. 2019, 45, 1849. [Google Scholar] [CrossRef]
- Nderitu, P.; Ursell, P. Factors Affecting Cataract Surgery Operating Time among Trainees and Consultants. J. Cataract Refract. Surg. 2019, 45, 816–822. [Google Scholar] [CrossRef] [PubMed]
- Mariani, A.; Pellegrini, E.; De Momi, E. Skill-Oriented and Performance-Driven Adaptive Curricula for Training in Robot-Assisted Surgery Using Simulators: A Feasibility Study. IEEE Trans. Biomed. Eng. 2021, 68, 685–694. [Google Scholar] [CrossRef] [PubMed]
- Shi, C.; Madera, J.; Boyea, H.; Fey, A.M. Haptic Guidance Using a Transformer-Based Surgeon-Side Trajectory Prediction Algorithm for Robot-Assisted Surgical Training. In Proceedings of the 2023 32nd IEEE International Conference on Robot and Human Interactive Communication (RO-MAN), Busan, Republic of Korea, 28–31 August 2023; pp. 1942–1949. [Google Scholar] [CrossRef]
- Rota, A.; Sun, X.F.; De Momi, E. Performance-Driven Tasks with Adaptive Difficulty for Enhanced Surgical Robotics Training. In Proceedings of the 2024 10th IEEE RAS/EMBS International Conference for Biomedical Robotics and Biomechatronics (BioRob), Heidelberg, Germany, 1–4 September 2024; pp. 465–470. [Google Scholar] [CrossRef]
- Fan, K.; Marzullo, A.; Pasini, N.; Rota, A.; Pecorella, M.; Ferrigno, G.; De Momi, E. A Unity-based Da Vinci Robot Simulator for Surgical Training. In Proceedings of the 2022 9th IEEE RAS/EMBS International Conference for Biomedical Robotics and Biomechatronics (BioRob), Seoul, Republic of Korea, 21–24 August 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Zheng, Y. Toward Augmenting Surgical Performance Using Motion Analysis and Haptic Guidance. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2024. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Alambeigi, F.; Zimmer-Galler, I.E.; Gehlbach, P.; Taylor, R.H.; Iordachita, I. Toward Improving Patient Safety and Surgeon Comfort in a Synergic Robot-Assisted Eye Surgery: A Comparative Study. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 7075–7082. [Google Scholar] [CrossRef]
- Liu, W.; Su, Y.; Wu, W.; Xin, C.; Hou, Z.G.; Bian, G.B. An operating smooth man–machine collaboration method for cataract capsulorhexis using virtual fixture. Future Gener. Comput. Syst. 2019, 98, 522–529. [Google Scholar] [CrossRef]
- Nasseri, M.A.; Gschirr, P.; Eder, M.; Nair, S.; Kobuch, K.; Maier, M.; Zapp, D.; Lohmann, C.; Knoll, A. Virtual fixture control of a hybrid parallel-serial robot for assisting ophthalmic surgery: An experimental study. In Proceedings of the 5th IEEE RAS and EMBS International Conference on Biomedical Robotics and Biomechatronics, Sao Paulo, Brazil, 12–15 August 2014; pp. 732–738. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Urias, M.; Patel, N.; He, C.; Taylor, R.H.; Gehlbach, P.; Iordachita, I. Towards securing the sclera against patient involuntary head movement in robotic retinal surgery. In Proceedings of the 2019 28th IEEE International Conference on Robot and Human Interactive Communication, RO-MAN 2019, New Delhi, India, 14–18 October 2019. [Google Scholar] [CrossRef]
- Gudiño-Lau, J.; Chávez-Montejano, F.; Alcalá, J.; Charre-Ibarra, S. Direct and inverse kinematic model of the OMNI PHANToM Modelo cinemático directo e inverso del OMNI PHANToM. ECORFAN Boliv. J. 2018, 5, 25–32. [Google Scholar]
- Al-Gailani, M.Y.; Grantner, J.L.; Shebrain, S.; Sawyer, R.G.; Abdel-Qader, I. Force Measurement Methods for Intelligent Box-Trainer System? Artificial Bowel Suturing Procedure. Acta Polytech. Hung. 2022, 19, 43–64. [Google Scholar] [CrossRef]
- Bowyer, S.A.; Davies, B.L.; Rodriguez y Baena, F. Active Constraints/Virtual Fixtures: A Survey. IEEE Trans. Robot. 2014, 30, 138–157. [Google Scholar] [CrossRef]
- Bettini, A.; Marayong, P.; Lang, S.; Hager, G.D. Vision-assisted control for manipulation using virtual fixtures. IEEE Trans. Robot. 2004, 20, 953–966. [Google Scholar] [CrossRef]
- Mieling, R.; Stapper, C.; Gerlach, S.; Neidhardt, M. Proximity-Based Haptic Feedback for Collaborative Robotic Needle Insertion. In Haptics: Science, Technology, Applications; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2022; Volume 13316, pp. 301–309. [Google Scholar] [CrossRef]
- Karg, P.; Kienzle, A.; Kaub, J.; Varga, B.; Hohmann, S. Trustworthiness of Optimality Condition Violation in Inverse Dynamic Game Methods Based on the Minimum Principle. In Proceedings of the 2024 IEEE Conference on Control Technology and Applications (CCTA), Newcastle upon Tyne, UK, 21–23 August 2024; pp. 824–831. [Google Scholar] [CrossRef]
- Kille, S.; Leibold, P.; Karg, P.; Varga, B.; Hohmann, S. Human-Variability-Respecting Optimal Control for Physical Human-Machine Interaction. In Proceedings of the 2024 33rd IEEE International Conference on Robot and Human Interactive Communication (ROMAN), Pasadena, CA, USA, 26–30 August 2024; pp. 1595–1602. [Google Scholar] [CrossRef]
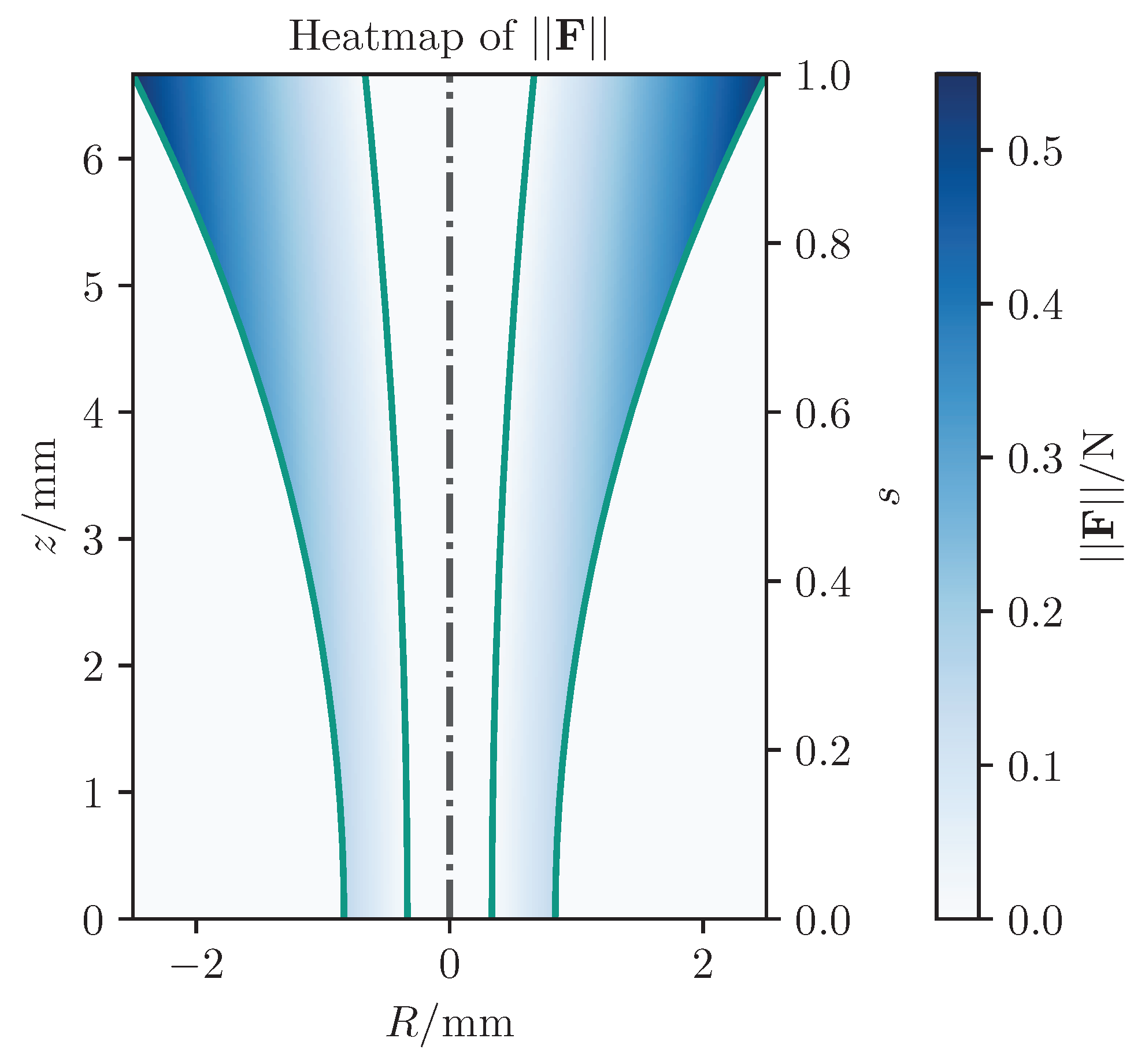
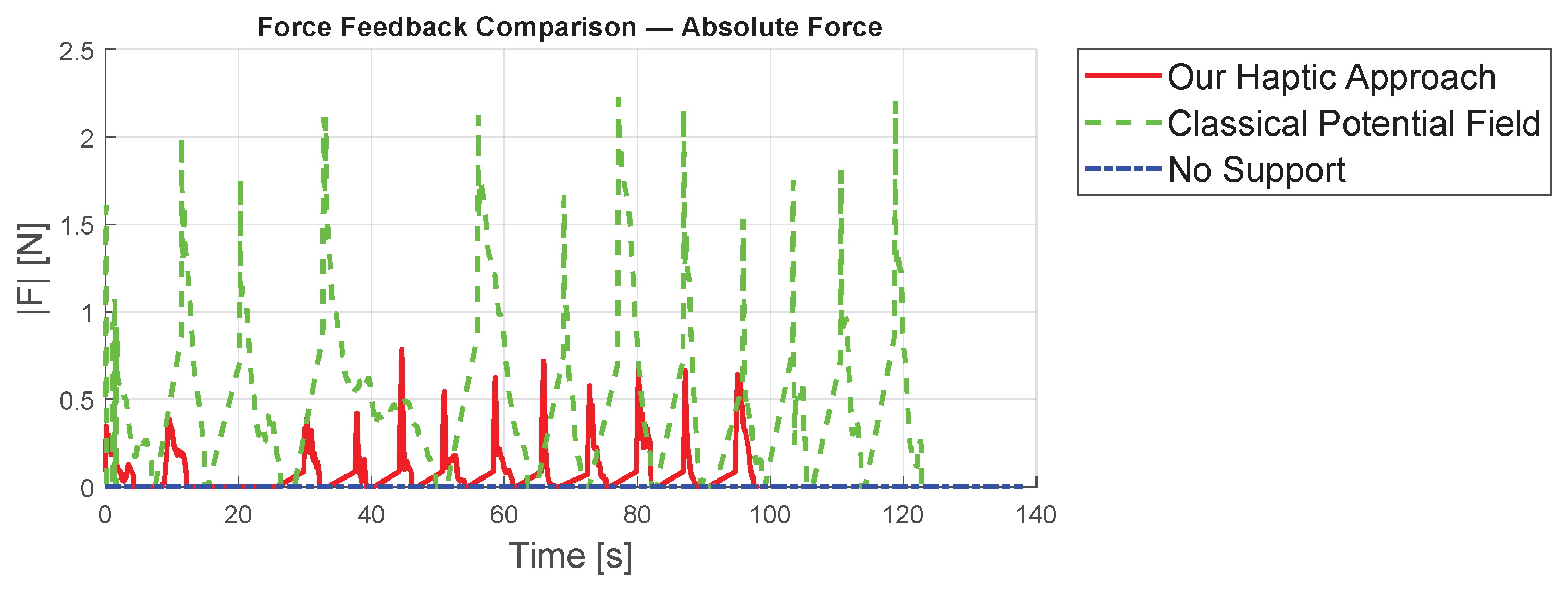
| No haptic support | s | s | mm |
| Classical potential-field-based shared control | s | s | mm |
| Our virtual-fixture-based shared control | s | s | mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varga, B.; Poncelet, M. A Shared Control Approach to Robot-Assisted Cataract Surgery Training for Novice Surgeons. Sensors 2025, 25, 5165. https://doi.org/10.3390/s25165165
Varga B, Poncelet M. A Shared Control Approach to Robot-Assisted Cataract Surgery Training for Novice Surgeons. Sensors. 2025; 25(16):5165. https://doi.org/10.3390/s25165165
Chicago/Turabian StyleVarga, Balint, and Michael Poncelet. 2025. "A Shared Control Approach to Robot-Assisted Cataract Surgery Training for Novice Surgeons" Sensors 25, no. 16: 5165. https://doi.org/10.3390/s25165165
APA StyleVarga, B., & Poncelet, M. (2025). A Shared Control Approach to Robot-Assisted Cataract Surgery Training for Novice Surgeons. Sensors, 25(16), 5165. https://doi.org/10.3390/s25165165






