AI-Powered Structural Health Monitoring Using Multi-Type and Multi-Position PZT Networks
Abstract
1. Introduction
Contributions
- Novel Multi-Sensor Monitoring Framework: Development of a new SHM framework that deploys multiple piezoelectric sensors at different locations on concrete elements to continuously monitor the impact-induced response, providing a more comprehensive view of curing progress than single-point tests.
- Early-Age Strength Prediction Model: Implementation of a machine learning model trained on multi-sensor data to predict concrete compressive strength at early ages (well before 28 days), improving the accuracy and lead time of strength estimations compared to traditional NDT or empirical maturity methods.
- Integration with Industry Standards: Demonstration of how the proposed system can complement and enhance standard practices (ASTM C39 cylinder tests, ASTM C805 rebound hammer, ASTM C597 UPV, and ACI guidelines for formwork removal) by offering real-time, in situ strength insights. The method is calibrated and validated against standard compressive tests to ensure results are grounded in established benchmarks.
- Practical Impact on Construction Scheduling and Safety: Evidence that our multi-sensor approach can reliably determine when concrete reaches key strength thresholds (e.g., 70% of for safe formwork stripping), thereby enabling more optimal timing of construction operations and reducing the risk of premature loading or unnecessary delays.
- Contribution to SHM Research: Expansion of the SHM knowledge base by introducing multi-position sensing for material property estimation. The study illustrates the benefits of data fusion from multiple sensors in a civil engineering context and provides an open dataset and guidelines for future researchers to build upon this multi-sensor machine learning approach for concrete strength monitoring.
2. Methodology
2.1. Materials
2.2. Piezoelectric Sensors and Layout
2.3. Experimental Procedure
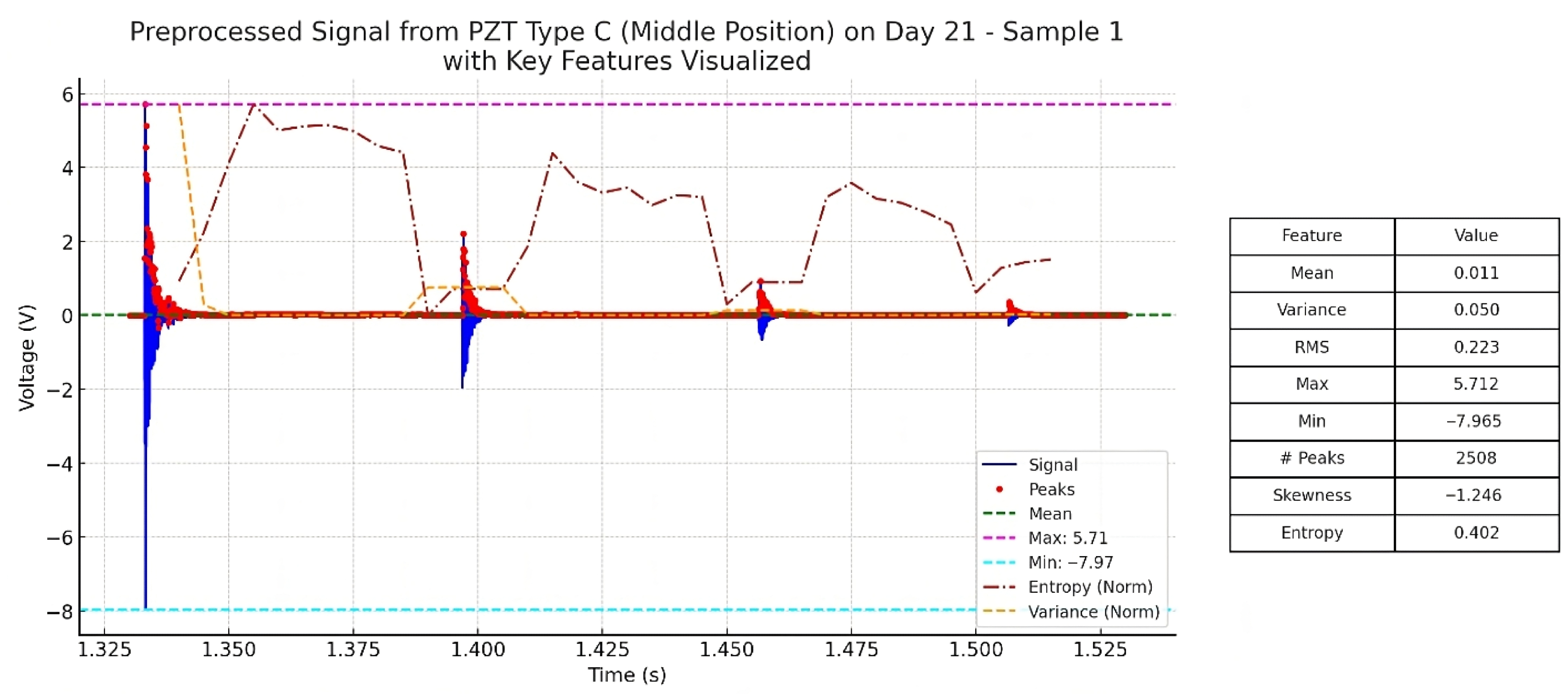
2.4. Preprocessing and Data Preparation
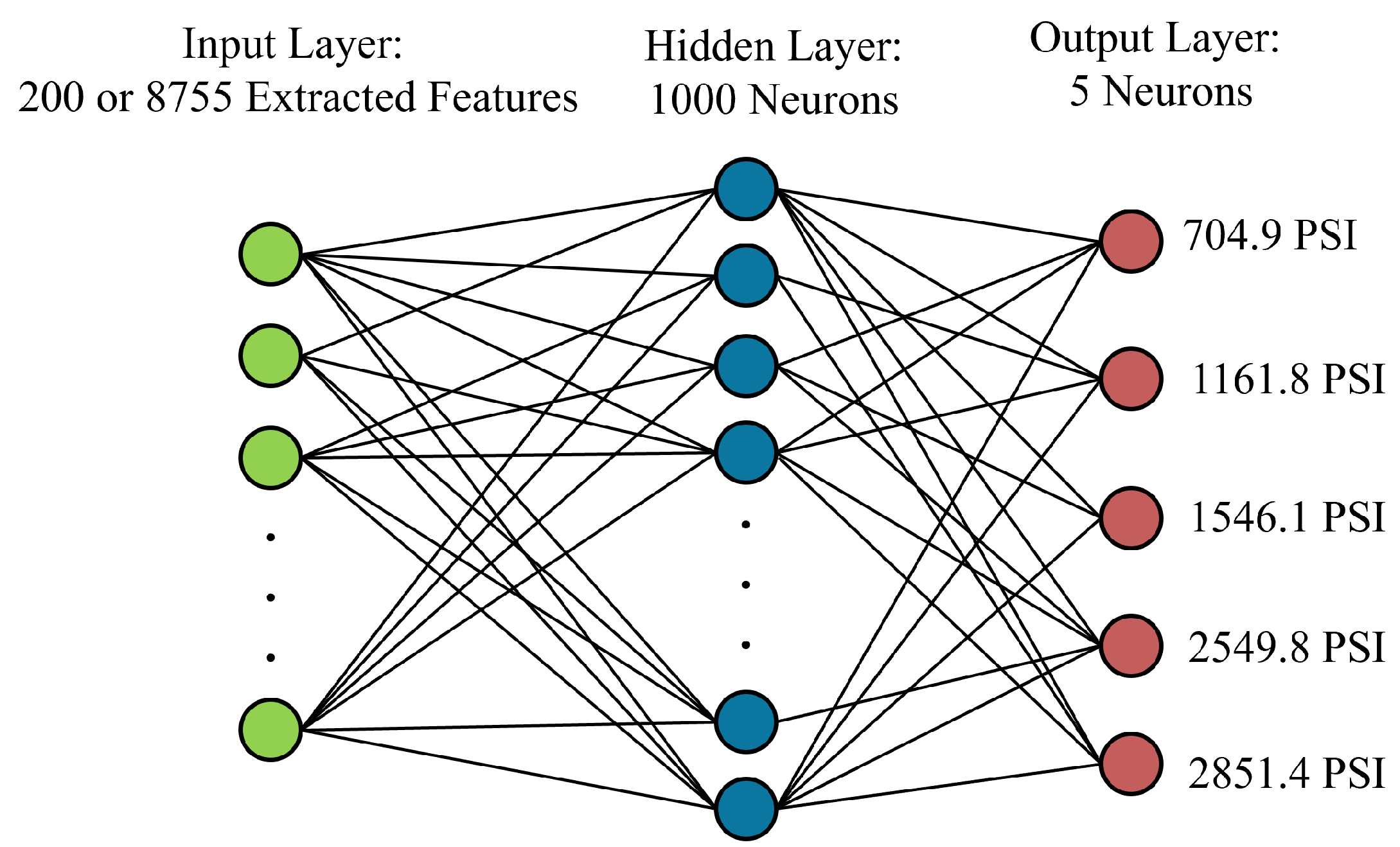
2.5. Feature Extraction
3. Results
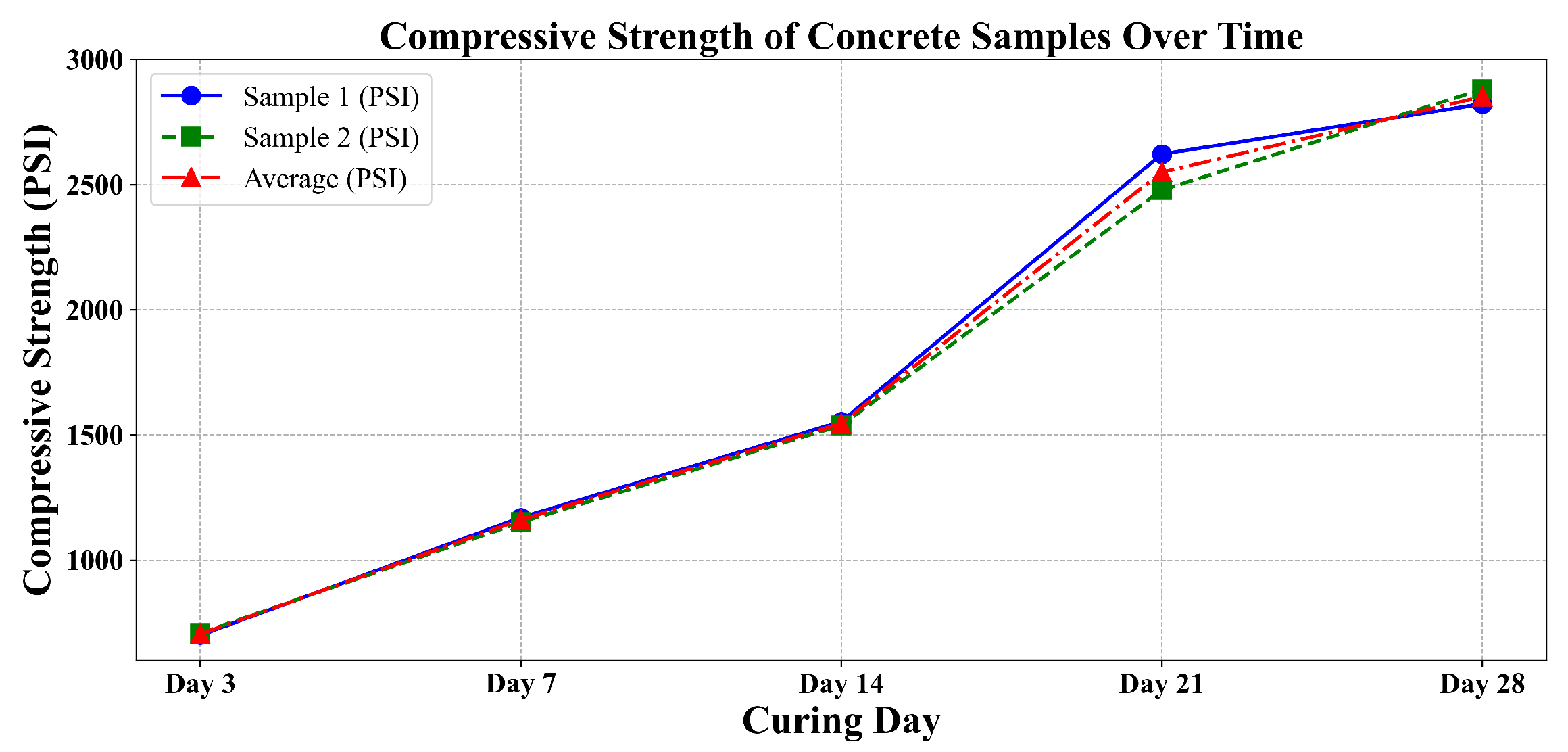
3.1. Strength Analysis
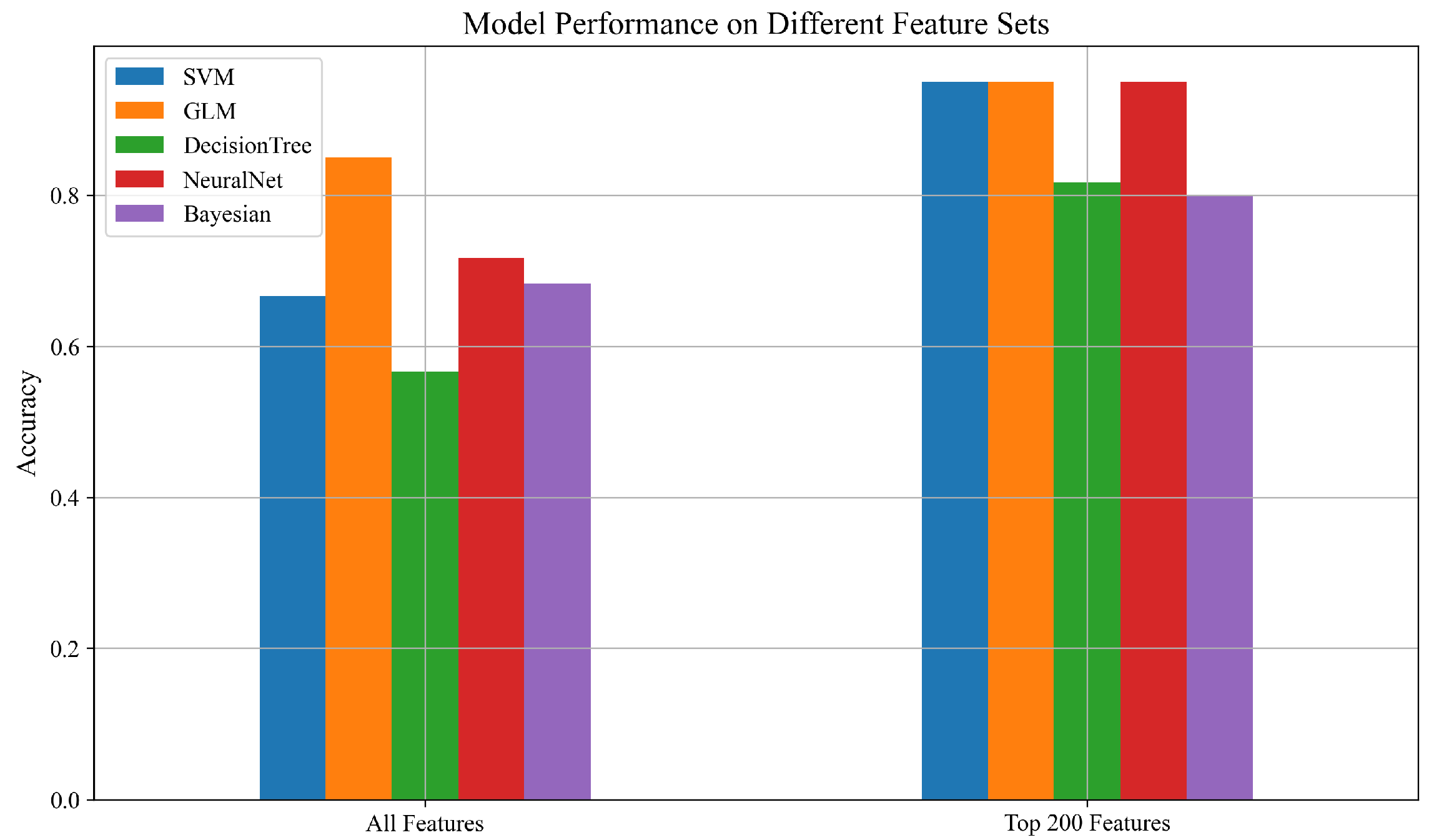
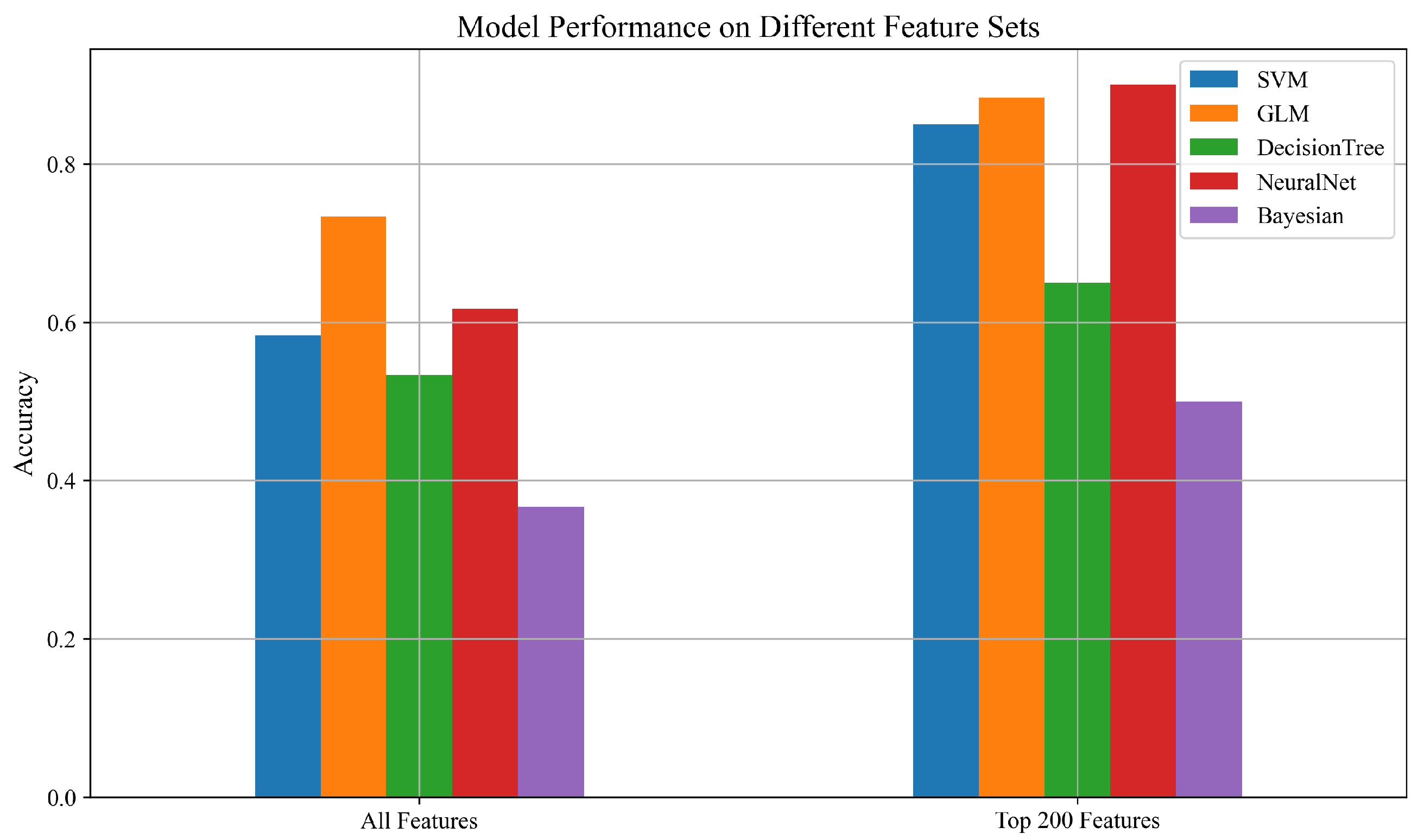
3.2. Model Performance Using Combined Sensor Data
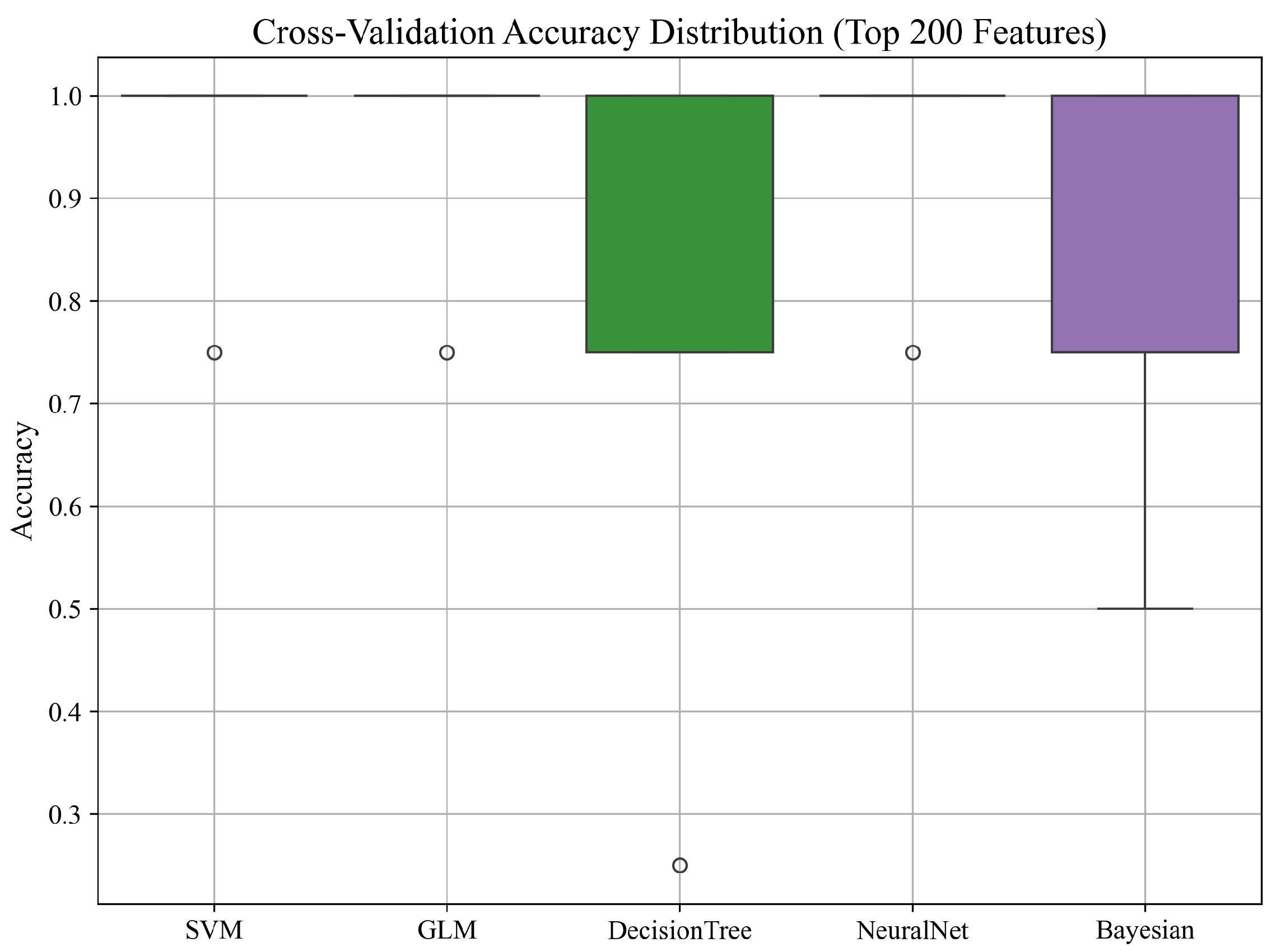
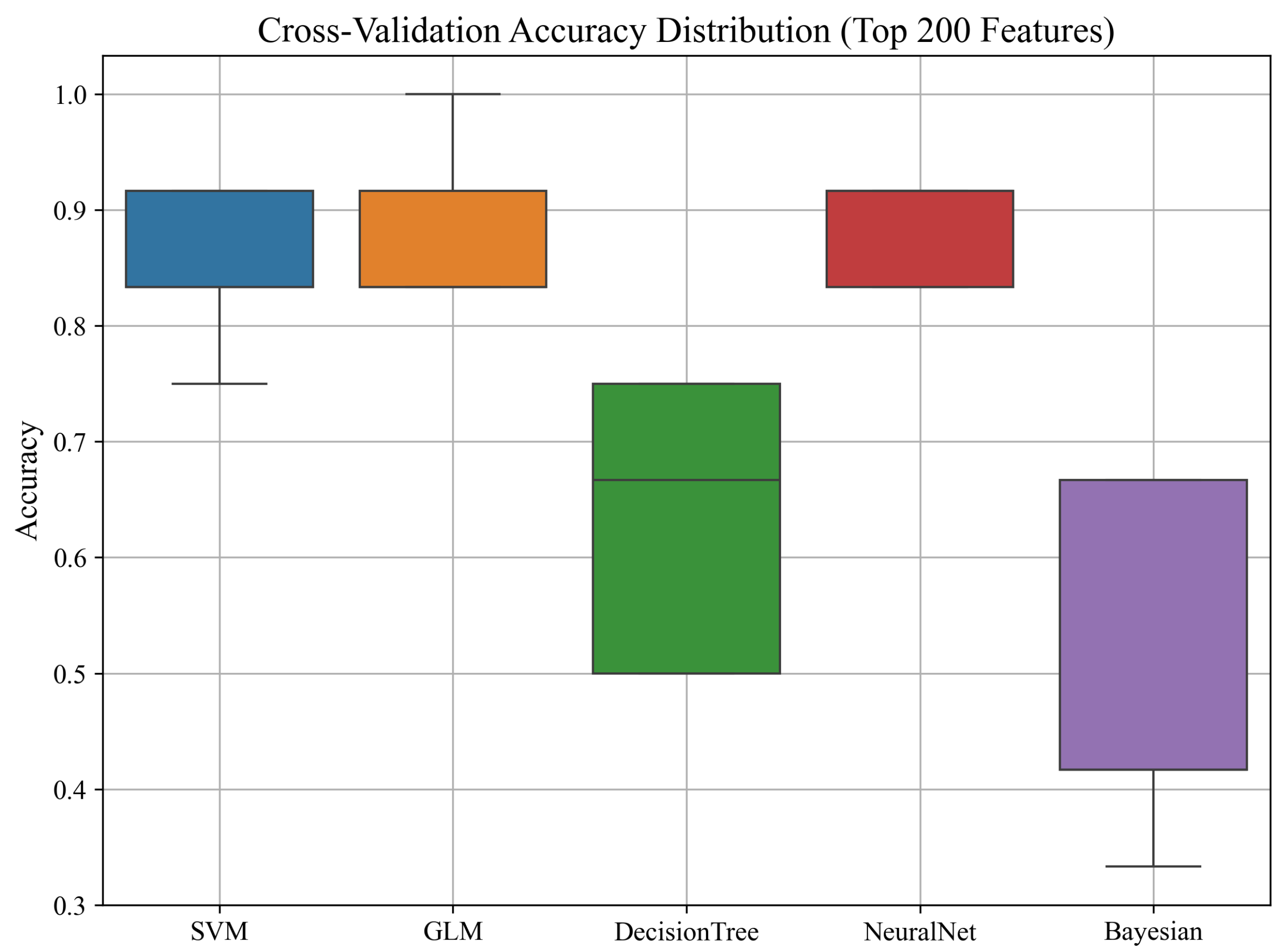
3.2.1. Cross-Validation Accuracy Distribution
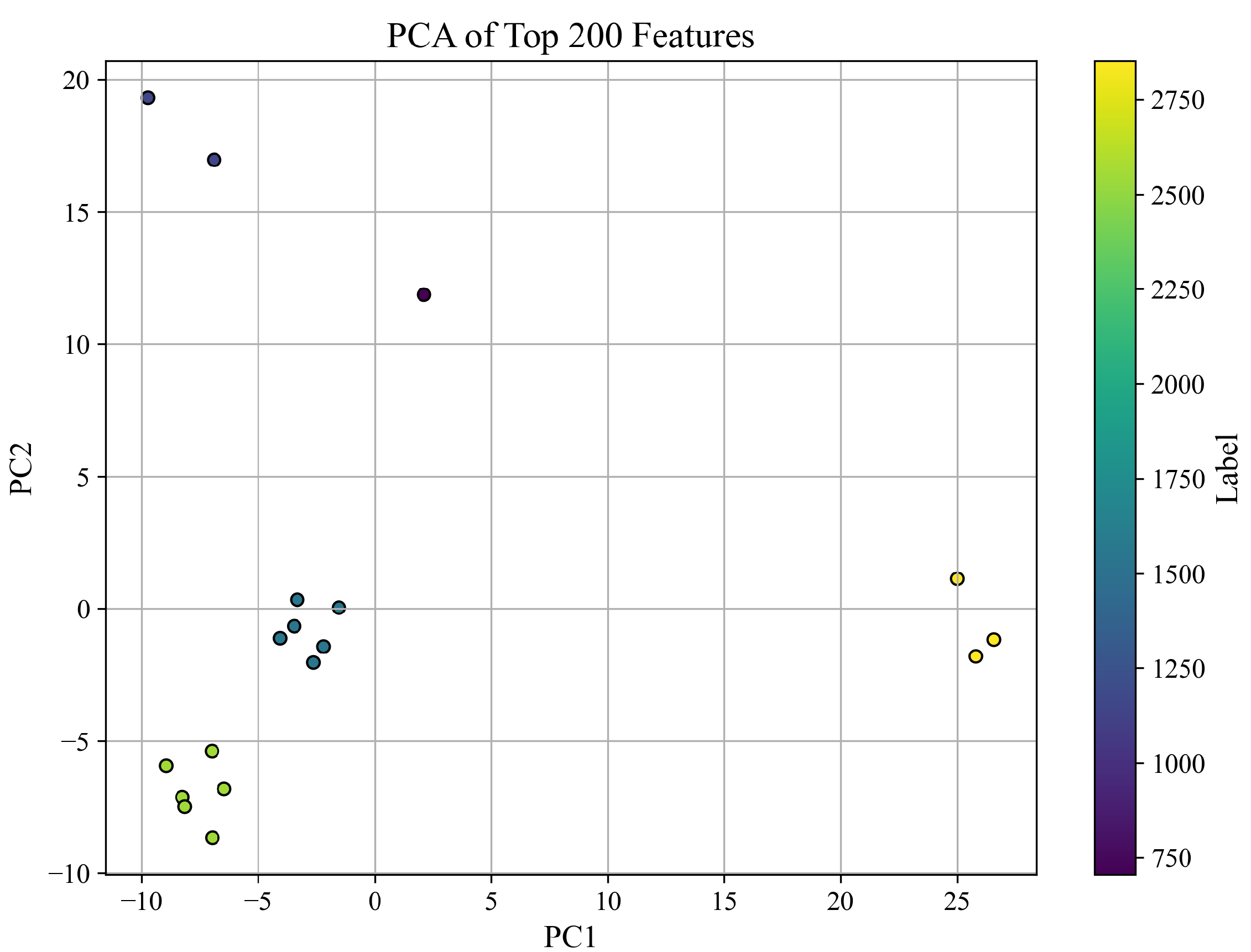
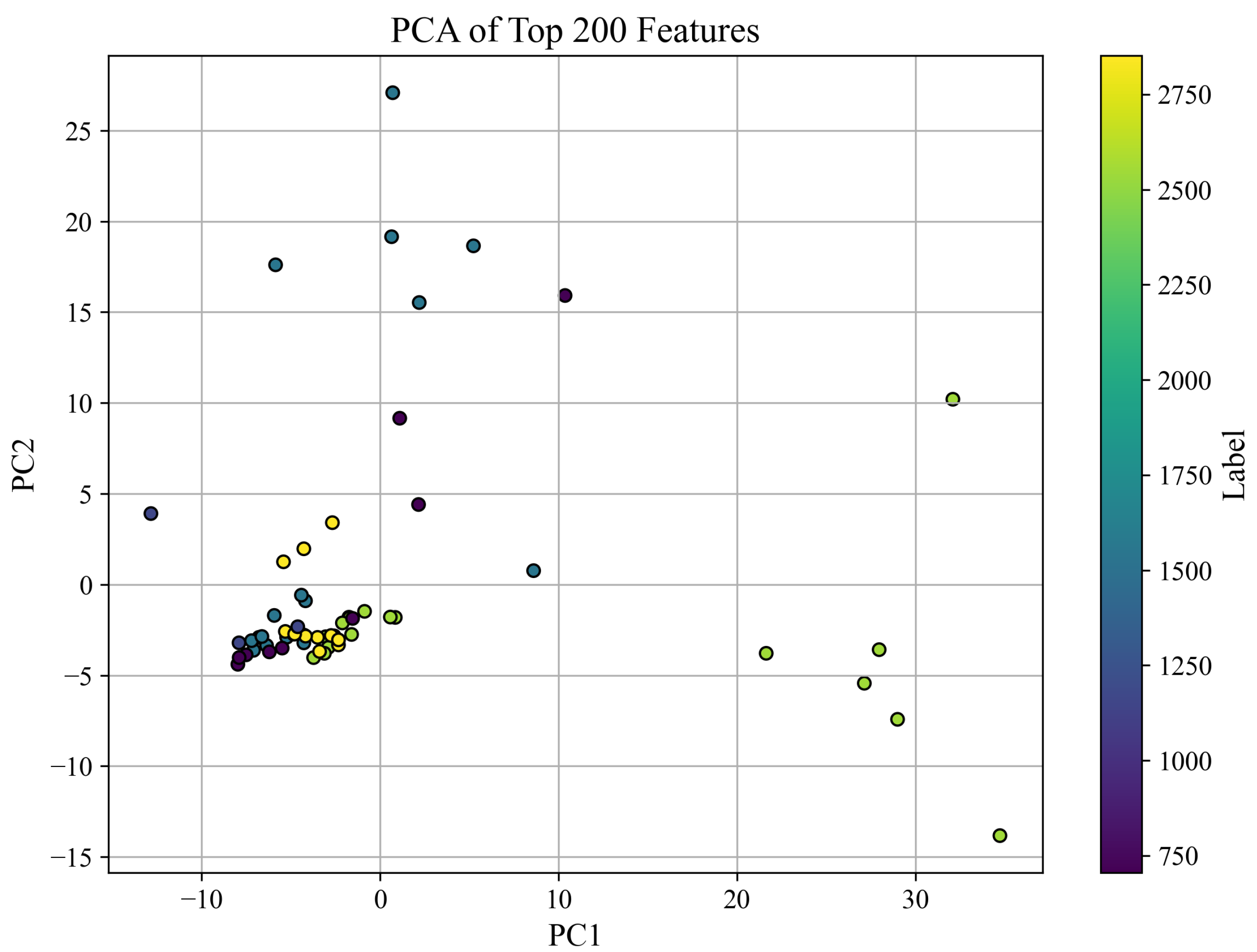
3.2.2. PCA Visualization of Feature Space
3.2.3. Feature Importance Analysis
- ratio_beyond_r_sigma, which captures signal amplitude dispersion and outliers;
- number_cwt_peaks, indicative of oscillatory behavior;
- partial_autocorrelation and ar_coefficient, which reflect temporal dependency and spectral resonance.
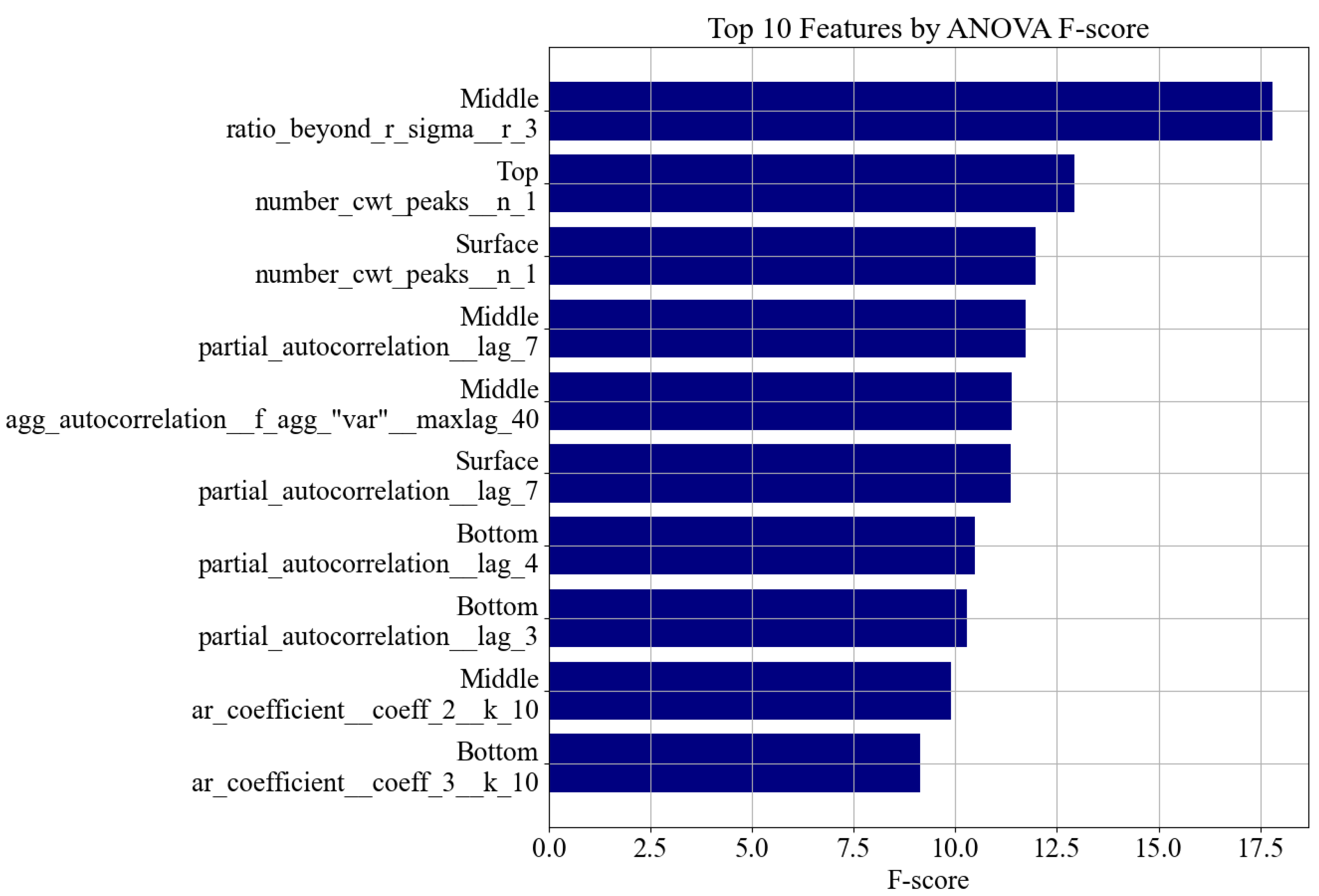
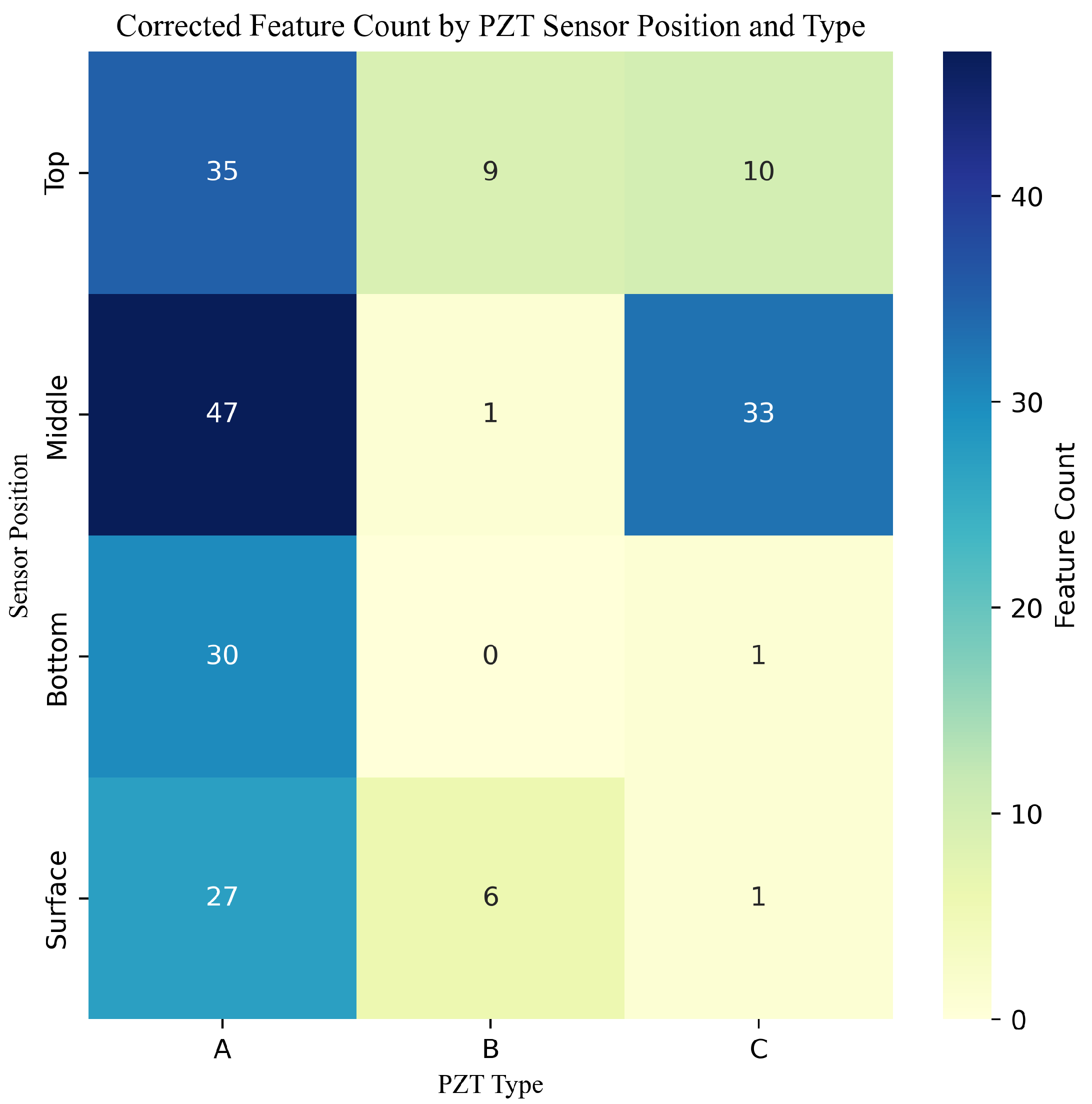
3.2.4. Sensor-Wise Contribution of Important Features
3.3. Model Performance by Individual PZT Type
- All Features: The complete cleaned tsfresh feature set, a total of 2934 features.
- Top 200 Features: A reduced subset selected using ANOVA F-score ranking.
3.3.1. Cross-Validation Performance by Individual PZT Type
3.3.2. PCA Visualization Using a Single PZT Type
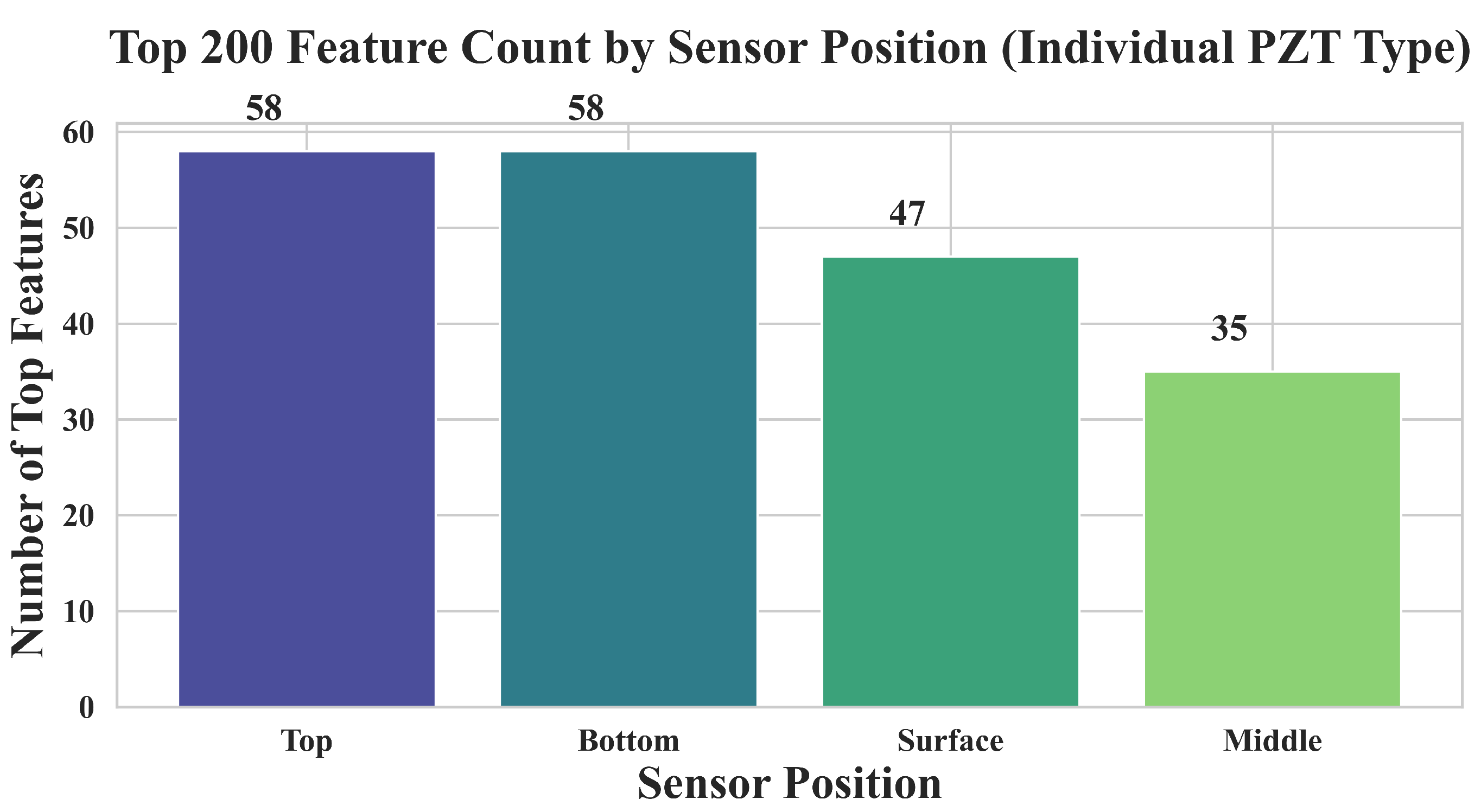
3.3.3. Feature Importance Distribution by Sensor Position (Single PZT Type)
4. Discussion
4.1. Interpretation of Model Performance and Feature Selection
4.2. Methodological Contributions of Automated Feature Engineering
4.3. Implications for Sensor Design and Multi-PZT Arrangements
4.4. Comparison with Existing Studies and Techniques
4.5. Practical Applications in Structural Health Monitoring
4.6. Limitations
4.7. Future Research Directions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SHM | Structural Health Monitoring |
| NDT | Non-Destructive Testing |
| PZT | Lead Zirconate Titanate Piezoelectric, |
| ML | Machine Learning |
| SVM | Support Vector Machine |
| GLM | Generalized Linear Model |
| PCA | Principal Component Analysis |
| UPV | Ultrasonic Pulse Velocity |
| ASTM | American Society for Testing and Materials |
| ACI | American Concrete Institute |
| DAQ | Data Acquisition |
| tsfresh | Time Series Feature Extraction based on Scalable Hypothesis tests |
References
- Asmara, Y.P. Concrete Structure. In Concrete Reinforcement Degradation and Rehabilitation: Damages, Corrosion and Prevention; Springer: Berlin/Heidelberg, Germany, 2023; pp. 7–24. [Google Scholar]
- Richardson, M.G. Fundamentals of Durable Reinforced Concrete; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- ASTM C39/C39M-23; Misc Test Method for Compressive Strength of Cylindrical Concrete Specimens. ASTM International: West Conshohocken, PA, USA, 2023.
- ACI 347R-14; Guide to Formwork for Concrete. ACI Committee 347: Farmington Hills, MI, USA, 2014.
- ASTM C805/C805M-18; Misc Test Method for Rebound Number of Hardened Concrete. ASTM International: West Conshohocken, PA, USA, 2018.
- ASTM C597-16; Standard Test Method for Pulse Velocity Through Concrete. ASTM International: West Conshohocken, PA, USA, 2016.
- Taylor, P.C. Curing Concrete; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Zhu, W.; Gibbs, J.C.; Bartos, P.J. Uniformity of in situ properties of self-compacting concrete in full-scale structural elements. Cem. Concr. Compos. 2001, 23, 57–64. [Google Scholar] [CrossRef]
- Huang, J.; Xing, L.; Ali, A.H.; El-Arab, I.E.; Elshekh, A.E.; Abbas, M.; Abdullah, N.; Elattar, S.; Hashmi, A.; Ali, E.; et al. Predicting concrete strength early age using a combination of machine learning and electromechanical impedance with nano-enhanced sensors. Environ. Res. 2024, 258, 119248. [Google Scholar] [CrossRef] [PubMed]
- Jalili, N. Piezoelectric-Based Vibration Control: From Macro to Micro/Nano Scale Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- ASTM C143/C143M-20; Standard Test Method for Slump of Hydraulic-Cement Concrete. ASTM International: West Conshohocken, PA, USA, 2020.
- ASTM C192/C192M-23; Standard Practice for Making and Curing Concrete Test Specimens in the Laboratory. ASTM International: West Conshohocken, PA, USA, 2023.
- ASTM C109/C109M-21; Standard Test Method for Compressive Strength of Hydraulic Cement Mortars (Using 2-in. or [50-mm] Cube Specimens). ASTM International: West Conshohocken, PA, USA, 2021.
- Christ, M.; Braun, N.; Neuffer, J.; Kempa-Liehr, A.W. Time series feature extraction on basis of scalable hypothesis tests (tsfresh—A python package). Neurocomputing 2018, 307, 72–77. [Google Scholar] [CrossRef]
- Bai, L.; Samavatian, M.; Samavatian, V. Machine learning-enabled characterization of concrete mechanical strength through correlation of flexural and torsional resonance frequencies. Phys. Scr. 2024, 99, 076002. [Google Scholar] [CrossRef]
- Jena, T.; Raj, A.K.; Saravanan, T.J.; Bansal, T. Deep learning neural networks for monitoring early-age concrete strength through a surface-bonded PZT sensor configuration. Measurement 2025, 241, 115698. [Google Scholar] [CrossRef]
- Shan, C.; Yao, Q.; Cao, S.; Zheng, C.; Xu, Q.; Xia, Z.; Shang, X.; Huang, G. Analysis of cracks development and damage evolution in red sandstone under dry-wet cycles based on temporal and frequency characteristics of acoustic emission. J. Build. Eng. 2024, 94, 109849. [Google Scholar] [CrossRef]
- Bansal, T.; Talakokula, V.; Sathujoda, P. Machine learning-based monitoring and predicting the compressive strength of different blended cementitious systems using embedded piezo-sensor data. Measurement 2022, 205, 112204. [Google Scholar] [CrossRef]
- Abazarsa, M.; Yu, T. Multiphysical characterization for predicting compressive strength of Portland cement concrete using synthetic aperture radar, ultrasonic testing, and rebound hammer. Sci. Rep. 2025, 15, 6058. [Google Scholar] [CrossRef]
- Kaur, N.; Negi, P. In situ strength assessment of rapid set concrete in real time using resonant peak parameters of embedded PZT transducers. Sci. Rep. 2025, 15, 11281. [Google Scholar] [CrossRef] [PubMed]
- Mangalathu, S.; Hwang, S.H.; Jeon, J.S. Failure mode and effects analysis of RC members based on machine-learning-based SHapley Additive exPlanations (SHAP) approach. Eng. Struct. 2020, 219, 110927. [Google Scholar] [CrossRef]



| Type | Brand/Model (Company, City, Country) | Size (mm) | Resonant Frequency |
|---|---|---|---|
| A | SM111/SMD25T85F234S (STEMINC, Miami, FL, USA) | 25 × 8.5 | 235 kHz |
| B | DZS Elec (DZS Elec, Shenzhen, China) | 27 × 0.15 | 3.5 ± 0.5 kHz |
| C | YQBOOM (YQBOOM, Shenzhen, China) | 41 × 0.30 | 3–5 kHz |
| Day | Sample 1 (PSI) | Sample 2 (PSI) | Difference (PSI) | Average (PSI) |
|---|---|---|---|---|
| Day 3 | 700.5 | 709.2 | 8.7 | 704.9 |
| Day 7 | 1170.5 | 1151.6 | 20.3 | 1161.8 |
| Day 14 | 1553.4 | 1538.8 | 14.5 | 1546.1 |
| Day 21 | 2622.2 | 2478.7 | 143.6 | 2549.8 |
| Day 28 | 2822.4 | 2880.4 | 58 | 2851.4 |
| Model | All Features | Top 200 Features |
|---|---|---|
| SVM | 0.67 | 0.95 |
| GLM | 0.85 | 0.95 |
| DecisionTree | 0.78 | 0.88 |
| NeuralNet | 0.76 | 0.95 |
| Bayesian | 0.68 | 0.80 |
| Sensor Position | PZT Type | Example Feature(s) | Category |
|---|---|---|---|
| Top | A | variance_larger_than_std, number_peaks_n_10 | Variability, Peaks |
| Top | C | augmented_dickey_fuller, fft_coeff_57 | Stationarity, Frequency |
| Middle | A | linear_trend_pvalue, skewness, entropy | Trend, Shape, Entropy |
| Middle | C | spkt_welch_density_coeff_2, fft_coeff_76 | Frequency Spectrum |
| Middle | B | fft_coefficient_real_22 | Frequency (Real Part) |
| Bottom | A | large_standard_deviation, permutation_entropy | Variability, Entropy |
| Surface | A | duplicate_max, ratio_value_to_length, entropy | Repetition, Complexity |
| Surface | B | augmented_dickey_fuller_pvalue, ratio_beyond_r_sigma | Stationarity, Spread |
| Feature | Sensor Position | Category |
|---|---|---|
| Middle__ratio_beyond_r_sigma__r_3 | Middle | Statistical Spread |
| Top__number_cwt_peaks__n_1 | Top | Peak Count |
| Surface__number_cwt_peaks__n_1 | Surface | Peak Count |
| Middle__partial_autocorrelation__lag_7 | Middle | Autocorrelation |
| Middle__agg_autocorrelation__f_agg_“var”__maxlag_40 | Middle | Autocorrelation |
| Surface__partial_autocorrelation__lag_7 | Surface | Autocorrelation |
| Bottom__partial_autocorrelation__lag_4 | Bottom | Autocorrelation |
| Bottom__partial_autocorrelation__lag_3 | Bottom | Autocorrelation |
| Middle__ar_coefficient__coeff_2__k_10 | Middle | AR Coefficient |
| Bottom__ar_coefficient__coeff_3__k_10 | Bottom | AR Coefficient |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gharavi, H.; Taban, F.; Korivand, S.; Jalili, N. AI-Powered Structural Health Monitoring Using Multi-Type and Multi-Position PZT Networks. Sensors 2025, 25, 5148. https://doi.org/10.3390/s25165148
Gharavi H, Taban F, Korivand S, Jalili N. AI-Powered Structural Health Monitoring Using Multi-Type and Multi-Position PZT Networks. Sensors. 2025; 25(16):5148. https://doi.org/10.3390/s25165148
Chicago/Turabian StyleGharavi, Hasti, Farshid Taban, Soroush Korivand, and Nader Jalili. 2025. "AI-Powered Structural Health Monitoring Using Multi-Type and Multi-Position PZT Networks" Sensors 25, no. 16: 5148. https://doi.org/10.3390/s25165148
APA StyleGharavi, H., Taban, F., Korivand, S., & Jalili, N. (2025). AI-Powered Structural Health Monitoring Using Multi-Type and Multi-Position PZT Networks. Sensors, 25(16), 5148. https://doi.org/10.3390/s25165148








