Visual Quantitative Characterization of External Corrosion in 3LPE Coated Pipes Based on Microwave Near-Field Reflectometry and Phase Unwrapping
Abstract
1. Introduction
2. Theory and Methodology
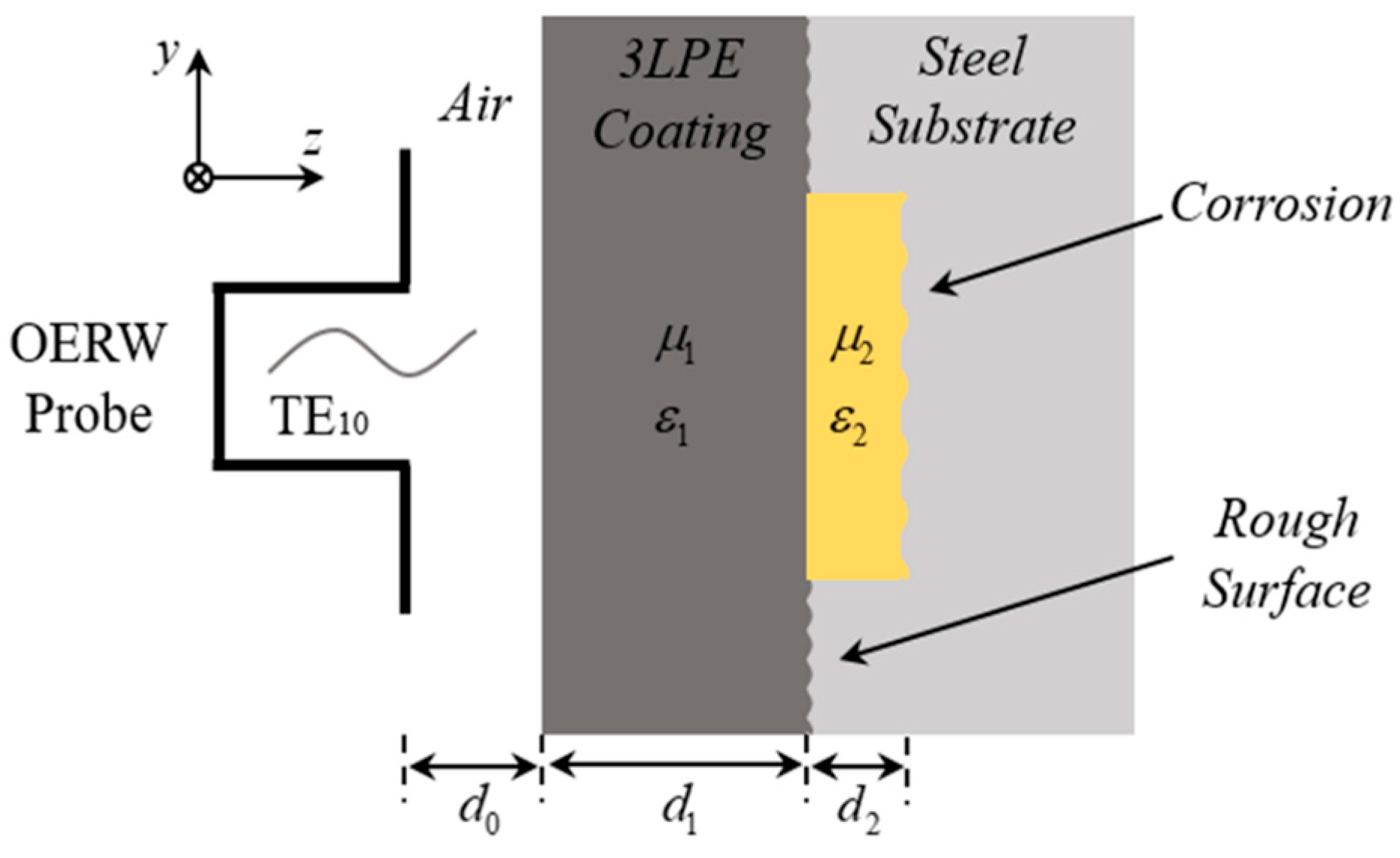
2.1. Theoretical Background
2.2. Proposition of Phase Unwrapping Algorithm
2.2.1. Residue Identification
2.2.2. Residue Pre-Processing
- Step 1. Take every residue as the center, search for the opposite residue from left to right and top to bottom in a 3 × 3-pixel diamond search box, place the cut as balanced and marked, and search for the next one until all the residues are processed.
- Step 2. If the box contains an image boundary, connect to it; if there is no opposite polarity residue in the search box, skip to the next residue and return to Step 1.
- Step 3. Check whether the rest positive and negative residues are equal (Npos = Nneg). If so, turn to Step 5. If there are not equal, proceed to Step 4.
- Step 4. Monopole compensation. If Npos > Nneg, calculate the closest distance of each positive residue to the image boundaries and sort them in ascending order; balance the first Npos–Nneg with the nearest boundary, and vice versa; then turn to Step 5.
- Step 5. Check whether the number of the remaining dipoles is smaller than the optimization threshold Nopt. If so, end the pre-processing; if not, increase the box size by 2 pixels, and return to Step 1 for a new search iteration.
2.2.3. Population Initialization and Selection Operation
2.2.4. Adaptive Crossover and Mutation Operation
- Step 1. Select two chromosomes sequentially, calculate their fitness values, and compute the crossover rate Pc using the larger fitness fc, as shown in the formula below:
- Step 2. Generate a random number. If it is less than Pc, perform the crossover operation; otherwise, copy the two parents to the offspring and return to Step 1.
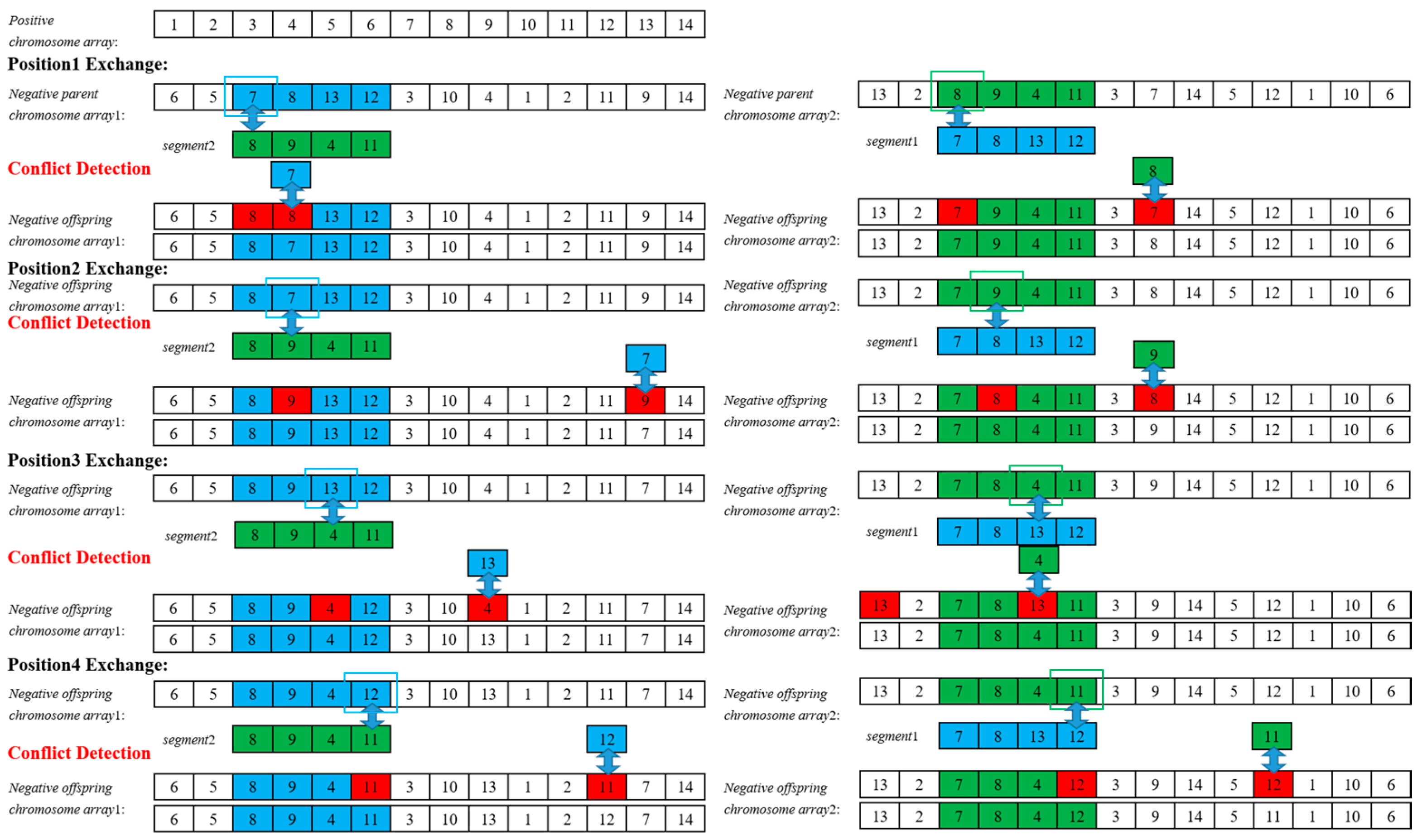
- Step 3. Randomly select a crossover region, and exchange the corresponding genes.
- Step 4. Conflict detection. If the genes in the crossover region conflict with others, replace them with genes from the original positions to produce the new offspring.
- Step 1. Select a chromosome sequentially from the population and calculate its fitness value fem. Then, compute the exchange mutation rate Pem using Equation (10):
- Step 2. Generate a random number. If it is less than Pem, perform the exchange mutation; otherwise, copy the parent genes to the new offspring and return to Step 1.
- Step 3. Randomly select two positions, and exchange genes to obtain the new offspring.
- Step 1. Select a chromosome sequentially from the population and calculate the fitness value fim, then calculate the inversion mutation rate Pim using Equation (11):
- Step 2. Generate a random number. If it is less than Pim, perform an inversion mutation; otherwise, copy the parent genes to the new offspring, and return to Step 1.
- Step 3. Randomly select a mutation region, and sort the genes to obtain offspring.
2.2.5. Update Population and Phase Integral
3. Numerical Simulations of the Phase Unwrapping Algorithm
4. Experiment and Discussion
4.1. Experimental System Setup
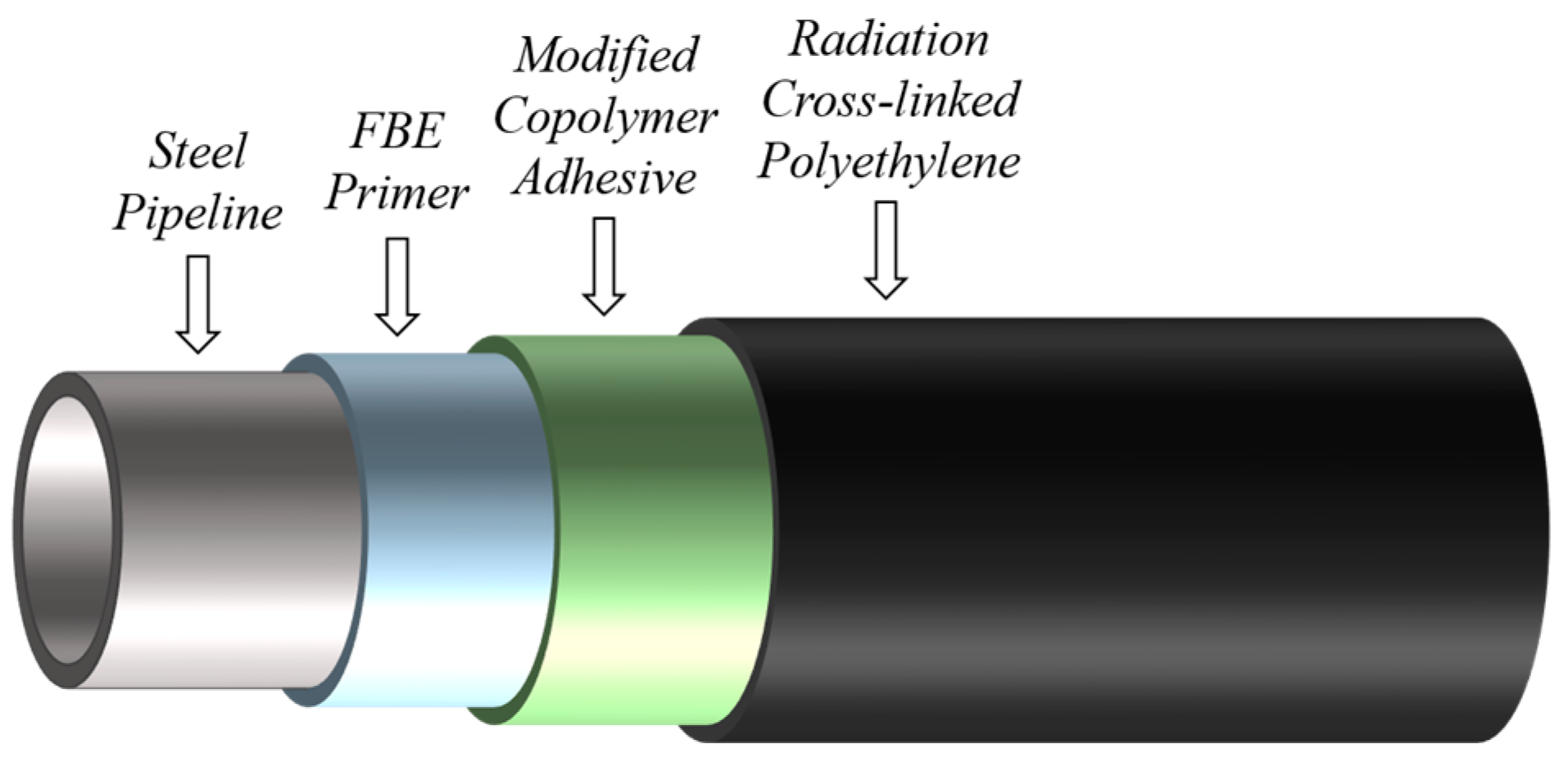
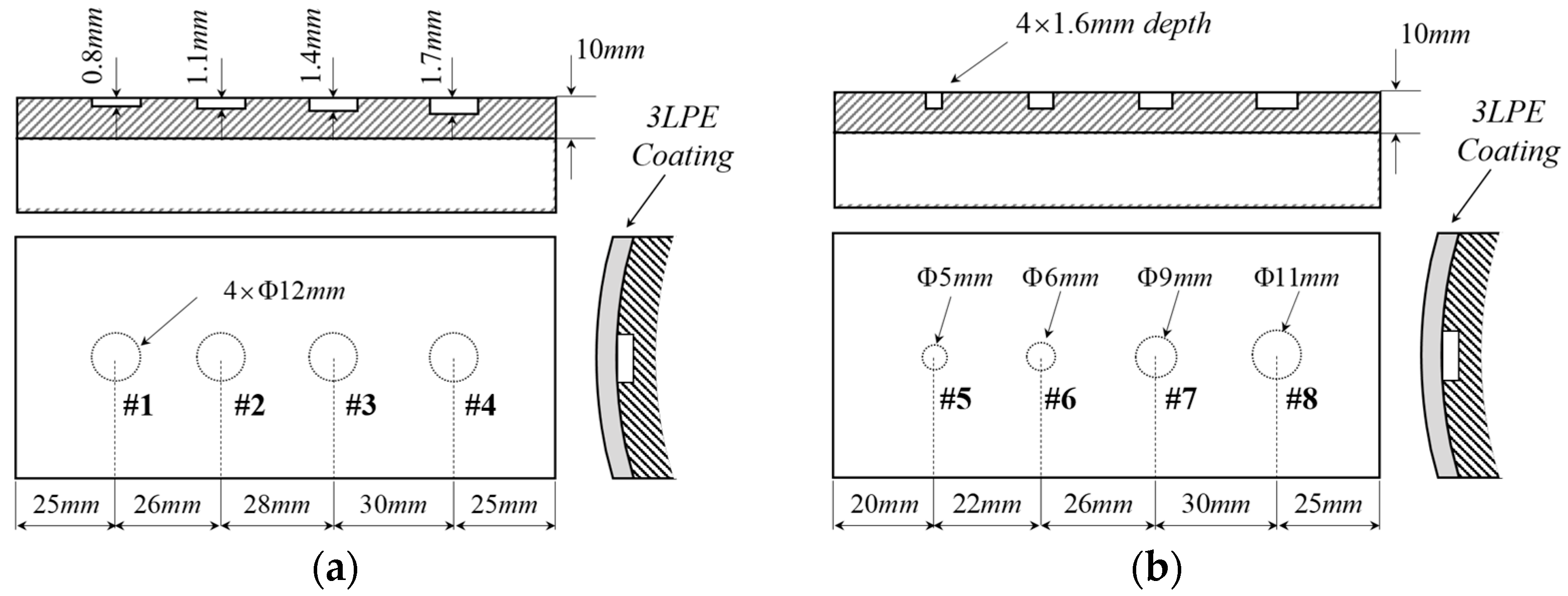
4.2. Specimen Preparation
4.3. Frequency Band Selection
4.4. Experimental Validation of the Phase Unwrapping Algorithm
4.5. Background Subtraction
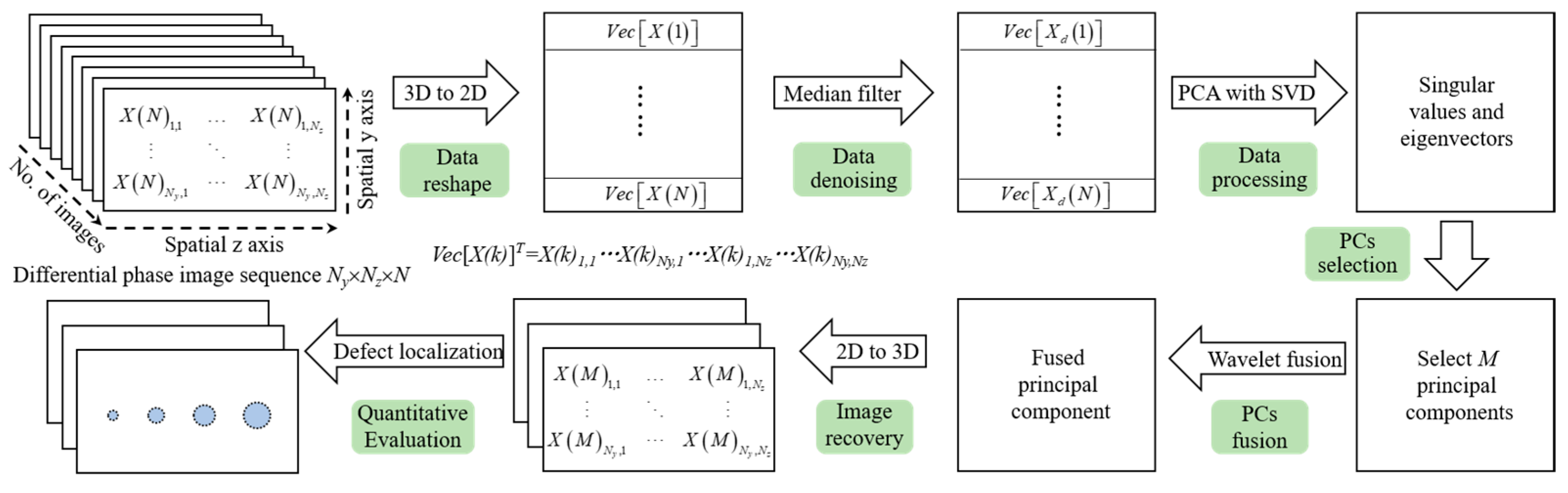
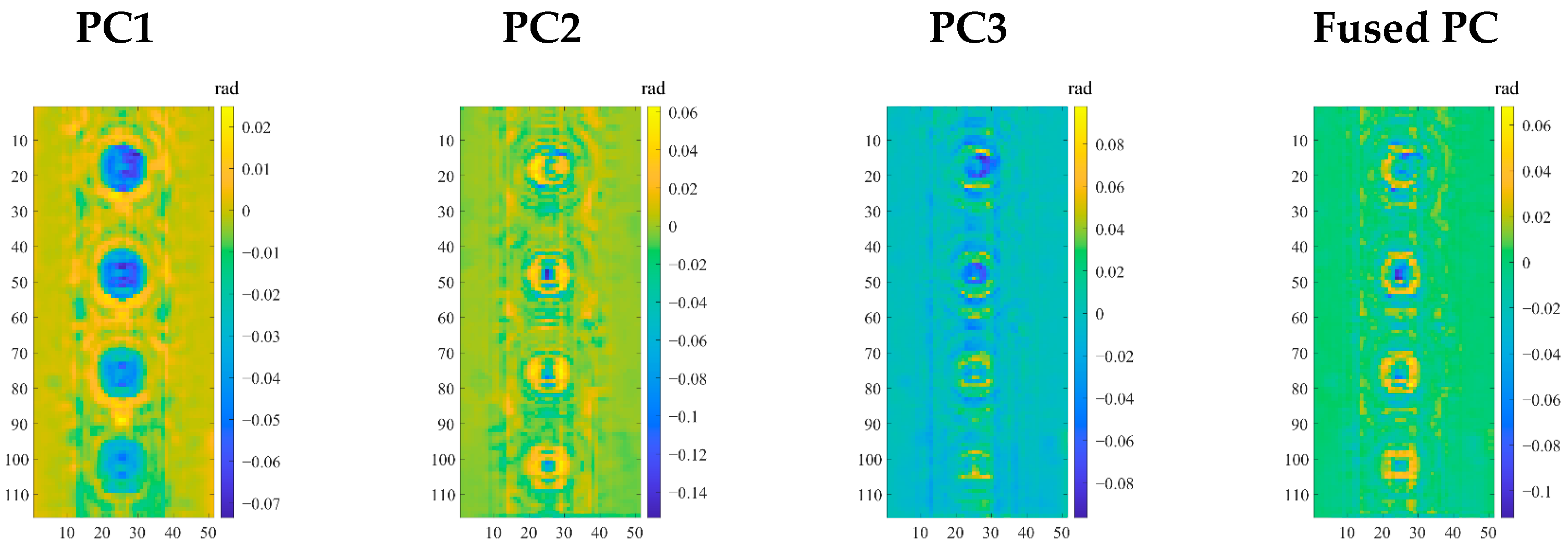
4.6. Principal Components Extraction and Fusion
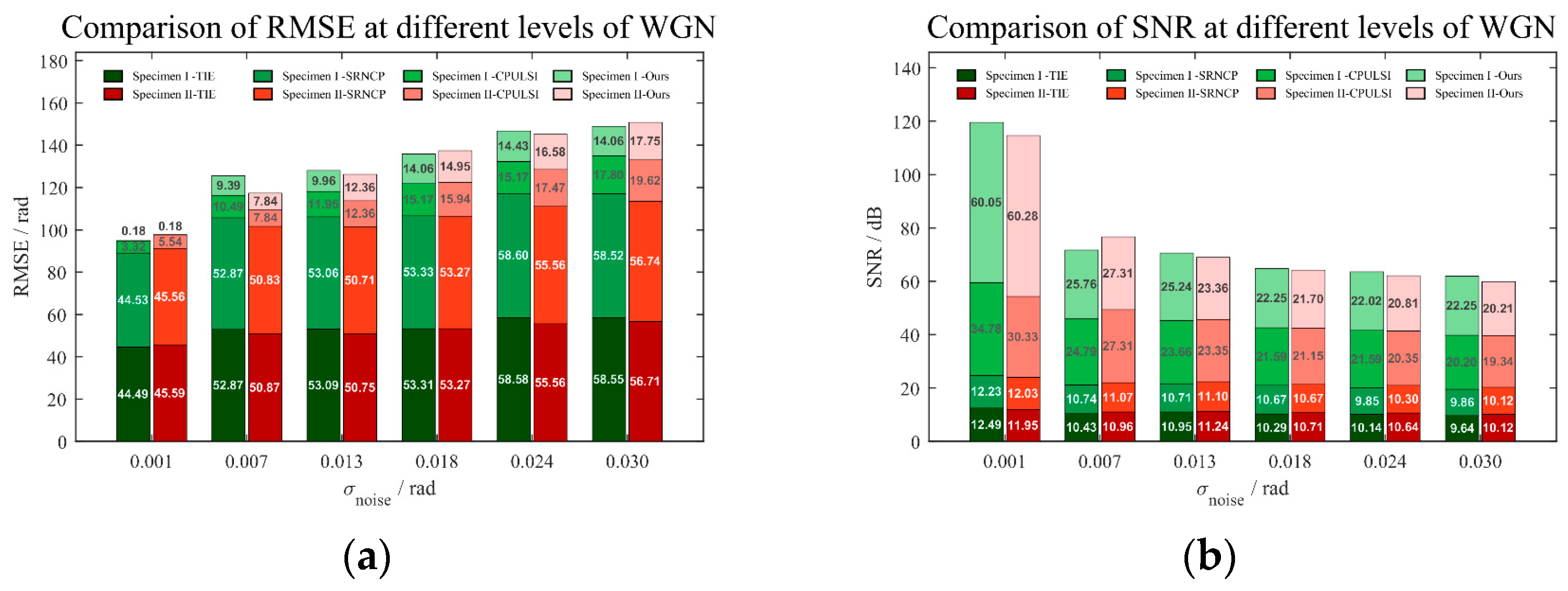
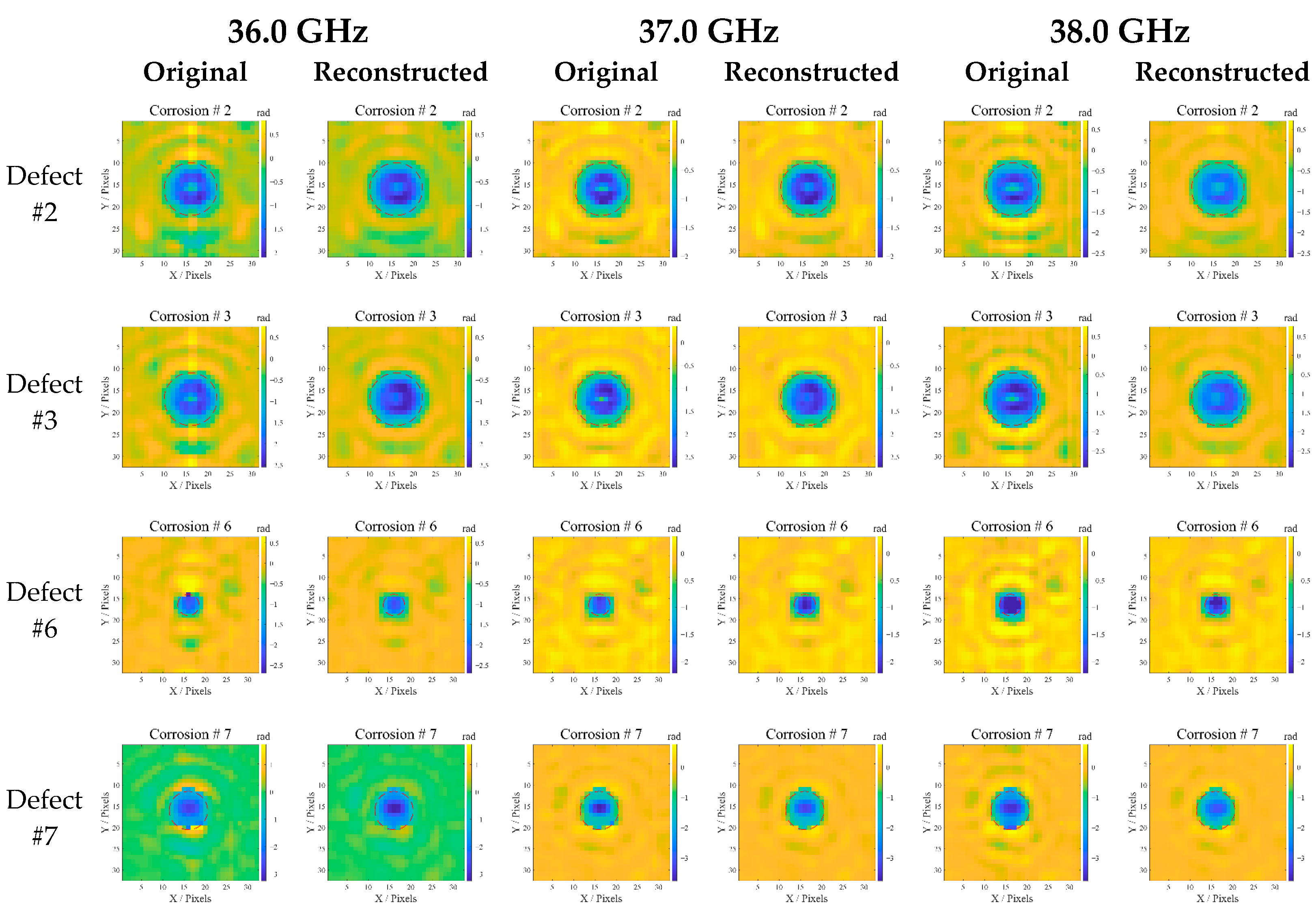
4.7. Corrosion Imaging
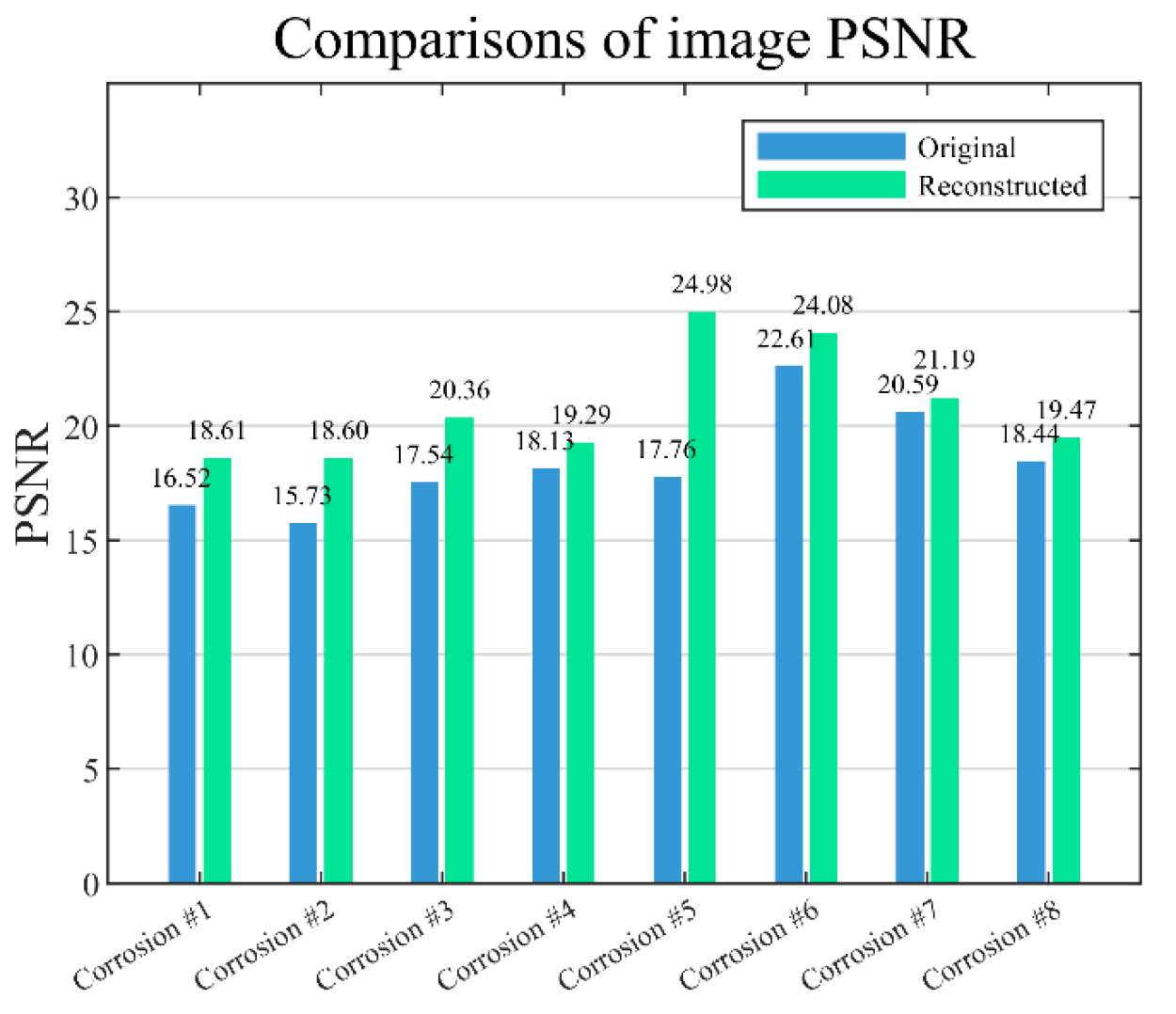
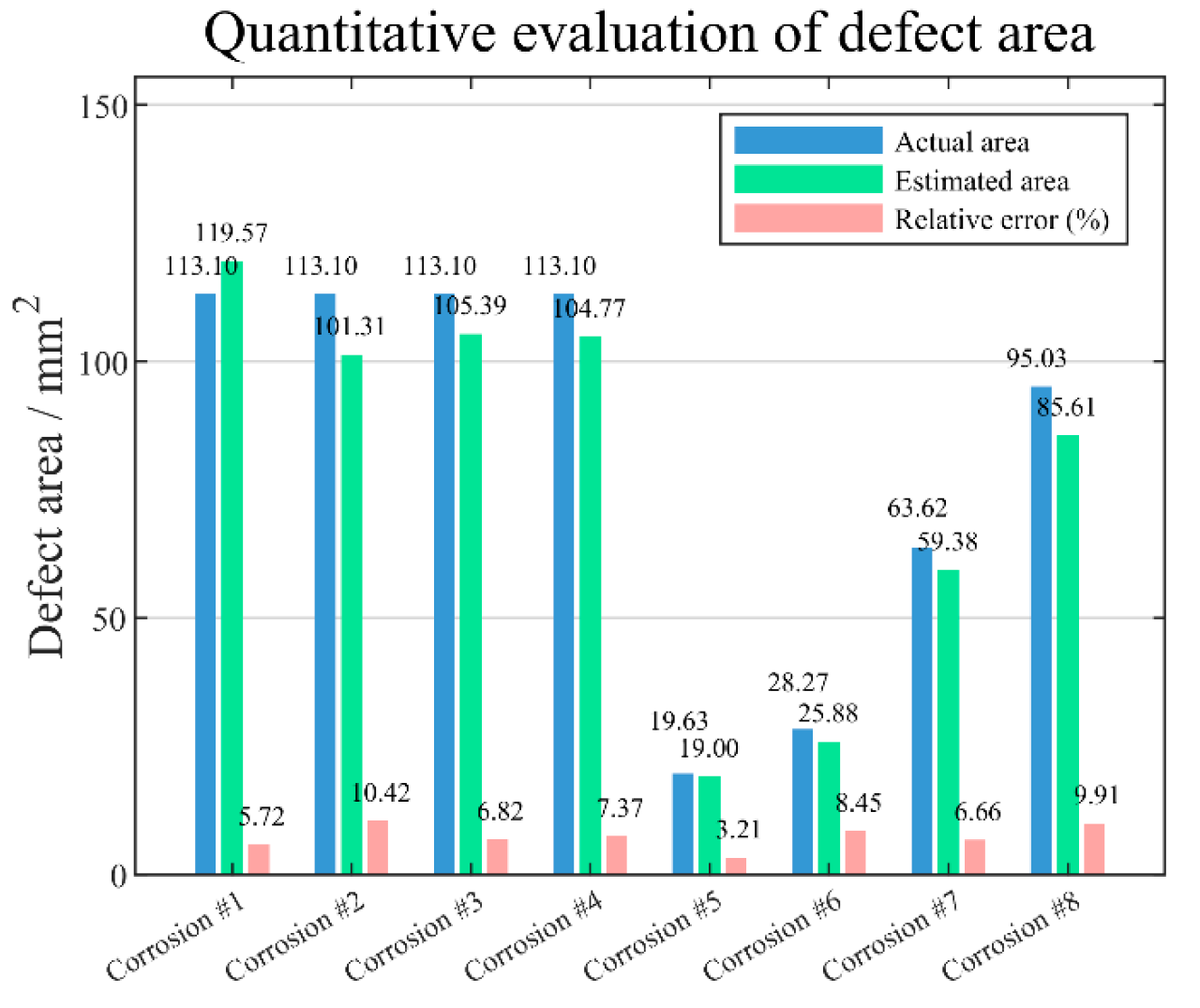
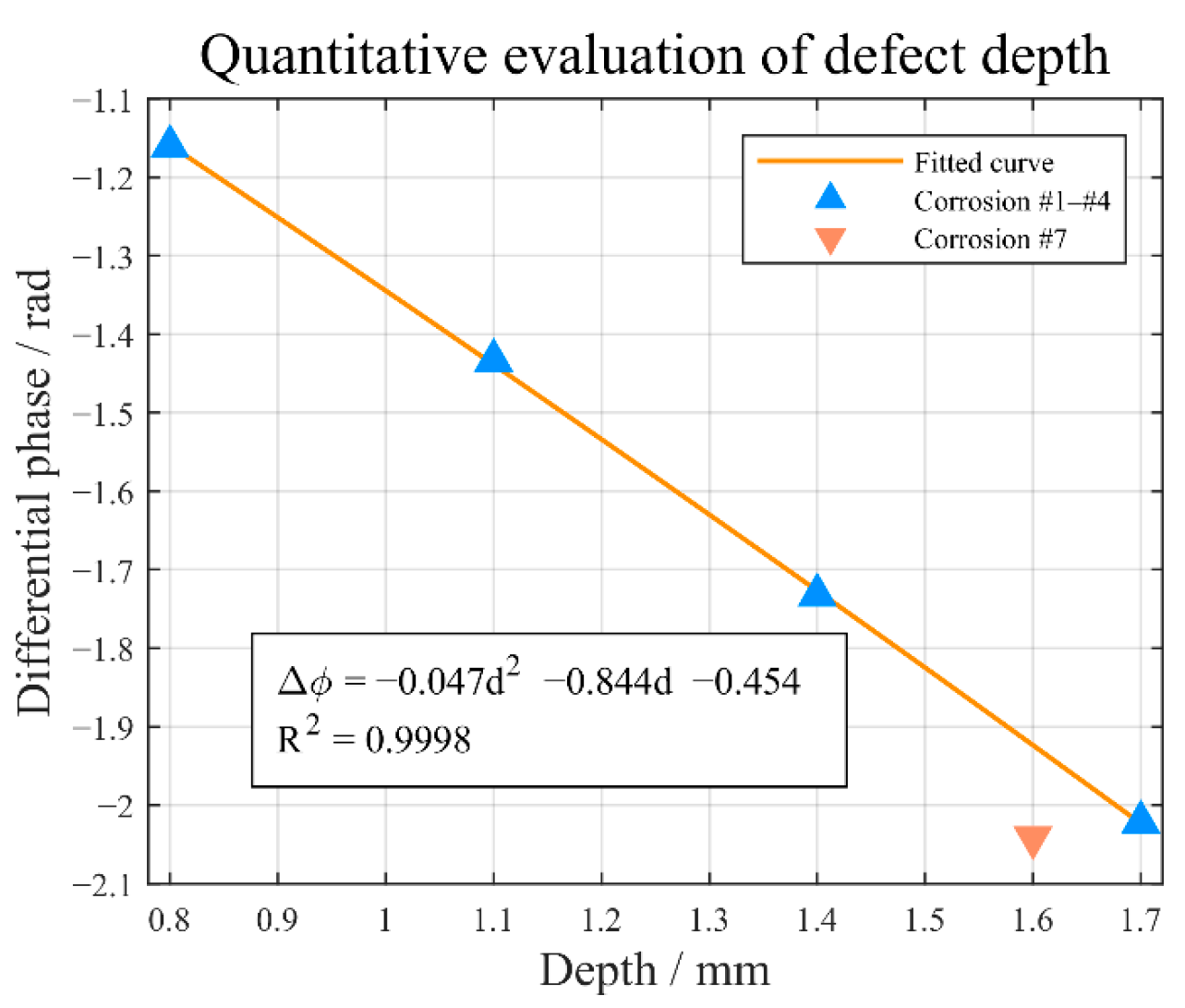
5. Defect Quantitative Evaluation
6. Conclusions and Future Work
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jena, H.; Satpathy, S.; Sahoo, S.; Sahu, S.; Nayak, B.B. Corrosion protection practices and integrity management challenges in oil and gas pipeline. In Transportation Systems Technology and Integrated Management; Springer: Berlin/Heidelberg, Germany, 2023; pp. 141–162. [Google Scholar]
- Xie, Y.; Chu, X.; Ouyang, P.; Jiang, L.; Xing, J.; Yao, H.; Zayed, T. A mini review on coated pipes: Materials, manufacturing and anti-corrosion protection. Corros. Eng. Sci. Technol. 2025, 60, 217–230. [Google Scholar] [CrossRef]
- Meroufel, A.; Gordon, A.; Thierry, D. Cathodic protection shielding of coated buried pipeline. J. Coat. Technol. Res. 2024, 21, 445–459. [Google Scholar] [CrossRef]
- QAZI, H.A.A. Integrity assessment of 3LPE coated pipes stored in open environment for several years. Eur. J. Mater. Sci. Eng. 2022, 7, 143–149. [Google Scholar] [CrossRef]
- Zishu, J.; Haonan, S.; Tianxiang, H.; Qinglong, L.; Xiaojun, L.; Wenxiang, W. Research on Chemical Properties of Anti-Corrosion Coatings for Natural Gas Pipelines and Economic Evaluation of Interconnection. Chem. Technol. Fuels Oils 2025, 61, 137–146. [Google Scholar] [CrossRef]
- Ma, Q.; Tian, G.; Zeng, Y.; Li, R.; Song, H.; Wang, Z.; Gao, B.; Zeng, K. Pipeline in-line inspection method, instrumentation and data management. Sensors 2021, 21, 3862. [Google Scholar] [CrossRef]
- Su, S.; Wang, P.; Shi, P.; Hao, S.; Liang, T. Experiment and simulation on testing steel plate with corrosion defects via magnetic flux leakage method. J. Magn. Magn. Mater. 2022, 560, 169595. [Google Scholar] [CrossRef]
- Feng, J.; Zhang, X.; Lu, S.; Yang, F. A single-stage enhancement-identification framework for pipeline MFL inspection. IEEE Trans. Instrum. Meas. 2022, 71, 1–13. [Google Scholar] [CrossRef]
- Gunarathna, R.; Sivahar, V. Challenges in monitoring metallic pipeline corrosion using ultrasonic waves—A review article. Eng. J. Inst. Eng. Sri Lanka 2021, 54, 67–75. [Google Scholar] [CrossRef]
- Cai, Z.; Yan, Y.; Tian, G. Enhancement of Lamb-EMAT signal using a modified one-side pitch-catch design. IEEE Access 2019, 7, 138556–138566. [Google Scholar] [CrossRef]
- Song, H.; Xiao, Q.; Wang, G.; Zhang, J.; Hu, W. A composite approach of electromagnetic acoustic transducer and eddy current for inner and outer corrosion defects detection. IEEE Trans. Instrum. Meas. 2023, 72, 1–11. [Google Scholar] [CrossRef]
- Hu, Y.; Zhou, J.; Yue, W. Research on crossing-pipe support structure defect detection of EMAT-Excited CSH wave. Sensors 2023, 23, 5535. [Google Scholar] [CrossRef]
- Wasif, R.; Tokhi, M.O.; Shirkoohi, G.; Marks, R.; Rudlin, J. Development of permanently installed magnetic eddy current sensor for corrosion monitoring of ferromagnetic pipelines. Appl. Sci. 2022, 12, 1037. [Google Scholar] [CrossRef]
- Su, L.; Gao, B.; Zhao, X.; Fu, Y.; Woo, W.L. RHiREM: Intelligent diagnostic framework for pipeline Eddy Current Internal Inspection based on reinforcement learning with hierarchical reward exploration mechanism. NDT E Int. 2024, 144, 103073. [Google Scholar] [CrossRef]
- Taheri, H.; Jones, C.; Taheri, M. Assessment and detection of stress corrosion cracking by advanced eddy current array nondestructive testing and material characterization. J. Nat. Gas Sci. Eng. 2022, 102, 104568. [Google Scholar] [CrossRef]
- Hou, Y.; Pojtanabuntoeng, T.; Salasi, M.; Iannuzzi, M.; McKechnie, J. Assessing the efficacy of non-destructive testing methods to detect pitting corrosion. Nondestruct. Test. Eval. 2023, 38, 373–393. [Google Scholar] [CrossRef]
- Amoah, P.; Owusu-Poku, S.; Ajubala, G.A. Investigation of wall thickness, corrosion, and deposits in industrial pipelines using radiographic technique. Int. J. Corros. 2023, 2023, 4924399. [Google Scholar] [CrossRef]
- Zuo, F.; Liu, J.; Zhang, H.; Chen, Z.; Yan, B.; Wang, L. A Complex Welding Defect Detection Method Based on Active Learning in Pipeline Transportation System. IEEE Trans. Instrum. Meas. 2025, 74, 1–12. [Google Scholar] [CrossRef]
- Allah, M.A.-A.; Toor, I.U.; Shams, A.; Siddiqui, O.K. Application of machine learning and deep learning techniques for corrosion and cracks detection in nuclear power plants: A review. Arab. J. Sci. Eng. 2025, 50, 3017–3045. [Google Scholar] [CrossRef]
- Zuo, F.; Liu, J.; Fu, M.; Wang, L.; Zhao, Z. An X-Ray-based multiexpert inspection method for automatic welding defect assessment in intelligent pipeline systems. IEEE/ASME Trans. Mechatron. 2024, 30, 1753–1764. [Google Scholar] [CrossRef]
- Siang, T.W.; Firdaus Akbar, M.; Nihad Jawad, G.; Yee, T.S.; Mohd Sazali, M.I.S. A Past, Present, and Prospective Review on Microwave Nondestructive Evaluation of Composite Coatings. Coatings 2021, 11, 913. [Google Scholar] [CrossRef]
- Abou-Khousa, M.A.; Rahman, M.S.U.; Donnell, K.M.; Al Qaseer, M.T. Detection of surface cracks in metals using microwave and millimeter-wave nondestructive testing techniques—A review. IEEE Trans. Instrum. Meas. 2023, 72, 1–18. [Google Scholar] [CrossRef]
- Ur Rahman, M.S.; Haryono, A.; Abou-Khousa, M.A. Microwave non-destructive evaluation of glass reinforced epoxy and high density polyethylene pipes. J. Nondestruct. Eval. 2020, 39, 26. [Google Scholar] [CrossRef]
- Amineh, R.K. Microwave nondestructive testing of nonmetallic pipes: An overview of the major developments. IEEE Instrum. Meas. Mag. 2024, 27, 54–66. [Google Scholar] [CrossRef]
- Brinker, K.; Dvorsky, M.; Al Qaseer, M.T.; Zoughi, R. Review of advances in microwave and millimetre-wave NDT&E: Principles and applications. Philos. Trans. R. Soc. A 2020, 378, 20190585. [Google Scholar]
- Zhang, H.; Gao, B.; Tian, G.Y.; Woo, W.L.; Bai, L. Metal defects sizing and detection under thick coating using microwave NDT. NDT E Int. 2013, 60, 52–61. [Google Scholar] [CrossRef]
- Bakhtiari, S.; Qaddoumi, N.; Ganchev, S.I.; Zoughi, R. Microwave noncontact examination of disbond and thickness variation in stratified composite media. IEEE Trans. Microw. Theory Tech. 1994, 42, 389–395. [Google Scholar] [CrossRef]
- Sutthaweekul, R.; Tian, G.Y. Steel corrosion stages characterization using open-ended rectangular waveguide probe. IEEE Sens. J. 2017, 18, 1054–1062. [Google Scholar] [CrossRef]
- Martinez-Carranza, J.; Falaggis, K.; Kozacki, T. Fast and accurate phase-unwrapping algorithm based on the transport of intensity equation. Appl. Opt. 2017, 56, 7079–7088. [Google Scholar] [CrossRef]
- Jia, Y.; Gao, Y.; Zhang, S.; Li, S.; Zhang, Y.; Li, M. A novel 2-D phase unwrapping method based on PUMA for aerospace topographic mapping systems. IEEE J. Miniaturization Air Space Syst. 2022, 3, 113–120. [Google Scholar] [CrossRef]
- Cheng, W.; Cheng, H.; Wen, Y.; Feng, Y. Comparison of weighted least-squares phase unwrapping algorithms in noise resistance, discontinuity characteristics, convergence speed, and accuracy. Opt. Eng. 2022, 61, 073105. [Google Scholar] [CrossRef]
- De Souza, J.; Oliveira, M.; Dos Santos, P. Branch-cut algorithm for optical phase unwrapping. Opt. Lett. 2015, 40, 3456–3459. [Google Scholar] [CrossRef]
- Herráez, M.A.; Burton, D.R.; Lalor, M.J.; Gdeisat, M.A. Fast two-dimensional phase-unwrapping algorithm based on sorting by reliability following a noncontinuous path. Appl. Opt. 2002, 41, 7437–7444. [Google Scholar] [CrossRef]
- Bentahar, T.; Bentahar, A.; Saidi, R.; Mayache, H.; Ferroudji, K. Hybrid technique of the branch-cut and the quality-guided for INSAR phase unwrapping. Int. J. Image Graph. 2021, 21, 2150040. [Google Scholar] [CrossRef]
- Karout, S.A.; Gdeisat, M.A.; Burton, D.R.; Lalor, M.J. Two-dimensional phase unwrapping using a hybrid genetic algorithm. Appl. Opt. 2007, 46, 730–743. [Google Scholar] [CrossRef]
- Buckland, J.; Huntley, J.; Turner, S. Unwrapping noisy phase maps by use of a minimum-cost-matching algorithm. Appl. Opt. 1995, 34, 5100–5108. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, J.; Tian, Z.; Sun, S.; Li, J.; Yang, J. A genetic algorithm with jumping gene and heuristic operators for traveling salesman problem. Appl. Soft Comput. 2022, 127, 109339. [Google Scholar] [CrossRef]
- Xia, H.; Montresor, S.; Guo, R.; Li, J.; Yan, F.; Cheng, H.; Picart, P. Phase calibration unwrapping algorithm for phase data corrupted by strong decorrelation speckle noise. Opt. Express 2016, 24, 28713–28730. [Google Scholar] [CrossRef]
- GB/T 23257-2017; Standard for Polyethylene Coating for Buried Steel Pipeline. Standardization administration of the People’s Republic of China: Beijing, China, 2017.
- Pozar, D.M. Microwave Engineering: Theory and Techniques; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Ferretti, A.; Monti-Guarnieri, A.; Prati, C.; Rocca, F.; Massonet, D. InSAR Principles-Guidelines for SAR Interferometry Processing and Interpretation; European Space Agency: Paris, France, 2007; Volume 19.
- He, Y.-L.; Ye, X.; Huang, D.-F.; Huang, J.Z.; Zhai, J.-H. Novel kernel density estimator based on ensemble unbiased cross-validation. Inf. Sci. 2021, 581, 327–344. [Google Scholar] [CrossRef]
- Li, X.; Cheng, X.; Xu, Y.; Jiao, Y.; Huang, W.; Cui, Y.; Shen, J.; Shao, W. Multi-frequency ultrasound imaging fusion method based on wavelet transform for guided screw insertion. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2023, 71, 395–407. [Google Scholar] [CrossRef]
- Yazid, H.; Basah, S.N.; Rahim, S.A.; Safar, M.J.A.; Basaruddin, K.S. Performance analysis of entropy thresholding for successful image segmentation. Multimed. Tools Appl. 2022, 81, 6433–6450. [Google Scholar] [CrossRef]


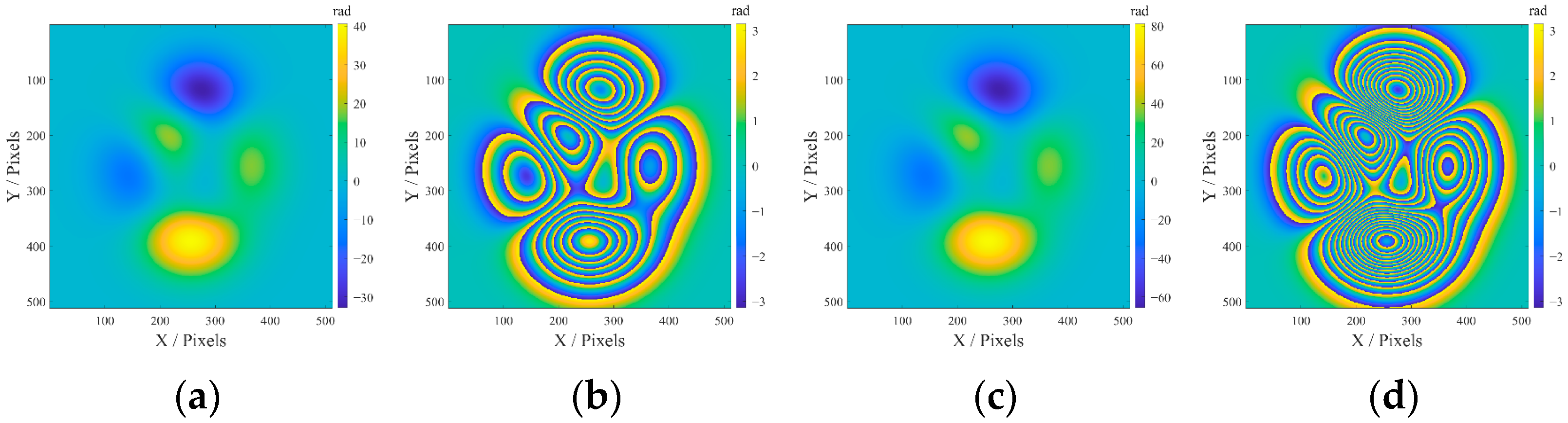

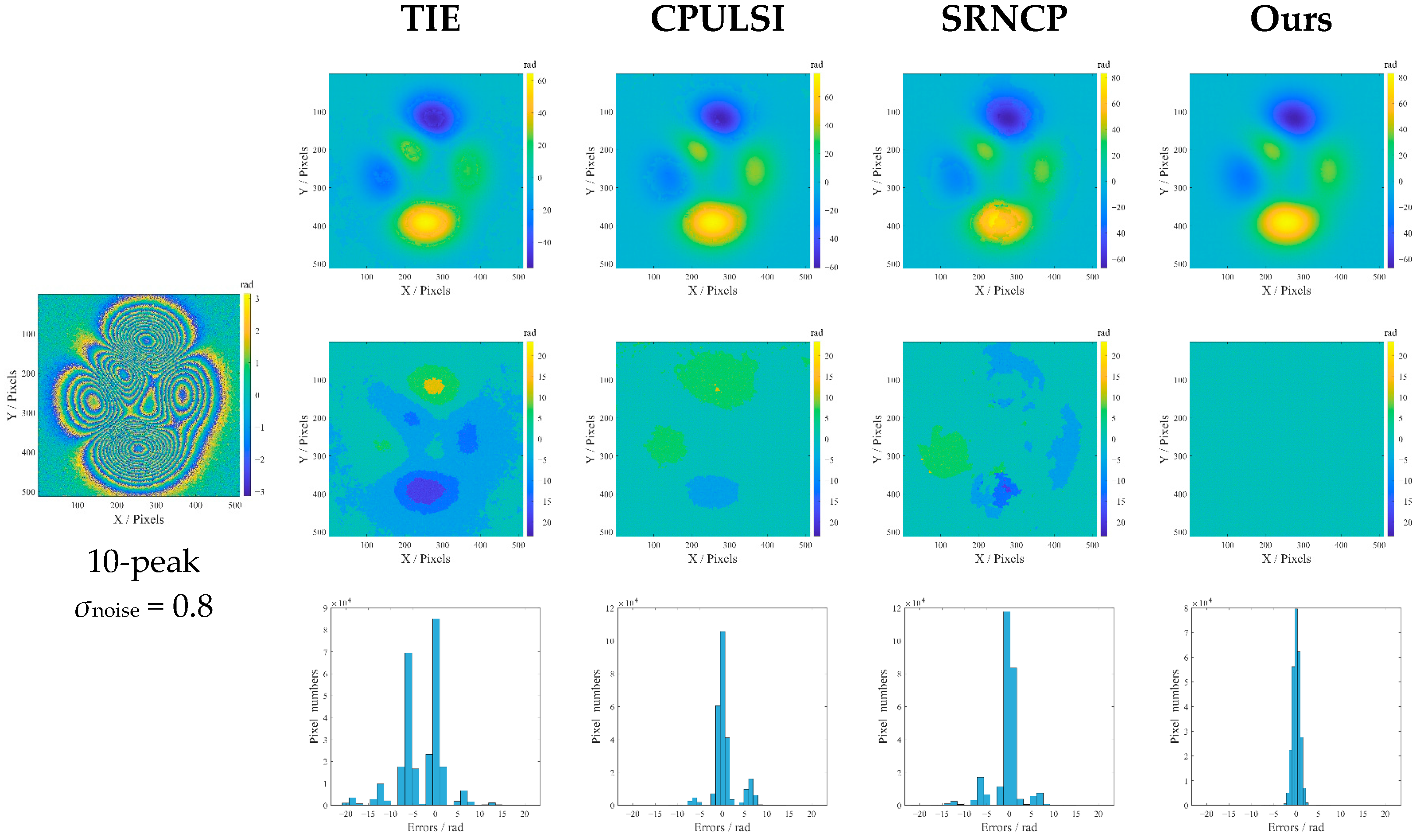




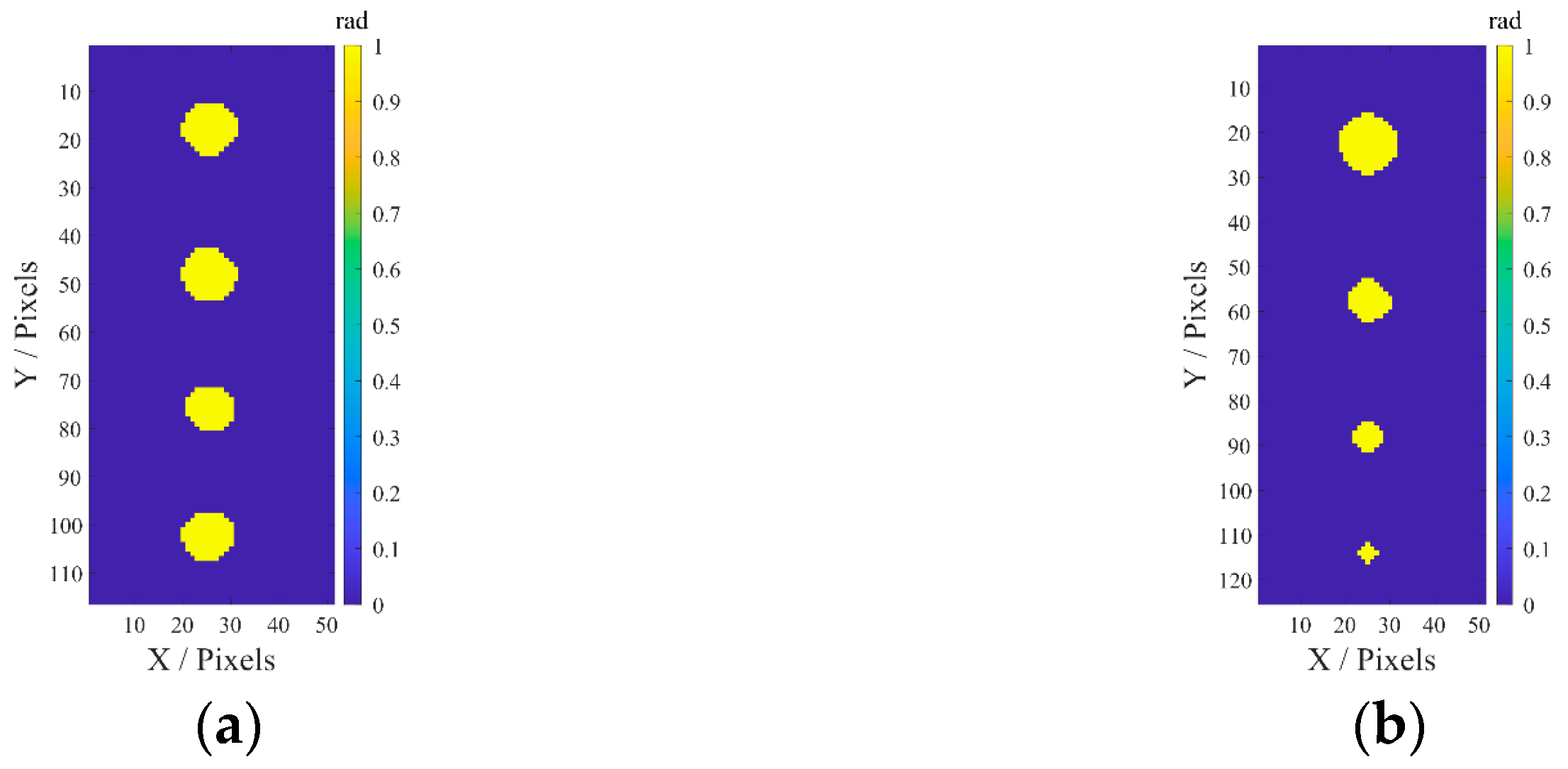
| Peaks | σnoise | Root Mean Square Error (rad) | Signal-to-Noise Ratio (dB) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| TIE | CPULSI | SRNCP | Ours | CPULSI | CPULSI | SRNCP | Ours | ||
| 5 | 0.3 | 1.425 | 1.425 | 1.425 | 1.425 | 38.842 | 38.842 | 38.842 | 38.842 |
| 0.5 | 1.984 | 1.984 | 1.984 | 1.983 | 35.969 | 35.970 | 35.968 | 35.971 | |
| 0.8 | 8.459 | 4.139 | 4.414 | 3.748 | 23.373 | 31.241 | 29.023 | 32.444 | |
| 10 | 0.3 | 0.692 | 0.692 | 0.692 | 0.692 | 45.118 | 45.119 | 45.119 | 45.119 |
| 0.5 | 1.323 | 1.090 | 1.092 | 1.091 | 37.076 | 41.172 | 41.165 | 41.169 | |
| 0.8 | 5.477 | 3.241 | 5.649 | 1.654 | 27.149 | 31.707 | 26.880 | 37.547 | |
| PCs | Specimen I | Specimen II | ||
|---|---|---|---|---|
| Component Contribution (%) | Cumulative Contribution (%) | Component Contribution (%) | Cumulative Contribution (%) | |
| PC1 | 81.37 | 81.37 | 70.84 | 70.84 |
| PC2 | 9.87 | 91.24 | 12.06 | 82.90 |
| PC3 | 4.05 | 95.28 | 8.10 | 91.00 |
| PC4 | 2.15 | 97.43 | 3.72 | 94.72 |
| PC5 | 1.27 | 98.71 | 2.58 | 97.30 |
| Defect Number | Actual Location | Evaluated Location | Relative Error (%) |
|---|---|---|---|
| #1 | (25.50, 102.00) | (25.19, 102.60) | (1.23, 0.59) |
| #2 | (25.50, 76.00) | (25.50, 76.00) | (0.00, 0.00) |
| #3 | (25.50, 48.00) | (25.48, 48.04) | (0.07, 0.09) |
| #4 | (25.50, 18.00) | (25.62, 17.69) | (0.46, 1.74) |
| #5 | (25.00, 114.00) | (25.00, 114.00) | (0.00, 0.00) |
| #6 | (25.00, 88.00) | (25.00, 88.00) | (0.00, 0.00) |
| #7 | (25.00, 58.00) | (25.31, 57.61) | (1.24, 0.68) |
| #8 | (25.00, 23.00) | (25.04, 22.48) | (0.18, 2.25) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W. Visual Quantitative Characterization of External Corrosion in 3LPE Coated Pipes Based on Microwave Near-Field Reflectometry and Phase Unwrapping. Sensors 2025, 25, 5126. https://doi.org/10.3390/s25165126
Li W. Visual Quantitative Characterization of External Corrosion in 3LPE Coated Pipes Based on Microwave Near-Field Reflectometry and Phase Unwrapping. Sensors. 2025; 25(16):5126. https://doi.org/10.3390/s25165126
Chicago/Turabian StyleLi, Wenjia. 2025. "Visual Quantitative Characterization of External Corrosion in 3LPE Coated Pipes Based on Microwave Near-Field Reflectometry and Phase Unwrapping" Sensors 25, no. 16: 5126. https://doi.org/10.3390/s25165126
APA StyleLi, W. (2025). Visual Quantitative Characterization of External Corrosion in 3LPE Coated Pipes Based on Microwave Near-Field Reflectometry and Phase Unwrapping. Sensors, 25(16), 5126. https://doi.org/10.3390/s25165126





