Virtual Observation Using Location-Dependent Statistical Information of Cyclists’ Movement for Estimation of Position and Uncertainty
Abstract
1. Introduction
- We propose a method for analyzing LDSI from accumulated low-level GNSS data.
- We propose a method for predicting the position and uncertainty of cyclists via virtual observation and virtual control input based on the LDSI.
2. Related Works
2.1. Cooperative Perception Methods for Traffic Safety of Vulnerable Road Users
2.2. Position Estimation Methods Considering Movement Characteristics Based on Accumulated Data
2.3. Virtual Observations and Virtual Control Inputs for Kalman Filter
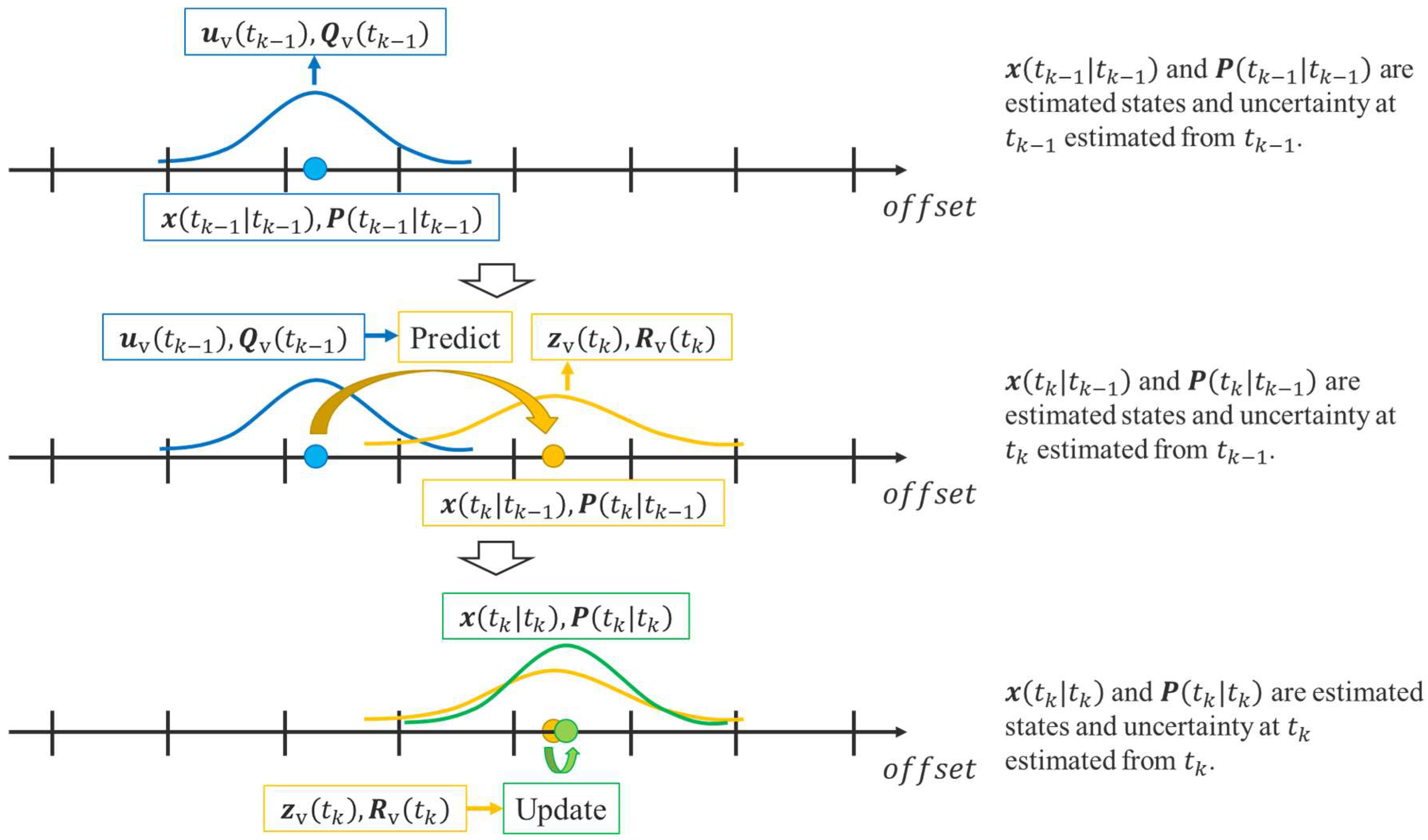
3. Method
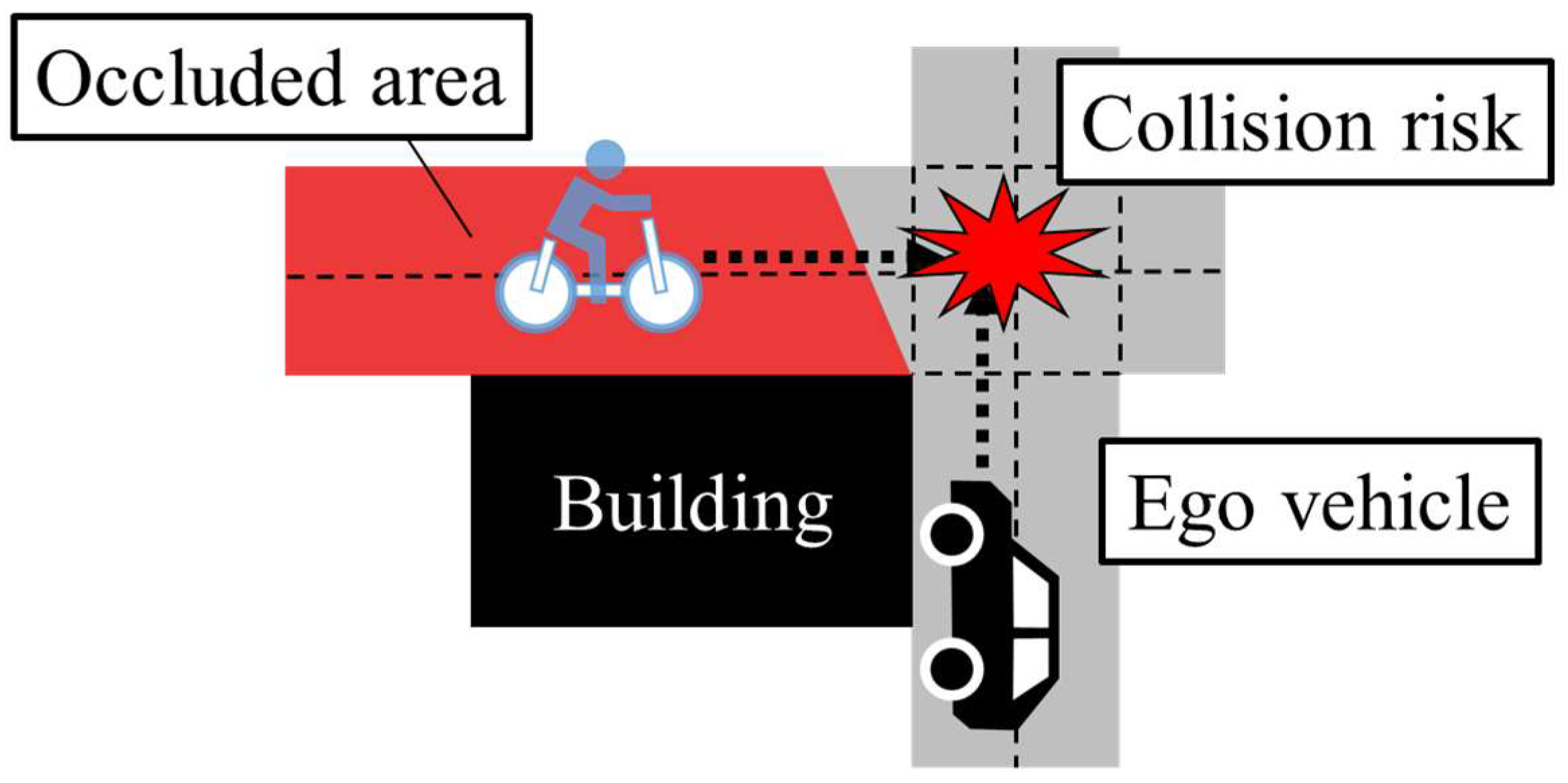
3.1. Investigated Situation
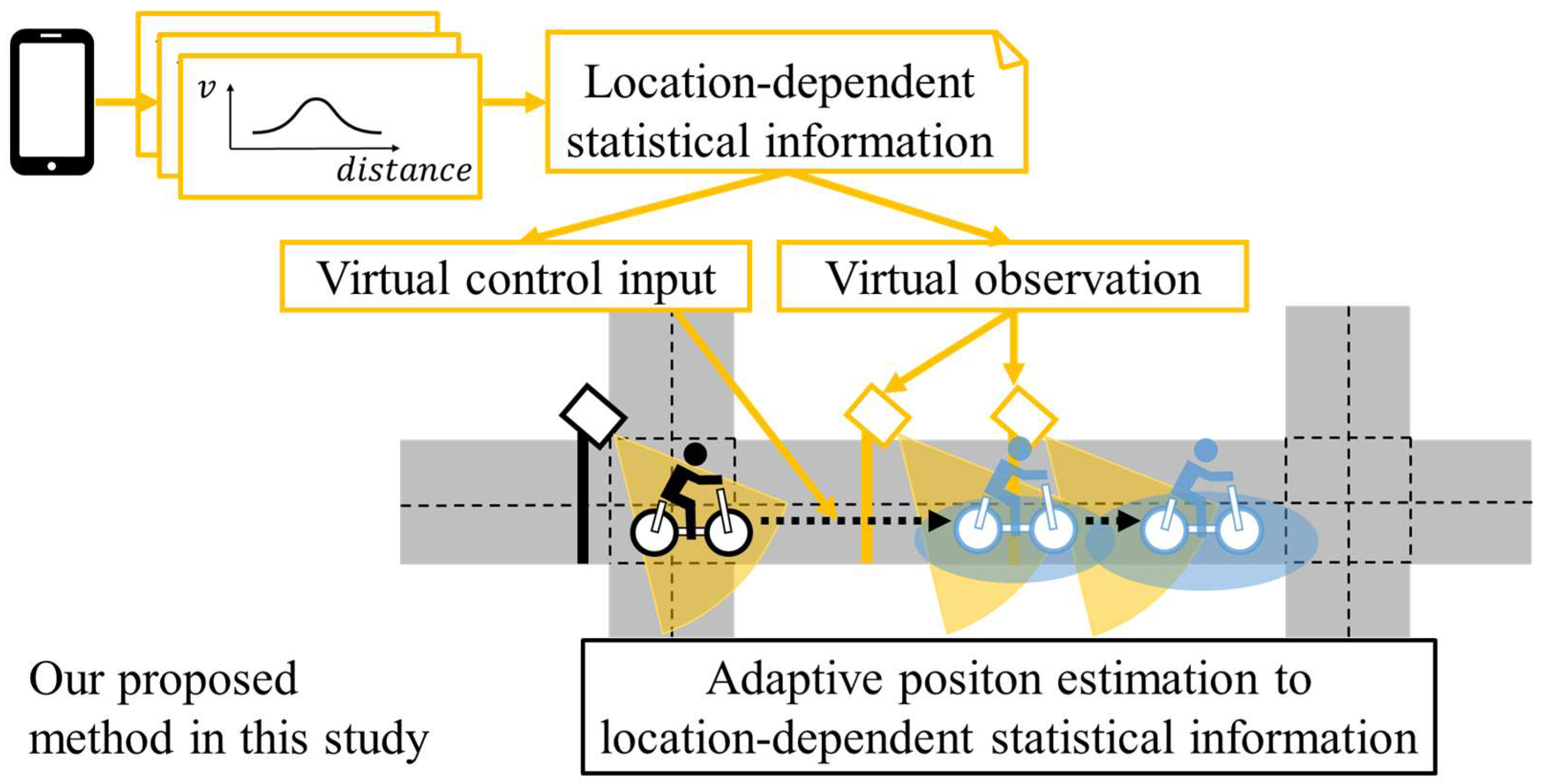
3.2. Conceptual Design
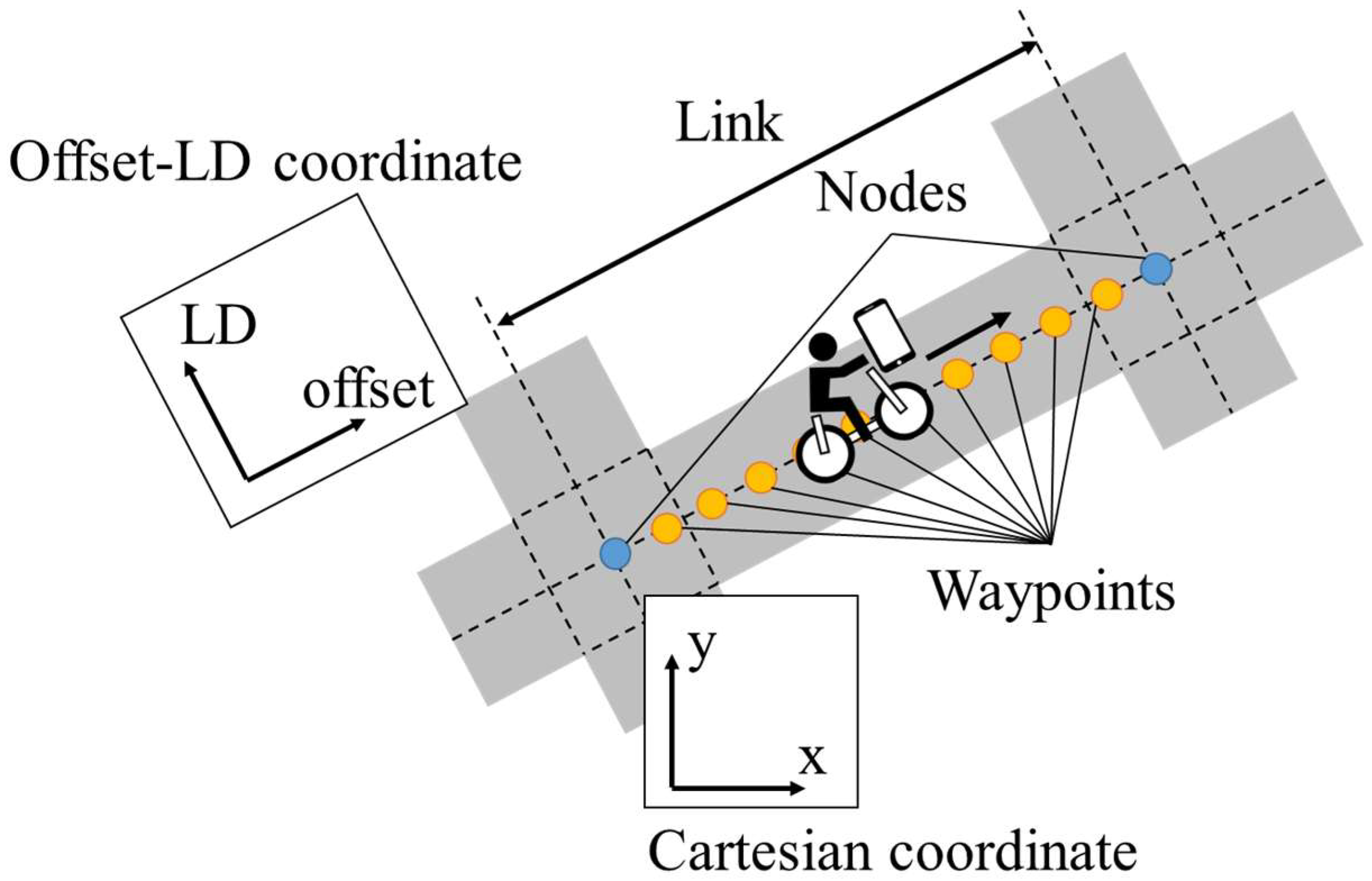
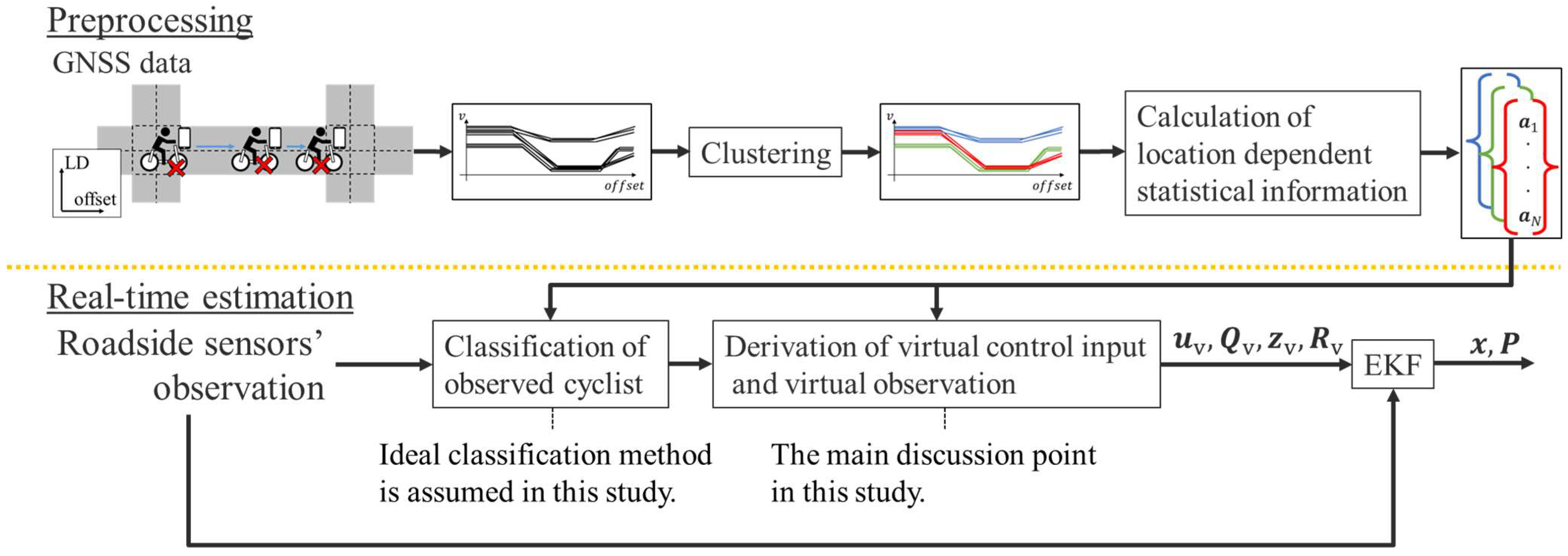
3.3. Preparation of LDSI
3.3.1. Movement State Estimation Using Kalman Smoother
3.3.2. Implementation of Observation
3.3.3. Clustering of Smoothed Data
3.4. Movement States Estimation Using LDSI
3.4.1. Real-Time Movement States Estimation Using Kalman Filter
3.4.2. Implementation of Actual Sensor Observation
3.4.3. Implementation of Virtual Control Input and Virtual Observation
4. Experiment for Preparing LDSI
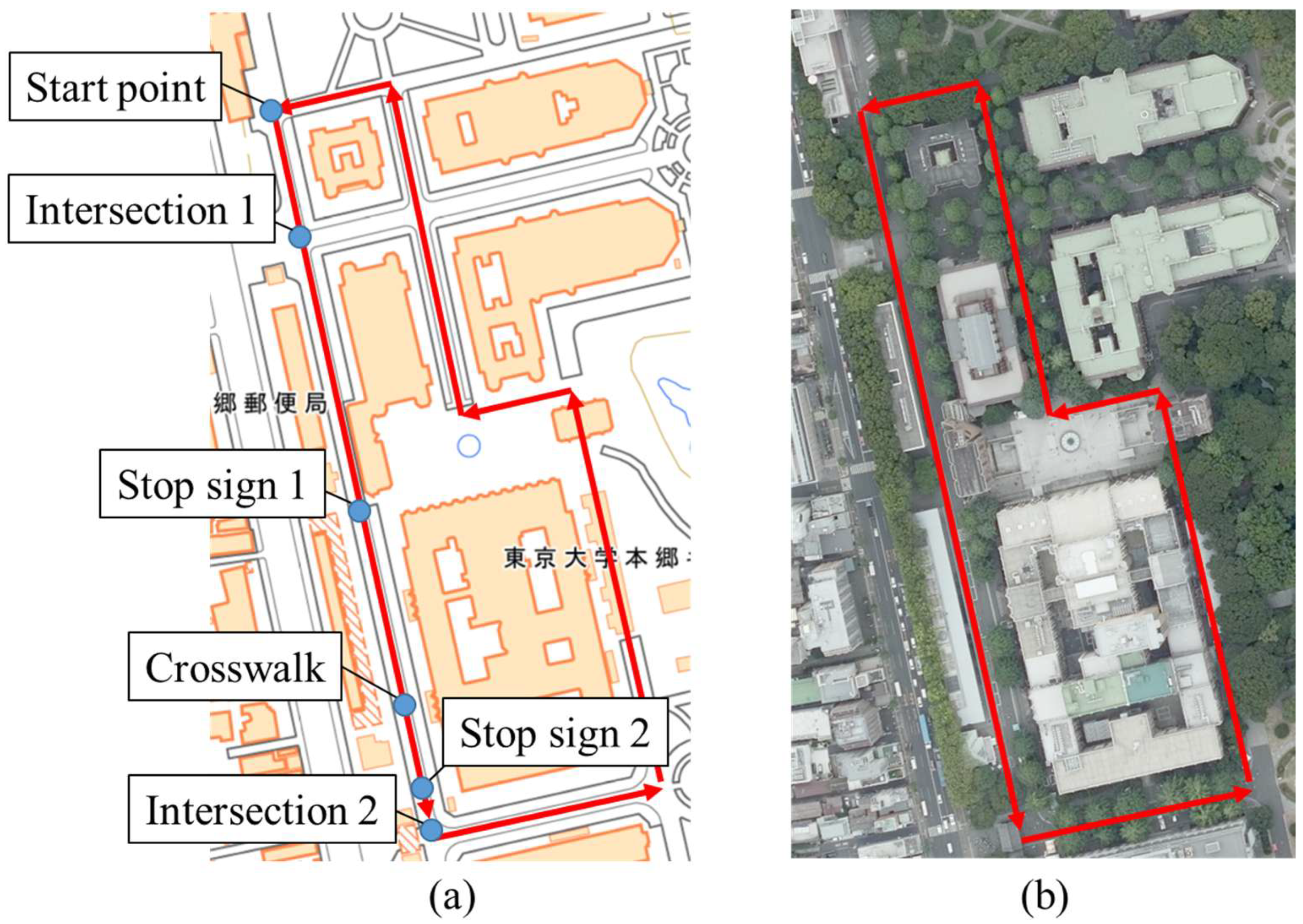
4.1. Experimental Setup
4.2. Parameters Related to GNSS Observation for Kalman Smoother
4.3. Clustering Result
5. Simulation Experiment of Position Estimation Using LDSI
5.1. Data for Simulation Experiment
5.2. Parameters of Roadside Sensor Observation
5.3. Conventional Method as a Baseline for Comparison
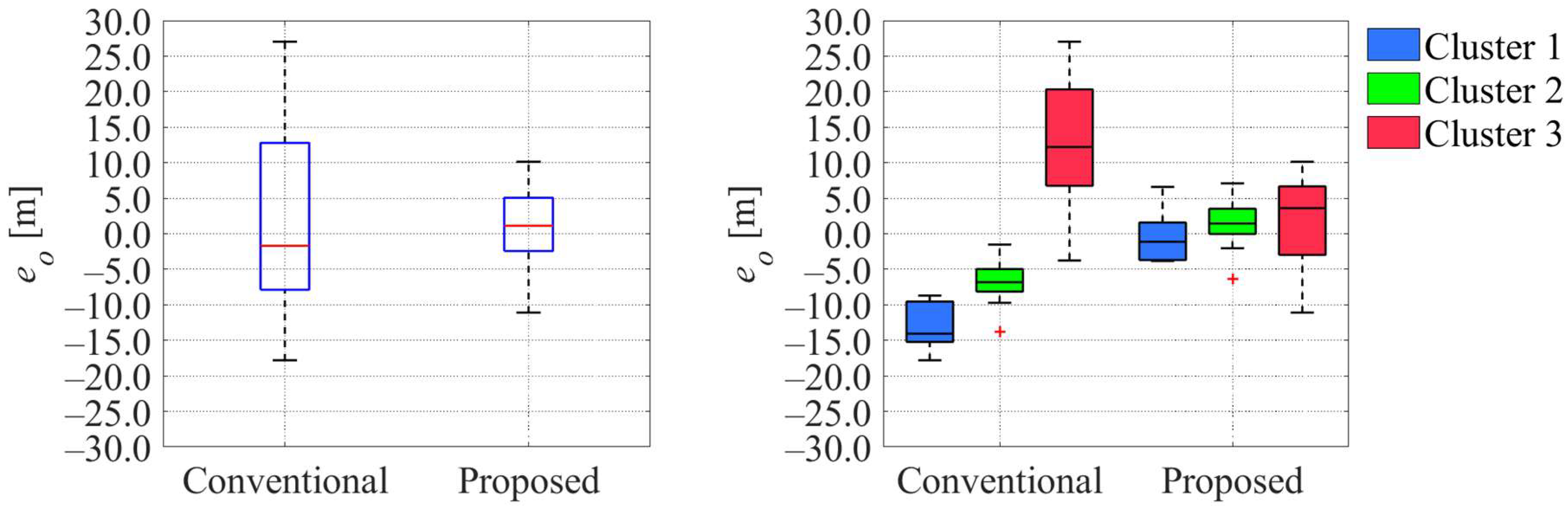
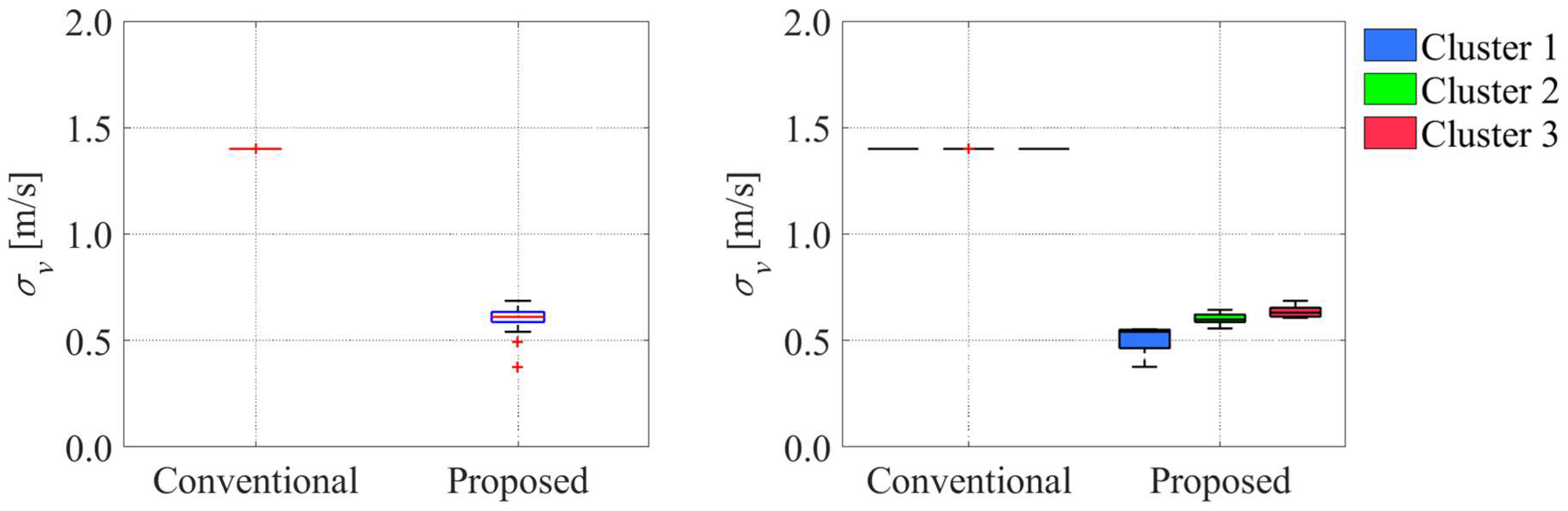
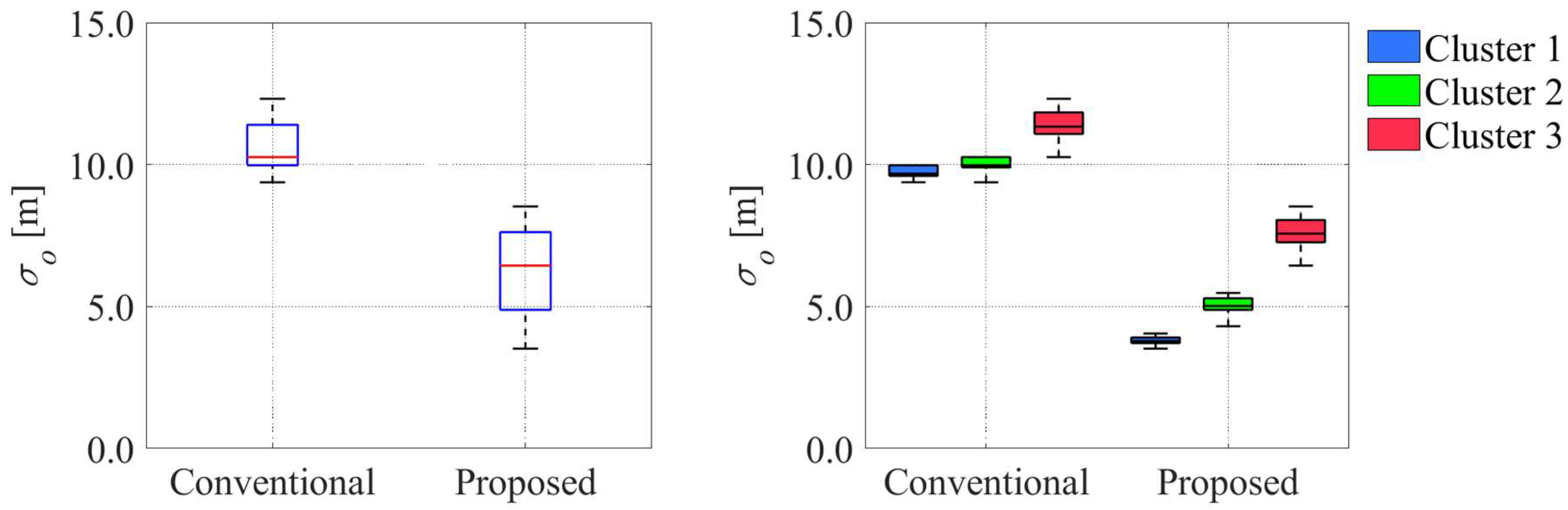
5.4. Results and Discussions
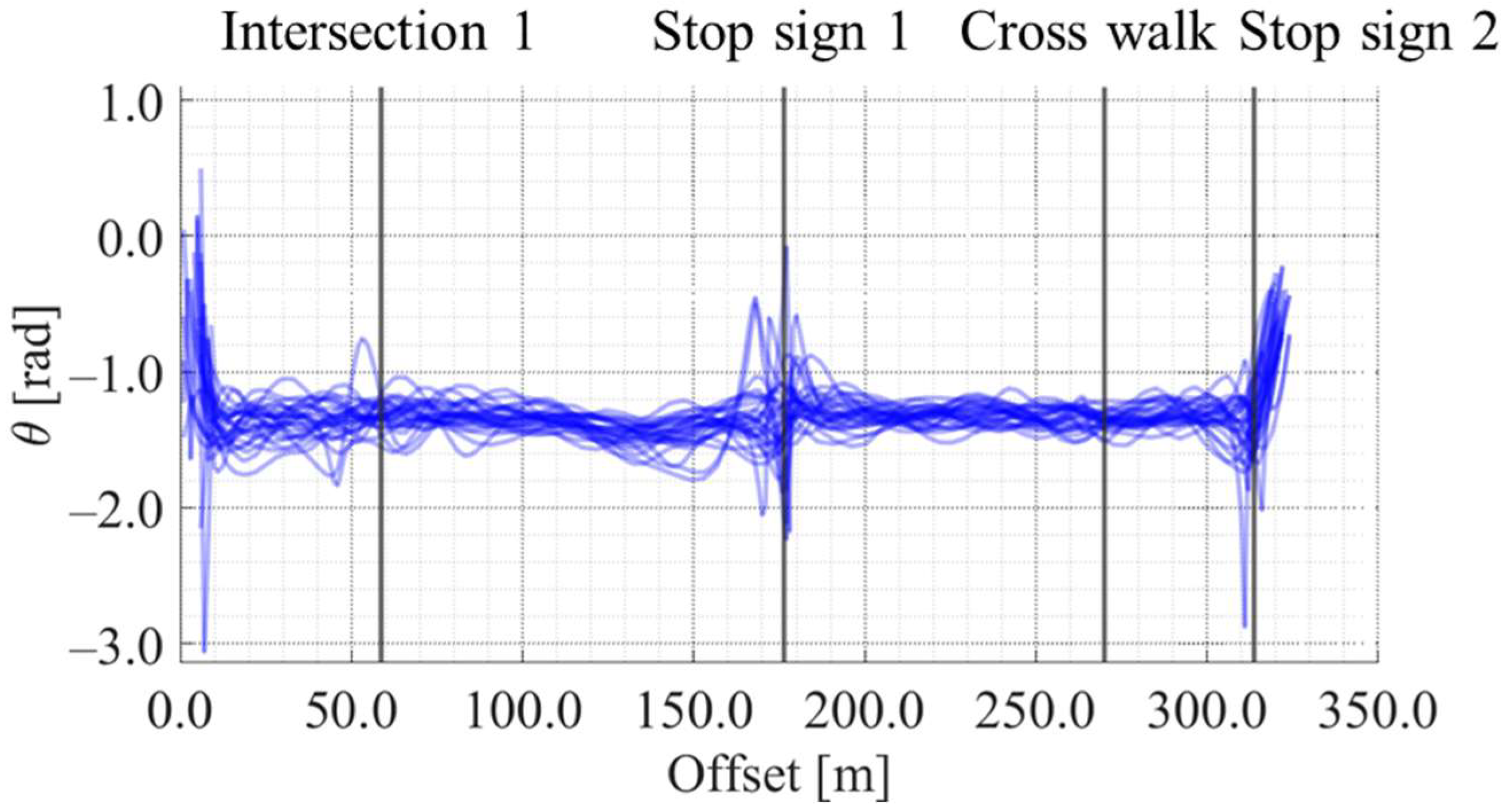
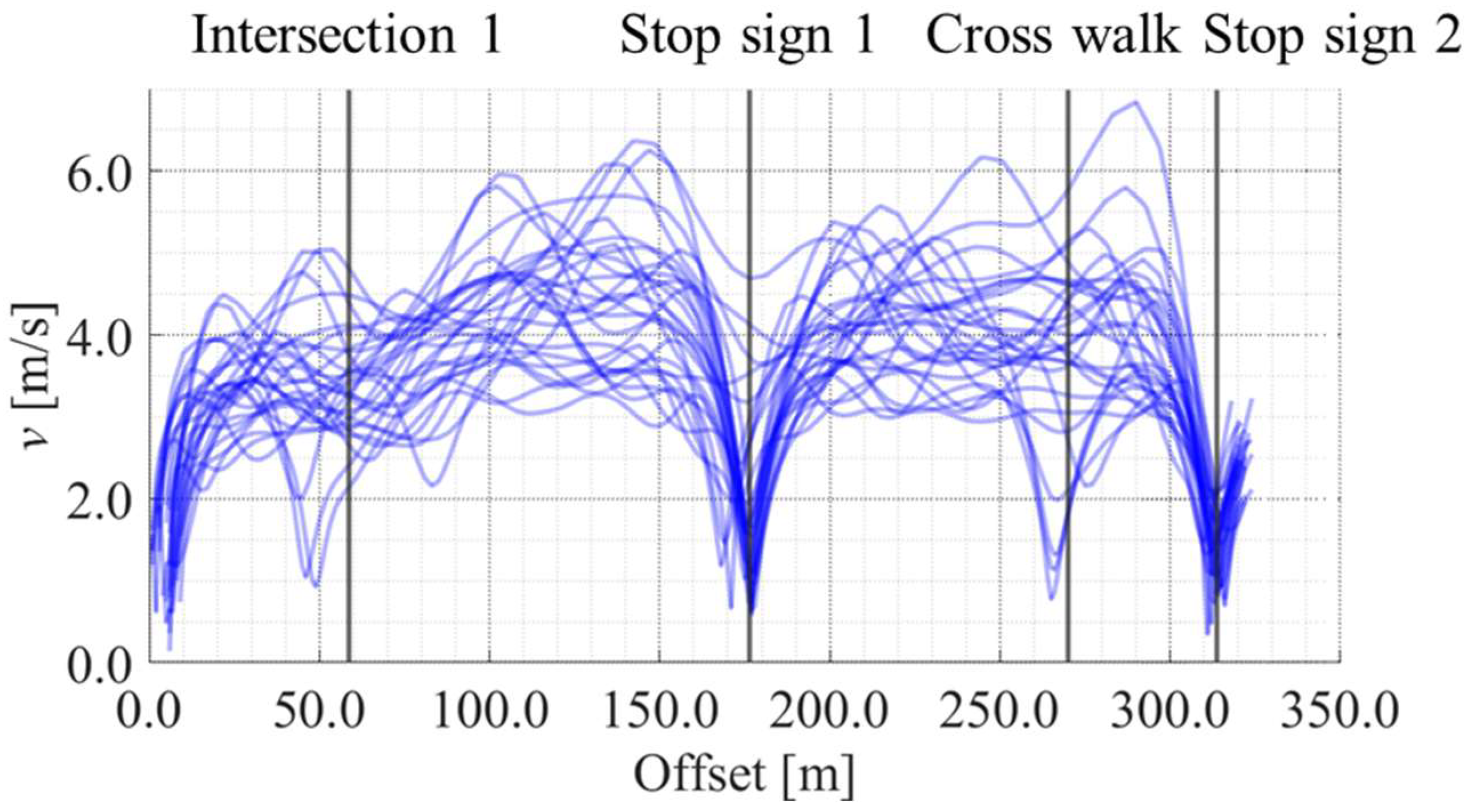
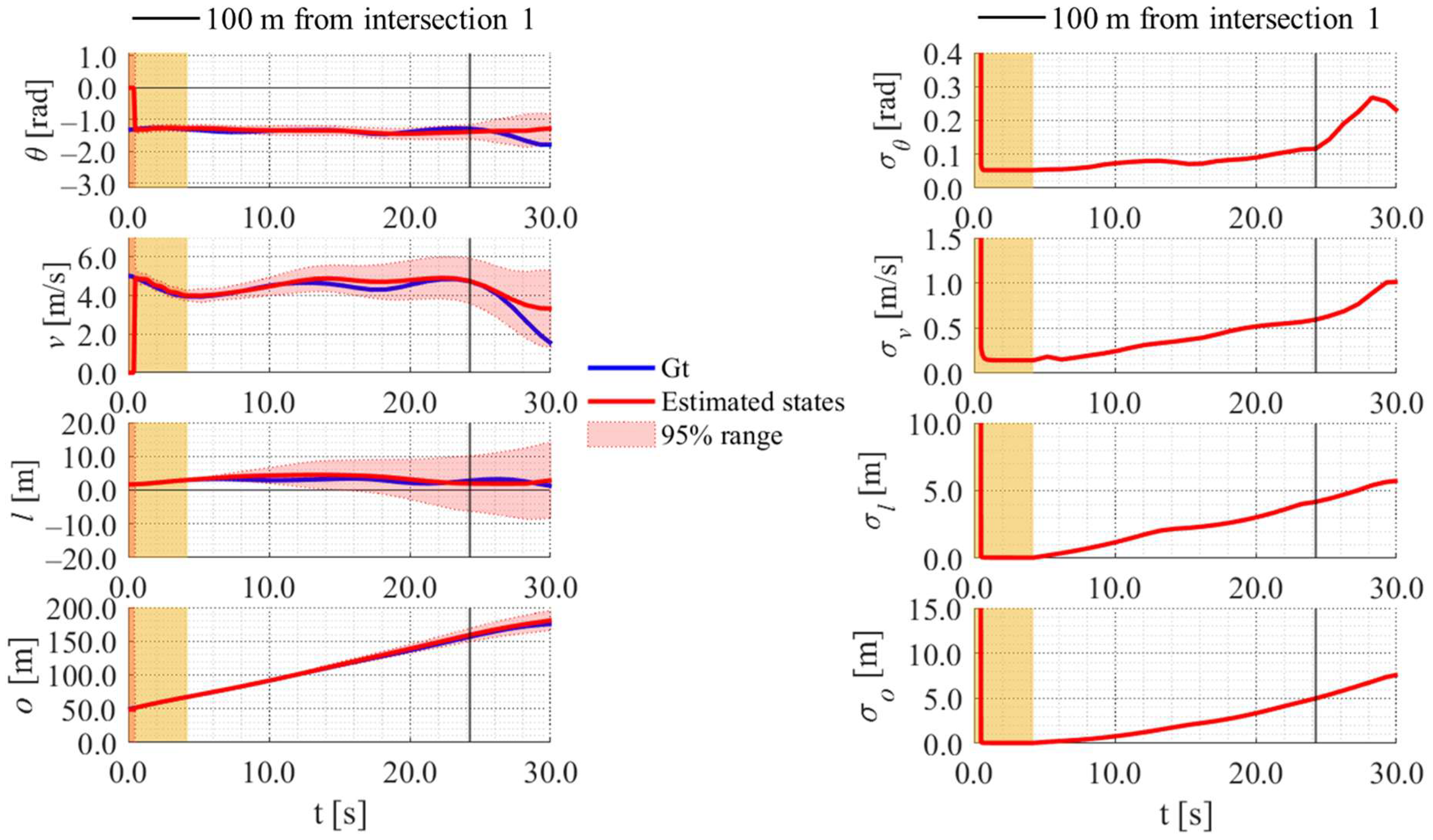
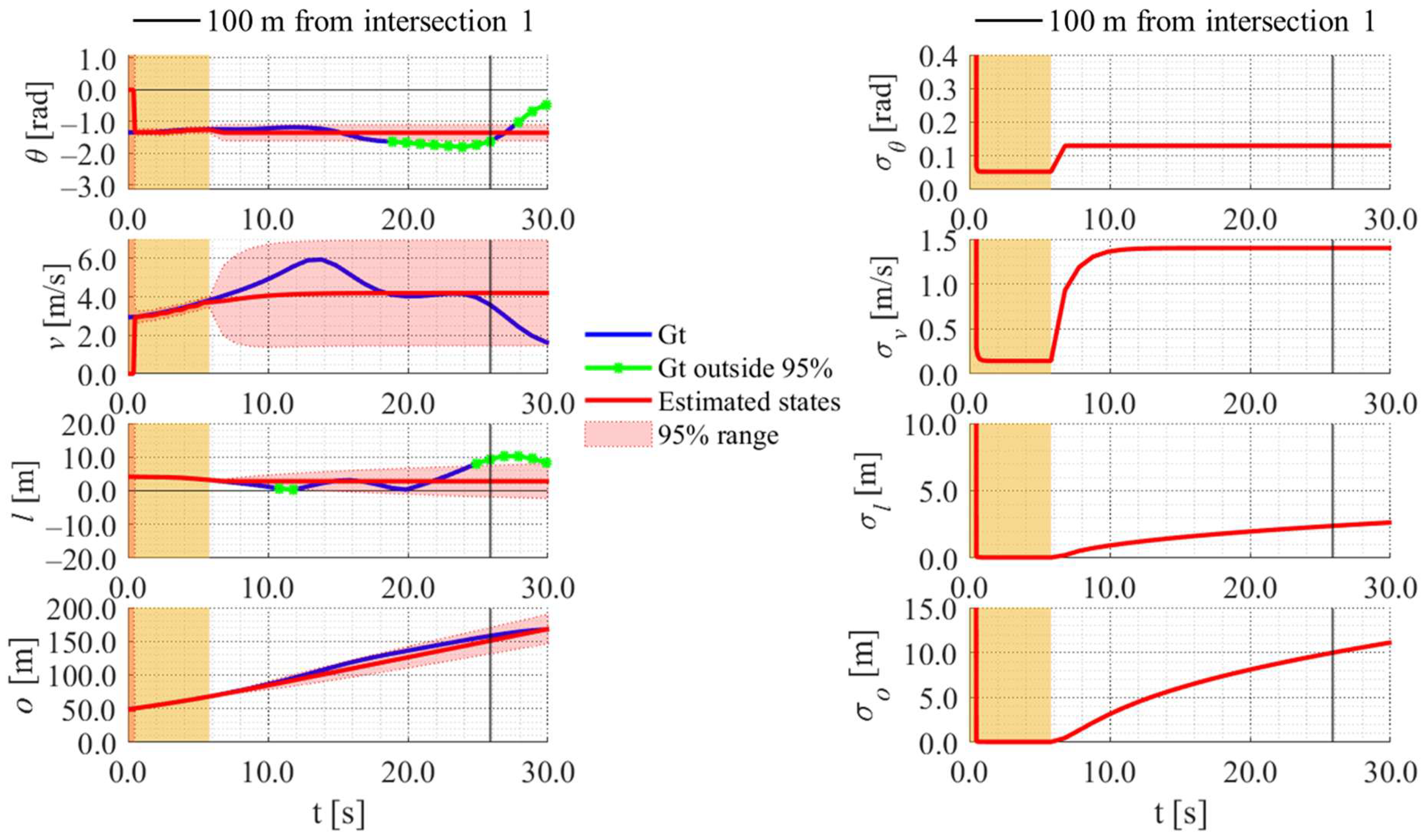
5.4.1. Position Estimation Results for Representative Cases
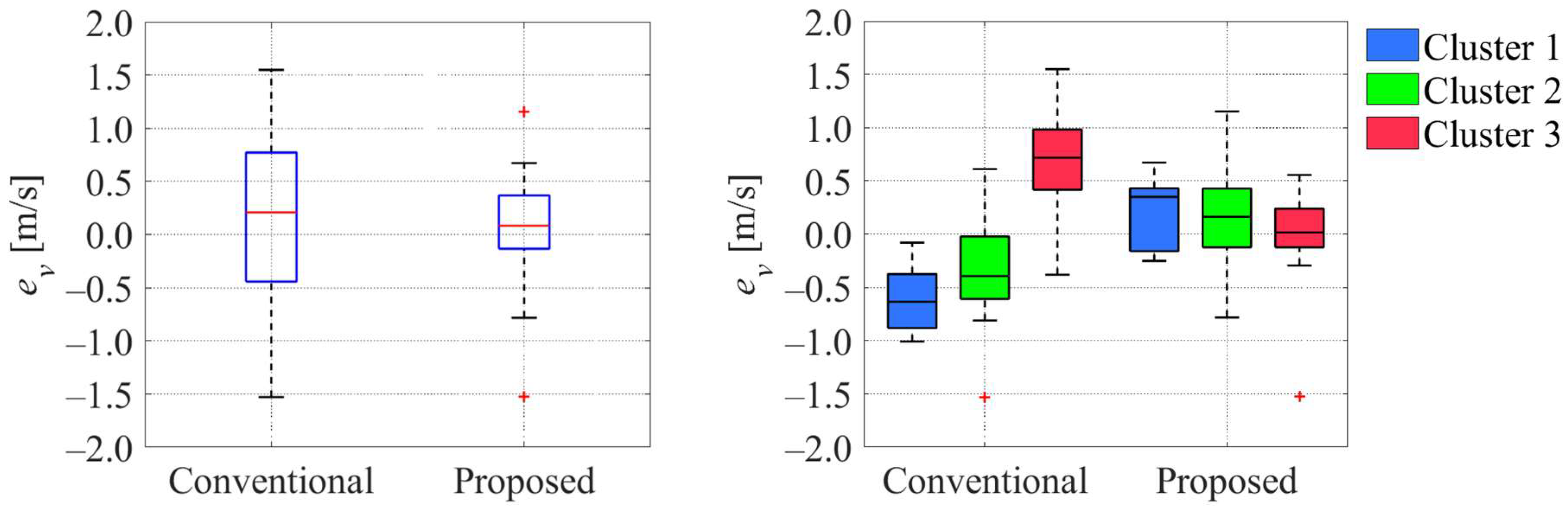
5.4.2. Evaluation Results for All Cases
5.4.3. Discussion
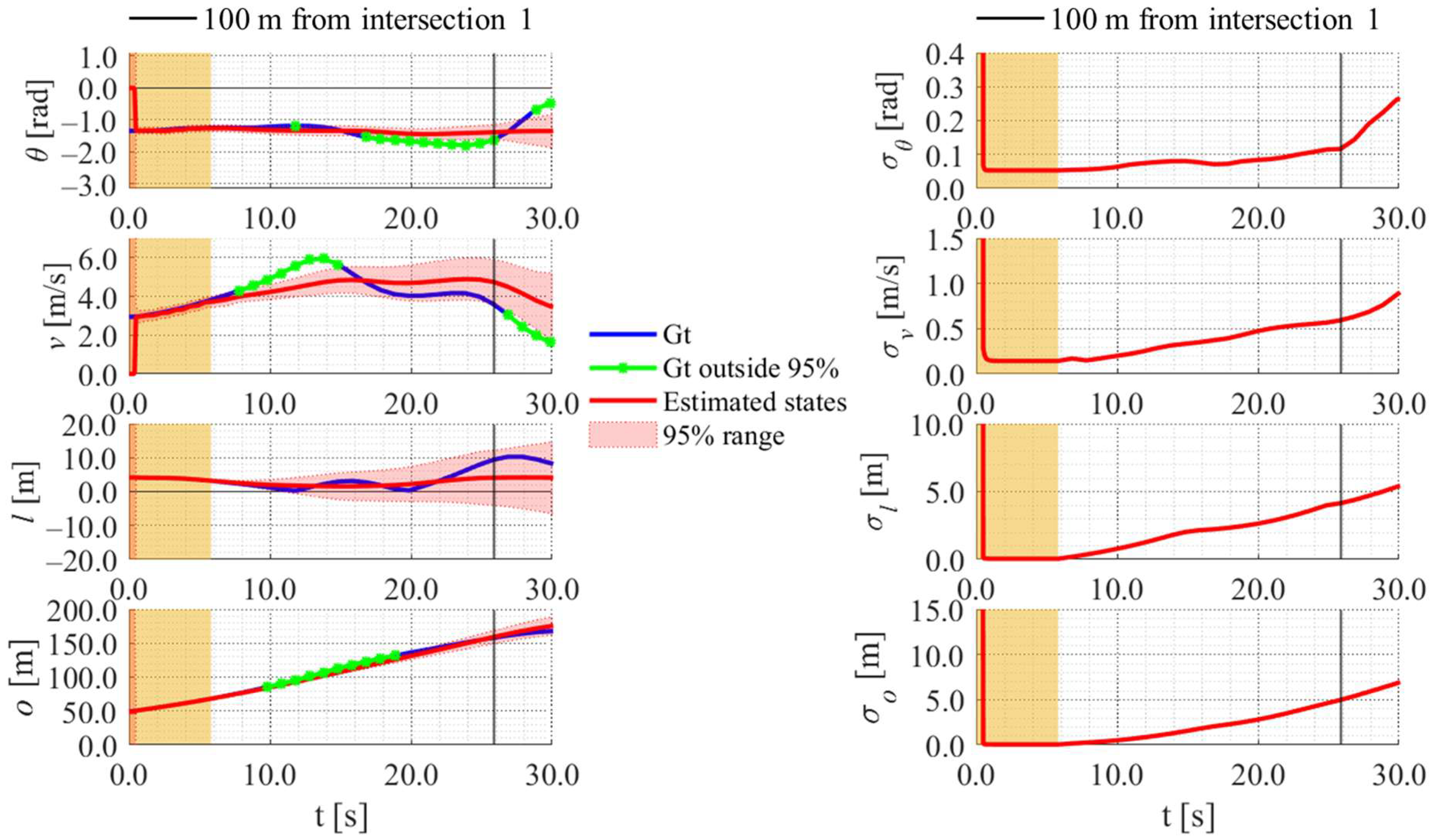
5.5. Position Estimation Results with Miss Classification
5.6. Limitations and Future Prospects
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GNSS | Global navigation satellite system |
| VRU | Vulnerable road user |
| ADAS | Advanced driver-assistance system |
| LDSI | Location-dependent statistical information |
| RSU | Roadside unit |
| V2P | Vehicle to pedestrian |
| V2I | Vehicle to infrastructure |
| P2I | Pedestrian to infrastructure |
| ML | Machine learning |
| LSTM | Long short-term memory |
| EKF | Extended Kalman filter |
| RNN | Recurrent neural network |
| NN | Neural network |
| LD | Lateral deviation |
| SWLDSI | Stochastically weighted location-dependent statistical information |
Appendix A
References
- Cabinet Office. White Paper on Traffic Safety in Japan 2023. Available online: https://www8.cao.go.jp/koutu/taisaku/r05kou_haku/english/pdf/wp2023.pdf (accessed on 29 January 2025).
- Cabinet Office. White Paper on Traffic Safety in Japan 2021. Available online: https://www8.cao.go.jp/koutu/taisaku/r03kou_haku/english/pdf/wp2021-1.pdf (accessed on 7 January 2025).
- National Police Agency. Annual Report by Traffic Accidents 2024 Trends in Traffic Accidents Involving Pedal Cyclist (Primary or Secondary Party) by Type of Accident. Available online: https://www.npa.go.jp/publications/statistics/koutsuu/toukeihyo_e.html (accessed on 2 July 2025).
- European Road Safety Observatory. European Commission (2024) Facts and Figures Cyclists. Available online: https://road-safety.transport.ec.europa.eu/document/download/5efc920c-99be-4870-9e4a-8f9c3029f9cb_en?filename=ff_cyclists_14082024.pdf (accessed on 28 July 2025).
- Zhang, G.; Tan, Y.; Jou, R.-C. Factors influencing traffic signal violations by car drivers, cyclists, and pedestrians: A case study from Guangdong, China. Transp. Res. Part F Traffic Psychol. Behav. 2016, 42, 205–216. [Google Scholar] [CrossRef]
- Ito, T. Connected Collision Avoidance System via Stochastic Localization on Community Roads. Int. J. Automot. Eng. 2025, 16, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, K.; Watanabe, K.; Yang, J.; Ito, T. Virtual Observation Using Statistical Information of Cyclist’s Velocity for Estimation of Position and Uncertainty. Int. J. Automot. Eng. 2025, 16, 54–65. [Google Scholar] [CrossRef] [PubMed]
- Bo Bo, N.; Slembrouck, M.; Veelaert, P.; Philips, W. Distributed Multi-Class Road User Tracking in Multi Camera Network for Smart Traffic Applications. Adv. Concepts Intell. Vis. Syst. 2020, 12002, 517–528. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, W.; Coifman, B.; Mills, J.P. Vehicle Tracking and Speed Estimation From Roadside Lidar. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5597–5608. [Google Scholar] [CrossRef]
- Zhang, R.; Zou, Z.; Shen, S.; Liu, H.X. Design, Implementation, and Evaluation of a Roadside Cooperative Perception System. Transp. Res. Rec. 2022, 2676, 273–284. [Google Scholar] [CrossRef]
- Sugimoto, C.; Nakamura, Y.; Hashimoto, T. Prototype of pedestrian-to-vehicle communication system for the prevention of pedestrian accidents using both 3G wireless and WLAN communication. In Proceedings of the 2008 3rd International Symposium on Wireless Pervasive Computing, Santorini, Greece, 7–9 May 2008; pp. 764–767. [Google Scholar] [CrossRef]
- Liu, W.; Muramatsu, S.; Okubo, Y. Cooperation of V2I/P2I Communication and Roadside Radar Perception for the Safety of Vulnerable Road Users. In Proceedings of the 2018 16th International Conference on Intelligent Transportation Systems Telecommunications (ITST), Lisboa, Portugal, 15–17 October 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Hussein, A.; García, F.; Armingol, J.M.; Olaverri-Monreal, C. P2V and V2P communication for Pedestrian warning on the basis of Autonomous Vehicles. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 2034–2039. [Google Scholar] [CrossRef]
- Li, P.; Guo, H.; Bao, S.; Kusari, A. A Probabilistic Framework for Estimating the Risk of Pedestrian Vehicle Conflicts at Intersections. IEEE Trans. Intell. Transp. Syst. 2023, 24, 14111–14120. [Google Scholar] [CrossRef]
- Zhou, S.; Xu, H.; Zhang, G.; Ma, T.; Yang, Y. Deep learning based pedestrian trajectory prediction and risk assessment at signalized intersections using trajectory data captured through roadside LiDAR. J. Intell. Transp. Syst. 2023, 28, 793–805. [Google Scholar] [CrossRef]
- Deo, N.; Trivedi, M.M. Convolutional Social Pooling for Vehicle Trajectory Prediction. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 1549–15498. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J.; Fang, L.; Jiang, Q.; Zhou, B. Multimodal Motion Prediction with Stacked Transformers. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 7573–7582. [Google Scholar] [CrossRef]
- Boulkroune, B.; Geebelen, K.; Wan, J.; van Nunen, E. Auto-tuning extended Kalman filters to improve state estimation. In Proceedings of the 2023 IEEE Intelligent Vehicles Symposium (IV), Anchorage, AK, USA, 4–7 June 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Jouaber, S.; Bonnabel, S.; Velasco-Forero, S.; Pilté, M. NNAKF: A Neural Network Adapted Kalman Filter for Target Tracking. In Proceedings of the ICASSP 2021—2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 4075–4079. [Google Scholar] [CrossRef]
- Jeong, Y.; Yi, K. Target Vehicle Motion Prediction-Based Motion Planning Framework for Autonomous Driving in Uncontrolled Intersections. IEEE Trans. Intell. Transp. Syst. 2021, 22, 168–177. [Google Scholar] [CrossRef]
- Yi, D.; Su, J.; Liu, C.; Chen, W.-H. Trajectory Clustering Aided Personalized Driver Intention Prediction for Intelligent Vehicles. Trans. Ind. Inform. 2019, 15, 3693–3702. [Google Scholar] [CrossRef]
- Tahk, M.; Speyer, J.L. Target tracking problems subject to kinematic constraints. IEEE Trans. Autom. Control. 1990, 35, 324–326. [Google Scholar] [CrossRef]
- Alouani, A.T.; Blair, W.D. Use of a kinematic constraint in tracking constant speed, maneuvering targets. IEEE Trans. Autom. Control. 1993, 38, 1107–1111. [Google Scholar] [CrossRef]
- Zhou, G.; Li, K.; Kirubarajan, T.; Xu, L. State Estimation With Trajectory Shape Constraints Using Pseudomeasurements. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 2395–2407. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, K.; Zhou, G. State Estimation with Heading Constraints for on-Road Vehicle Tracking. IEEE Trans. Intell. Transp. Syst. 2022, 23, 13614–13635. [Google Scholar] [CrossRef]
- Vargas-Meléndez, L.; Boada, B.L.; Boada, M.J.L.; Gauchía, A.; Díaz, V. A Sensor Fusion Method Based on an Integrated Neural Network and Kalman Filter for Vehicle Roll Angle Estimation. Sensors 2016, 16, 1400. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Kim, G.; Choi, S.; Huh, K. An Integrated Deep Ensemble-Unscented Kalman Filter for Sideslip Angle Estimation with Sensor Filtering Network. IEEE Access 2021, 9, 149681–149689. [Google Scholar] [CrossRef]
- Jiang, Y.; Nong, X. A Radar Filtering Model for Aerial Surveillance Base on Kalman Filter and Neural Network. In Proceedings of the 2020 IEEE 11th International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 16–18 October 2020; pp. 57–60. [Google Scholar] [CrossRef]
- Ito, T.; Mio, M.; Tohriyama, K.; Kamata, M. Novel Map Platform based on Primitive Elements of Traffic Environments for Automated Driving Technologies. Int. J. Automot. Eng. 2016, 7, 143–151. [Google Scholar] [CrossRef] [PubMed]
- Brown, R.G.; Hwang, P.Y.C. Introduction to Random Signals and Applied Kalman Filtering; John Wiley and Sons: Hoboken, NJ, USA, 2012; pp. 208–209. [Google Scholar]
- Japan Road Association. Explanation and Operation of Government Order on Road Design Standards; Japan Road Association: Tokyo, Japan, 2021; p. 517. (In Japanese) [Google Scholar]
- Japan Society of Traffic Engineers. Road Traffic Technology Handbook 2024; Japan Society of Traffic Engineers: Tokyo, Japan, 2024; p. 44. (In Japanese) [Google Scholar]
- Yuuki, K.; Hideo, Y.; Kensuke, K.; Shunsuke, Y. An analysis on characteristics of cycling behavior by elderly people at slopes and in starting to move. In Proceedings of the 39th Infrastructure Planning Conference, Tokushima, Japan, 13–14 January 2009. (In Japanese). [Google Scholar]
- Givens, C.R.; Shortt, R.M. A class of Wasserstein metrics for probability distributions. Mich. Math. J. 1984, 31, 231–240. [Google Scholar] [CrossRef]
- Kučera, V. The discrete Riccati equation of optimal control. Kybernetika 1972, 8, 430–447. [Google Scholar]
- Geospatial Information Authority of Japan. GSI Maps. Available online: https://maps.gsi.go.jp/ (accessed on 13 July 2025).
- Geospatial Information Authority of Japan. The Aerial Photograph by Geospatial Information Authority of Japan; Geospatial Information Authority of Japan: Ibaraki, Japan, 2019. [Google Scholar]
- Eom, S.; Kim, H.; Hasegawa, D.; Yamada, I. Pedestrian movement with large-scale GPS records and transit-oriented development attributes. Sustain. Cities Soc. 2024, 102, 105223. [Google Scholar] [CrossRef]





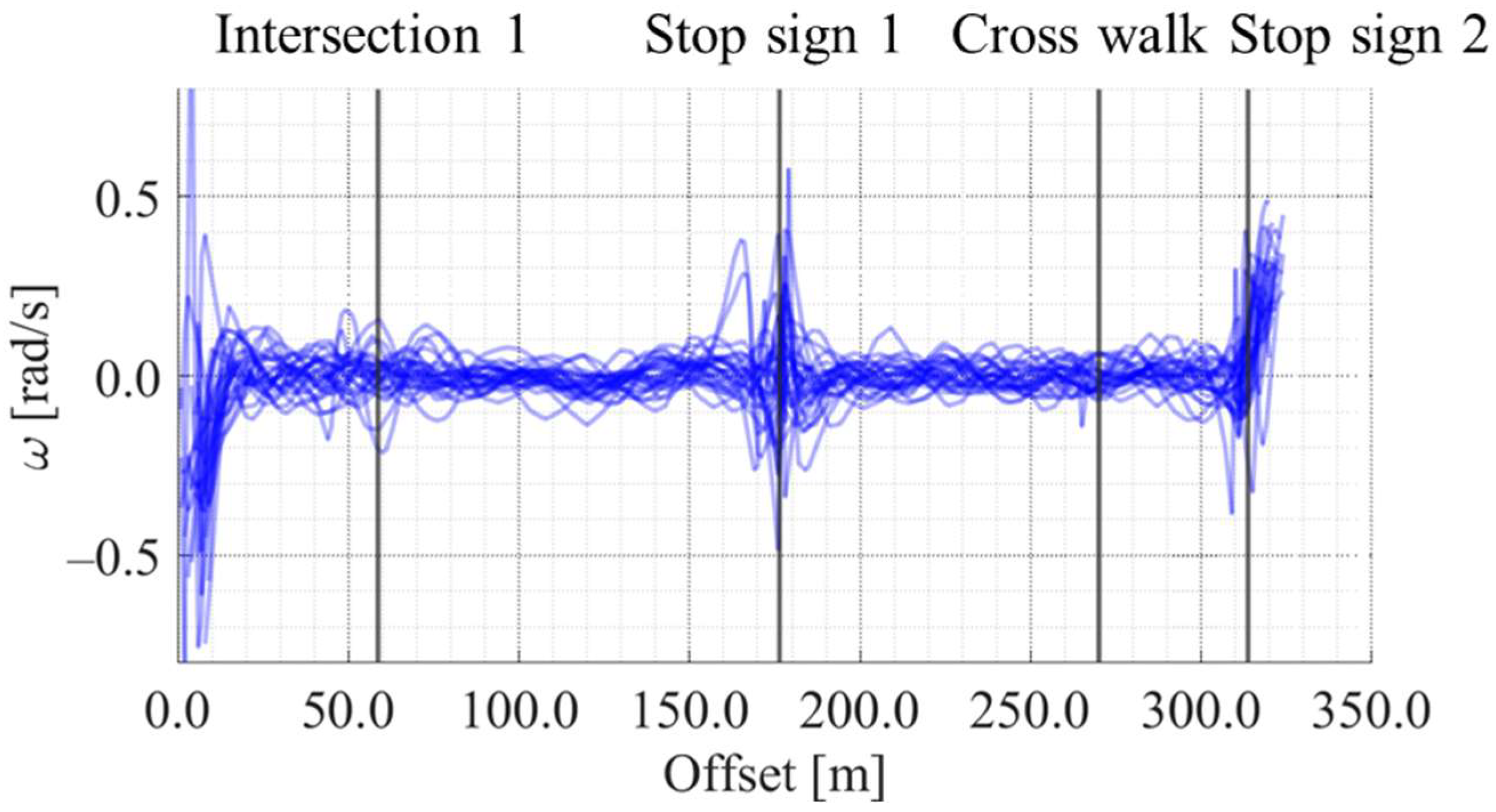
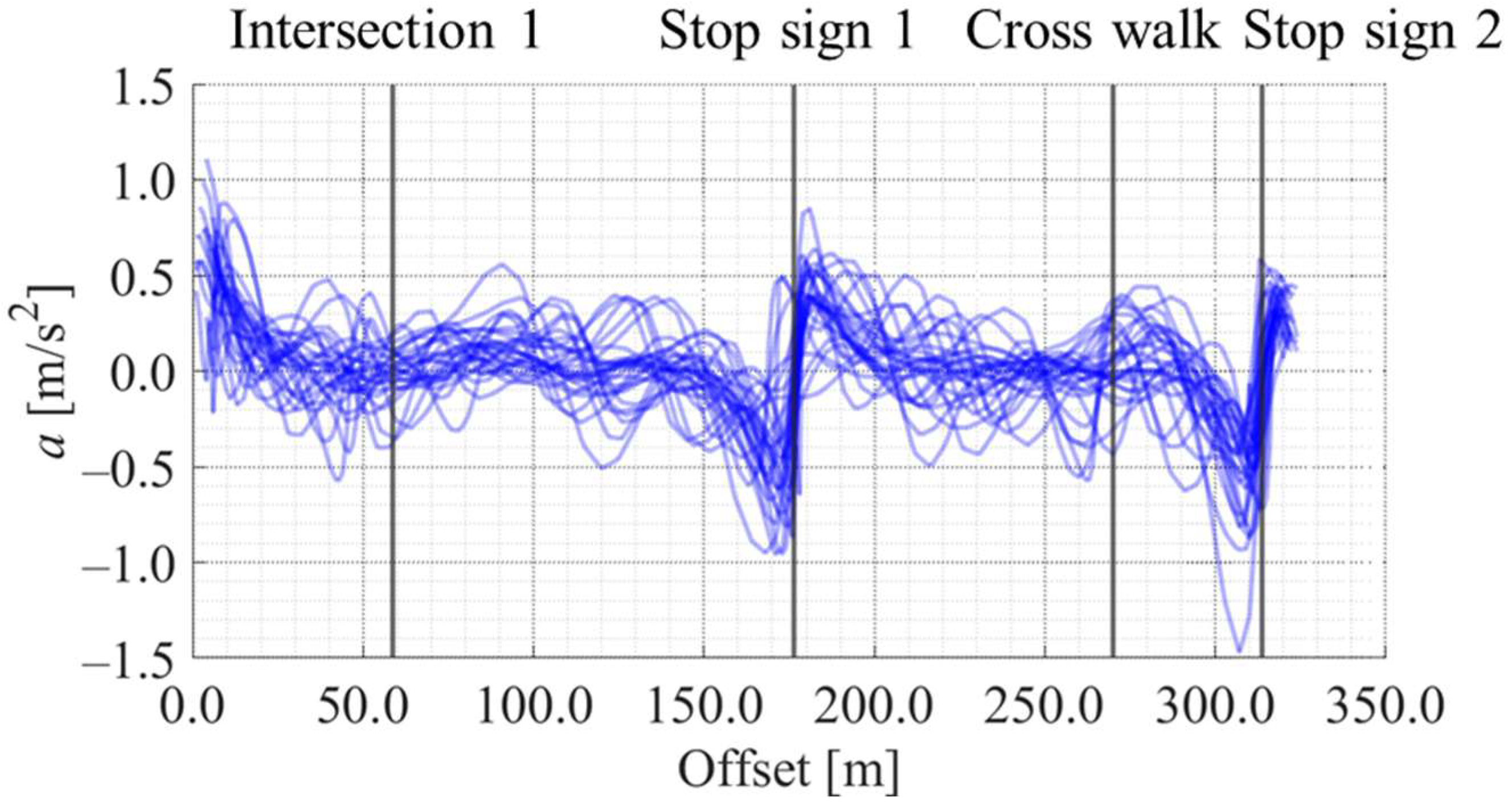
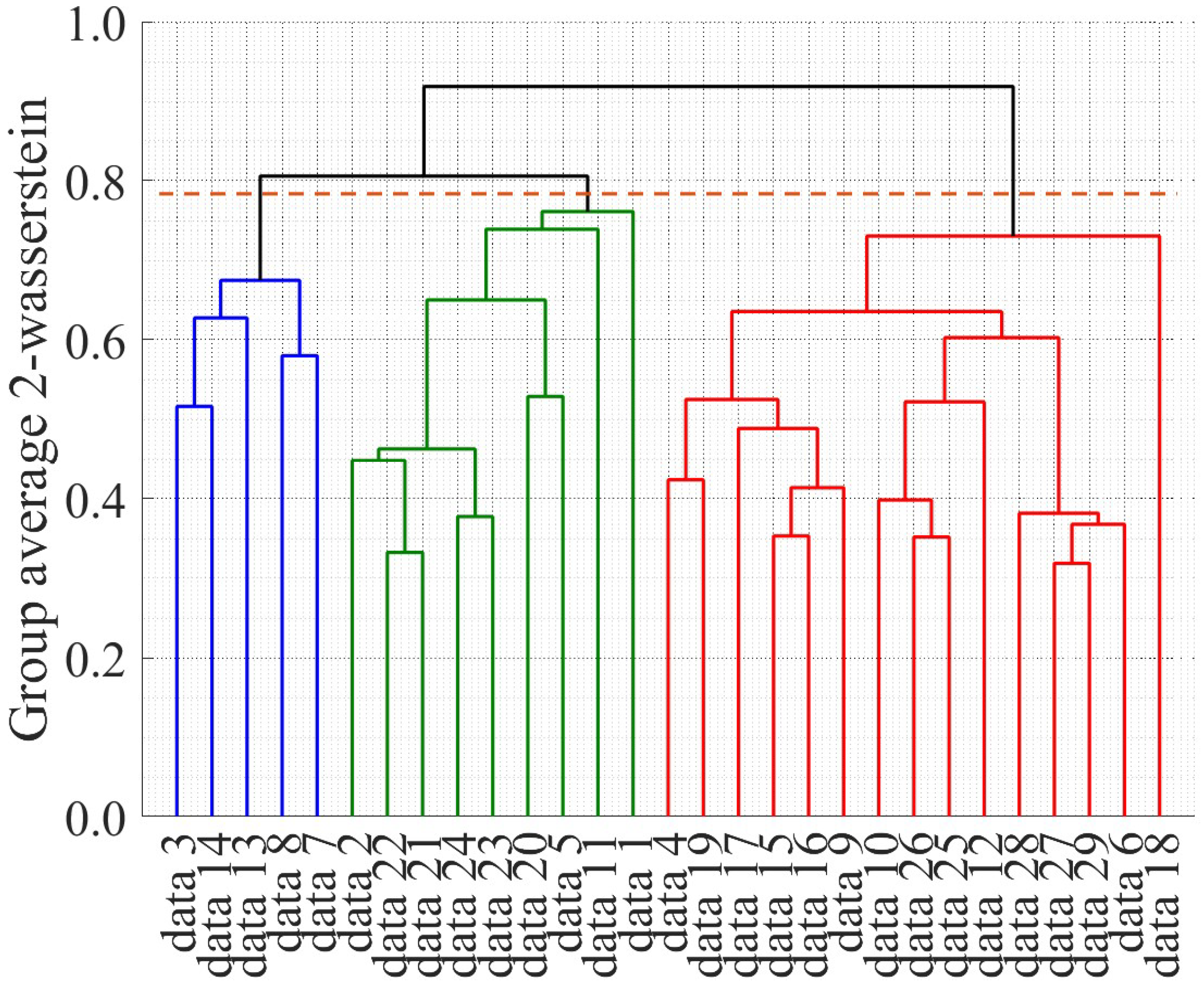
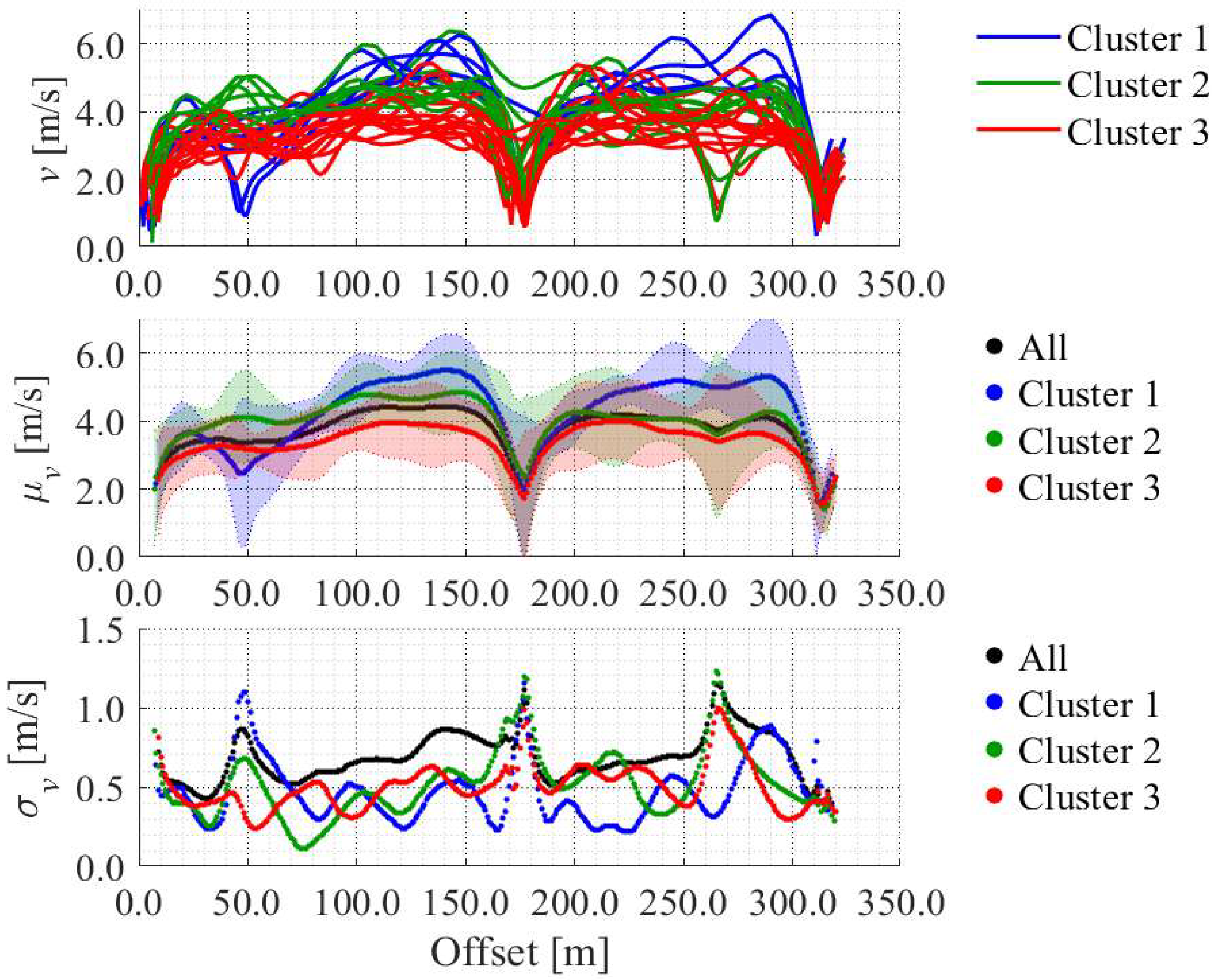
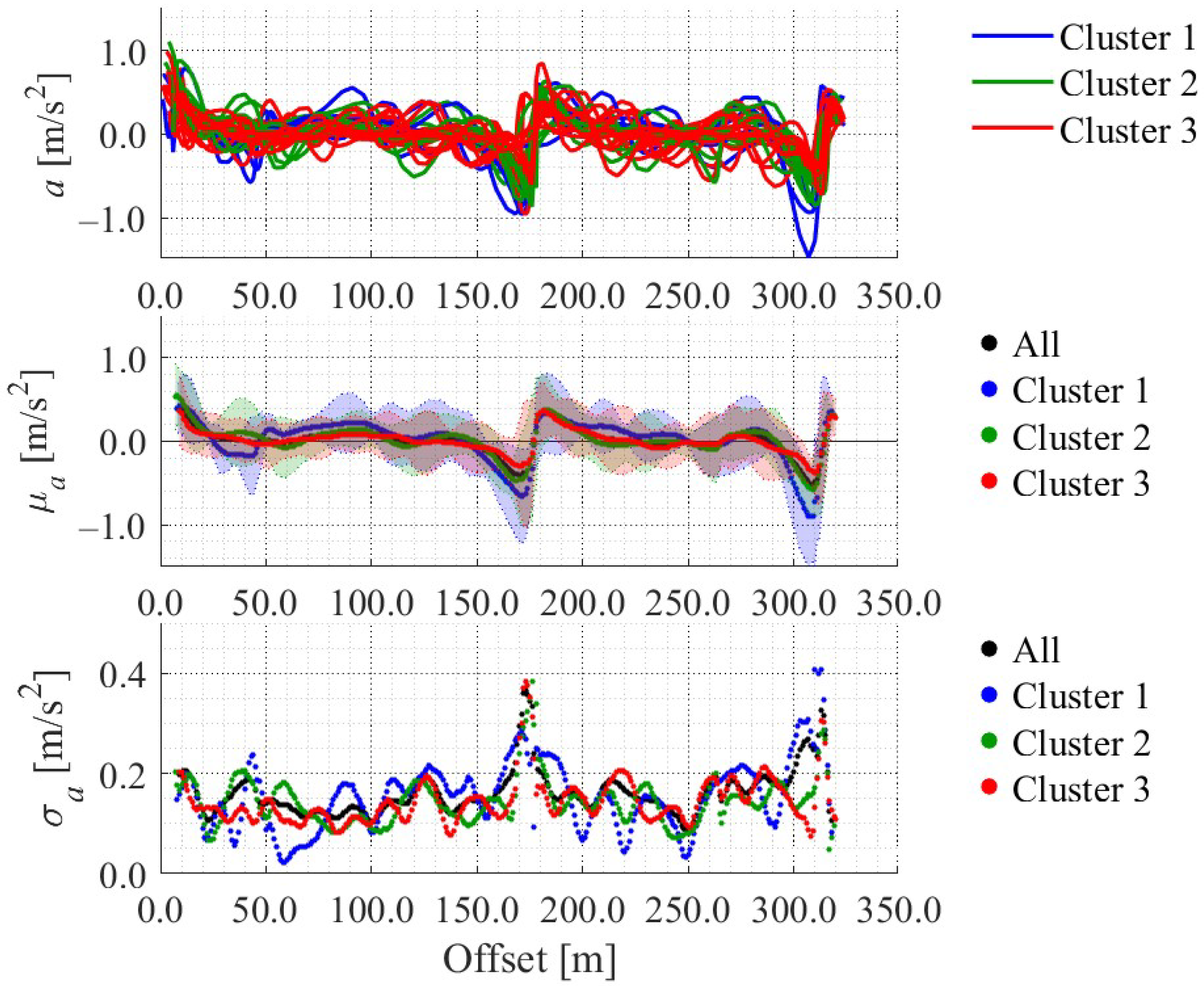
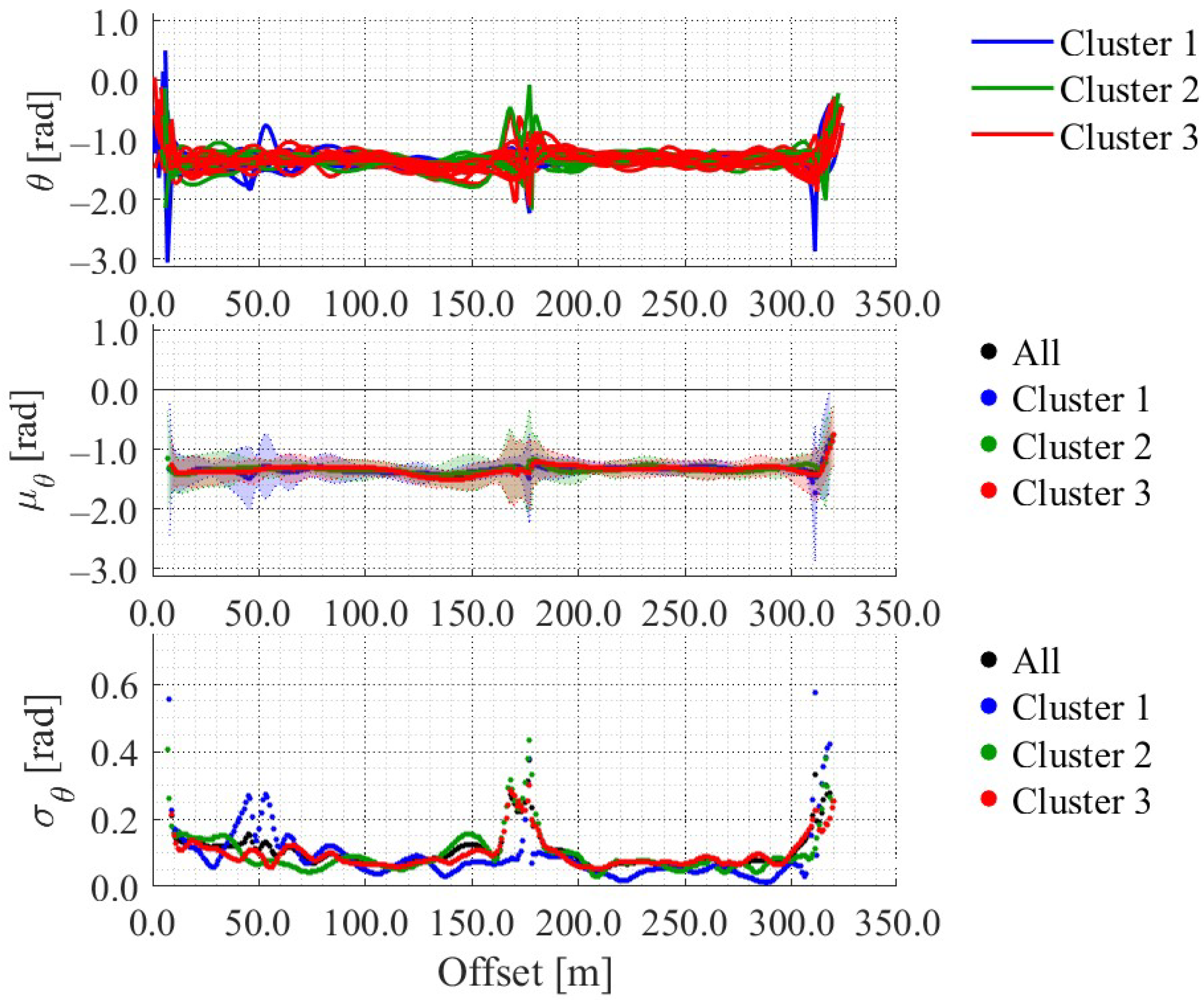

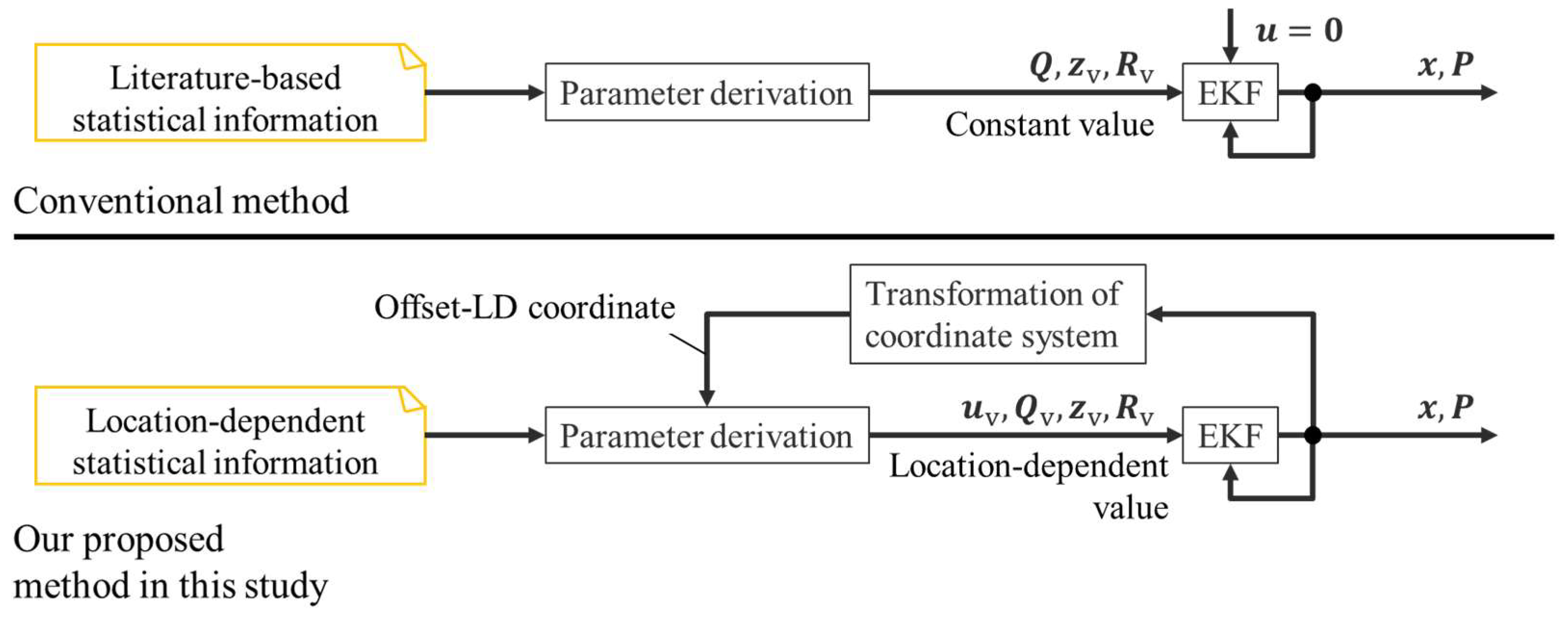
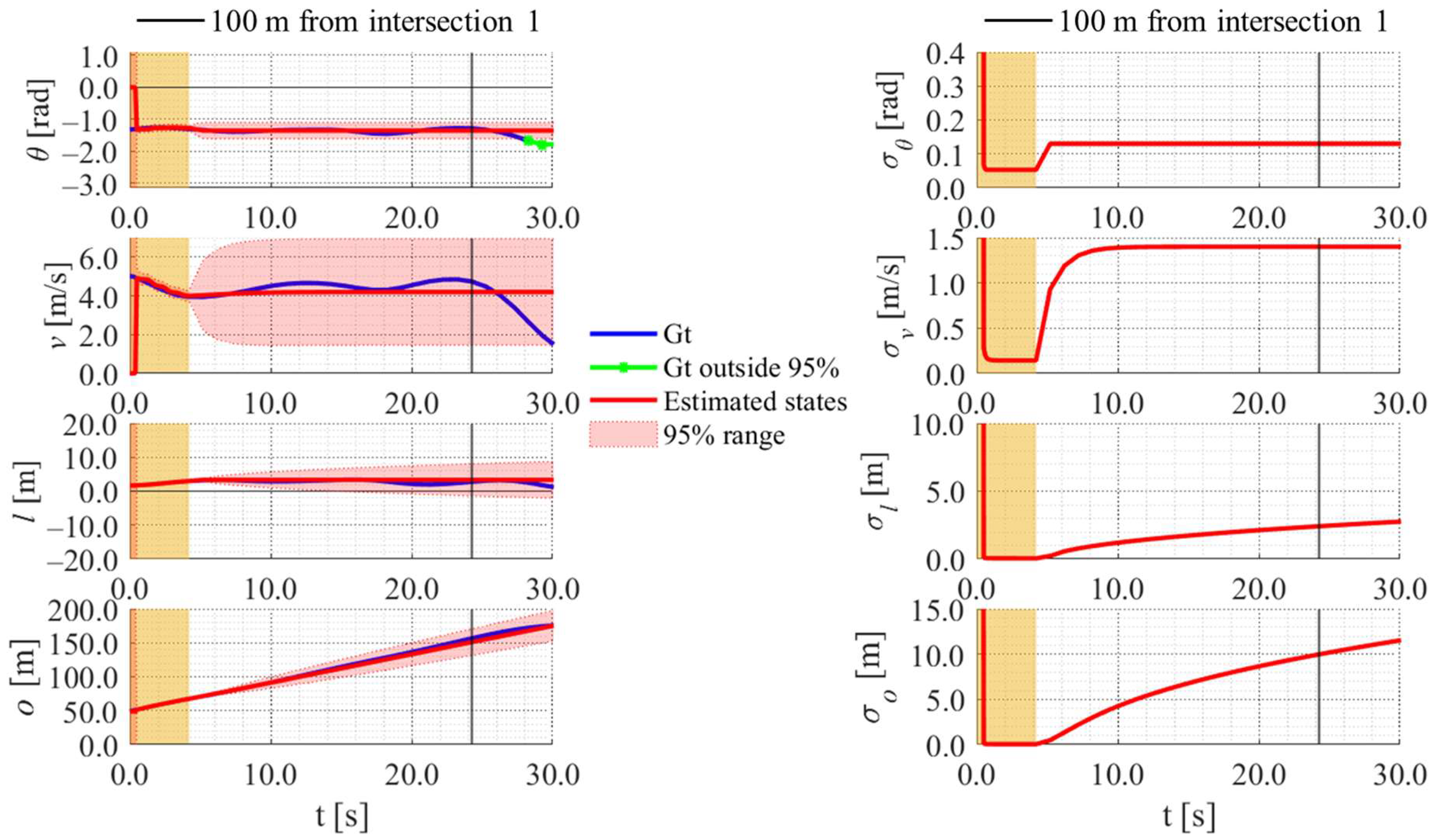
| Methods | All Data (29 Data) | Cluster 1 (5 Data) | Cluster 2 (9 Data) | Cluster 3 (15 Data) |
|---|---|---|---|---|
| Conventional | 1.00 | 1.00 | 1.00 | 1.00 |
| Proposed | 0.93 | 0.90 | 0.92 | 0.94 |
| Methods | All Data (29 Data) | Cluster 1 (5 Data) | Cluster 2 (9 Data) | Cluster 3 (15 Data) |
|---|---|---|---|---|
| Conventional | 0.97 | 1.00 | 1.00 | 0.95 |
| Proposed | 0.91 | 0.77 | 0.93 | 0.93 |
| GT Cluster | Cluster 1 (5 Data) | Cluster 2 (9 Data) | Cluster 3 (15 Data) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Classified Cluster | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |
| Correct | Wrong | Wrong | Wrong | Correct | Wrong | Wrong | Wrong | Correct | ||
| Average ratio within the confidence interval | Velocity | 0.90 | 0.72 | 0.37 | 0.61 | 0.92 | 0.89 | 0.40 | 0.46 | 0.94 |
| Offset | 0.77 | 0.65 | 0.36 | 0.54 | 0.93 | 0.82 | 0.24 | 0.15 | 0.93 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suzuki, K.; Ito, T. Virtual Observation Using Location-Dependent Statistical Information of Cyclists’ Movement for Estimation of Position and Uncertainty. Sensors 2025, 25, 5122. https://doi.org/10.3390/s25165122
Suzuki K, Ito T. Virtual Observation Using Location-Dependent Statistical Information of Cyclists’ Movement for Estimation of Position and Uncertainty. Sensors. 2025; 25(16):5122. https://doi.org/10.3390/s25165122
Chicago/Turabian StyleSuzuki, Kento, and Takuma Ito. 2025. "Virtual Observation Using Location-Dependent Statistical Information of Cyclists’ Movement for Estimation of Position and Uncertainty" Sensors 25, no. 16: 5122. https://doi.org/10.3390/s25165122
APA StyleSuzuki, K., & Ito, T. (2025). Virtual Observation Using Location-Dependent Statistical Information of Cyclists’ Movement for Estimation of Position and Uncertainty. Sensors, 25(16), 5122. https://doi.org/10.3390/s25165122





