Dynamic Calibration of Quartz Flexure Accelerometers
Abstract
Highlights
- A dynamic calibration model is developed based on a mechanistic analysis of quartz flexure accelerometers.
- A dynamic calibration method is designed utilizing a dual-axis precision centrifuge in conjunction with the dynamic model.
- The magnitude of dynamic measurement errors is significantly reduced by the proposed dynamic error model.
- The calibration of the dynamic parameter yields a relative standard deviation of −0.048%.
Abstract
1. Introduction
- is the sensor output (output unit);
- is the indicated sensor output (m/s2);
- is the bias (m/s2);
- is the scale factor [output units/(m/s2)];
- is the second-order coefficient [(m/s2)/(m/s2)2];
- is the third-order coefficient [(m/s2)/(m/s2)];
- are the cross-coupling coefficients [(m/s2)/(m/s2)];
- is the acceleration along sensor IA (m/s2);
- is the acceleration along sensor pendulous axis (PA) (m/s2);
- is the acceleration along sensor output axis (OA) (m/s2);
- is the misalignment angle between IA and case reference IA about OA (rad);
- is the misalignment angle between IA and case reference IA about PA (rad).
- Compared to precision vibration tables, they offer higher accuracy and independent control of excitation amplitude and frequency.
- Compared to precision turntables, they enable a wider adjustable acceleration range, allowing for enhanced calibration precision.
- Compared to Hopkinson bars, they provide better repeatability and consistency due to their mechanical stability and programmable control.
2. Accelerometer Error Model Incorporating Dynamic Terms
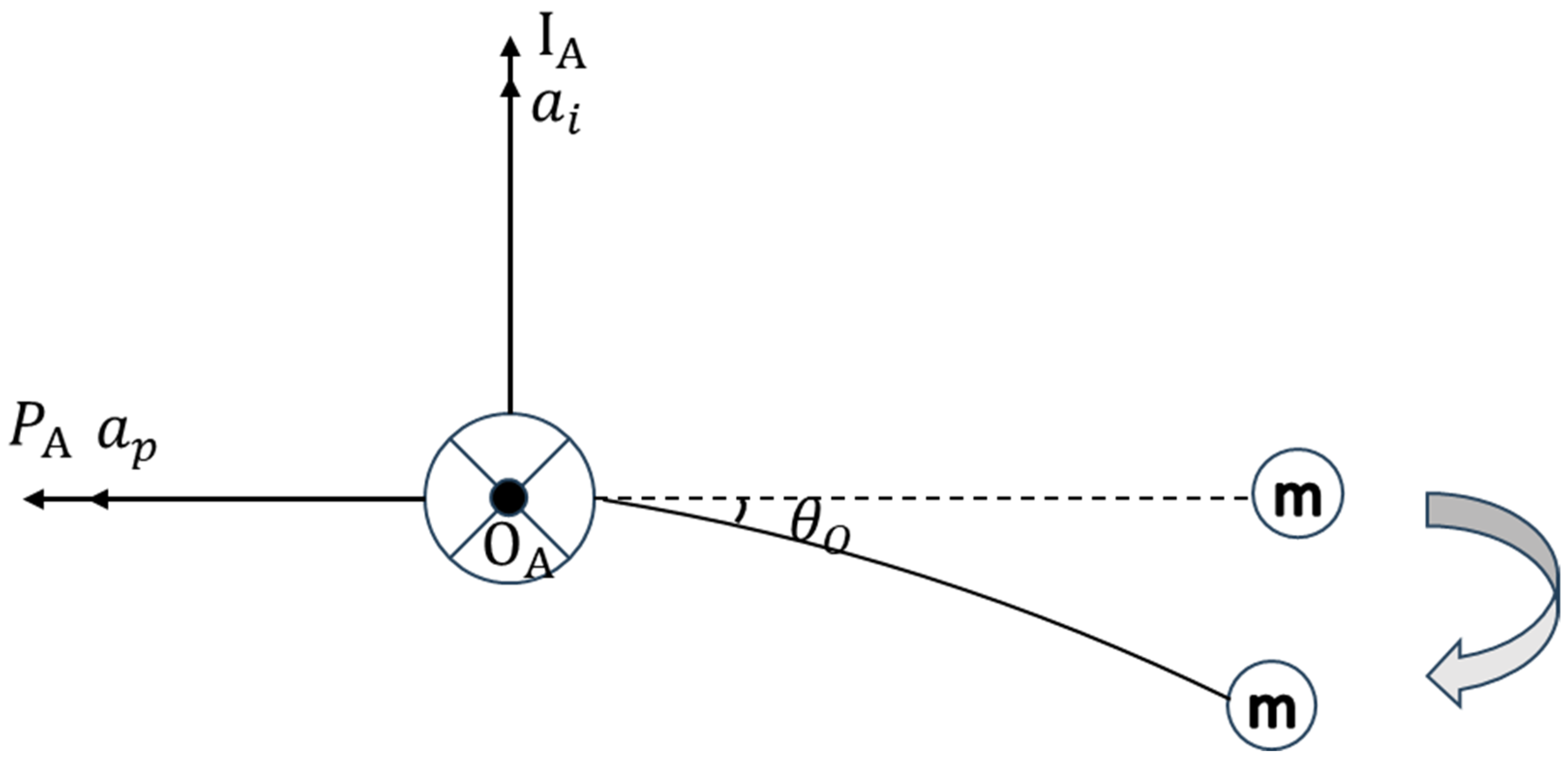
2.1. Mechanistic Modeling of Quartz Flexure Accelerometers
2.2. Analysis of Dynamic Response Characteristics
2.3. Development of a Calibration Model Incorporating Dynamic Terms
- is accelerometer output (output units);
- is the indicated sensor output (m/s2);
- is the scale factor [output units/(m/s2)];
- is random noise (m/s2);
- is the bias (m/s2);
- is the dynamic compensation coefficient (s);
- is the acceleration along sensor IA (m/s2);
- is the time derivative of acceleration along sensor IA (m/s3).
3. Performance Analysis of the Dynamic Model
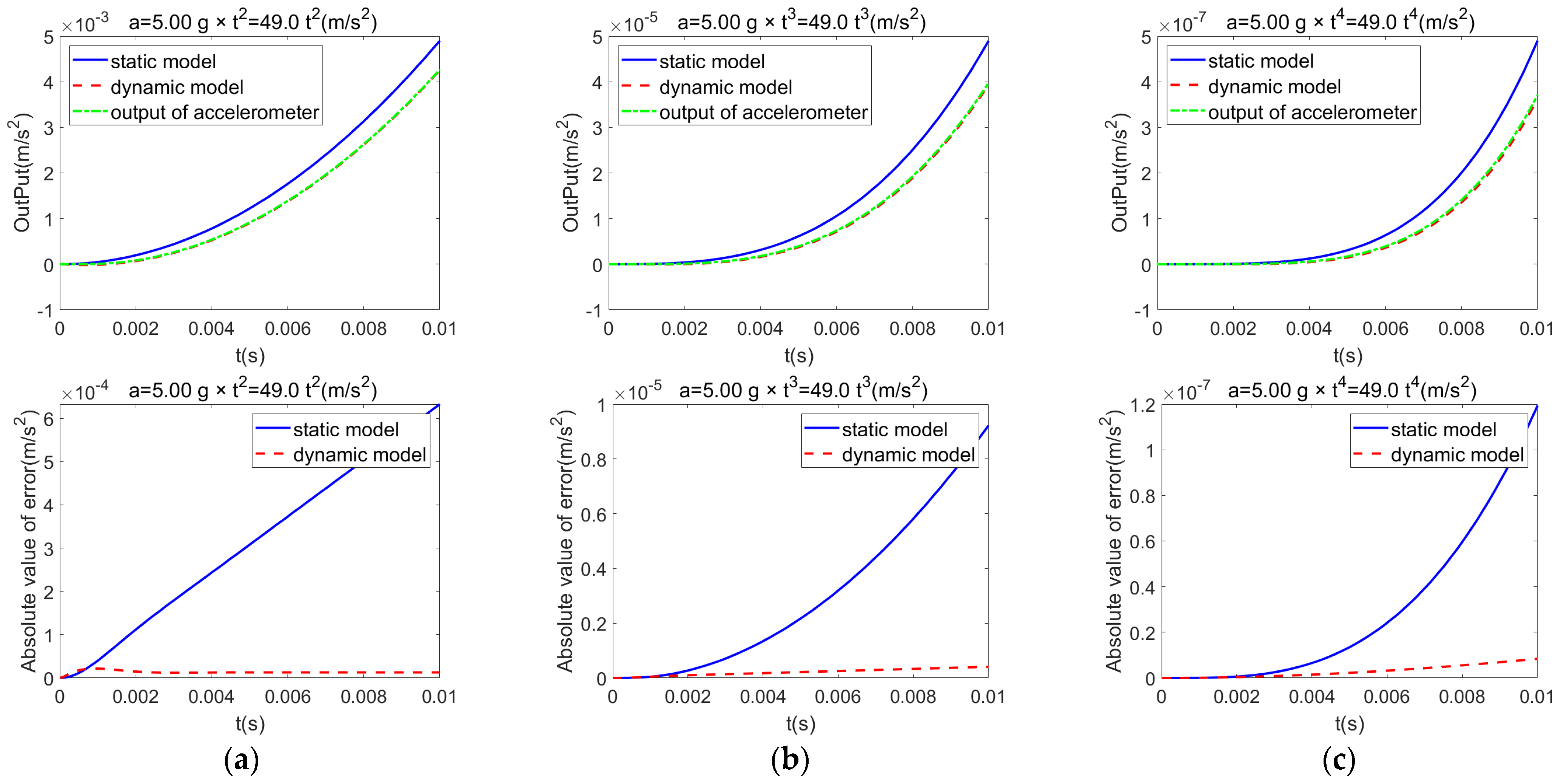
3.1. Analysis of Accelerometer Model Output
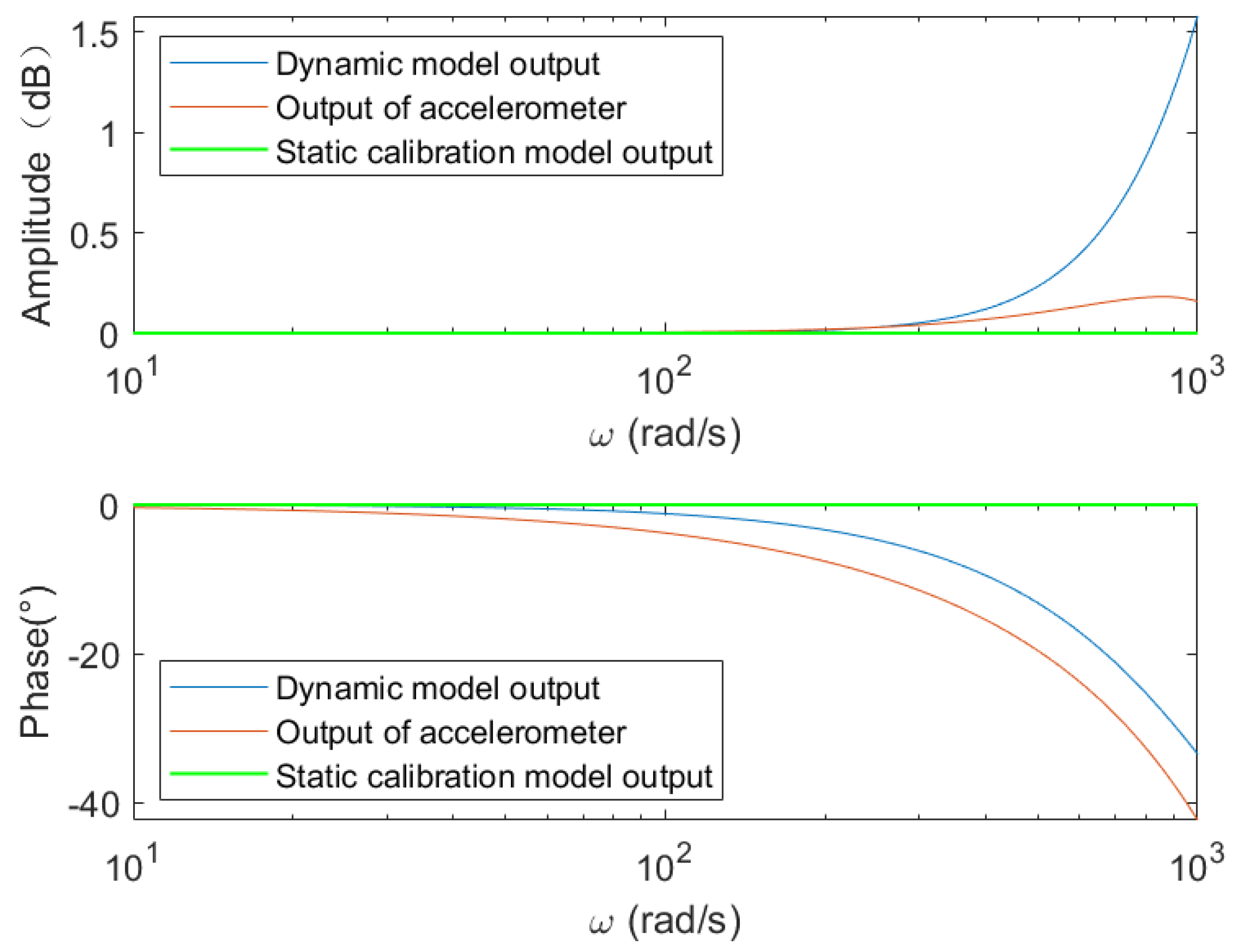
3.2. Dynamic Model Output Analysis
3.3. Model Performance Assessment
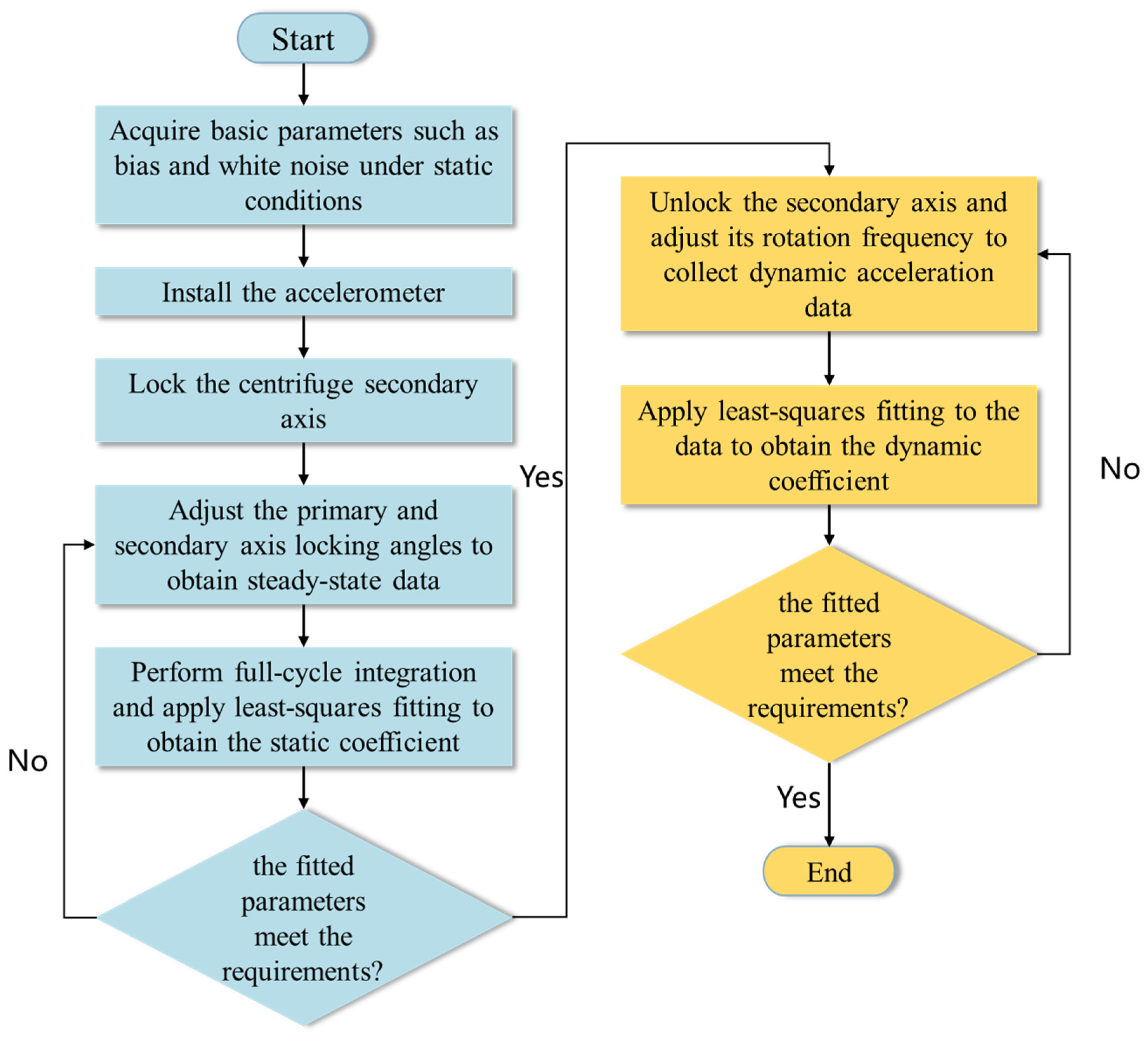
4. Design of Calibration Method
4.1. Error Source Analysis and Coordinate Transformation
- where:
4.2. Specific Force Input
4.2.1. Gravitational Acceleration Components on Each Axis
4.2.2. Components of Centripetal and Tangential Acceleration in the Accelerometer Coordinate Axes
4.2.3. Coriolis Acceleration Components Along the Three Axes of the Accelerometer Coordinate System
4.2.4. Composite Specific Force
4.3. Calibration Method Design
Error Calibration Model Development
5. Simulation Verification and Evaluation
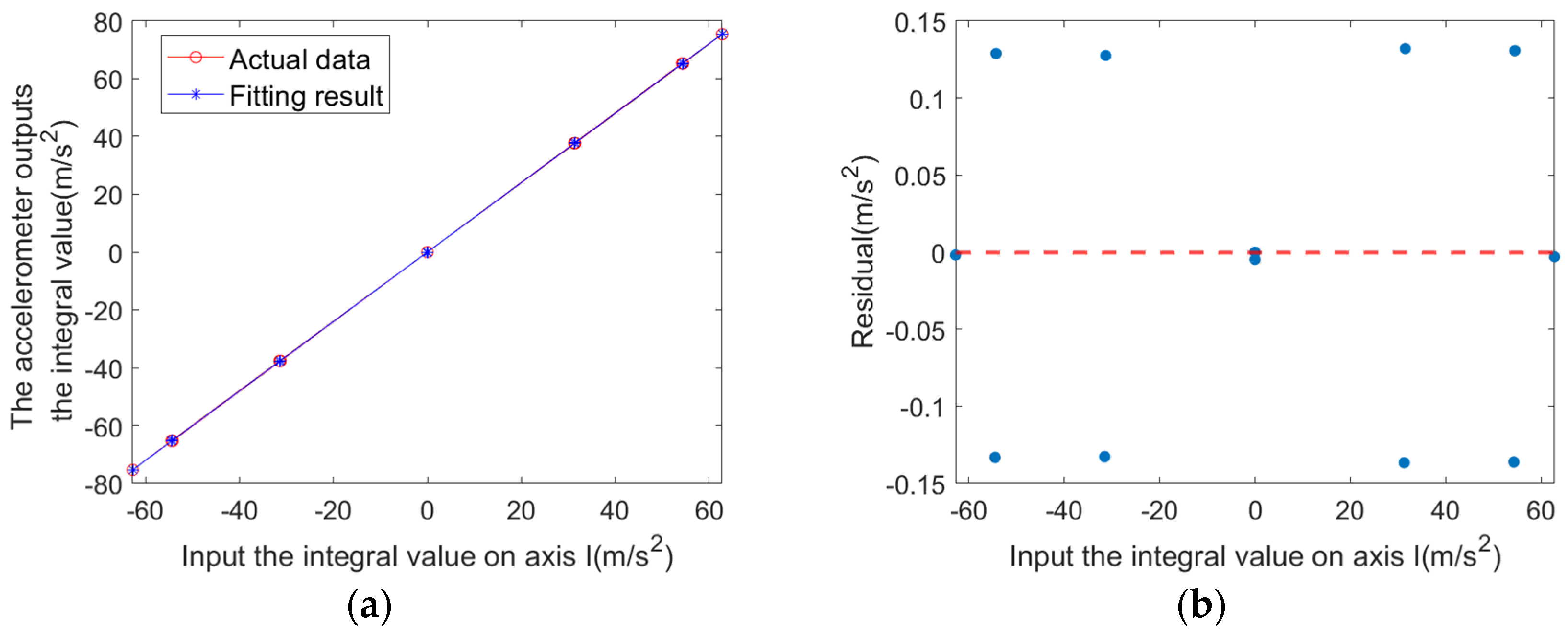
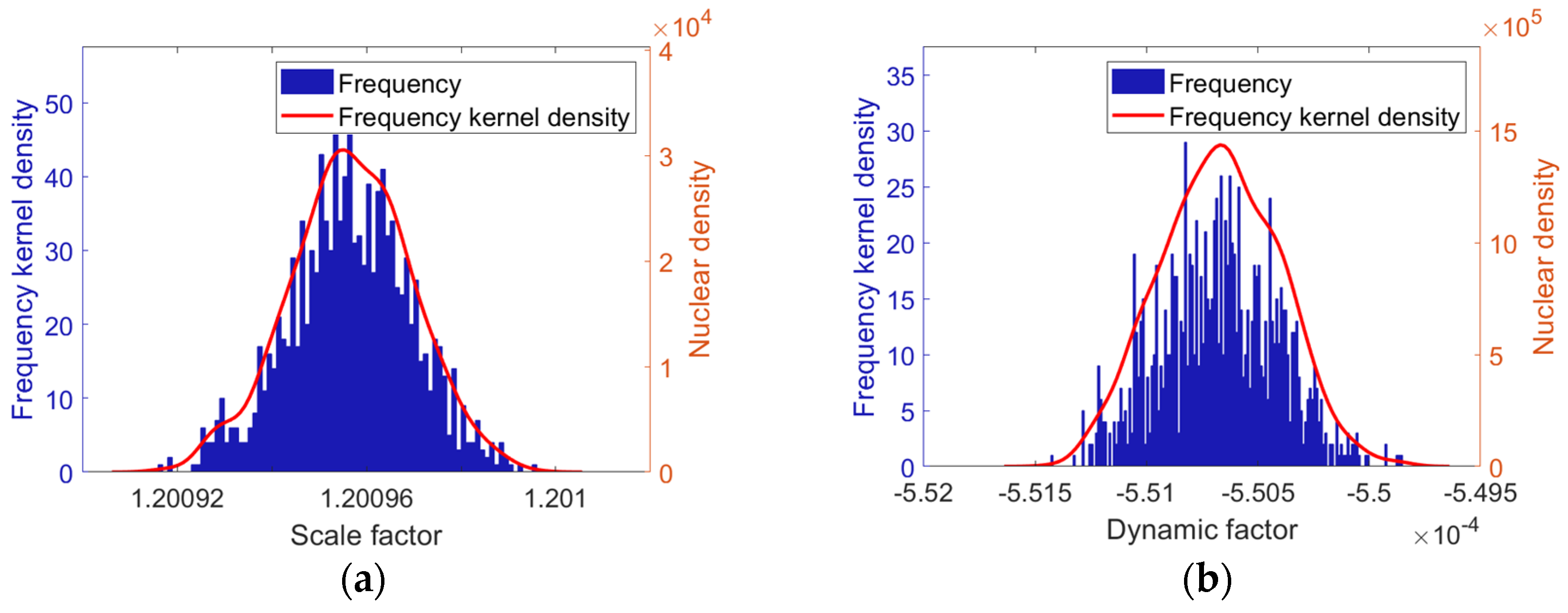
5.1. Single Static Test
- Scale factor: ;
- Mean squared error: ;
- Root mean squared error: ;
- Coefficient of determination: ;
- 95% confidence interval: [1.199332, 1.202562].
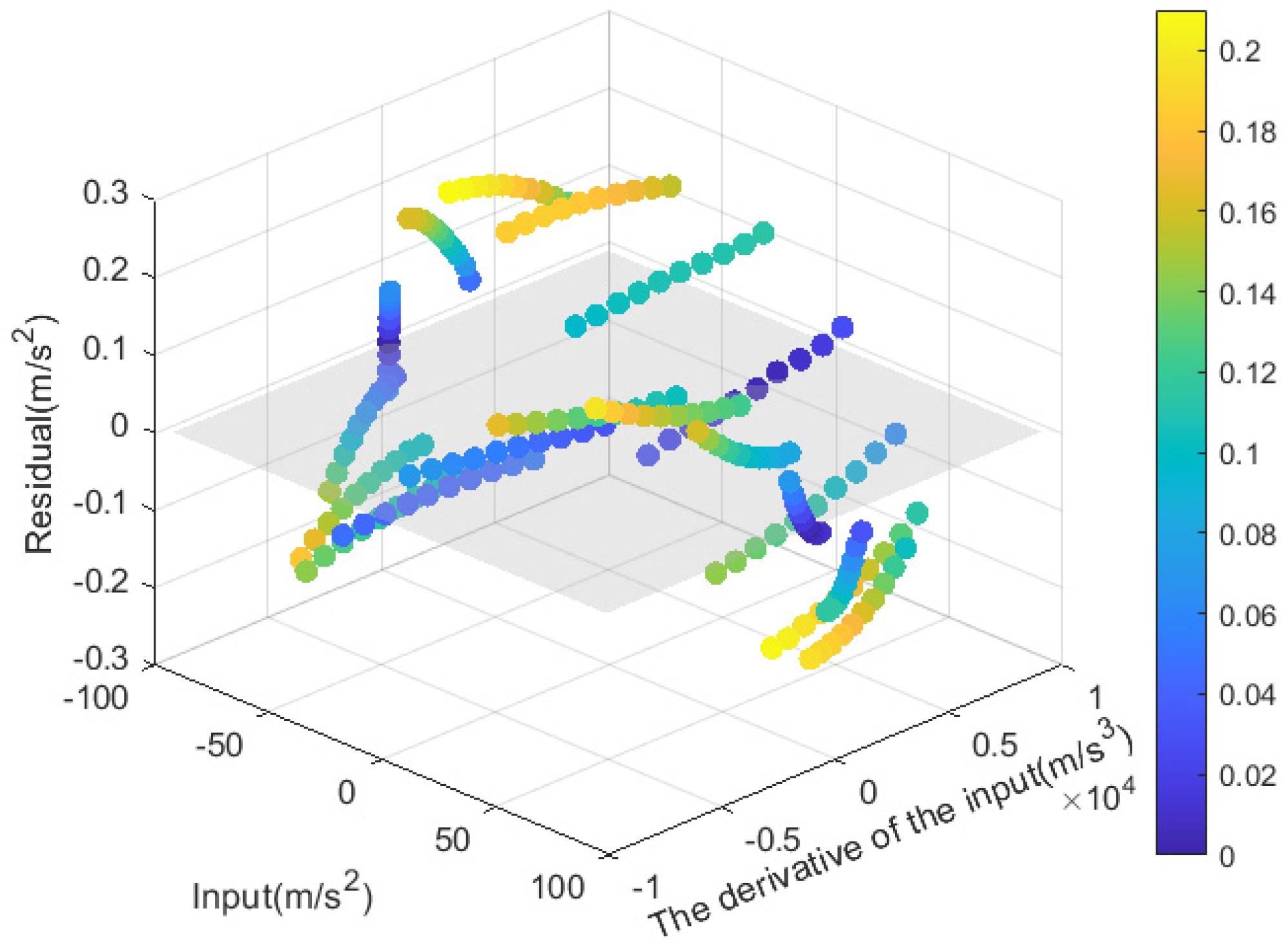
5.2. Single Dynamic Test
- Dynamic factor: ;
- (theoretical value is );
- Mean squared error: ;
- Root mean squared error: ;
- Coefficient of determination: ;
- 95% confidence interval: [−0.0005553, −0.0005471].
5.3. Monte Carlo Simulation-Based Analysis of Accelerometer Coefficient Uncertainty
6. Conclusions
- (a)
- The proposed dynamic calibration model effectively accounts for the time-varying characteristics of acceleration inputs and achieves higher accuracy than conventional static models.
- (b)
- For quartz flexure accelerometers exhibiting typical damping behavior, calibration with the proposed model significantly reduces dynamic errors within the standard operating range. Complete error compensation is achieved under ramp inputs, while sinusoidal inputs yield notable improvements in frequency domain accuracy.
- (c)
- The dual-axis centrifuge-based calibration method effectively estimates the dynamic model parameters, confirming both the scientific validity and practical feasibility of the proposed model. The calibration of the dynamic parameter yields a relative standard deviation of −0.048%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Wang, Y.; Huang, T.; Ye, L.; Zhu, Z.; Song, K. Evaluation of Accelerometer Dynamic Performance Based on Multiple Indices in the Time and Frequency Domain. IEEE Sens. J. 2024, 24, 22486–22501. [Google Scholar]
- Cheng, R.; Liu, Z.; Zhai, G.; Lv, Q.; Yang, M.; Cai, C. High-Acceleration Vibration Calibration System Based on Phase-Locked Resonance Control. Sensors 2022, 22, 7208. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Wang, X.; Song, L.; Ran, L. Temperature Hysteresis Mechanism and Compensation of Quartz Flexible Accelerometer in Aerial Inertial Navigation System. Sensors 2021, 21, 294. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Chen, F.; Wang, Y.; Sadeghpour, S.; Wang, C.; Baijot, M.; Esteves, R.; Zhao, C.; Bai, J.; Liu, H.; et al. Micromachined Accelerometers with Sub-Μg/√Hz Noise Floor: A Review. Sensors 2020, 20, 4054. [Google Scholar] [CrossRef]
- Ran, L.; Zhang, C.; Song, L.; Lu, J. The Estimation and Compensation of the Loop-Parameter-Drifting in the Digital Close-Loop Quartz Flexible Accelerometers. IEEE Access 2020, 8, 5678–5687. [Google Scholar] [CrossRef]
- El-Sheimy, N.; Youssef, A. Inertial Sensors Technologies for Navigation Applications: State of the Art and Future Trends. Satell. Navig. 2020, 1, 2. [Google Scholar] [CrossRef]
- IEEE Recommended Practice for Precision Centrifuge Testing of Linear Accelerometers. In IEEE Std 836-2009 (Revision of IEEE Std 836-2001); IEEE: New York, NY, USA, 2009; pp. 1–152.
- Pan, J.; Zhang, C.; Cai, Q. An Accurate Calibration Method for Accelerometer Nonlinear Scale Factor on a Low-Cost Three-Axis Turntable. Meas. Sci. Technol. 2014, 25, 025102. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, W.; Sun, C. Optimal Calibration Method of PIGA’s Orthogonal Poses for Gravity Field Testing. J. Sens. 2023, 2023, 7441499. [Google Scholar] [CrossRef]
- Shi, R.; Zhao, J.; Qiu, A.P.; Xia, G.M. Temperature Self-Compensation of Micromechanical Silicon Resonant Accelerometer. AMM 2013, 373, 373–381. [Google Scholar]
- Hewes, A.; Medvescek, J.I.; Mydlarski, L.; Baliga, B.R. Drift Compensation in Thermal Anemometry. Meas. Sci. Technol. 2020, 31, 045302. [Google Scholar] [CrossRef]
- Kaya, O.; Kose, T.; Azgin, K. Integrated Temperature Sensor for Temperature Compensation of Inertial Sensors. In Proceedings of the 2019 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Naples, FL, USA, 1–5 April 2019. [Google Scholar]
- Huang, L.; Yang, H.; Gao, Y.; Zhao, L.; Liang, J. Design and Implementation of a Micromechanical Silicon Resonant Accelerometer. Sensors 2013, 13, 15785–15804. [Google Scholar] [CrossRef]
- Mu, S.L.; Chen, F.B.; Gao, J.M.; Wu, Z.Z. Research on Temperature Compensation Method of Quartz Flexible Accelerometer. AMM 2013, 423–426, 2308–2312. [Google Scholar]
- Yang, H.; Li, J.; Xiao, X.; Wang, J.; Li, Y.; Li, K.; Li, Z.; Yang, H.; Wang, Q.; Yang, J.; et al. Topographic Design in Wearable MXene Sensors with In-Sensor Machine Learning for Full-Body Avatar Reconstruction. Nat. Commun. 2022, 13, 5311. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; Yu, H.; Liang, D.; Yang, X. Enhancing Pure Inertial Navigation Accuracy through a Redundant High-Precision Accelerometer-Based Method Utilizing Neural Networks. Sensors 2024, 24, 2566. [Google Scholar] [CrossRef] [PubMed]
- Carlsson, H.; Skog, I.; Hendeby, G.; Jaldén, J. Inertial Navigation Using an Inertial Sensor Array. arXiv 2022, arXiv:2201.11983. [Google Scholar] [CrossRef]
- Tian, J.; Yang, W.; Peng, Z.; Tang, T.; Li, Z. Application of MEMS Accelerometers and Gyroscopes in Fast Steering Mirror Control Systems. Sensors 2016, 16, 440. [Google Scholar] [CrossRef]
- ISO 16063-32:2016; Methods for the Calibration of Vibration and Shock Transducers—Part 32: Resonance Testing—Testing the Frequency and the Phase Response of Accelerometers by Means of Shock Excitation. ISO: Geneva, Switzerland, 2016.
- Bruns, T.; Kumme, R.; Kobusch, M.; Peters, M. From Oscillation to Impact: The Design of a New Force Calibration Device at PTB. Measurement 2002, 32, 85–92. [Google Scholar] [CrossRef]
- Geist, J.; Gaitan, M. Type A Uncertainty Analysis Validation of Type B Analysis for Three-Axis Accelerometer Calibrations. Metrologia 2022, 59, 052101. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Z.; Niu, L.; Zhang, D.; Zhang, Z. Frequency Characteristic Measurement of High-G Accelerometers Based on Down-Step Response. IEEE Sens. J. 2023, 23, 7312–7319. [Google Scholar] [CrossRef]
- Wei, Q.; Wang, J.; Han, R.; Yv, T.; Zhao, L. Dynamic Model Parameter Identification of Accelerometer Using Discrete Spectrum Correction and Least Square. J. Beijing Inst. Tech. 2018, 38, 1282–1288. [Google Scholar]
- Xiao, S.; Wang, S.; Zhuang, J.; Huang, Z.; Zhang, G. Nonlinear Dynamic Calibration and Correction of Acceleration Sensor Based on Adaptive Neural Network. Fractals 2022, 30, 2240098. [Google Scholar] [CrossRef]
- Ye, L.; Guo, Y.; Su, S.W. An Efficient Autocalibration Method for Triaxial Accelerometer. IEEE Trans. Instrum. Meas. 2017, 66, 2380–2390. [Google Scholar] [CrossRef]
- Li, X.; Song, B.; Wang, Y.; Niu, J.; Li, Z. Calibration and Alignment of Tri-Axial Magnetometers for Attitude Determination. IEEE Sens. J. 2018, 18, 7399–7406. [Google Scholar] [CrossRef]
- Schopp, P.; Graf, H.; Burgard, W.; Manoli, Y. Self-Calibration of Accelerometer Arrays. IEEE Trans. Instrum. Meas. 2016, 65, 1913–1925. [Google Scholar] [CrossRef]
- Stakkeland, M.; Prytz, G.; Booij, W.E.; Pedersen, S.T. Characterization of Accelerometers Using Nonlinear Kalman Filters and Position Feedback. IEEE Trans. Instrum. Meas. 2007, 56, 2698–2704. [Google Scholar] [CrossRef]
- Batista, P.; Silvestre, C.; Oliveira, P.; Cardeira, B. Accelerometer Calibration and Dynamic Bias and Gravity Estimation: Analysis, Design, and Experimental Evaluation. IEEE Trans. Contr. Syst. Technol. 2011, 19, 1128–1137. [Google Scholar] [CrossRef]
- Gao, P.; Li, K.; Wang, L.; Liu, Z. A Self-Calibration Method for Accelerometer Nonlinearity Errors in Triaxis Rotational Inertial Navigation System. IEEE Trans. Instrum. Meas. 2016, 66, 243–253. [Google Scholar] [CrossRef]
- Lu, Y.; Cheng, Y.; Sun, Y. Performance Evaluation of High g Accelerometers. J. Mech. Sci. Technol. 2013, 27, 3357–3362. [Google Scholar] [CrossRef]
- Ren, S.-Q.; Sun, C. A New Method for Calibrating Nonlinear Coefficients of PIGA on Linear Vibrator. IEEE Trans. Instrum. Meas. 2019, 68, 2898–2906. [Google Scholar] [CrossRef]
- Guan, W.; Meng, X.; Dong, X. Accelerometer Transverse Sensitivity Testing with Double Turntable Centrifuge. In Proceedings of the 2014 IEEE International Instrumentation and Measurement Technology Conference (I2MTC) Proceedings, Montevideo, Uruguay, 12–15 May 2014. [Google Scholar]
- Yang, Y.; Huo, X. Measuring and Balancing Dynamic Unbalance of Precision Centrifuge. In Proceedings of the Fifth International Symposium on Instrumentation Science and Technology, Shenyang, China, 15–18 September 2008; Tan, J., Wen, X., Eds.; SPIE: Bellingham, WA, USA, 2009. [Google Scholar]
- Liu, Y.; Yu, Z.; Ren, S. On Pseudo Second-Order Term of Pendulous Integrating Gyro Accelerometer Calibrated in Dual-Axis Precision Centrifuge. IEEE Trans. Instrum. Meas. 2023, 72, 1007109. [Google Scholar] [CrossRef]
- Qiao, Y.; Liu, Y.; Su, B. Study on PIGA Test Method on Centrifuge. In Proceedings of the 2007 International Conference on Computational Intelligence and Security (CIS 2007), Harbin, China, 15–19 December 2007. [Google Scholar]
- Sohrabi, H.; Ebadollahi, S. Accuracy Enhancement of MEMS Accelerometer by Determining Its Nonlinear Coefficients Using Centrifuge Test. Measurement 2017, 112, 29–37. [Google Scholar] [CrossRef]
- Sun, C.; Ren, S.; Wang, Z. Calibration Method of Accelerometer on Precision Centrifuge and Its Error Analysis. J. Chin. Inert. Technol. 2019, 27, 121–128. [Google Scholar]
- Sun, C.; Ren, S.; Wang, C. Revised Error Calibration Model of Linear Accelerometer on Precision Centrifuge. Rev. Sci. Instrum. 2019, 90, 085002. [Google Scholar] [CrossRef]
- Sun, C.; Ren, S.; Zeng, M.; Wang, C.; Huo, R. Sequential Calibration Method of Nonlinear Errors of PIGA on Counter-Rotating Platform Centrifuge. IEEE Trans. Instrum. Meas. 2020, 70, 1001811. [Google Scholar] [CrossRef]
- Tian, B.; Liu, H.; Yang, N.; Zhao, Y.; Jiang, Z. Design of a Piezoelectric Accelerometer with High Sensitivity and Low Transverse Effect. Sensors 2016, 16, 1587. [Google Scholar] [CrossRef]
- Xu, D.; Chen, Y.; Kang, R. Study of Accelerated Stability Test Method for Quartz Flexible Accelerometer. IEEE Trans. Device Mater. Reliab. 2011, 11, 148–156. [Google Scholar] [CrossRef]
- Zhu, M.; Chang, J.; Wang, X.; Duan, R.; Xiong, Q. Temperature Compensation for Quartz Flexible Accelerometer Based on IAPSO-RBF. Measurement 2025, 247, 116603. [Google Scholar] [CrossRef]
- Dong, X.; Jiao, J.; Lu, W.; Zeng, R.; Liu, H.; Xu, L.; Wen, J. The Method of Damping Parameters Close-Loop Detection Technology of Quartz Flexible Accelerometers. Flight Control Detect. 2023, 6, 95–99. [Google Scholar]
- Wang, C.; Li, X.; Dong, J. Analysis of squeeze film damping in quartz flexible accelerometer. J. Electron. Meas. Instrum. 2016, 218–224. [Google Scholar] [CrossRef]
- Jiang, S. Research on Measurement Method of Inertial Instrument and System Using Centrifuge. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2022. [Google Scholar]
- Tomczyk, K. Application of the Monte Carlo Method for Parametric Identification of Accelerometers in the Frequency Domain. PAR 2020, 24, 31–38. [Google Scholar] [CrossRef]
- Ning, F. Error Analysis and Uncertainty Research in Calibration of Linear Accelerometers. Master’s Thesis, Institute of Structural Mechanics China Academy of Engineering Physics, Mianyang, China, 2014. [Google Scholar]



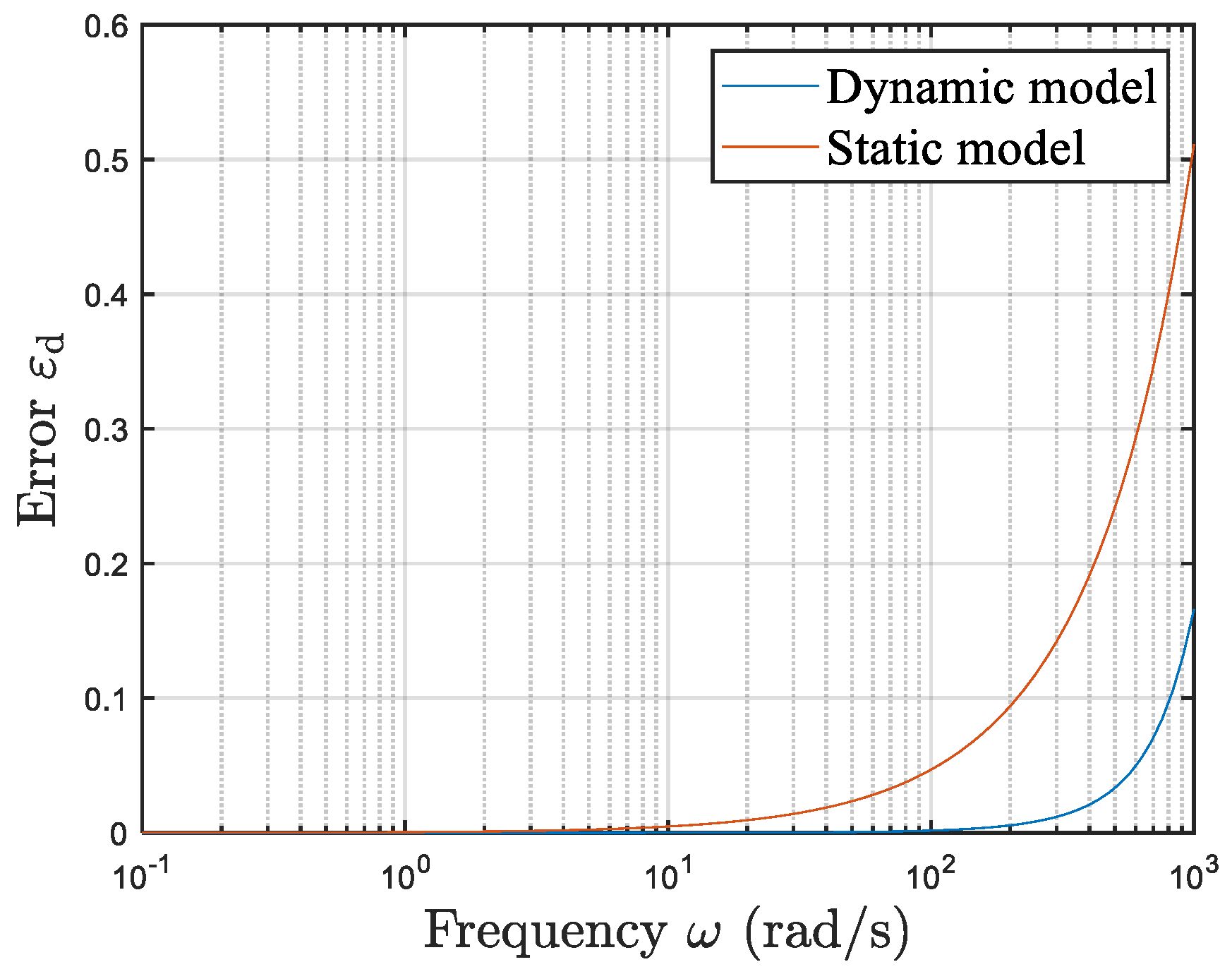
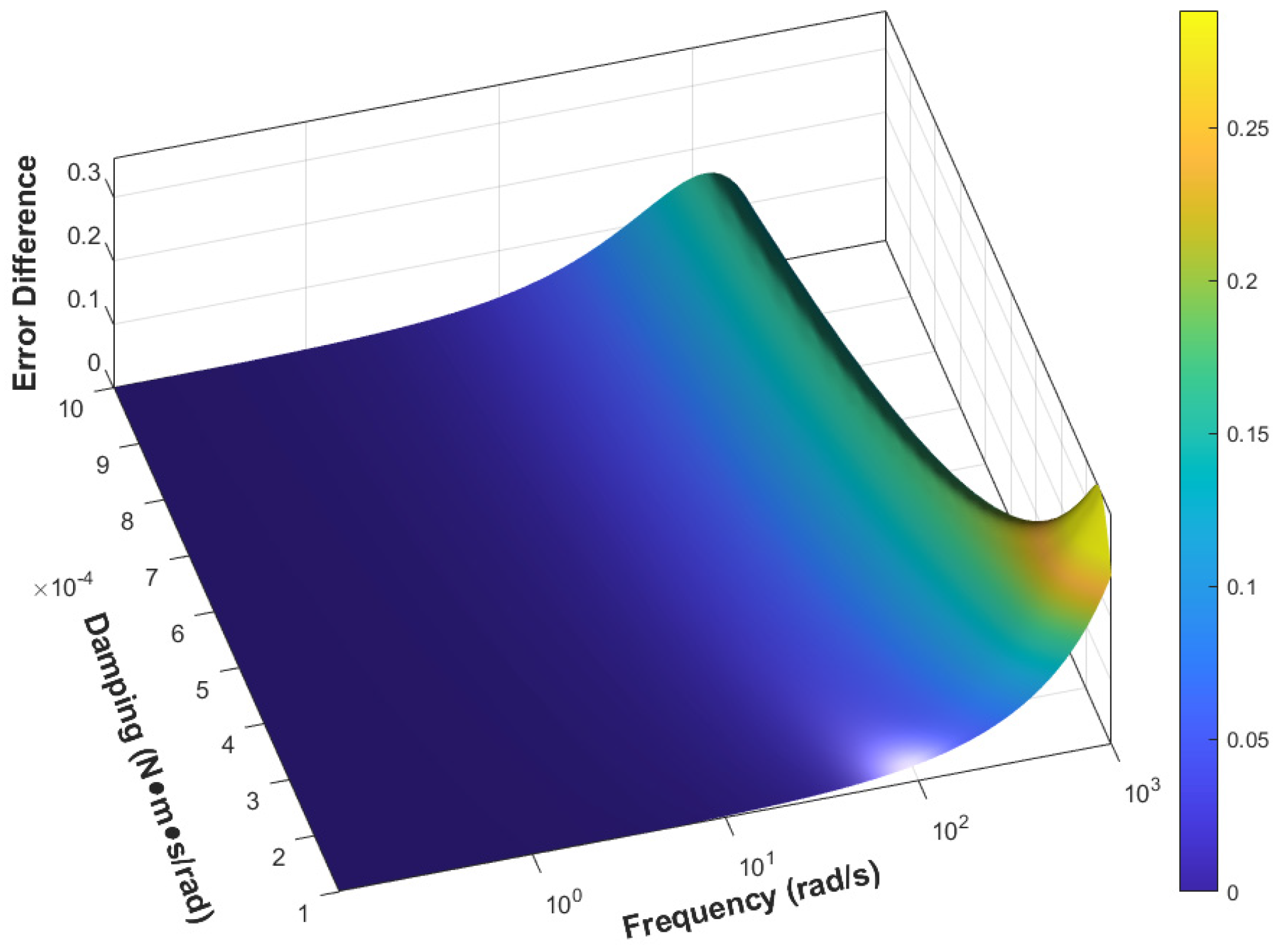



| Frequency (rad/s) | 0.100 | 0.231 | 0.586 | 1.485 | 3.765 | 9.546 |
| Static model error | 6.61 × 10−5 | 3.87 × 10−4 | 9.78 × 10−4 | 2.431 × 10−3 | 5.458 × 10−3 | 1.008 × 10−2 |
| Dynamic model error | 3.323 × 10−6 | 7.674 × 10−6 | 4.933 × 10−6 | 1.251 × 10−4 | 3.172 × 10−4 | 8.073 × 10−4 |
| Frequency (rad/s) | 24.201 | 61.359 | 155.568 | 572.237 | 830.218 | 1000 |
| Static model error | 2.832 × 10−2 | 7.253 × 10−2 | 1.880 × 10−1 | 2.797 × 10−1 | 4.192 × 10−1 | 5.126 × 10−1 |
| Dynamic model error | 2.086 × 10−3 | 5.908 × 10−3 | 2.382 × 10−2 | 4.910 × 10−2 | 1.135 × 10−1 | 1.781 × 10−1 |
| Coordinate System | Error Term | Coordinate Transformation Matrix |
|---|---|---|
| Geographic reference frame | ||
| Main axis sleeve reference frame | ||
| Main axis reference frame | ||
| Azimuth axis reference frame | ||
| Accelerometer casing reference frame | ||
| Accelerometer pendulum assembly reference frame |
| Integral value of the I-axis input (m/s2) | −75.3898240 | −65.2895028 | −37.6949120 | 0 | 37.6949120 | 65.2895028 |
| Accelerometer measured output (m/s2) | −62.7768581 | −54.4759719 | −31.4982265 | −0.0000477 | 31.4975864 | 54.4738495 |
| Integral value of the I-axis input (m/s2) | 75.3898240 | 65.2895028 | 37.694912 | 0 | −37.6949120 | −65.2895028 |
| Accelerometer measured output (m/s2) | 62.7727251 | 54.2516002 | 31.2738693 | −0.0040528 | −31.2814464 | −54.2577276 |
| Ideal input along the I-axis (m/s2) | −90.8328217 | 84.4223511 | −75.7923064 | 65.2545809 | −52.6749421 | 39.036774 |
| Derivative of ideal I-axis input (m/s3) | 619.6807592 | −1367.4047251 | 2350.8017103 | −3512.5138427 | 4806.0646933 | −5255.3148971 |
| Actual accelerometer output (m/s2) | −76.132558500 | 70.9614870 | −64.6024280 | 56.1267940 | −46.6890485 | 35.2704721 |
| Ideal input along the I-axis (m/s2) | −23.673606 | 8.0139039 | 8.0563864 | −23.5288197 | ||
| Derivative of ideal I-axis input (m/s3) | 6506.7094863 | −7650.6523934 | 8612.7862156 | −9318.9423288 | ||
| Actual accelerometer output (m/s2) | −23.4083424 | 10.8270773 | 1.9438143 | −14.4080055 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, X.; Wang, X.; Chen, W.; Shu, Y.; Zhang, K. Dynamic Calibration of Quartz Flexure Accelerometers. Sensors 2025, 25, 5096. https://doi.org/10.3390/s25165096
Sheng X, Wang X, Chen W, Shu Y, Zhang K. Dynamic Calibration of Quartz Flexure Accelerometers. Sensors. 2025; 25(16):5096. https://doi.org/10.3390/s25165096
Chicago/Turabian StyleSheng, Xuan, Xizhe Wang, Wenying Chen, Yang Shu, and Kai Zhang. 2025. "Dynamic Calibration of Quartz Flexure Accelerometers" Sensors 25, no. 16: 5096. https://doi.org/10.3390/s25165096
APA StyleSheng, X., Wang, X., Chen, W., Shu, Y., & Zhang, K. (2025). Dynamic Calibration of Quartz Flexure Accelerometers. Sensors, 25(16), 5096. https://doi.org/10.3390/s25165096





