Personalized Federated Learning Based on Dynamic Parameter Fusion and Prototype Alignment
Abstract
1. Introduction
- We propose a class-wise dynamic parameter fusion mechanism that achieves fine-grained fusion of classifier parameters. This mechanism adaptively weights and fuses local and global classifier parameters based on class prediction performance, enhancing both personalization and generalization capabilities of the local model.
- We introduce a prototype alignment mechanism based on global and historical information, which jointly constrains local features through global and historical alignment. This effectively mitigates cross-client semantic shifts and enhances the stability of local feature spaces.
- We conduct extensive experiments under various typical Non-IID scenarios, demonstrating that the proposed method surpasses baseline algorithms in both personalization performance and convergence stability.
2. Related Work
2.1. Knowledge Transfer-Based Personalized Federated Learning
2.2. Parameter Fusion-Based Personalized Federated Learning
2.3. Parameter Decoupling-Based Personalized Federated Learning
3. Preliminaries
3.1. Non-IID Data in Federated Learning
3.2. Federated Learning Framework and Objective
3.3. Problem Definition
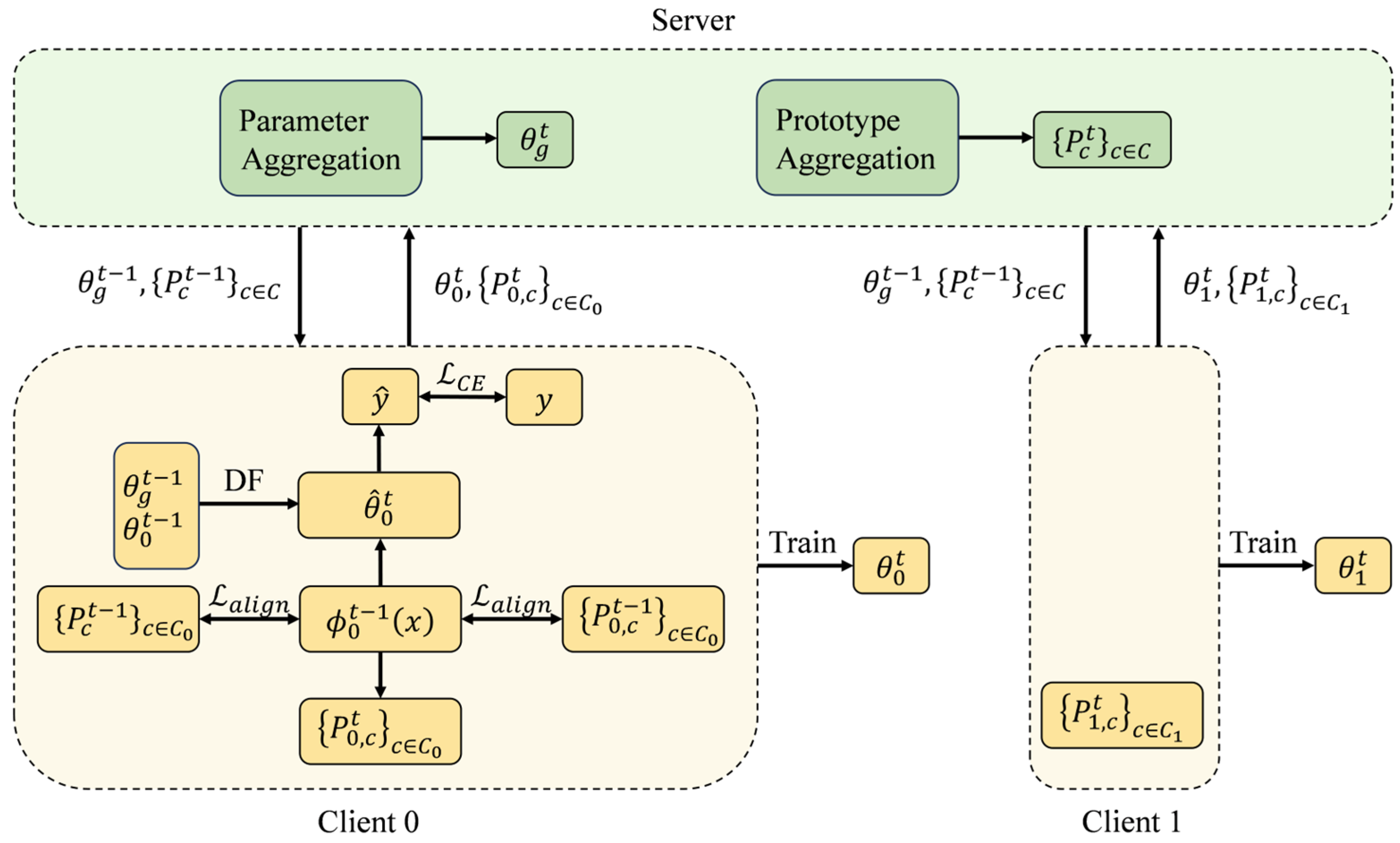
4. The Proposed FedDFPA Approach
4.1. Class-Wise Dynamic Parameter Fusion
4.2. Prototype Alignment Based on Global and Historical Information
4.3. The Process of FedDFPA
| Algorithm 1. FedDFPA |
| Input: , Total clients; , Client sampling ratio per round; , Total communication rounds; , Global category set; , Small positive constant; , Learning rate of local models |
| Output: personalized local models |
| Initialization: Server initializes global classifier randomly, and empty global prototype set , each client initializes local model , identifies local class set from dataset |
| 1: for communication round do |
| 2: Server: |
| 3: Sample client subset with ratio |
| 4: Send and to clients in |
| 5: Client (Parallel): |
| 6: for each class : |
| 7: if : |
| 8: Calculate local accuracy and global accuracy |
| 9: Calculate fusion coefficient by |
| 10: Update classifier: |
| 11: if , retain |
| 12: end for |
| 13: Calculate local prototypes |
| 14: Calculate cross-entropy loss with |
| 15: Calculate prototype alignment loss |
| 16: Update local model: |
| 17: Upload and to server |
| 18: Server: |
| 19: Update global classifier: |
| 20: Update global prototypes for each class : |
| 21: end for |
| 22: return personalized local models |
5. Experiments
5.1. Datasets and Non-IID Settings
- Practical Non-IID Setting [29]: The data is partitioned using a Dirichlet distribution Dir (), where the parameter controls the degree of data heterogeneity. A smaller results in more skewed and imbalanced label distributions across clients. We set the value of to 0.1.
5.2. Training Details
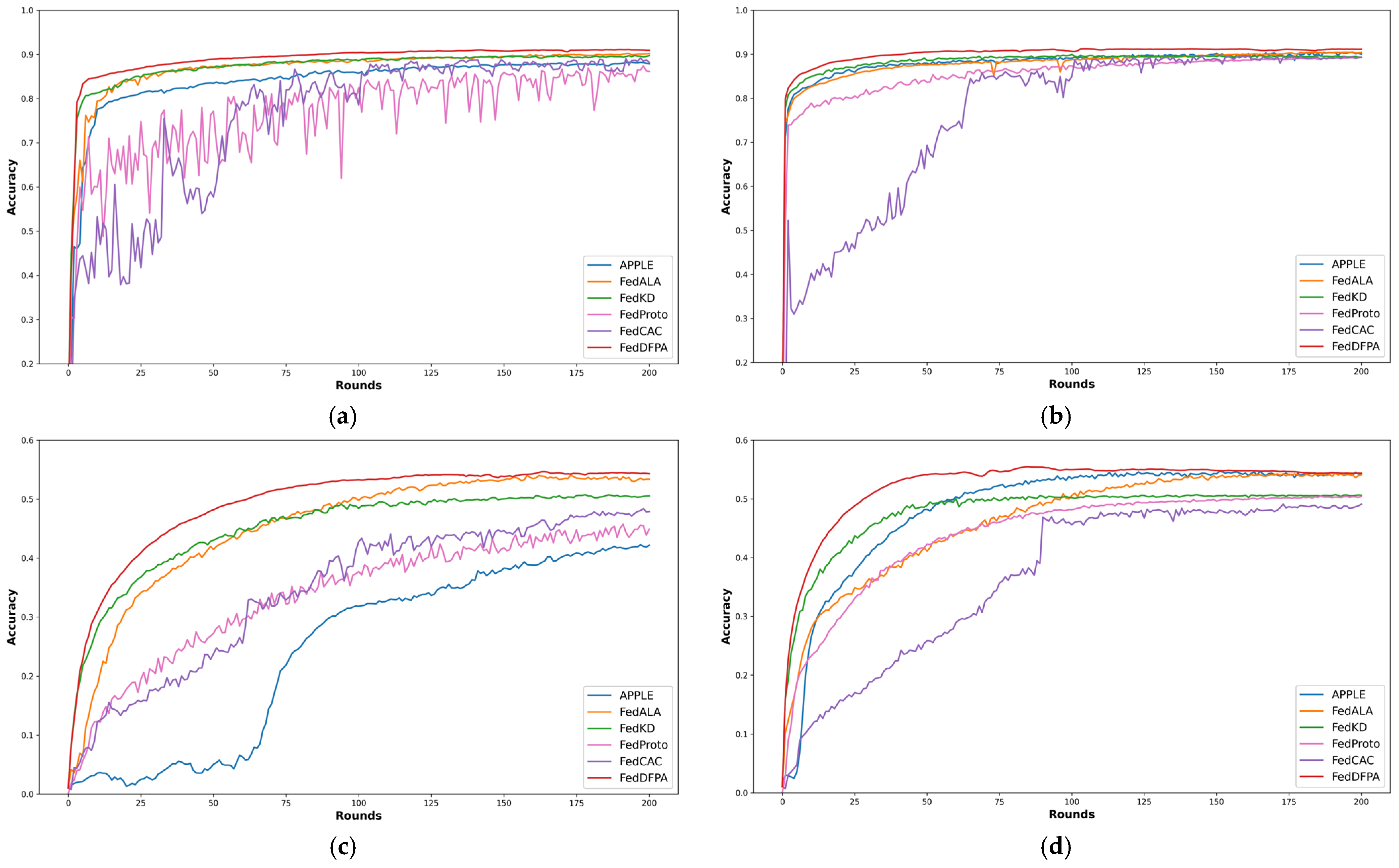
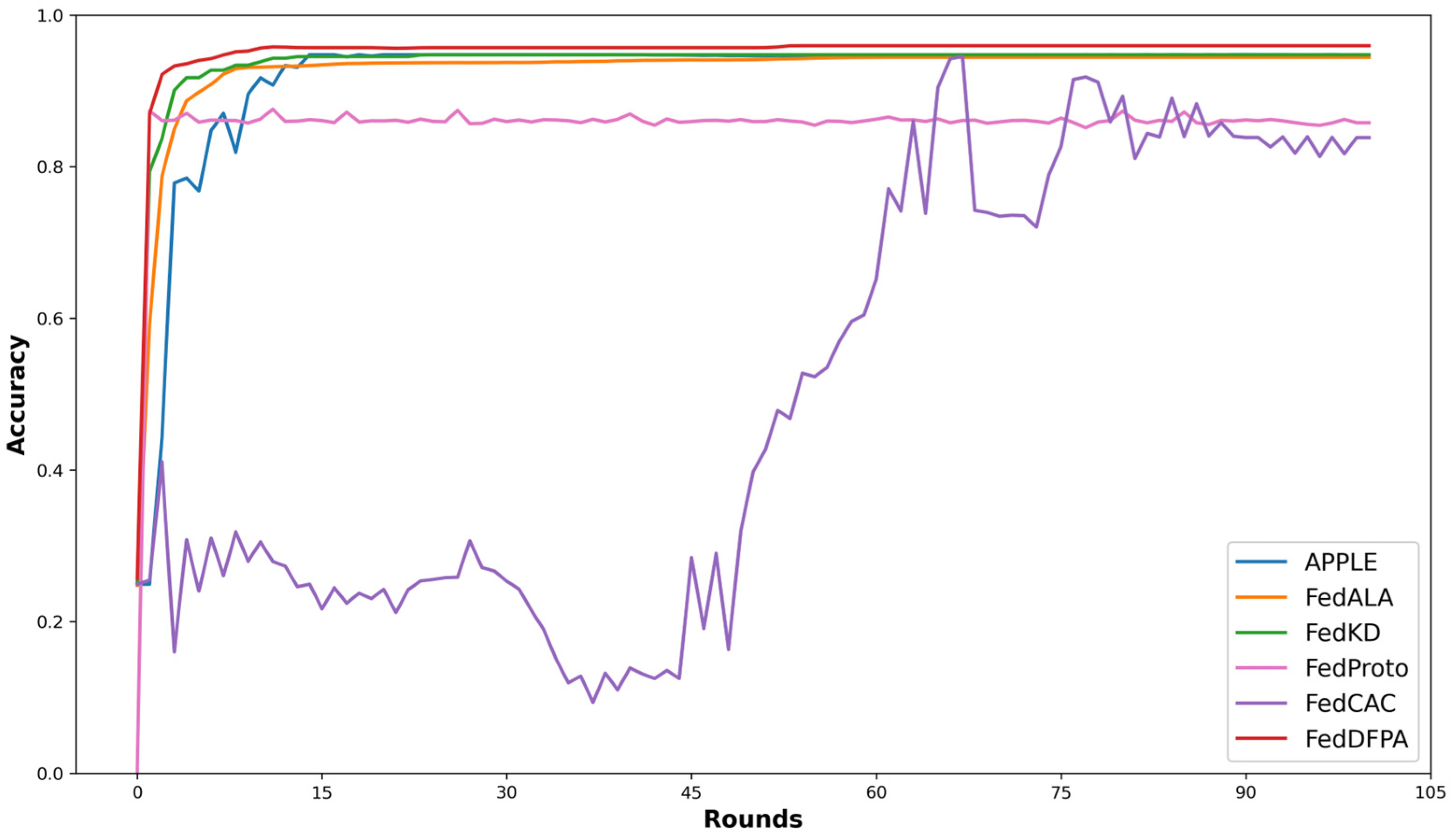
5.3. Results and Discussion
5.4. Communication Cost Analysis
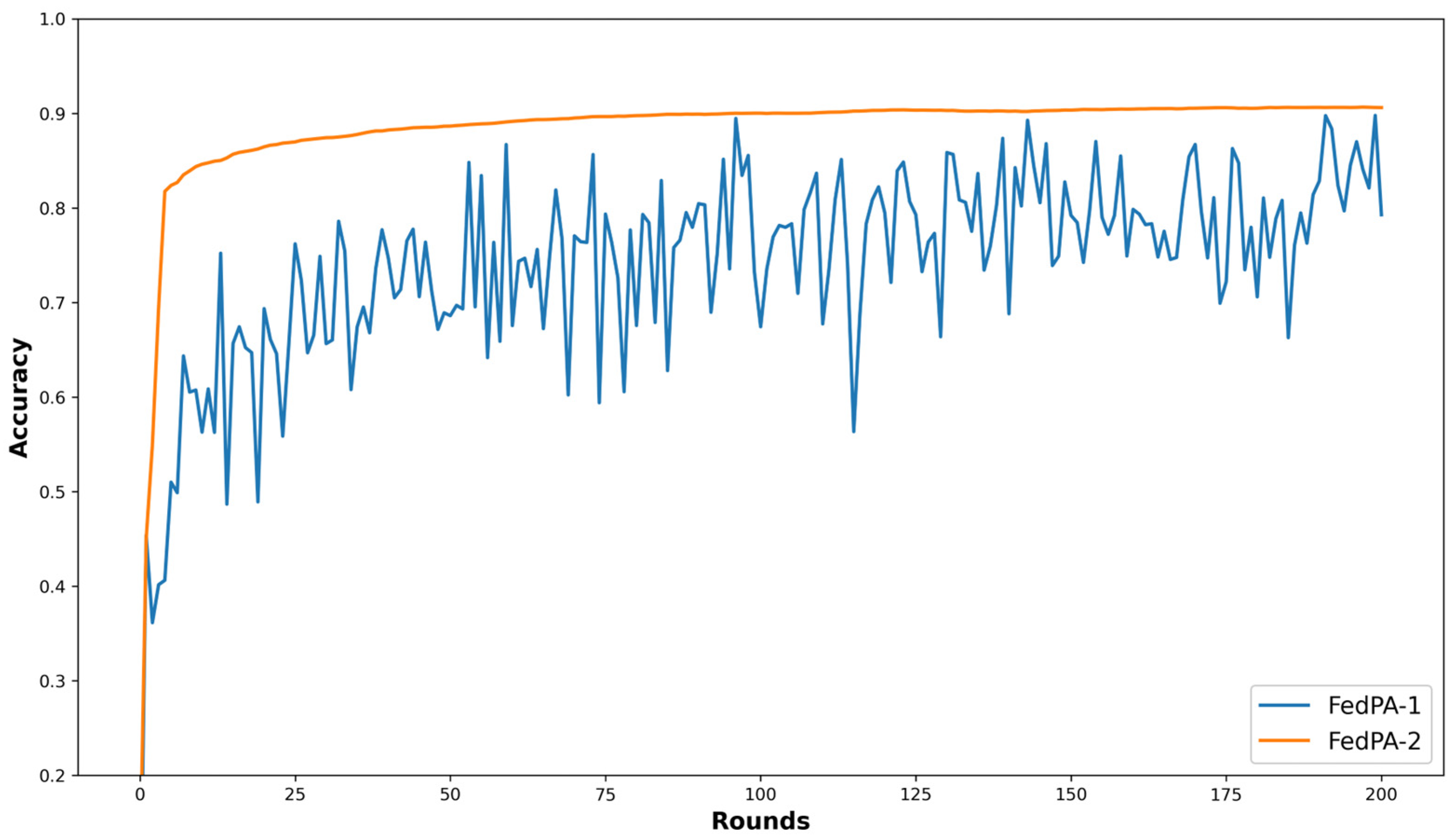
5.5. Ablation Study
6. Limitations and Future Work
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Li, Z.; Sharma, V.; Mohanty, S.P. Preserving data privacy via federated learning: Challenges and solutions. IEEE Consum. Electron. Mag. 2020, 9, 8–16. [Google Scholar] [CrossRef]
- Ma, X.; Zhu, J.; Lin, Z.; Chen, S.; Qin, Y. A state-of-the-art survey on solving non-iid data in federated learning. Future Gener. Comput. Syst. 2022, 135, 244–258. [Google Scholar] [CrossRef]
- Tan, A.Z.; Yu, H.; Cui, L.; Yang, Q. Towards personalized federated learning. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 9587–9603. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated optimization in heterogeneous networks. Proc. Mach. Learn. Syst. 2020, 2, 429–450. [Google Scholar]
- Karimireddy, S.P.; Kale, S.; Mohri, M.; Reddi, S.; Stich, S.; Suresh, A.T. Scaffold: Stochastic controlled averaging for federated learning. In Proceedings of the 37th International Conference on Machine Learning, Online, 13–18 July 2020; pp. 5132–5143. [Google Scholar]
- Sabah, F.; Chen, Y.; Yang, Z.; Azam, M.; Ahmad, N.; Sarwar, R. Model optimization techniques in personalized federated learning: A survey. Expert Syst. Appl. 2024, 243, 122874. [Google Scholar] [CrossRef]
- Ye, M.; Fang, X.; Du, B.; Yuen, P.C.; Tao, D. Heterogeneous federated learning: State-of-the-art and research challenges. ACM Comput. Surv. 2023, 56, 1–44. [Google Scholar] [CrossRef]
- Chen, H.; Vikalo, H. The best of both worlds: Accurate global and personalized models through federated learning with data-free hyper-knowledge distillation. arXiv 2023, arXiv:2301.08968. [Google Scholar]
- Tan, Y.; Long, G.; Liu, L.; Zhou, T.; Lu, Q.; Jiang, J.; Zhang, C. Fedproto: Federated prototype learning across heterogeneous clients. In Proceedings of the 36th AAAI Conference on Artificial Intelligence, Virtual, 22 February–1 March 2022; pp. 8432–8440. [Google Scholar]
- Deng, Y.; Kamani, M.M.; Mahdavi, M. Adaptive personalized federated learning. arXiv 2020, arXiv:2003.13461. [Google Scholar] [CrossRef]
- Zhang, M.; Sapra, K.; Fidler, S.; Yeung, S.; Alvarez, J.M. Personalized federated learning with first order model optimization. arXiv 2020, arXiv:2012.08565. [Google Scholar]
- Huang, Y.; Chu, L.; Zhou, Z.; Wang, L.; Liu, J.; Pei, J.; Zhang, Y. Personalized cross-silo federated learning on non-iid data. In Proceedings of the 35th AAAI conference on artificial intelligence, Virtual, 2–9 February 2021; pp. 7865–7873. [Google Scholar]
- Luo, J.; Wu, S. Adapt to adaptation: Learning personalization for cross-silo federated learning. In Proceedings of the Thirty-First International Joint Conference on Artificial Intelligence, Vienna, Austria, 23–29 July 2022; pp. 2166–2173. [Google Scholar]
- Mei, Y.; Guo, B.; Xiao, D.; Wu, W. FedVF: Personalized federated learning based on layer-wise parameter updates with variable frequency. In Proceedings of the 2021 IEEE International Performance, Computing, and Communications Conference (IPCCC), Austin, TX, USA, 29–31 October 2021; pp. 1–9. [Google Scholar]
- Oh, J.; Kim, S.; Yun, S.-Y. Fedbabu: Towards enhanced representation for federated image classification. arXiv 2021, arXiv:2106.06042. [Google Scholar]
- Wu, X.; Liu, X.; Niu, J.; Zhu, G.; Tang, S. Bold but cautious: Unlocking the potential of personalized federated learning through cautiously aggressive collaboration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 19375–19384. [Google Scholar]
- Wu, C.; Wu, F.; Lyu, L.; Huang, Y.; Xie, X. Communication-efficient federated learning via knowledge distillation. Nat. Commun. 2022, 13, 2032. [Google Scholar] [CrossRef] [PubMed]
- Jin, H.; Bai, D.; Yao, D.; Dai, Y.; Gu, L.; Yu, C.; Sun, L. Personalized edge intelligence via federated self-knowledge distillation. IEEE Trans. Parallel Distrib. Syst. 2022, 34, 567–580. [Google Scholar] [CrossRef]
- Dai, Y.; Chen, Z.; Li, J.; Heinecke, S.; Sun, L.; Xu, R. Tackling data heterogeneity in federated learning with class prototypes. In Proceedings of the 37th AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; pp. 7314–7322. [Google Scholar]
- Ma, X.; Zhang, J.; Guo, S.; Xu, W. Layer-wised model aggregation for personalized federated learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10092–10101. [Google Scholar]
- Zhang, J.; Hua, Y.; Wang, H.; Song, T.; Xue, Z.; Ma, R.; Guan, H. Fedala: Adaptive local aggregation for personalized federated learning. In Proceedings of the 37th AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; pp. 11237–11244. [Google Scholar]
- Collins, L.; Hassani, H.; Mokhtari, A.; Shakkottai, S. Exploiting shared representations for personalized federated learning. In Proceedings of the 38th International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 2089–2099. [Google Scholar]
- Zhu, G.; Liu, X.; Tang, S.; Niu, J. Aligning before aggregating: Enabling cross-domain federated learning via consistent feature extraction. In Proceedings of the 2022 IEEE 42nd International Conference on Distributed Computing Systems (ICDCS), Bologna, Italy, 10–13 July 2022; pp. 809–819. [Google Scholar]
- Chen, H.-Y.; Chao, W.-L. On bridging generic and personalized federated learning for image classification. arXiv 2021, arXiv:2107.00778. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the 37th International Conference on Machine Learning, Online, 13–18 July 2020; pp. 1597–1607. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. 2009. Available online: http://www.cs.utoronto.ca/~kriz/learning-features-2009-TR.pdf (accessed on 13 August 2025).
- Zhang, X.; Zhao, J.; LeCun, Y. Character-level convolutional networks for text classification. Adv. Neural Inf. Process. Syst. 2015, 28. [Google Scholar] [CrossRef]
- Lin, T.; Kong, L.; Stich, S.U.; Jaggi, M. Ensemble distillation for robust model fusion in federated learning. Adv. Neural Inf. Process. Syst. 2020, 33, 2351–2363. [Google Scholar]
- Shamsian, A.; Navon, A.; Fetaya, E.; Chechik, G. Personalized federated learning using hypernetworks. In Proceedings of the 38th International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 9489–9502. [Google Scholar]


| Algorithm | CIFAR-10 | CIFAR-100 | ||
|---|---|---|---|---|
| APPLE | 88.20 ± 0.19 | 90.42 ± 0.19 | 42.24 ± 0.25 | 54.70 ± 0.21 |
| FedALA | 90.19 ± 0.11 | 90.47 ± 0.09 | 54.06 ± 0.10 | 54.36 ± 0.10 |
| FedKD | 89.73 ± 0.13 | 89.91 ± 0.11 | 50.74 ± 0.15 | 50.71 ± 0.13 |
| FedProto | 87.36 ± 0.52 | 89.24 ± 0.55 | 45.71 ± 0.51 | 50.42 ± 0.50 |
| FedCAC | 89.16 ± 0.54 | 89.70 ± 0.51 | 48.37 ± 0.57 | 49.10 ± 0.58 |
| FedDFPA | 91.08 ± 0.16 | 91.19 ± 0.15 | 54.64 ± 0.19 | 55.45 ± 0.18 |
| Algorithm | CIFAR-10 | CIFAR-100 | ||
|---|---|---|---|---|
| APPLE | 88.08 ± 0.21 | 89.49 ± 0.20 | 56.80 ± 0.26 | 62.43 ± 0.22 |
| FedALA | 90.48 ± 0.09 | 90.59 ± 0.09 | 63.25 ± 0.10 | 63.58 ± 0.09 |
| FedKD | 88.75 ± 0.11 | 88.58 ± 0.11 | 65.83 ± 0.11 | 66.06 ± 0.12 |
| FedProto | 89.03 ± 0.53 | 89.51 ± 0.50 | 59.47 ± 0.51 | 66.53 ± 0.51 |
| FedCAC | 90.03 ± 0.55 | 90.27 ± 0.54 | 62.92 ± 0.57 | 62.43 ± 0.54 |
| FedDFPA | 91.29 ± 0.14 | 91.56 ± 0.14 | 66.36 ± 0.16 | 67.24 ± 0.17 |
| Algorithm | Upload | Download |
|---|---|---|
| APPLE | Local model | Multiple other client models |
| FedALA | Local model | Global model |
| FedKD | Compressed Mentee gradients | Compressed Mentee gradients |
| FedProto | Local class prototypes | Global class prototypes |
| FedCAC | Local model and binary mask | Global model and customized global model |
| FedDFPA | Local prototypes and classifier | Global prototypes and classifier |
| Algorithm | CIFAR-10 | CIFAR-100 | ||
|---|---|---|---|---|
| FedDF | 90.25 ± 0.21 | 90.44 ± 0.18 | 54.19 ± 0.22 | 54.28 ± 0.20 |
| FedPA | 90.62 ± 0.19 | 90.95 ± 0.18 | 54.40 ± 0.21 | 55.01 ± 0.21 |
| FedDFPA | 91.08 ± 0.16 | 91.19 ± 0.15 | 54.64 ± 0.19 | 55.45 ± 0.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Wen, J.; Liang, S.; Chen, Z.; Huang, B. Personalized Federated Learning Based on Dynamic Parameter Fusion and Prototype Alignment. Sensors 2025, 25, 5076. https://doi.org/10.3390/s25165076
Chen Y, Wen J, Liang S, Chen Z, Huang B. Personalized Federated Learning Based on Dynamic Parameter Fusion and Prototype Alignment. Sensors. 2025; 25(16):5076. https://doi.org/10.3390/s25165076
Chicago/Turabian StyleChen, Ying, Jing Wen, Shaoling Liang, Zhaofa Chen, and Baohua Huang. 2025. "Personalized Federated Learning Based on Dynamic Parameter Fusion and Prototype Alignment" Sensors 25, no. 16: 5076. https://doi.org/10.3390/s25165076
APA StyleChen, Y., Wen, J., Liang, S., Chen, Z., & Huang, B. (2025). Personalized Federated Learning Based on Dynamic Parameter Fusion and Prototype Alignment. Sensors, 25(16), 5076. https://doi.org/10.3390/s25165076





