Collaborative Swarm Robotics for Object Transport via Caging
Abstract
1. Introduction
2. Object Collective Transport Problem
2.1. Problem Definition
2.2. Main Challenges
3. Related Works
3.1. Distributed Swarm Transport
3.2. Coordinated Swarm Transport
3.3. Advancement in Swarm Transport
4. Proposed Model for Object Transport
4.1. Swarm Size
4.2. Proportional–Integral–Derivative Controllers
| Algorithm 1 PID() |
| Ensure: u; ; ; ; ; if then ; ; end if if ∧ then ; ; end if |
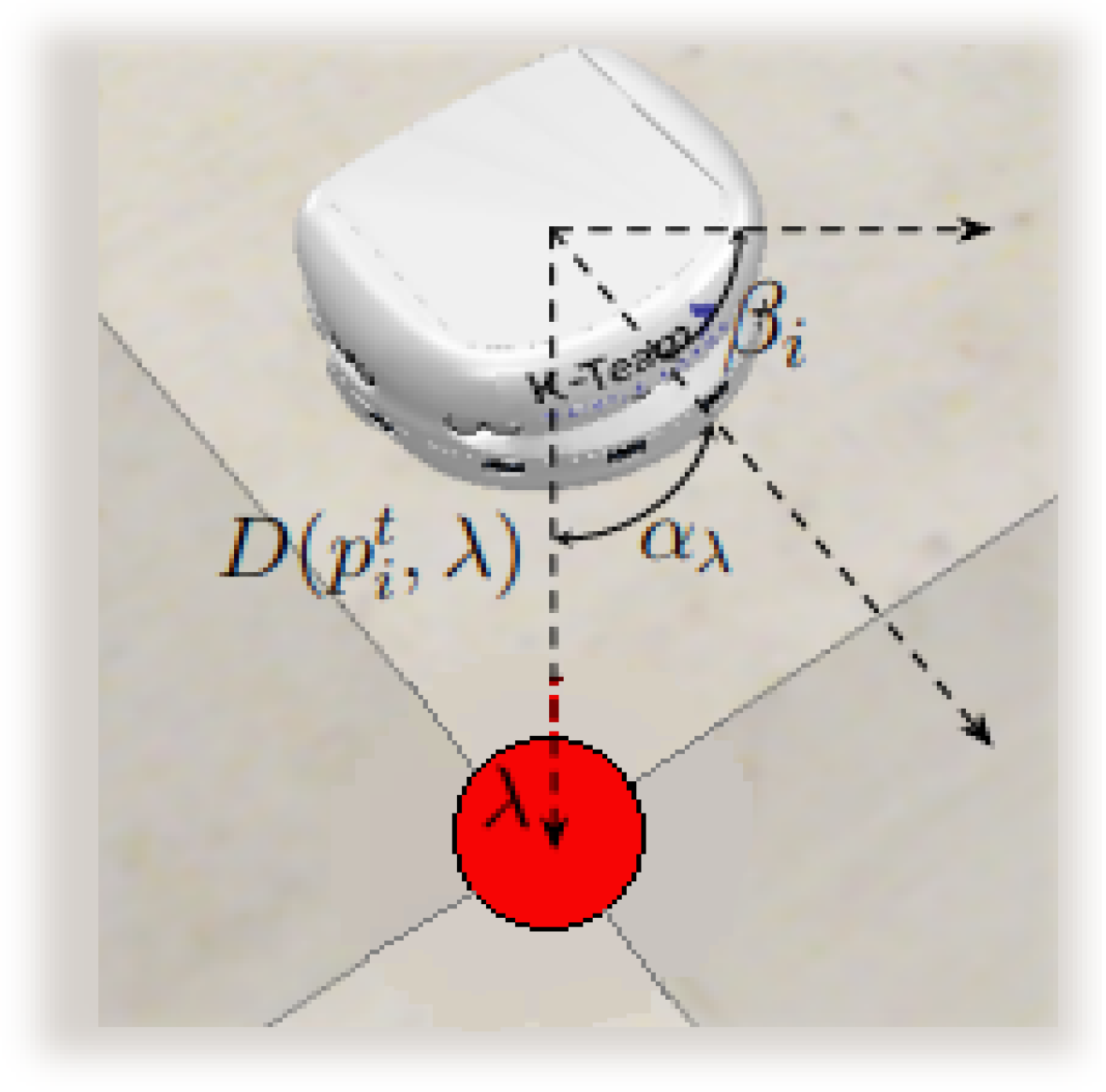
4.3. Robot Navigation Control
| Algorithm 2 Move() in robot i |
| Require: ; Ensure: ; Compute with Equation (3); Compute with Equation (4); Normalize so that ; PID(); PID(); Compute with Braitenberg(); if then state ; else if state = ∧ then state ; else if state = ∧ then state end if end if end if if state = then ; ; else if state = then ; ; end if end if |
| Algorithm 3 Turn() at robot i |
| Require: ; Ensure: ; Compute using Equation (4); Normalize such that ; PID(); if then state ; else if state = ∧ then state ; else if state = ∧ then state end if end if end if if state = then ; ; else if state = then ; ; end if end if |
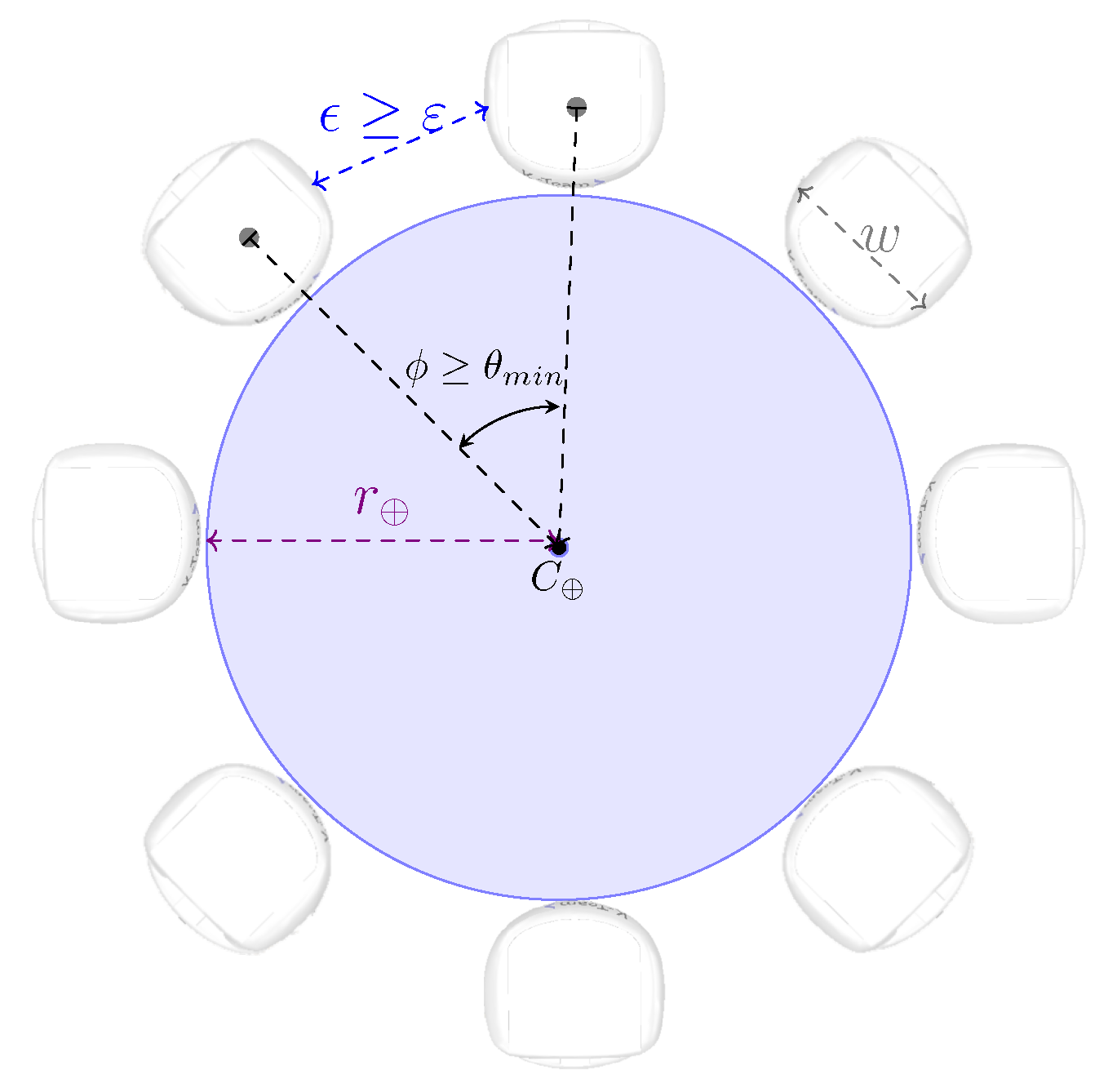
| Algorithm 4 Caging(, , , , , , ) at robot i |
Initialize caging at robot i; Apply (); Apply (); |
| Algorithm 5 Initialize caging at robot i |
| Ensure: ; Compute with Equation (3); Compute ; with Equation (3); Compute with Equation (4); Compute and ; Normalize e such that e ; ControlTrsp (); |
| Algorithm 6 ControlTrsp() at robot i |
| Ensure: ; PID(); PID(); PID(); PID(); PID(); PID(); PID(); |
5. Algorithms for the Caging Strategy
| Algorithm 7 Collective transport by caging |
Arena Initialization; parallel do Object Search; parallel do Robot Recruitment(); parallel do Object Transport; |
5.1. Arena Initialization
| Algorithm 8 Arena initialization |
| Require: , , Ensure: , , for ; for do Generate Randomly within arena; for do Define ; Generate randomly within arena; for do Generate randomly by the arena border; for do Define ; end for |
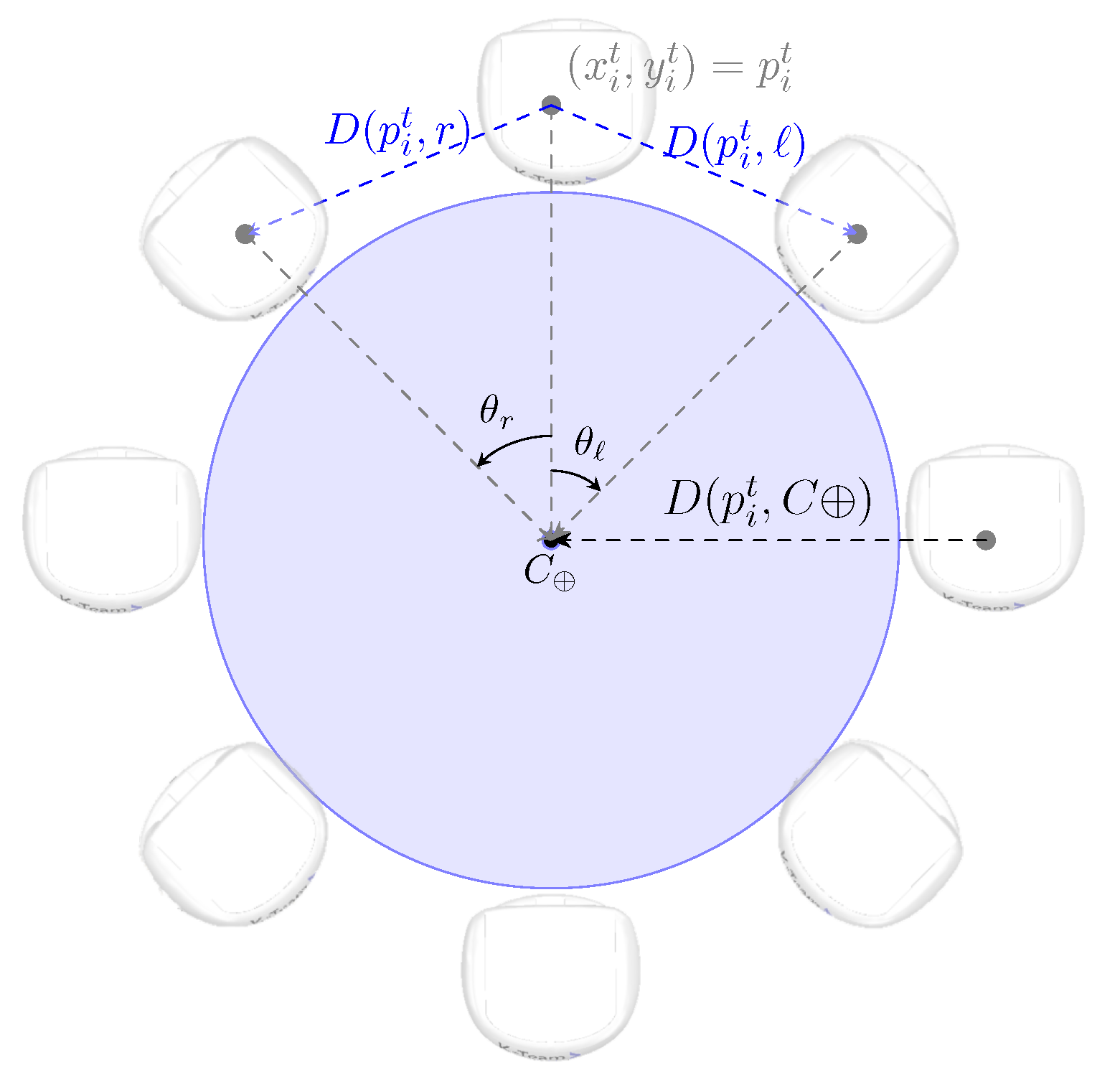
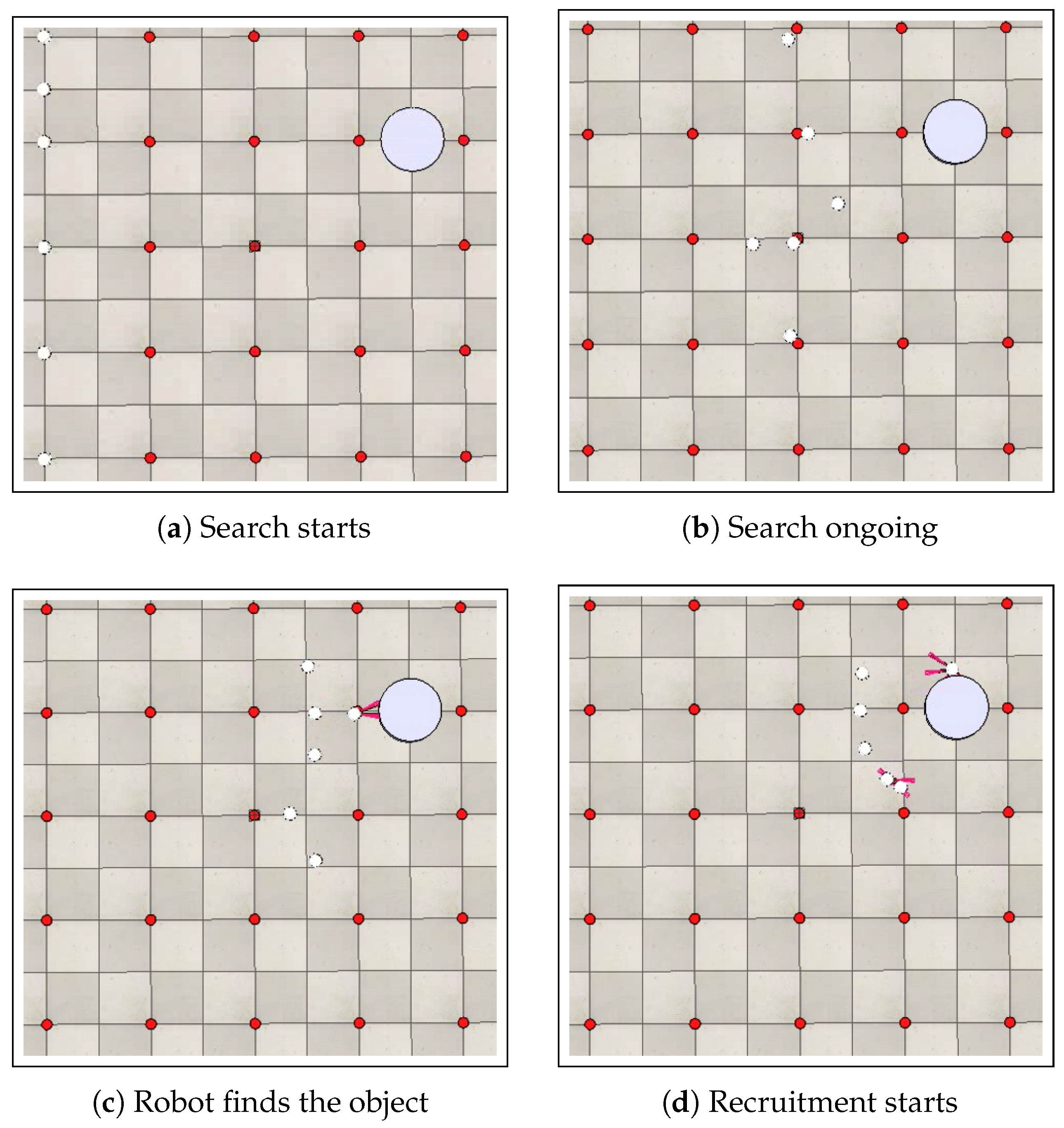
5.2. Object Search
| Algorithm 9 Object search at robot i |
| Require: L, Ensure: , , ; ; ; ; Select randomly ; repeat Compute with Equation (3); Compute with Equation (4); Move(); for do if then ; ; for do if then Send , ; end for end if end for if then Receive ; if then ; ; ; else if then Append to ; ; Select randomly ; ; end if end if end if until |
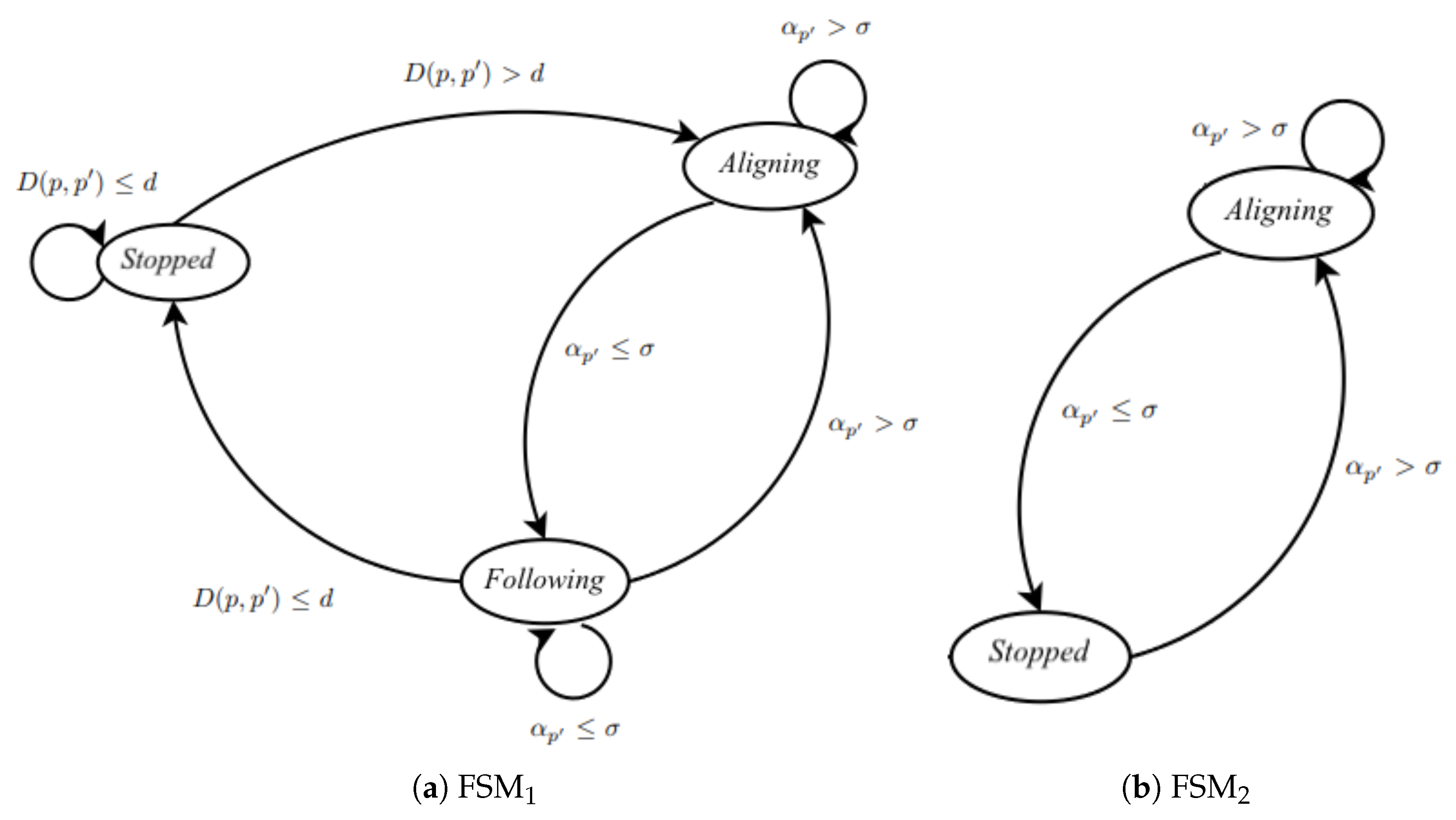
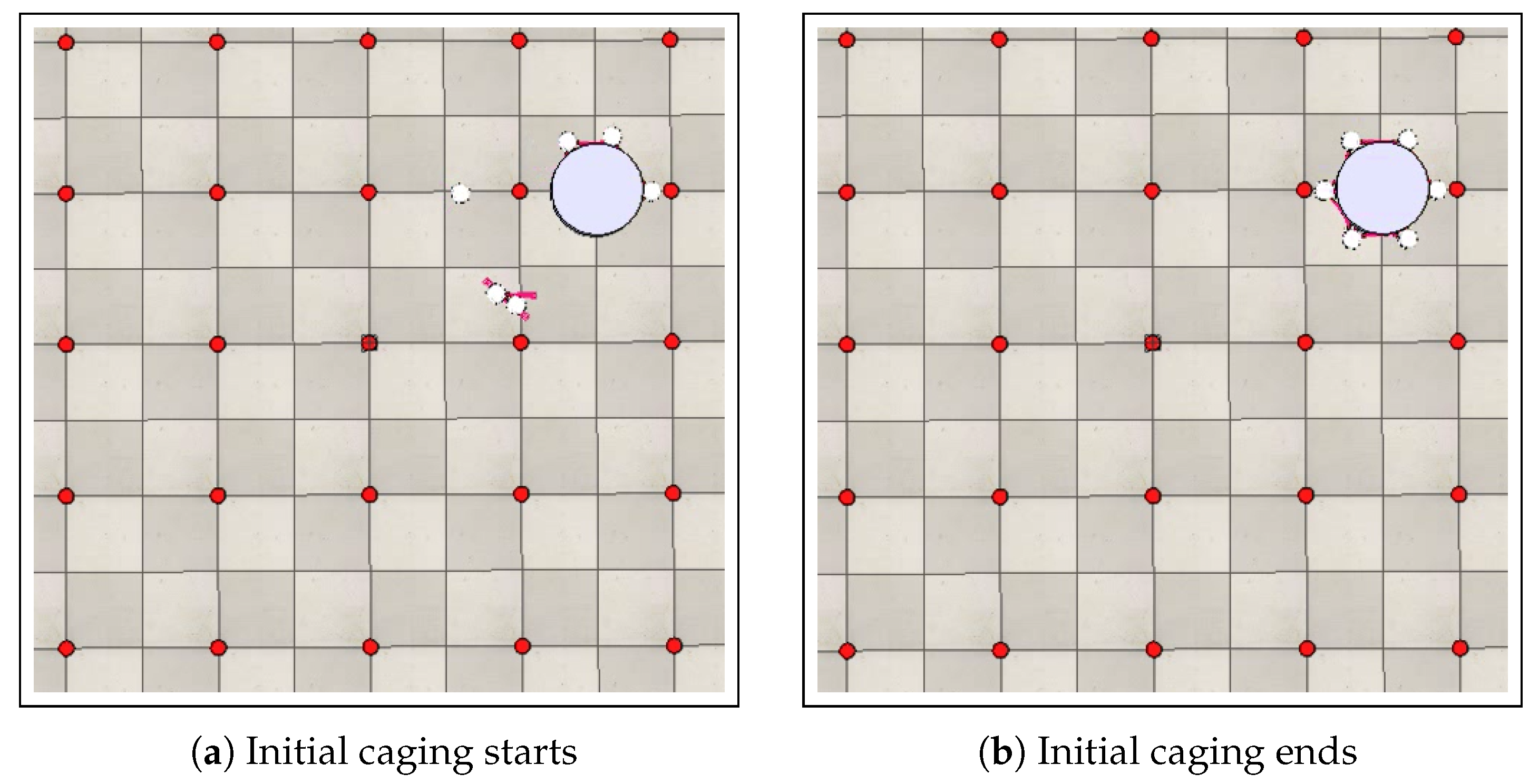
5.3. Robot Recruitment and Caging
| Algorithm 10 Robot recruitment () at robot i |
if
then Recruiter(); else Recruited(); end if |
| Algorithm 11 Recruiter() at robot i |
while
do Compute with Equation (3); Move(); end while for
do ; Send ; repeat Receive ; until ; end for |
| Algorithm 12 Recruited() at robot i |
while
do Move(); Compute with Equation (3); Compute with Equation (4); Receive ; end while if then Receive ; if
then while do Compute with Equation (3); end while for do if then Send ; end for end if |
5.4. Object Transport
| Algorithm 13 Object transport at robot i |
; while
do Receive ; if ( then ; end while for
do ; repeat Compute with Equation (4); Turn(); until for do if then Send ; end for while do Receive ; if ( then ; end while repeat Compute =, = with Equation (3); Compute =,= with Equation (3) Compute , with Equation (4); Caging(, , , , , , ); until for do Send ; ; while do Receive ; if (then ; end while end for |
6. Implementation Issues and Setup
7. Performance Results
7.1. Results Regarding Search and Recruitment
7.2. Results Regarding Transport
7.2.1. Robot Number Impact
7.2.2. Impact of Object Characteristics
7.2.3. Arena Discretization Impact
7.3. Statistical Confidence Results
7.4. Performance Comparison: Pushing vs. Caging
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Berman, S.; Lindsey, Q.; Sakar, M.S.; Kumar, V.; Pratt, S.C. Experimental Study and Modeling of Group Retrieval in Ants as an Approach to Collective Transport in Swarm Robotic Systems. Proc. IEEE 2011, 99, 1470–1481. [Google Scholar] [CrossRef]
- Vardharajan, V.S.; Soma, K.; Beltrame, G. Collective Transport via Sequential Caging. In Proceedings of the Distributed Autonomous Robotic Systems, Kyoto, Japan, 1–4 June 2021. [Google Scholar]
- Wang, Z.; Kumar, V. Object closure and manipulation by multiple cooperating mobile robots. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation (Cat. No.02CH37292), Washington, DC, USA, 11–15 May 2002; pp. 394–399. [Google Scholar]
- Chen, J.; Gauci, M.; Li, W.; Kolling, A.; Groß, R. Occlusion-based cooperative transport with a swarm of miniature mobile robots. IEEE Trans. Robot. 2015, 31, 307–321. [Google Scholar] [CrossRef]
- Sudsang, A.; Ponce, J. On grasping and manipulating polygonal objects with disc-shaped robots in the plane. In Proceedings of the 1998 IEEE International Conference on Robotics and Automation (Cat. No.98CH36146), Leuven, Belgium, 20 May 1998; pp. 2740–2746. [Google Scholar]
- Ferreira, G.B.; Nadia, N.; Luiza, d.M.M. Transporte cooperativo de objeto por multi-robôs 2022. Master’s Thesis, State University of Rio de Janeiro University, Rio de Janeiro, Brazil, 2022. Available online: https://www.pel.uerj.br/dissertacoes/ (accessed on 1 August 2025).
- Sasaki, J.; Ota, J.; Yoshida, E.; Kurabayashi, D.; Arai, T. Cooperating grasping of a large object by multiple mobile robots. In Proceedings of the 1995 IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995; pp. 1205–1210. [Google Scholar]
- Dorigo, M.; Gambardella, L. Ant colony system: A cooperative learning approach to the traveling salesman problem. IEEE Trans. Evol. Comput. 1997, 1, 53–66. [Google Scholar] [CrossRef]
- Braitenberg, V. Vehicles: Experiments in Synthetic Psychology; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Lambrinos, D.; Scheier, C. Extended Braitenberg Architectures; Technical Report for AI Lab, No. IFI-AI-95.10; AI LabComputer Science Department University of Zurich: Zurich, Switzerland, 1995; Available online: https://citeseerx.ist.psu.edu/ (accessed on 1 August 2025).
- Fink, J.; Michael, N.; Kumar, V. Composition of vector fields for multi-robot manipulation via caging. In Proceedings of the Conference Robotics: Science and Systems, Atlanta, GA, USA, 27–30 June 2007; Volume 3. [Google Scholar]
- Farrugia, J.L.; Fabri, S.G. Swarm robotics for object transportation. In Proceedings of the 2018 UKACC 12th International Conference on Control (CONTROL), Sheffield, UK, 5–7 September 2018; pp. 353–358. [Google Scholar]
- Becker, A.; Ertel, C.; McLurkin, J. Crowdsourcing swarm manipulation experiments: A massive online user study with large swarms of simple robots. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 2825–2830. [Google Scholar]
- Wan, W.; Shi, B.; Wang, Z.; Fukui, R. Multirobot Object Transport via Robust Caging. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 270–280. [Google Scholar] [CrossRef]
- Wang, Z.; Takano, Y.; Hirata, Y.; Kosuge, K. A pushing leader based decentralized control method for cooperative object transportation. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Sendai, Japan, 28 September–2 October 2004; pp. 1035–1040. [Google Scholar]
- Obradović, J.; Križmančić, M.; Bogdan, S. Decentralized multi-robot formation control using reinforcement learning. In Proceedings of the 2023 XXIX International Conference on Information, Communication and Automation Technologies (ICAT), Sarajevo, Bosnia and Herzegovina, 11–14 June 2023; pp. 1–7. [Google Scholar]
- Nguyen, K.; Dang, V.T.; Pham, D.D.; Dao, P.N. Formation control scheme with reinforcement learning strategy for a group of multiple surface vehicles. Int. J. Robust Nonlinear Control 2024, 34, 2252–2279. [Google Scholar] [CrossRef]
- Venturini, F.; Mason, F.; Pase, F.; Chiariotti, F.; Testolin, A.; Zanella, A.; Zorzi, M. Distributed reinforcement learning for flexible and efficient UAV swarm control. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 955–969. [Google Scholar] [CrossRef]
- Yang, J.; Wang, X.; Bauer, P. Extended PSO Based Collaborative Searching for Robotic Swarms With Practical Constraints. IEEE Access 2019, 7, 76328–76341. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, H.; Wang, H.; Li, X.; Wang, C. Heterogeneous unmanned swarm formation containment control based on reinforcement learning. Aerosp. Sci. Technol. 2024, 150, 109186. [Google Scholar] [CrossRef]
- Croll, J.G.A. Force Systems and Equilibrium; Chatto & Windus: London, UK, 1974. [Google Scholar]
- Leao, W. Controle PID Aplicado em Robo Móvel de Rodas (Parte 2). Available online: https://www.youtube.com/watch?v=PSt96KnCNxc&list=PL1WrY7PmiW_iwesX41-rS6ddHlvbrpe0O&index=34 (accessed on 1 August 2025).
- CoppeliaSim: Robotics Simulation Plataform. Available online: https://www.coppeliarobotics.com (accessed on 1 August 2025).
- Khepera-III: User Manual. Available online: https://www.cyberbotics.com/doc/guide/khepera3?version=R2021a (accessed on 1 August 2025).
- Mukhametzyanov, I.Z. Normalization of Multidimensional Data for Multi-Criteria Decision Making Problems, 1st ed.; International Series in Operations Research & Management Science; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Nedjah, N.; Ferreira, G.B.; de Macedo Mourelle, L. Swarm robotics for collaborative object transport using a pushing strategy. Expert Syst. Appl. 2025, 271, 126610. [Google Scholar] [CrossRef]
- Dorigo, M.; Stutzle, T. Ant Colony Optimization, 1st ed.; The MIT Press: Cambridge, UK, 2004. [Google Scholar]
- Wilson, S.; Glotfelter, P.; Wang, L.; Mayya, S.; Notomista, G.; Mote, M.; Egerstedt, M. The Robotarium: Globally Impactful Opportunities, Challenges, and Lessons Learned in Remote-Access, Distributed Control of Multirobot Systems. IEEE Control Syst. Mag. 2020, 40, 26–44. [Google Scholar] [CrossRef]
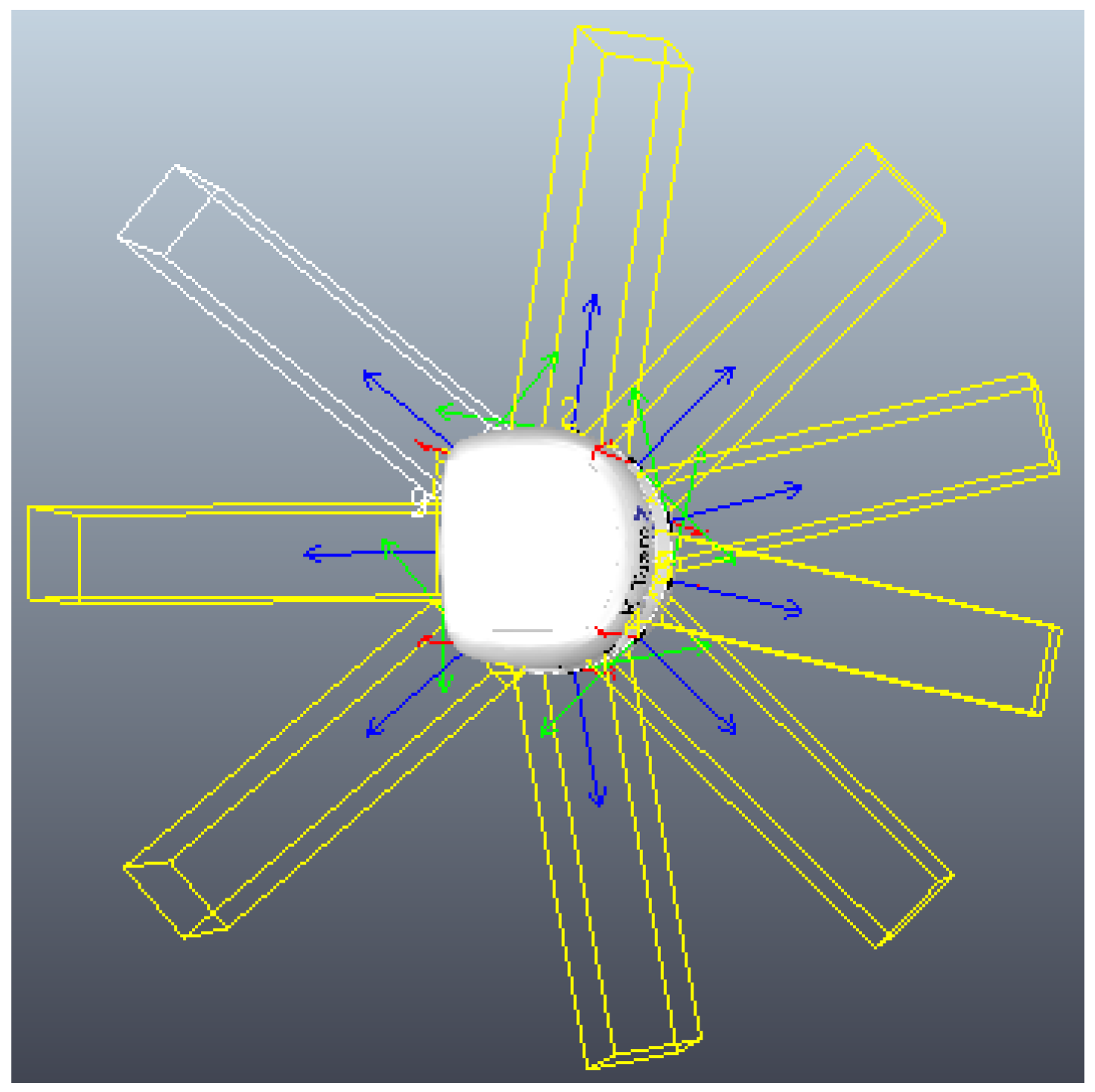



| PIDs | , | , | |||
|---|---|---|---|---|---|
| 1 | 1 | 1 | |||
| w (m) | m (kg) | a (m/s2) | (m) | c (m) | (m) | d (m) | (°) |
|---|---|---|---|---|---|---|---|
| 0.00354 | 3 |
| Arena (m) | Step (m) | (s) | (%) | ||
|---|---|---|---|---|---|
| 2.334 | [68.886, 72.226] | 2.366 | |||
| 1.841 | [58.803, 61.437] | 2.190 | |||
| 7.400 | [216.871, 227.458] | 2.383 | |||
| 3.307 | [195.170, 199.901] | 1.197 |
| (m) | (m) | E (m) | (%) | (s) | (s) | ES | |
|---|---|---|---|---|---|---|---|
| 6 | 2.67 | ||||||
| 7 | 1.45 | ||||||
| 8 | 2.16 |
| (m) | M (kg) | (m) | (m) | E (m) | E (%) | (s) | (s) | ES |
|---|---|---|---|---|---|---|---|---|
| 3.91 | ||||||||
| 1.38 | ||||||||
| 2.49 |
| (m) | (m) | (m) | E (m) | (%) | (s) | (s) | ES | |
|---|---|---|---|---|---|---|---|---|
| 6 | 4.90 | |||||||
| 5.51 | ||||||||
| 7 | 4.33 | |||||||
| 5.56 | ||||||||
| 8 | 4.46 | |||||||
| 5.28 |
| (m) | M (kg) | (m) | (m) | (m) | E (m) | (%) | (s) | (s) | ES |
|---|---|---|---|---|---|---|---|---|---|
| 1.59 | |||||||||
| 4.18 | |||||||||
| 1.43 | |||||||||
| 2.88 | |||||||||
| 2.04 | |||||||||
| 3.95 |
| Step (m) | (s) | (%) | (s) | (%) | |||||
|---|---|---|---|---|---|---|---|---|---|
| 6 | 123.925 | 2.576 | [122.082, 125.768] | 1.487 | 287.849 | 3.625 | [285.256, 290.442] | 0.901 | |
| 7 | 129.051 | 6.823 | [124.170, 133.932] | 3.782 | 306.623 | 7.851 | [301.007, 312.239] | 1.831 | |
| 8 | 130.271 | 7.001 | [125.263, 135.279] | 3.844 | 322.716 | 6.970 | [317.730, 327.702] | 1.545 | |
| 6 | 74.630 | 3.145 | [72.380, 76.880] | 3.014 | 209.018 | 12.257 | [200.250, 217.786] | 4.195 | |
| 7 | 78.739 | 9.270 | [72.600, 79.078] | 4.270 | 235.218 | 3.672 | [232.591, 237.844] | 1.116 | |
| 8 | 78.325 | 4.412 | [75.169, 81.481] | 4.029 | 250.097 | 7.435 | [244.779, 255.415] | 2.126 |
| Step (m) | (m) | (%) | (m) | (%) | |||||
|---|---|---|---|---|---|---|---|---|---|
| 6 | 0.246 | 0.0147 | [0.236, 0.257] | 4.267 | 5.022 | 0.2820 | [4.820, 5.224] | 4.017 | |
| 7 | 0.264 | 0.0146 | [0.253, 0.274] | 3.965 | 4.998 | 0.3440 | [4.752, 5.244] | 4.923 | |
| 8 | 0.316 | 0.0134 | [0.307, 0.326] | 3.036 | 5.142 | 0.2381 | [4.972, 5.312] | 3.312 | |
| 6 | 0.169 | 0.0111 | [0.161, 0.177] | 4.690 | 5.500 | 0.1820 | [5.369, 5.630] | 2.367 | |
| 7 | 0.205 | 0.0630 | [0.175, 0.184] | 2.532 | 5.998 | 0.2669 | [5.807, 6.189] | 3.183 | |
| 8 | 0.206 | 0.0377 | [0.158, 0.174] | 4.897 | 5.229 | 0.311 | [5.006, 5.451] | 4.254 |
| Strategy | Arena () | #WP | M (kg) | (m) | Platform | |
|---|---|---|---|---|---|---|
| Pushing ([26]) | 7 | 27 | 0.18 | 0.3 | Robotarium Sim | |
| Caging (proposed) | 7 | 25 | 0.3 | 0.3 | CoppeliaSim |
| Strategy | Step | Search | (m) | (m) | E (m) | E (%) | (s) | (s) | ES |
|---|---|---|---|---|---|---|---|---|---|
| Pushing ([26]) | – | Rand | 7.84 | ||||||
| – | Opt | 9.67 | |||||||
| Caging (proposed) | 0.5 | Rand | 4.37 | ||||||
| 1.0 | 17.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nedjah, N.; Cardoso, K.d.S.; Mourelle, L.d.M. Collaborative Swarm Robotics for Object Transport via Caging. Sensors 2025, 25, 5063. https://doi.org/10.3390/s25165063
Nedjah N, Cardoso KdS, Mourelle LdM. Collaborative Swarm Robotics for Object Transport via Caging. Sensors. 2025; 25(16):5063. https://doi.org/10.3390/s25165063
Chicago/Turabian StyleNedjah, Nadia, Karen da Silva Cardoso, and Luiza de Macedo Mourelle. 2025. "Collaborative Swarm Robotics for Object Transport via Caging" Sensors 25, no. 16: 5063. https://doi.org/10.3390/s25165063
APA StyleNedjah, N., Cardoso, K. d. S., & Mourelle, L. d. M. (2025). Collaborative Swarm Robotics for Object Transport via Caging. Sensors, 25(16), 5063. https://doi.org/10.3390/s25165063









