PG-Mamba: An Enhanced Graph Framework for Mamba-Based Time Series Clustering
Abstract
1. Introduction
Contributions of the Paper
2. Materials and Methods
2.1. Datasets
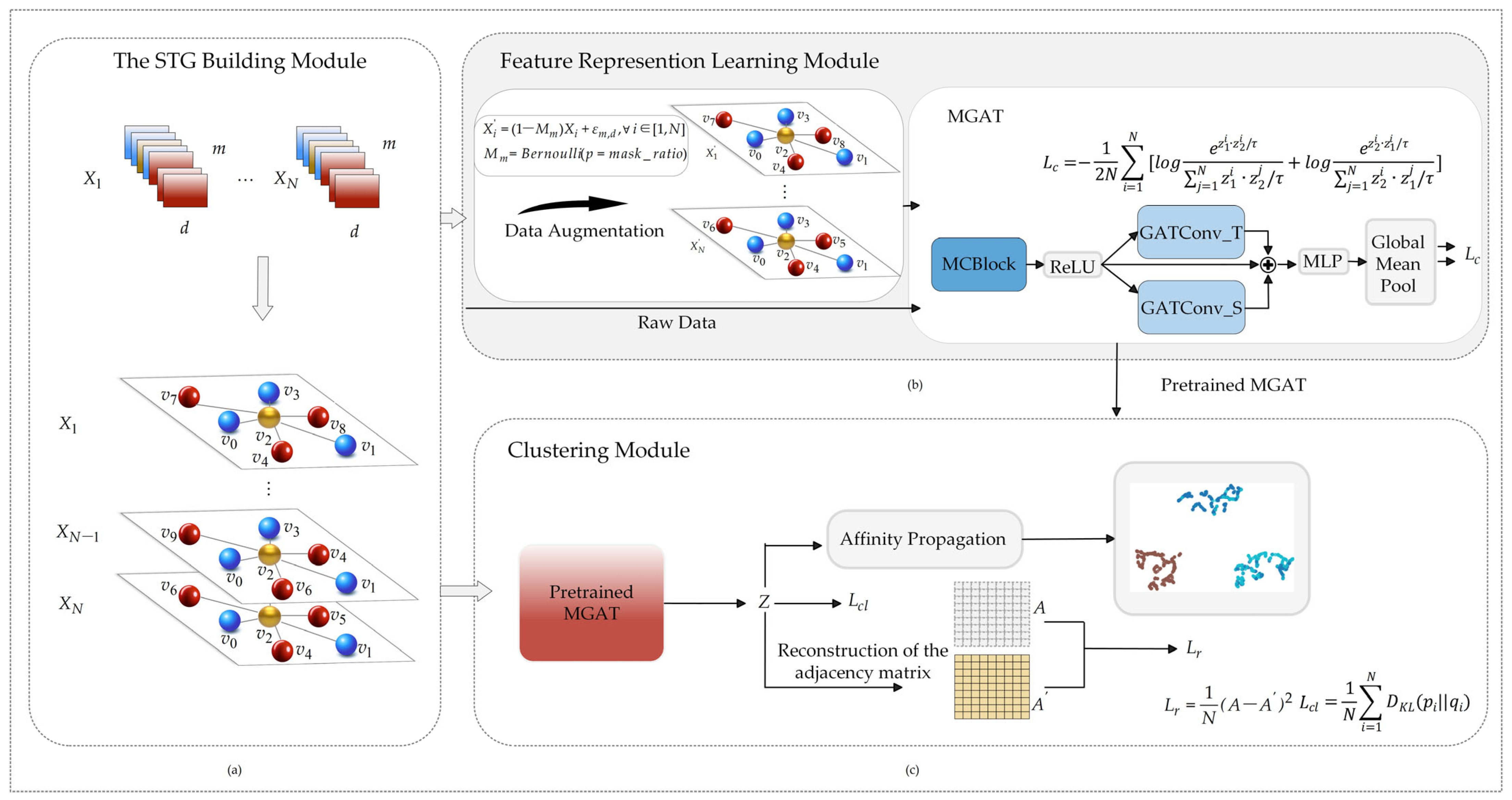
2.2. The STG Building Module
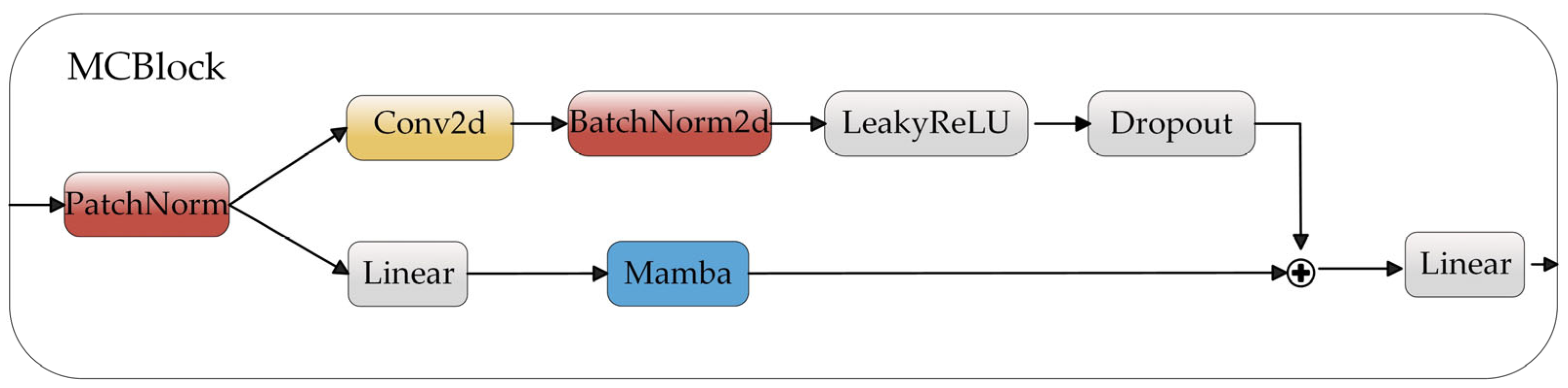
2.3. Feature Representation Learning Module
2.4. Feature Representation Learning Pre-Training
2.5. Cluster Module
2.6. Cluster Validity Indices
3. Results
3.1. Training Setting
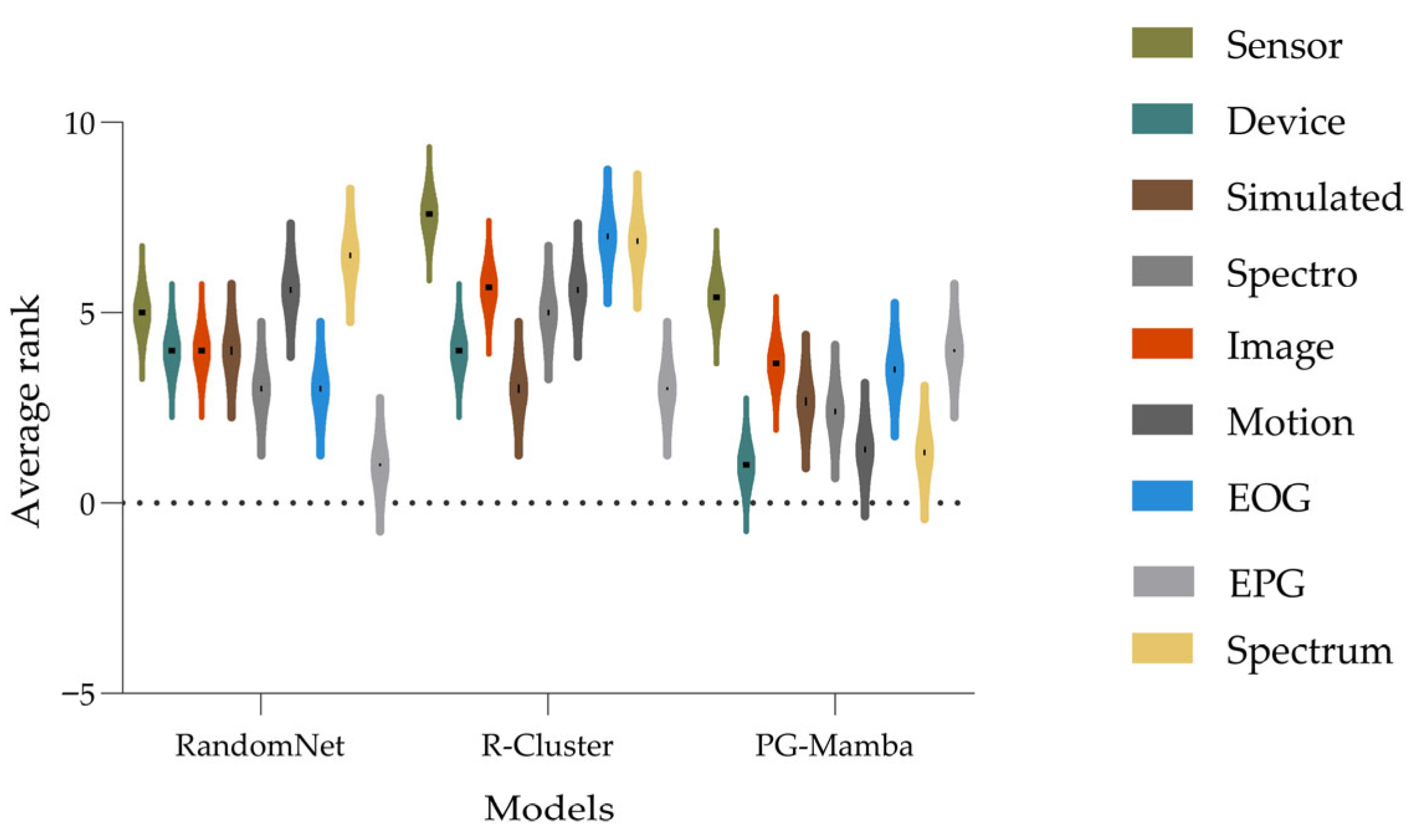
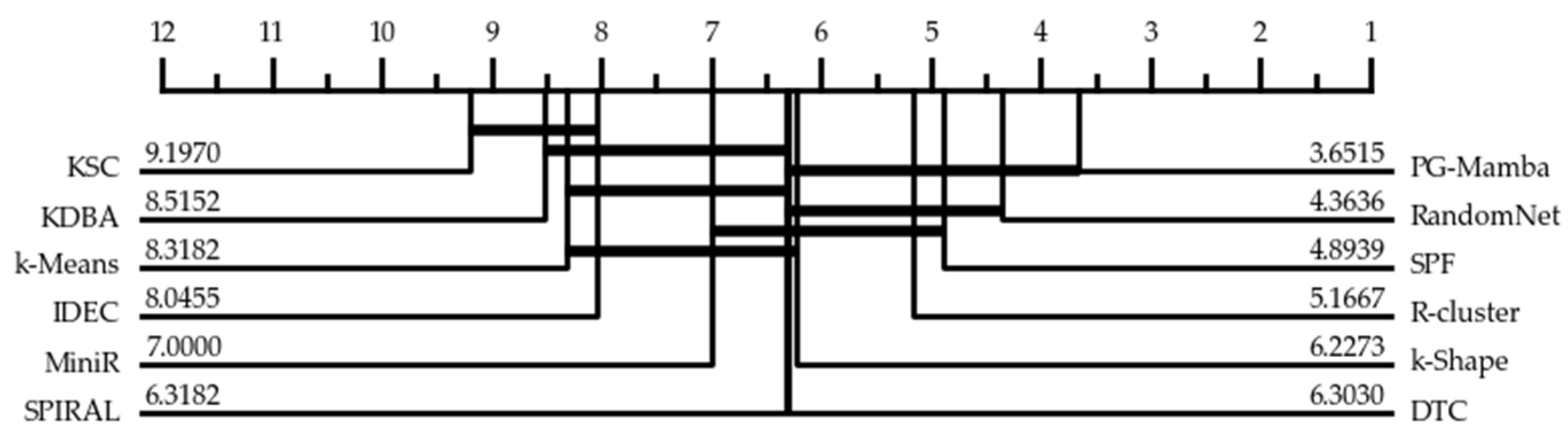
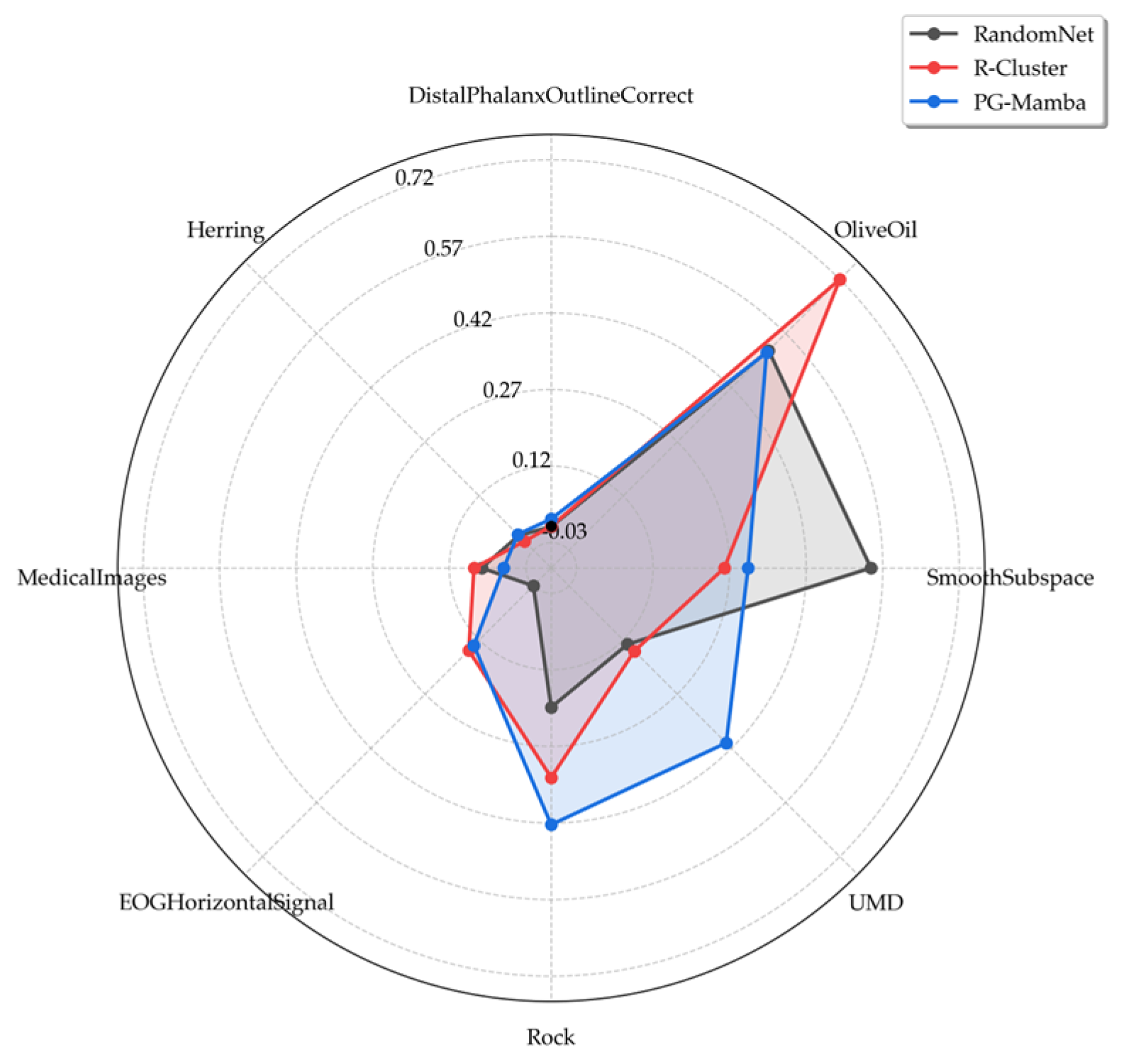
3.2. Experimental Results
- K-Means [1] accomplishes the clustering task by assigning samples to the nearest clusters by calculating the Euclidean distance and continuously updating the cluster centers.
- DBA [2] flexibly aligns the time series to the average series based on DTW path backtracking by calculating the DTW distance from each time series to the average series.
- KSC [3] takes into account that the time series should still maintain the same shape when the time axis is panned and captures the evolutionary pattern of the time-series data through different scaling methods when clustering.
- K-shape [4] aligns the nearest clusters by SBD values and uses Rayleigh Quotient maximization to find the center of the representation clusters that have the greatest similarity to all time series.
- SPF [6] converts the timing data into symbol patterns after time window division and randomly selects the symbol patterns with SPT, which together form the SPF to correct the deviation of SPT in a global view.
- IDEC [7] fine-tunes the clustering loss by pre-training a denoising self-encoder to preserve the distribution of the data.
- DTC [8] uses CNN and BiLSTM as encoder layers to capture spatial and temporal feature dependencies independently.
- Minirocket [10] determines the initialization of the weighted convolution kernel by means of predefined rules to simulate the convolution operation in a linear computation to achieve the classification task.
- Randomnet [12] utilizes a combined module of multi-branch CNN and LSTM to independently extract temporal and spatial features of time-series data and integrates them through multi-branch clustering to obtain the final clustering labels.
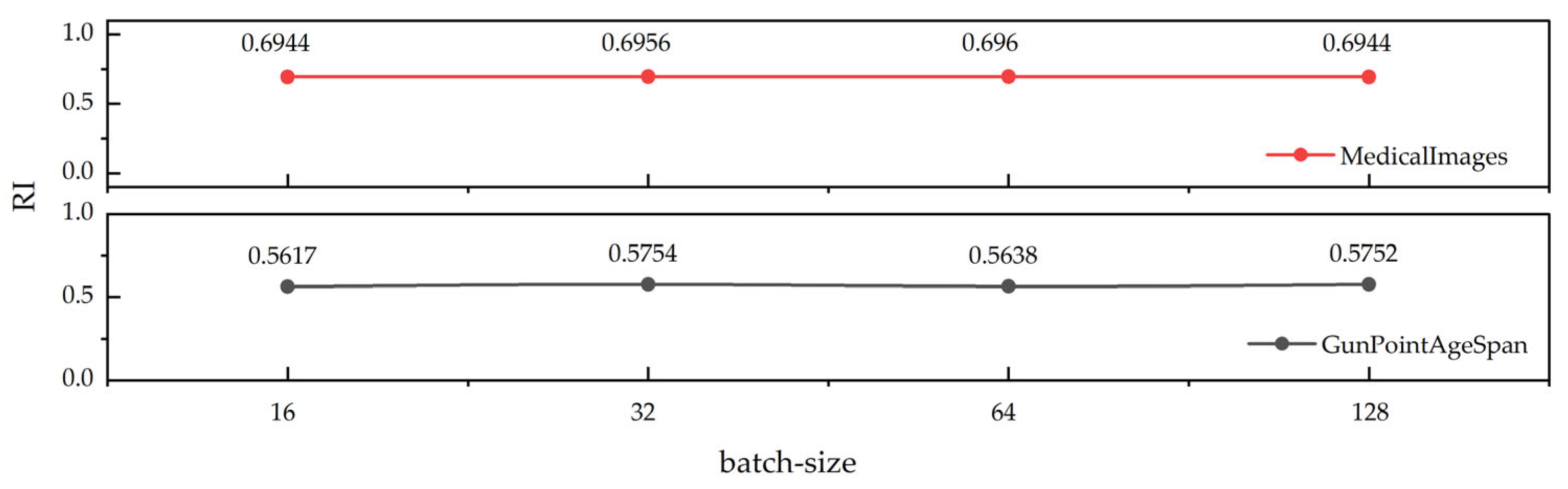
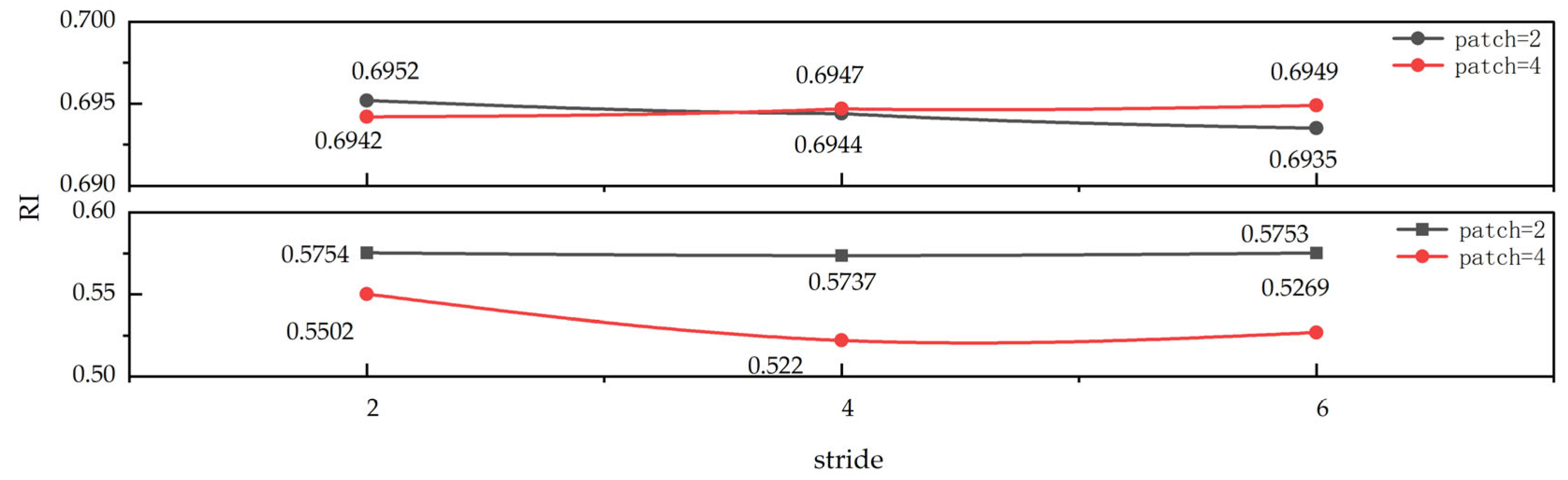
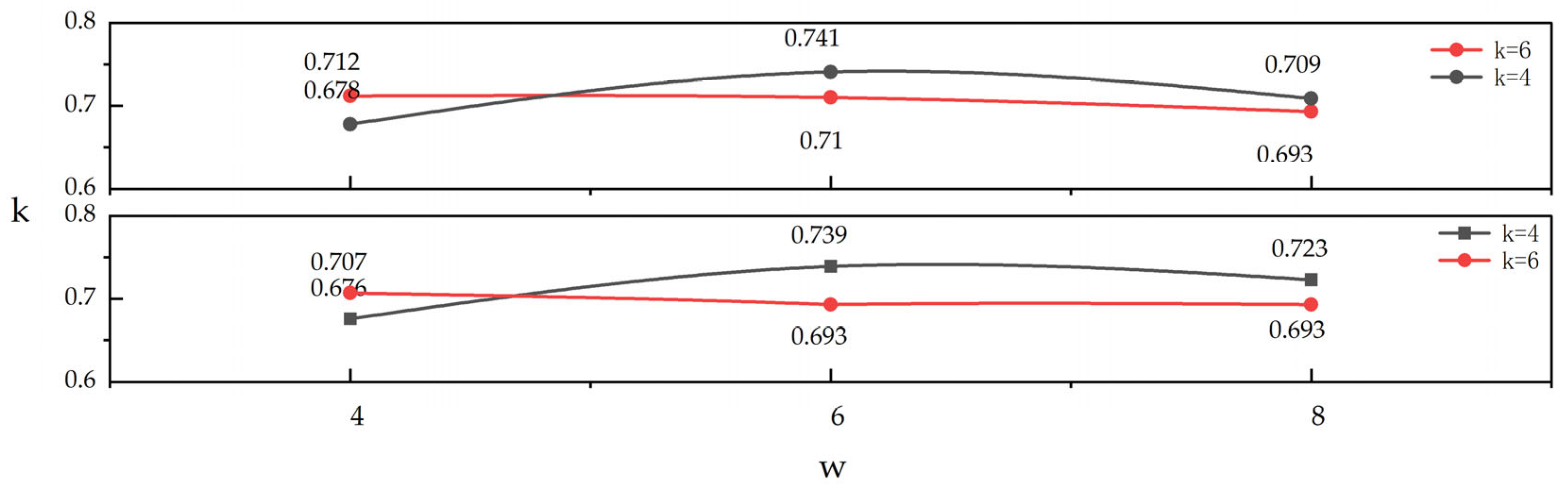
3.3. Analyzing Parameter Sensitivity
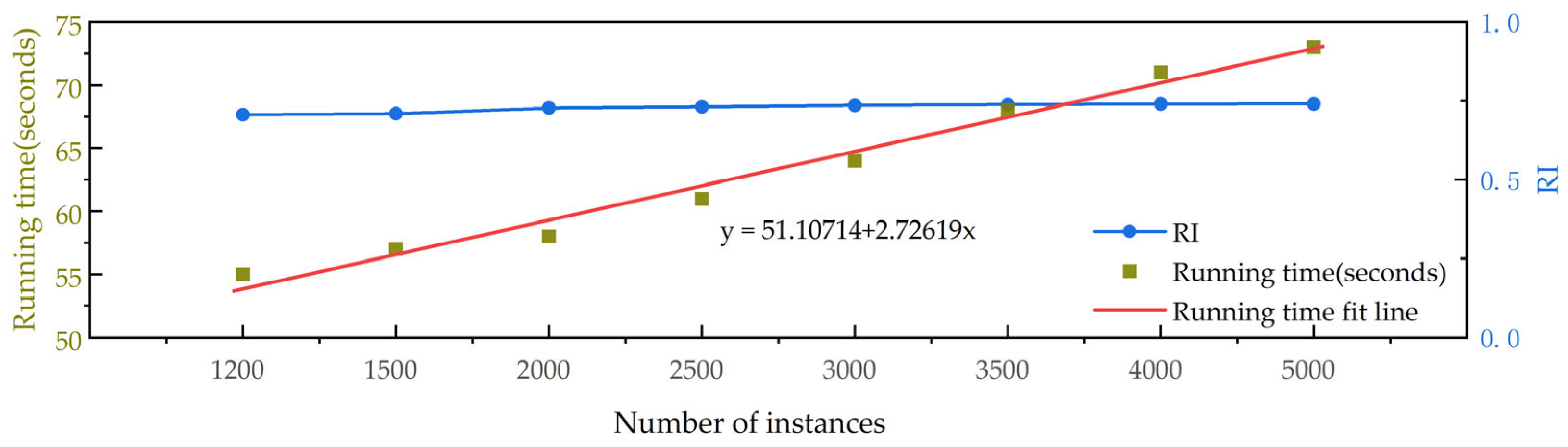
3.4. Analyzing the Time Complexity
3.5. Ablation Study
4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Los Angeles, CA, USA, 1 January 1967; University of California Press: Los Angeles, CA, USA, 1967. [Google Scholar]
- Petitjean, F.; Ketterlin, A.; Gançarski, P. A global averaging method for dynamic time warping, with applications to clustering. Pattern Recognit. 2011, 44, 678–693. [Google Scholar] [CrossRef]
- Yang, J.; Leskovec, J. Patterns of temporal variation in online media. In Proceedings of the fourth ACM international conference on Web search and data mining, Hong Kong, China, 9–12 February 2011. [Google Scholar]
- Lines, J.; Bagnall, A. Time series classification with ensembles of elastic distance measures. Data. Min. Knowl. Disc. 2015, 29, 565–592. [Google Scholar] [CrossRef]
- Lei, Q.; Yi, J.; Vaculin, R.; Wu, L.; Dhillon, I.S. Similarity preserving representation learning for time series clustering. arXiv 2017, arXiv:1702.03584. [Google Scholar]
- Li, X.; Lin, J.; Zhao, L. Linear Time Complexity Time Series Clustering with Symbolic Pattern Forest. In Proceedings of the Nineth International Joint Conference on Artificial Intelligence, Macau, China, 10–16 August 2019. [Google Scholar]
- Guo, X.; Gao, L.; Liu, X. Improved deep embedded clustering with local structure preservation. In Proceedings of the 17th International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017. [Google Scholar]
- Madiraju, N.S. Deep Temporal Clustering: Fully Unsupervised Learning of Time-Domain Features. Master’s Thesis, Arizona State University, Tempe, AZ, USA, 2018. [Google Scholar]
- Dempster, A.; Schmidt, D.F.; Webb, G.I. Minirocket: A very fast (almost) deterministic transform for time series classification. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Virtual Event Singapore, 14–18 August 2021. [Google Scholar]
- Dempster, A.; Petitjean, F.; Webb, G.I. ROCKET: Exceptionally fast and accurate time series classification using random convolutional kernels. Data. Min. Knowl. Disc. 2020, 34, 1454–1495. [Google Scholar] [CrossRef]
- Jorge, M.B.; Rubén, C. Time series clustering with random convolutional kernels. Data. Min. Knowl. Disc. 2024, 8, 1862–1888. [Google Scholar] [CrossRef]
- Li, X.; Xi, W.; Lin, J. Randomnet: Clustering time series using untrained deep neural networks. Data. Min. Knowl. Disc. 2024, 38, 3473–3502. [Google Scholar] [CrossRef]
- Fern, X.Z.; Brodley, C.E. Solving cluster ensemble problems by bipartite graph partitioning. In Proceedings of the Twenty-First International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004. [Google Scholar]
- Gu, A.; Dao, T. Mamba: Linear-time sequence modeling with selective state spaces. arXiv 2023. [Google Scholar] [CrossRef]
- He, Y.; Tu, B.; Liu, B.; Li, J.; Plaza, A. 3DSS-Mamba: 3D-spectral-spatial mamba for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5534216. [Google Scholar] [CrossRef]
- Wu, R.; Liu, Y.; Liang, P.; Chang, Q. Ultralight vm-unet: Parallel vision mamba significantly reduces parameters for skin lesion segmentation. arXiv 2024, arXiv:2403.20035. [Google Scholar] [CrossRef]
- Chen, H.; Song, J.; Han, C.; Xia, J.; Yokoya, N. Changemamba: Remote sensing change detection with spatio-temporal state space model. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4409720. [Google Scholar]
- Zhang, Z.; Peng, B.; Zhao, T. An ultra-lightweight network combining Mamba and frequency-domain feature extraction for pavement tiny-crack segmentation. Expert. Syst. Appl. 2025, 264, 125941. [Google Scholar] [CrossRef]
- Li, L.; Wang, H.; Zhang, W.; Coster, A. Stg-mamba: Spatial-temporal graph learning via selective state space model. arXiv 2024, arXiv:2403.12418. [Google Scholar]
- Dau, H.A.; Bagnall, A.; Kamgar, K.; Yeh, C.C.M.; Zhu, Y.; Gharghabi, S.; Ratanamahatana, C.A.; Keogh, E. The ucr time series archive. J. Autom. Sin. 2019, 6, 1293–1305. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, L.; Pal, S.; Zhang, Y.; Coates, M. Multi-resolution time-series transformer for long-term forecasting. In Proceedings of the 27th International Conference on Artificial Intelligence and Statistics, Valencia, Spain, 2–4 May 2024. [Google Scholar]
- Abdel-Sater, R.; Ben Hamza, A. A federated large language model for long-term time series forecasting. In Proceedings of the 27th European Conference on Artificial Intelligence, Santiago de Compostela, Spain, 19–24 October 2024. [Google Scholar]
- Huang, L.; Chen, Y.; He, X. Spectral-spatial mamba for hyperspectral image classification. arXiv 2024, arXiv:2404.18401. [Google Scholar] [CrossRef]
- Milligan, G.W.; Cooper, M.C. A study of the comparability of external criteria for hierarchical cluster analysis. Multivar. Behav. Res. 1986, 21, 441–458. [Google Scholar] [CrossRef] [PubMed]
- Demšar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]

| Dataset Name | Data Type | Train Size | Test Size | Length | Class |
|---|---|---|---|---|---|
| AllGestureWiimoteX | Sensor | 300 | 700 | 500 | 10 |
| Chinatown | Traffic | 20 | 343 | 24 | 2 |
| Coffee | Spectro | 28 | 28 | 286 | 2 |
| CricketY | Motion | 390 | 390 | 300 | 12 |
| DistalPhalanxOutlineCorrect | Image | 600 | 276 | 80 | 2 |
| DodgerLoopGame | Sensor | 20 | 138 | 288 | 2 |
| ECGFiveDays | ECG | 23 | 861 | 136 | 2 |
| EOGHorizontalSignal | EOG | 362 | 362 | 1250 | 12 |
| EOGVerticalSignal | EOG | 362 | 362 | 1250 | 12 |
| EthanolLevel | Spectro | 504 | 500 | 1751 | 4 |
| FordA | Sensor | 3601 | 1320 | 500 | 2 |
| Fungi | HRM | 18 | 186 | 201 | 18 |
| GesturePebbleZ1 | Sensor | 132 | 172 | 455 | 6 |
| GunPoint | Motion | 50 | 150 | 150 | 2 |
| GunPointAgeSpan | Motion | 135 | 316 | 150 | 2 |
| Herring | Image | 64 | 64 | 512 | 2 |
| InlineSkate | Motion | 100 | 550 | 1882 | 7 |
| InsectEPGSmallTrain | EPG | 17 | 249 | 601 | 3 |
| Meat | Spectro | 60 | 60 | 448 | 3 |
| MedicalImages | Image | 381 | 760 | 99 | 10 |
| OliveOil | Spectro | 30 | 30 | 570 | 4 |
| Phoneme | Sensor | 214 | 1896 | 1024 | 39 |
| PigAirwayPressure | Hemodynamics | 104 | 208 | 2000 | 52 |
| RefrigerationDevices | Device | 375 | 375 | 720 | 3 |
| Rock | Spectrum | 20 | 50 | 2844 | 4 |
| ScreenType | Device | 375 | 375 | 720 | 3 |
| SemgHandMovementCh2 | Spectrum | 450 | 450 | 1500 | 6 |
| SemgHandSubjectCh2 | Spectrum | 450 | 450 | 1500 | 5 |
| SmoothSubspace | Simulated | 150 | 150 | 15 | 3 |
| UMD | Simulated | 36 | 144 | 150 | 3 |
| Wine | Spectro | 57 | 54 | 234 | 2 |
| Worms | Motion | 181 | 77 | 900 | 5 |
| TwoPatterns | Simulated | 1000 | 4000 | 128 | 4 |
| Datasets | Data Type | k-Means | KSC | k-Shape | SPF | SPIRAL | KDBA | IDEC | DTC | MiniR | RandomNet | R-Cluster | PG-Mamba |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AllGestureWiimoteX | Sensor | 0.83 | 0.099 | 0.854 | 0.836 | 0.835 | 0.819 | 0.824 | 0.817 | 0.82 | 0.834 | 0.812 | 0.878 |
| Chinatown | Traffic | 0.527 | 0.526 | 0.526 | 0.633 | 0.787 | 0.569 | 0.513 | 0.527 | 0.582 | 0.592 | 0.579 | 0.489 |
| Coffee | Spectro | 0.751 | 0.805 | 0.751 | 0.834 | 0.805 | 0.777 | 0.492 | 0.492 | 0.75 | 1 | 0.777 | 0.815 |
| CricketY | Motion | 0.854 | 0.514 | 0.876 | 0.871 | 0.856 | 0.805 | 0.858 | 0.848 | 0.869 | 0.868 | 0.876 | 0.884 |
| DistalPhalanxOutlineCorrect | Image | 0.499 | 0.499 | 0.499 | 0.5 | 0.501 | 0.502 | 0.526 | 0.521 | 0.501 | 0.501 | 0.500 | 0.499 |
| DodgerLoopGame | Sensor | 0.503 | 0.639 | 0.585 | 0.517 | 0.529 | 0.515 | 0.556 | 0.597 | 0.502 | 0.529 | 0.510 | 0.513 |
| ECGFiveDays | ECG | 0.5 | 0.871 | 0.879 | 0.578 | 0.53 | 0.511 | 0.506 | 0.596 | 0.761 | 0.531 | 0.512 | 0.507 |
| EOGHorizontalSignal | EOG | 0.857 | 0.422 | 0.877 | 0.869 | 0.866 | 0.797 | 0.082 | 0.855 | 0.569 | 0.874 | 0.857 | 0.859 |
| EOGVerticalSignal | EOG | 0.856 | 0.603 | 0.876 | 0.87 | 0.851 | 0.8 | 0.855 | 0.838 | 0.786 | 0.861 | 0.840 | 0.871 |
| EthanolLevel | Spectro | 0.623 | 0.621 | 0.623 | 0.626 | 0.606 | 0.553 | 0.613 | 0.689 | 0.621 | 0.627 | 0.673 | 0.741 |
| FordA | Sensor | 0.5 | 0.505 | 0.578 | 0.501 | 0.5 | 0.5 | 0.5 | 0.51 | 0.5 | 0.501 | 0.503 | 0.507 |
| Fungi | HRM | 0.938 | 0.794 | 0.798 | 0.99 | 0.993 | 0.398 | 0.959 | 0.926 | 0.999 | 0.976 | 1.000 | 0.930 |
| GesturePebbleZ1 | Sensor | 0.802 | 0.213 | 0.87 | 0.904 | 0.795 | 0.75 | 0.838 | 0.841 | 0.832 | 0.818 | 0.796 | 0.826 |
| GunPoint | Motion | 0.497 | 0.507 | 0.497 | 0.497 | 0.498 | 0.497 | 0.498 | 0.53 | 0.497 | 0.507 | 0.497 | 0.512 |
| GunPointAgeSpan | Motion | 0.628 | 0.518 | 0.53 | 0.514 | 0.546 | 0.518 | 0.499 | 0.559 | 0.499 | 0.499 | 0.519 | 0.575 |
| Herring | Image | 0.5 | 0.499 | 0.504 | 0.504 | 0.506 | 0.499 | 0.504 | 0.489 | 0.502 | 0.508 | 0.507 | 0.777 |
| InlineSkate | Motion | 0.736 | 0.76 | 0.749 | 0.759 | 0.693 | 0.669 | 0.749 | 0.763 | 0.738 | 0.759 | 0.749 | 0.832 |
| InsectEPGSmallTrain | EPG | 0.564 | 0.574 | 0.707 | 0.732 | 0.722 | 0.629 | 0.628 | 0.635 | 0.775 | 1 | 0.768 | 0.749 |
| Meat | Spectro | 0.785 | 0.785 | 0.729 | 0.83 | 0.852 | 0.8 | 0.328 | 0.578 | 0.768 | 0.86 | 0.854 | 0.872 |
| MedicalImages | Image | 0.665 | 0 | 0.668 | 0.667 | 0.668 | 0.684 | 0.682 | 0.651 | 0.678 | 0.677 | 0.674 | 0.694 |
| OliveOil | Spectro | 0.739 | 0.845 | 0.745 | 0.875 | 0.872 | 0.828 | 0.288 | 0.288 | 0.775 | 0.815 | 0.882 | 0.816 |
| Phoneme | Sensor | 0.911 | 0.491 | 0.929 | 0.93 | 0.928 | 0.789 | 0.922 | 0.082 | 0.928 | 0.932 | 0.929 | 0.921 |
| PigAirwayPressure | Hemodynamics | 0.914 | 0.016 | 0.903 | 0.936 | 0.96 | 0.84 | 0.938 | 0.883 | 0.967 | 0.969 | 0.967 | 0.925 |
| RefrigerationDevices | Device | 0.555 | 0.332 | 0.556 | 0.558 | 0.587 | 0.588 | 0.554 | 0.518 | 0.538 | 0.58 | 0.578 | 0.662 |
| Rock | Spectrum | 0.664 | 0.38 | 0.689 | 0.719 | 0.657 | 0.675 | 0.66 | 0.722 | 0.734 | 0.695 | 0.747 | 0.777 |
| ScreenType | Device | 0.562 | 0.332 | 0.557 | 0.568 | 0.566 | 0.525 | 0.562 | 0.635 | 0.559 | 0.569 | 0.591 | 0.642 |
| SemgHandMovementCh2 | Spectrum | 0.735 | 0.638 | 0.739 | 0.756 | 0.604 | 0.732 | 0.743 | 0.783 | 0.762 | 0.743 | 0.743 | 0.822 |
| SemgHandSubjectCh2 | Spectrum | 0.734 | 0.645 | 0.721 | 0.734 | 0.568 | 0.661 | 0.73 | 0.797 | 0.698 | 0.7 | 0.696 | 0.782 |
| SmoothSubspace | Simulated | 0.709 | 0.333 | 0.682 | 0.645 | 0.896 | 0.629 | 0.585 | 0.638 | 0.631 | 0.816 | 0.662 | 0.741 |
| UMD | Simulated | 0.557 | 0.559 | 0.612 | 0.622 | 0.626 | 0.557 | 0.614 | 0.682 | 0.616 | 0.621 | 0.762 | 0.739 |
| Wine | Spectro | 0.496 | 0.496 | 0.496 | 0.5 | 0.495 | 0.496 | 0.496 | 0.496 | 0.503 | 0.502 | 0.507 | 0.660 |
| Worms | Motion | 0.646 | 0.52 | 0.656 | 0.683 | 0.666 | 0.644 | 0.263 | 0.701 | 0.648 | 0.687 | 0.655 | 0.724 |
| TwoPatterns | Simulated | 0.628 | 0.537 | 0.675 | 0.693 | 0.656 | 0.945 | 0.63 | 0.705 | 0.638 | 0.725 | 0.743 | 0.741 |
| Average Rand Index | 0.675 | 0.511 | 0.695 | 0.705 | 0.698 | 0.652 | 0.606 | 0.642 | 0.683 | 0.717 | 0.705 | 0.736 | |
| Average rank | 8.364 | 9.212 | 6.303 | 4.894 | 6.318 | 8.545 | 8.076 | 6.303 | 7.030 | 4.379 | 4.970 | 3.606 | |
| Number Best | 1 | 1 | 4 | 1 | 2 | 1 | 1 | 2 | 0 | 4 | 3 | 13 |
| Datasets | k-Means | KSC | k-Shape | SPF | SPIRAL | KDBA | IDEC | DTC | MiniR | RandomNet | R-Cluster | PG-Mamba |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sensor | 8.80 | 8.00 | 2.40 | 3.90 | 7.00 | 9.60 | 6.40 | 5.80 | 8.10 | 5.00 | 7.60 | 5.40 |
| Device | 7.75 | 12.00 | 8.50 | 8.50 | 4.50 | 6.50 | 8.25 | 6.50 | 9.50 | 4.00 | 4.00 | 1.00 |
| Image | 10.00 | 11.17 | 8.17 | 7.33 | 5.50 | 5.17 | 3.33 | 8.33 | 5.67 | 4.00 | 5.67 | 3.67 |
| Simulated | 8.83 | 11.33 | 7.00 | 6.00 | 4.33 | 7.50 | 9.67 | 5.33 | 8.33 | 4.00 | 3.00 | 2.67 |
| Spectro | 8.20 | 6.60 | 8.50 | 3.80 | 6.90 | 7.70 | 10.70 | 8.90 | 7.70 | 3.60 | 3.00 | 2.40 |
| Motion | 7.80 | 7.40 | 6.30 | 6.30 | 6.70 | 10.10 | 8.60 | 3.60 | 8.60 | 5.60 | 5.60 | 1.40 |
| EOG | 6.00 | 11.50 | 1.00 | 3.00 | 5.50 | 9.50 | 9.00 | 8.50 | 10.50 | 3.00 | 7.00 | 3.50 |
| EPG | 12.00 | 11.00 | 7.00 | 5.00 | 6.00 | 9.00 | 10.00 | 8.00 | 2.00 | 1.00 | 3.00 | 4.00 |
| HRM | 7.00 | 11.00 | 10.00 | 4.00 | 3.00 | 12.00 | 6.00 | 9.00 | 2.00 | 5.00 | 1.00 | 8.00 |
| Spectrum | 7.17 | 11.33 | 7.00 | 4.17 | 11.67 | 9.33 | 7.17 | 2.33 | 4.67 | 6.50 | 5.33 | 1.33 |
| Average rank | 9.05 | 10.30 | 6.60 | 4.95 | 5.90 | 8.90 | 7.95 | 6.45 | 7.25 | 3.25 | 4.05 | 2.70 |
| Num. Top-1 | 0 | 0 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 5 |
| Model Configuration | Average Rand Index | Average FLOPs (G) |
|---|---|---|
| PG-Mamba | 0.736 (+0.040) | 49.851 (+6.828) |
| PG-Mamba w/o Conv | 0.715 (+0.019) | 44.751 (+1.728) |
| PG-Mamba w/o Mamba | 0.708 (+0.012) | 49.188 (+6.165) |
| PG-Mamba w/o Conv and Mamba | 0.696 | 43.023 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Zuo, D.; Gao, J. PG-Mamba: An Enhanced Graph Framework for Mamba-Based Time Series Clustering. Sensors 2025, 25, 5043. https://doi.org/10.3390/s25165043
Sun Y, Zuo D, Gao J. PG-Mamba: An Enhanced Graph Framework for Mamba-Based Time Series Clustering. Sensors. 2025; 25(16):5043. https://doi.org/10.3390/s25165043
Chicago/Turabian StyleSun, Yao, Dongshi Zuo, and Jing Gao. 2025. "PG-Mamba: An Enhanced Graph Framework for Mamba-Based Time Series Clustering" Sensors 25, no. 16: 5043. https://doi.org/10.3390/s25165043
APA StyleSun, Y., Zuo, D., & Gao, J. (2025). PG-Mamba: An Enhanced Graph Framework for Mamba-Based Time Series Clustering. Sensors, 25(16), 5043. https://doi.org/10.3390/s25165043





