Coverage Analysis of 5G Intelligent High-Speed Railway System Based on Beamwidth-Adaptive Free-Space Optical Communication
Abstract
1. Introduction
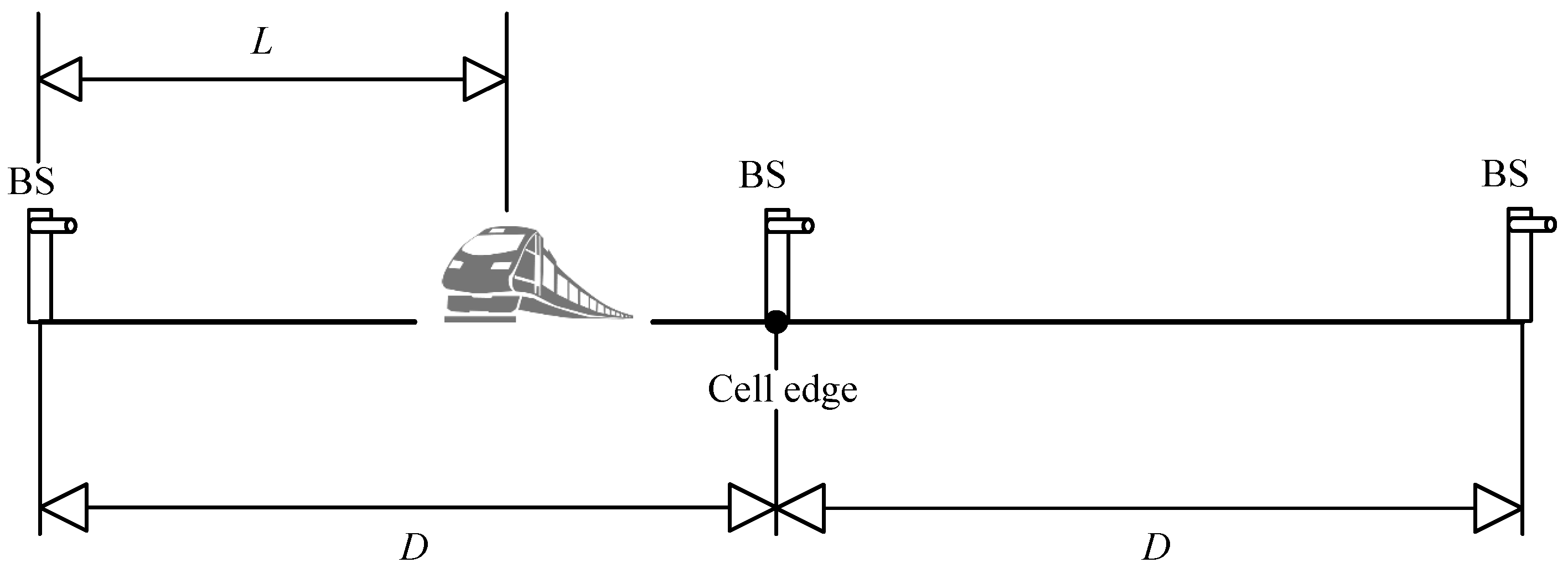
- We construct a model of an intelligent HSR system based on beamwidth-adaptive FSO communication with narrow-strip-shaped cells. In this model, the cell diameter and cell edge are defined, and two scenarios of transmitter beamwidth (i.e., wide beam and narrow beam) are considered. When the transmitter emits a wide beam, the channel gain includes geometric loss, atmospheric attenuation, and atmospheric turbulence. When the transmitter emits a narrow beam, the channel gain includes pointing error, atmospheric attenuation, and atmospheric turbulence.
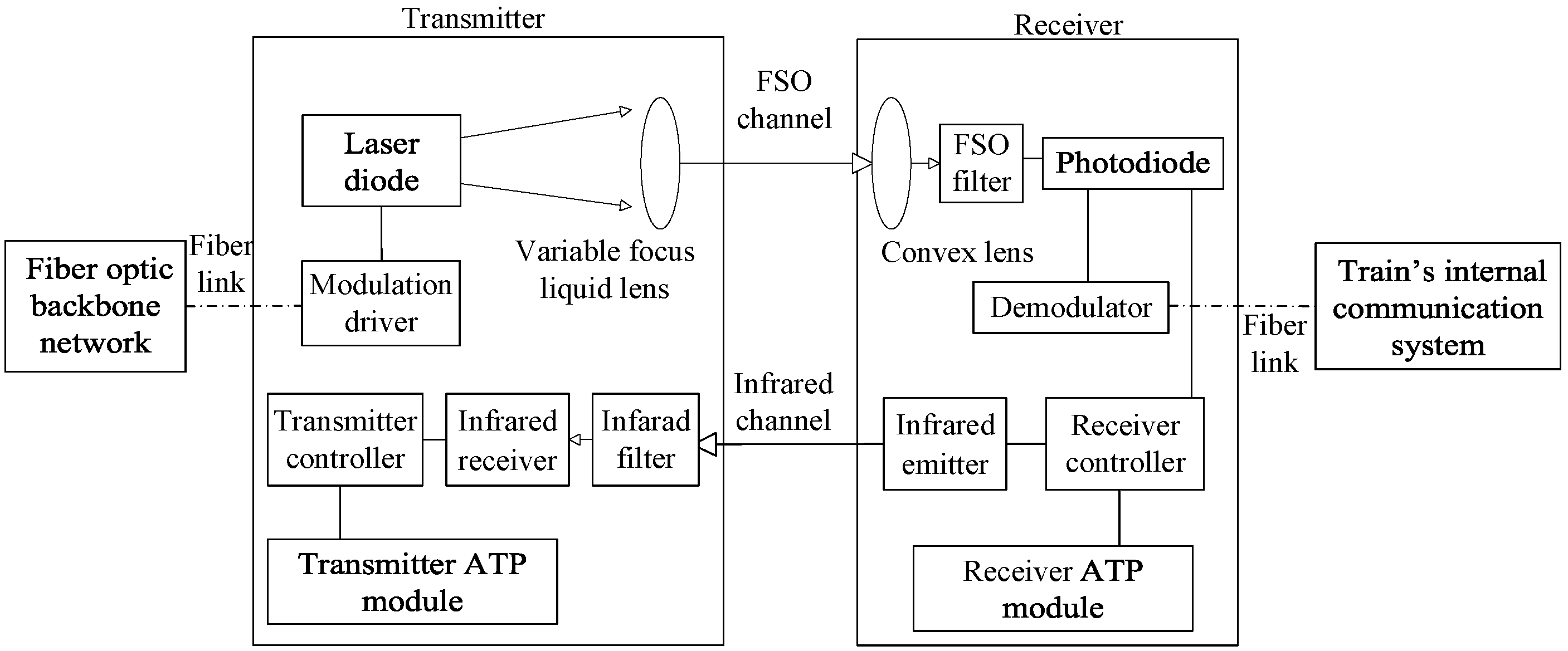
- We propose a beamwidth-adaptive FSO communication system. By incorporating an additional transmitter controller and infrared emitter into the transmitter unit, as well as an additional receiver controller and infrared receiver into the receiver unit, the system is capable of adaptively managing the on or off state of the ATP module.
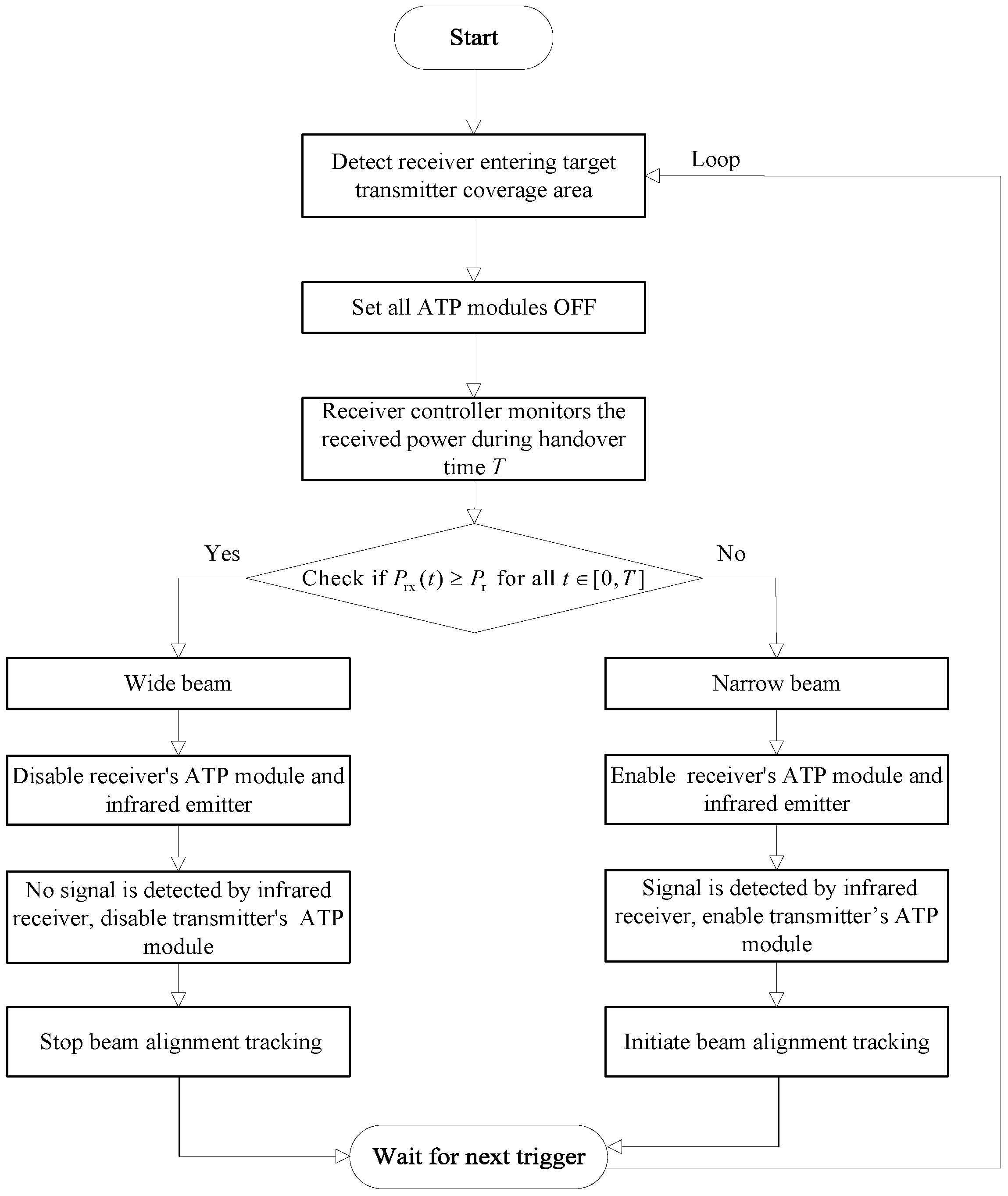
- We propose a beamwidth-adaptive method. During the handover process, the receiver controller assesses the beam width of the target transmitter by detecting the signal strength received from the target transmitter. In conjunction with the infrared emitter, infrared receiver, and transmitter controller, it adaptively controls the on or off state of the ATP modules in both the transmitter and receiver, thereby achieving dynamic alignment and tracking of the optical beams. Specifically, when the target transmitter emits a wide beam, the system keeps the ATP module off to conserve energy; when a narrow beam is transmitted, the ATP module is activated to ensure precise beam alignment between the transmitter and receiver.
- We analyze the coverage performance at the cell edge by studying the statistical characteristics of the received signal-to-noise ratio (SNR). Based on the definition of ECP and utilizing integral formulas of the Meijer’s G-function, closed-form expressions of ECP are derived for both the wide-beam and narrow-beam cases.
- We present the average coverage performance of the cells, which is characterized by the percentage of CCA. The closed-form expressions of the percentage of CCA for the cases of wide beams and narrow beams are derived by utilizing the mathematical definition, the integral formula of the Meijer’s G-function, and the composite trapezoidal integration approximation method.
- Numerical results are presented, showing good agreement between theoretical and simulation results, thereby validating the accuracy of the derived expressions. In addition, the effects of cell diameter, transmit power, SNR threshold, and weather visibility on coverage performance are analyzed.
2. System and Channel Models
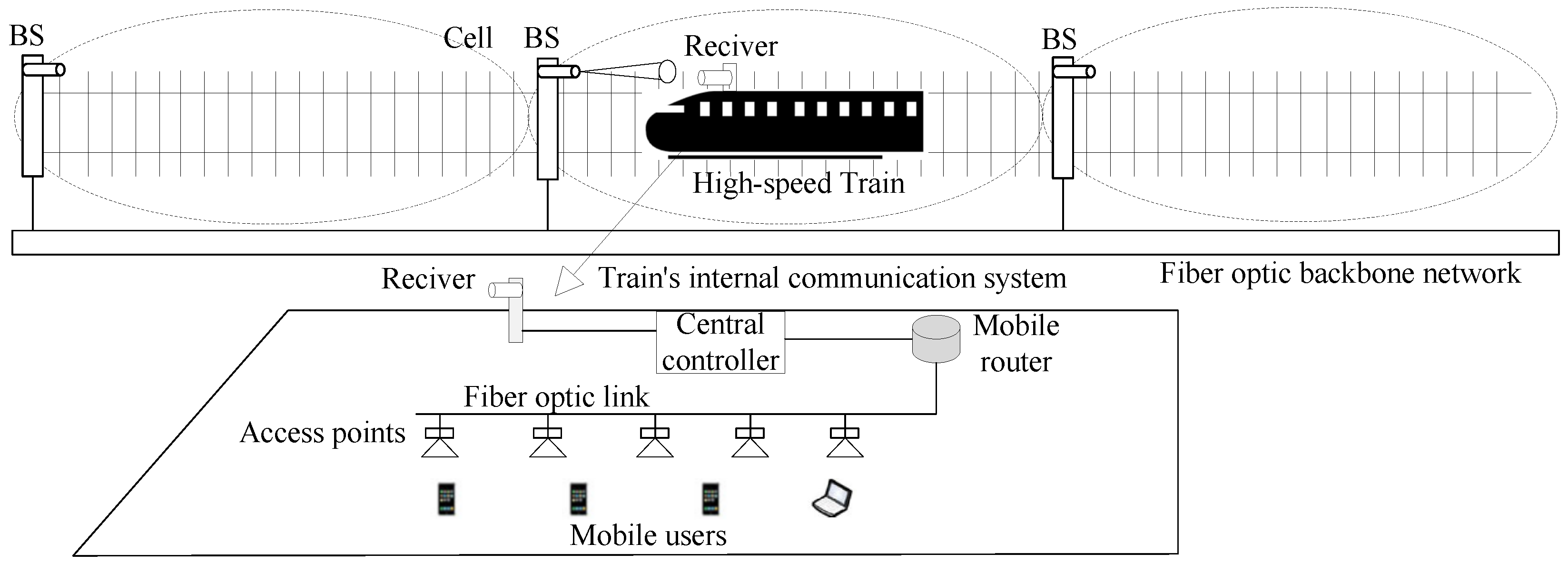
2.1. System Model
2.2. Channel Model
2.2.1. Geometric Loss
2.2.2. Atmospheric Attenuation
2.2.3. Atmospheric Turbulence
2.2.4. Pointing Error
3. Proposed Beamwidth-Adaptive FSO Communication System and Method
3.1. Beamwidth-Adaptive System
3.2. Beamwidth-Adaptive Method
| Algorithm 1 Beamwidth-adaptive Method |
|
4. Coverage Performance Analysis
4.1. ECP Analysis
4.2. Percentage of CCA Analysis
5. Numerical Results
| Algorithm 2 Monte-Carlo simulation method |
|
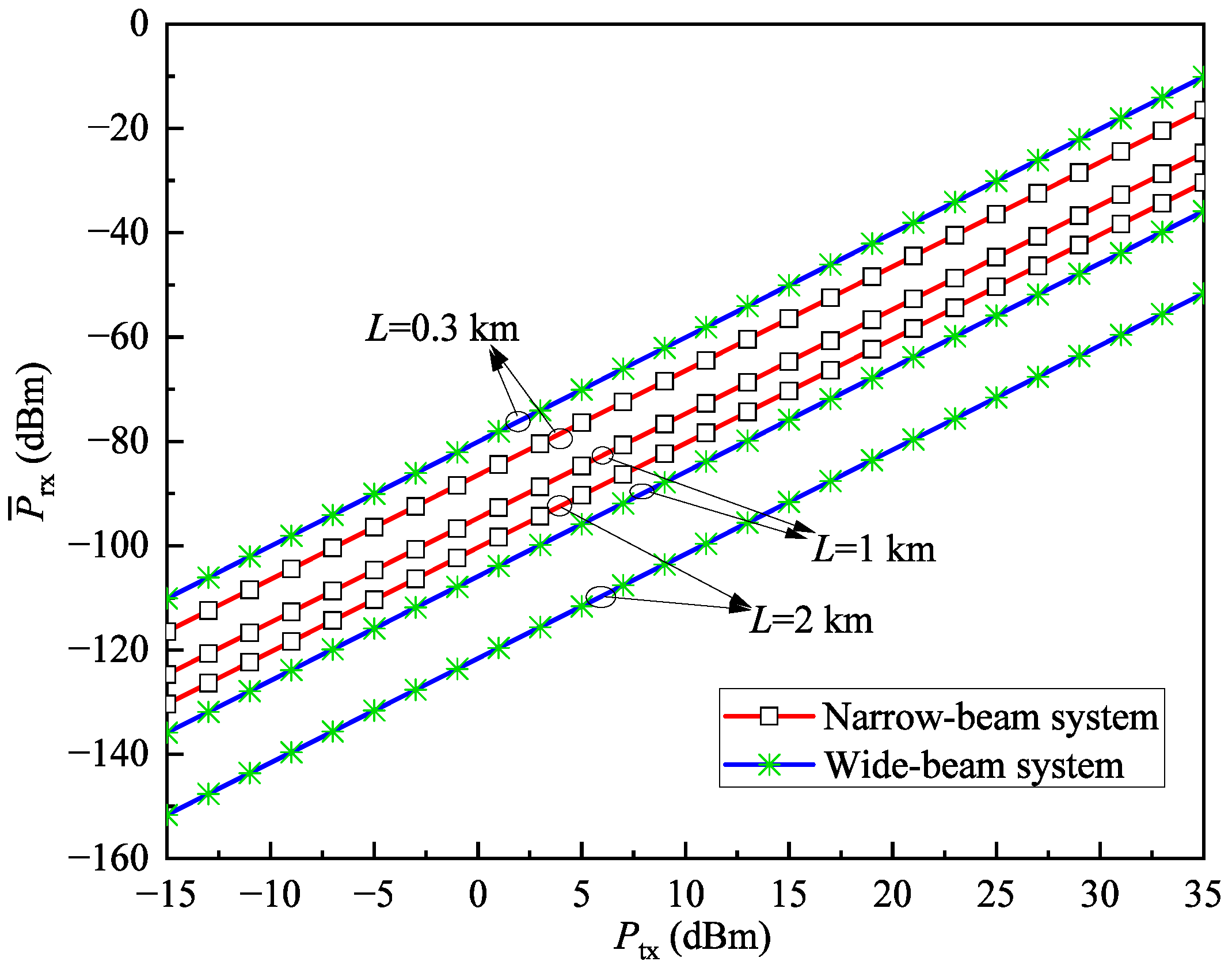
5.1. Power Consumption Comparison
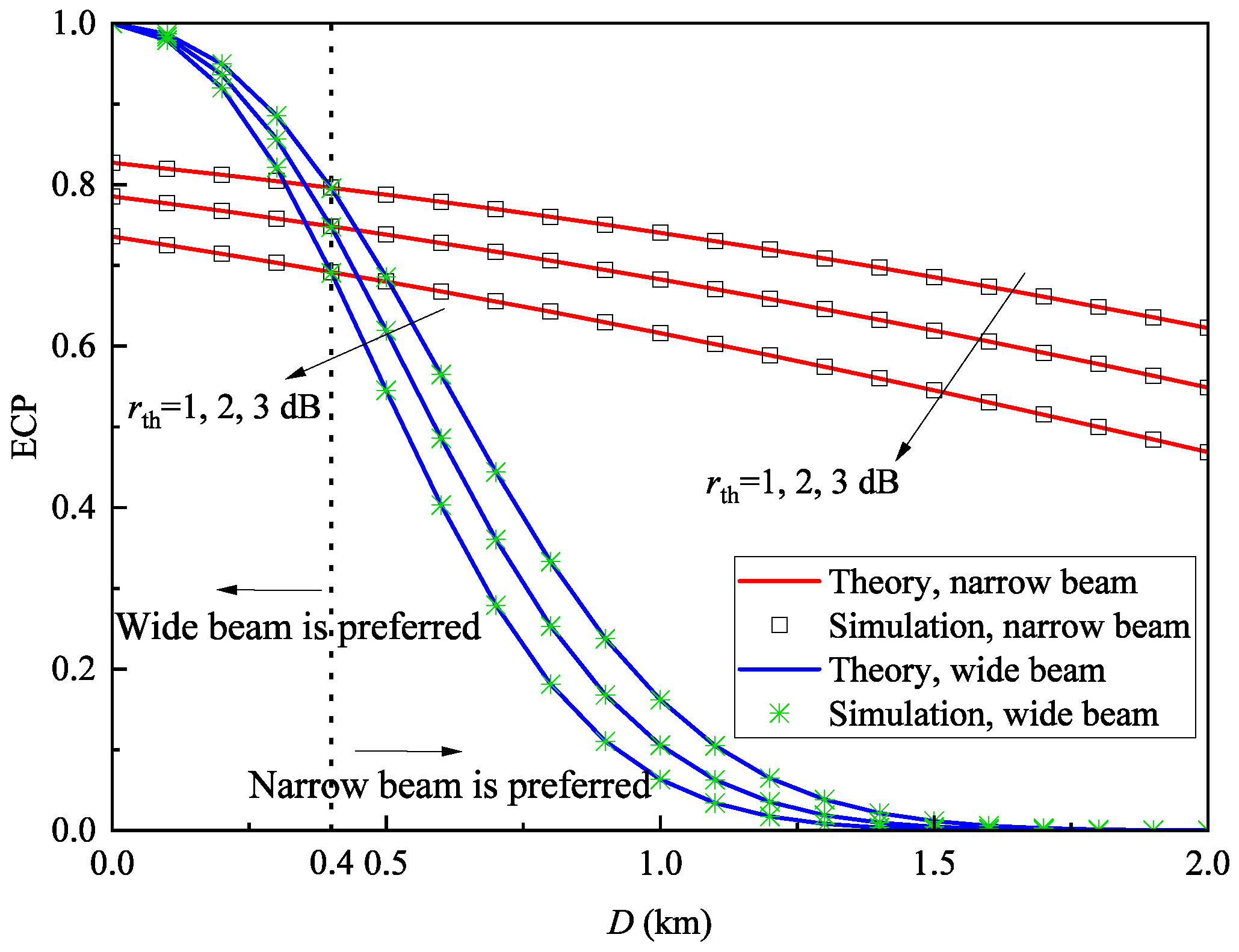
5.2. Results of ECP
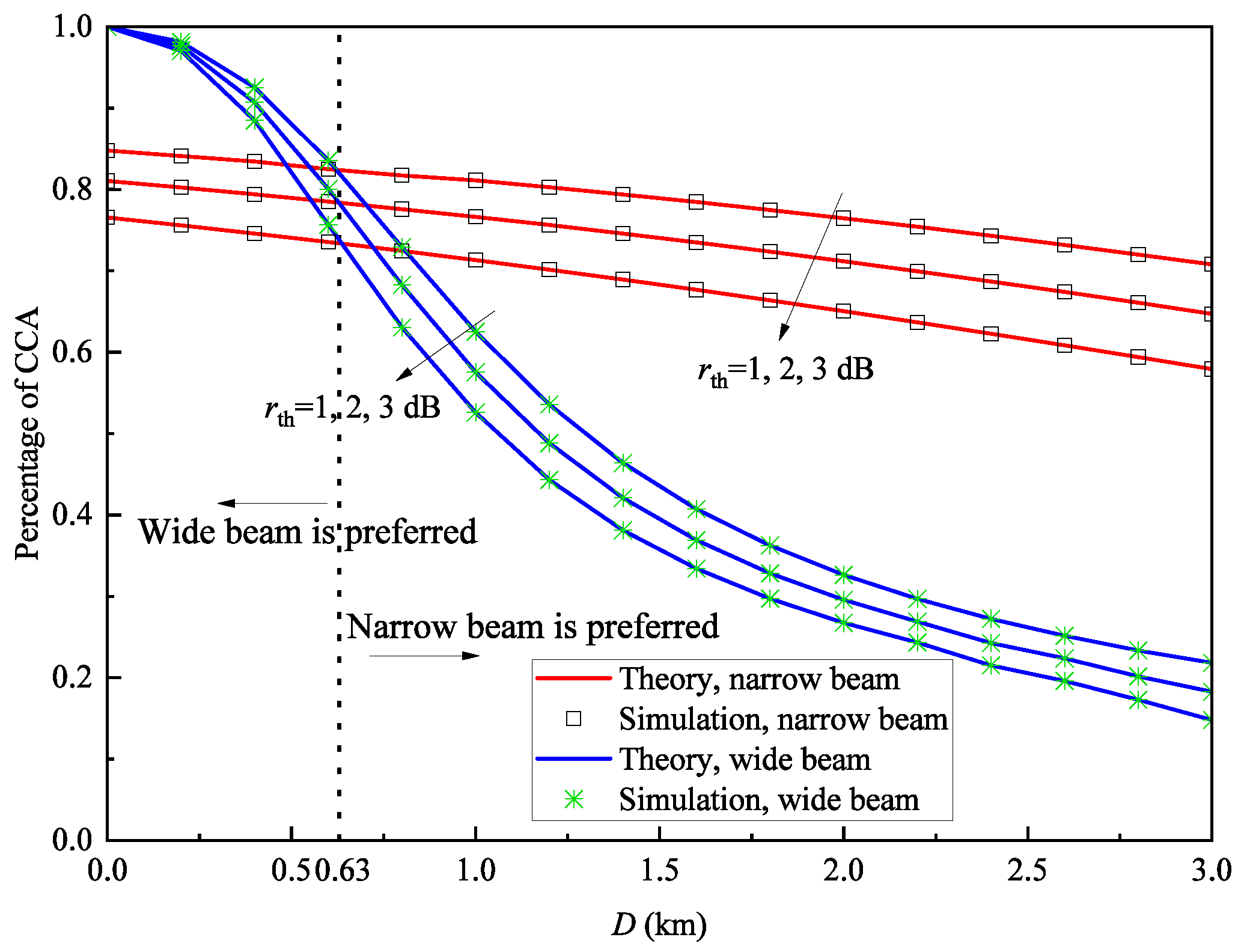
5.3. Results of Percentage of CCA
6. Conclusions
- We propose a beamwidth-adaptive FSO communication system and a beamwidth-adaptive method. When the target transmitter emits a wide beam, the system keeps the ATP module off to conserve energy; when a narrow beam is transmitted, the ATP module is activated to ensure precise beam alignment between the transmitter and receiver. This method effectively enables the system to adaptively adjust the state of the ATP module based on the target transmitter’s width during receiver movement, utilizing handover detection and signal power threshold judgment, thereby enhancing communication reliability and energy efficiency.
- For the HSR system based on a beam-adaptive FSO communication system, closed-form expressions of the ECP and the percentage of CCA are derived. All theoretical results match well with simulations, demonstrating the accuracy of the derived expressions for performance evaluation without time-consuming simulations.
- The wide-beam system should be prioritized in small coverage scenarios to ensure coverage quality while saving energy consumption from ATP system activation. The narrow-beam configuration is preferred for large coverage scenarios to meet coverage performance requirements.
- The wide-beam systems perform better in low-power deployment scenarios due to their tolerance to alignment errors, ensuring better initial cell coverage. Narrow-beam systems excel in high-power scenarios, as their energy concentration enables more significant performance improvements with increasing power. System designers should select appropriate beam configurations based on power constraints to optimize the percentage of CCA.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 5G-R | Fifth generation-railway |
| ATP | Acquisition-tracking-pointing |
| BSs | Base stations |
| CCA | Cell coverage area |
| ECP | Edge coverage probability |
| FSO | Free-space optical |
| GSM-R | Global system for mobile communication-railway |
| HSR | High-speed railway |
| LTE-R | Long term evolution-railway |
| OOK | On-off keying |
| Probability density function | |
| RF | Radio frequency |
| SNR | Signal-to-noise ratio |
Appendix A
Appendix B
Appendix C
Appendix D
References
- Koide, Y.; Wakayama, N.; Maeda, T.; Watanabe, H.; Narusue, Y.; Morikawa, H. Propagation characteristics and quality improvement in millimeter-wave communication for ultra-high-speed maglev train. In Proceedings of the 27th International Symposium on Wireless Personal Multimedia Communications, Greater Noida, India, 17–20 November 2024; pp. 1–5. [Google Scholar]
- Liu, T.; Hu, F.; Ling, Z.; Li, C.; Liang, Y.-C. Multi-agent cooperation-based deep reinforcement learning for multisensor perception communication system in HSR tunnel scenario. IEEE Trans. Commun. 2025, 73, 1816–1832. [Google Scholar] [CrossRef]
- Liu, X.; Chen, J.; Xie, J.; Chang, Y. Generating HSR bogie vibration signals via pulse voltage-guided conditional diffusion model. IEEE Trans. Intell. Transp. Syst. 2025, 26, 116–127. [Google Scholar] [CrossRef]
- Yan, L.; Fang, X.; Fang, Y.; Hao, L.; Xue, Q.; Xu, C. KF-LSTM based beam tracking for UAV-assisted mmWave HSR wireless networks. IEEE Trans. Veh. Technol. 2022, 71, 10796–10807. [Google Scholar] [CrossRef]
- Zheng, R.; Kong, Y.; Chan, E.H.W.; Cao, Y.; Wang, X.; Feng, X.; Guan, B. Photonics based microwave frequency shifter for doppler shift compensation in high-speed railways. In Proceedings of the Conference on Lasers and Electro-Optics Pacific Rim, Hong Kong, China, 29 July–3 August 2018; pp. 1–2. [Google Scholar]
- Hu, J.; Wu, W.; Wang, S.; Wu, Y.; Zhang, Z. Error probability of MPSK with phase errors in dual-hop FSO communication systems. IEEE Photonics Technol. Lett. 2025, 37, 231–234. [Google Scholar] [CrossRef]
- Du, X.; Yu, K.; Wang, Q.; Kam, P.-Y. Non-data-aided ML estimation of timing offset and carrier phase for M-APSK modulated FSO systems. IEEE Photonics Technol. Lett. 2025, 37, 559–562. [Google Scholar] [CrossRef]
- Songsriboonsit, N.; Rodrigues, T.K.; Kawamoto, Y.; Yamashita, Y.; Morikawa, M.; Kato, N. Prediction-based link selection with machine learning in HAP-assisted FSO networks. IEEE Wirel. Commun. Lett. 2025, 14, 1024–1028. [Google Scholar] [CrossRef]
- Mori, K.; Ishikawa, S. Fast handover mechanism for high data rate ground-to-train free-space optical communication system. In Proceedings of the IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014; pp. 499–504. [Google Scholar]
- Weyrauch, T.; Vorontsov, M. Free-space laser communications with adaptive optics: Atmospheric compensation experiments. J. Opt. Commmun. Rep. 2004, 1, 355–379. [Google Scholar] [CrossRef]
- Lee, J.H.; Shin, S.; Park, G.N.; Rhee, H.-G.; Yang, H.-S. Atmospheric turbulence simulator for adaptive optics evaluation on an optical test bench. Curr. Opt. Photonics 2017, 1, 107–112. [Google Scholar] [CrossRef]
- Galaktionov, I.; Sheldakova, J.; Nikitin, A.; Samarkin, V.; Parfenov, V.; Kudryashov, A. Laser beam focusing through a moderately scattering medium using a bimorph mirror. Opt. Exp. 2020, 28, 38061–38075. [Google Scholar] [CrossRef]
- Giggenbach, D.; Shrestha, A. Atmospheric absorption and scattering impact on optical satellite-ground links. Int. J. Satell. Commun. Netw. 2022, 40, 157–176. [Google Scholar] [CrossRef]
- Khuwaja, A.A.; Zheng, G.; Chen, Y.; Feng, W. Optimum deployment of multiple UAVs for coverage area maximization in the presence of co-channel interference. IEEE Access 2019, 7, 85203–85212. [Google Scholar] [CrossRef]
- Wang, X.; Turgut, E.; Gursoy, M.C. Coverage in downlink heterogeneous mmWave cellular networks with user-centric small cell deployment. IEEE Trans. Veh. Technol. 2019, 68, 3513–3533. [Google Scholar] [CrossRef]
- Lin, S.; Wang, H.; Li, W.; Wang, J. Coverage analysis for high-speed railway communications with narrow-strip-shaped cells over Suzuki fading channels. Entropy 2024, 26, 657. [Google Scholar] [CrossRef]
- Lin, S.-H.; Xu, Y.; Wang, J.-Y. Coverage analysis and optimization for high-speed railway communication systems with narrow-strip-shaped cells. IEEE Trans. Veh. Technol. 2020, 69, 11544–11556. [Google Scholar] [CrossRef]
- Khalighi, M.A.; Uysal, M. Survey on free space optical communication: A communication theory perspective. IEEE Commun. Surv. Tutor. 2014, 16, 2231–2258. [Google Scholar] [CrossRef]
- Taheri, M.; Ansari, N.; Feng, J.; Rojas-Cessa, R.; Zhou, M. Provisioning internet access using FSO in high-speed rail networks. IEEE Netw. 2017, 31, 96–101. [Google Scholar] [CrossRef]
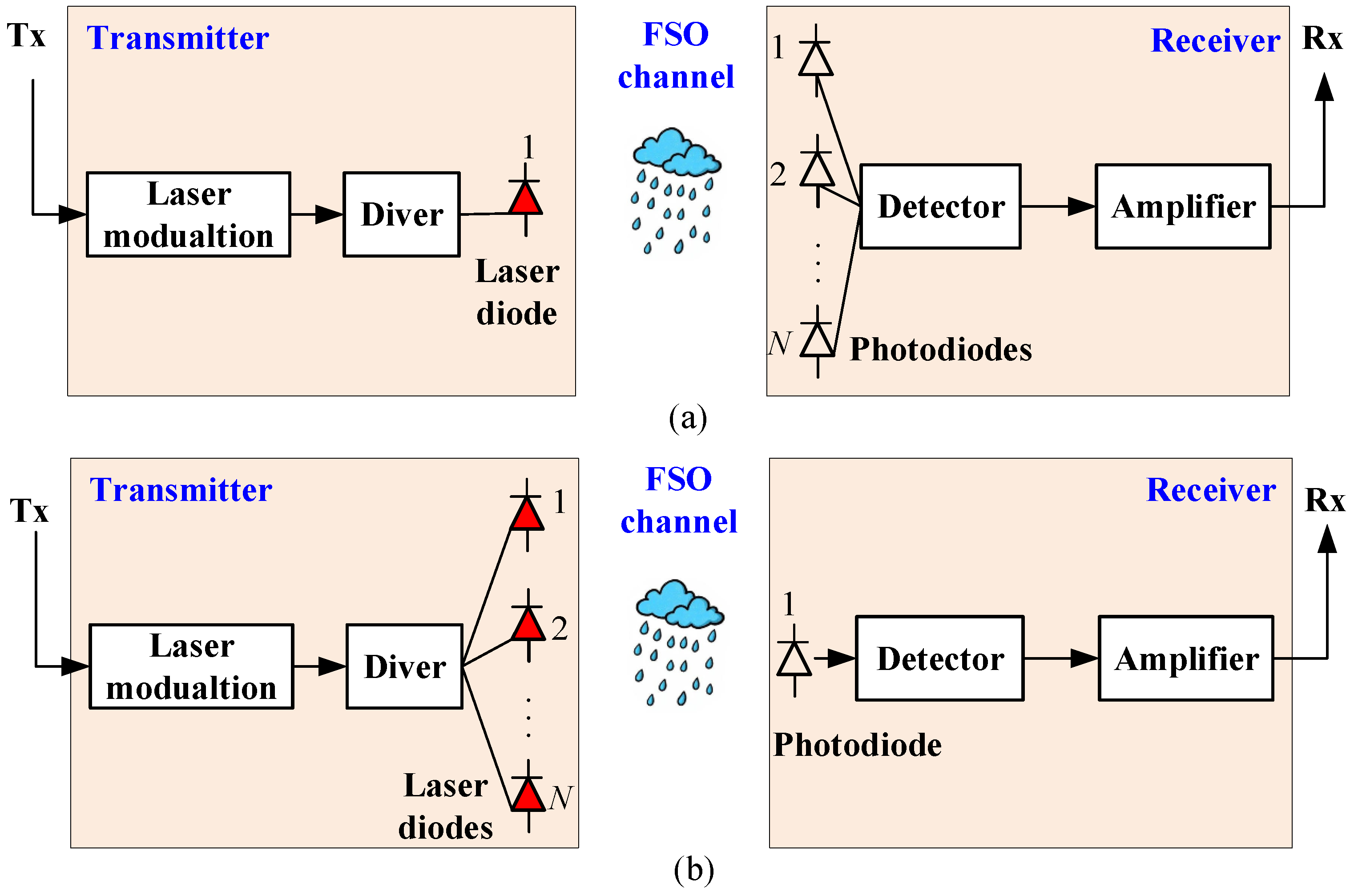
- Mabrouk, W.A.; Abdullah, M.F.L.; Gismalla, M.S.M. Enhancement of link range for FSO ground to train communications using multiple transmitters concept. In Proceedings of the International Conference on Software Technologies, Karachi, Pakistan, 2–4 October 2019; pp. 1–7. [Google Scholar]
- Fan, Q.; Taheri, M.; Ansari, N.; Feng, J.-H.; Rojas-Cessa, R.; Zhou, M.-C.; Zhang, T.-R. Reducing the impact of handovers in ground-to-train free space optical communications. IEEE Trans. Veh. Technol. 2018, 67, 1292–1301. [Google Scholar] [CrossRef]
- Lin, S.-H.; Xu, Y.; Wang, L.; Wang, J.-Y. Coverage analysis and chance-constrained optimization for HSR communications with carrier aggregation. IEEE Trans. Intel. Transport. Syst. 2022, 23, 15107–15120. [Google Scholar] [CrossRef]
- Zhang, J.; Du, H.; Zhang, P.; Cheng, J.; Yang, L. Performance analysis of 5G mobile relay systems for high-speed trains. IEEE J. Sel. Areas Commun. 2020, 38, 2760–2772. [Google Scholar] [CrossRef]
- Nace, D.; Pióro, M.; Poss, M.; D’Andreagiovanni, F.; Kalesnikau, I.; Shehaj, M.; Tomaszewski, A. An optimization model for robust FSO network dimensioning. Opt. Switch. Netw. 2019, 32, 25–40. [Google Scholar] [CrossRef]
- Farid, A.A.; Hranilovic, S. Optimization of beam width, bit error rate and availability for free-space optical links. In Proceedings of the 6th International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP), Graz, Austria, 23–25 June 2008; pp. 92–96. [Google Scholar]
- Mohammad, A.B. Optimization of FSO system in tropical weather using multiple beams. In Proceedings of the IEEE 5th International Conference on Photonics (ICP), Kuala Lumpur, Malaysia, 2–4 September 2014; pp. 109–112. [Google Scholar]
- Bloom, S.; Korevaar, E.; Schuster, J.; Willebrand, H. Understanding the performance of free-space optics [invited]. J. Opt. Netw. 2003, 2, 178–200. [Google Scholar] [CrossRef]
- Kaymak, Y.; Rojas-Cessa, R.; Feng, J.; Ansari, N.; Zhou, M. On divergence-angle efficiency of a laser beam in free-space optical communications for high-speed trains. IEEE Trans. Veh. Technol. 2017, 66, 7677–7687. [Google Scholar] [CrossRef]
- Killinger, D. Free space optics for laser communication through the air. Opt. Photonics News. 2002, 13, 36–42. [Google Scholar] [CrossRef]
- Wang, J.-Y.; Wang, J.-B.; Chen, M.; Tang, Y.; Zhang, Y. Outage analysis for relay-aided free-space optical communications over turbulence channels with nonzero boresight pointing errors. IEEE Photonics J. 2014, 6, 7901815. [Google Scholar]
- He, J.; Norwood, R.A.; Brandt-Pearce, M.; Djordjevic, I.B.; Cvijetic, M.; Subramaniam, S.; Himmelhuber, R.; Reynolds, C.; Blanche, P.; Lynn, B.; et al. A survey on recent advances in optical communications. Comput. Electr. Eng. 2014, 40, 216–240. [Google Scholar] [CrossRef]
- Turan, H.; Subaşi, Ö. Development of fine tracking unit for hybrid ATP mechanism in free-space optical communication. In Proceedings of the 29th Signal Processing and Communications Applications Conference, Istanbul, Turkey, 9–11 June 2021; pp. 1–4. [Google Scholar]
- Mai, V.; Kim, H. Beam steering and divergence control using variable focus liquid lenses for WDM FSO communications. IEEE Photonics Technol. Lett. 2022, 34, 1226–1229. [Google Scholar] [CrossRef]
- Paudel, R.; Ghassemlooy, Z.; Le-Minh, H.; Rajbhandari, S. Modelling of free space optical link for ground-to-train communications using a gaussian source. IET Optoelectron. 2013, 7, 1–8. [Google Scholar] [CrossRef]
- Fan, Q.; Ansari, N.; Feng, J.; Rojas-Cessa, R.; Zhou, M.; Zhang, T. Reducing the number of FSO base stations with dual transceivers for next-generation ground-to-train communications. IEEE Trans. Veh. Technol. 2018, 67, 11143–11153. [Google Scholar] [CrossRef]
- Lv, L.; Yang, Z.; Fang, Y.; Guizani, M. Adaptive interleaver and rate-compatible PLDPC code design for MIMO FSO-RF systems. IEEE Trans. Veh. Technol. 2024, 73, 15757–15762. [Google Scholar] [CrossRef]
- Rakia, T.; Yang, H.-C.; Alouini, M.-S.; Gebali, F. Outage analysis of practical FSO/RF system with adaptive combining. IEEE Commun. Lett. 2015, 19, 1366–1369. [Google Scholar] [CrossRef]
- Xu, G.; Xu, M.; Zhang, Q.; Song, Z. Cooperative FSO/RF space-air-ground integrated network system with adaptive combining: A performance analysis. IEEE Trans. Wirel. Commun. 2024, 23, 17279–17293. [Google Scholar] [CrossRef]
- Ansari, I.S.; Yilmaz, F.; Alouini, M.-S. Performance analysis of free-space optical links over Málaga (M) turbulence channels with pointing errors. IEEE Trans. Wirel. Commun. 2016, 15, 91–102. [Google Scholar] [CrossRef]
- Khatib, M. Contemporary Issues in Wireless Communications; IntechOpen: Rijeka, Croatia, 2014; pp. 159–212. [Google Scholar]
- Navas, A.J.; Balsells, J.M.G.; Paris, J.F.; Vazquez, M.C.; Notario, A.P. Impact of pointing errors on the performance of generalized atmospheric optical channels. Opt. Express 2012, 20, 12550–12562. [Google Scholar] [CrossRef]
- Elsawy, Y.; Alatawi, A.S.; Abaza, M.; Moawad, A.; Agoune, E.-H. Next-generation dual transceiver FSO communication system for high-speed trains in neom smart city. Photonics 2024, 11, 483. [Google Scholar] [CrossRef]
- IEC 60825-1:2007; Safety of Laser Products-Part 1: Equipment Classification and Requirements. IEC: Geneva, Switzerland, 2007.
- Ai, B.; He, R.; Li, G.; Guan, K.; He, D.; Shi, G.; Zhong, Z. Determination of cell coverage area and its applications in high-speed railway environments. IEEE Trans. Veh. Technol. 2017, 66, 3515–3525. [Google Scholar] [CrossRef]
- Adamchik, V.S.; Marichev, O.I. The algorithm for calculating integrals of hypergeometric type functions and its realization in REDUCE system. In Proceedings of the International Symposium on Symbolic and Algebraic Computation (ISSAC), Tokyo, Japan, 20–24 August 1990; pp. 212–224. [Google Scholar]
- Wolfram. The Wolfram Functions Site. Available online: http://functions.wolfram.com/ (accessed on 7 August 2025).




| Parameters | Symbols | Values |
|---|---|---|
| Photoelectric conversion efficiency | R | 0.8 |
| Receiver diameter | B | 0.2 m |
| Divergence angle | 0.01 rad | |
| Noise standard deviation | A/Hz | |
| Beam wavelength | 850 nm | |
| Effective number of large-scale cells | 3.99 | |
| Amount of fading parameter | 2 | |
| Average optical power of the classic scattering component received by off-axis eddies | 0.2 | |
| Average optical power of the coherent contributions | 0.5 | |
| Beam waist radius | ||
| Number of sub-intervals in the composite trapezoidal integral | n | 1000 |
| Number of Snapshots | N |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, S.; Zeng, Z.-Z.; Zhang, D.-T.; Sun, Z.-Q.; Wang, J.-Y. Coverage Analysis of 5G Intelligent High-Speed Railway System Based on Beamwidth-Adaptive Free-Space Optical Communication. Sensors 2025, 25, 4906. https://doi.org/10.3390/s25164906
Dong S, Zeng Z-Z, Zhang D-T, Sun Z-Q, Wang J-Y. Coverage Analysis of 5G Intelligent High-Speed Railway System Based on Beamwidth-Adaptive Free-Space Optical Communication. Sensors. 2025; 25(16):4906. https://doi.org/10.3390/s25164906
Chicago/Turabian StyleDong, Shuai, Zhi-Zhao Zeng, Dan-Ting Zhang, Zi-Qi Sun, and Jin-Yuan Wang. 2025. "Coverage Analysis of 5G Intelligent High-Speed Railway System Based on Beamwidth-Adaptive Free-Space Optical Communication" Sensors 25, no. 16: 4906. https://doi.org/10.3390/s25164906
APA StyleDong, S., Zeng, Z.-Z., Zhang, D.-T., Sun, Z.-Q., & Wang, J.-Y. (2025). Coverage Analysis of 5G Intelligent High-Speed Railway System Based on Beamwidth-Adaptive Free-Space Optical Communication. Sensors, 25(16), 4906. https://doi.org/10.3390/s25164906









