High-Performance Capacitive Ultrasonic Transducer for Non-Destructive Testing of Concrete Compressive Strength
Abstract
1. Introduction
2. Materials and Methods
2.1. Finite Element Numerical Simulation
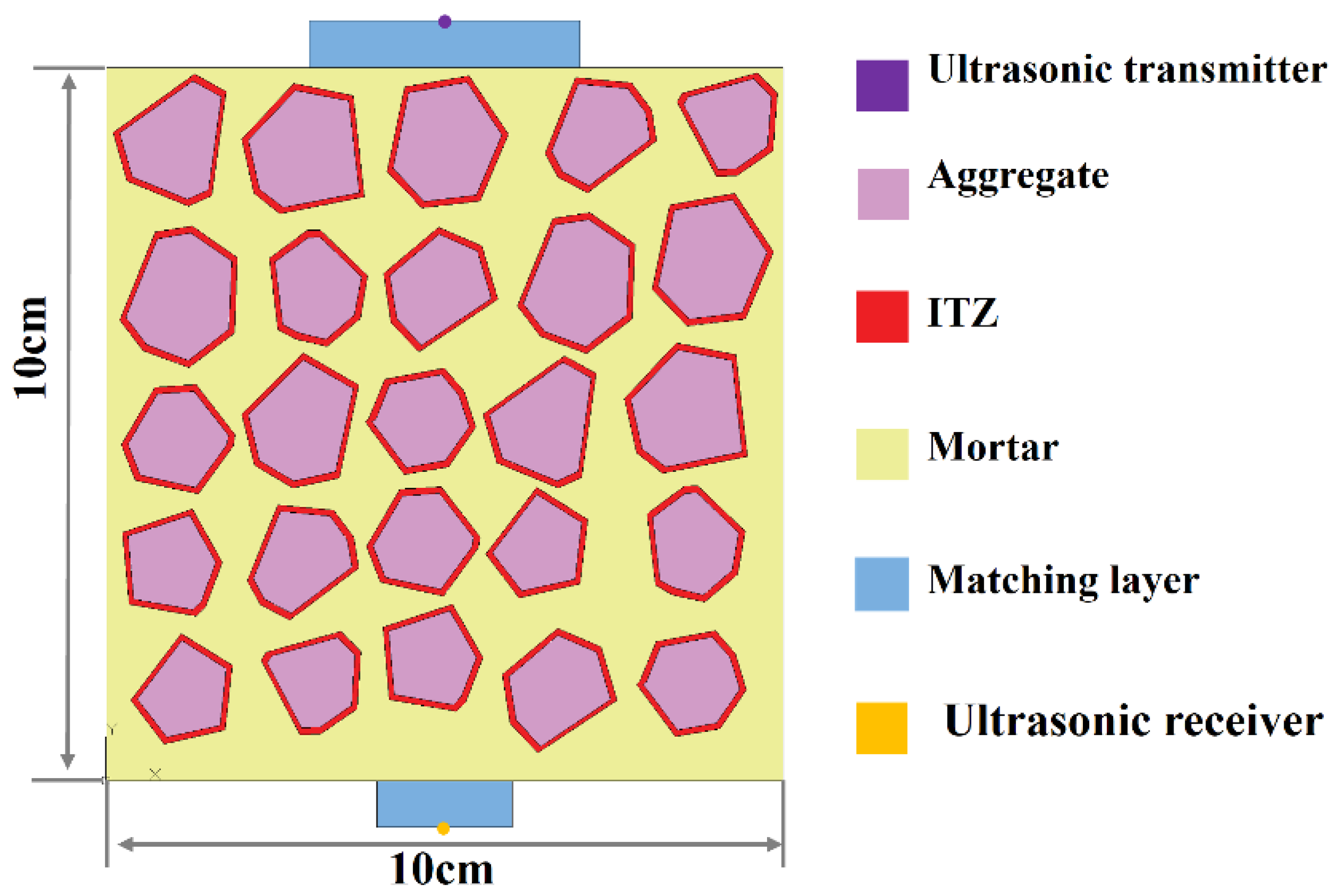
2.1.1. Geometrical Model
2.1.2. Ultrasonic Excitation
2.1.3. Medium Material
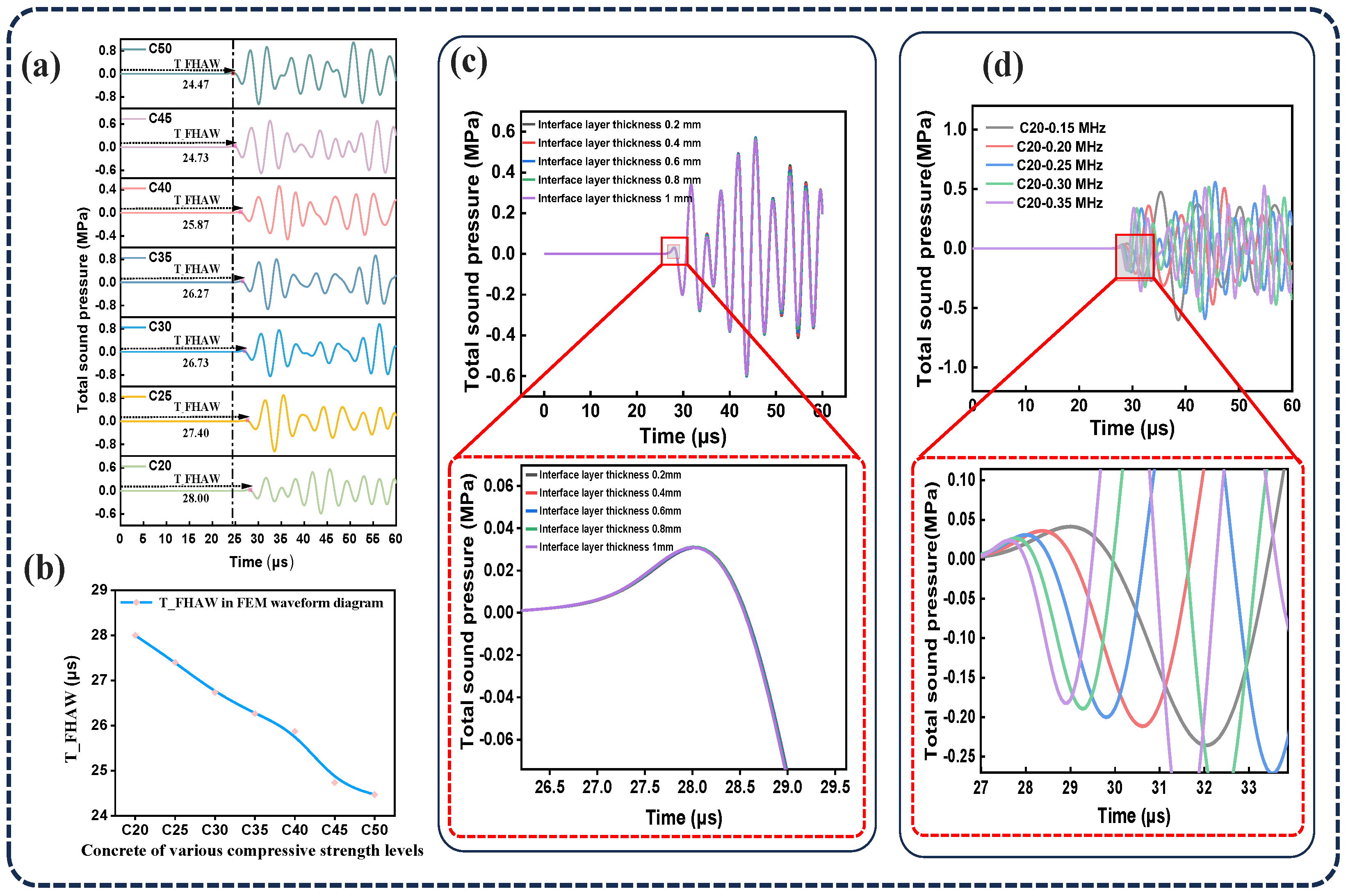
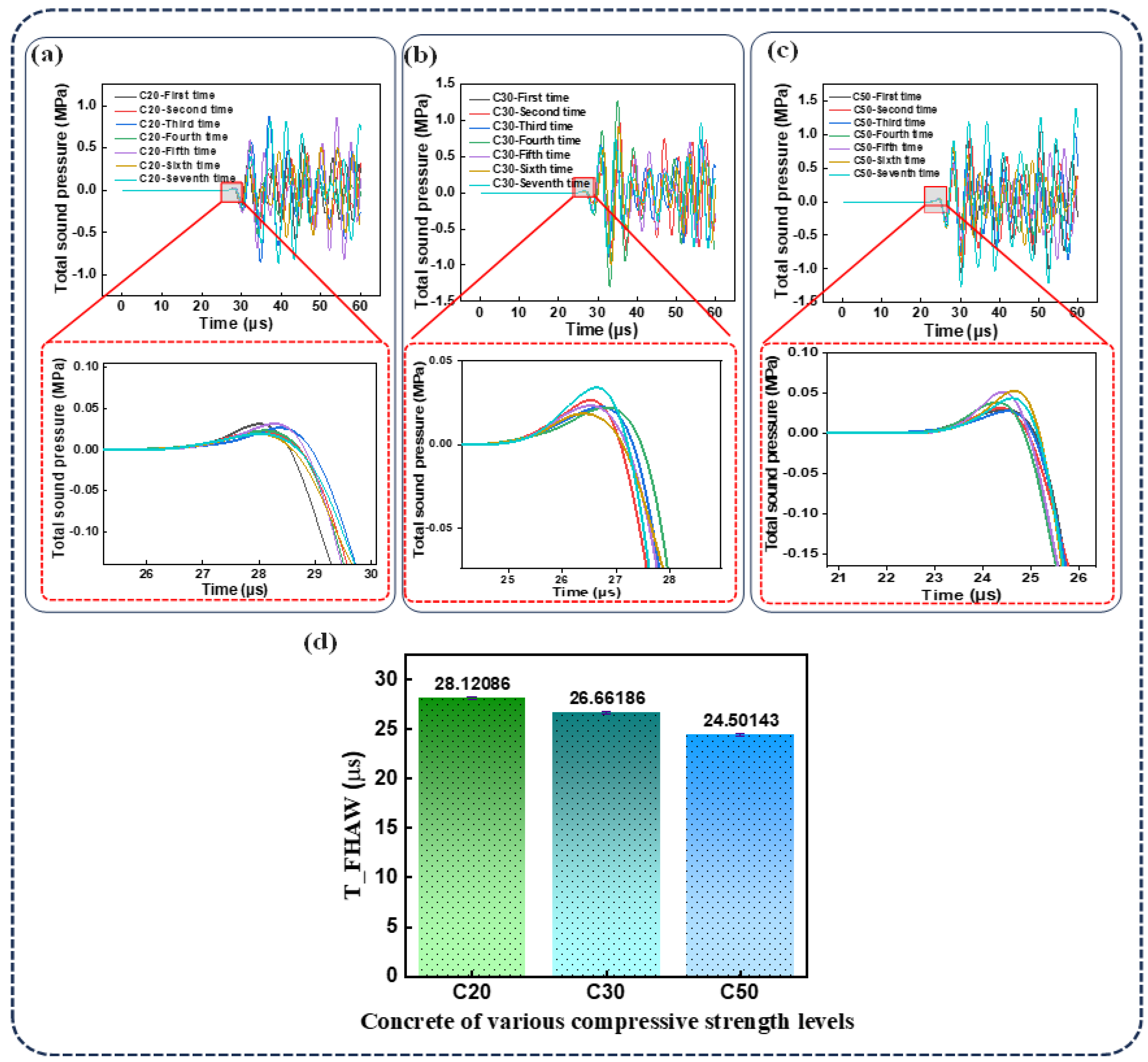
2.2. Simulation Validation Results
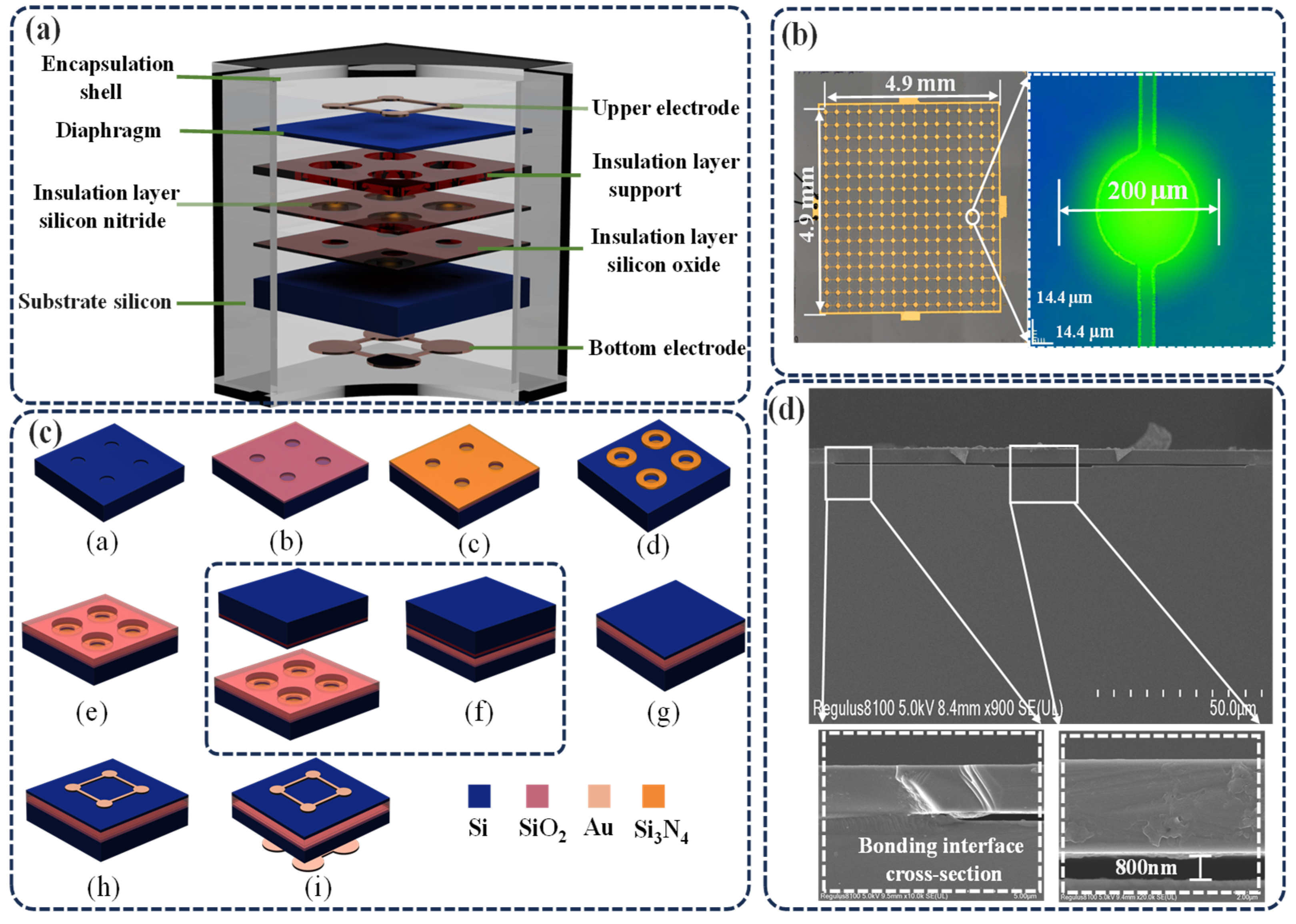
3. Design and Preparation of CMUT Chip
4. Encapsulation of the CMUT Chip
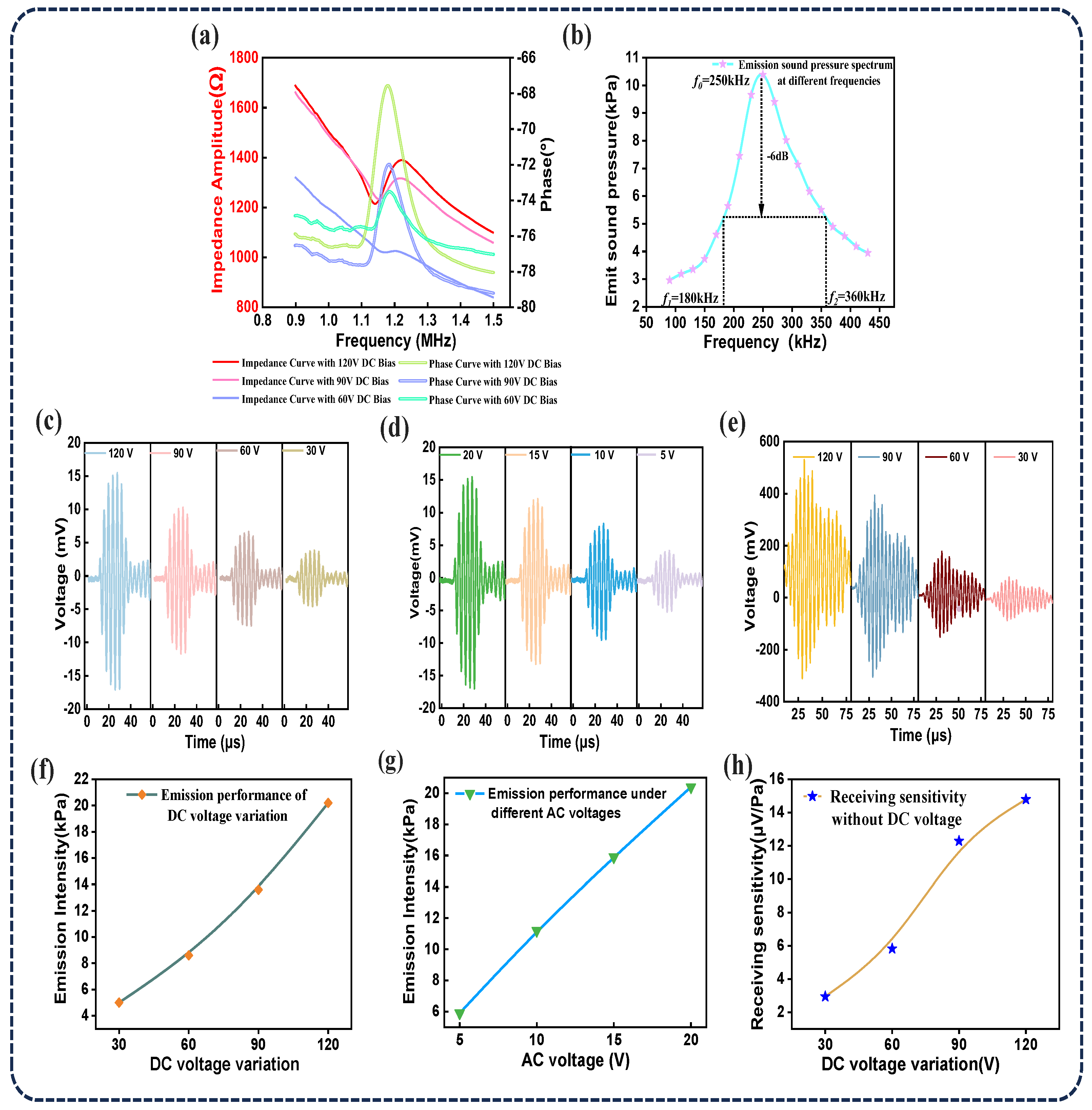
5. Performance Testing of the CMUT Chip
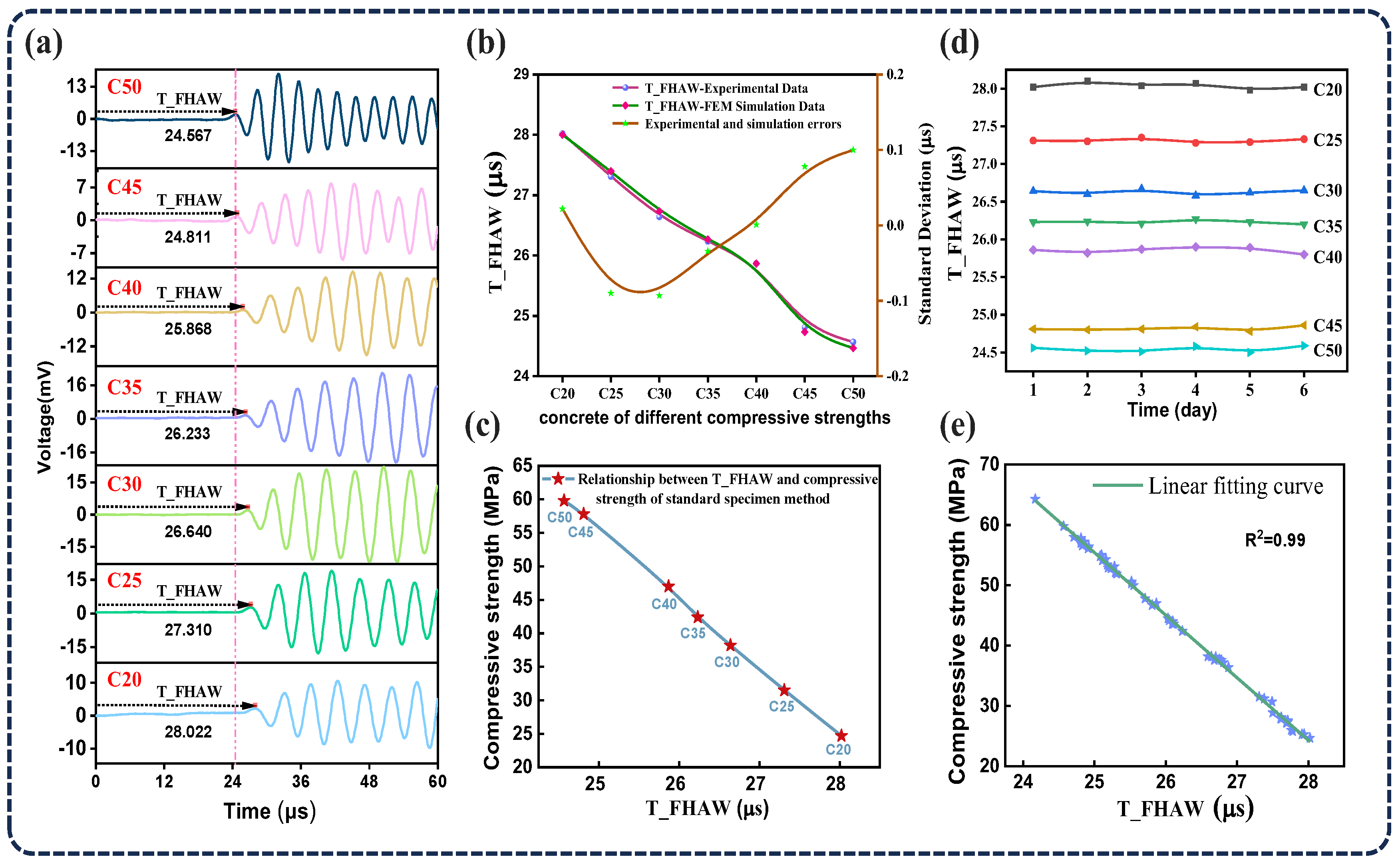
6. Ultrasonic Time-of-Flight Testing in Concrete
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, L.; Song, D.; Liu, N.; Tian, W. Study on Mechanical Properties of Basalt Fiber-Reinforced Concrete with High Content of Stone Powder at High Temperatures. Adv. Mater. Sci. Eng. 2021, 2021, 7517049. [Google Scholar] [CrossRef]
- Moccia, F.; Yu, Q.; Fernández Ruiz, M.; Muttoni, A. Concrete Compressive Strength: From Material Characterization to a Structural Value. Struct. Concr. 2021, 22, E634–E654. [Google Scholar] [CrossRef]
- Sandhu, H.K.; Bodda, S.S.; Gupta, A. A Future with Machine Learning: Review of Condition Assessment of Structures and Mechanical Systems in Nuclear Facilities. Energies 2023, 16, 2628. [Google Scholar] [CrossRef]
- Chew, A.W.Z.; He, R.; Zhang, L. Physics Informed Machine Learning (PIML) for Design, Management and Resilience-Development of Urban Infrastructures: A Review. Arch. Comput. Methods Eng. 2025, 32, 399–439. [Google Scholar] [CrossRef]
- Ismail, M.; Muhammad, B.; Ismail, M.E. Compressive Strength Loss and Reinforcement Degradations of Reinforced Concrete Structure Due to Long-Term Exposure. Constr. Build. Mater. 2010, 24, 898–902. [Google Scholar] [CrossRef]
- Yan, C.; Tu, J.; Li, D.; Guo, S.; Liang, H. The Failure Mechanism of Concrete Gravity Dams Considering Different Nonlinear Models under Strong Earthquakes. Shock. Vib. 2021, 2021, 5558284. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, L.; Wen, S.; Huang, S. A Review on Concrete Structural Properties and Damage Evolution Monitoring Techniques. Sensors 2024, 24, 620. [Google Scholar] [CrossRef]
- Kontani, O.; Ishikawa, S.; Nishioka, T.; Masaki, H.; Tanaka, N.; Goto, Y.; Ishioka, S. Properties of Concrete Subjected to Severe Accident Conditions at Fukushima Daiichi Nuclear Power Plant. J. Adv. Concr. Technol. 2022, 20, 152–187. [Google Scholar] [CrossRef]
- Rasheed, P.A.; Nayar, S.K.; AlFantazi, A. Concrete Corrosion in Nuclear Power Plants and Other Nuclear Installations and Its Mitigation Techniques: A Review. Corros. Rev. 2024, 42, 57–73. [Google Scholar] [CrossRef]
- Ibragimov, R.; Korolev, E.; Deberdeev, T.; Dolbin, I. Influence of Electromagnetic Radiation on the Degradation of Reinforced Concrete Structures—Review. Case Stud. Constr. Mater. 2022, 17, e01454. [Google Scholar] [CrossRef]
- Haavisto, J.; Husso, A.; Laaksonen, A. Compressive Strength of Core Specimens Drilled from Concrete Test Cylinders. Struct. Concr. 2021, 22, E683–E695. [Google Scholar] [CrossRef]
- Byeon, H.; Park, J. Statistical Analysis of Effects of Test Conditions on Compressive Strength of Cement Solidified Radioactive Waste. Nucl. Eng. Technol. 2023, 55, 876–883. [Google Scholar] [CrossRef]
- Demir, T.; Ulucan, M.; Alyamaç, K.E. Development of Combined Methods Using Non-Destructive Test Methods to Determine the in-Place Strength of High-Strength Concretes. Processes 2023, 11, 673. [Google Scholar] [CrossRef]
- Kouddane, B.; Sbartaï, Z.M.; Elachachi, S.M.; Lamdouar, N. New Multi-Objective Optimization to Evaluate the Compressive Strength and Variability of Concrete by Combining Non-Destructive Techniques. J. Build. Eng. 2023, 77, 107526. [Google Scholar] [CrossRef]
- Jodhani, J.; Handa, A.; Gautam, A.; Ashwni; Rana, R. Ultrasonic Non-Destructive Evaluation of Composites: A Review. Mater. Today Proc. 2023, 78, 627–632. [Google Scholar] [CrossRef]
- Ali-Benyahia, K.; Kenai, S.; Ghrici, M.; Sbartaï, Z.-M.; Elachachi, S.-M. Analysis of the Accuracy of In-Situ Concrete Characteristic Compressive Strength Assessment in Real Structures Using Destructive and Non-Destructive Testing Methods. Constr. Build. Mater. 2023, 366, 130161. [Google Scholar] [CrossRef]
- Saleh, E.F.; Tarawneh, A.N.; Katkhuda, H.N. A Comprehensive Evaluation of Existing and New Model-Identification Approaches for Non-Destructive Concrete Strength Assessment. Constr. Build. Mater. 2022, 334, 127447. [Google Scholar] [CrossRef]
- Jung, J.; Lee, W.; Kang, W.; Shin, E.; Ryu, J.; Choi, H. Review of Piezoelectric Micromachined Ultrasonic Transducers and Their Applications. J. Micromech. Microeng. 2017, 27, 113001. [Google Scholar] [CrossRef]
- Smith, G.L.; Pulskamp, J.S.; Sanchez, L.M.; Potrepka, D.M.; Proie, R.M.; Ivanov, T.G.; Rudy, R.Q.; Nothwang, W.D.; Bedair, S.S.; Meyer, C.D.; et al. PZT-Based Piezoelectric MEMS Technology. J. Am. Ceram. Soc. 2012, 95, 1777–1792. [Google Scholar] [CrossRef]
- Zhang, W. Biomarker Detection Based on Nanoparticle-Induced Ultrasonic Rayleigh Scattering. Microsyst. Nanoeng. 2024, 10, 182. [Google Scholar] [CrossRef]
- Joseph, J.; Ma, B.; Khuri-Yakub, B.T. Applications of Capacitive Micromachined Ultrasonic Transducers: A Comprehensive Review. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 456–467. [Google Scholar] [CrossRef] [PubMed]
- Savoia, A.S.; Mauti, B.; Caliano, G. A Low Frequency Broadband Flextensional Ultrasonic Transducer Array. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2016, 63, 128–138. [Google Scholar] [CrossRef] [PubMed]
- Omidvar, A.; Cretu, E.; Rohling, R.; Cresswell, M.; Hodgson, A.J. Flexible PolyCMUTs: Fabrication and Characterization of a Flexible Polymer-based Capacitive Micromachined Ultrasonic Array for Conformal Ultrasonography. Adv. Mater. Technol. 2023, 8, 2201316. [Google Scholar] [CrossRef]
- Bolborea, B.; Baera, C.; Dan, S.; Gruin, A.; Burduhos-Nergis, D.-D.; Vasile, V. Concrete Compressive Strength by Means of Ultrasonic Pulse Velocity and Moduli of Elasticity. Materials 2021, 14, 7018. [Google Scholar] [CrossRef]
- Lin, Y.; Lai, C.-P.; Yen, T. Prediction of Ultrasonic Pulse Velocity (UPV) in Concrete. Mater. J. 2003, 100, 21–28. [Google Scholar] [CrossRef]
- Zhang, J.; Dong, Z.-H.; Wang, X.-B.; Shi, W.-Z.; Wang, X.; Tang, Q. Study on Characteristics of Radiation Sound Field of Line-Focusing Angled SV Wave EMAT. In Proceedings of the 2020 IEEE Far East NDT New Technology & Application Forum (FENDT), Kunming, China, 20 November 2020; pp. 125–129. [Google Scholar]
- Luo, J.; Xie, Z.; Li, X. Asymmetric Windows and Their Application in Frequency Estimation. J. Algorithms Comput. Technol. 2015, 9, 389–412. [Google Scholar] [CrossRef]
- Hasannejad, M.; Berenjian, J.; Pouraminian, M.; Sadeghi Larijani, A. Studying of Microstructure, Interface Transition Zone and Ultrasonic Wave Velocity of High Strength Concrete by Different Aggregates. J. Build. Rehabil. 2022, 7, 9. [Google Scholar] [CrossRef]
- Fang, M.; Park, D.; Singuranayo, J.L.; Chen, H.; Li, Y. Aggregate Gradation Theory, Design and Its Impact on Asphalt Pavement Performance: A Review. Int. J. Pavement Eng. 2019, 20, 1408–1424. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, J.; Wang, Z.; Zhao, T.; Wang, Z. A Review of the Interfacial Transition Zones in Concrete: Identification, Physical Characteristics, and Mechanical Properties. Eng. Fract. Mech. 2024, 300, 109979. [Google Scholar] [CrossRef]
- Wong, C.-M.; Chan, S.-F.; Wu, W.C.; Suen, C.-H.; Yau, H.-M.; Wang, D.Y.; Li, S.; Dai, J.Y. Tunable High Acoustic Impedance Alumina Epoxy Composite Matching for High Frequency Ultrasound Transducer. Ultrasonics 2021, 116, 106506. [Google Scholar] [CrossRef]
- GB/T 50081-2019; Standards for Test Methods of Mechanical Properties of Ordinary Concrete. National Development and Reform Commission of the PRC: Beijing, China, 2019. (In Chinese)
- Ofuyatan, O.; Olowofoyeku, A.; Oluwafemi, J.; Ighalo, J. Predicting the Compressive Strength of Concrete by Ultrasonic Pulse Velocity. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1036, 012053. [Google Scholar] [CrossRef]
- Panzera, T.H.; Christoforo, A.L.; Cota, F.P.; Borges, P.R.; Bowen, C.R. Ultrasonic Pulse Velocity Evaluation of Cementitious Materials. In Advances in Composite Materials—Analysis of Natural and Man-Made Materials; InTech: Rijeka, Croatia, 2011; ISBN 978-953-307-449-8. [Google Scholar]
- Zárate, D.M.; Cárdenas, F.; Forero, E.F.; Peña, F.O. Strength of Concrete through Ultrasonic Pulse Velocity and Uniaxial Compressive Strength. Int. J. Technol. 2022, 13, 103–114. [Google Scholar] [CrossRef]
- Bezerra, A.K.L.; Melo, A.R.S.; Freitas, I.L.B.; Babadopulos, L.F.A.L.; Carret, J.-C.; Soares, J.B. Determination of Modulus of Elasticity and Poisson’s Ratio of Cementitious Materials Using S-Wave Measurements to Get Consistent Results between Static, Ultrasonic and Resonant Testing. Constr. Build. Mater. 2023, 398, 132456. [Google Scholar] [CrossRef]
- Mata, R.; Ruiz, R.O.; Nuñez, E. Correlation between Compressive Strength of Concrete and Ultrasonic Pulse Velocity: A Case of Study and a New Correlation Method. Constr. Build. Mater. 2023, 369, 130569. [Google Scholar] [CrossRef]


| Strength Grade | Water (Kg/m3) | Cement (Kg/m3) | Fly Ash (Kg/m3) | Fine Aggregate (Kg/m3) | Superplasticizer (Kg/m3) | Coarse Aggregate (Kg/m3) |
|---|---|---|---|---|---|---|
| C20 | 165 | 200 | 80 | 850 | 3.92 | 1090 |
| C25 | 163 | 220 | 90 | 820 | 4.65 | 1097 |
| C30 | 165 | 250 | 80 | 785 | 5.28 | 1120 |
| C35 | 165 | 285 | 90 | 734 | 6.75 | 1126 |
| C40 | 160 | 320 | 95 | 690 | 7.88 | 1147 |
| C45 | 155 | 350 | 95 | 640 | 8.9 | 1167 |
| C50 | 150 | 410 | 85 | 597 | 10.89 | 1188 |
| Test Method | Production Materials | Linear Range | Linear Coefficient R2 | Ref |
|---|---|---|---|---|
| PZT Bulk | Lead Zirconate Titanate (toxic) | C15–C35 | 0.71 | [33] |
| PZT Bulk | Lead Zirconate Titanate (toxic) | C20–C50 | 0.88 | [34] |
| PZT Bulk | Lead Zirconate Titanate (toxic) | C10–C35 | 0.951 | [35] |
| PZT Bulk | Lead Zirconate Titanate (toxic) | C10–C35 | 0.9453 | [36] |
| PZT Bulk | Lead Zirconate Titanate (toxic) | C20–C65 | 0.3063 | [37] |
| CMUT | Si (non-toxic) | C20–C50 | 0.99 | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Yang, J.; Ren, L.; Dou, H.; Chen, X.; Jia, H.; Mao, Y.; Zhang, J.; Xu, W.; Zhou, H.; et al. High-Performance Capacitive Ultrasonic Transducer for Non-Destructive Testing of Concrete Compressive Strength. Sensors 2025, 25, 4903. https://doi.org/10.3390/s25164903
Zhang W, Yang J, Ren L, Dou H, Chen X, Jia H, Mao Y, Zhang J, Xu W, Zhou H, et al. High-Performance Capacitive Ultrasonic Transducer for Non-Destructive Testing of Concrete Compressive Strength. Sensors. 2025; 25(16):4903. https://doi.org/10.3390/s25164903
Chicago/Turabian StyleZhang, Wangyang, Jiaqian Yang, Lei Ren, Hanjie Dou, Xianglong Chen, Haoliang Jia, Yuchen Mao, Jixuan Zhang, Wanyu Xu, Hong Zhou, and et al. 2025. "High-Performance Capacitive Ultrasonic Transducer for Non-Destructive Testing of Concrete Compressive Strength" Sensors 25, no. 16: 4903. https://doi.org/10.3390/s25164903
APA StyleZhang, W., Yang, J., Ren, L., Dou, H., Chen, X., Jia, H., Mao, Y., Zhang, J., Xu, W., Zhou, H., & Mu, X. (2025). High-Performance Capacitive Ultrasonic Transducer for Non-Destructive Testing of Concrete Compressive Strength. Sensors, 25(16), 4903. https://doi.org/10.3390/s25164903








