Exact SER Analysis of Partial-CSI-Based SWIPT OAF Relaying over Rayleigh Fading Channels and Insights from a Generalized Non-SWIPT OAF Approximation
Abstract
1. Introduction
- 1.
- Operational Protocol Proposal: A practical protocol and operational scenario are proposed for efficient SWIPT OAF relaying under partial-CSI (P-CSI) and energy harvesting constraints.
- 2.
- Exact SER Analysis: Exact closed-form expressions for the SER of P-CSI-based SWIPT OAF relaying systems over Rayleigh fading channels are derived using moment-generating function (MGF)-based techniques.
- 3.
- Generalized Non-SWIPT OAF Approximation: An analytical approximation modeling the SWIPT OAF relay as a generalized non-SWIPT OAF relay is introduced, enabling a unified and tractable performance analysis.
- 4.
- Analysis of Best Relay Selection: The framework incorporates scenarios involving best relay selection, addressing practical issues such as relay unavailability or selection inaccuracies.
- 5.
- Asymptotic Performance Insights: Asymptotic SER expressions in the high signal-to-noise ratio (SNR) regime are derived, providing insights into the harmonic mean behavior of end-to-end SNR and the influence of PS ratios.
- 6.
- Simulation Validation: Extensive simulations confirm the analytical results and quantify performance trade-offs associated with PS factors, relay selection strategies, and partial CSI.
2. SWIPT OAF Relaying Systems
2.1. SWIPT Relaying System Model
Indirect (SRD) Link SNR
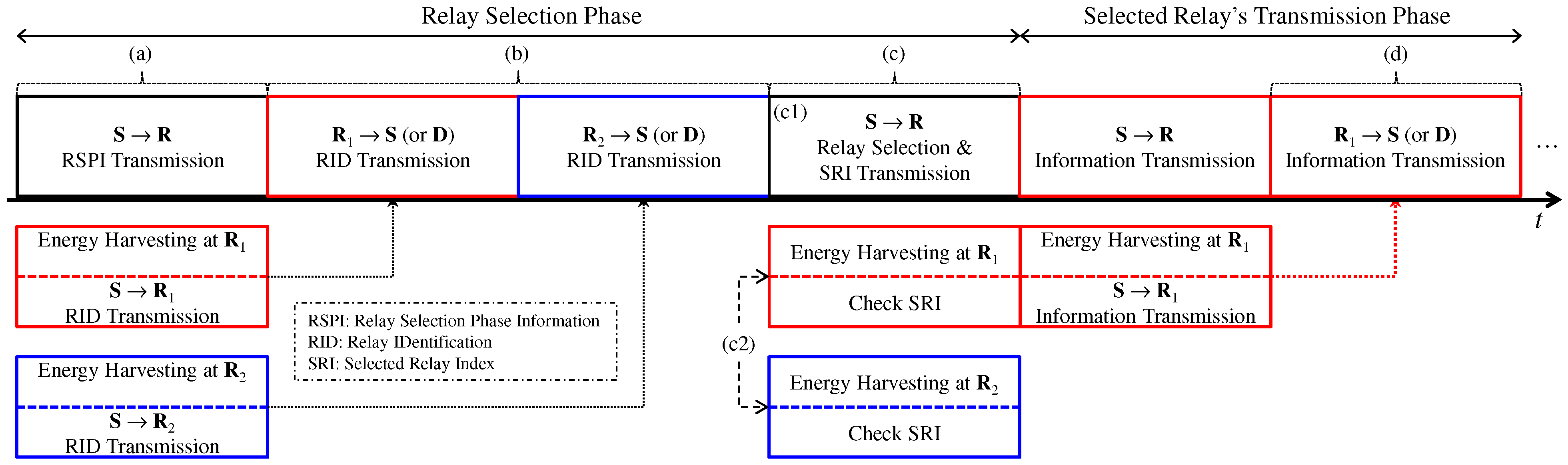
2.2. SWIPT Relay Selection Scenario for SRD Link
- (a)
- Source node: Broadcasts basic information (i.e., relay selection phase information, RSPI) to all SWIPT relays.
- (b)
- Each SWIPT relay: Performs EH and responds to both the source and destination nodes by transmitting its relay identification (RID) (e.g., an assigned Walsh–Hadamard code [35]).
- (c1)
- Source node: Computes the instantaneous SR link SNR, selects the best relay, and broadcasts the selected relay index (SRI) to all relays.
- (c2)
- Each SWIPT relay: Receives the SRI and compares it with its own RID.
- (d)
- Selected relay: Participates in the AF transmission phase.
2.2.1. RSP(a): S→R Subphase
2.2.2. RSP(b): S→R (Non-AF) →S Subphase
2.2.3. RSP(c1): CSI at Source Node
2.2.4. RSP(c2) & (d): Source Transmits the Selected Relay Index
3. Performance Analysis for the SWIPT OAF Relaying System: P-CSI Based on SR Link
3.1. Nth Best Selection Probability
3.1.1. Relay Selection Probability for the ith Relay
3.1.2. Joint PDF
3.2. Error Rate Expressions
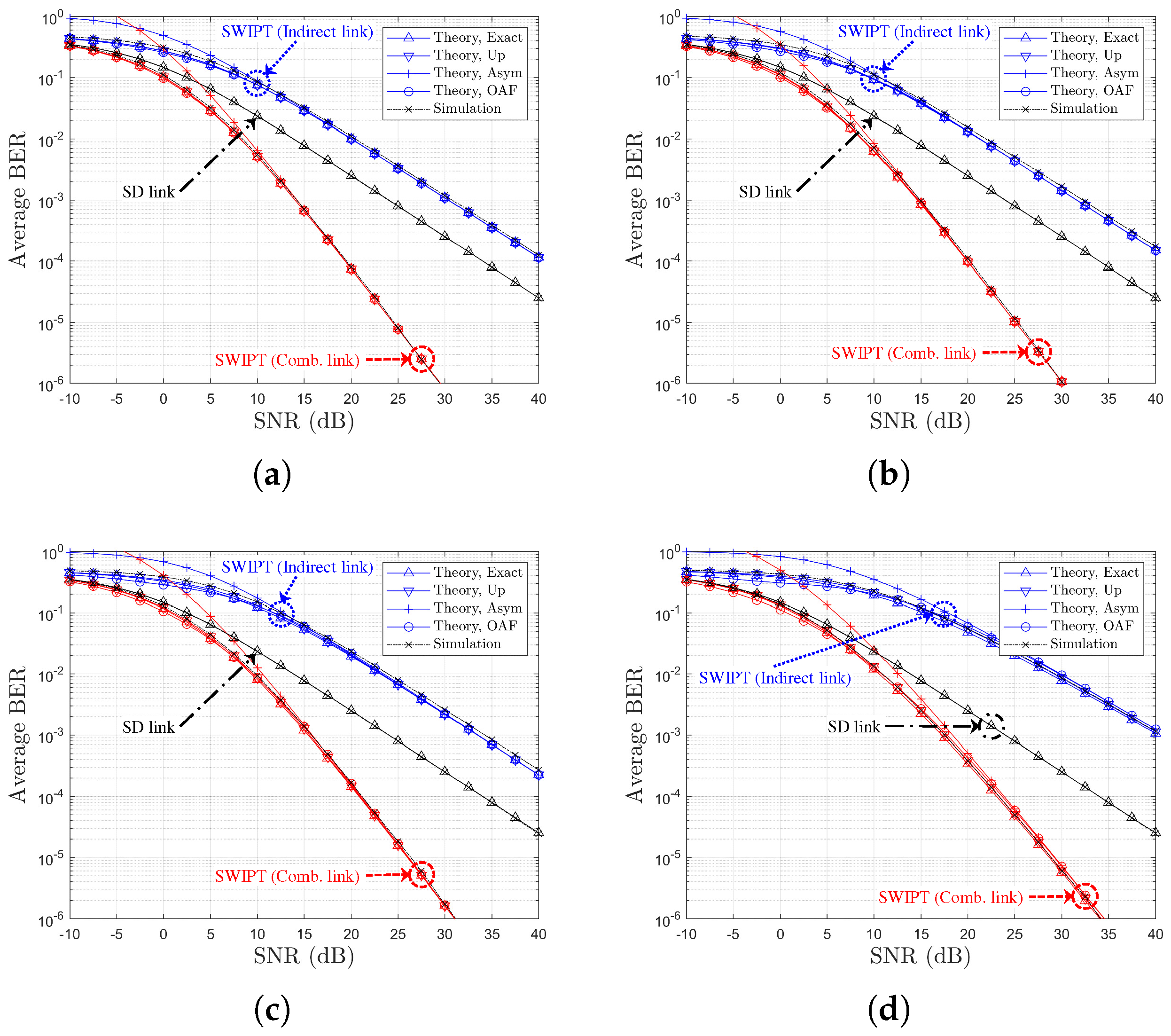
3.2.1. Exact and Upper-Bounded ASER Expressions
3.2.2. Asymptotic BER Expressions
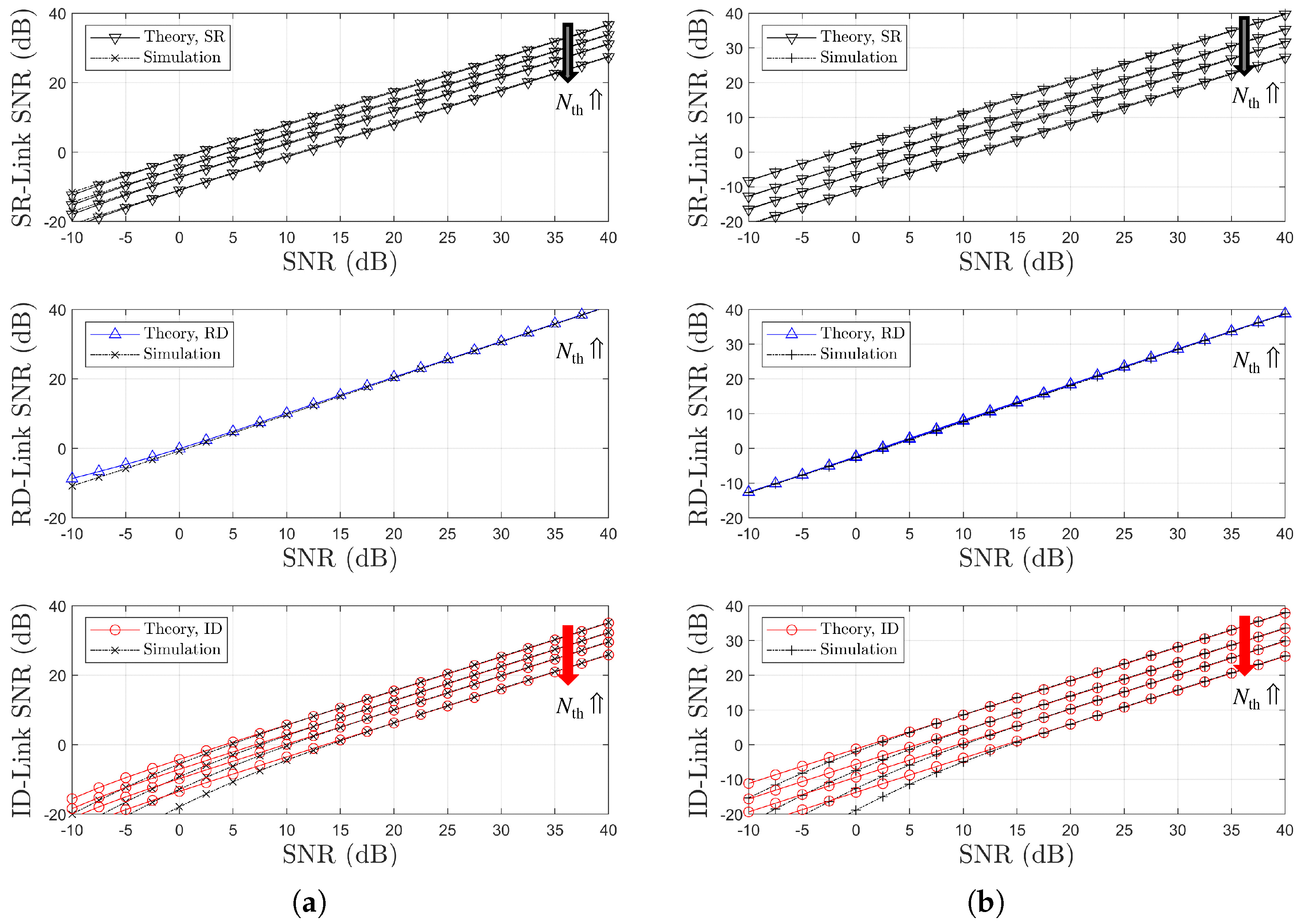
3.3. Average Link SNR Derivation
3.3.1. SR Link
3.3.2. RD Link
3.3.3. Indirect Link
3.4. Approximation SWIPT OAF Relay to General OAF Relay
- Relay selection based on partial CSIs of SR links.
- Approximation of the SWIPT indirect link as a conventional AF indirect link.
- Minimum-based approximation for the indirect link SNR pair.
3.4.1. PDFs (SWIPT OAF → General OAF)
3.4.2. ABER Expressions Based on Min-Approximation of OAF Links
4. Performance Analysis for the SWIPT OAF Relaying System: P-CSI Based on RD Link
4.1. Nth Best Selection Probability
4.1.1. Relay Selection Probability for the ith Relay
4.1.2. Joint PDF
4.2. Error Rate Expressions
4.2.1. Exact and Upper Bounded ASER Expressions
4.2.2. Asymptotic BER Expressions
4.3. Average Link SNR Derivation
4.3.1. SR Link
4.3.2. RD Link
4.3.3. Indirect Link
4.4. Approximation SWIPT OAF Relay to General OAF Relay
- Relay selection based on partial CSI of RD links.
- Approximation of the SWIPT indirect link as a conventional AF indirect link.
- Minimum-based approximation for the indirect link SNR pair.
4.4.1. PDFs (SWIPT OAF → General OAF)
4.4.2. Approximated Closed-Form Expression of ABRE
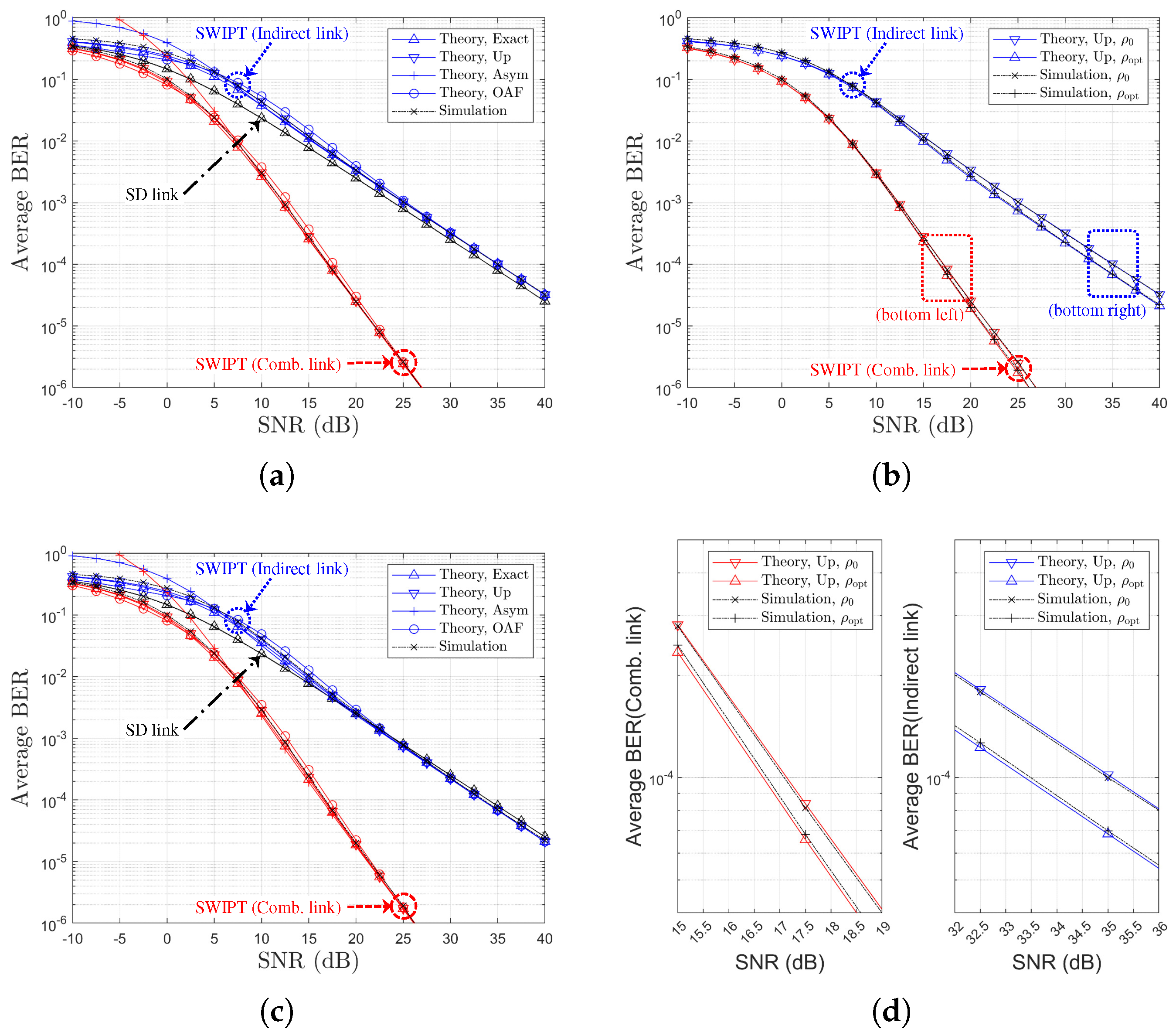
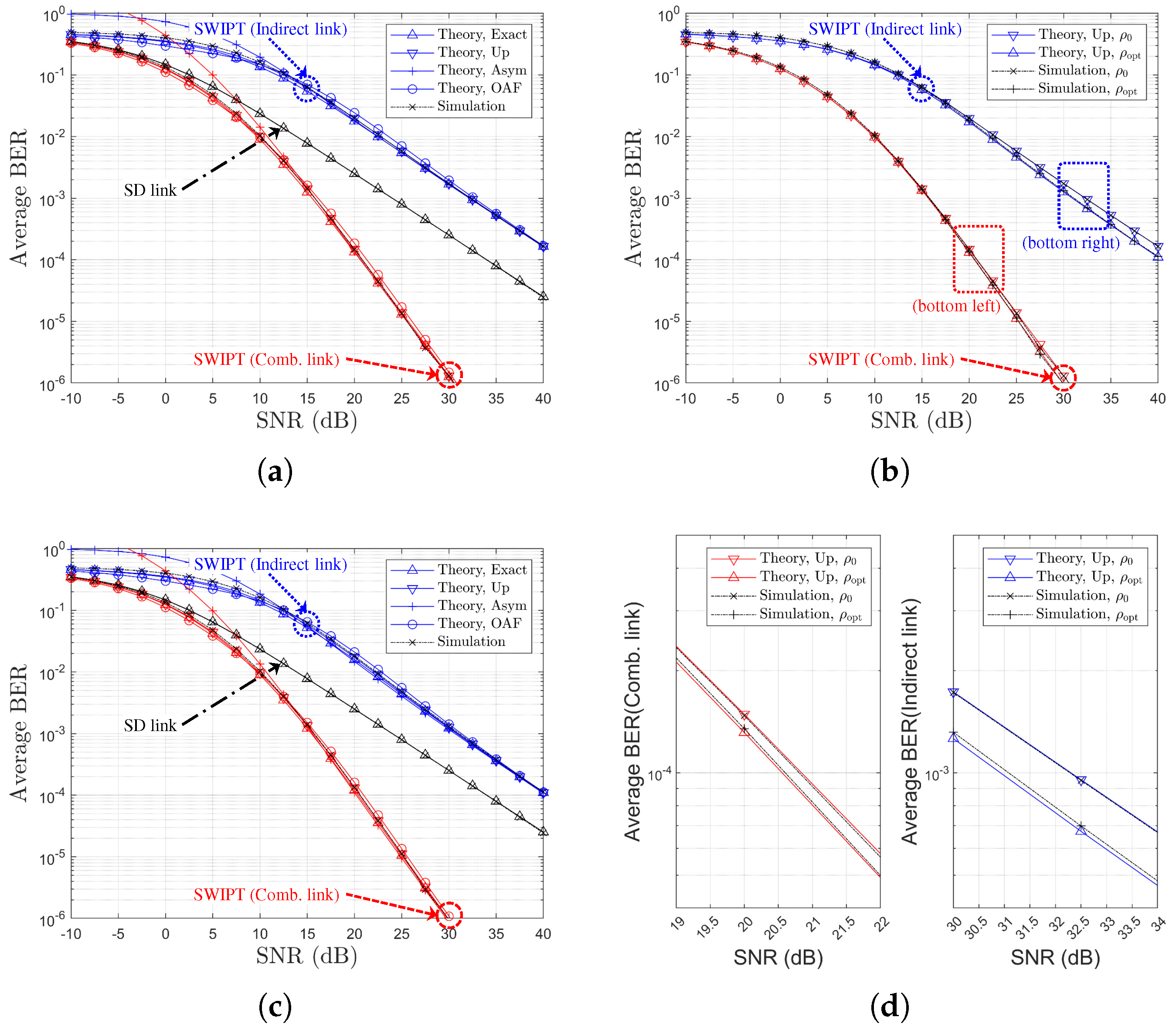
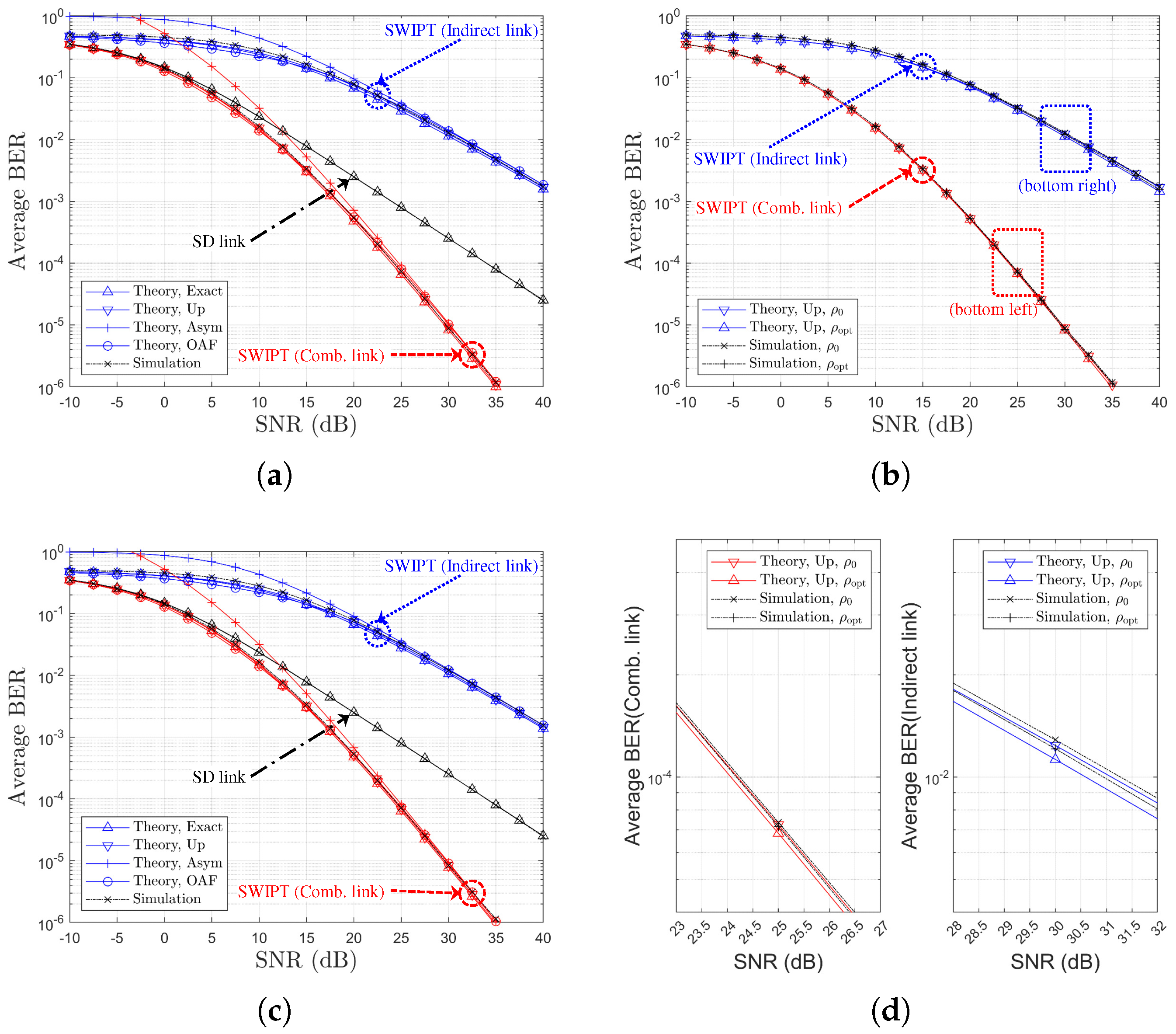
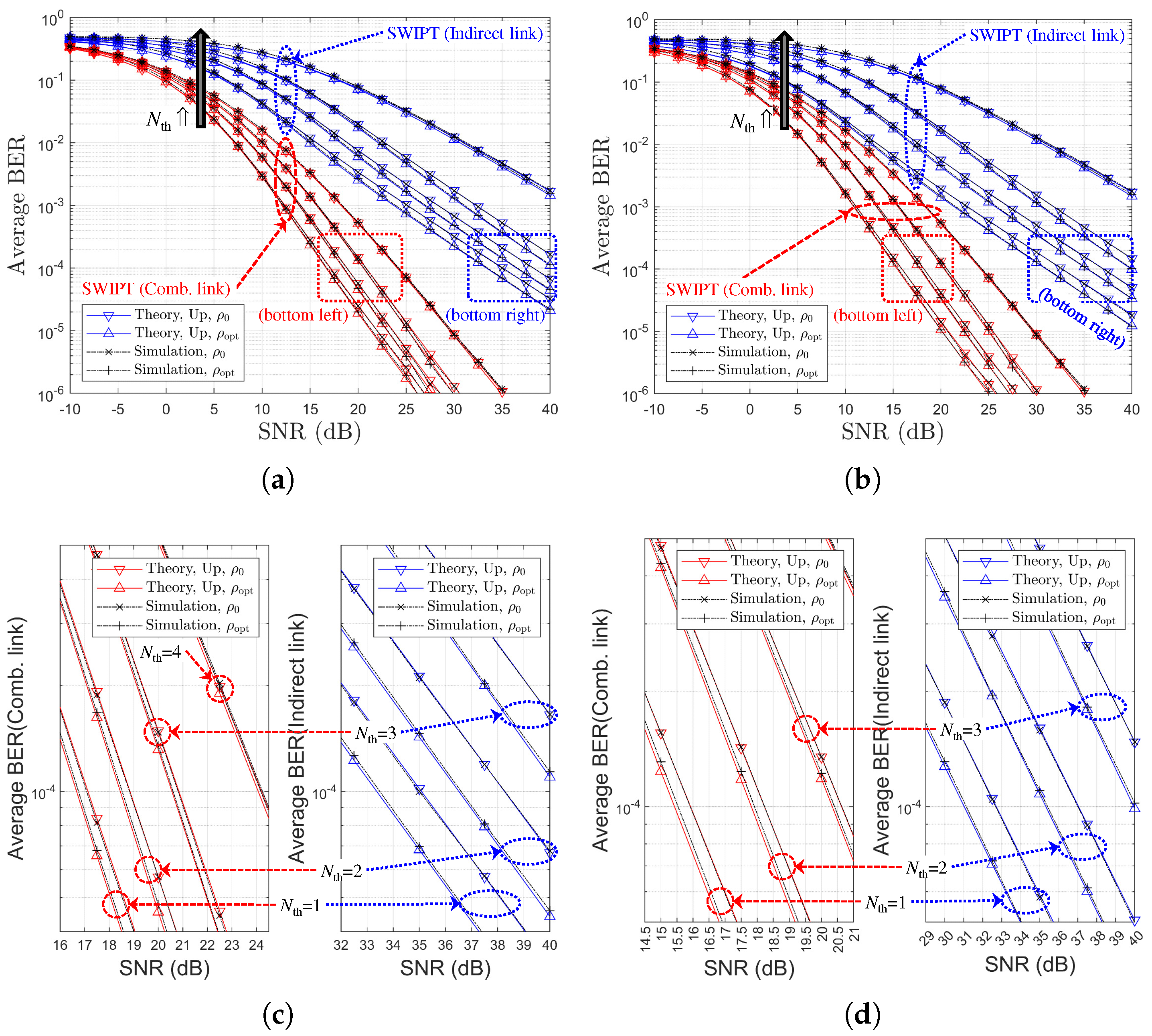
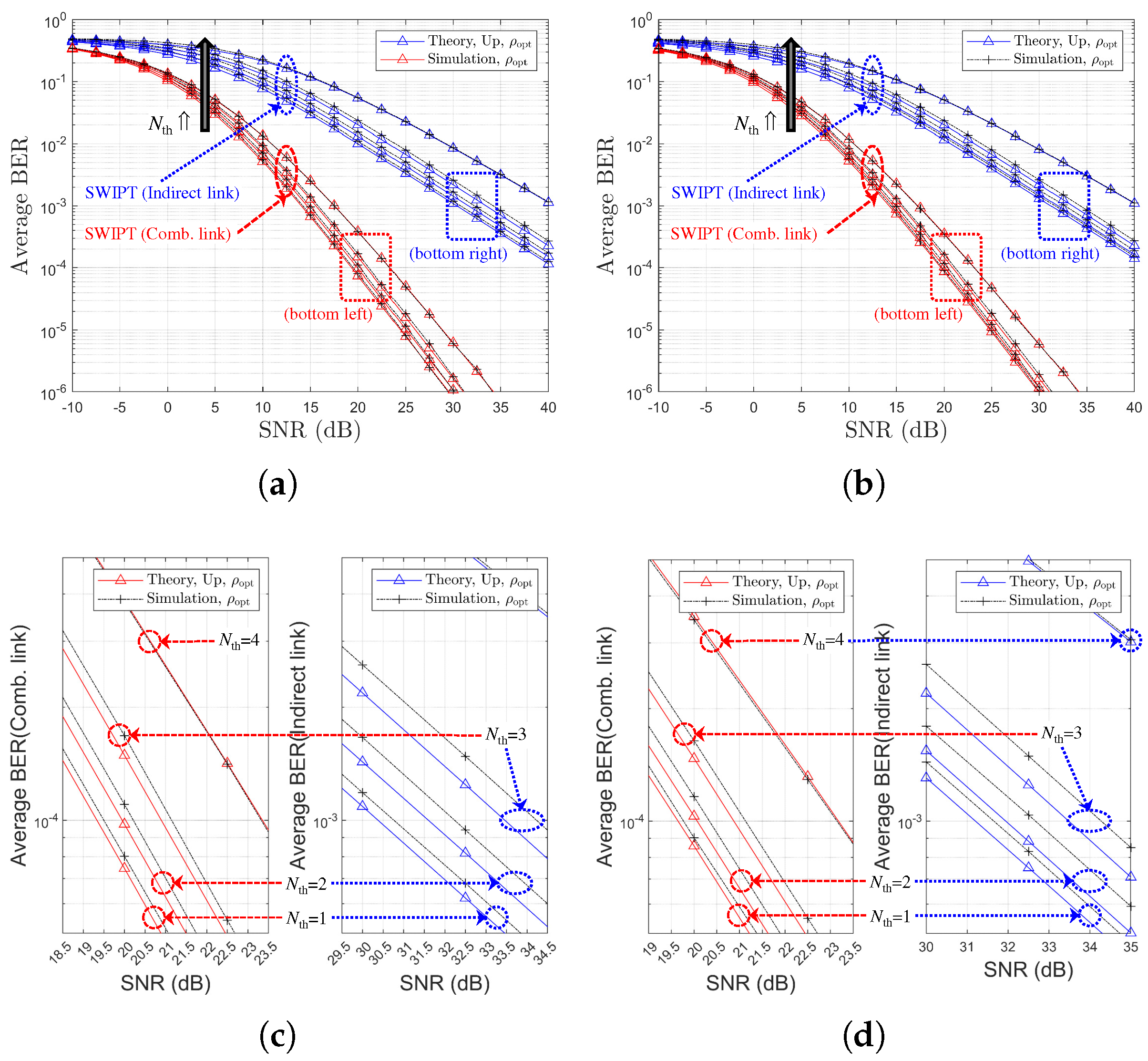
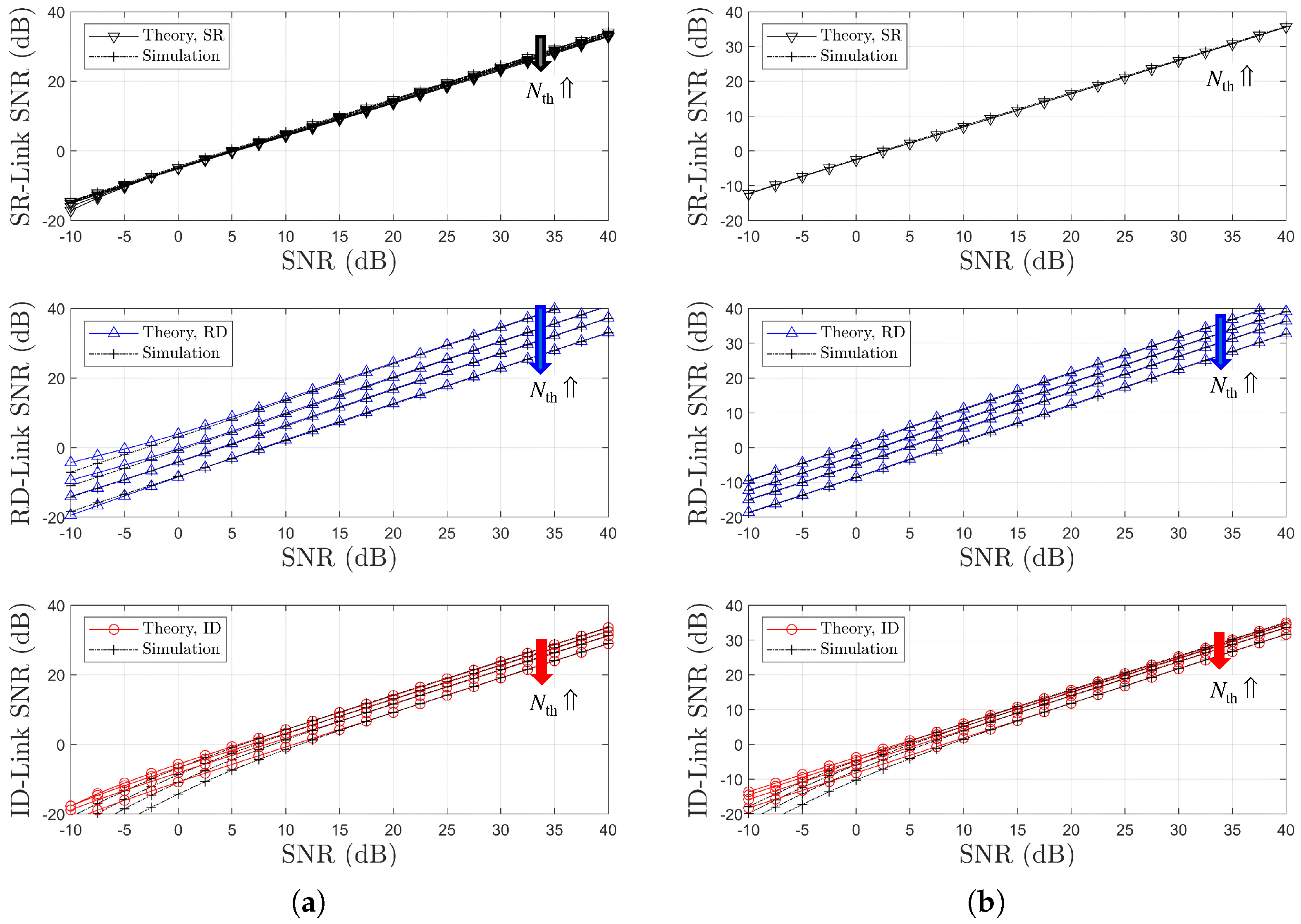
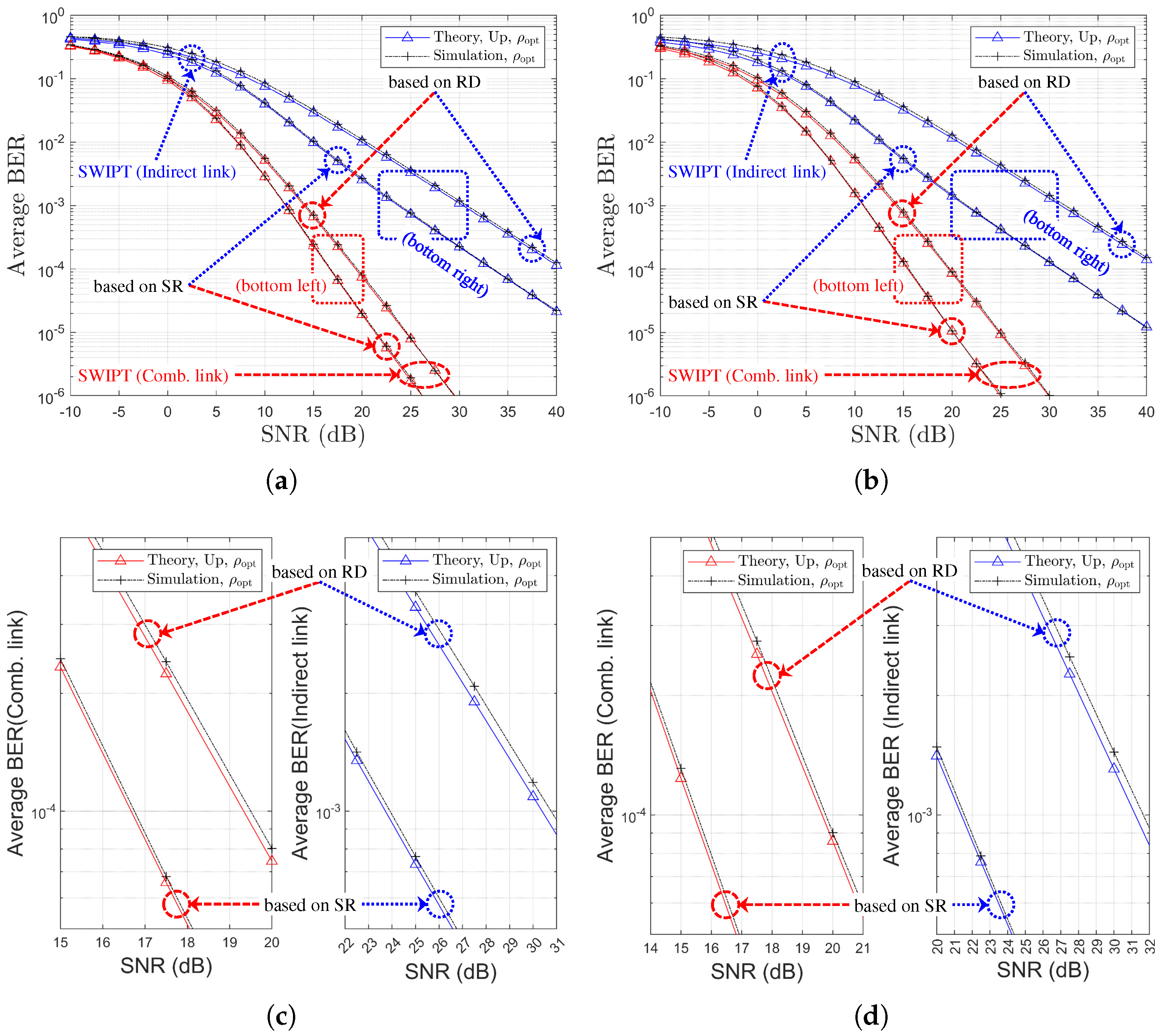
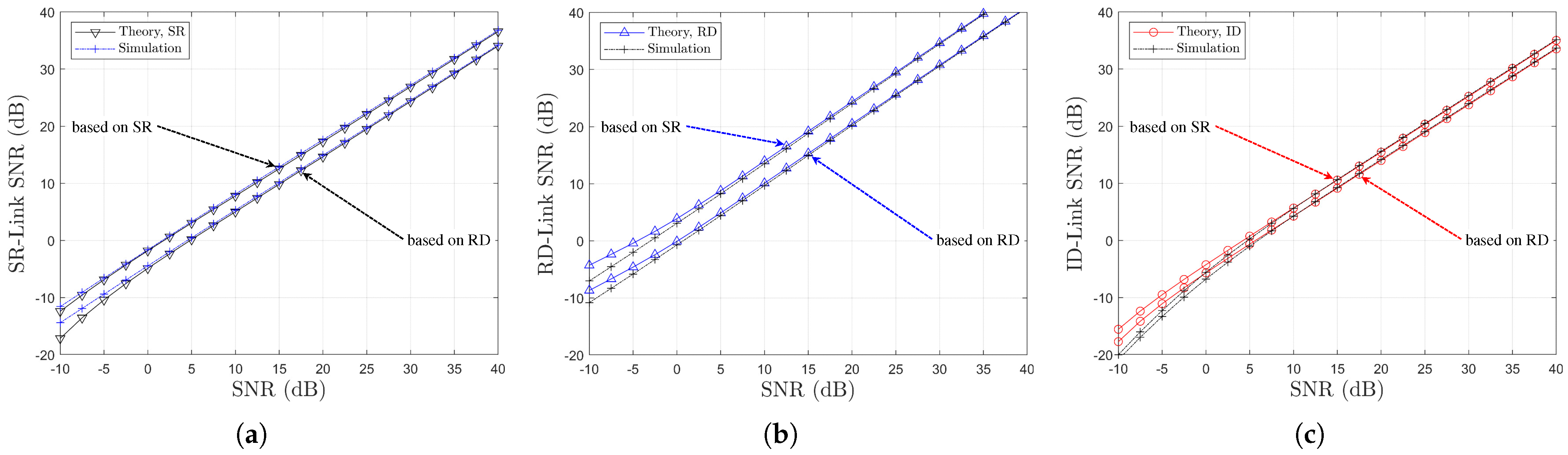
5. Numerical and Simulation Results
5.1. SWIPT OAF Relaying System Using P-CSIs Based on SR Links
5.2. SWIPT OAF Relaying System Using P-CSIs Based on RD Links
5.3. Performance Comparison by Relay Selection Method: SR Links vs. RD Links
6. Conclusions
Future Work
- Nonlinear EH Modeling and Efficiency Variability: Practical energy harvesting (EH) circuits often exhibit nonlinear characteristics and time-varying conversion efficiencies due to hardware limitations, temperature, and other environmental factors. Incorporating nonlinear EH models, as discussed in [41], and analyzing the impact of efficiency variability can enhance the accuracy and robustness of performance evaluations and system design for real-world deployment.
- Machine-Learning-Based PS Optimization: Adaptive power splitting (PS) control using machine learning techniques—such as deep reinforcement learning and predictive modeling [42]—could improve system adaptability and energy efficiency under dynamic wireless environments with partial CSI constraints.
- Advanced Optimization Algorithms: Employing advanced nonlinear optimization methods, including those surveyed in [40], may provide more efficient solutions to nonconvex optimization problems typically encountered in SWIPT OAF relaying systems.
- Analysis under Generalized Fading: Extending the current analytical framework to incorporate more general channel models, such as Rician, Nakagami-m, or - fading, may provide valuable insights into the performance of SWIPT systems under line-of-sight (LoS) or composite fading conditions prevalent in practical deployment scenarios.
- Cross-Layer and System-Level Design: Integrating higher-layer design aspects such as MAC-layer scheduling, delay constraints, and buffer management could lead to a more comprehensive and practically viable design for SWIPT OAF relay networks in next-generation IoT and wireless systems.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AF | amplify-and-forward |
| AWGN | additive white Gaussian noise |
| BER | bit error rate |
| BPSK | binary phase shift keying |
| CDF | cumulative distribution function |
| CSI | channel state information |
| DF | decode-and-forward |
| D2D | Device-to-Device |
| EH | energy harvesting |
| IP | information processing |
| MGF | moment-generating function |
| OAF | opportunistic amplify-and-forward |
| probability density function | |
| PS | power splitting |
| PSF | power splitting factor |
| RD | relay-to-destination |
| RF | radio frequency |
| SD | source-to-destination |
| SRD | source-relay-destination |
| SER | symbol error rate |
| SNR | signal-to-noise ratio |
| SR | source-to-relay |
| SWIPT | simultaneous wireless information and power transfer |
| TS | time splitting |
| WPCN | wireless powered communication network |
Appendix A. Generalized Interpretation of SWIPT AF Relaying as Conventional AF Relaying [36]
Appendix A.1. MGF and Upper Bounded Exprassions
Appendix A.2. Asymptotic BER Expression
Appendix A.3. SWIPT AF Relaying Modeled as Conventional AF Relaying
Appendix B. Nth Order Statistic for a Set of Independent RVs
- PDF of the RV Y:
- CDF of the RV Y:
Appendix B.1. Nth Order Statistic for IID Case
Appendix B.2. Nth Order Statistic for IID Rayleigh RVs
Appendix B.3. Nth Order Statistic for INID Case
Appendix B.4. Nth Order Statistic for INID Rayleigh RVs [33]
References
- Nasir, A.; Zhou, X.; Durrani, S.; Kennedy, R. Relaying Protocols for Wireless Energy Harvesting and Information Processing. IEEE Trans. Wireless Commun. 2013, 7, 3622–3636. [Google Scholar] [CrossRef]
- Lee, H.; Song, C.; Choi, S.; Lee, I. Outage Probability Analysis and Power Splitter Designs for SWIPT Relaying Systems with Direct Link. IEEE Commun. Lett. 2017, 3, 648–651. [Google Scholar] [CrossRef]
- Song, C.; Jeon, Y. Weighted MMSE Precoder Designs for Sum-Utility Maximization in Multi-User SWIPT Network-MIMO with Per-BS Power Constraints. IEEE Trans. Veh. Technol. 2018, 3, 2809–2813. [Google Scholar] [CrossRef]
- Chen, H.; Zhou, X.; Li, Y.; Wang, P.; Vucetic, B. Harvest-Then-Cooperate: Wireless-Powered Cooperative Communications. IEEE Trans. Signal Process. 2015, 7, 1700–1711. [Google Scholar] [CrossRef]
- Mahama, S.; Asiedu, D.K.P.; Lee, K.-J. Simultaneous wireless information and power transfer for cooperative relay networks with battery. IEEE Access 2017, 5, 13171–13178. [Google Scholar] [CrossRef]
- Lee, H.; Lee, K.-J.; Kim, H.; Lee, I. Wireless information and power exchange for energy-constrained device-to-device communications. IEEE Internet Things J. 2018, 5, 3175–3185. [Google Scholar] [CrossRef]
- Asiedu, D.K.P.; Lee, H.; Lee, K.-J. Simultaneous wireless information and power transfer for decode-and-forward Multi-hop Relay systems in energy-constrained IoT networks. IEEE Internet Things J. 2019, 6, 9413–9426. [Google Scholar] [CrossRef]
- Liu, Z.; Ye, Y.; Lu, G.; Hu, R.Q. System Outage Performance of SWIPT Enabled Full-Duplex Two-Way Relaying with Residual Hardware Impairments and Self-Interference. IEEE Syst. J. 2023, 1, 337–348. [Google Scholar] [CrossRef]
- He, S.; Xie, K.; Chen, W.; Zhang, D.; Wen, J. Energy-aware routing for SWIPT in multi-hop energy-constrained wireless network. IEEE Access 2018, 6, 17996–18008. [Google Scholar] [CrossRef]
- Zhang, Z.; Pang, H.; Georgiadis, A.; Cecati, C. Wireless power transfer—An overview. IEEE Trans. Ind. Elect. 2018, 66, 1044–1058. [Google Scholar] [CrossRef]
- Kim, K.; Asiedu, D.K.P.; Anokye, P.; Kim, E.; Lee, K.-J. Transmit Power Optimization in Multihop Amplify-and-Forward Relay Systems with Simultaneous Wireless Information and Power Transfer. Electronics 2024, 13, 4232. [Google Scholar] [CrossRef]
- Ghosh, S.; Acharya, T.; Maity, S.P. Outage Analysis in SWIPT Enabled Cooperative AF/DF Relay Assisted Two-Way Spectrum Sharing Communication. IEEE Trans. Cogn. Commun. Netw. 2022, 3, 1434–1443. [Google Scholar] [CrossRef]
- Ghadi, F.R.; Lopez-Martinez, F.J. Performance Analysis of SWIPT Relay Networks Over Arbitrary Dependent Fading Channels. IEEE Trans. Commun. 2024, 6, 3651–3663. [Google Scholar] [CrossRef]
- Kumar, P.; Dhaka, K. Performance of wireless powered DF relay system under Nakagami-m fading: Relay assists energy-constrained source. IEEE Syst. J. 2020, 2, 2497–2507. [Google Scholar] [CrossRef]
- Babaei, M.; Durak-Ata, L.; Aygolu, U. Performance analysis of dual-hop AF relaying with non-linear/linear energy harvesting. Sensors 2022, 22, 5987. [Google Scholar] [CrossRef]
- Ashraf, N.; Sheihkh, S.A.; Khan, S.A.; Shayea, I.; Jalal, M. Simultaneous Wireless Information and Power Transfer with Cooperative Relaying for Next-Generation Wireless Networks: A Review. IEEE Access 2021, 9, 71482–71504. [Google Scholar] [CrossRef]
- Rossi, P.S.; Ciuonzo, D.; Kansanen, K.; Ekman, T. Performance analysis of energy detection for MIMO decision fusion in wireless sensor networks over arbitrary fading channels. IEEE Trans. Wireless Commun. 2016, 15, 7794–7806. [Google Scholar] [CrossRef]
- Liu, X.; Wen, Z.; Liu, D.; Zou, J.; Li, S. Joint source and relay beamforming design in wireless multi-hop sensor networks with SWIPT. Sensors 2019, 19, 182. [Google Scholar] [CrossRef]
- Lou, Y.; Yu, Q.; Cheng, J.; Zhao, H. Exact BER analysis of selection combining for differential SWIPT relaying systems. IEEE Signal Process. Lett. 2016, 8, 1198–1202. [Google Scholar] [CrossRef]
- Krikidis, I.; Thompson, J.; Mclaughlin, S.; Goertz, N. Amplify-and-forward with partial relay selection. IEEE Commun. Lett. 2008, 4, 235–237. [Google Scholar] [CrossRef]
- Hasna, M.; Alouini, M. End-to-End performance of transmission systems with relays over Rayleigh-fading channels. IEEE Trans. Wireless Commun. 2003, 6, 1126–1131. [Google Scholar] [CrossRef]
- Anghel, P.; Kaveh, M. Exact symbol error probability of a cooperative network in a Rayleigh-fading environment. IEEE Trans. Wireless Commun. 2004, 9, 1416–1421. [Google Scholar] [CrossRef]
- Laneman, J.N.; Tse, D.N.C.; Wornell, G.W. Cooperative diversity in wireless networks: Efficient protocols and outage behavior. IEEE Trans. Info. Theory 2004, 12, 3062–3080. [Google Scholar] [CrossRef]
- Bletsas, A.; Khisti, A.; Reed, D.P.; Lippman, A. A simple cooperative diversity method based on network path selection. IEEE J. Sel. Areas Commun. 2006, 3, 659–672. [Google Scholar] [CrossRef]
- Zhao, Y.; Adve, R.; Lim, T.J. Symbol error rate of selection amplify-and-forward relay systems. IEEE Commun. Lett. 2006, 11, 757–759. [Google Scholar] [CrossRef]
- Ikki, S.S.; Ahmed, M.H. Performance of Multiple-Relay Cooperative Diversity Systems with Best Relay Selection over Rayleigh Fading Channels. EURASIP J. Adv. Signal Process. 2008, 2008, 580368. [Google Scholar] [CrossRef]
- Maham, B.; Hjorungnes, A. Performance analysis of amplify-and-forward opportunistic relaying in Rician fading. IEEE Signal Process. Lett. 2009, 8, 643–646. [Google Scholar] [CrossRef]
- Ikki, S.S.; Ahmed, M.H. Performance Analysis of Adaptive Decode-and-Forward Cooperative Diversity Networks with Best-Relay Selection. IEEE Trans. Commun. 2010, 1, 68–72. [Google Scholar] [CrossRef]
- Ikki, S.S.; Ahmed, M.H. On the Performance of Cooperative-Diversity Networks with the Nth Best-Relay Selection Scheme. IEEE Trans. on Commun. 2010, 11, 3062–3069. [Google Scholar] [CrossRef]
- He, Y.; Huang, F.; Wang, D.; Zhang, R. Outage Probability Analysis of MISO-NOMA Downlink Communications in UAV-Assisted Agri-IoT with SWIPT and TAS Enhancement. IEEE Trans. Netw. Sci. Eng. 2025, 3, 2151–2164. [Google Scholar] [CrossRef]
- Lin, G.; Zhou, Y.; Jiang, W.; He, X.; Zhou, X.; He, G.; Yang, P. LF-SWIPT: Outage Analysis for SWIPT Relaying Networks Using Lossy Forwarding with QoS Guaranteed. IEEE Internet Things J. 2022, 19, 18737–18748. [Google Scholar] [CrossRef]
- Nam, S.; Ko, K.; Hong, D. Exact Average SER Performance Analysis for the Nth Best Opportunistic Amplify-and-Forward Relay Systems. IEICE Trans. Commun. 2012, 5, 1852–1855. [Google Scholar] [CrossRef]
- Ko, K.; Woo, C. Outage Probability and Channel Capacity for Nth Best Relay Selection AF Relaying over INID Rayleigh Fading Channels. Int. J. Commun. Syst. 2012, 11, 1496–1504. [Google Scholar] [CrossRef]
- Lim, S.; Ko, K. Approximation of Multi-hop Relay to Dual-hop Relay and Its Error Performance Analysis. IEEE Commun. Lett. 2017, 2, 342–345. [Google Scholar] [CrossRef]
- Woo, C.; Lim, S.; Ko, K. Effects of CEE and Feedback Error on Performance for AF-ORS with PSA-CE Schemes Over Quasi-Static Rayleigh Fading channels. Wireless Pers. Commun. 2017, 3, 3619–3643. [Google Scholar] [CrossRef]
- Ko, K.; Lim, S. Error Performance Analysis and PS factor Optimization for SWIPT AF Relaying Systems over Rayleigh Fading Channels: Interpretation SWIPT AF relay as non-SWIPT AF relay. Electronics 2025, 14, 2597. [Google Scholar] [CrossRef]
- Gradshteyn, I.; Ryzhik, I. Table of Integrals, Series and Products, 7th ed.; Academic Press: San Diego, CA, USA, 2007. [Google Scholar]
- Exponential Integral. Available online: https://en.wikipedia.org/wiki/Exponential_integral (accessed on 19 March 2025).
- Proakis, J. Digital Communication, 3rd ed.; McGraw Hill: Boston, MA, UAS, 1995. [Google Scholar]
- Khalaf, Q.; Sali, A.; Ismail, A.; Ahmad, M.; Hussein, Y.; Shah, J. Advanced Nonlinear Optimization Techniques in SWIPT: A Review. IEEE Access 2024, 12, 192743–192766. [Google Scholar] [CrossRef]
- Mushtaq, M.U.; Venter, H.; Singh, A.; Owais, M. Advances in Energy Harvesting for Sustainable Wireless Sensor Networks: Challenges and Opportunities. Hardware 2025, 3, 1. [Google Scholar] [CrossRef]
- Alamu, O.; Olwal, T.; Migabo, E. Machine Learning Applications in Energy Harvesting Internet of Things Networks: A Review. IEEE Access 2025, 13, 4235–4266. [Google Scholar] [CrossRef]
- Popoulis, A.; Pillai, S. Probability, Random Variables, and Stochastic Processes, 4th ed.; McGraw Hill: Boston, MA, UAS, 2002. [Google Scholar]
- Simon, M.; Alouini, M. Digital Communication over Fading Channels; John Wiley & Sons: New York, NY, UAS, 2000. [Google Scholar]




| Ch. Model | Link | Channel Power | R |
|---|---|---|---|
| 1 | SD | 4 | |
| SR | |||
| RD | |||
| 2 | SD | 4 | |
| SR | |||
| RD |
| Legend | Symbol | Equation(s) | Remarks |
|---|---|---|---|
| Theory,Exact | , | (26) | Exact MGF |
| Theory,Up | , | (27) | Upper Bound MGF |
| Theory,Asym | , | (28), (29) | Asymptotic Bound |
| Theory,OAF | , | (39), (40) | OAF Approximation |
| Theory,SR | (30) | Exact | |
| Theory,RD | (32) | Exact | |
| Theory,ID | (33) | High SNR Approximation |
| Legend | Symbol | Equation(s) | Remarks |
|---|---|---|---|
| Theory,Exact | , | (52) | Exact MGF |
| Theory,Up | , | (53) | Upper Bound MGF |
| Theory,Asym | , | (54), (55) | Asymptotic Bound |
| Theory,OAF | , | (63), (64) | OAF Approximation |
| Theory,SR | (56) | Exact | |
| Theory,RD | (58) | Exact | |
| Theory,ID | (59) | High SNR Approximation |
| Ch. Model | Gain for Comb. Link 1 | Gain for Indirect Link 2 | Figures | |
|---|---|---|---|---|
| 1 | Figure 12a,c | |||
| 2 | Figure 14a,c | |||
| 3 | Figure 15a,c | |||
| 1 | Figure 12b,d | |||
| 2 | Figure 14b,d | |||
| 3 | Figure 15b,d |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ko, K.; Song, S. Exact SER Analysis of Partial-CSI-Based SWIPT OAF Relaying over Rayleigh Fading Channels and Insights from a Generalized Non-SWIPT OAF Approximation. Sensors 2025, 25, 4872. https://doi.org/10.3390/s25154872
Ko K, Song S. Exact SER Analysis of Partial-CSI-Based SWIPT OAF Relaying over Rayleigh Fading Channels and Insights from a Generalized Non-SWIPT OAF Approximation. Sensors. 2025; 25(15):4872. https://doi.org/10.3390/s25154872
Chicago/Turabian StyleKo, Kyunbyoung, and Seokil Song. 2025. "Exact SER Analysis of Partial-CSI-Based SWIPT OAF Relaying over Rayleigh Fading Channels and Insights from a Generalized Non-SWIPT OAF Approximation" Sensors 25, no. 15: 4872. https://doi.org/10.3390/s25154872
APA StyleKo, K., & Song, S. (2025). Exact SER Analysis of Partial-CSI-Based SWIPT OAF Relaying over Rayleigh Fading Channels and Insights from a Generalized Non-SWIPT OAF Approximation. Sensors, 25(15), 4872. https://doi.org/10.3390/s25154872





