FPCR-Net: Front Point Cloud Regression Network for End-to-End SMPL Parameter Estimation
Abstract
1. Introduction
- FPCR-Net is the first network designed to directly regress SMPL pose and shape parameters from single-view front point clouds, eliminating the need for iterative registration.
- FPCR-Net extracts SO(3) equivariant features separately from front and back point clouds to reduce rotational ambiguity and interference, while employing soft aggregation and self-attention mechanisms for differentiable, accurate SMPL pose and shape regression.
2. Related Work
2.1. Advances in Human Body Reconstruction
2.2. Advances in Point Cloud Completion
3. Method
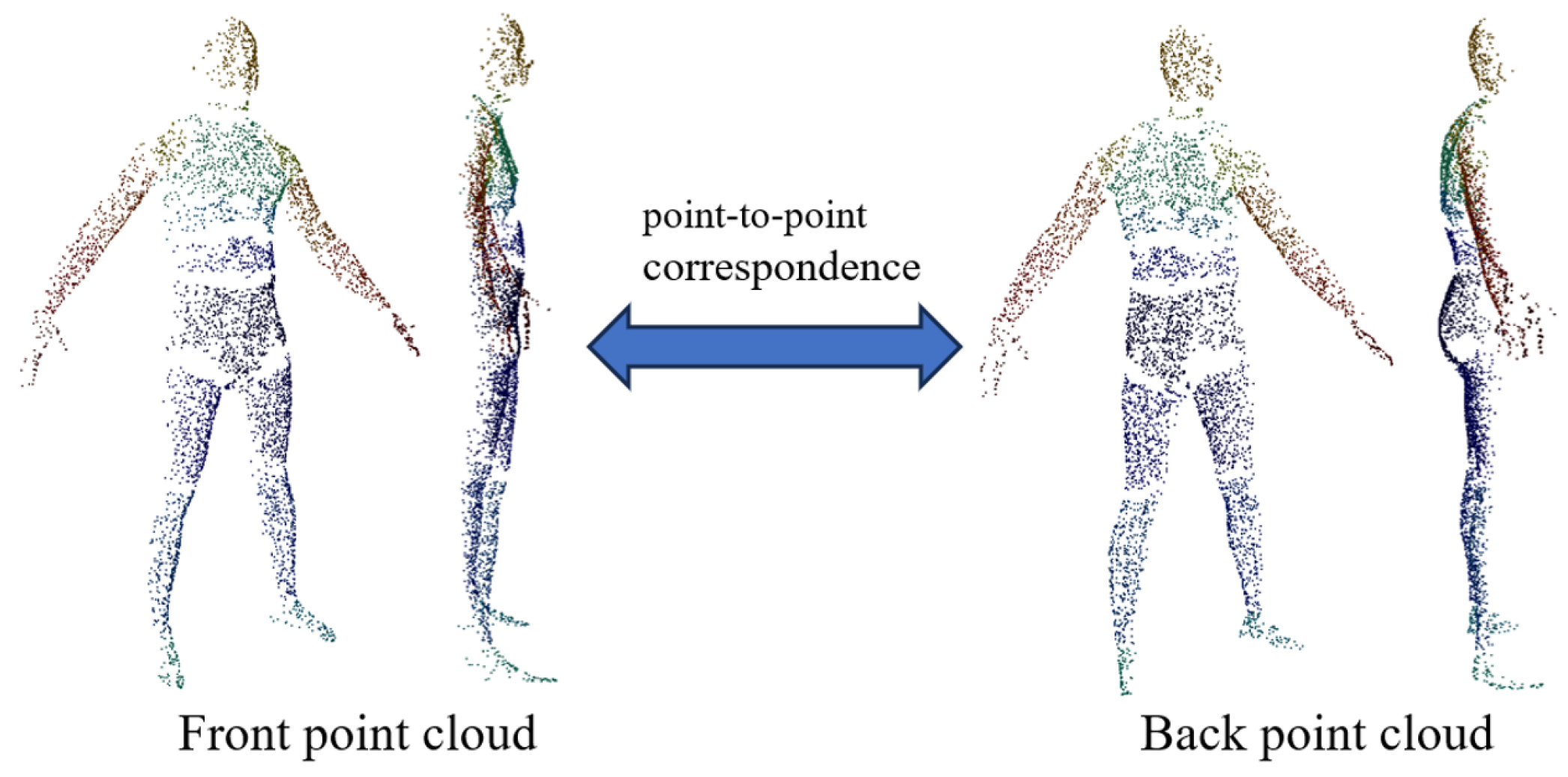
3.1. Back Point Cloud Prediction
3.2. Point Cloud Equivariant Feature Extraction
3.3. Pose Parameter Prediction Module
3.4. Shape Parameter Prediction Module
3.5. FPCR-Net Construction Details
4. Dataset Construction
5. Training Details
6. Experimental Results and Analysis
6.1. Implementation Details
6.2. Effectiveness of Body Point Cloud Completion
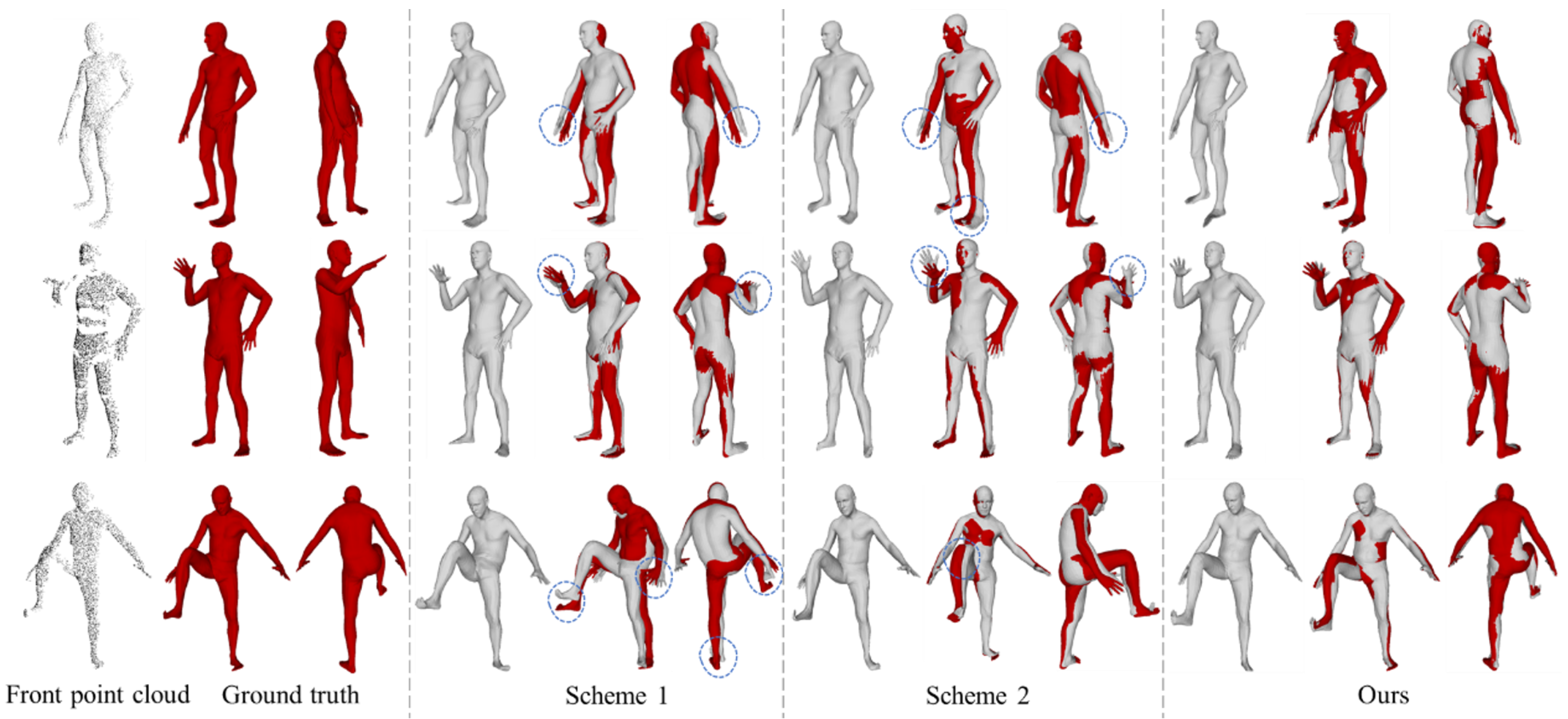
6.3. Ablation Experiment on Point Cloud Equivariant Feature Extraction Scheme
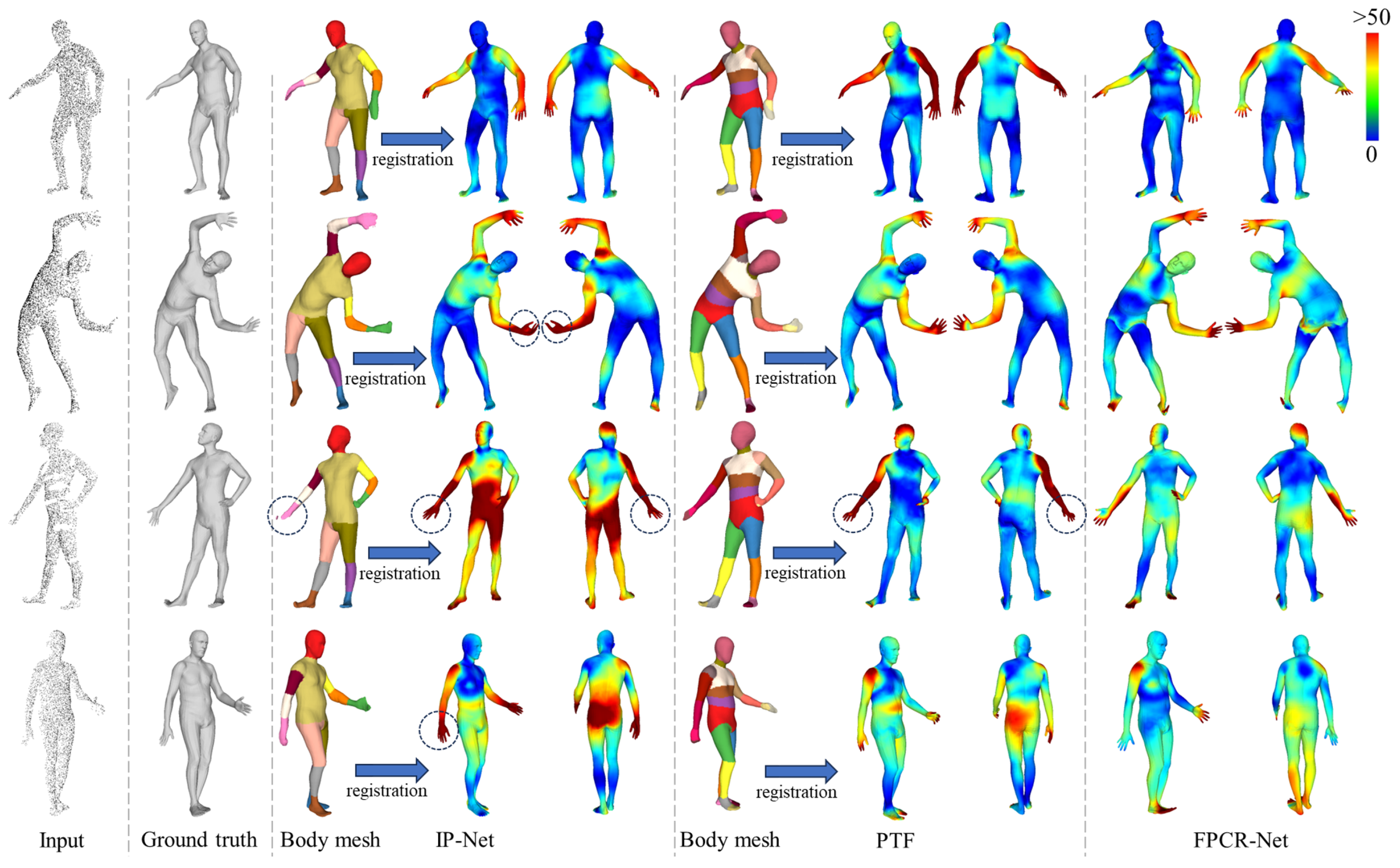
6.4. SMPL Body Shape and Pose Prediction
7. Limitations and Discussions
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, X.; Li, G.; Li, M.; Liu, K.; Mitrouchev, P. 3D human body modeling with orthogonal human mask image based on multi-channel Swin transformer architecture. Image Vis. Comput. 2023, 137, 104795. [Google Scholar] [CrossRef]
- Chen, D.; Song, Y.; Liang, F.; Ma, T.; Zhu, X.; Jia, T. 3D human body reconstruction based on SMPL model. Vis. Comput. 2023, 39, 1893–1906. [Google Scholar] [CrossRef]
- Wang, Y.; Daniilidis, K. Refit: Recurrent fitting network for 3d human recovery. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 14644–14654. [Google Scholar]
- Xie, H.; Zhong, Y. Structure-consistent customized virtual mannequin reconstruction from 3D scans based on optimization. Text. Res. J. 2020, 90, 937–950. [Google Scholar] [CrossRef]
- Yan, S.; Wirta, J.; Kämäräinen, J.K. Anthropometric clothing measurements from 3D body scans. Mach. Vis. Appl. 2020, 31, 7. [Google Scholar] [CrossRef]
- Alhwarin, F.; Schiffer, S.; Ferrein, A.; Scholl, I. An optimized method for 3D body scanning applications based on KinectFusion. In Proceedings of the Biomedical Engineering Systems and Technologies: 11th International Joint Conference, BIOSTEC 2018, Funchal, Madeira, Portugal, 19–21 January 2018; Revised Selected Papers 11. Springer: Cham, Switzerland, 2019; pp. 100–113. [Google Scholar]
- Loper, M.; Mahmood, N.; Romero, J.; Pons-Moll, G.; Black, M.J. SMPL: A skinned multi-person linear model. In Seminal Graphics Papers: Pushing the Boundaries; Association for Computing Machinery: New York, NY, USA, 2023; Volume 2, pp. 851–866. [Google Scholar]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Proceedings of the Sensor Fusion IV: Control Paradigms and Data Structures, Boston, MA, USA, 12–15 November 1991; Volume 1611, pp. 586–606. [Google Scholar]
- Li, J.; Hu, Q.; Zhang, Y.; Ai, M. Robust symmetric iterative closest point. ISPRS J. Photogramm. Remote Sens. 2022, 185, 219–231. [Google Scholar] [CrossRef]
- Wang, K.; Xie, J.; Zhang, G.; Liu, L.; Yang, J. Sequential 3D human pose and shape estimation from point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 7275–7284. [Google Scholar]
- Feng, H.; Kulits, P.; Liu, S.; Black, M.J.; Abrevaya, V.F. Generalizing neural human fitting to unseen poses with articulated se (3) equivariance. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 7977–7988. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. In Proceedings of the NIPS’17: 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar] [CrossRef]
- Chen, H.; Liu, S.; Chen, W.; Li, H.; Hill, R. Equivariant point network for 3d point cloud analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 19–25 June 2021; pp. 14514–14523. [Google Scholar]
- Liu, B.; Liu, X.; Yang, Z.; Wang, C.C. Concise and effective network for 3D human modeling from orthogonal silhouettes. J. Comput. Inf. Sci. Eng. 2022, 22, 051004. [Google Scholar] [CrossRef]
- Pavlakos, G.; Choutas, V.; Ghorbani, N.; Bolkart, T.; Osman, A.A.; Tzionas, D.; Black, M.J. Expressive body capture: 3d hands, face, and body from a single image. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 10975–10985. [Google Scholar]
- Choutas, V.; Müller, L.; Huang, C.H.P.; Tang, S.; Tzionas, D.; Black, M.J. Accurate 3D body shape regression using metric and semantic attributes. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022; pp. 2718–2728. [Google Scholar]
- Muller, L.; Osman, A.A.; Tang, S.; Huang, C.H.P.; Black, M.J. On self-contact and human pose. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 19–25 June 2021; pp. 9990–9999. [Google Scholar]
- Song, Y.P.; Wu, X.; Yuan, Z.; Qiao, J.J.; Peng, Q. Posturehmr: Posture transformation for 3d human mesh recovery. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–21 June 2024; pp. 9732–9741. [Google Scholar]
- Bhatnagar, B.L.; Sminchisescu, C.; Theobalt, C.; Pons-Moll, G. Loopreg: Self-supervised learning of implicit surface correspondences, pose and shape for 3d human mesh registration. Adv. Neural Inf. Process. Syst. 2020, 33, 12909–12922. [Google Scholar]
- Li, X.; Li, G.; Li, T.; Mitrouchev, P. Human body construction based on combination of parametric and nonparametric reconstruction methods. Vis. Comput. 2024, 40, 5557–5573. [Google Scholar] [CrossRef]
- Wang, S.; Geiger, A.; Tang, S. Locally aware piecewise transformation fields for 3d human mesh registration. In Proceedings of the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 19–25 June 2021; pp. 7639–7648. [Google Scholar]
- Bhatnagar, B.L.; Sminchisescu, C.; Theobalt, C.; Pons-Moll, G. Combining implicit function learning and parametric models for 3d human reconstruction. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 311–329. [Google Scholar]
- Lunscher, N.; Zelek, J. Deep learning whole body point cloud scans from a single depth map. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1095–1102. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Yu, X.; Rao, Y.; Wang, Z.; Liu, Z.; Lu, J.; Zhou, J. Pointr: Diverse point cloud completion with geometry-aware transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Virtual, 11–17 October 2021; pp. 12498–12507. [Google Scholar]
- Yu, X.; Rao, Y.; Wang, Z.; Lu, J.; Zhou, J. AdaPoinTr: Diverse Point Cloud Completion With Adaptive Geometry-Aware Transformers. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 14114–14130. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Lee, H.; Shin, D. Proxyformer: Nyström-based linear transformer with trainable proxy tokens. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 13418–13426. [Google Scholar]
- Leng, S.; Zhang, Z.; Zhang, L. A point contextual transformer network for point cloud completion. Expert Syst. Appl. 2024, 249, 123672. [Google Scholar] [CrossRef]
- Wang, J.; Cui, Y.; Guo, D.; Li, J.; Liu, Q.; Shen, C. Pointattn: You only need attention for point cloud completion. In Proceedings of the Proceedings of the AAAI Conference on artificial intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 5472–5480. [Google Scholar]
- Hartley, R.; Trumpf, J.; Dai, Y.; Li, H. Rotation averaging. Int. J. Comput. Vis. 2013, 103, 267–305. [Google Scholar] [CrossRef]
- Ma, Q.; Yang, J.; Ranjan, A.; Pujades, S.; Pons-Moll, G.; Tang, S.; Black, M.J. Learning to dress 3d people in generative clothing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 6469–6478. [Google Scholar]
- Loper, M.M.; Black, M.J. OpenDR: An approximate differentiable renderer. In Proceedings of the 13th European Conference on Computer Vision—ECCV 2014, Zurich, Switzerland, 6–12 September 2014; Springer: Cham, Switzerland, 2014; pp. 154–169. [Google Scholar]
- Fuchs, F.; Worrall, D.; Fischer, V.; Welling, M. Se (3)-transformers: 3d roto-translation equivariant attention networks. Adv. Neural Inf. Process. Syst. 2020, 33, 1970–1981. [Google Scholar]
- Yuan, W.; Khot, T.; Held, D.; Mertz, C.; Hebert, M. Pcn: Point completion network. In Proceedings of the 2018 International Conference on 3D vision (3DV), Verona, Italy, 5–8 September 2018; pp. 728–737. [Google Scholar]










| Method | CD | EMD | Parameter | Time |
|---|---|---|---|---|
| PoinTr [25] | 402.2 | 30.4 | 40.5 M | 3.3 s |
| AdaPoinTr [26] | 231.7 | 22.4 | 31.0 M | 2.5 s |
| Ours | 187.8 | 17.2 | 7.86 M | 0.9 s |
| Design Schemes | Parameter | Vertex Error | Joint Position Error | Time |
|---|---|---|---|---|
| Scheme 1 | 2.0 M | 60.2 | 49.3 | 2.2 s |
| Scheme 2 | 10.3 M | 49.7 | 57.0 | 3.0 s |
| Ours | 10.6 M | 37.8 | 40.2 | 3.2 s |
| Method | Input | Parameters | Vertex | Joint Position | Time |
|---|---|---|---|---|---|
| PostureHMR [18] | Front RGB image | 29.4 M | 71.4 | 82.7 | 1.2 s |
| ArtEq [11] | Front point cloud | 0.9 M | 66.5 | 73.1 | 2.3 s |
| FPCR-Net | Front point cloud | 10.6 M | 37.8 | 40.2 | 3.2 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Cheng, X.; Chen, F.; Shi, F.; Li, M. FPCR-Net: Front Point Cloud Regression Network for End-to-End SMPL Parameter Estimation. Sensors 2025, 25, 4808. https://doi.org/10.3390/s25154808
Li X, Cheng X, Chen F, Shi F, Li M. FPCR-Net: Front Point Cloud Regression Network for End-to-End SMPL Parameter Estimation. Sensors. 2025; 25(15):4808. https://doi.org/10.3390/s25154808
Chicago/Turabian StyleLi, Xihang, Xianguo Cheng, Fang Chen, Furui Shi, and Ming Li. 2025. "FPCR-Net: Front Point Cloud Regression Network for End-to-End SMPL Parameter Estimation" Sensors 25, no. 15: 4808. https://doi.org/10.3390/s25154808
APA StyleLi, X., Cheng, X., Chen, F., Shi, F., & Li, M. (2025). FPCR-Net: Front Point Cloud Regression Network for End-to-End SMPL Parameter Estimation. Sensors, 25(15), 4808. https://doi.org/10.3390/s25154808






