Research on Q-Learning-Based Cooperative Optimization Methodology for Dynamic Task Scheduling and Energy Consumption in Underwater Pan-Tilt Systems
Abstract
1. Introduction
2. Composition and Energy Consumption Modeling of Underwater Pan-Tilt Systems
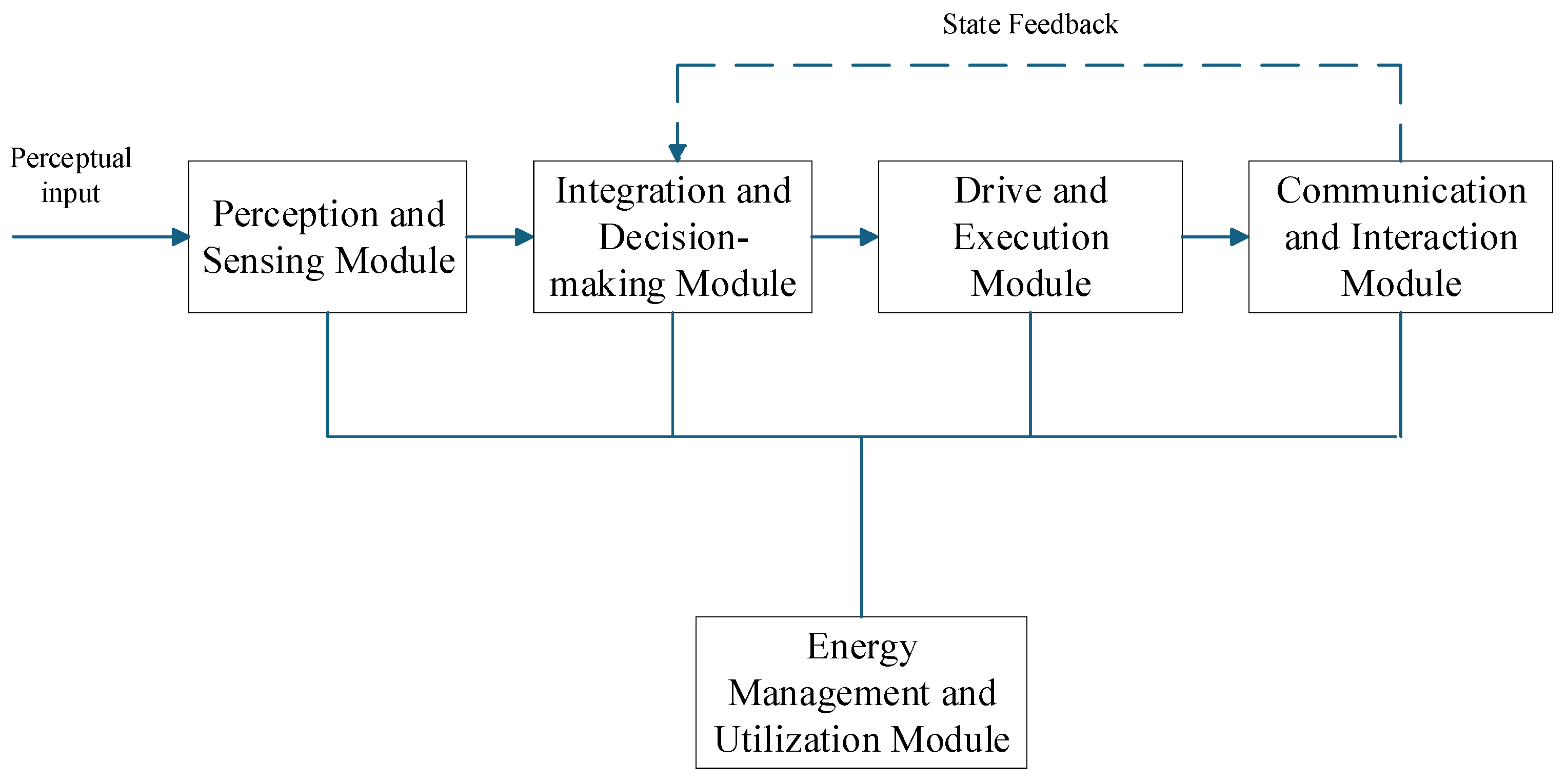
2.1. Underwater Pan-Tilt Systems
2.2. Underwater Pan-Tilt Systems’ Energy Consumption Model
3. Q-Learning Algorithm for Optimizing Control Strategies
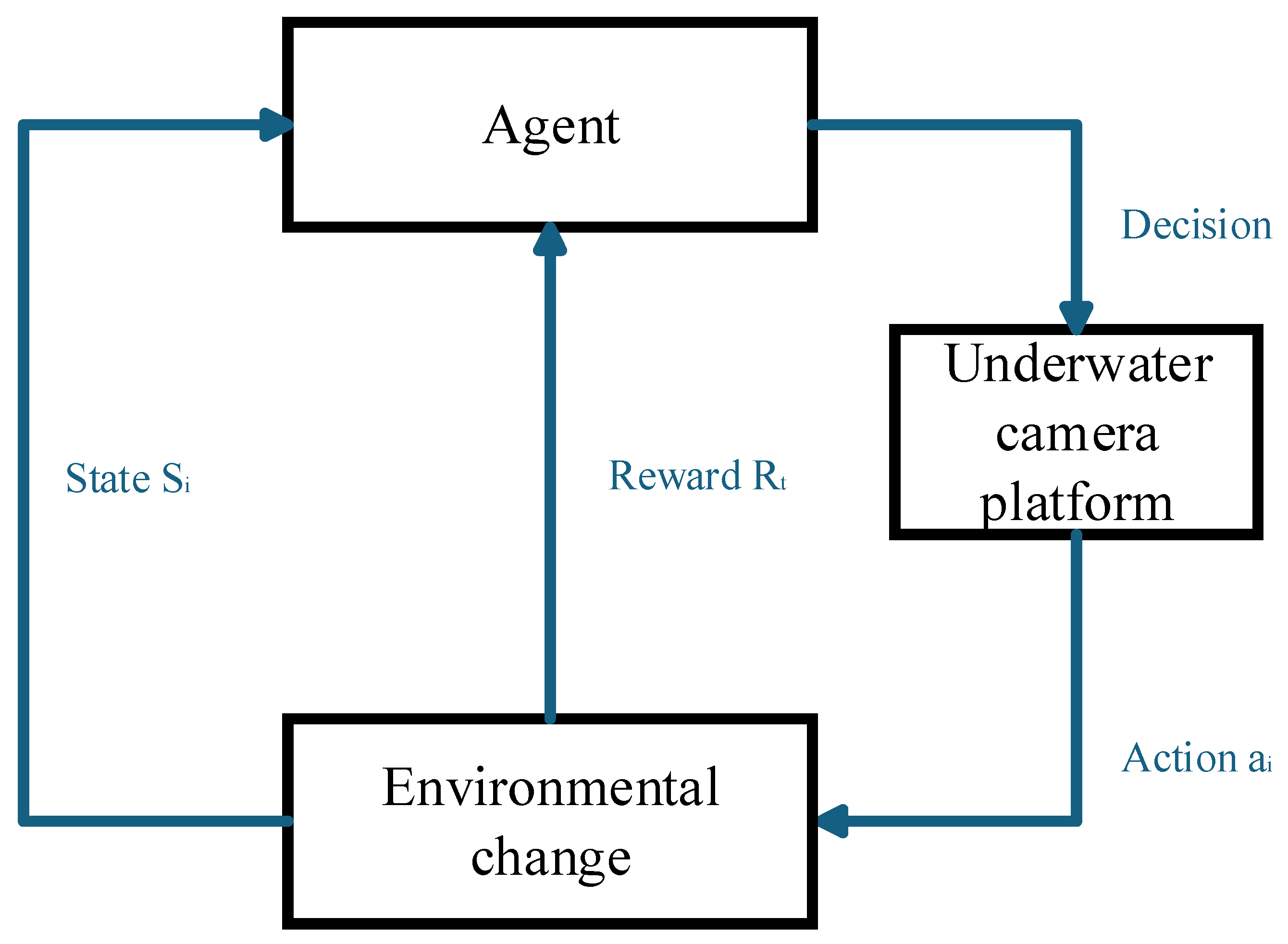
3.1. Q-Learning Algorithm
3.2. Design of Q-Learning Algorithm
3.2.1. State Space
3.2.2. Action Space
- Observe the current state.
- Generate a random number randomly .
- Compare with . If , the intelligent agent will randomly select an action from the current state’s action set; if , the intelligent agent will choose the action with the maximum Q-value in the current state.
3.2.3. Reward Function
3.3. Underwater Pan-Tilt Systems’ Energy Management Strategy
- Set the learning rate and exploration rate for the intelligent agent.
- Initialization of the agent function.
- Set the parameters for the state space, action space and reward function.
- The agent acquires the current state and makes action selections using the ε-greedy strategy.
- Update the Q-value continuously through the reward function.
- Repeat steps 4 and 5, and iterate until the Q value stabilizes.
4. Simulation Experiments and Result Analysis
4.1. Parameter Settings
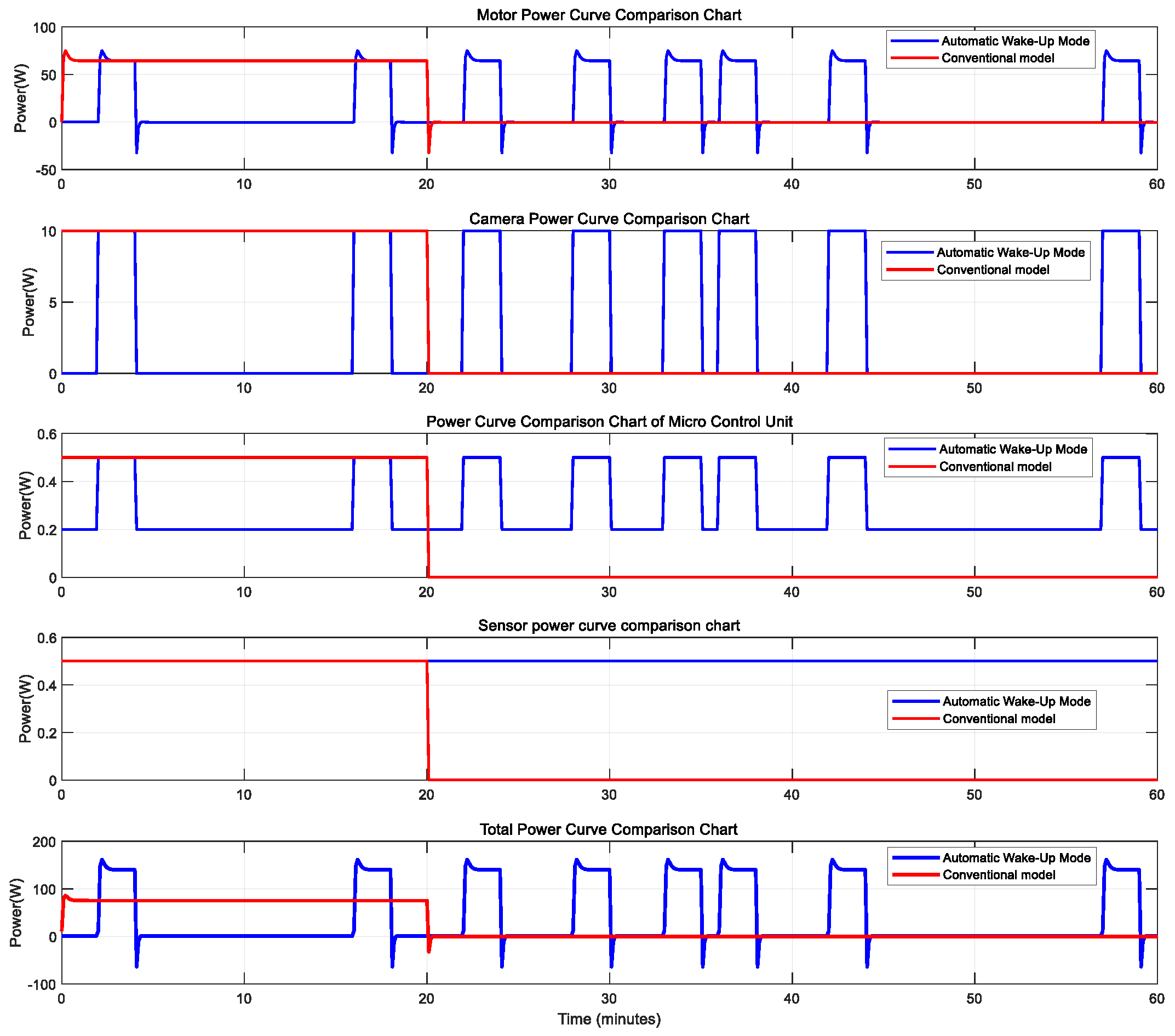
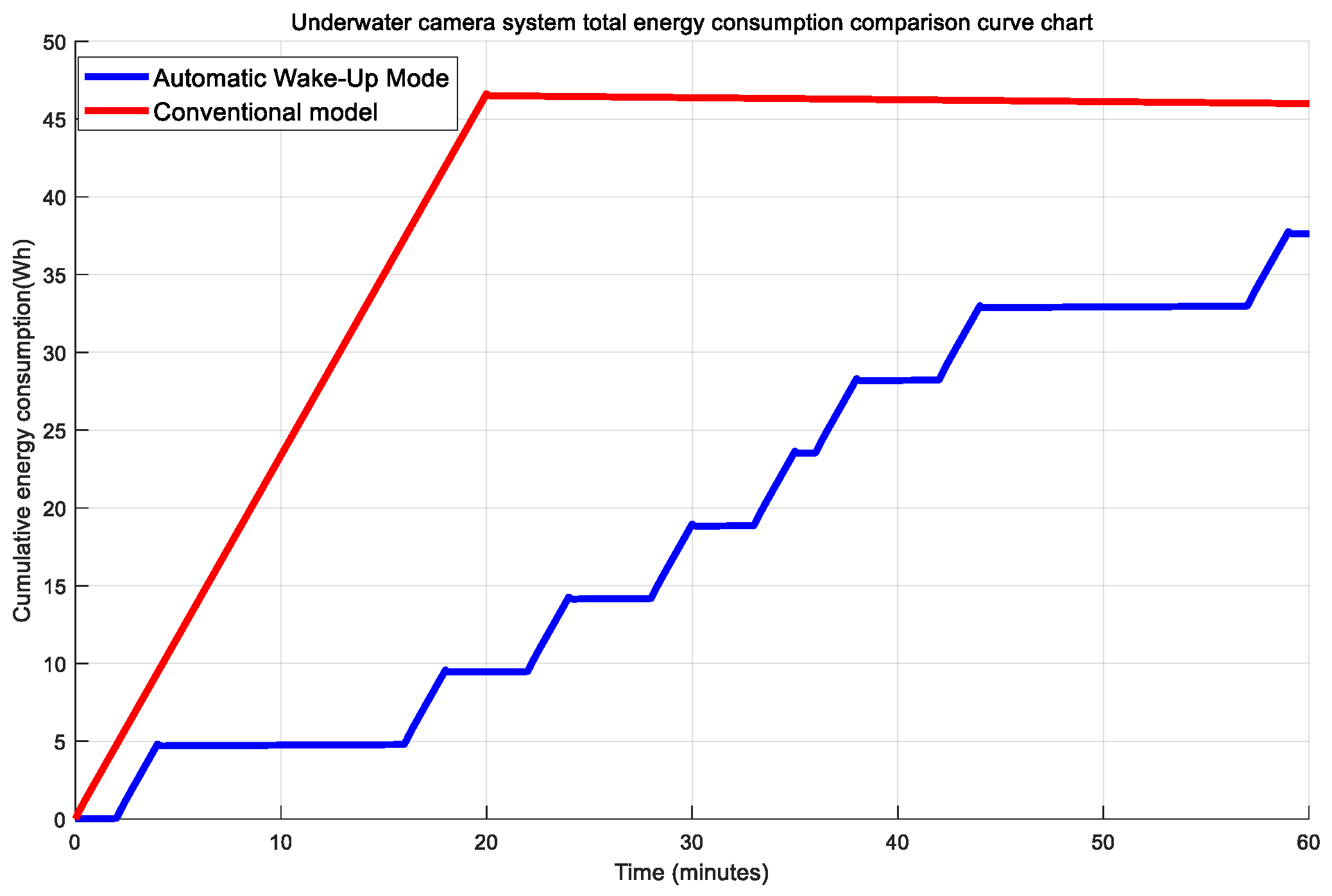
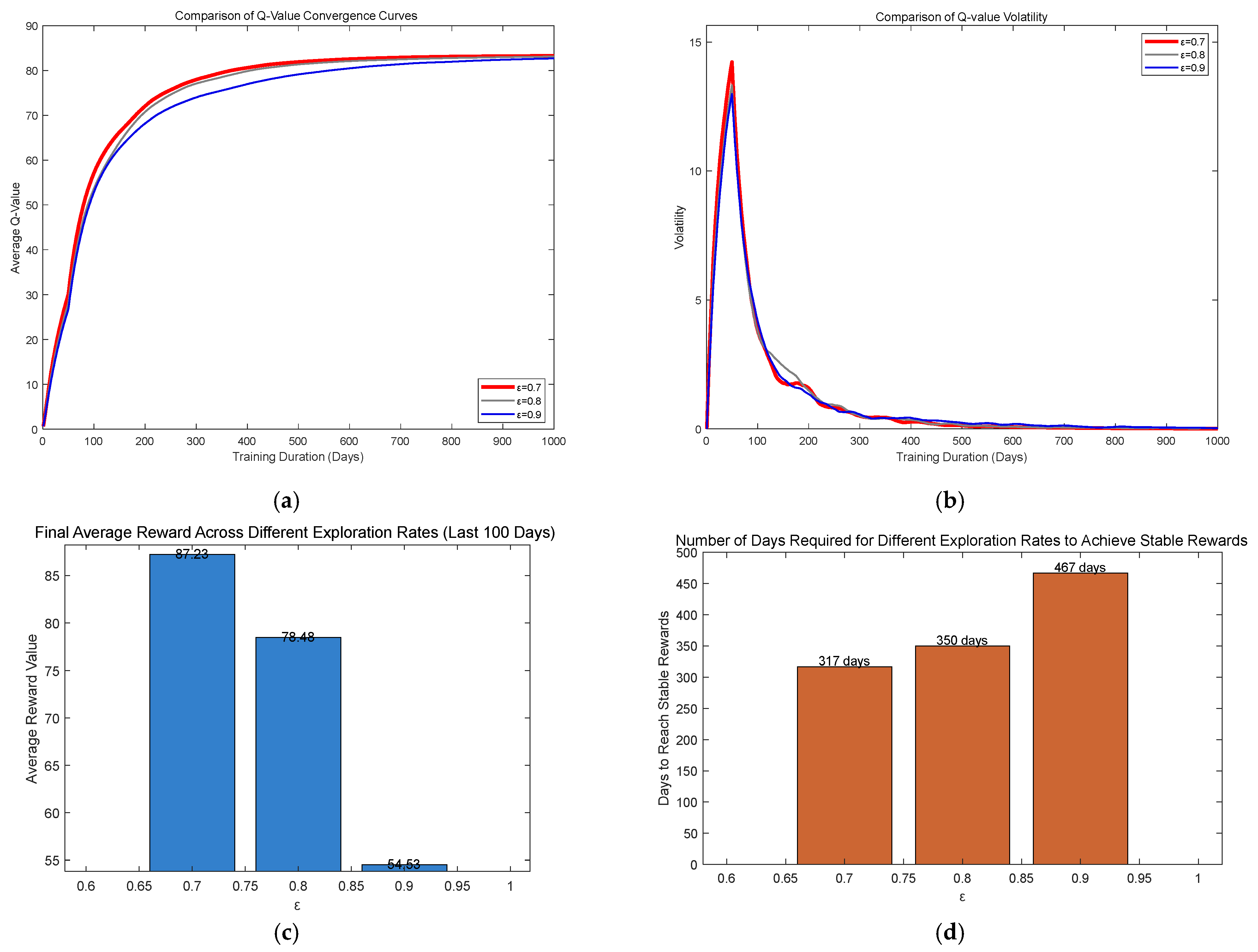
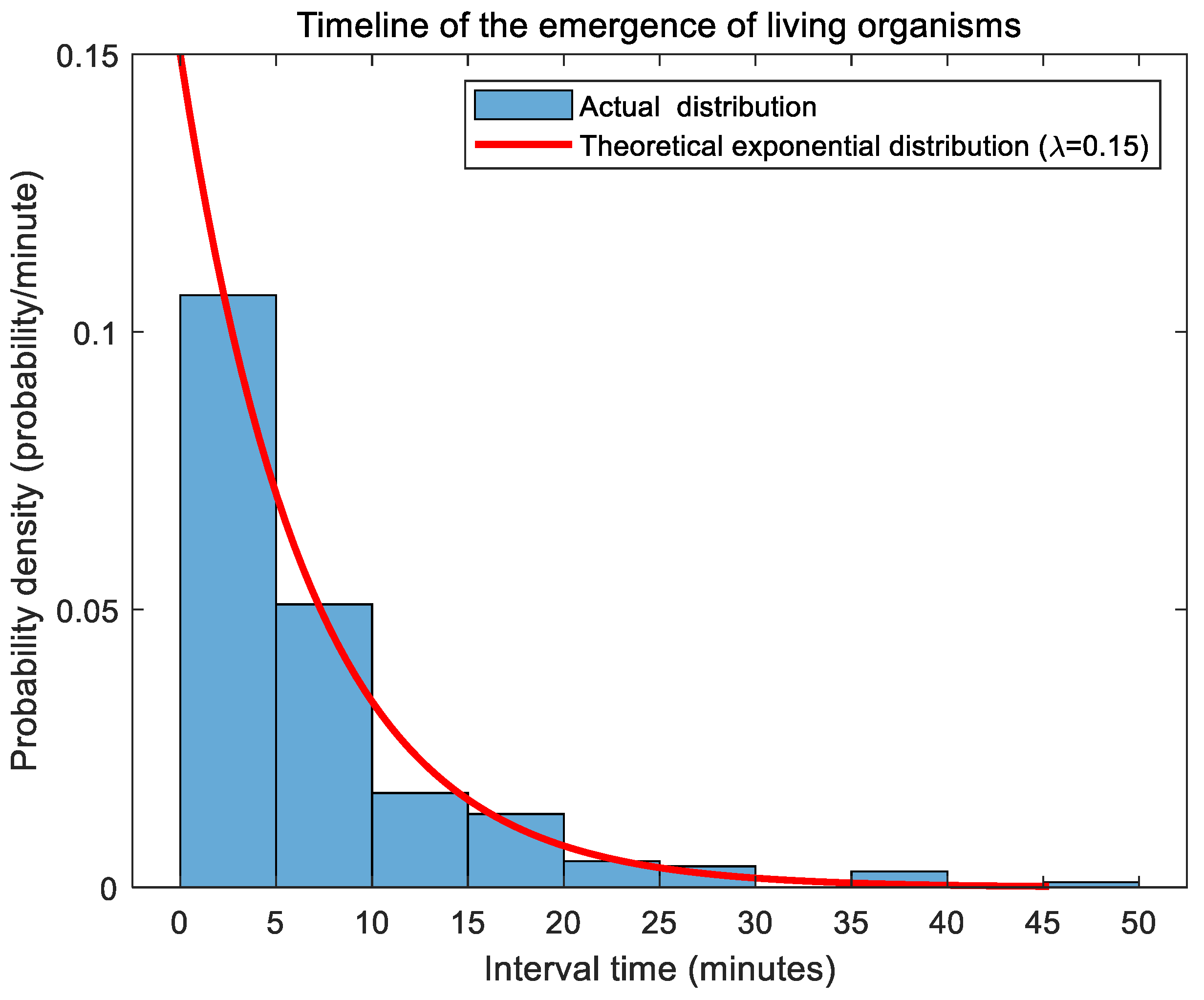
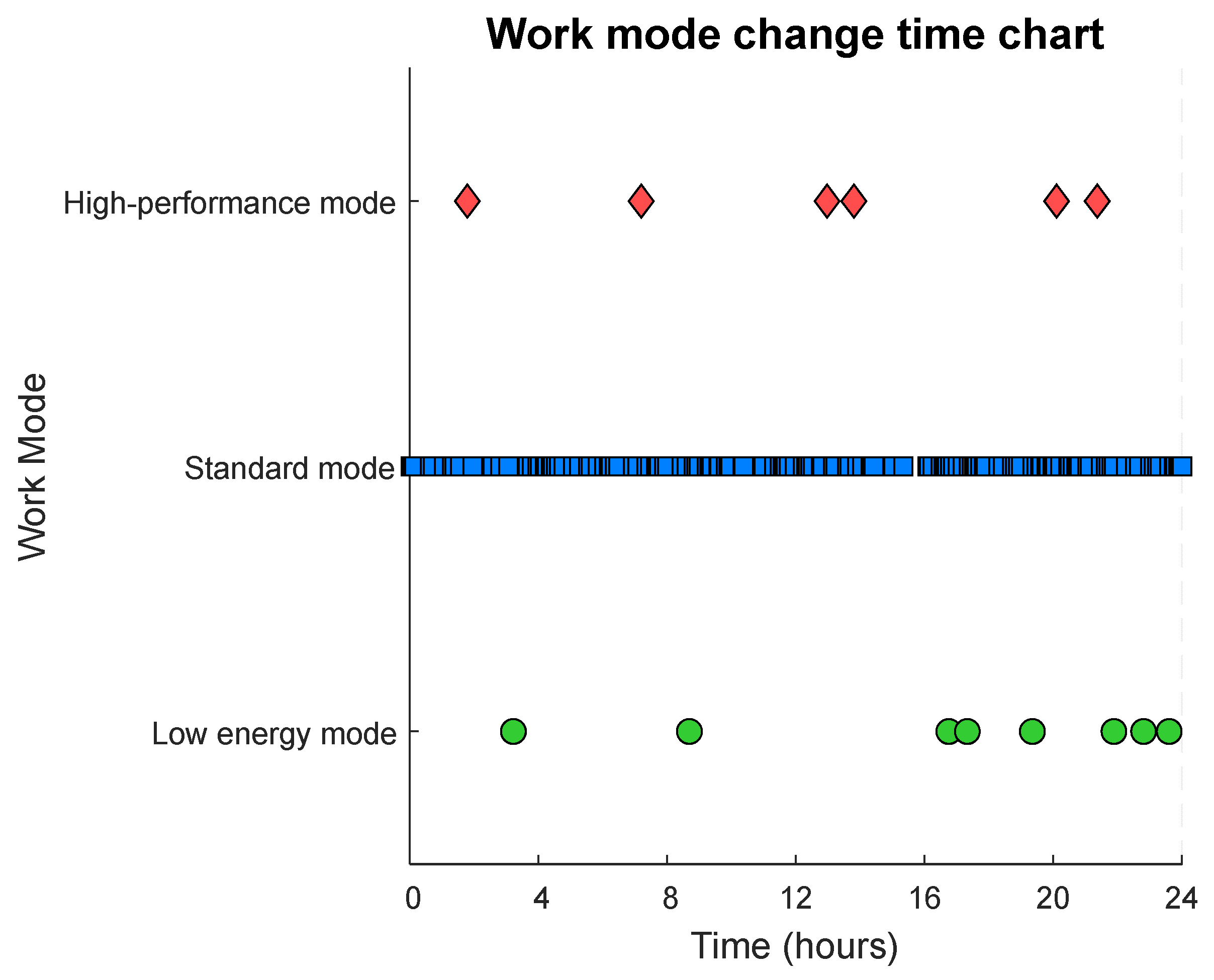
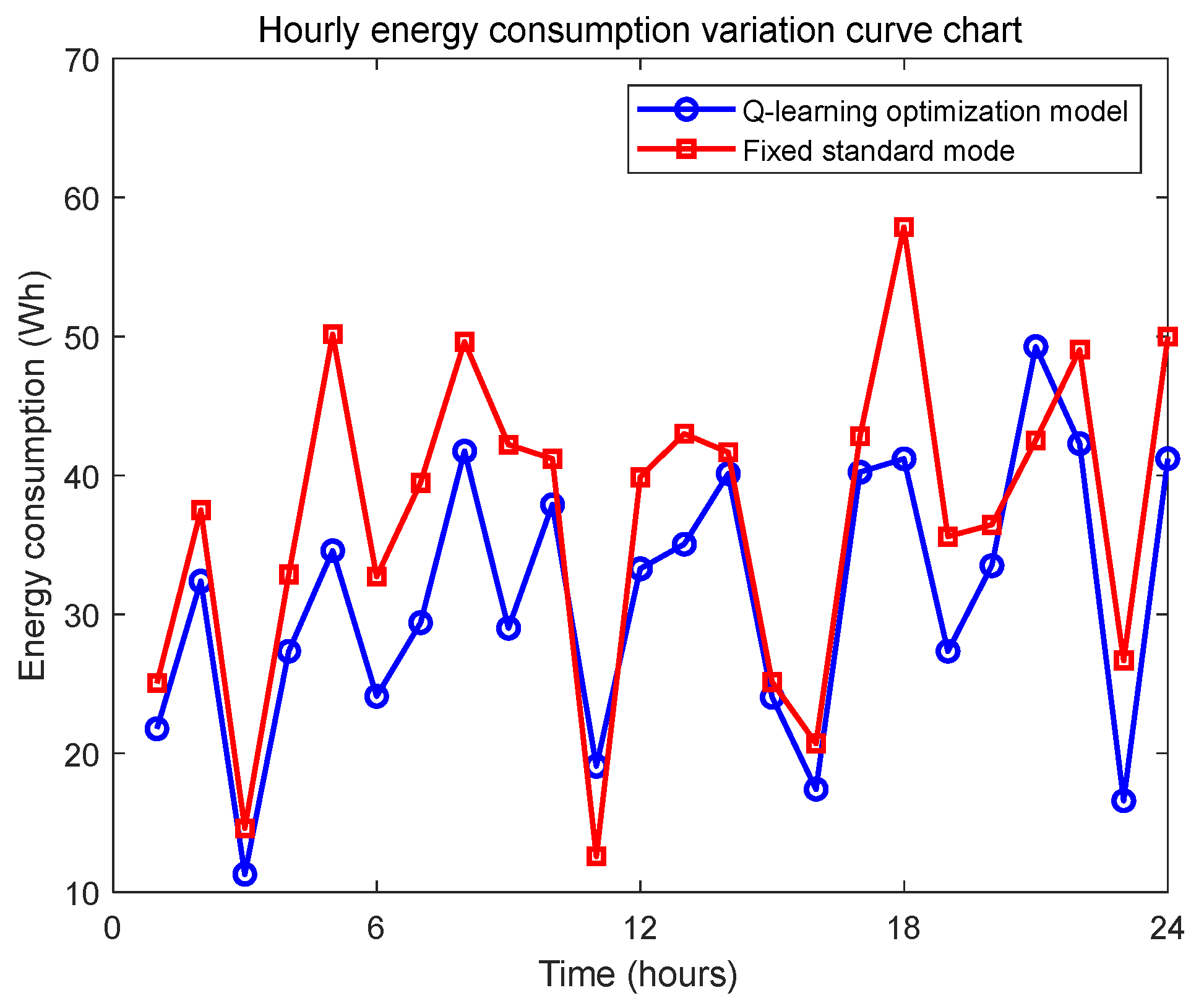
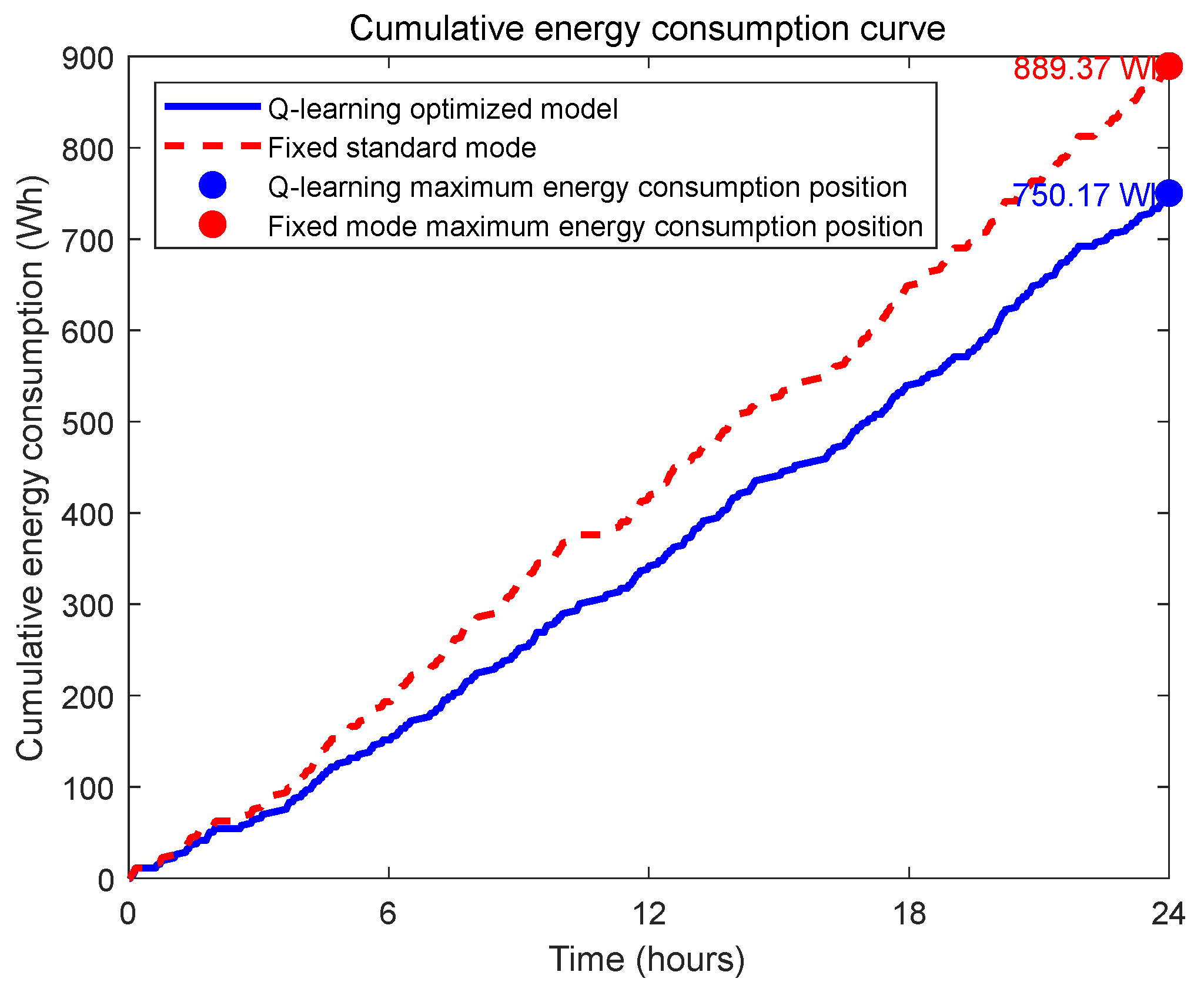
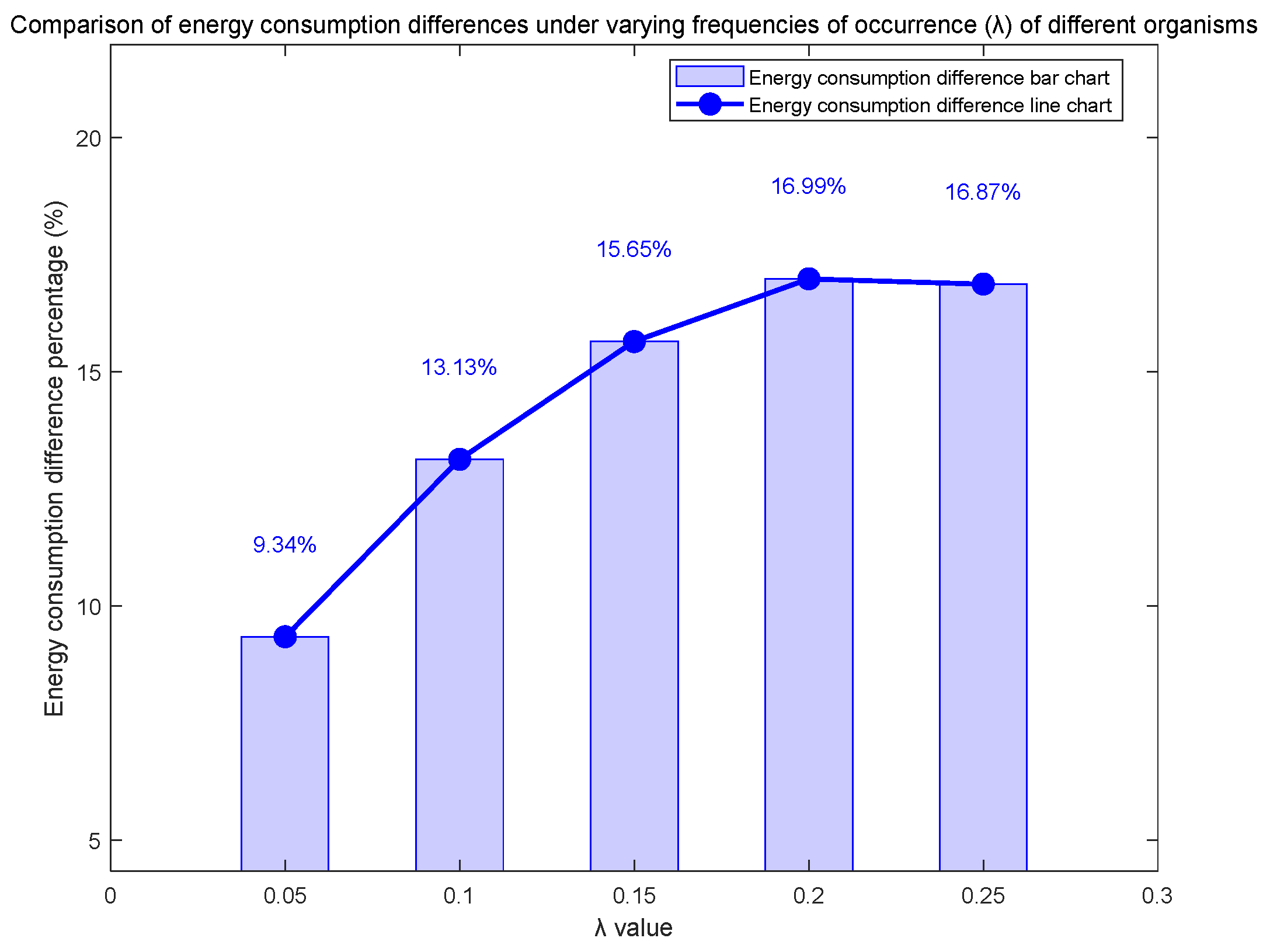
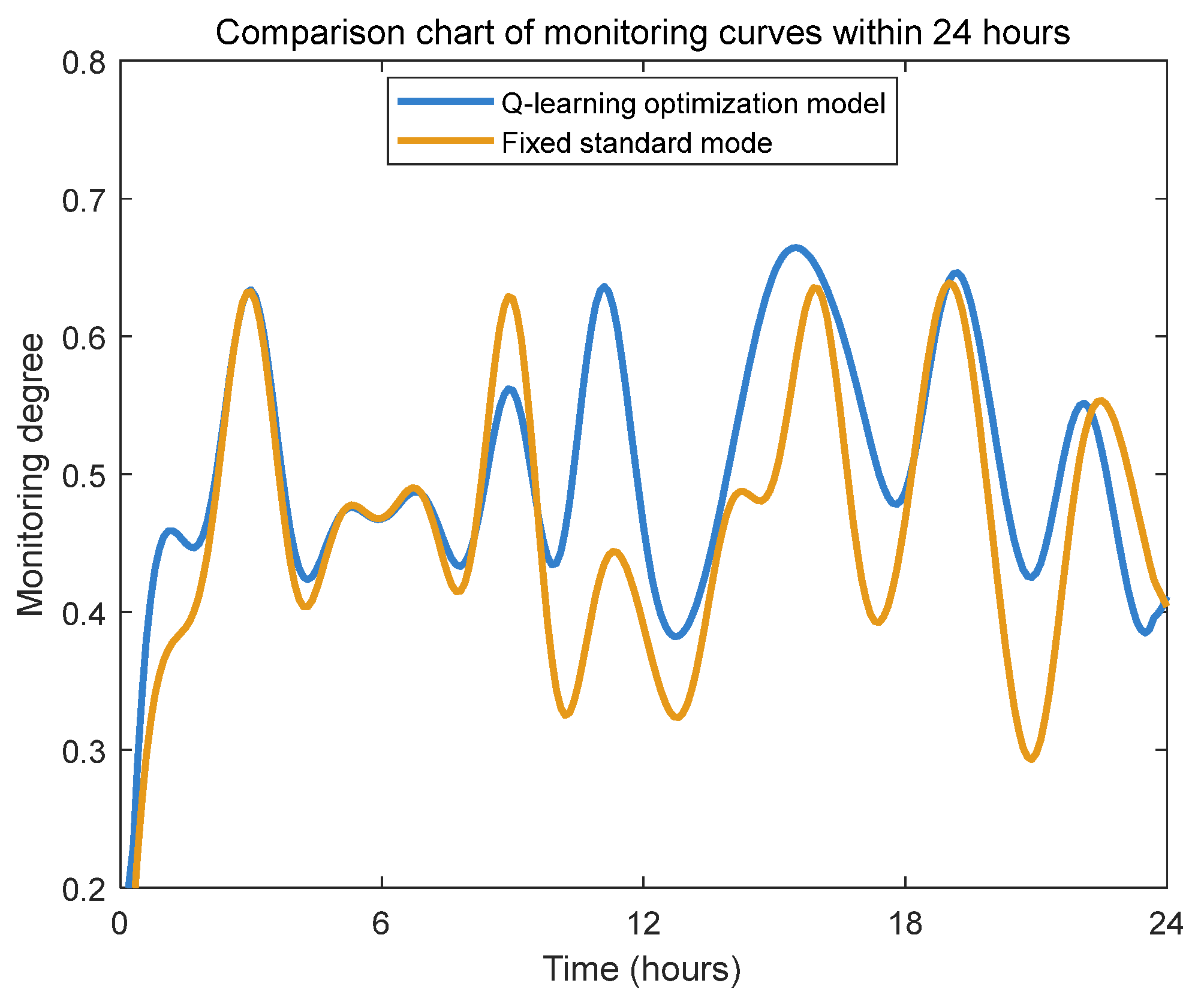
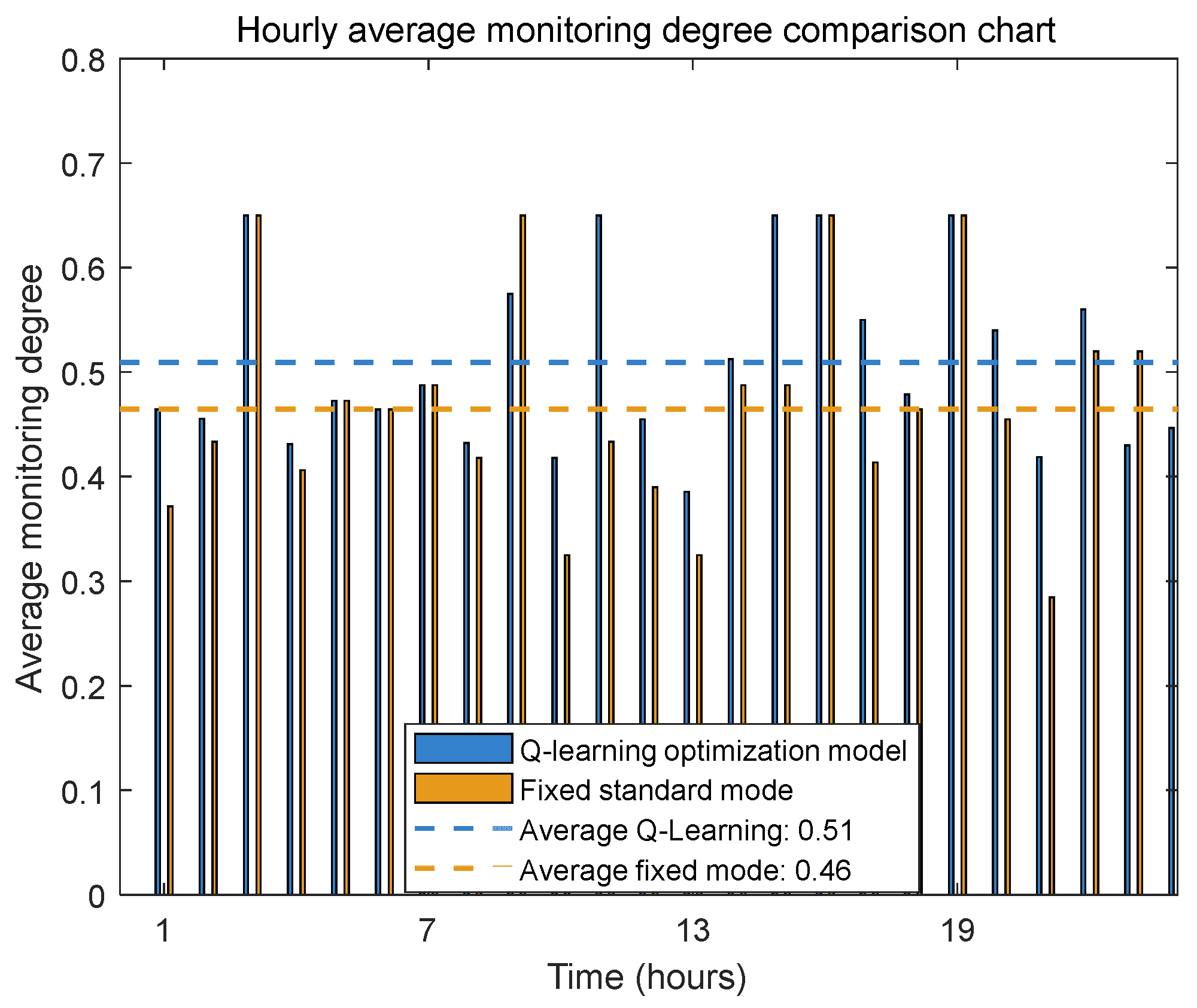
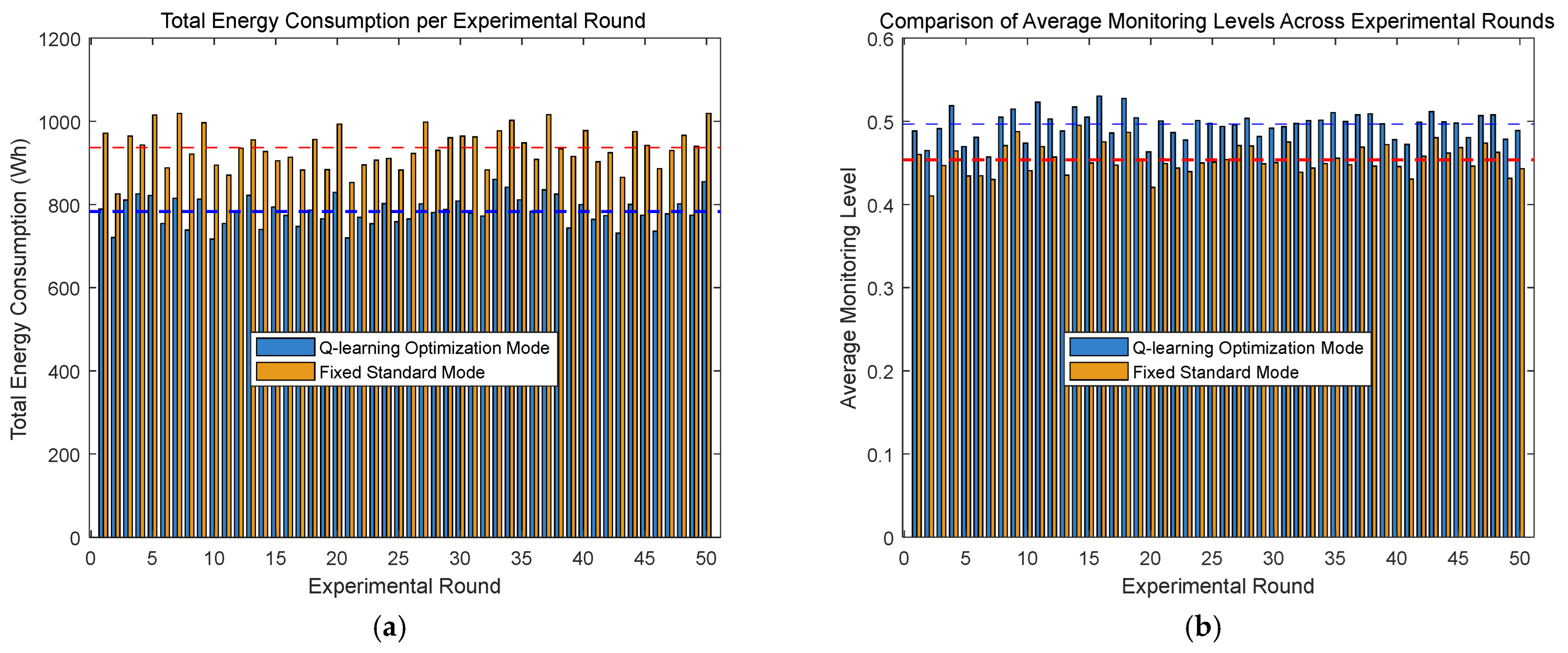
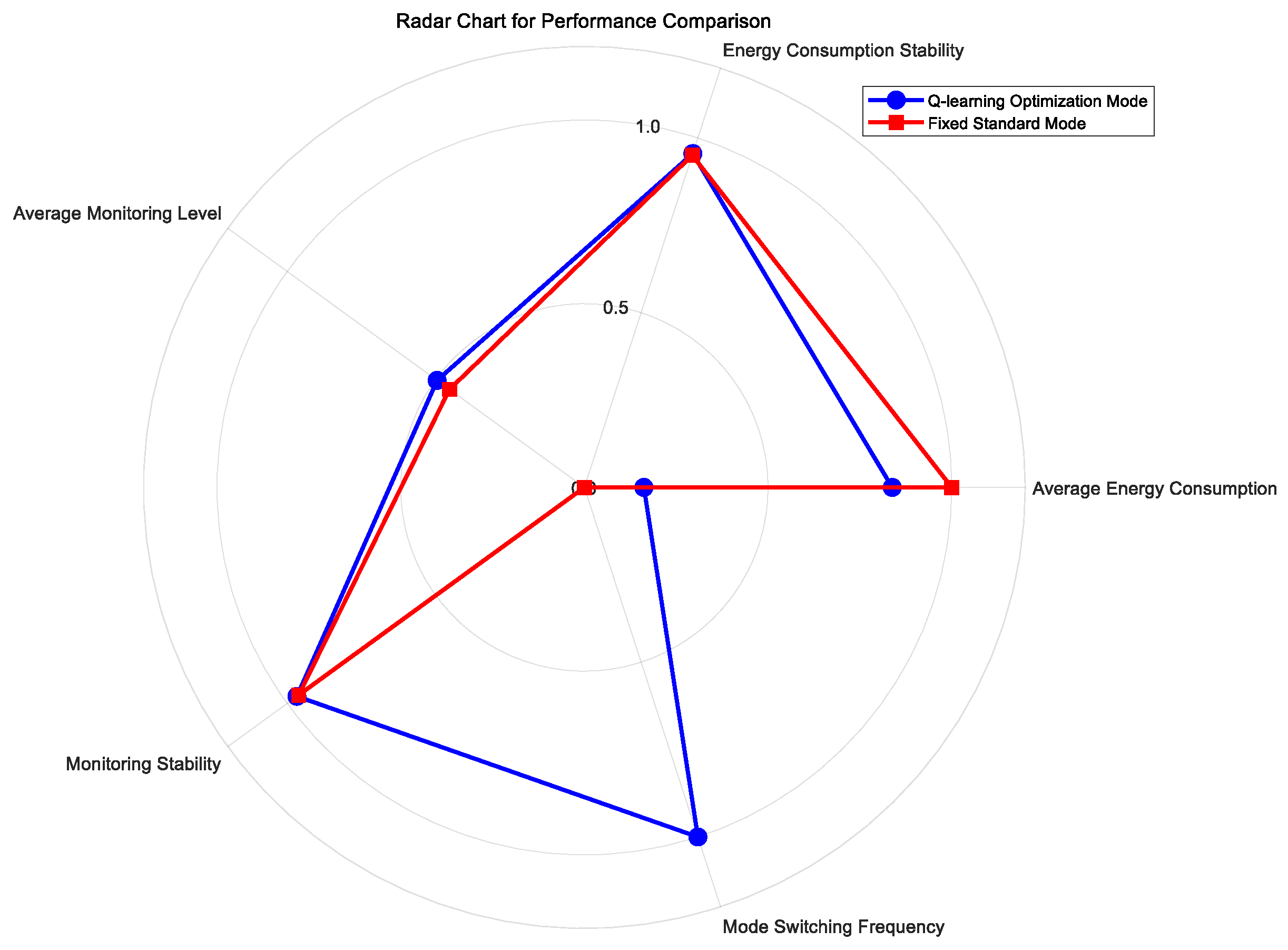
4.2. Experimental Analysis and Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, N.; Chang, D.; Amini, M.R.; Johnson-Roberson, M.; Sun, J. Energy Management for Autonomous Underwater Vehicles Using Economic Model Predictive Control. In Proceedings of the 2019 Annual American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019. [Google Scholar]
- Wang, S.Q.; Zheng, H.C.; Xu, J.W.; Yu, Z.; Li, B.B.; Kong, X. Research on Hybrid Energy System of Underwater Platform Based on Super Capacitor. Mar. Electr. Electron. Eng. 2024, 44, 42–45. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, H.L. Current Status and Trends of Electric Energy Supply Technology Development for Underwater Energy Supply Platforms. Mar. Electr. Electron. Eng. 2023, 43, 15–19. (In Chinese) [Google Scholar] [CrossRef]
- Chen, X.C. Research and Design of Full-Ocean-Depth Underwater Pan-Tilt Control System. Master’s Thesis, Shanghai Ocean University, Shanghai, China, 2019. (In Chinese). [Google Scholar]
- Li, X.X. Research on Energy Management Strategies for Fuel Cell Hybrid Electric Ships. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2023. (In Chinese). [Google Scholar]
- Sufán, V.; Troni, G. Swim4Real: Deep Reinforcement Learning-Based Energy-Efficient and Agile 6-DOF Control for Underwater Vehicles. IEEE Robot. Autom. Lett. 2025, 10, 7326–7333. [Google Scholar] [CrossRef]
- Rybak, L.A.; Behera, L.; Averbukh, M.A.; Sapryka, A.V. Development of an Algorithm for Managing a Multi-Robot System for Cargo Transportation Based on Reinforcement Learning in a Virtual Environment. IOP Conf. Ser. Mater. Sci. Eng. 2020, 945, 012083. [Google Scholar] [CrossRef]
- Chorney, L. Multi-Agent Reinforcement Learning for Guidance and Control of Unmanned Underwater Vehicles in Dynamic Docking Scenarios. Master’s Thesis, The Pennsylvania State University, State College, PA, USA, May 2025. [Google Scholar]
- Fang, W.; Liao, Z.; Bai, Y. Improved ACO Algorithm Fused with Improved Q-Learning Algorithm for Bessel Curve Global Path Planning of Search and Rescue Robots. Robot. Auton. Syst. 2024, 182, 104822. [Google Scholar] [CrossRef]
- Carlucho, I.; De Paula, M.; Wang, S.; Petillot, Y.; Acosta, G.G. Adaptive Low-Level Control of Autonomous Underwater Vehicles Using Deep Reinforcement Learning. Robot. Auton. Syst. 2018, 107, 71–86. [Google Scholar] [CrossRef]
- Liang, Z.B.; Li, Q.; Fu, G.D. Multi-UAV Collaborative Search and Attack Mission Decision-Making in Unknown Environments. Sensors 2023, 23, 7398. [Google Scholar] [CrossRef]
- Luo, Y.; Ball, P. Adaptive Production Strategy in Vertical Farm Digital Twins with Q-Learning Algorithms. Sci. Rep. 2025, 15, 15129. [Google Scholar] [CrossRef] [PubMed]
- Korivand, S.; Galvani, G.; Ajoudani, A.; Gong, J.; Jalili, N. Optimizing Human–Robot Teaming Performance through Q-Learning-Based Task Load Adjustment and Physiological Data Analysis. Sensors 2024, 24, 2817. [Google Scholar] [CrossRef] [PubMed]
- Collins, W.P.; Bellwood, D.R.; Morais, R.A.; Waltham, N.J.; Siqueira, A.C. Diel Movement Patterns in Nominally Nocturnal Coral Reef Fishes (Haemulidae and Lutjanidae): Intra vs. Interspecific Variation. Coral Reefs 2024, 1749–1760. [Google Scholar] [CrossRef]
- Song, Y.X.; Song, C. Aristotle’s Meteorological Thought on Marine Fish Activities and Its System Concept. Chin. J. Syst. Sci. 2025, 33, 43–49. (In Chinese) [Google Scholar]
- Villafuerte, R.; Kufner, M.B.; Delibes, M.; Moreno, S. Environmental Factors Influencing the Seasonal Daily Activity of the European Rabbit (Oryctolagus Cuniculus) in a Mediterranean Area. Mammalia 2009, 57, 341–348. [Google Scholar] [CrossRef]
- Chyba, M.; Haberkorn, T.; Singh, S.B.; Smith, R.N.; Choi, S.K. Increasing Underwater Vehicle Autonomy by Reducing Energy Consumption. Ocean Eng. 2008, 36, 62–73. [Google Scholar] [CrossRef]
- Ariche, S.; Boulghasoul, Z.; Ouardi, A.E.; Elbacha, A.; Tajer, A.; Espié, S. Enhancing Energy Management in Battery Electric Vehicles: A Novel Approach Based on Fuzzy Q-Learning Controller. Eng. Sci. Technol. Int. J. 2025, 67, 102070. [Google Scholar] [CrossRef]
- Ramesh, S.; Sukanth, B.N.; Sathyavarapu, S.J.; Sharma, V.; Kumaar, A.A.N.; Khanna, M. Comparative Analysis of Q-Learning, SARSA, and Deep Q-Network for Microgrid Energy Management. Sci. Rep. 2025, 15, 694. [Google Scholar] [CrossRef]
- Puterman, M.L. Markov Decision Processes: Discrete Stochastic Dynamic Programming; John Wiley and Sons: Hoboken, NJ, USA, 1994. [Google Scholar]
- Sutton, R.; Barto, A. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Xu, Y.J.; Li, H. Secondary Voltage Control Strategy for DC Microgrid Based on Reinforcement Learning. Mech. Electr. Eng. Technol. 2025, 54, 173–178. (In Chinese) [Google Scholar]
- Chen, D.; Wang, H.; Hu, D.; Xian, Q.; Wu, B. Q-Learning Improved Golden Jackal Optimization Algorithm and Its Application to Reliability Optimization of Hydraulic System. Sci. Rep. 2024, 14, 24587. [Google Scholar] [CrossRef]
- Dong, X.; Zhang, H.; Xie, X.; Ming, Z. Data-Driven Distributed H∞ Current Sharing Consensus Optimal Control of DC Microgrids via Reinforcement Learning. IEEE Trans. Circuits Syst. Regul. Pap. 2024, 71, 2824–2834. [Google Scholar] [CrossRef]
- Wang, J.J.; Zhou, H.M.; Guo, J.; Si, H.W.; Xu, C.; Zhang, M.H.; Zhang, Y.Q.; Zhou, G.X. A Q-Learning-Based Deep Deterministic Policy Gradient Algorithm for the Re-Entrant Hybrid Flow Shop Joint Scheduling Problem with Dual-Gripper. Eng. Lett. 2025, 33, 1632–1647. [Google Scholar]
- Wang, X.; Zhu, Q.X.; Zhu, Y.H.; Miao, L.Y. Path Planning for Mobile Robots Based on Improved Q-Learning Algorithm. Comput. Simul. 2025, 42, 371–377. (In Chinese) [Google Scholar]
- Zhou, Y.X.; Cheng, K.T.; Liu, L.M.; He, X.J.; Huang, Z.G. Research on Trajectory Optimization Based on Q-Learning. J. Ordnance Equip. Eng. 2022, 43, 191–196. (In Chinese) [Google Scholar]
- Benini, L.; de Micheli, G. System-Level Power Optimization: Techniques and Tools. In Proceedings of the 1999 International Symposium on Low Power Electronics and Design (Cat. No.99TH8477), San Diego, CA, USA, 16–17 August 1999; pp. 288–293. [Google Scholar]
- Paolo, D. Context-Dependent Variability in the Components of Fish Escape Response: Integrating Locomotor Performance and Behavior. J. Exp. Zool. Part Ecol. Genet. Physiol. 2010, 313, 59–79. [Google Scholar]
- Ma, M.M.; Dong, L.P.; Liu, X.J. Energy Management Strategy of Multi-Agent Microgrid Based on Q-Learning Algorithm. J. Syst. Simul. 2023, 35, 1487–1496. (In Chinese) [Google Scholar] [CrossRef]
- Mao, Y.Z.; He, B.N.; Wang, D.S.; Jiang, R.Z.; Zhou, Y.Y.; Zhang, J.R.; He, X.M.; Dong, Y.C. Optimization Method for Smart Multi-Microgrid Control Based on Improved Deep Reinforcement Learning. Smart Power 2021, 49, 19–25+58. (In Chinese) [Google Scholar]
- Kim, S.Y.; Ko, H. Energy-Efficient Cooperative Transmission in Ultra-Dense Millimeter-Wave Network: Multi-Agent Q-Learning Approach. Sensors 2024, 24, 7750. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.Q.; Mu, C.D.; Zhao, M.; Yao, T. Frequency Coordination Control Strategy of Multiple Photovoltaic-Battery Virtual Synchronous Generators Based on Reinforcement Learning. Electr. Drive 2021, 51, 36–42. [Google Scholar] [CrossRef]
- Yang, Q. Research on Adaptive Scheduling of Automated Warehousing System Based on Q-Learning. Master’s Thesis, Hangzhou Dianzi University, Hangzhou, China, 2025. (In Chinese). [Google Scholar]




| Parameter | Numerical/W |
|---|---|
| The working power consumption of the motor | 75 |
| The standby power consumption of the motor | 1.5 |
| The power consumption of the camera during operation | 10 |
| The standby power consumption of the camera | 1 |
| Power consumption during the wake-up process of the microcontroller unit | 0.5 |
| Power consumption during the sleep mode of the microcontroller unit | 0.02 |
| Power consumption of underwater sensors on the underwater pan-tilt-system | 0.5 |
| Power consumption of the photoelectric sensor | 0.5 |
| Key Components in MDP Decision-Making Framework | Energy Consumption Model of Underwater Pan-Tilt System | Design Elements |
|---|---|---|
| Environment | Energy Consumption System | Simulation Environment |
| Action | Real-time Rules | Mode Transition Logic |
| State | Runtime Status | Operational Mode Characteristics |
| Reward | Reward Mechanism | Key Performance Indicators |
| Action Space | Working Hours (Min) | Energy Consumption (Wh) | Monitoring Degree | η | μ |
|---|---|---|---|---|---|
| Low energy mode | 1 | 1.5 | 0.2 | 0.15 | 0.7 |
| Standard mode | 3 | 5.5 | 0.65 | 0.55 | 0.55 |
| High-performance mode | 5 | 9 | 0.85 | 0.8 | 0.25 |
| Parameter | Numerical |
|---|---|
| α | 0.2 |
| β | 0.95 |
| ε | 0.7 |
| Mode | Mean Total Energy Consumption (Wh) | Total Energy Std Dev (Wh) | Mean Monitoring Accuracy | Monitoring Accuracy Std Dev |
|---|---|---|---|---|
| Q-learning | 783.52 | ±35.15 | 0.50 | ±0.02 |
| Fixed Standard Mode | 935.05 | ±46.59 | 0.45 | ±0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, S.; Yang, L.; Zhang, X.; Zhao, S.; Liu, K.; Tian, X.; Xu, H. Research on Q-Learning-Based Cooperative Optimization Methodology for Dynamic Task Scheduling and Energy Consumption in Underwater Pan-Tilt Systems. Sensors 2025, 25, 4785. https://doi.org/10.3390/s25154785
Tao S, Yang L, Zhang X, Zhao S, Liu K, Tian X, Xu H. Research on Q-Learning-Based Cooperative Optimization Methodology for Dynamic Task Scheduling and Energy Consumption in Underwater Pan-Tilt Systems. Sensors. 2025; 25(15):4785. https://doi.org/10.3390/s25154785
Chicago/Turabian StyleTao, Shan, Lei Yang, Xiaobo Zhang, Shengya Zhao, Kun Liu, Xinran Tian, and Hengxin Xu. 2025. "Research on Q-Learning-Based Cooperative Optimization Methodology for Dynamic Task Scheduling and Energy Consumption in Underwater Pan-Tilt Systems" Sensors 25, no. 15: 4785. https://doi.org/10.3390/s25154785
APA StyleTao, S., Yang, L., Zhang, X., Zhao, S., Liu, K., Tian, X., & Xu, H. (2025). Research on Q-Learning-Based Cooperative Optimization Methodology for Dynamic Task Scheduling and Energy Consumption in Underwater Pan-Tilt Systems. Sensors, 25(15), 4785. https://doi.org/10.3390/s25154785







