Dual-Path Adversarial Denoising Network Based on UNet
Abstract
1. Introduction
- We design a dual-path adversarial structure that takes a set of clean and noisy images as input during training. The model can continuously optimize itself through the adversarial structure, thereby enhancing the denoising performance.
- We modify the UNet architecture and propose a new dual-U-shaped network model. This model can extract image features more finely and effectively reduce image noise.
- We also verify other multi-U-shaped network designs through experiments, demonstrating the practical reliability of the proposed dual-U-shaped network.
2. Related Work
3. Network Structure
3.1. Overall Structure
| Algorithm 1 Dual-path adversarial denoising network training procedure |
|
3.2. Denoiser Double-Layer U-Denoise Network
3.2.1. Multi-Receptive Field Perception Denoise Module
3.2.2. Enlarging the Receptive Field Module
3.3. Generator U-Shaped Imitation Noise Generation Network
3.4. Discriminator Dual-Channel Adversarial Discriminator
3.5. Loss Function
4. Experiment and Result Analysis
4.1. Measurement Standards
4.2. Experimental Dataset
4.3. Comparison Method
4.3.1. Comparison of Key Methods
4.3.2. Original Design Proposal
4.3.3. Computational Efficiency
4.4. Comparative Experiments
4.5. Ablation Studies
- Experimental settings:
- Dataset: SIDD, consistent with previous comparative experiments.
- Parameters: All experimental parameters were strictly set to the same values for accuracy and reproducibility of the results.
- Experimental operation:
- We removed the lower U-shaped structure (), retaining only the upper U-shaped structure ().
- We removed the MRDB module. When the MRDB module was removed, the ASPP module was also excluded due to its inherent association with it.
- We removed the ASPP module.
- Results:
- Compared to having no modules, the PSNR was improved by 2.83 dB, 2.89 dB, and 2.39 dB.
- Compared to having no modules, the SSIM was improved 4.14%, 5.4%, and 5.31%.
- Impact of removing all modules: the PSNR decreased by 2.96 dB and the SSIM by 0.056%, indicating a significant performance drop.
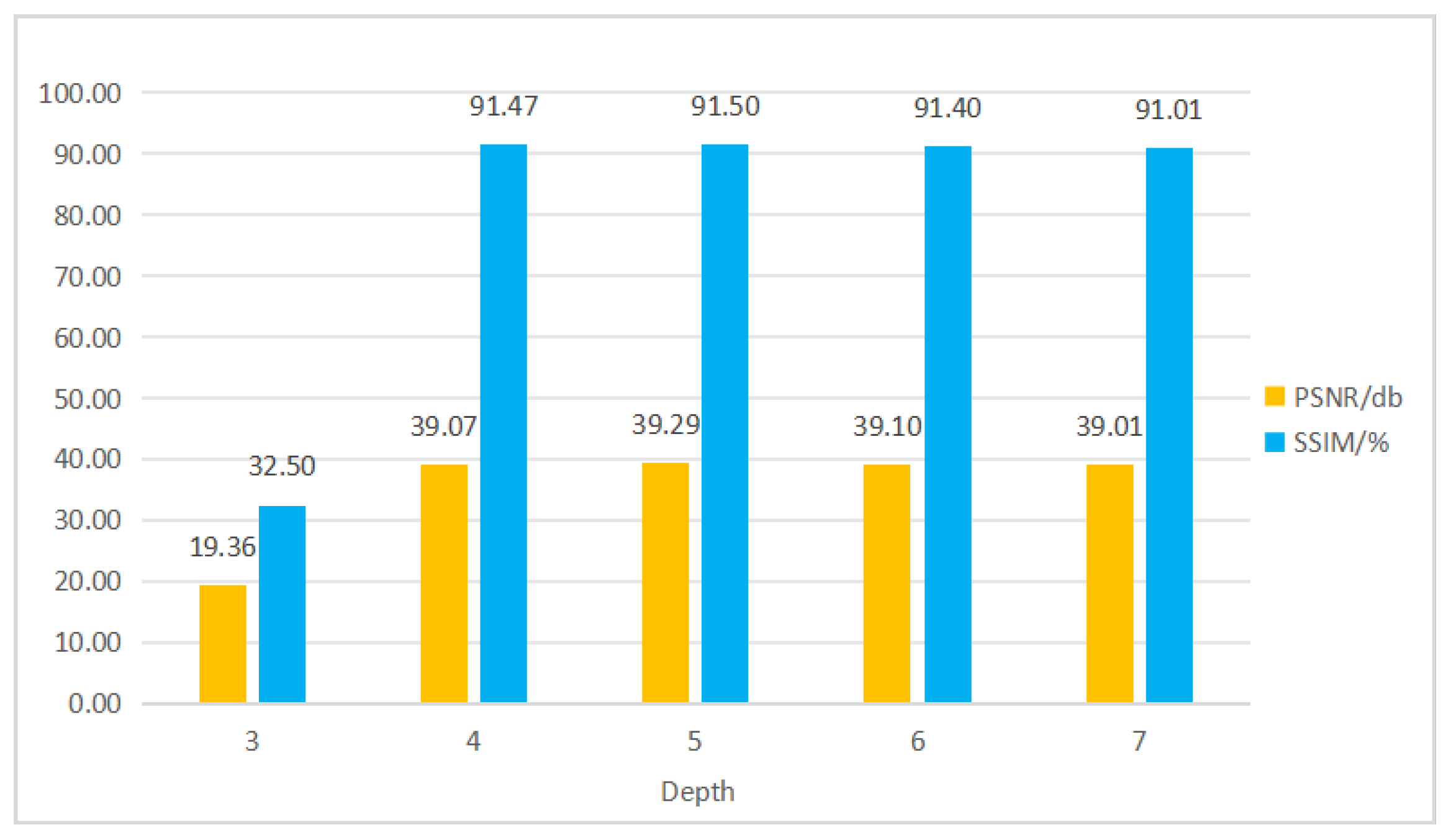
4.6. Superparameter Experiment and Result Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Elad, M.; Aharon, M. Image Denoising Via Sparse and Redundant Representations over Learned Dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef]
- Coupé, P.; Hellier, P.; Kervrann, C.; Barillot, C. Nonlocal Means-Based Speckle Filtering for Ultrasound Images. IEEE Trans. Image Process. 2009, 18, 3736–3745. [Google Scholar] [CrossRef]
- Sattar, F.; Floreby, L. Image Enhancement Based on a Nonlinear Multi-scale Method. IEEE Trans. Image Process. 1997, 6, 888–895. [Google Scholar] [CrossRef]
- Wu, W.; Chen, M.; Xiang, Y.; Zhang, Y.; Yang, Y. Recent Progress in Image Denoising: A Training Strategy Perspective. IET Image Process. 2023, 17, 1627. [Google Scholar] [CrossRef]
- Ilesanmi, A.E.; Ilesanmi, T.O. Methods for Image Denoising Using Convolutional Neural Network: A Review. Complex Intell. Syst. 2021, 7, 2179–2198. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.-M. Non-Local Means Denoising. Image Process. Line 2011, 1, 208–212. [Google Scholar] [CrossRef]
- Kaur, R.; Karmakar, G.; Imran, M. Impact of Traditional and Embedded Image Denoising on CNN-Based Deep Learning. Appl. Sci. 2023, 13, 11560. [Google Scholar] [CrossRef]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image Denoising by Sparse 3-D Transform-Domain Collaborative Filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef]
- Khan, A.; Jin, W.; Haider, A.; Rahman, M.; Wang, D. Adversarial Gaussian Denoiser for Multiple-Level Image Denoising. Sensors 2021, 21, 2998. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Trans. Image Process. 2016, 26, 3142–3155. [Google Scholar] [CrossRef]
- Lehtinen, J.; Munkberg, J.; Hasselgren, J.; Laine, S.; Karras, T.; Aittala, M.; Aila, T. Noise2Noise: Learning Image Restoration without Clean Data. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Chen, S.; Shi, D.; Sadiq, M.; Cheng, X. Image Denoising with Generative Adversarial Networks and Its Application to Cell Image Enhancement. IEEE Access 2020, 8, 82819–82831. [Google Scholar] [CrossRef]
- Wang, L.F.; Ren, W.J.; Guo, X.D.; Zhang, R.G.; Hu, L.H. Multi-Feature Generative Adversarial Network for Low-Dose CT Image Denoising. J. Comput. Appl. 2025, 1–12. Available online: https://link.cnki.net/urlid/51.1307.TP.20250327.0948.002 (accessed on 27 March 2025).
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2015; Volume 9351, pp. 234–241. [Google Scholar] [CrossRef]
- Zhou, Z.; Siddiquee, M.M.R.; Tajbakhsh, N.; Liang, J. UNet++: A Nested U-Net Architecture for Medical Image Segmentation. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support; DLMIA ML-CDS 2018; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; Volume 11045, pp. 3–11. [Google Scholar] [CrossRef]
- Chen, H.; Han, Y.; Xu, P.; Li, Y.; Li, K.; Yin, J. MS-UNet-v2: Adaptive Denoising Method and Training Strategy for Medical Image Segmentation with Small Training Data. arXiv 2023, arXiv:2309.03686. [Google Scholar]
- Huang, G.; Liu, Z.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar] [CrossRef]
- Zhao, J.; Li, Q.; Li, H.; Zhang, L. Automated Segmentation of Cervical Nuclei in Pap Smear Images Using Deformable Multi-Path Ensemble Model. In Proceedings of the 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), Venice, Italy, 8–11 April 2019; pp. 1514–1518. [Google Scholar] [CrossRef]
- Yu, F.; Koltun, V. Multi-Scale Context Aggregation by Dilated Convolutions. arXiv 2015, arXiv:1511.07122. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Chen, L.-C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking Atrous Convolution for Semantic Image Segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar] [CrossRef]
- Wang, P.; Chen, P.; Yuan, Y.; Liu, D.; Huang, Z.; Hou, X.; Cottrell, G. Understanding Convolution for Semantic Segmentation. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 1451–1460. [Google Scholar] [CrossRef]
- Jia, X.; Peng, Y.; Ge, B.; Li, J.Y.; Liu, S.; Wang, W. A Multi-scale Dilated Residual Convolution Network for Image Denoising. Neural Process. Lett. 2022, 55, 1231–1246. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.C.; Bengio, Y. Generative Adversarial Nets. Adv. Neural Inf. Process. Syst. 2014, 2, 2672–2680. [Google Scholar]
- Isola, P.; Zhu, J.-Y.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5967–5976. [Google Scholar] [CrossRef]
- Lai, W.-S.; Huang, J.-B.; Ahuja, N.; Yang, M.-H. Fast and Accurate Image Super-Resolution with Deep Laplacian Pyramid Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 41, 2599–2613. [Google Scholar] [CrossRef] [PubMed]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein GAN. arXiv 2017, arXiv:1701.07875. [Google Scholar]
- Tai, Y.; Yang, J.; Liu, X.; Xu, C. MemNet: A Persistent Memory Network for Image Restoration. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 4549–4557. [Google Scholar] [CrossRef]
- Wang, Z.; Fu, Y.; Liu, J.; Zhang, Y. LG-BPN: Local and Global Blind-Patch Network for Self-Supervised Real-World Denoising. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 18156–18165. [Google Scholar] [CrossRef]
- Wu, W.; Liu, S.; Zhou, Y.; Zhang, Y.; Xiang, Y. Dual Residual Attention Network for Image Denoising. Pattern Recognit. 2023, 149, 110291. [Google Scholar] [CrossRef]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef]
- Eigen, D.; Fergus, R. Predicting Depth, Surface Normals and Semantic Labels with a Common Multi-Scale Convolutional Architecture. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 2650–2658. [Google Scholar] [CrossRef]
- Takahashi, N.; Mitsufuji, Y. Densely Connected Multidilated Convolutional Networks for Dense Prediction Tasks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 19–25 June 2021; pp. 993–1002. [Google Scholar]
- Chen, J.; Chen, J.; Chao, H.; Yang, M. Image Blind Denoising with Generative Adversarial Network Based Noise Modeling. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3155–3164. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.H.; Wu, L.Y.; Zhao, S.B. A CT Image Denoising Method Based on Improved GAN. Digit. Technol. Appl. 2024, 42, 201–203. [Google Scholar]
- Toxigon. Dive Deep Into GANs: Generative Adversarial Networks Explained. Toxigon Blog. Available online: https://toxigon.com/deep-dive-into-gans-generative-adversarial-networks (accessed on 1 January 2025).
- Horé, A.; Ziou, D. Image Quality Metrics: PSNR vs. SSIM. In Proceedings of the 20th International Conference on Pattern Recognition, ICPR 2010, Istanbul, Turkey, 23–26 August 2010. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Abdelhamed, A.; Lin, S.; Brown, M.S. A High-Quality Denoising Dataset for Smartphone Cameras. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1692–1700. Available online: https://ieeexplore.ieee.org/document/8578280 (accessed on 1 January 2025).
- Plotz, T.; Roth, S. Benchmarking Denoising Algorithms with Real Photographs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 22–25 July 2017; pp. 1586–1595. [Google Scholar] [CrossRef]
- Xu, J.; Li, H.; Liang, Z.; Zhang, D.; Zhang, L. Real-world Noisy Image Denoising: A New Benchmark. arXiv 2018, arXiv:1804.02603. [Google Scholar] [CrossRef]
- Kim, Y.; Soh, J.W.; Park, G.Y.; Cho, N.I. Transfer Learning From Synthetic to Real-Noise Denoising With Adaptive Instance Normalization. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR 2020), Seattle, WA, USA, 14–19 June 2020; pp. 3479–3489. [Google Scholar] [CrossRef]
- Guo, S.; Yan, Z.; Zhang, K.; Zuo, W.; Zhang, L. Toward Convolutional Blind Denoising of Real Photographs. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 1712–1722. [Google Scholar] [CrossRef]
- Jiang, Y. Image Denoising Algorithm Research Based on CNN-Transformer Multi-Interaction. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2023. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Zhang, L. FFDNet: Toward a Fast and Flexible Solution for CNN based Image Denoising. IEEE Trans. Image Process. 2018, 27, 4608–4622. [Google Scholar] [CrossRef] [PubMed]
- Anwar, S.; Barnes, N. Real Image Denoising With Feature Attention. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3155–3164. [Google Scholar]
- Xu, J.; Zhang, L.; Zhang, D. A Trilateral Weighted Sparse Coding Scheme for Real-World Image Denoising. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 20–36. [Google Scholar]











| Method | PSNR/dB | SSIM/% | FOM | TT/s |
|---|---|---|---|---|
| ID-MSE-WGAN | 29.28 | 37.14 | 0.538 | - |
| ADGN | 26.01 | 87.09 | 0.7251 | 0.064 |
| CS-PCN | 38.53 | 90.56 | 0.9119 | 0.059 |
| Trident GAN | 38.40 | 90.40 | 0.9120 | 0.047 |
| Ours | 39.29 | 91.50 | 0.9121 | 0.051 |
| Method | PSNR/dB | SSIM/% |
|---|---|---|
| WNet | 23.67 | 33.38 |
| XNet | 12.87 | 37.37 |
| U3Net | 37.72 | 89.28 |
| Module | Parameter (M) | FLOPs (G) | Single Epoch Training (min) | Single Image Reasoning (ms) |
|---|---|---|---|---|
| Generator (32 channel) | ≈ 7.8 | 34.2 | 9 | 18 |
| Denoiser | ≈15.6 | 68.9 | 18 | 38 |
| Discriminator | ≈4.2 | 9.1 | 5 | 12 |
| Overall | 27.6 | 112.2 | 32 | 55 |
| Configuration | Parameter |
|---|---|
| Operating system | Ubuntu 20.04.6 LTS |
| GPU | Tesla V100S-PCIE-32 GB |
| CPU | Intel(R) Xeon(R) Gold 5220R CPU @ 2.20 GHz |
| Deep learning framework | PyTorch 1.3.1 |
| Python version | 3.7.4 |
| Method | PSNR/dB | SSIM/% | FOM/% | ||||||
|---|---|---|---|---|---|---|---|---|---|
| DnCNN | 23.66 | 24.67 | 24.52 | 58.30 | 57.37 | 62.57 | 62.57 | 62.58 | 62.77 |
| BM3D | 25.65 | 25.71 | 25.67 | 68.50 | 68.61 | 68.71 | 68.50 | 68.61 | 68.71 |
| TWSC | 26.02 | 27.95 | 27.82 | 62.02 | 61.95 | 63.82 | 67.02 | 66.95 | 67.82 |
| FFDNet | 33.07 | 33.28 | 33.48 | 62.25 | 62.30 | 62.50 | 72.67 | 72.75 | 72.52 |
| CBDNet | 30.77 | 35.71 | 38.02 | 76.37 | 86.30 | 86.80 | 77.25 | 77.16 | 77.34 |
| RIDNet | 32.25 | 32.31 | 32.36 | 81.16 | 80.28 | 80.97 | 79.27 | 79.65 | 79.85 |
| AINDNet | 32.22 | 32.32 | 32.41 | 80.21 | 80.15 | 81.03 | 79.11 | 80.01 | 80.21 |
| Trident GAN | 38.10 | 38.40 | 38.69 | 90.10 | 90.40 | 90.19 | 89.10 | 91.20 | 91.19 |
| CS-PCN | 38.34 | 38.53 | 38.73 | 90.22 | 90.56 | 90.89 | 89.98 | 91.19 | 91.21 |
| Ours | 38.91 | 39.29 | 39.10 | 91.13 | 91.50 | 92.01 | 91.03 | 91.21 | 91.30 |
| Method | PSNR/dB | SSIM/% | FOM/% | ||||||
|---|---|---|---|---|---|---|---|---|---|
| DnCNN | 32.47 | 32.43 | 32.75 | 79.13 | 79.11 | 79.07 | 68.57 | 68.51 | 67.77 |
| BM3D | 34.51 | 33.20 | 34.89 | 85.15 | 85.10 | 85.24 | 69.70 | 69.61 | 69.68 |
| TWSC | 34.12 | 33.15 | 34.82 | 84.02 | 84.95 | 84.82 | 70.01 | 71.32 | 71.82 |
| FFDNet | 34.25 | 34.45 | 34.50 | 84.25 | 84.60 | 84.50 | 77.55 | 77.99 | 78.50 |
| CBDNet | 38.05 | 37.71 | 38.02 | 84.07 | 84.21 | 84.02 | 78.77 | 78.71 | 78.72 |
| RIDNet | 38.25 | 38.21 | 38.26 | 85.16 | 85.28 | 85.05 | 79.76 | 80.02 | 80.15 |
| AINDNet | 38.37 | 38.41 | 38.39 | 85.21 | 85.05 | 85.15 | 80.21 | 80.17 | 80.35 |
| Trident GAN | 38.90 | 39.10 | 39.19 | 93.10 | 93.40 | 93.19 | 93.10 | 93.19 | 93.20 |
| CS-PCN | 39.01 | 39.02 | 39.09 | 93.11 | 93.30 | 93.89 | 93.11 | 93.30 | 93.89 |
| Ours | 39.23 | 39.48 | 39.31 | 94.03 | 94.48 | 94.52 | 94.01 | 94.22 | 94.36 |
| Method | PSNR/dB | SSIM/% |
|---|---|---|
| None | 36.33 ± 0.10 | 85.91 ± 0.11 |
| Dual UNet | 39.16 ± 0.15 | 90.05 ± 0.17 |
| Dual UNet without ASPP | 39.22 ± 0.12 | 91.31 ± 0.15 |
| MRDB | 38.72 ± 0.11 | 91.22 ± 0.14 |
| Ours | 39.29 ± 0.05 | 91.50 ± 0.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Zhou, Y.; Sun, M.; Wang, D. Dual-Path Adversarial Denoising Network Based on UNet. Sensors 2025, 25, 4751. https://doi.org/10.3390/s25154751
Yu J, Zhou Y, Sun M, Wang D. Dual-Path Adversarial Denoising Network Based on UNet. Sensors. 2025; 25(15):4751. https://doi.org/10.3390/s25154751
Chicago/Turabian StyleYu, Jinchi, Yu Zhou, Mingchen Sun, and Dadong Wang. 2025. "Dual-Path Adversarial Denoising Network Based on UNet" Sensors 25, no. 15: 4751. https://doi.org/10.3390/s25154751
APA StyleYu, J., Zhou, Y., Sun, M., & Wang, D. (2025). Dual-Path Adversarial Denoising Network Based on UNet. Sensors, 25(15), 4751. https://doi.org/10.3390/s25154751






