Obtaining Rotational Stiffness of Wind Turbine Foundation from Acceleration and Wind Speed SCADA Data
Abstract
1. Introduction
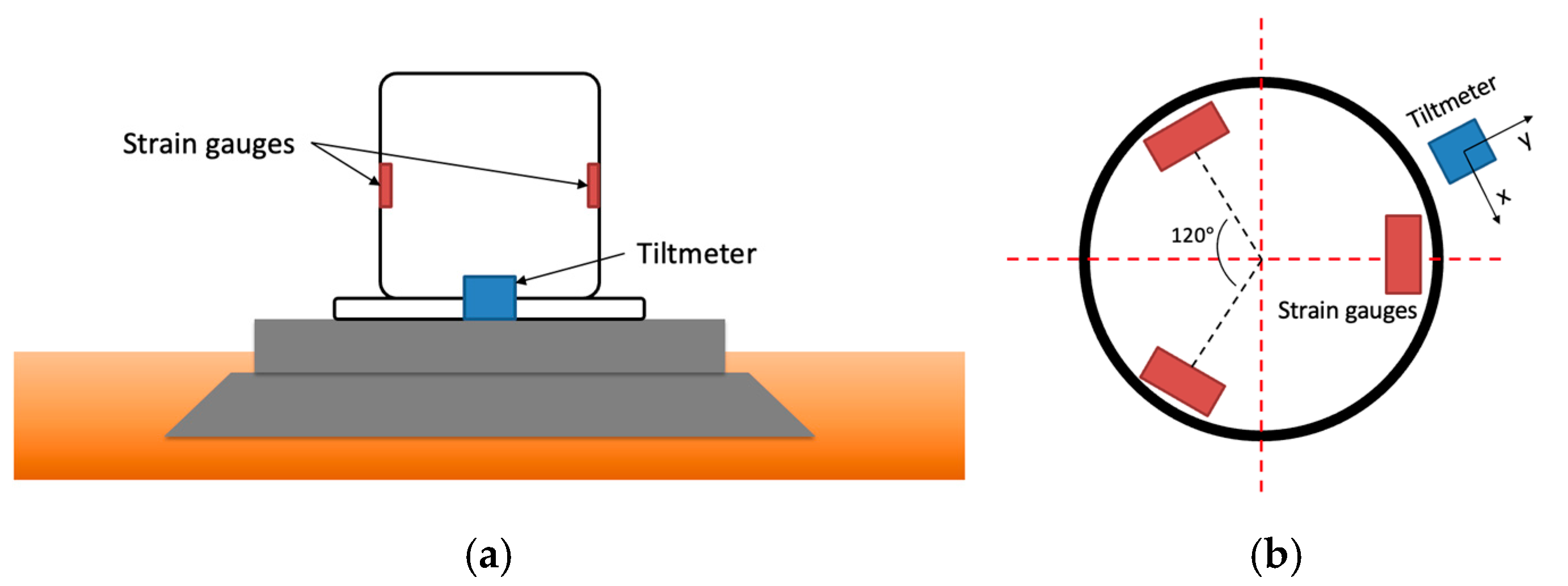
2. Dataset and Data Preprocessing
3. Mapping Model
3.1. Architecture of CNN Model
- (i)
- Input Layer—Accepts a sequence of 2-channel time-series/frequency map data over a window of size T.
- (ii)
- First Convolutional Block—A 1D convolution layer with 32 filters of a kernel size 3. Then, ReLU (Rectified Linear Unit) activation is applied, followed by a max pooling layer that reduces the temporal dimension by a factor of 2
- (iii)
- Second Convolutional Block—The feature map output of the first convolution block is passed through a second convolution layer with 64 filters (also with a kernel size 3, ReLU activation), followed by another max pooling layer
- (iv)
- Flatten and Dense Layers—The pooled features are flattened into a 1D vector and passed through a fully connected layer with 128 units and ReLU activation
- (v)
- Dropout Layer—To prevent overfitting, a dropout layer with a rate of 0.2 is added.
- (vi)
- Output Layer—Finally, a dense layer with linear activation is used to output a 2D vector representing the estimated tilt and moment
3.2. Window Size Selection
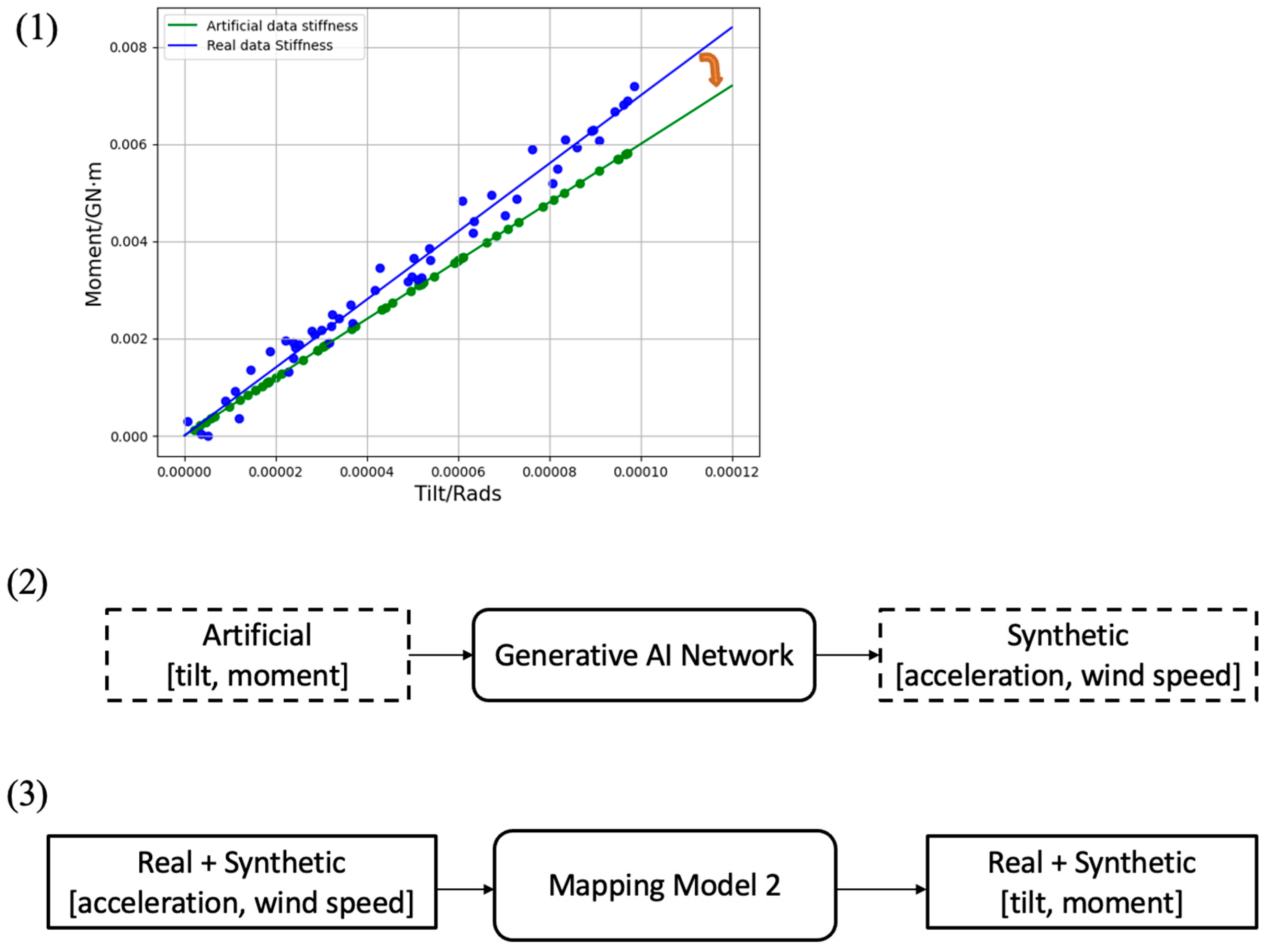
4. Synthetic Data Generation
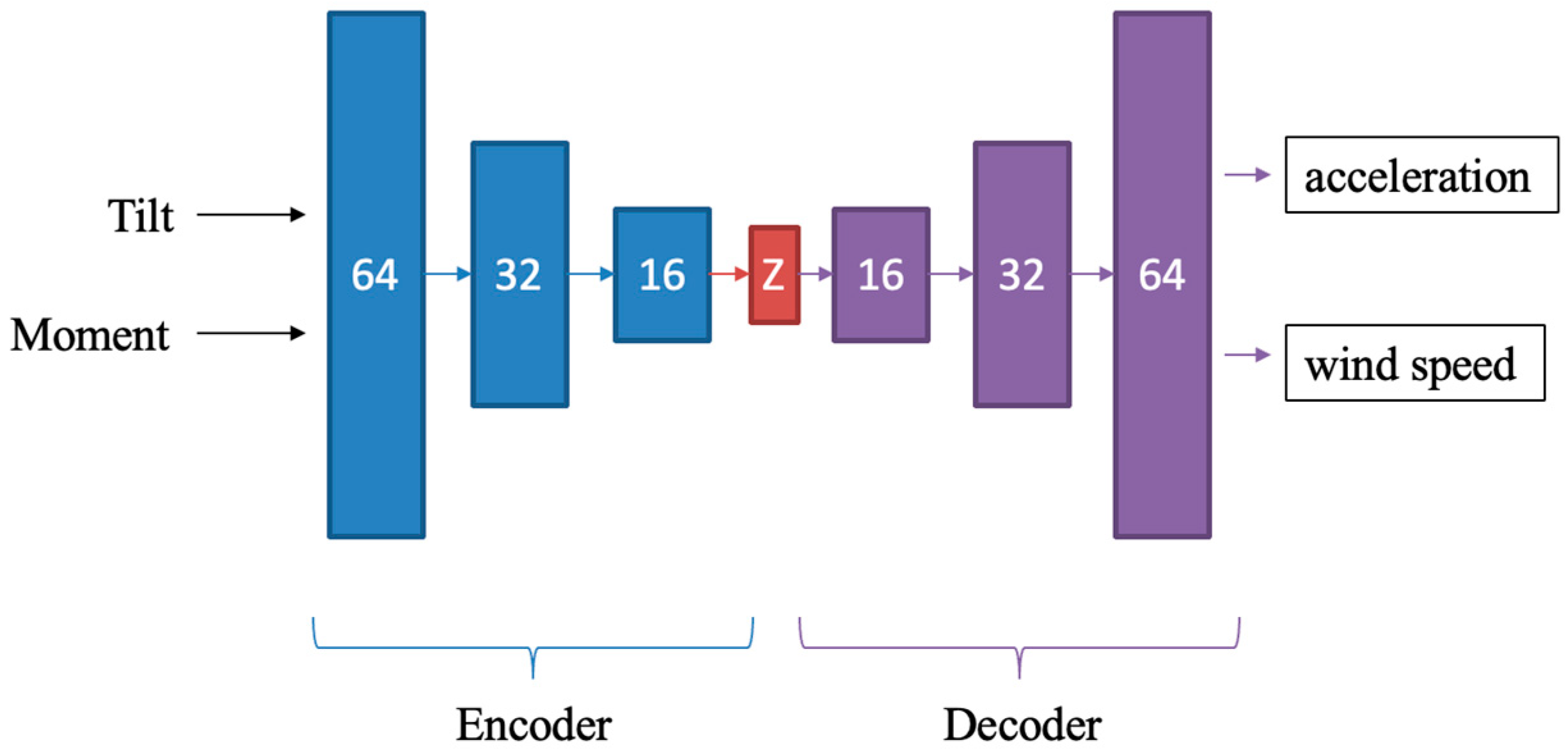
Architecture of Autoencoder Network
5. Results and Discussion
5.1. Results of Estimating Stiffness by the Mapping Model
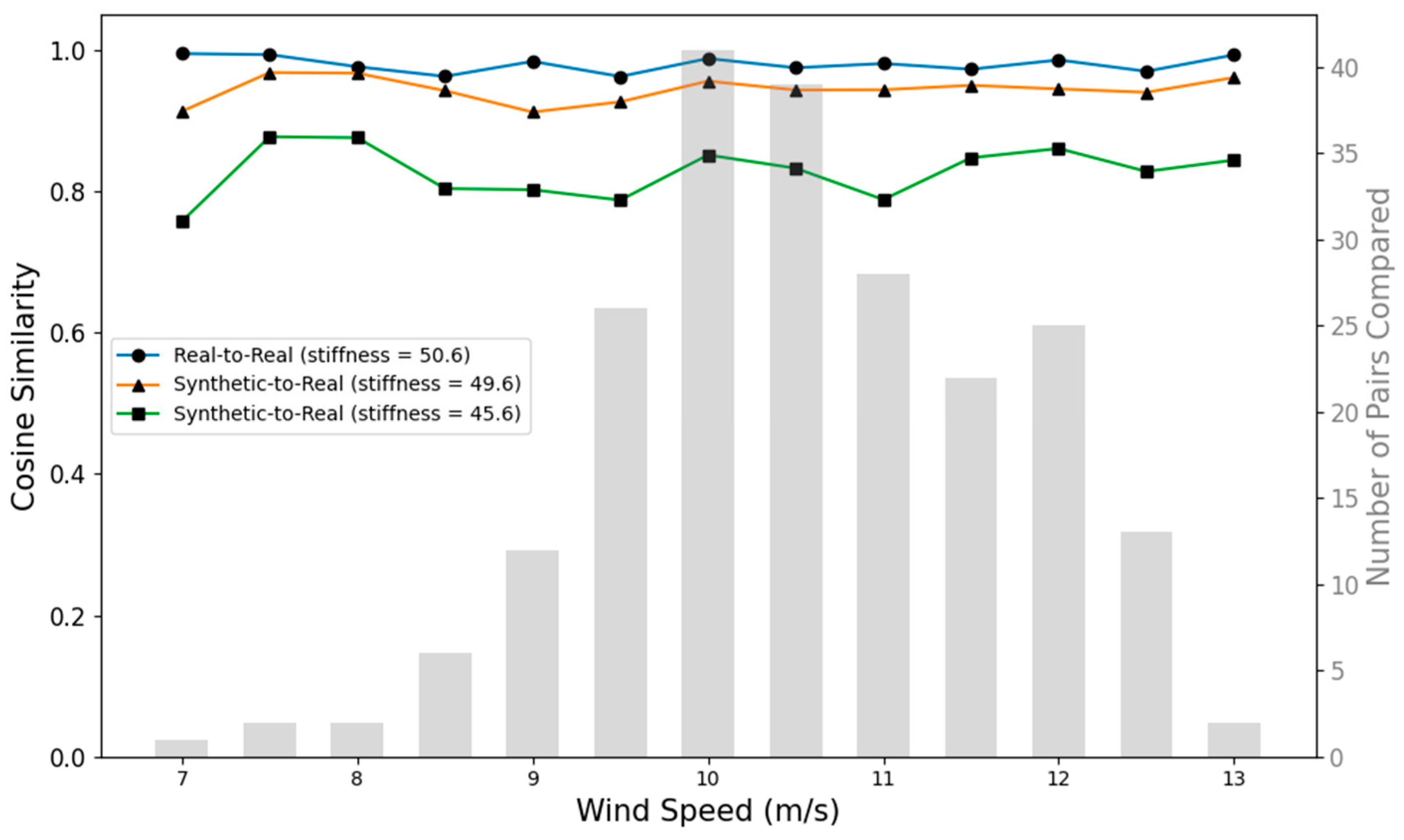
5.2. Results of Detecting a Drop in Stiffness
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dai, J.; Zhang, Y.; Rotea, M.; Kehtarnavaz, N. A Review of Machine Learning Approaches for Prediction of Icing on Wind Turbines. In Proceedings of the 2024 IEEE 19th Conference on Industrial Electronics and Applications (ICIEA), Kristiansand, Norway, 5–8 August 2024; pp. 1–7. [Google Scholar]
- Thompson, J.M.T.; Byrne, B.W.; Houlsby, G.T. Foundations for Offshore Wind Turbines. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 2003, 361, 2909–2930. [Google Scholar] [CrossRef]
- McAlorum, J.; Perry, M.; Fusiek, G.; Niewczas, P.; McKeeman, I.; Rubert, T. Deterioration of Cracks in Onshore Wind Turbine Foundations. Eng. Struct. 2018, 167, 121–131. [Google Scholar] [CrossRef]
- Duan, Y.; Pan, W.; Ping, T.; Mou, B.; Young, B. Effects of Module-to-Module Connection Rotational Stiffness on the Structural Performance of High-Rise Steel Modular Buildings. J. Build. Eng. 2024, 82, 108187. [Google Scholar] [CrossRef]
- Faulkner, K.; Brownjohn, J.M.W.; Wang, Y.; Huseynov, F. Tracking Bridge Tilt Behaviour Using Sensor Fusion Techniques. J. Civ. Struct. Health Monit. 2020, 10, 543–555. [Google Scholar] [CrossRef]
- Silva, A.L.; Varanis, M.; Mereles, A.G.; Oliveira, C.; Balthazar, J.M. A Study of Strain and Deformation Measurement Using the Arduino Microcontroller and Strain Gauges Devices. Rev. Bras. Ensino Fís. 2018, 41, 20180206. [Google Scholar] [CrossRef]
- Liu, C.; Park, J.-W.; Spencer, B.F.; Moon, D.-S.; Fan, J. Sensor Fusion for Structural Tilt Estimation Using an Acceleration-Based Tilt Sensor and a Gyroscope. Smart Mater. Struct. 2017, 26, 105005. [Google Scholar] [CrossRef]
- Gulgec, N.S.; Takáč, M.; Pakzad, S.N. Structural Sensing with Deep Learning: Strain Estimation from Acceleration Data for Fatigue Assessment. Comput. Aided Civ. Infrastruct. Eng. 2020, 35, 1349–1364. [Google Scholar] [CrossRef]
- Jahani, K.; Langlois, R.G.; Afagh, F.F. Structural Dynamics of Offshore Wind Turbines: A Review. Ocean. Eng. 2022, 251, 111136. [Google Scholar] [CrossRef]
- Maes, K.; Iliopoulos, A.; Weijtjens, W.; Devriendt, C.; Lombaert, G. Dynamic Strain Estimation for Fatigue Assessment of an Offshore Monopile Wind Turbine Using Filtering and Modal Expansion Algorithms. Mech. Syst. Signal Process. 2016, 76–77, 592–611. [Google Scholar] [CrossRef]
- Tarpø, M.; Nabuco, B.; Skafte, A.; Kristoffersen, J.; Vestermark, J.; Amador, S.; Brincker, R. Operational Modal Analysis Based Prediction of Actual Stress in an Offshore Structural Model. Procedia Eng. 2017, 199, 2262–2267. [Google Scholar] [CrossRef]
- McAdam, R.A.; Chatzis, M.N.; Kuleli, M.; Anderson, E.F.; Byrne, B.W. Monopile Foundation Stiffness Estimation of an Instrumented Offshore Wind Turbine through Model Updating. Struct. Control. Health Monit. 2023, 2023, 4474809. [Google Scholar] [CrossRef]
- Wondra, B.; Malek, S.; Botz, M.; Glaser, S.D.; Grosse, C.U. Wireless High-Resolution Acceleration Measurements for Structural Health Monitoring of Wind Turbine Towers. Data Enabled Discov. Appl. 2019, 3, 4. [Google Scholar] [CrossRef]
- García, D.; Tcherniak, D. An Experimental Study on the Data-Driven Structural Health Monitoring of Large Wind Turbine Blades Using a Single Accelerometer and Actuator. Mech. Syst. Signal Process. 2019, 127, 102–119. [Google Scholar] [CrossRef]
- Kilic, G.; Unluturk, M.S. Testing of Wind Turbine Towers Using Wireless Sensor Network and Accelerometer. Renew. Energy 2015, 75, 318–325. [Google Scholar] [CrossRef]
- Vidal Seguí, Y.; Rubias, J.L.; Pozo Montero, F. Wind turbine health monitoring based on accelerometer data. In Proceedings of the 9th ECCOMAS Thematic Conference on Smart Structures and Materials, Paris, France, 8–12 July 2019; pp. 1604–1611. [Google Scholar]
- Jewell Instruments. LS Series Precision Inclinometers Operating Manual; Jewell Instruments: Manchester, NH, USA, 2018; Available online: https://jewellinstruments.com/wp-content/uploads/L00255-C801-Rev-D.pdf (accessed on 20 June 2025).
- OMEGA Engineering. KFH Series Foil Strain Gauges Datasheet; OMEGA Engineering: Norwalk, CT, USA, 2020; Available online: https://assets.omega.com/pdf/test-and-measurement-equipment/strain-gauges/KFH.pdf (accessed on 20 June 2025).
- Gere, J.M.; Goodno, B.J. Mechanics of Materials, 8th ed.; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Kong, Z.; Tang, B.; Deng, L.; Liu, W.; Han, Y. Condition Monitoring of Wind Turbines Based on Spatio-Temporal Fusion of SCADA Data by Convolutional Neural Networks and Gated Recurrent Units. Renew. Energy 2020, 146, 760–768. [Google Scholar] [CrossRef]
- Chen, H.; Liu, H.; Chu, X.; Liu, Q.; Xue, D. Anomaly Detection and Critical SCADA Parameters Identification for Wind Turbines Based on LSTM-AE Neural Network. Renew. Energy 2021, 172, 829–840. [Google Scholar] [CrossRef]
- Amini, A.; Kanfoud, J.; Gan, T.-H. An Artificial Intelligence Neural Network Predictive Model for Anomaly Detection and Monitoring of Wind Turbines Using SCADA Data. Appl. Artif. Intell. 2022, 36, 2034718. [Google Scholar] [CrossRef]
- Lutz, M.-A.; Vogt, S.; Berkhout, V.; Faulstich, S.; Dienst, S.; Steinmetz, U.; Gück, C.; Ortega, A. Evaluation of Anomaly Detection of an Autoencoder Based on Maintenace Information and Scada-Data. Energies 2020, 13, 1063. [Google Scholar] [CrossRef]
- Jin, X.; Wang, H.; Kong, Z.; Xu, Z.; Qiao, W. Condition Monitoring of Wind Turbine Generators Based on SCADA Data and Feature Transfer Learning. IEEE Access 2023, 11, 9441–9450. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, Z. Wind Turbine Gearbox Failure Detection Based on SCADA Data: A Deep Learning-Based Approach. IEEE Trans. Instrum. Meas. 2021, 70, 3507911. [Google Scholar] [CrossRef]
- Nazir, S.; Patel, S.; Patel, D. Autoencoder Based Anomaly Detection for SCADA Networks. IJAIML 2021, 11, 83–99. [Google Scholar] [CrossRef]





| Turbine Number | Ground Truth Stiffness (GN·m/rads) | Number of Data Samples | R2 |
|---|---|---|---|
| 24 | 73.1 | 7200 | 0.95 |
| 37 | 66.5 | 2620 | 0.96 |
| 40 | 50.6 | 6610 | 0.81 |
| 44 | 41.2 | 6010 | 0.82 |
| 46 | 74.7 | 5780 | 0.93 |
| Window Size (Samples) | Stiffness Estimation Absolute Error (GN·m/Rads) |
|---|---|
| 10 | 4.5 |
| 20 | 2.7 |
| 30 | 1.3 |
| 40 | 4.2 |
| Turbine Number | Ground Truth Stiffness (GN·m/rads) | Estimated Stiffness (GN·m/rads) Mean ± Std | t-Distribution 95% Confidence Interval |
|---|---|---|---|
| 24 | 73.1 | 74.4 ± 3.9 | [73.2, 75.4] |
| 37 | 66.5 | 69.9 ± 6.8 | [67.9, 71.8] |
| 40 | 50.6 | 53.2 ± 6.9 | [51.3, 55.2] |
| 44 | 41.2 | 44.1 ± 3.4 | [43.2, 45.1] |
| 46 | 74.7 | 77.2 ± 3.3 | [76.3, 78.2] |
| Turbine Number | Ground Truth Stiffness (GN·m/rads) | Estimated Stiffness (Moment Only) (GN·m/rads) Mean ± Std | t-Distribution 95% Confidence Interval |
|---|---|---|---|
| 24 | 73.1 | 73.4 ± 2 | [72.8, 74.0] |
| 37 | 66.5 | 66.5 ± 2.3 | [65.9, 67.1] |
| 40 | 50.6 | 51.4 ± 3.7 | [50.3, 52.4] |
| 44 | 41.2 | 43.4 ± 3.0 | [42.6, 44.3] |
| 46 | 74.7 | 77.1 ± 1.4 | [76.7, 77.6] |
| Turbine 24 | Artificial drop in stiffness | −1 | −2 | −3 | −4 | −5 |
| Measured stiffness | Estimated stiffness | 72.6 | 72.8 | 72.5 | 72.5 | 72.0 |
| 73.1 | Detected drop in stiffness | −0.1 | −0.7 | −1.0 | −1.4 | −1.6 |
| Turbine 37 | Artificial drop in stiffness | −1 | −2 | −3 | −4 | −5 |
| Measured stiffness | Estimated stiffness | 67.6 | 67.2 | 67.7 | 67.6 | 68.2 |
| 66.5 | Detected drop in stiffness | −0.9 | −1.3 | −2.3 | −3.0 | −4.8 |
| Turbine 40 | Artificial drop in stiffness | −1 | −2 | −3 | −4 | −5 |
| Measured stiffness | Estimated stiffness | 50.7 | 50.3 | 50.9 | 50.6 | 50.0 |
| 50.6 | Detected drop in stiffness | −0.1 | −0.2 | −0.9 | −1.3 | −1.6 |
| Turbine 44 | Artificial drop in stiffness | −1 | −2 | −3 | −4 | −5 |
| Measured stiffness | Estimated stiffness | 41.2 | 41.3 | 41.3 | 41.9 | 41.6 |
| 41.2 | Detected drop in stiffness | −0.9 | −1.6 | −2.2 | −3.6 | −4.1 |
| Turbine 46 | Artificial drop in stiffness | −1 | −2 | −3 | −4 | −5 |
| Measured stiffness | Estimated stiffness | 74.8 | 74.8 | 74.5 | 74.3 | 74.3 |
| 74.7 | Detected drop in stiffness | −0.4 | −0.7 | −0.8 | −1.3 | −1.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, J.; Rotea, M.; Kehtarnavaz, N. Obtaining Rotational Stiffness of Wind Turbine Foundation from Acceleration and Wind Speed SCADA Data. Sensors 2025, 25, 4756. https://doi.org/10.3390/s25154756
Dai J, Rotea M, Kehtarnavaz N. Obtaining Rotational Stiffness of Wind Turbine Foundation from Acceleration and Wind Speed SCADA Data. Sensors. 2025; 25(15):4756. https://doi.org/10.3390/s25154756
Chicago/Turabian StyleDai, Jiazhi, Mario Rotea, and Nasser Kehtarnavaz. 2025. "Obtaining Rotational Stiffness of Wind Turbine Foundation from Acceleration and Wind Speed SCADA Data" Sensors 25, no. 15: 4756. https://doi.org/10.3390/s25154756
APA StyleDai, J., Rotea, M., & Kehtarnavaz, N. (2025). Obtaining Rotational Stiffness of Wind Turbine Foundation from Acceleration and Wind Speed SCADA Data. Sensors, 25(15), 4756. https://doi.org/10.3390/s25154756










