Optimal Coherence Length Control in Interferometric Fiber Optic Hydrophones via PRBS Modulation: Theory and Experiment
Abstract
1. Introduction
2. Theory and Methodology
2.1. Impact of PRBS Phase Modulation on Laser Coherence Length
2.2. Impact of Coherence Length on IFOH System Background Noise
2.3. Simulation of Introduced Phase Noise
3. Experimental Results and Discussion
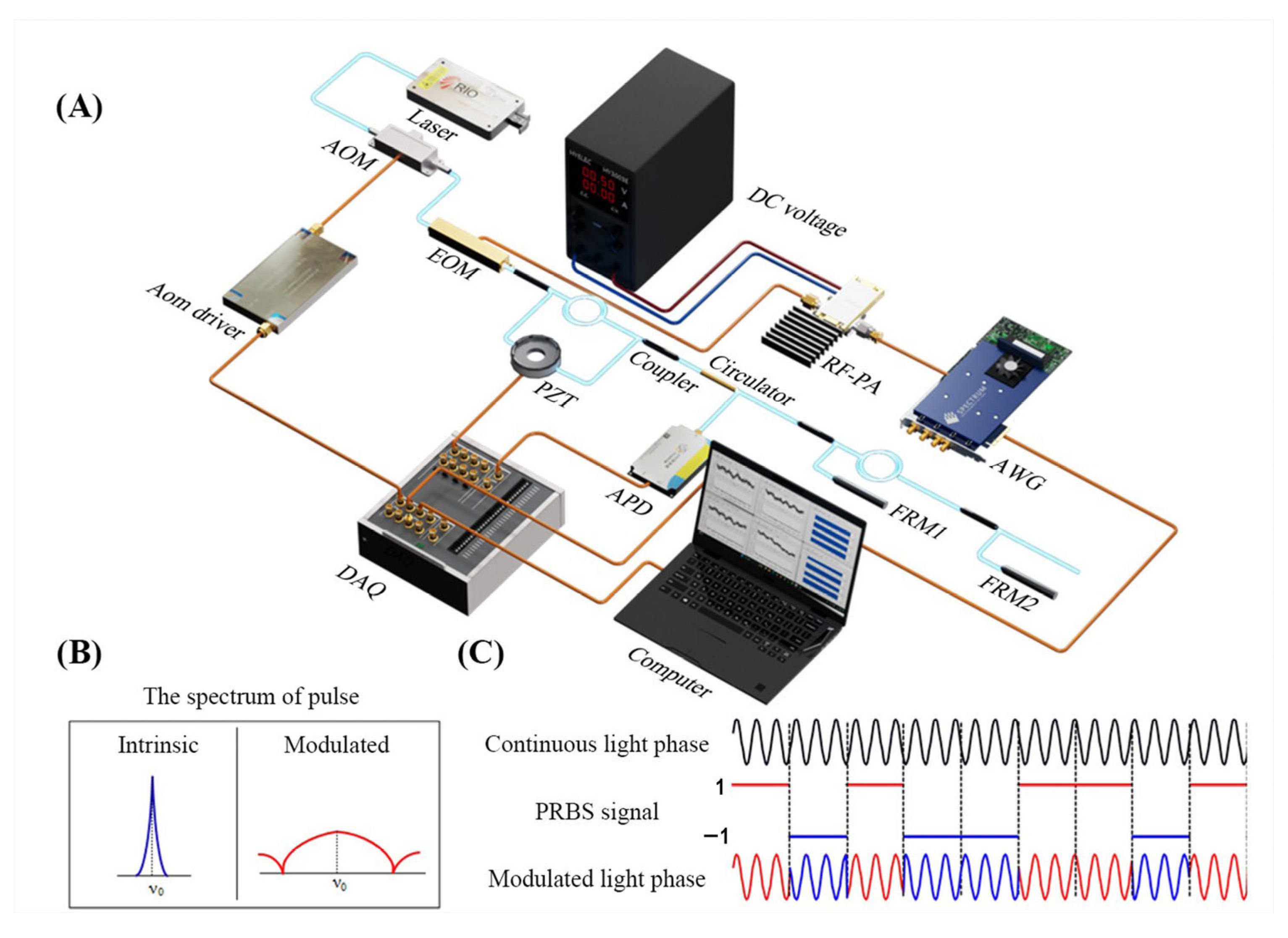
3.1. System Configuration
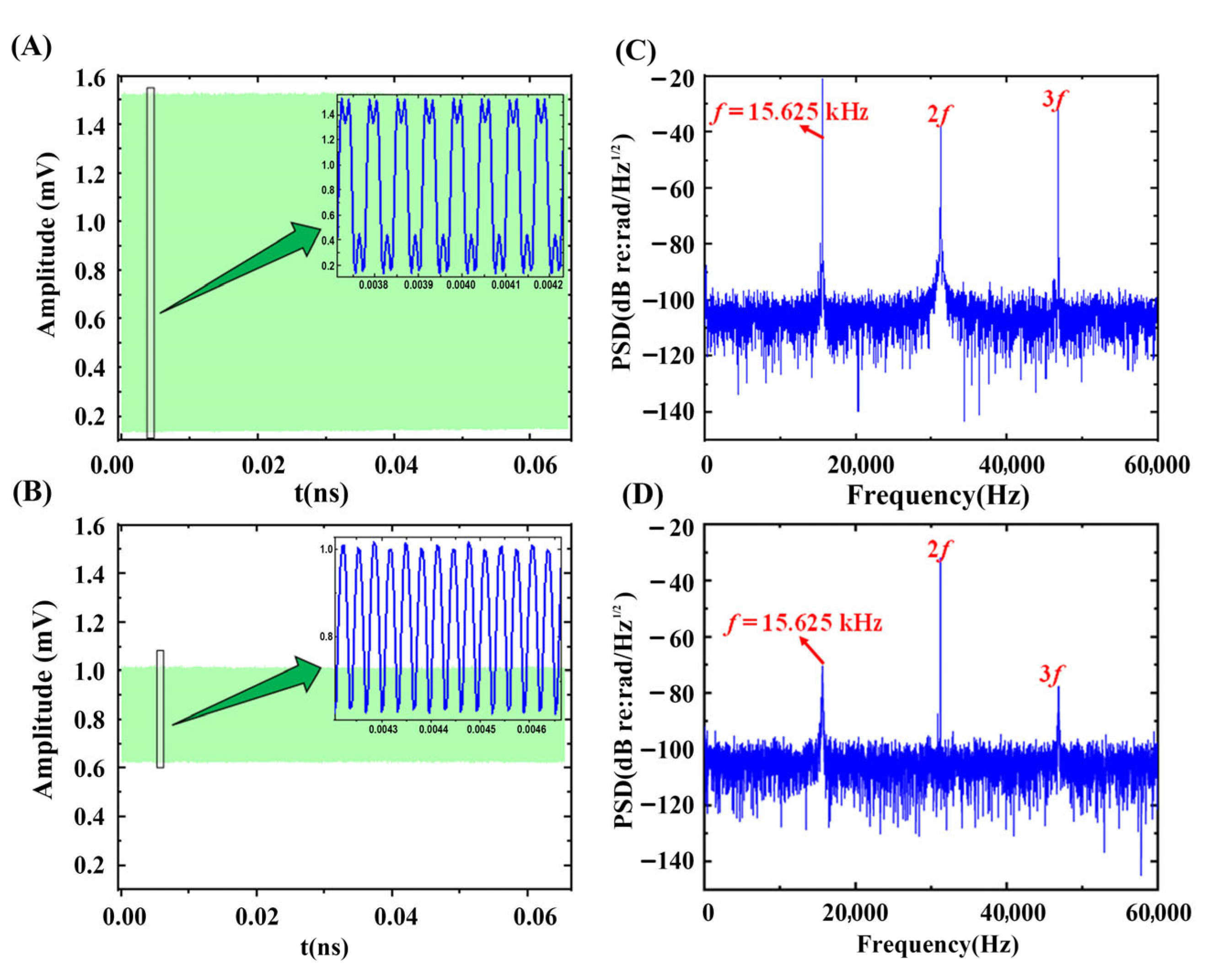
3.2. The Influence of Coherence Length on Interference Visibility
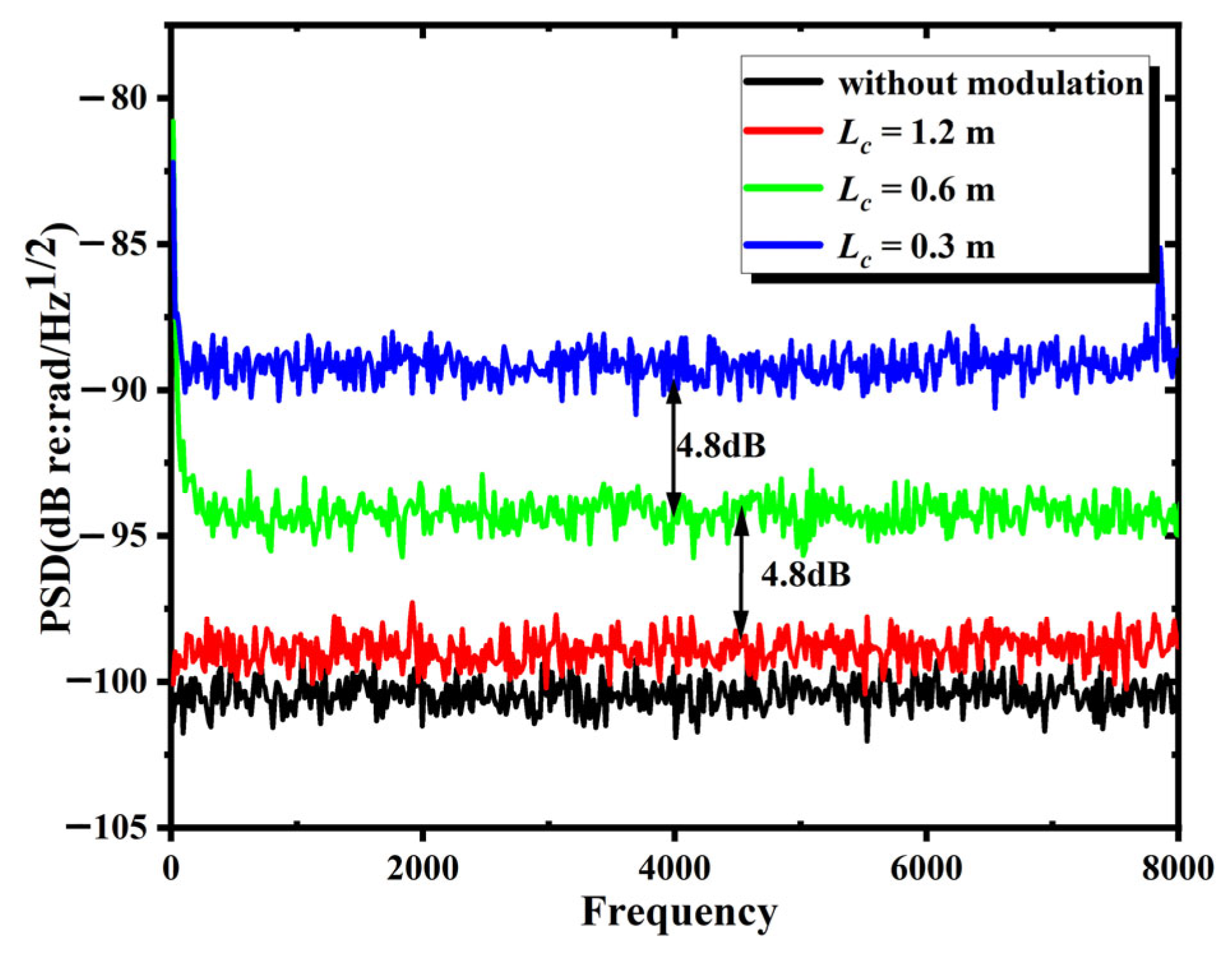
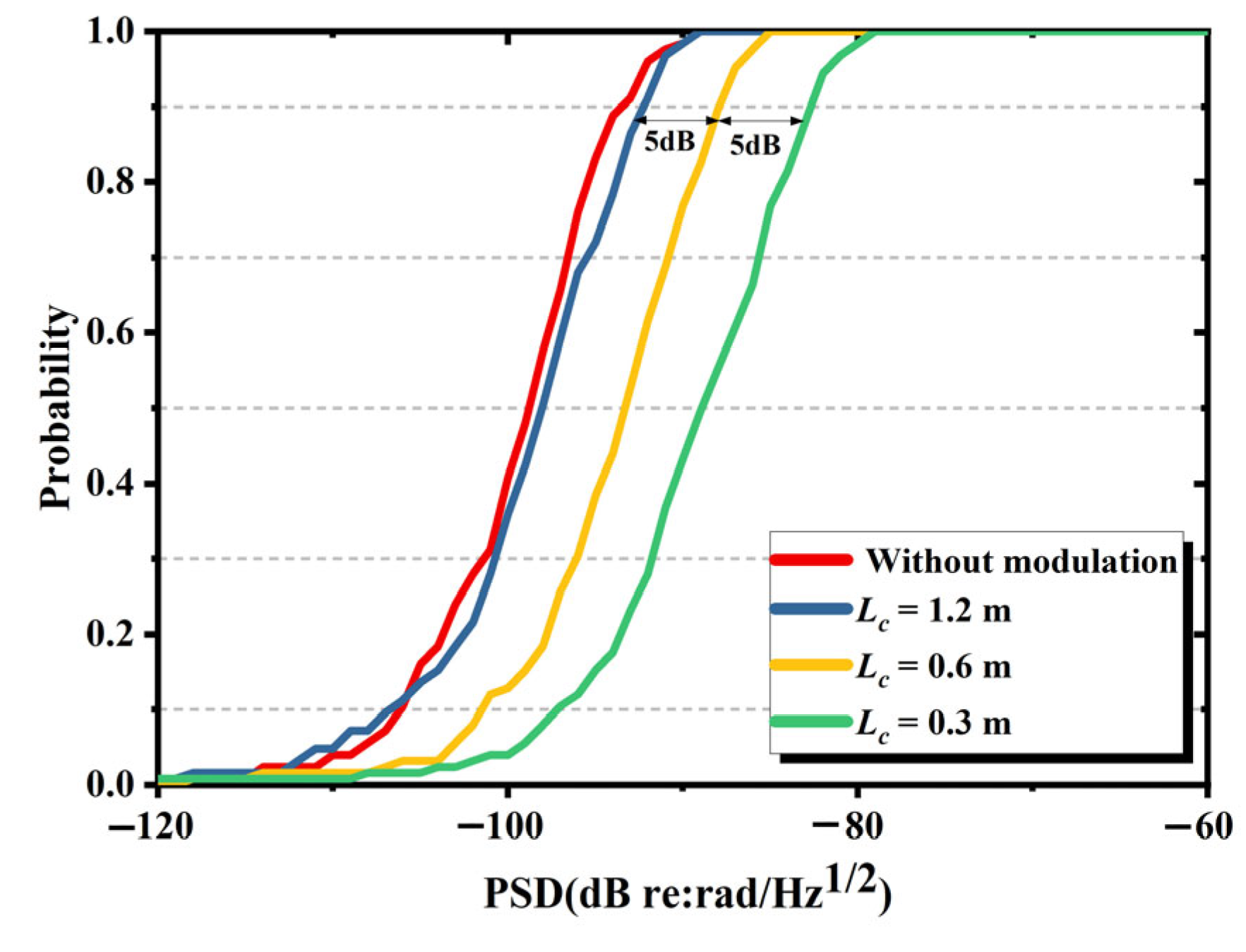
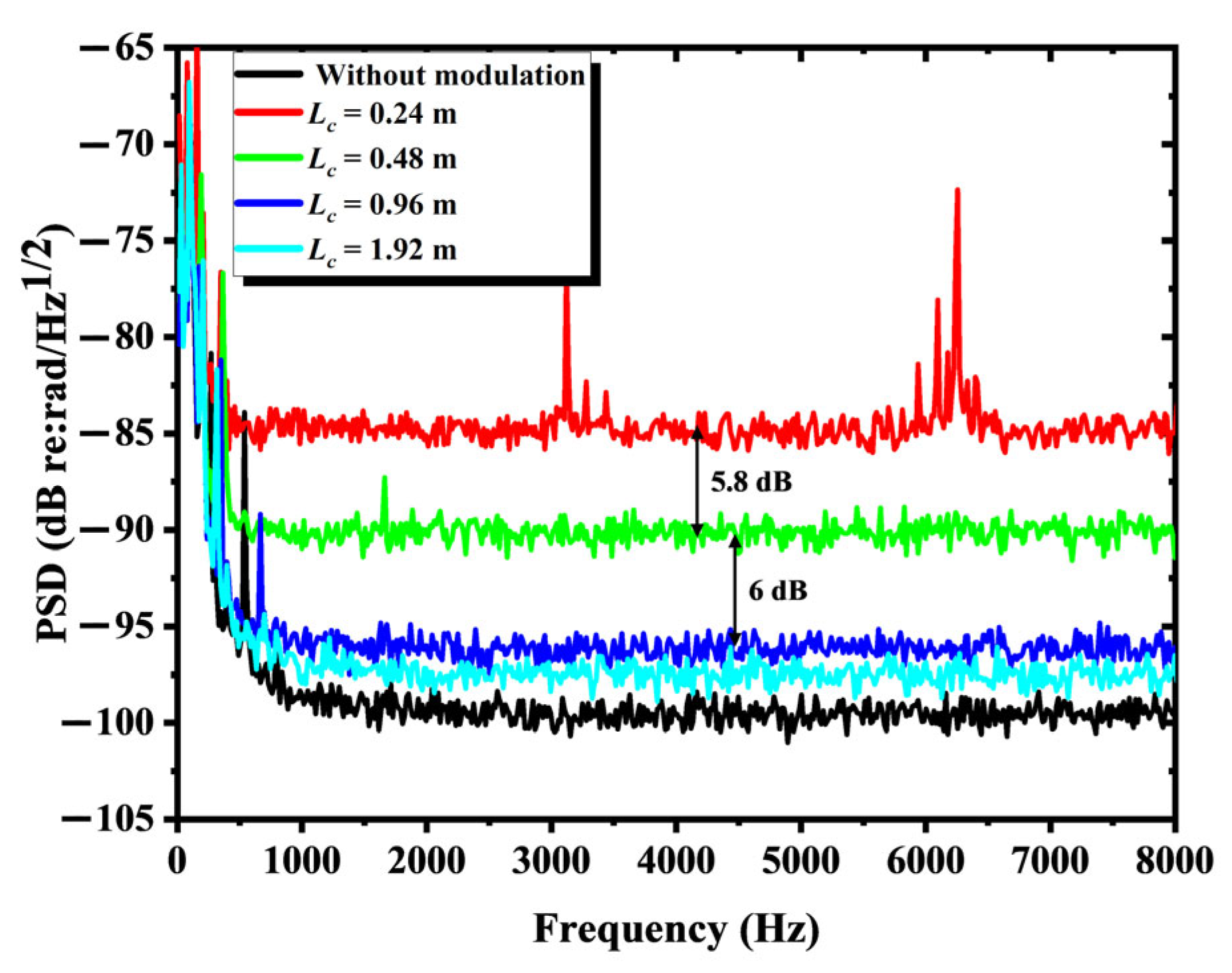
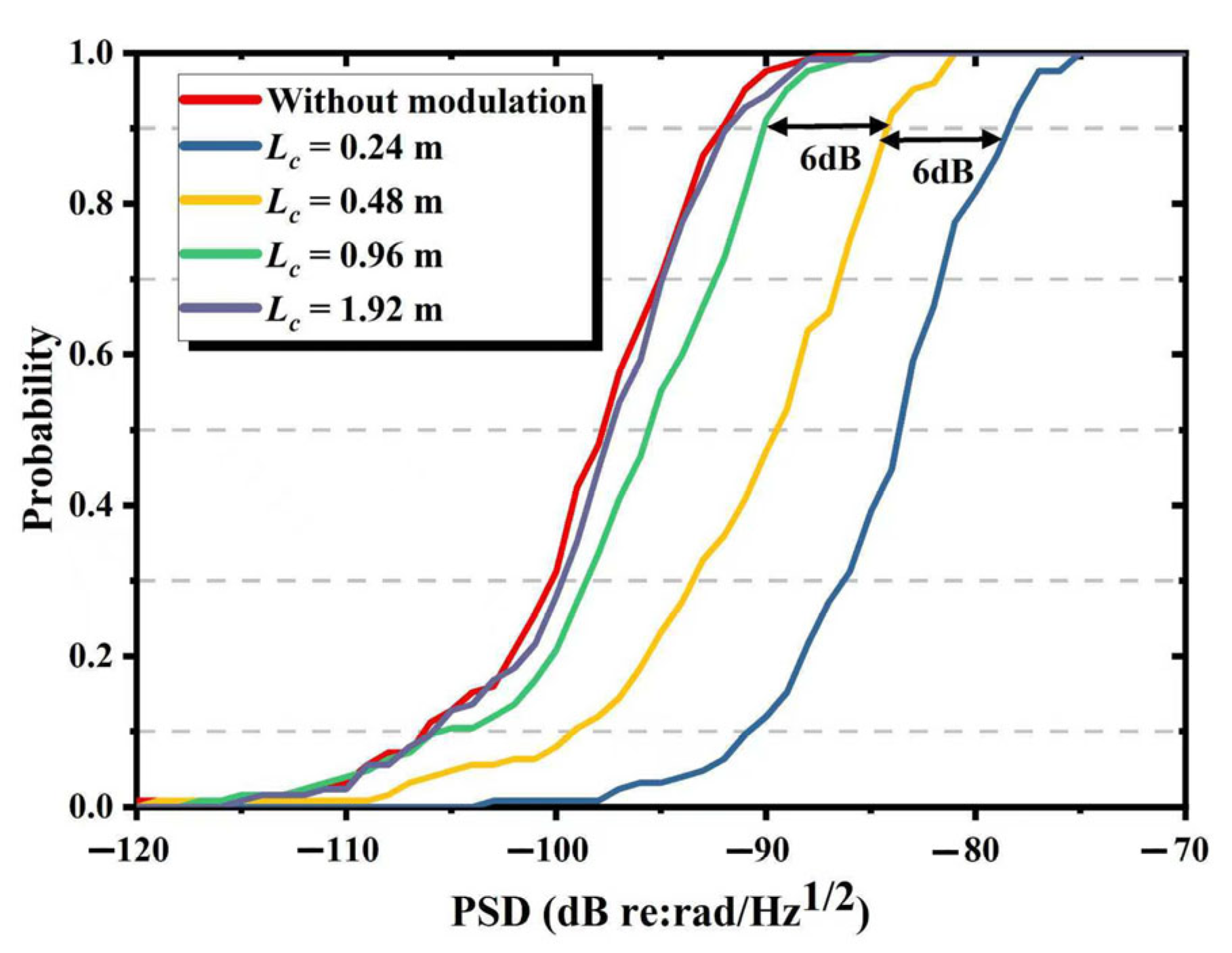
3.3. The Influence of Coherence Length on Background Noise of IFOH Without Parasitic Interference
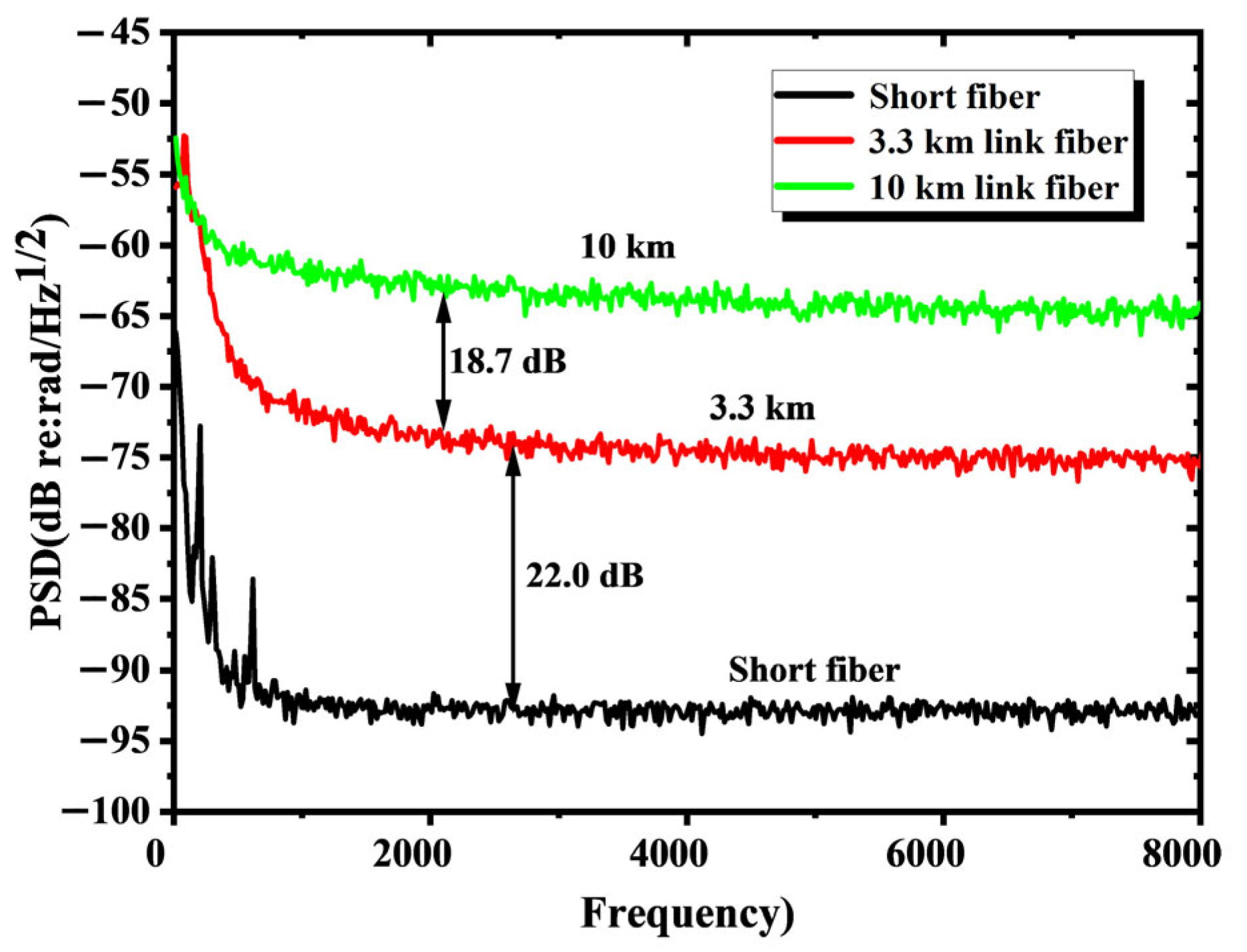
3.4. The Optimal Coherence Length Under Different Fiber Link Lengths
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Denisov, A.; Soto, M.A.; Thévenaz, L. Going beyond 1000000 Resolved Points in a Brillouin Distributed Fiber Sensor: Theoretical Analysis and Experimental Demonstration. Light Sci. Appl. 2016, 5, e16074. [Google Scholar] [CrossRef] [PubMed]
- Soriano-Amat, M.; Durán, V.; Martins, H.F.; Preciado, J.; Martin-Lopez, S.; Gonzalez-Herraez, M.; Fernández-Ruiz, M.R. Time-Domain Expansion in Phase-Sensitive Optical Time Domain Reflectometry. In Optical Fiber Sensors Conference 2020 Special Edition, Proceedings of the Optical Fiber Sensors Conference 2020, Washington, DC, USA, 8–12 June 2020; Optica Publishing Group: Washington, DC, USA, 2021. [Google Scholar]
- Li, J.; Zhu, W.; Biondi, E.; Zhan, Z. Earthquake Focal Mechanisms with Distributed Acoustic Sensing. Nat. Commun. 2023, 14, 4181. [Google Scholar] [CrossRef] [PubMed]
- Dandridge, A. Fiber Optic Interferometric Sensors at Sea. Opt. Photonics News 2019, 30, 34–41. [Google Scholar] [CrossRef]
- Hu, Q.; Shang, F.; Ma, L.; Wang, W.; Yu, Y.; Bian, Y.; Zhu, X.; Song, J. Revolutionizing Underwater Sensor Performance: Tackling Rayleigh Scattering Challenges by Pseudo Random Noise. Adv. Sci. 2024, 12, 2411967. [Google Scholar] [CrossRef]
- Dandridge, A.; Cogdell, G.B. Fiber Optic Sensors for Navy Applications. IEEE LCS 1991, 2, 81–89. [Google Scholar] [CrossRef]
- Davis, A.R.; Kirkendall, C.K.; Dandridge, A.; Kersey, A.D. 64 Channel All Optical Deployable Acoustic Array. In Fiber Sensors For Industrial Applications, Proceedings of the 12th International Conference on Optical Fiber Sensors, Williamsburg, VA, USA, 28–31 October 1997; OSA: Washington, DC, USA, 1997; p. OFA6. [Google Scholar]
- Cranch, G.A.; Crickmore, R.; Kirkendall, C.K.; Bautista, A.; Daley, K.; Motley, S.; Salzano, J.; Latchem, J.; Nash, P.J. Acoustic Performance of a Large-Aperture, Seabed, Fiber-Optic Hydrophone Array. J. Acoust. Soc. Am. 2004, 115, 2848–2858. [Google Scholar] [CrossRef]
- Cranch, G.A.; Nash, P.J.; Kirkendall, C.K. Large-Scale Remotely Interrogated Arrays of Fiber-Optic Interferometric Sensors for Underwater Acoustic Applications. IEEE Sens. J. 2003, 3, 19–30. [Google Scholar] [CrossRef]
- Vlasov, A.A.; Plotnikov, M.Y.; Volkovsky, S.A.; Aleinik, A.S.; Motorin, E.A.; Sharkov, I.A.; Makarenko, A.A. Development of the Passive Vibroacoustic Isolation System for the Path Matched Differential Interferometry Based Fiber-Optic Sensors. Opt. Fiber Technol. 2020, 57, 102241. [Google Scholar] [CrossRef]
- Kirkendall, C.; Cole, J.H.; Tveten, A.B.; Dandridge, A. Progress in Fiber Optical Acoustic and Seismic Sensing. In Optical Fiber Sensors, Proceedings of the Optical Fiber Sensors, Cancún, Mexico, 23–27 October 2006; OSA: Washington, DC, USA, 2006; p. ThB1. [Google Scholar]
- Giallorenzi, T.G. All-Optical Towed and Conformal Arrays. U.S. Patent 4,648,083, 3 March 1987. [Google Scholar]
- De Freitas, J.M. Recent Developments in Seismic Seabed Oil Reservoir Monitoring Applications Using Fibre-Optic Sensing Networks. Meas. Sci. Technol. 2011, 22, 052001. [Google Scholar] [CrossRef]
- Kringlebotn, J.T.; Nakstad, H.; Eriksrud, M. Fibre Optic Ocean Bottom Seismic Cable System: From Innovation to Commercial Success. In Proceedings of SPIE, Proceedings of the 20th International Conference on Optical Fibre Sensors 2009, Edinburgh, UK, 5–9 October 2009; Jones, J.D.C., Ed.; SPIE: Bellingham, WA, USA, 2009; p. 75037U. [Google Scholar]
- Knudsen, S.; Havsgard, G.B.; Berg, A.; Nakstad, H.; Bostick, T. Permanently Installed High-Resolution Fiber Optic 3C/4D Seismic Sensor Systems for in-Well Imaging and Monitoring Applications. In Proceedings of the Sixth Pacific Northwest Fiber Optic Sensor Workshop, Troutdale, OR, USA, 14–15 November 2003; p. 51. [Google Scholar]
- Nakstad, H.; Kringlebotn, J.T. Realisation of a Full-Scale Fibre Optic Ocean Bottom Seismic System. In Proceedings of the SPIE, Proceedings of the 19th International Conference on Optical Fibre Sensors, Perth, Australia, 15–18 April 2008; Sampson, D.D., Ed.; SPIE: Bellingham, WA, USA, 2008; p. 700436. [Google Scholar]
- Ajo-Franklin, J.B.; Dou, S.; Lindsey, N.J.; Monga, I.; Tracy, C.; Robertson, M.; Rodriguez Tribaldos, V.; Ulrich, C.; Freifeld, B.; Daley, T.; et al. Distributed Acoustic Sensing Using Dark Fiber for Near-Surface Characterization and Broadband Seismic Event Detection. Sci. Rep. 2019, 9, 1328. [Google Scholar] [CrossRef]
- Muñoz, F.; Soto, M.A. Enhancing Fibre-Optic Distributed Acoustic Sensing Capabilities with Blind near-Field Array Signal Processing. Nat. Commun. 2022, 13, 4019. [Google Scholar] [CrossRef]
- Bao, X.; Wang, Y. Recent Advancements in Rayleigh Scattering-Based Distributed Fiber Sensors. Adv. Devices Instrum. 2021, 2021, 8696571. [Google Scholar] [CrossRef]
- Huy, D.Q.; Sadjoli, N.; Azam, A.B.; Elhadidi, B.; Cai, Y.; Seet, G. Object Perception in Underwater Environments: A Survey on Sensors and Sensing Methodologies. Ocean Eng. 2023, 267, 113202. [Google Scholar] [CrossRef]
- Fabricante, B.R.; Król, M.; Wurdack, M.; Pieczarka, M.; Steger, M.; Snoke, D.W.; West, K.; Pfeiffer, L.N.; Truscott, A.G.; Ostrovskaya, E.A.; et al. Narrow-Linewidth Exciton-Polariton Laser. Optica 2024, 11, 838–845. [Google Scholar] [CrossRef]
- Duan, J.; Huang, H.; Lu, Z.G.; Poole, P.J.; Wang, C.; Grillot, F. Narrow Spectral Linewidth in InAs/InP Quantum Dot Distributed Feedback Lasers. Appl. Phys. Lett. 2018, 112, 121102. [Google Scholar] [CrossRef]
- Shu, H.; Chang, L.; Tao, Y.; Shen, B.; Xie, W.; Jin, M.; Netherton, A.; Tao, Z.; Zhang, X.; Chen, R.; et al. Microcomb-Driven Silicon Photonic Systems. Nature 2022, 605, 457–463. [Google Scholar] [CrossRef]
- Zhu, T.; Huang, S.; Shi, L.; Huang, W.; Liu, M.; Chiang, K. Rayleigh Backscattering: A Method to Highly Compress Laser Linewidth. Chin. Sci. Bull. 2014, 59, 4631–4636. [Google Scholar] [CrossRef]
- Cranch, G.A.; Nash, P.J. Large-Scale Multiplexing of Interferometric Fiber-Optic Sensors Using TDM and DWDM. J. Light. Technol. 2001, 19, 687–699. [Google Scholar] [CrossRef]
- Liao, Y.; Austin, E.; Nash, P.J.; Kingsley, S.A.; Richardson, D.J. Phase Sensitivity Characterization in Fiber-Optic Sensor Systems Using Amplifiers and TDM. J. Light. Technol. 2013, 31, 1645–1653. [Google Scholar] [CrossRef]
- Sakai, I.; Parry, G. Multiplexing Interferometric Fiber Sensors by Frequency Modulation Techniques. In Proceedings of the Optical Fiber Sensors, San Diego, CA, USA, 20–23 August 1985; p. ThBB5. [Google Scholar]
- Fang, G.; Xu, T.; Feng, S.; Li, F. Phase-Sensitive Optical Time Domain Reflectometer Based on Phase-Generated Carrier Algorithm. J. Light. Technol. 2015, 33, 2811–2816. [Google Scholar] [CrossRef]
- Cranch, G.A.; Dandridge, A.; Kirkendall, C.K. Suppression of Double Rayleigh Scattering-Induced Excess Noise in Remotely Interrogated Fiber-Optic Interferometric Sensors. IEEE Photonics Technol. Lett. 2003, 15, 1582–1584. [Google Scholar] [CrossRef]
- Chang, D.; Sun, Y.; Wang, J.; Yin, Z.; Hu, P.; Tan, J. Multiple-Beam Grating Interferometry and Its General Airy Formulae. Opt. Lasers Eng. 2023, 164, 107534. [Google Scholar] [CrossRef]
- Gao, W.; Liu, J.; Guo, H.; Jiang, X.; Sun, S.; Yu, H. Multi-Wavelength Ultra-Weak Fiber Bragg Grating Arrays for Long-Distance Quasi-Distributed Sensing. Photonic Sens. 2022, 12, 185–195. [Google Scholar] [CrossRef]
- Kocal, E.B.; Wuilpart, M.; Yüksel, K. Analysis of Crosstalk Effects in Phase-OTDR System Using Fiber Bragg Grating Array. Opt. Fiber Technol. 2023, 75, 103176. [Google Scholar] [CrossRef]
- Shang, F.; Yu, Y.; Ma, L.; Qi, Y.; Song, J. Analysis on Leading-Fiber-Induced Doppler Noise in Interferometric FBG Sensor Arrays Using Polarization Switching and PGC Hybrid Processing Method. Opt. Express 2021, 29, 16118–16134. [Google Scholar] [CrossRef] [PubMed]
- Zhu, M.; Wang, X.; Chang, J.; Zhou, H. Improved PGC Demodulation Algorithm for Fiber Optic Interferometric Sensors. Opt. Express 2024, 32, 2162–2178. [Google Scholar] [CrossRef] [PubMed]
- Marrone, M.J.; Kersey, A.D.; Villarruel, C.A.; Kirkendall, C.K.; Dandridge, A. Elimination of Coherent Rayleigh Backscatter Induced Noise in Fibre Michelson Interferometers. Electron. Lett. 1992, 28, 1803–1804. [Google Scholar] [CrossRef]
- Digonnet, M.; Blin, S.; Kim, H.K.; Dangui, V.; Kino, G. Sensitivity and Stability of an Air-Core Fibre-Optic Gyroscope. Meas. Sci. Technol. 2007, 18, 3089–3097. [Google Scholar] [CrossRef]
- Gundavarapu, S.; Belt, M.; Huffman, T.A.; Tran, M.A.; Komljenovic, T.; Bowers, J.E.; Blumenthal, D.J. Interferometric Optical Gyroscope Based on an Integrated Si3N4 Low-Loss Waveguide Coil. J. Light. Technol. 2018, 36, 1185–1191. [Google Scholar] [CrossRef]
- Wheeler, J.M.; Chamoun, J.N.; Digonnet, M.J.F. Optimizing Coherence Suppression in a Laser Broadened by Phase Modulation with Noise. J. Light. Technol. 2021, 39, 2994–3001. [Google Scholar] [CrossRef]
- Flores, A.; Robin, C.; Lanari, A.; Dajani, I. Pseudo-Random Binary Sequence Phase Modulation for Narrow Linewidth, Kilowatt, Monolithic Fiber Amplifiers. Opt. Express 2014, 22, 17735–17744. [Google Scholar] [CrossRef]
- Belthangady, C.; Chuu, C.-S.; Yu, I.A.; Yin, G.Y.; Kahn, J.M.; Harris, S.E. Hiding Single Photons with Spread Spectrum Technology. Phys. Rev. Lett. 2010, 104, 223601. [Google Scholar] [CrossRef]
- Chamoun, J.; Digonnet, M.J.F. Pseudo-Random-Bit-Sequence Phase Modulation for Reduced Errors in a Fiber Optic Gyroscope. Opt. Lett. 2016, 41, 5664–5667. [Google Scholar] [CrossRef]
- Chan, A.O.; Wong, J.; Sibley, P.G.; Bandutunga, C.P. Narrow-Band Readout and Compression of a Single Acousto-Optic Frequency Comb Using Digitally Enhanced Heterodyne Interferometry. Opt. Express 2025, 33, 11876–11886. [Google Scholar] [CrossRef]
- Shaddock, D.A. Digitally Enhanced Heterodyne Interferometry. Opt. Lett. 2007, 32, 3355–3357. [Google Scholar] [CrossRef]
- Bandutunga, C.P.; Zhang, Y.; McRae, T.G.; Gray, M.B.; Chow, J.H. Coherent Rayleigh Backscatter Phase Noise in Digitally Enhanced Fiber Interferometers. J. Light. Technol. 2021, 39, 2625–2630. [Google Scholar] [CrossRef]
- Lahiri, A. Basic Optics: Principles and Concepts; Elsevier: Amsterdam, The Netherlands, 2016; ISBN 978-0-12-805357-7. [Google Scholar]
- Hu, Q.; Wang, W.; Ma, L.; Zhu, X. Efficient Inhibition of Rayleigh Scattering in Interferometric Sensor through Random Phase Noise. In Proceedings of SPIE, Proceedings of the 29th International Conference on Optical Fiber Sensors, Porto, Portugal, 25–30 May 2025; Lopez-Amo Sainz, M., Santos, J.L., Sun, T., Eds.; SPIE: Bellingham, WA, USA; p. 446.



| C | fPGC | fAOM | Lc | ||
|---|---|---|---|---|---|
| 2.2 kHz | 2.37 | 15.625 kHz | 250 kHz | 1.2, 0.6, 0.3 m | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Hu, Q.; Ma, L.; Shang, F.; Leng, H.; Song, J. Optimal Coherence Length Control in Interferometric Fiber Optic Hydrophones via PRBS Modulation: Theory and Experiment. Sensors 2025, 25, 4711. https://doi.org/10.3390/s25154711
Wang W, Hu Q, Ma L, Shang F, Leng H, Song J. Optimal Coherence Length Control in Interferometric Fiber Optic Hydrophones via PRBS Modulation: Theory and Experiment. Sensors. 2025; 25(15):4711. https://doi.org/10.3390/s25154711
Chicago/Turabian StyleWang, Wujie, Qihao Hu, Lina Ma, Fan Shang, Hongze Leng, and Junqiang Song. 2025. "Optimal Coherence Length Control in Interferometric Fiber Optic Hydrophones via PRBS Modulation: Theory and Experiment" Sensors 25, no. 15: 4711. https://doi.org/10.3390/s25154711
APA StyleWang, W., Hu, Q., Ma, L., Shang, F., Leng, H., & Song, J. (2025). Optimal Coherence Length Control in Interferometric Fiber Optic Hydrophones via PRBS Modulation: Theory and Experiment. Sensors, 25(15), 4711. https://doi.org/10.3390/s25154711






