Application of Array Imaging Algorithms for Water Holdup Measurement in Gas–Water Two-Phase Flow Within Horizontal Wells
Abstract
1. Introduction
2. Methodology
2.1. Experimental Summary
2.2. CAT Instrument Description and Measurement Principle
2.3. Analysis of CAT Response Characteristics
3. Water Holdup Calculation Methods
3.1. Experimental Data Analysis
3.2. Water Holdup Calculation Methods
4. Imaging Algorithms of Gas–Water Two-Phase Flow
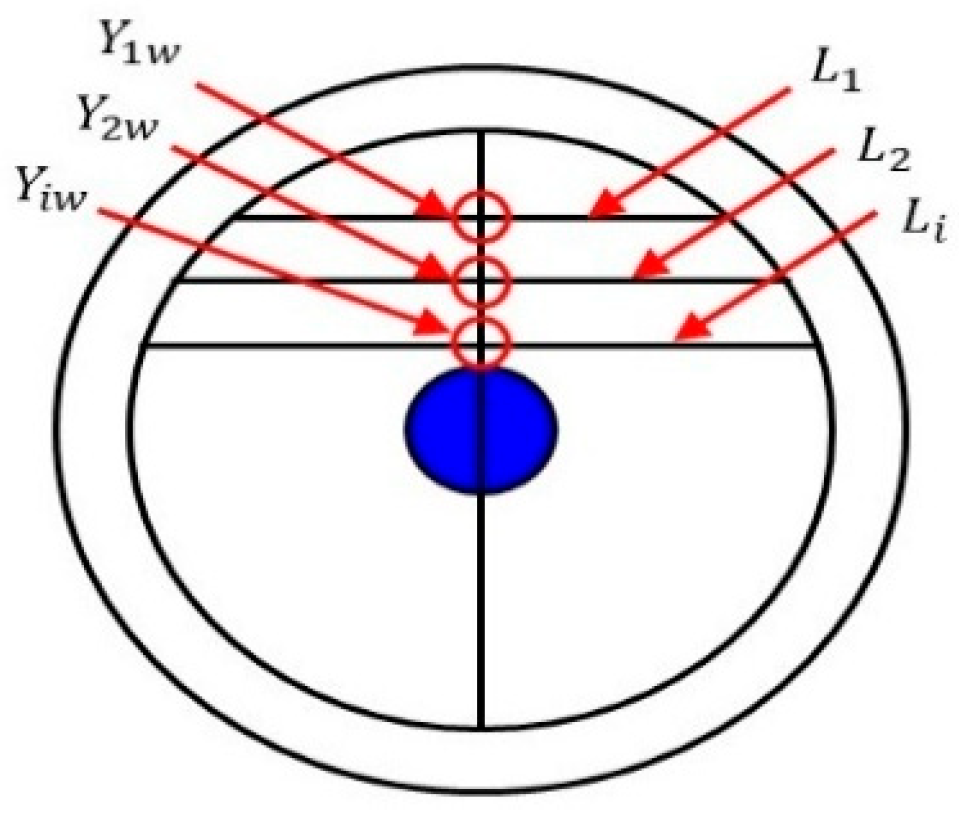
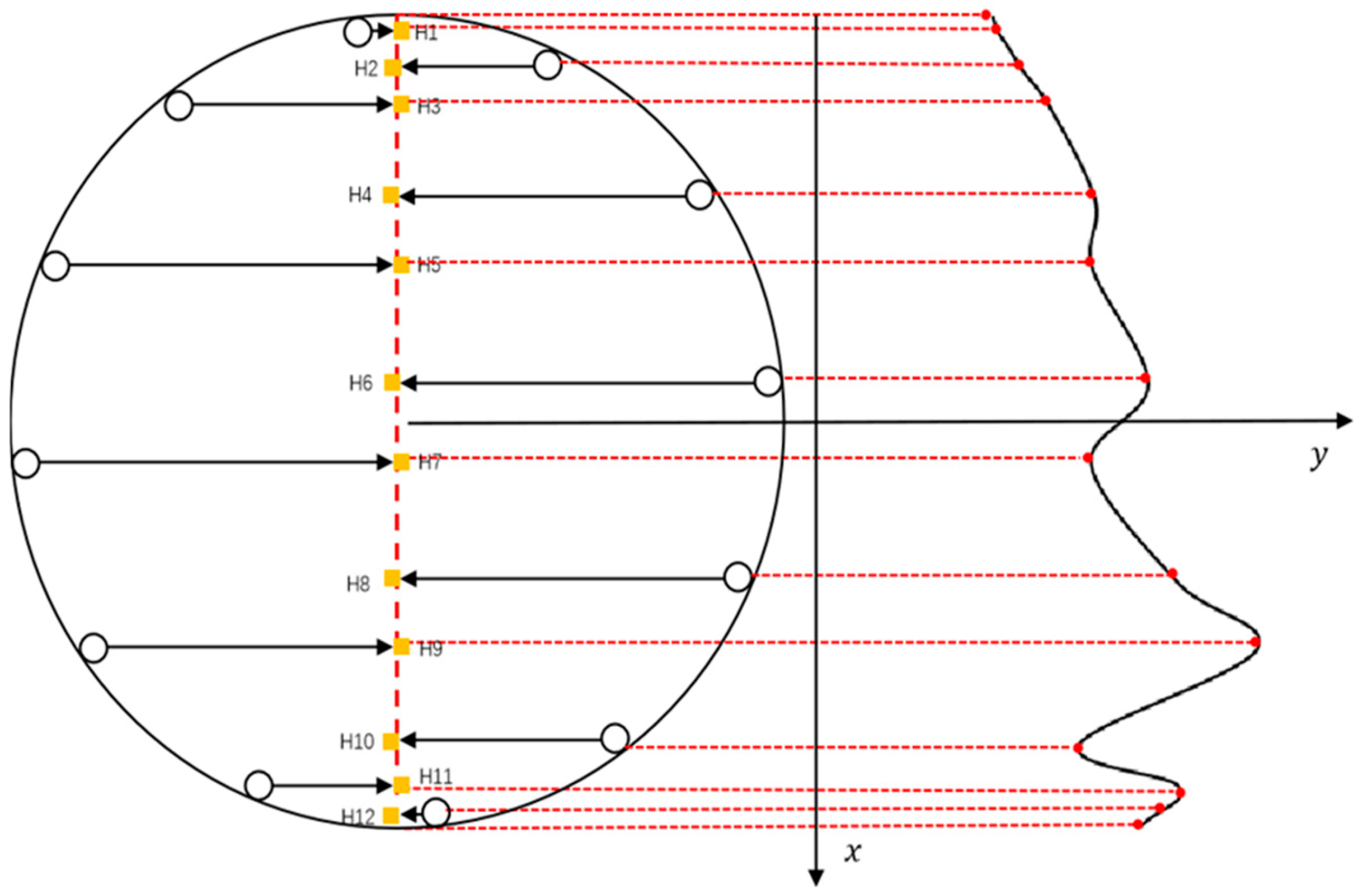
4.1. Data Preprocessing of CAT Measurement
4.2. Simple Linear Interpolation (SLI)
4.3. Inverse Distance Weighted (IDW) Interpolation
4.4. Lagrangian Nonlinear Interpolation (LNI)
5. Results and Discussion
6. Conclusions
- (1)
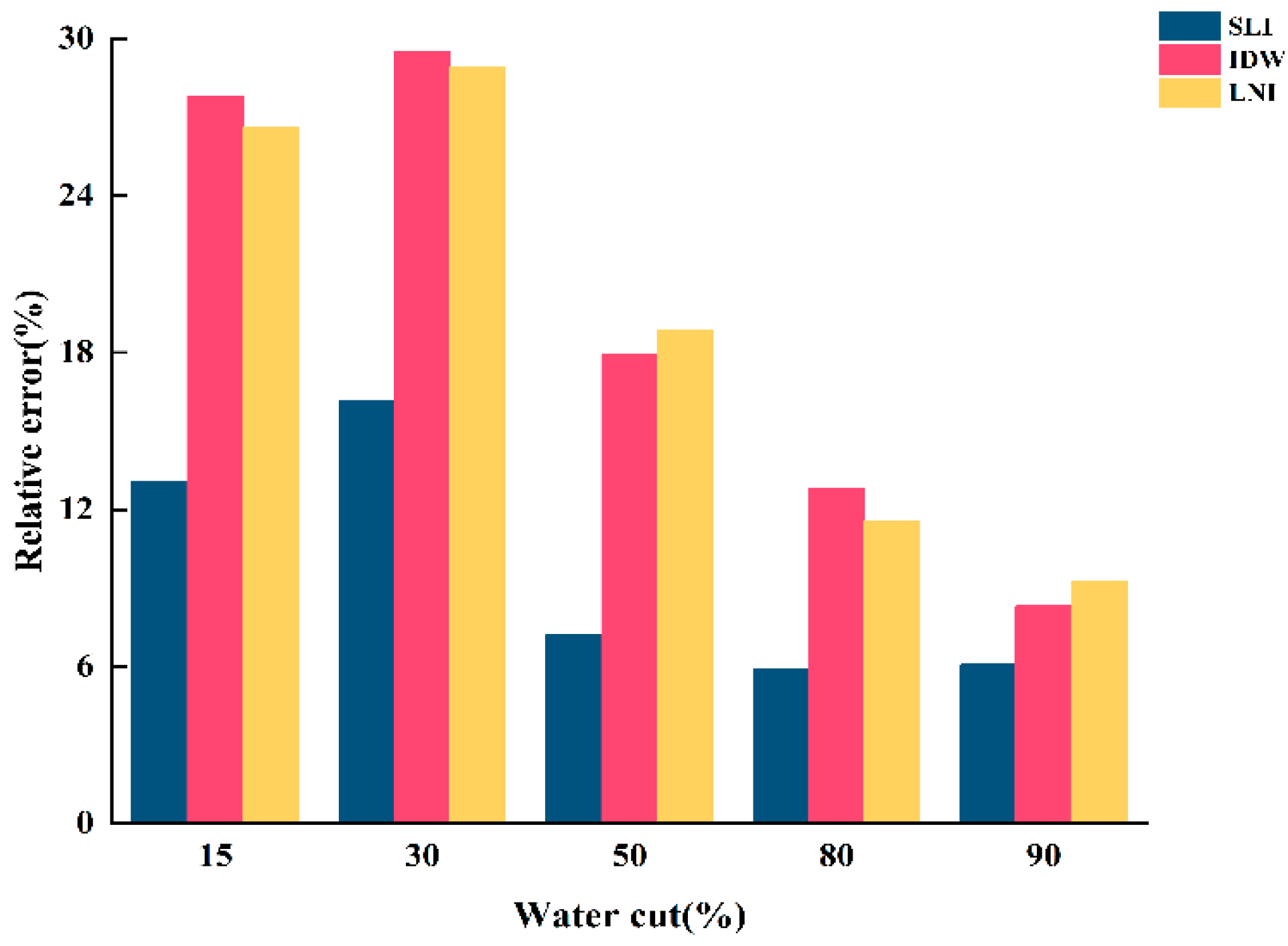
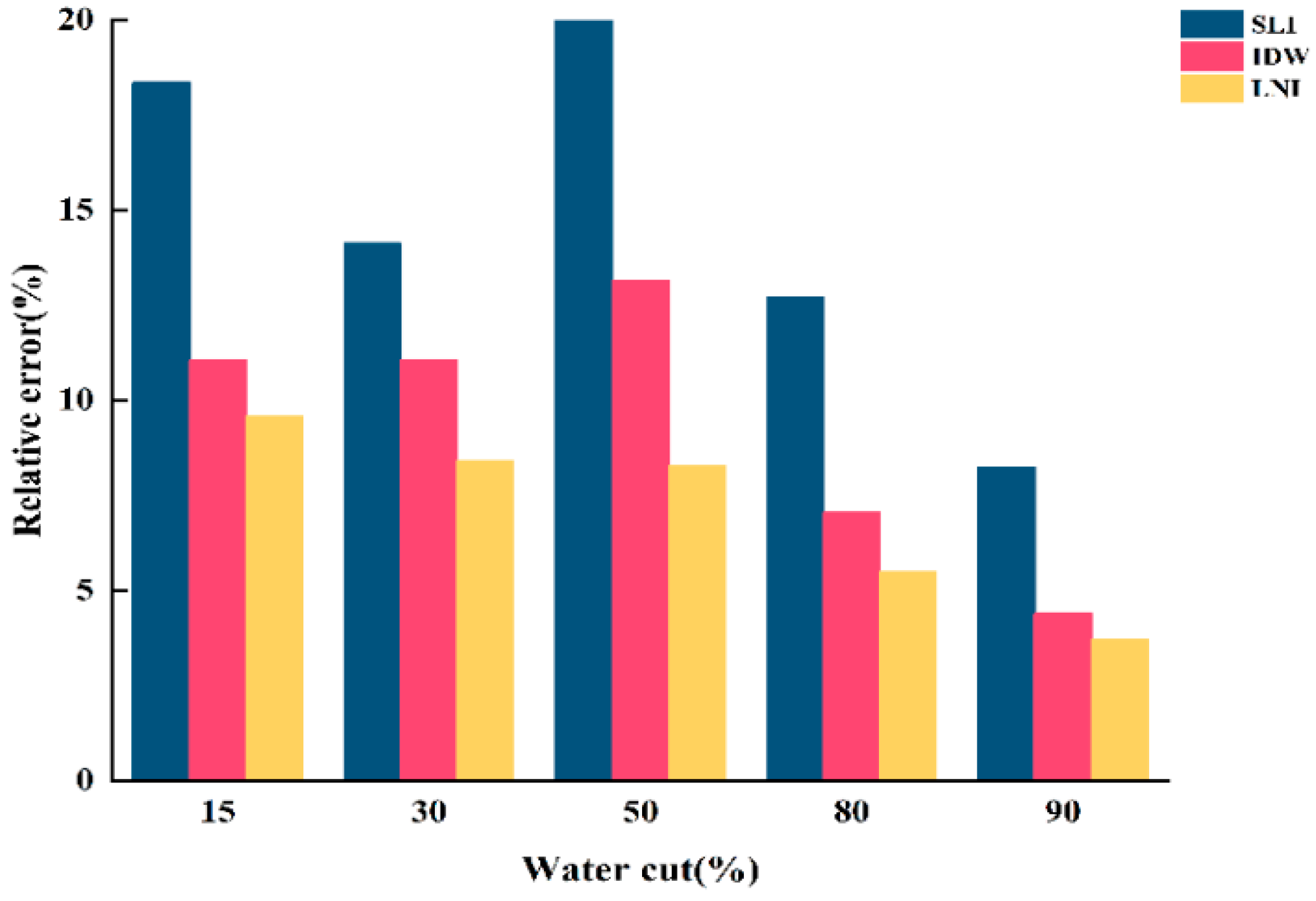
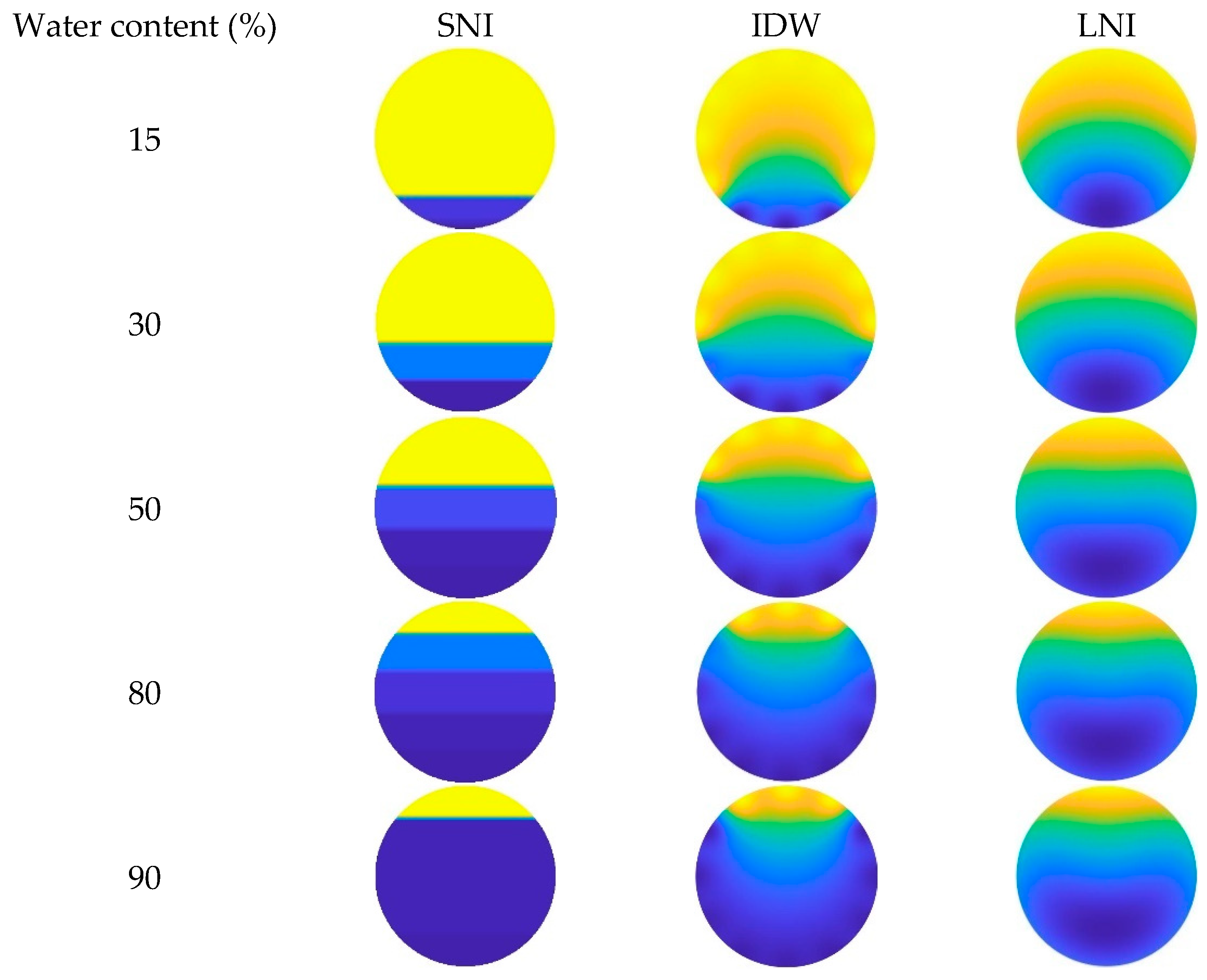
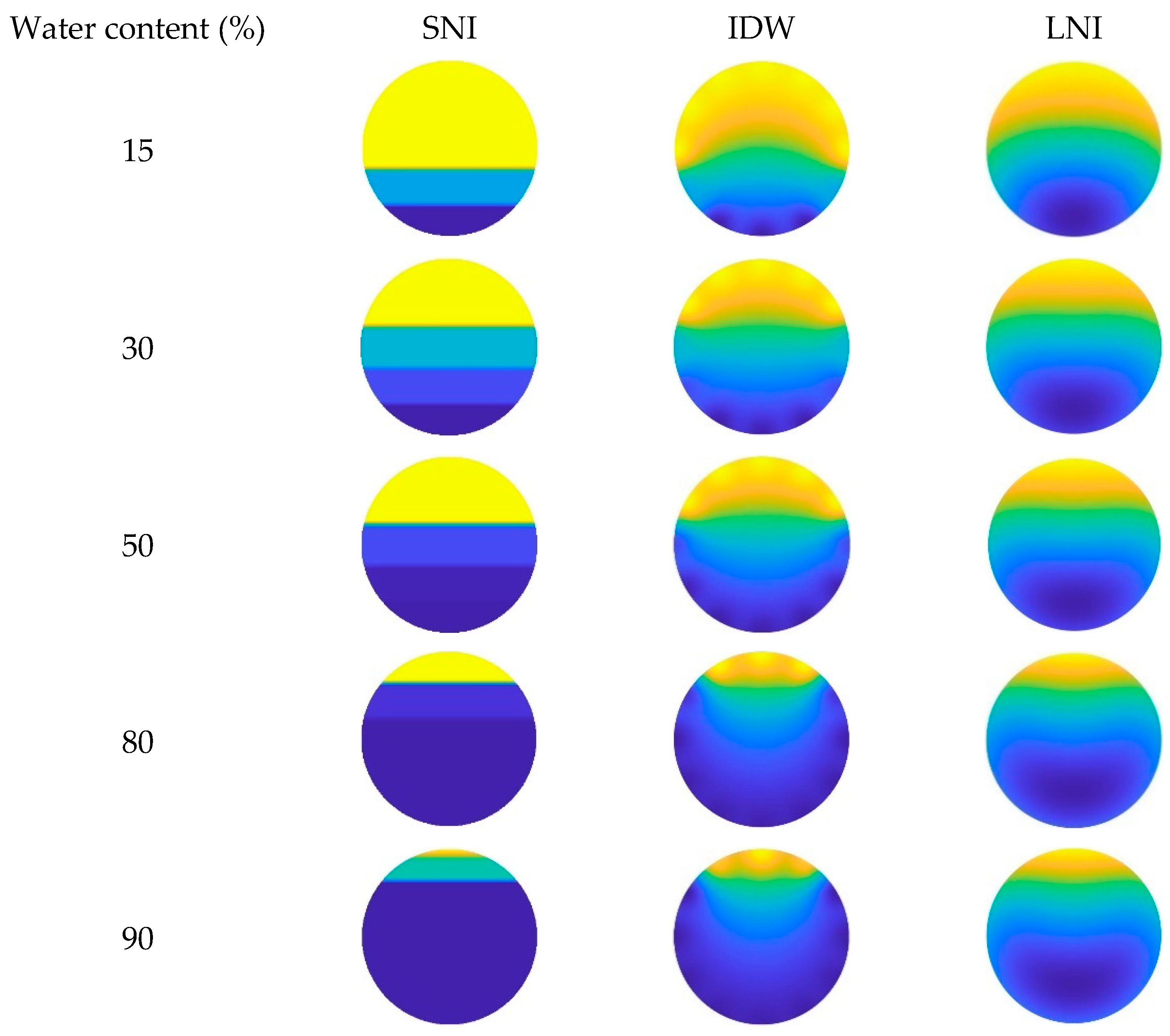
- When the total flow is 300 m3/d, the fluid in the simulated wellbore exhibits stratified flow regardless of changes in water content, with a clearly visible interface between the gas and water phases. Among the three interpolation algorithms, the simple linear interpolation (SLI) algorithm produced the best imaging results, demonstrating the highest consistency with the actual experimental observations. It also yielded the lowest relative error in water holdup calculation under this flow condition, indicating that SLI is best suited for low-flow, stratified scenarios due to its ability to accurately capture the gas–water interface.
- (2)
- When the total flow is 500 m3/d, the flow pattern remains stratified under low- and medium-water-content conditions, where SLI still performs better than the other two methods in terms of both image fidelity and holdup accuracy. However, as the water content increases, the flow pattern gradually transitions into dispersed flow. Under these conditions, the Lagrange nonlinear interpolation (LNI) algorithm shows superior performance, closely matching the observed distribution of the gas and water phases. In terms of water holdup calculation, LNI achieves higher accuracy under high-water-content conditions, while the inverse distance weighted (IDW) algorithm also performs well, though slightly less accurately than LNI. Both LNI and IDW offer practical advantages in capturing the gradual and nonlinear transitions of the flow structure.
- (3)
- When the total flow is 700 m3/d, the influence of water content on the flow pattern becomes more pronounced. At low water content, the flow remains stratified, and SLI continues to provide satisfactory imaging and holdup estimation. However, with increasing water content, the flow becomes highly dispersed, and both LNI and IDW outperform SLI in reconstructing the complex fluid distribution. Particularly, LNI yields the lowest relative error in water holdup and provides the most accurate visualization of the internal gas–water distribution under these high-flow, high-complexity conditions.
- (4)
- With the continuous advancement of technology, particularly the development of artificial intelligence, neural network interpolation algorithms have gained increasing attention and practical application in solving interpolation problems. With strong generalization and self-learning capabilities, neural networks can automatically extract patterns from complex, nonlinear datasets, making them well-suited for modeling and predicting fluid distributions in wellbore cross-sections. Future research will focus on incorporating neural networks to enhance the fusion and optimization of multiple interpolation results, and on developing intelligent interpolation models with adaptive strategy selection capabilities. Such models will be able to dynamically adjust interpolation strategies based on sensor response characteristics and wellbore flow conditions, thereby improving the accuracy and robustness of imaging results under varying flow regimes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kochbeck, B.; Lindert, M.; Hempel, D.C. Determination of local phase holdups in airlift reactors by means of time-domain-reflectometry. Chem. Eng. Technol. Ind. Chem. Plant Equip. Process Eng. Biotechnol. 1997, 20, 533–537. [Google Scholar] [CrossRef]
- Bruvik, E.M.; Hjertaker, B.T.; Folgerø, K.; Meyer, S.K. Monitoring oil–water mixture separation by time domain reflectometry. Meas. Sci. Technol. 2012, 23, 125303. [Google Scholar] [CrossRef]
- Dziallas, H.; Michele, V.; Hempel, D.C. Measurement and modelling of local phase holdup and flow structure in three-phase bubble columns. In International Symposium on Multiphase Flow and Transport Phenomena; Begel House Inc.: Danbury, CT, USA, 1997. [Google Scholar]
- Yang, W.Q.; York, T.A. New AC-based capacitance tomography system. IEE Proc. Sci. Meas. Technol. 1999, 146, 47–53. [Google Scholar] [CrossRef]
- Vadlakonda, B.; Mangadoddy, N. Hydrodynamic study of two phase flow of column flotation using electrical resistance tomography and pressure probe techniques. Sep. Purif. Technol. 2017, 184, 168–187. [Google Scholar] [CrossRef]
- Meng, Z.; Huang, Z.; Wang, B.; Ji, H.; Li, H.; Yan, Y. Air–water two-phase flow measurement using a Venturi meter and an electrical resistance tomography sensor. Flow Meas. Instrum. 2010, 21, 268–276. [Google Scholar] [CrossRef]
- Razzak, S.A.; Barghi, S.; Zhu, J.X. Electrical resistance tomography for flow characterization of a gas–liquid–solid three-phase circulating fluidized bed. Chem. Eng. Sci. 2007, 62, 7253–7263. [Google Scholar] [CrossRef]
- Wang, H.; Wang, C.; Yin, W. A pre-iteration method for the inverse problem in electrical impedance tomography. IEEE Trans. Instrum. Meas. 2004, 53, 1093–1096. [Google Scholar] [CrossRef]
- Dong, F.; Jiang, Z.X.; Qiao, X.T.; Xu, L.A. Application of electrical resistance tomography to two-phase pipe flow parameters measurement. Flow Meas. Instrum. 2003, 14, 183–192. [Google Scholar] [CrossRef]
- Basavaraj, M.G.; Gupta, G.S.; Naveen, K.; Rudolph, V.; Bali, R. Local liquid holdups and hysteresis in a 2-D packed bed using X-ray radiography. AIChE J. 2005, 51, 2178–2189. [Google Scholar] [CrossRef]
- Zhai, L.S.; Jin, N.D.; Gao, Z.K.; Wang, Z.Y.; Li, D.M. The ultrasonic measurement of high water volume fraction in dispersed oil-in-water flows. Chem. Eng. Sci. 2013, 94, 271–283. [Google Scholar] [CrossRef]
- Zhao, A.; Han, Y.F.; Ren, Y.Y.; Zhai, L.S.; In, N.D. Ultrasonic method for measuring water holdup of low velocity and high-water-cut oil-water two-phase flow. Appl. Geophys. 2016, 13, 179–193. [Google Scholar] [CrossRef]
- Su, Q.; Tan, C.; Dong, F. Measurement of oil–water two-phase flow phase fraction with ultrasound attenuation. IEEE Sens. J. 2017, 18, 1150–1159. [Google Scholar] [CrossRef]
- Su, Q.; Tan, C.; Dong, F. Mechanism modeling for phase fraction measurement with ultrasound attenuation in oil–water two-phase flow. Meas. Sci. Technol. 2017, 28, 035304. [Google Scholar] [CrossRef]
- Chakrabarti, D.P.; Das, G.; Das, P.K. Identification of stratified liquid–liquid flow through horizontal pipes by a non-intrusive optical probe. Chem. Eng. Sci. 2007, 62, 1861–1876. [Google Scholar] [CrossRef]
- Jana, A.K.; Mandal, T.K.; Chakrabarti, D.P.; Das, G.; Das, P.K. An optical probe for liquid–liquid two-phase flows. Meas. Sci. Technol. 2007, 18, 1563. [Google Scholar] [CrossRef]
- Shang, L.; Shi, J.; Wang, Y. Measuring the concentration of mineral oil in water by optical fiber fluorescence method. In Advanced Sensor Systems and Applications; SPIE: Bellingham, WA, USA, 2002; Volume 4920, pp. 566–571. [Google Scholar]
- Suehara, K.I.; Tsunematsu, T.; Tasaka, T.; Kohda, J.; Nakano, Y.; Fujii, E.; Yano, T. Development of an air–oil and oil–water interface detector using plastic optical fiber and its application for measurement of oil layer thickness of industrial kitchen wastewater in a grease trap. J. Chem. Eng. Jpn. 2006, 39, 670–677. [Google Scholar] [CrossRef]
- Meng, D.; Xuan, H.; Zhang, M.; Lai, S.; Liao, Y. Performance analysis of an in-line optical fiber analysis system for well crude oil. In Fundamental Problems of Optoelectronics and Microelectronics III; SPIE: Bellingham, WA, USA, 2007; Volume 6595, pp. 907–915. [Google Scholar]
- Wang, D.; Jin, N.; Zhai, L.; Ren, Y. Measurement of gas holdup in oil-gas-water flows using combined conductance sensors. IEEE Sens. J. 2021, 21, 12171–12178. [Google Scholar] [CrossRef]
- Shi, H.; Song, H.; Guo, H.; Ma, H. Comparative study on data processing methods of oil-water two-phase array water holdup instrument in low-yield horizontal wells. China Sci. 2021, 16, 12–20. [Google Scholar]
- Li, J.; Ma, H.; Li, H.; Zhao, J.; Song, W.; Guo, H. Calculation method of water holdup in horizontal wells of offshore oilfields based on array capacitance. Well Logging Technol. 2023, 47, 55–62. [Google Scholar]
- Song, H.; Guo, H. Analysis on imaging interpolation algorithm for logging data of water holdup array tool in horizontal wells. J. Oil Gas Technol. 2016, 1, 24–32. [Google Scholar] [CrossRef]
- Niu, Y. Numerical Simulation and Experimental Study of Gas-Water Two-Phase Flow Pattern in Horizontal Wells. Master’s Thesis, Yangtze University, Jingzhou, China, 2022. [Google Scholar]

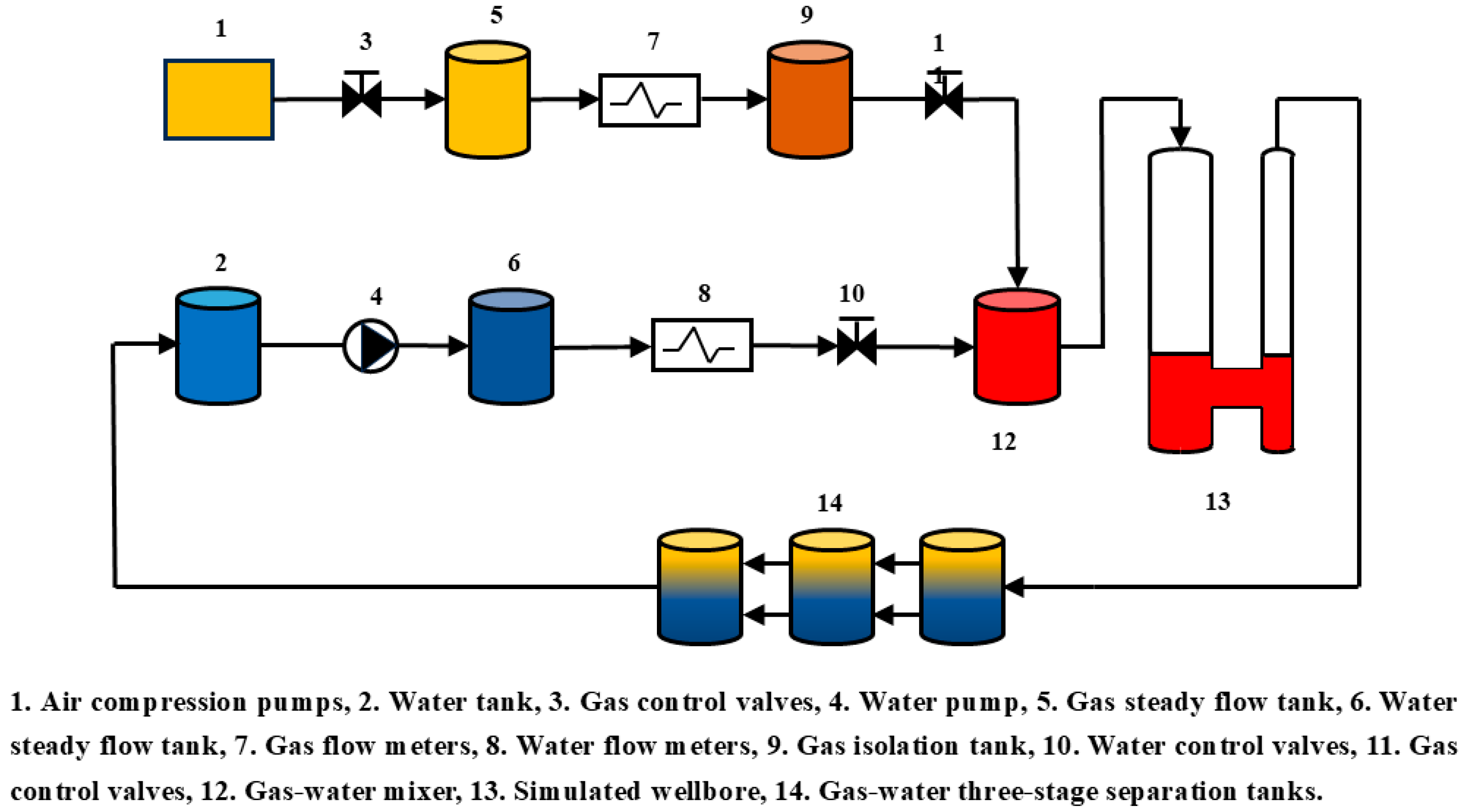
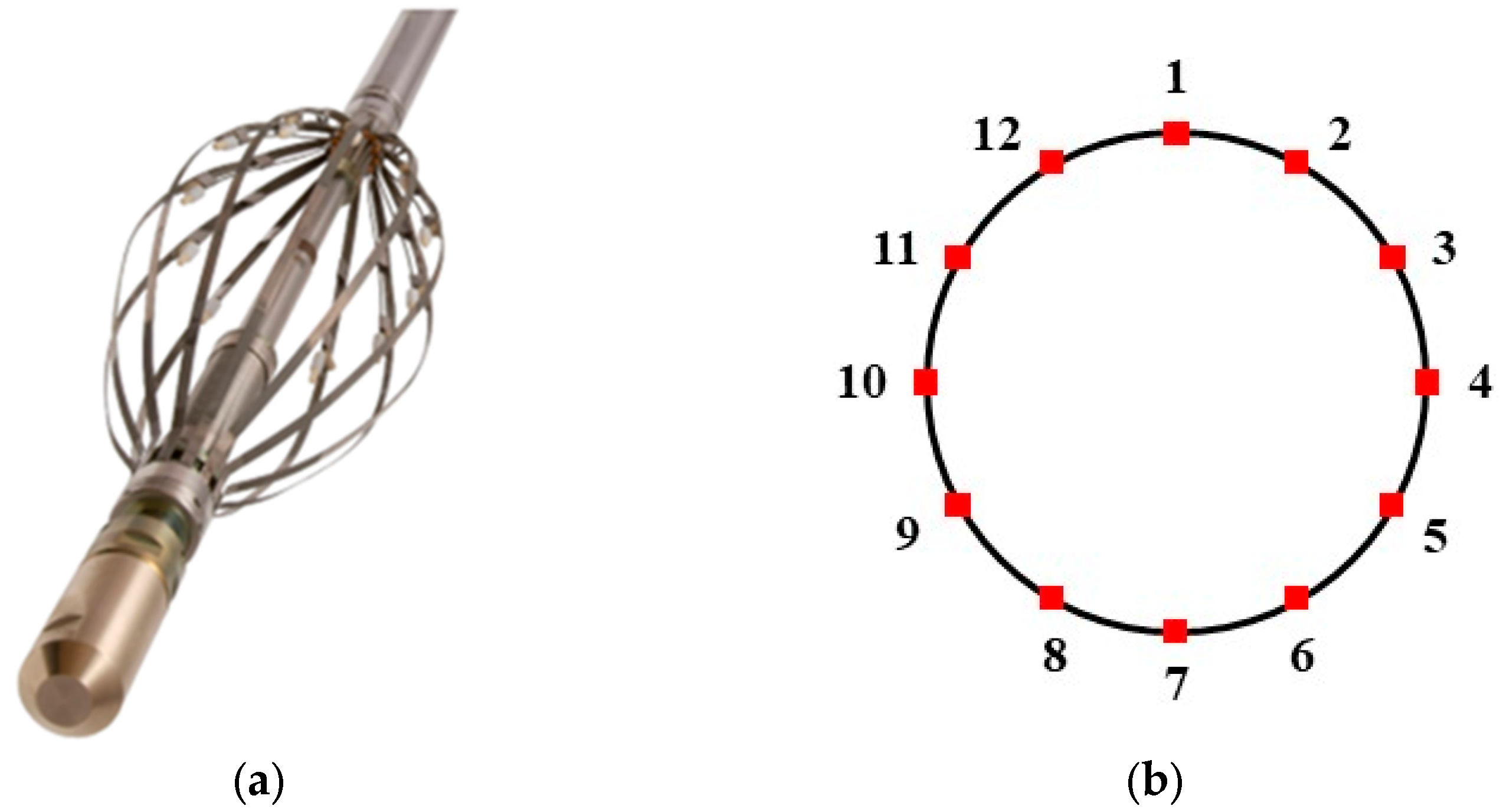
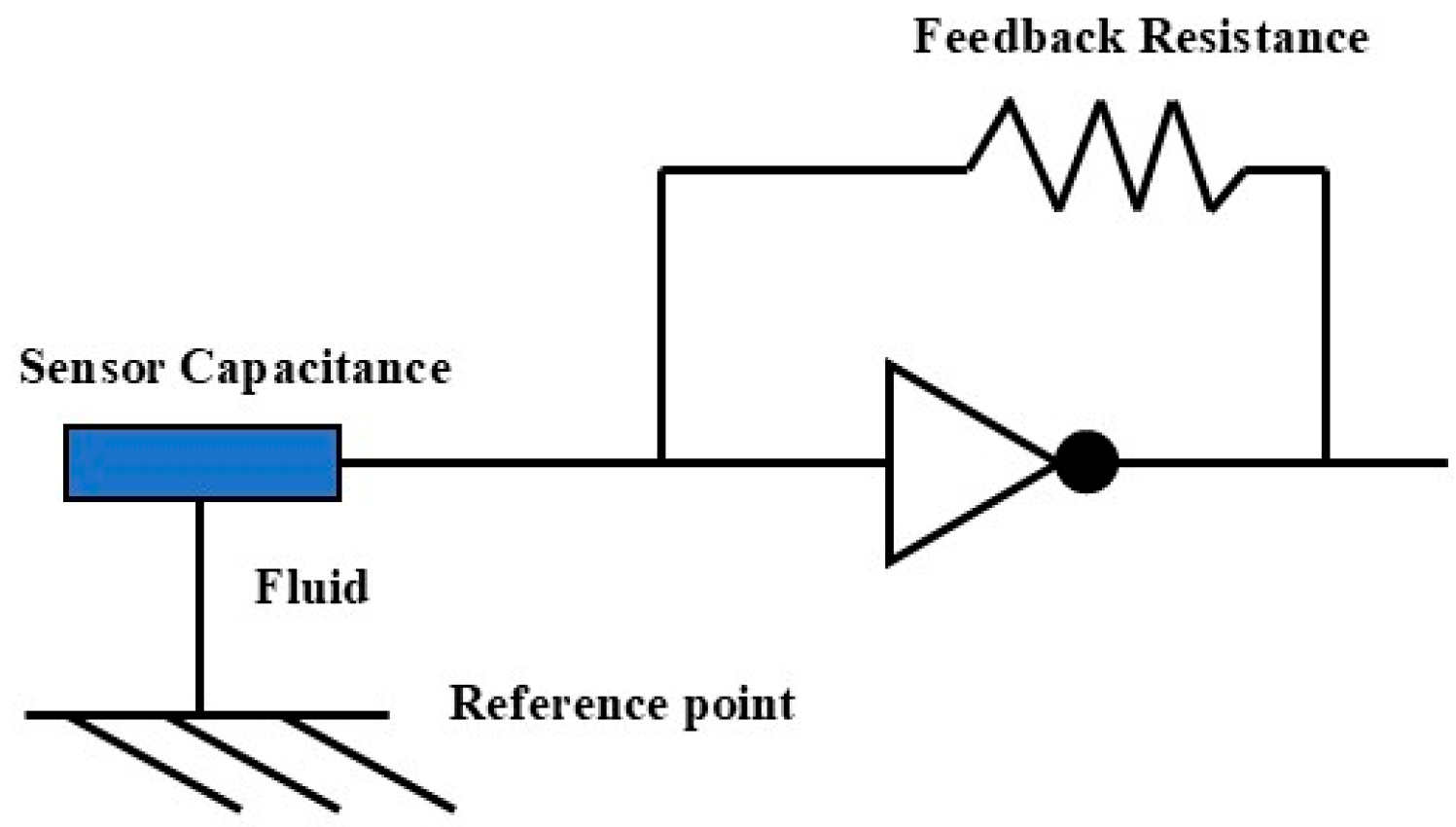


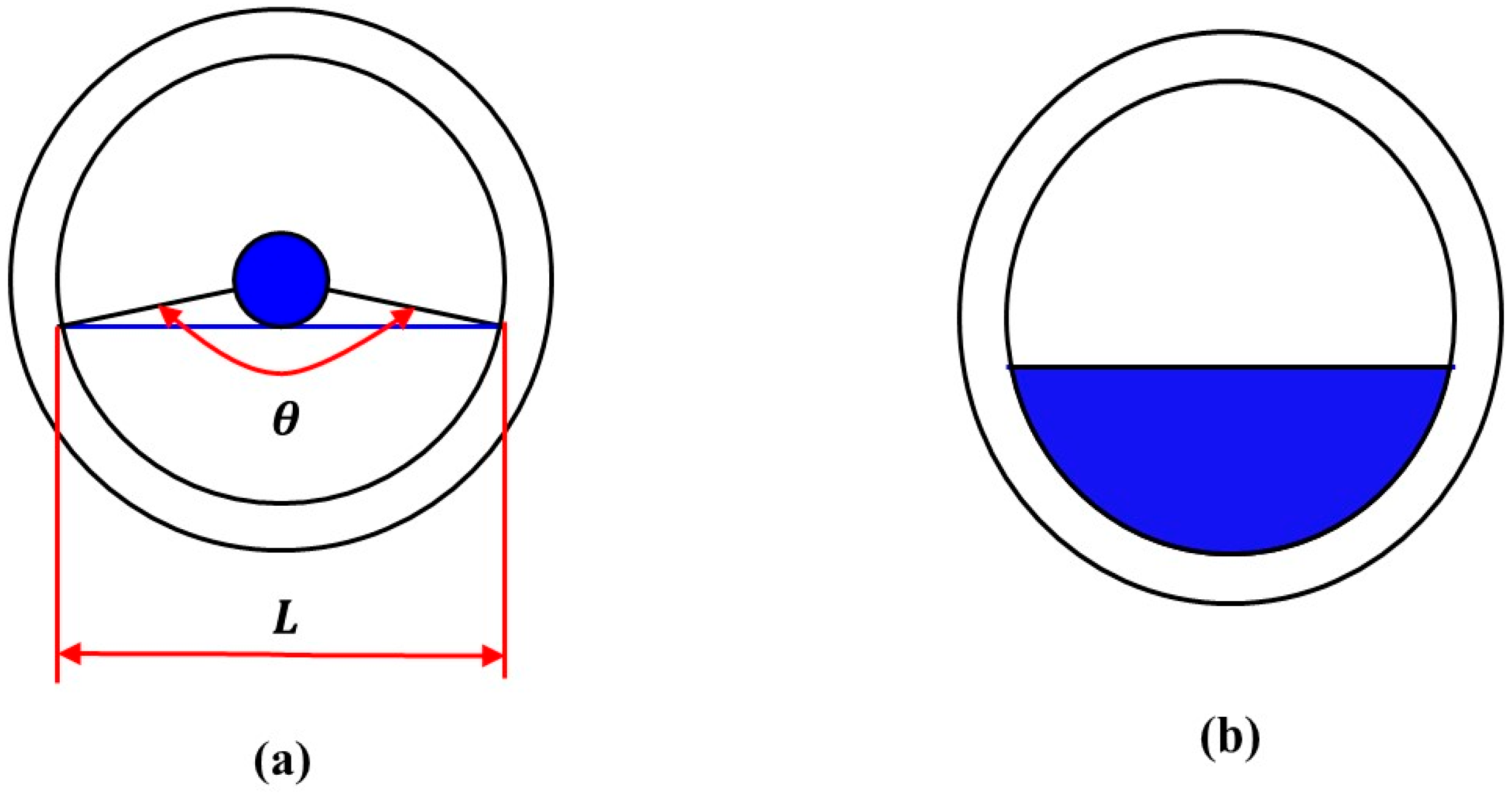

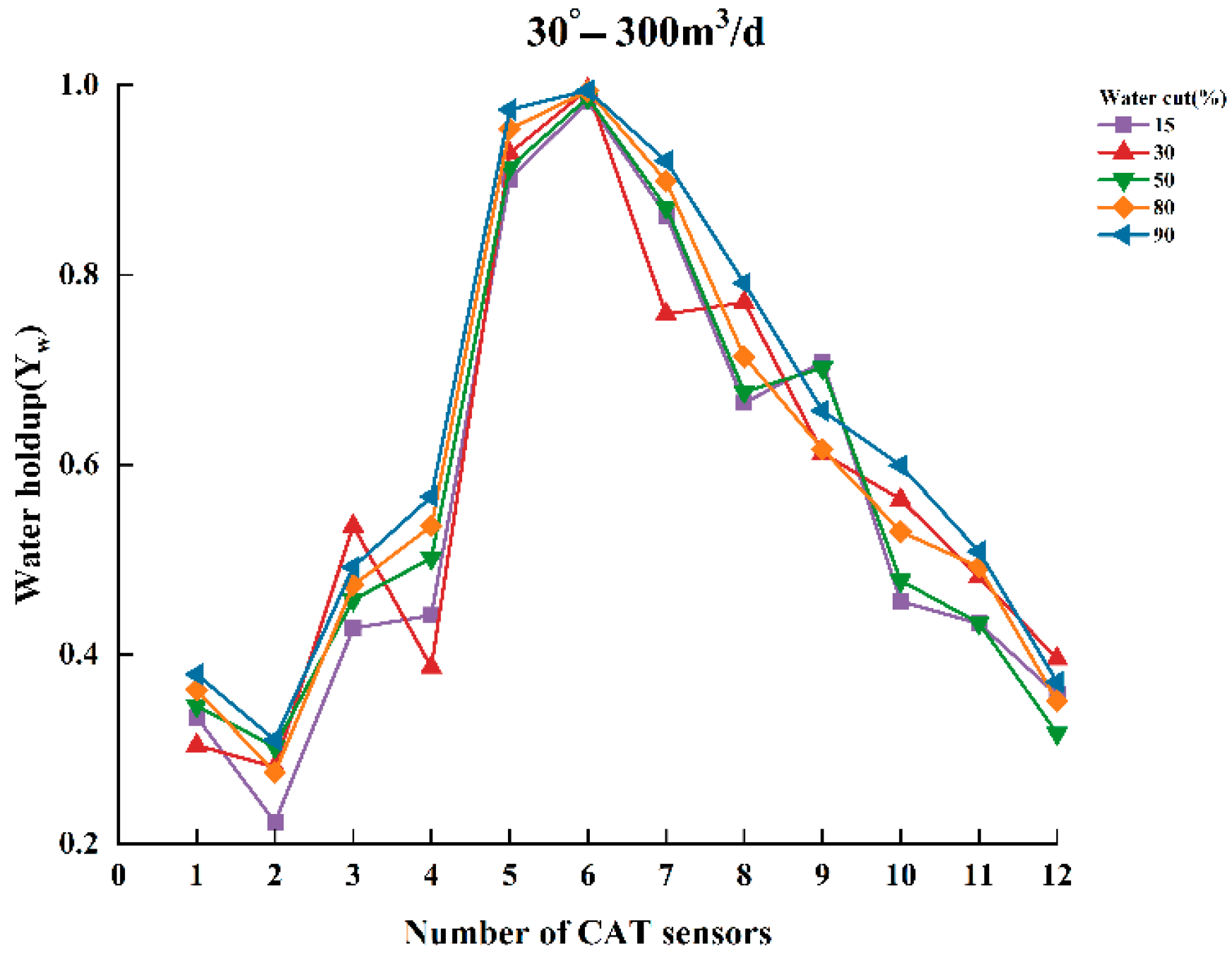
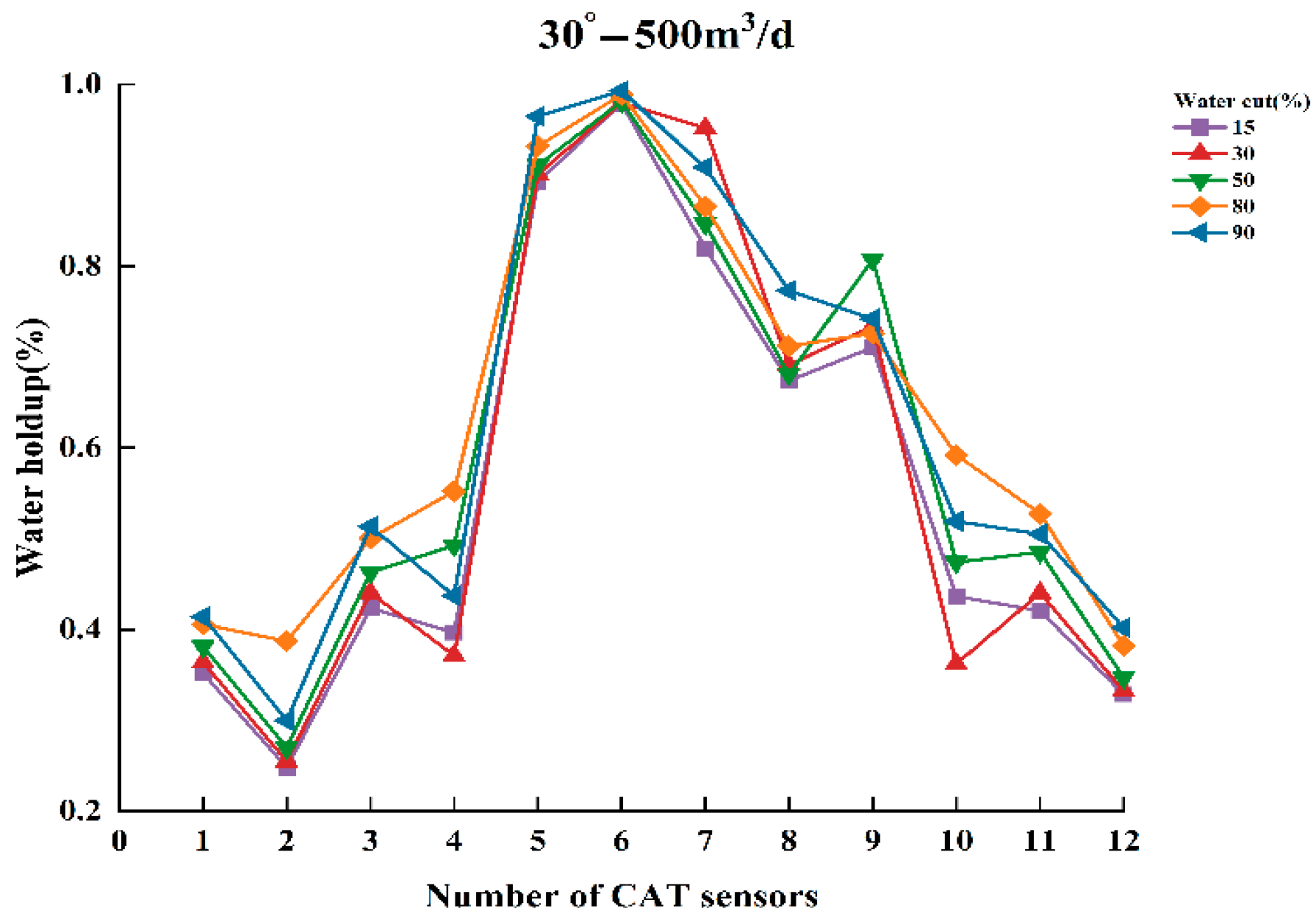
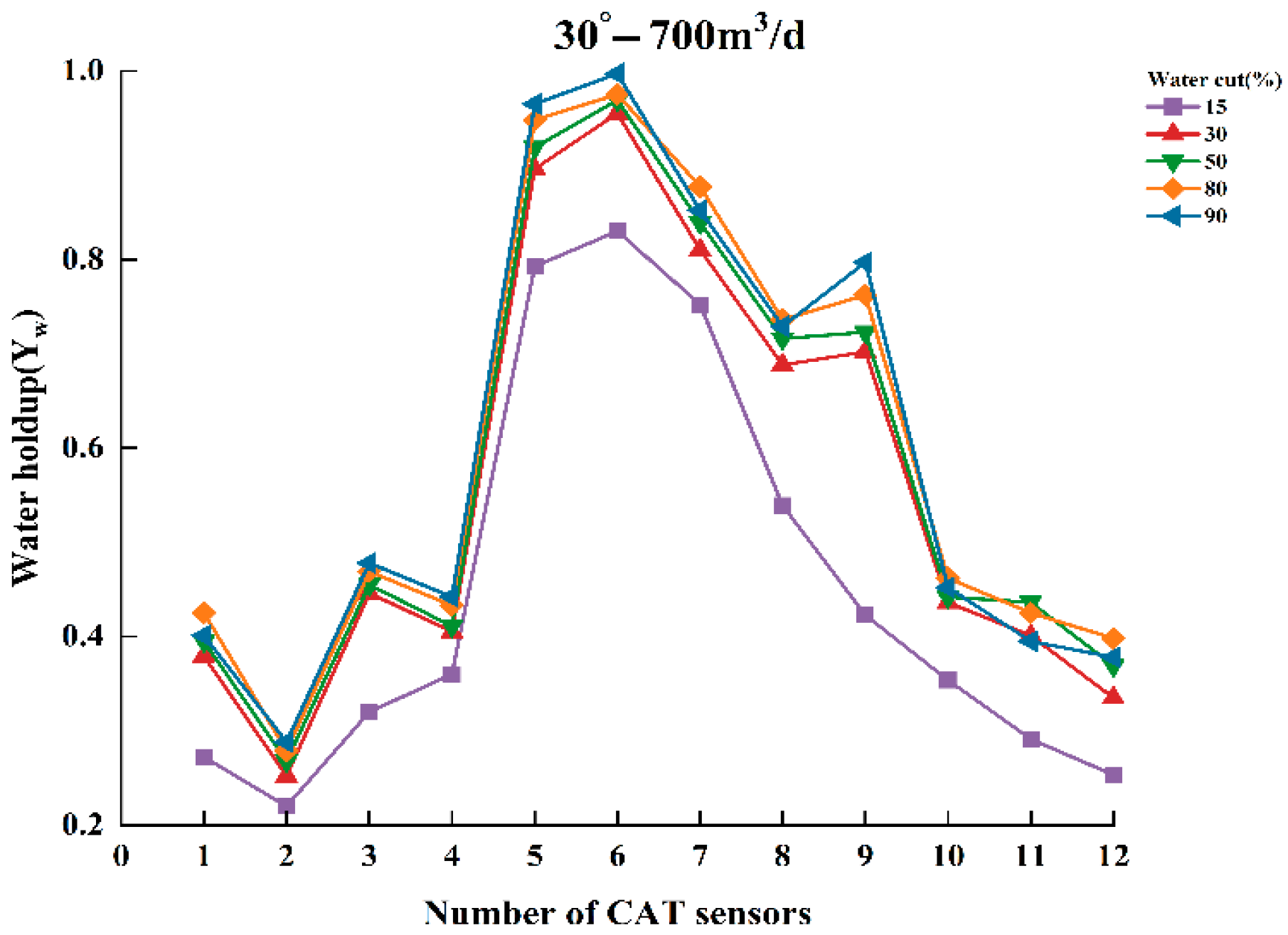

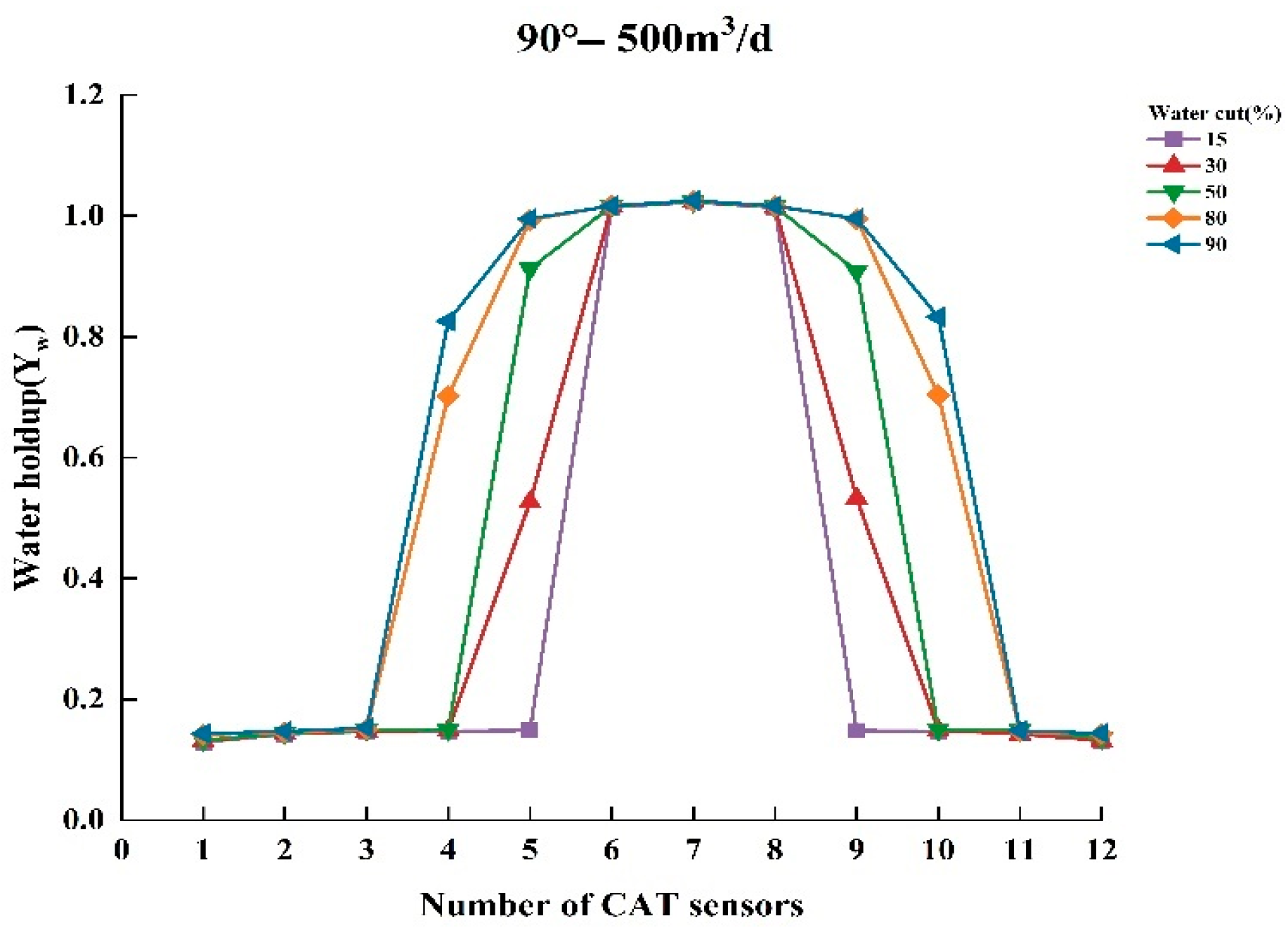









| Well Deviation () | Total Flowrate () | Water Content (%) |
|---|---|---|
| 30, 90 | 300, 500, 700 | 15, 30, 50, 80, 90 |
| Water Content (%) | 15 | 30 | 50 | 80 | 90 |
|---|---|---|---|---|---|
| 1 | 0.1226 | 0.1249 | 0.1311 | 0.1409 | 0.1418 |
| 2 | 0.1389 | 0.1352 | 0.1405 | 0.1421 | 0.1433 |
| 3 | 0.1436 | 0.1345 | 0.1455 | 0.1462 | 0.1481 |
| 4 | 0.1455 | 0.1459 | 0.1465 | 0.6488 | 0.7521 |
| 5 | 0.144 | 0.4445 | 0.8139 | 0.9895 | 0.9956 |
| 6 | 1.0134 | 1.0155 | 1.0159 | 1.0166 | 1.0171 |
| 7 | 1.0227 | 1.0235 | 1.0238 | 1.0241 | 1.0245 |
| 8 | 1.0168 | 1.0142 | 1.0141 | 1.0145 | 1.0144 |
| 9 | 0.1449 | 0.4563 | 0.8146 | 0.9926 | 0.9963 |
| 10 | 0.1411 | 0.1452 | 0.1458 | 0.6518 | 0.7439 |
| 11 | 0.135 | 0.1378 | 0.1382 | 0.1383 | 0.1491 |
| 12 | 0.1233 | 0.1252 | 0.1305 | 0.1315 | 0.1411 |
| Water Content (%) | 15 | 30 | 50 | 80 | 90 |
|---|---|---|---|---|---|
| 1 | 0.1309 | 0.1522 | 0.1636 | 0.201 | 0.2539 |
| 2 | 0.1435 | 0.1551 | 0.1672 | 0.2066 | 0.2577 |
| 3 | 0.1472 | 0.1586 | 0.1691 | 0.2085 | 0.662 |
| 4 | 0.1491 | 0.1599 | 0.1705 | 0.8536 | 0.9515 |
| 5 | 0.1499 | 0.6353 | 0.9511 | 0.996 | 0.9962 |
| 6 | 1.0145 | 0.6353 | 1.0165 | 1.0171 | 1.017 |
| 7 | 1.0236 | 1.016 | 1.0235 | 1.024 | 1.0242 |
| 8 | 1.0143 | 1.0229 | 1.016 | 1.0168 | 1.0166 |
| 9 | 0.1488 | 0.6412 | 0.9489 | 0.9963 | 0.9969 |
| 10 | 0.1482 | 0.1593 | 0.1715 | 0.8622 | 0.9513 |
| 11 | 0.1477 | 0.1579 | 0.1699 | 0.209 | 0.689 |
| 12 | 0.1338 | 0.154 | 0.1651 | 0.2051 | 0.2526 |
| Water Content (%) | 15 | 30 | 50 | 80 | 90 |
|---|---|---|---|---|---|
| 1 | 0.1292 | 0.1311 | 0.1325 | 0.1421 | 0.1433 |
| 2 | 0.1423 | 0.1428 | 0.1439 | 0.1455 | 0.1469 |
| 3 | 0.1466 | 0.1475 | 0.1491 | 0.1512 | 0.1525 |
| 4 | 0.1472 | 0.1487 | 0.1495 | 0.7027 | 0.8261 |
| 5 | 0.1485 | 0.5266 | 0.9127 | 0.9936 | 0.9957 |
| 6 | 1.0141 | 1.0158 | 1.0162 | 1.0169 | 1.0168 |
| 7 | 1.0233 | 1.0233 | 1.0235 | 1.025 | 1.0253 |
| 8 | 1.0146 | 1.0151 | 1.0151 | 1.0163 | 1.0166 |
| 9 | 0.1479 | 0.5327 | 0.5327 | 0.9954 | 0.9955 |
| 10 | 0.1475 | 0.1489 | 0.1489 | 0.7039 | 0.8329 |
| 11 | 0.1470 | 0.1424 | 0.1424 | 0.1461 | 0.1477 |
| 12 | 0.1301 | 0.1316 | 0.1356 | 0.1426 | 0.1439 |
| Water Content (%) | Integral | SLI | IDW | LNI |
|---|---|---|---|---|
| 15 | 0.2813 | 0.3226 | 0.3327 | 0.3351 |
| 30 | 0.3689 | 0.4131 | 0.4262 | 0.4159 |
| 50 | 0.5914 | 0.6624 | 0.6321 | 0.6215 |
| 80 | 0.8135 | 0.8567 | 0.8469 | 0.841 |
| 90 | 0.9016 | 0.9695 | 0.9482 | 0.9433 |
| Water Content (%) | Integral | SLI | IDW | LNI |
|---|---|---|---|---|
| 15 | 0.2931 | 0.3469 | 0.3255 | 0.3212 |
| 30 | 0.3427 | 0.3911 | 0.3806 | 0.3715 |
| 50 | 0.5576 | 0.6927 | 0.631 | 0.6037 |
| 80 | 0.8243 | 0.9292 | 0.8823 | 0.8696 |
| 90 | 0.9141 | 0.9895 | 0.9542 | 0.9481 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, H.; Li, A.; Sun, Y.; Yu, L.; Peng, W.; Ouyang, M.; Wang, D.; Guo, Y. Application of Array Imaging Algorithms for Water Holdup Measurement in Gas–Water Two-Phase Flow Within Horizontal Wells. Sensors 2025, 25, 4557. https://doi.org/10.3390/s25154557
Guo H, Li A, Sun Y, Yu L, Peng W, Ouyang M, Wang D, Guo Y. Application of Array Imaging Algorithms for Water Holdup Measurement in Gas–Water Two-Phase Flow Within Horizontal Wells. Sensors. 2025; 25(15):4557. https://doi.org/10.3390/s25154557
Chicago/Turabian StyleGuo, Haimin, Ao Li, Yongtuo Sun, Liangliang Yu, Wenfeng Peng, Mingyu Ouyang, Dudu Wang, and Yuqing Guo. 2025. "Application of Array Imaging Algorithms for Water Holdup Measurement in Gas–Water Two-Phase Flow Within Horizontal Wells" Sensors 25, no. 15: 4557. https://doi.org/10.3390/s25154557
APA StyleGuo, H., Li, A., Sun, Y., Yu, L., Peng, W., Ouyang, M., Wang, D., & Guo, Y. (2025). Application of Array Imaging Algorithms for Water Holdup Measurement in Gas–Water Two-Phase Flow Within Horizontal Wells. Sensors, 25(15), 4557. https://doi.org/10.3390/s25154557




