Road-Adaptive Precise Path Tracking Based on Reinforcement Learning Method
Abstract
1. Introduction
- By utilizing the motor energy efficiency map, the energy-efficient output control strategy based on the SAC method ensures that the motor of the autonomous vehicle operates in an efficient state at all times. This approach not only saves energy but also prolongs the service life of the motor.
- By adopting U-Net and pavement image segmentation methods, we developed a real-time detection system for road surfaces to better address the complexities of road conditions. By incorporating the results into the soft actor–critic (SAC) controller, it can effectively handle external disturbances caused by changes in the friction coefficient, thereby enhancing its stability.
- Our work directly uses the results of road segmentation to determine the category to which each pixel belongs (such as normal road, unpaved road, etc.) by performing semantic segmentation on the input image. The segmented pixel information is then input into the SAC network. Unlike directly inputting image features into the SAC network, this method enables the SAC network to obtain the road type of each pixel, thereby enhancing its adaptability.
- The SAC controller can better represent the vehicle’s dynamic model and make future predictions based on the reference path, thereby improving the ability to handle disturbances during tracking.
- The SACPP controller only needs to obtain the nominal values of the vehicle parameters without requiring the actual values. In addition, due to its simplified network structure and geometric control method, the amount of calculation is significantly reduced, thereby improving the practicality of this algorithm.
2. Problem Formulation
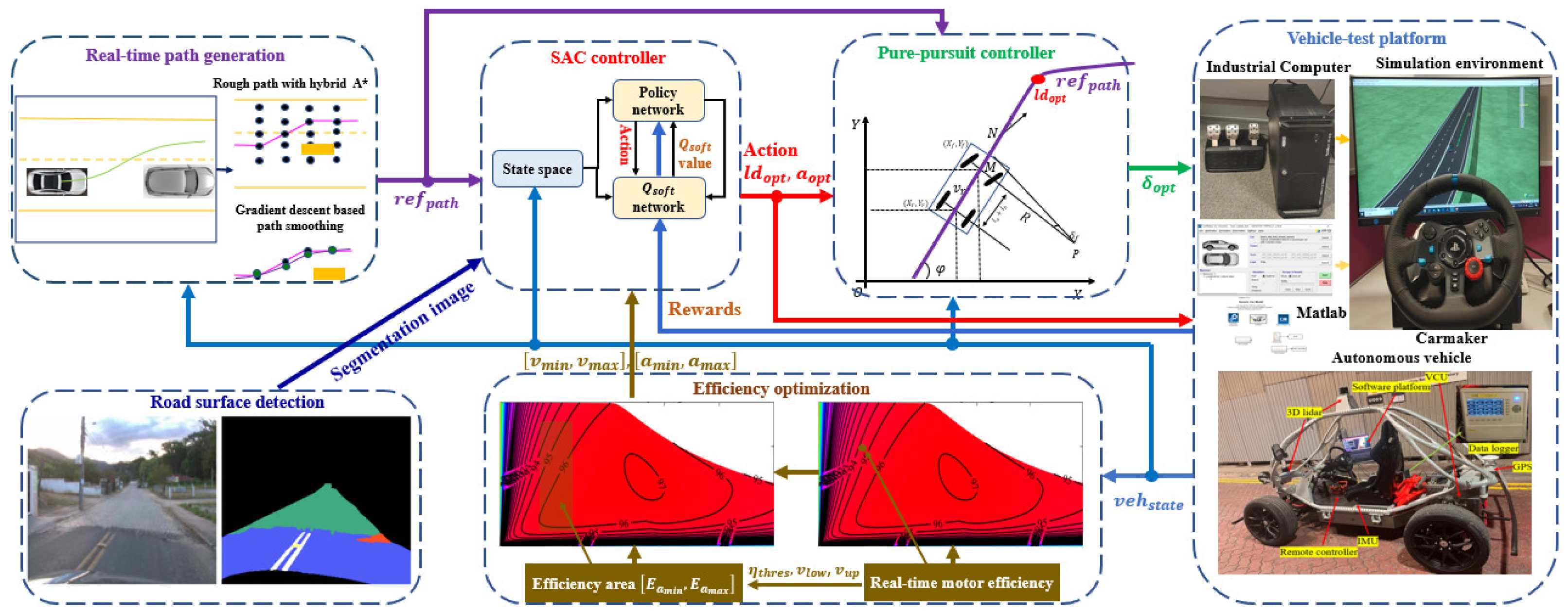
- In the real-time path generation module, the hybrid A* method [19] is used to generate and avoid obstacles according to the generated cost function to generate a safe driving path while avoiding obstacles. However, in complex environments, this path may have some uneven parts. Thus, a gradient descent smoother is adopted to optimize the path, focusing on the curvature and smoothness to improve the overall driving experience and provide the reference path .
- The vision-based road semantic segmentation algorithm and U-Net network structure are used to segment the state of the road surface in real time during driving [20,21], as shown in the road surface detection module. It can directly semantically segment different types of roads, each corresponding to a specific category and indirectly reflecting different friction coefficients. These classification results will be input into the RL model as feature values, thereby enhancing its perception of the external environment.
- The vehicle’s driving stability, safety, and motor output efficiency are always considered to ensure that the motor operates within the efficient output range, as demonstrated in the efficiency optimization module. First, a motor energy efficiency model is built to describe the energy consumption at different speeds and accelerations . Then, we include energy efficiency as part of the reward function to encourage the algorithm to choose a more efficient driving speed.
- Based on input information such as , semantic information on road segmentation, , and , SAC controller can adjust the vehicle’s optimal acceleration and forward distance in real-time, as shown in the SAC controller module.
- The PP geometric tracking method used in the pure-pursuit controller is used to reduce the amount of algorithm calculation. and are directly used to calculate the optimal front wheel angle . It has almost negligible calculation time while meeting the tracking accuracy, which significantly improves practicality.
- As demonstrated in the vehicle-test platform, the simulation platform is mainly composed of an industrial computer, the CarMaker, and a Logitech steering wheel and brake throttle system. The platform is mainly used for data collection and network training. Additionally, the actual vehicle is used to finally verify the performance of our work.
3. Real-Time Path Generation
- 1.
- Initialize the waypoint to the original waypoint.
- 2.
- Compute the gradient for each path point , and calculate the objective function with respect to the gradient of gradient in (4):Curvature gradient:Smooth gradient:
- 3.
- Waypoint update equation is given in (5):where is the learning rate, which controls the update step size. It is crucial to choose an appropriate , as a learning rate that is too large may cause algorithm instability, while one that is too small will slow down the convergence speed. Adjust the two weights and according to the specific scenario to achieve the ideal path-smoothing effect and path fidelity. The parameters selected in this paper are 0.001, and are set to 0.6 and 0.4, respectively. In each iteration, the algorithm calculates the gradient of the objective function and updates the positions of the path points using the conjugate gradient method [23]. Finally, the smooth path will be output as the navigation reference path.
4. Optimal Speed Generation
4.1. Road Surface Detection
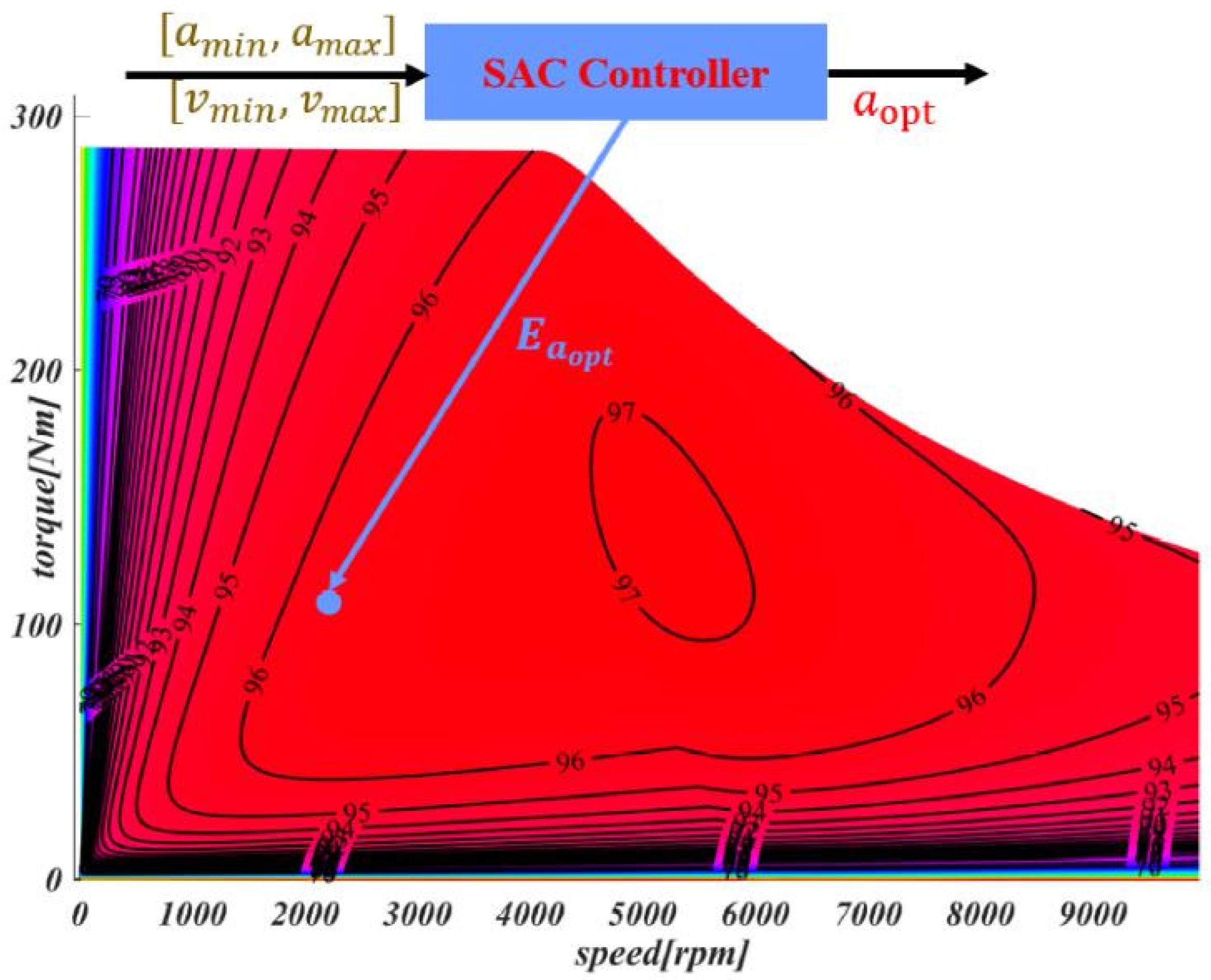
4.2. Motor Efficiency Optimization
4.3. SAC Controller
- 1.
- Path tracking error: The tracking error includes the lateral tracking error (cross-track error, ()) and the heading tracking error . During the tracking process, as long as the tracking error of the controller is kept within a reasonable range, the safety of driving can be ensured. Therefore, the reward function will encourage the controller to minimize both the lateral and heading errors, especially the lateral error.Since the heading deviation has a significant impact on driving safety, the reward function will decrease exponentially as increases. This design is intended to encourage the controller to pay more attention to the heading error to ensure driving safety.
- 2.
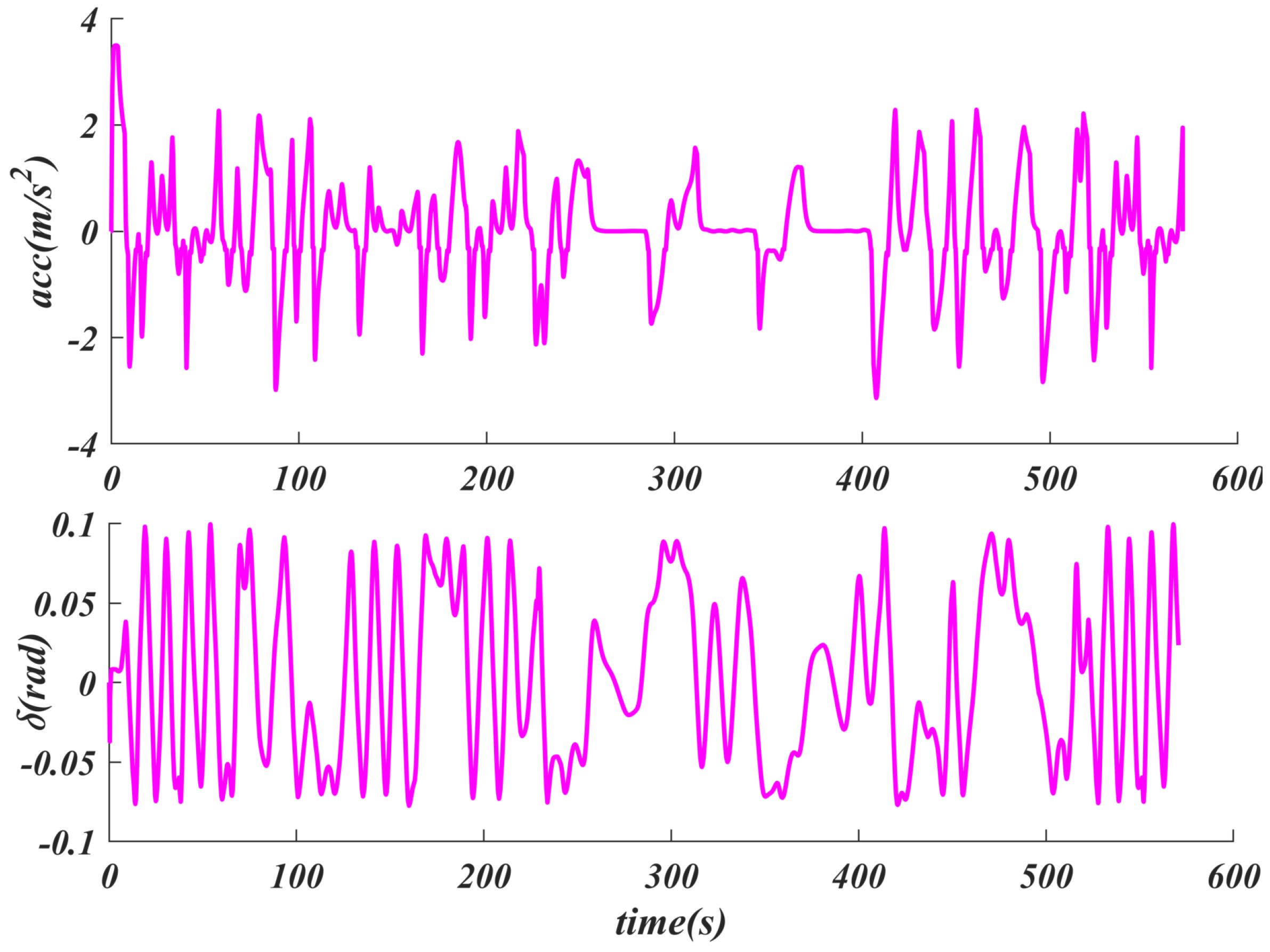
- Velocity tracking error: In terms of tracking efficiency and comfort, we have established a reward mechanism: within the speed limit of the road, the faster the speed, the higher the efficiency. Therefore, we introduced a speed reward. When the vehicle speed is lower than a certain set value, a negative reward will be given to ensure that the vehicle can maintain a certain initial speed.The acceleration of the vehicle directly affects ride comfort, so we have also established an acceleration reward mechanism. Specifically, the smaller the acceleration, the smoother the driving process, thus improving the ride comfort experience.
- 3.
- Energy efficiency: Energy consumption is a crucial factor in high-speed path tracking. The motor running at a low energy efficiency point will directly lead to a shortened actual mileage of the vehicle and also shorten the service life of the battery and motor. Therefore, it is very necessary to keep the motor output at a high-efficiency point during driving. As given in the efficiency optimization module, can be defined. When exceeds this threshold, the corresponding reward will be given; if it is lower than the set threshold, the reward will be negative.
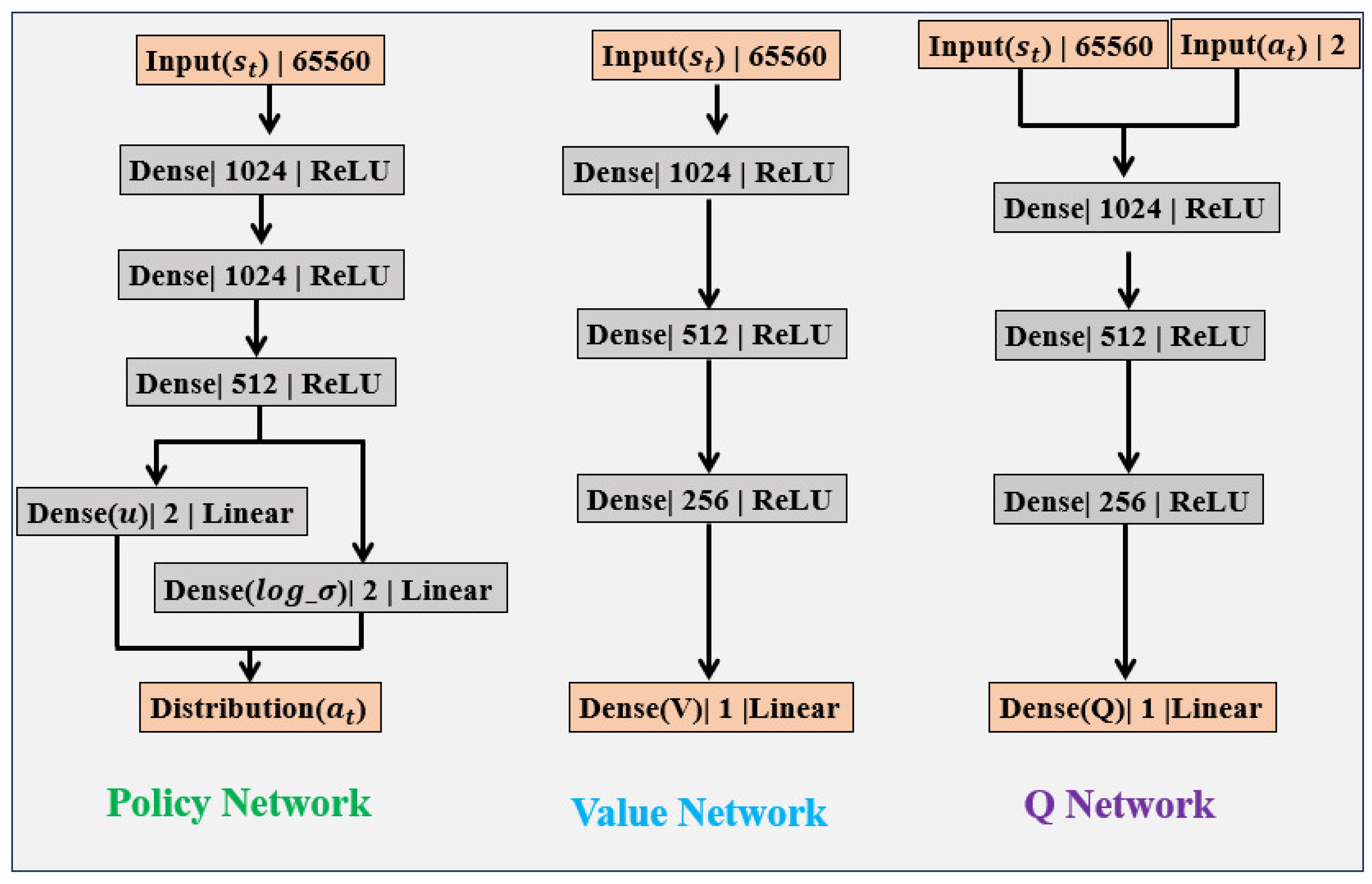
4.4. Network
| Algorithm 1: SAC path-tracking training method with prioritized experience replay |
 |
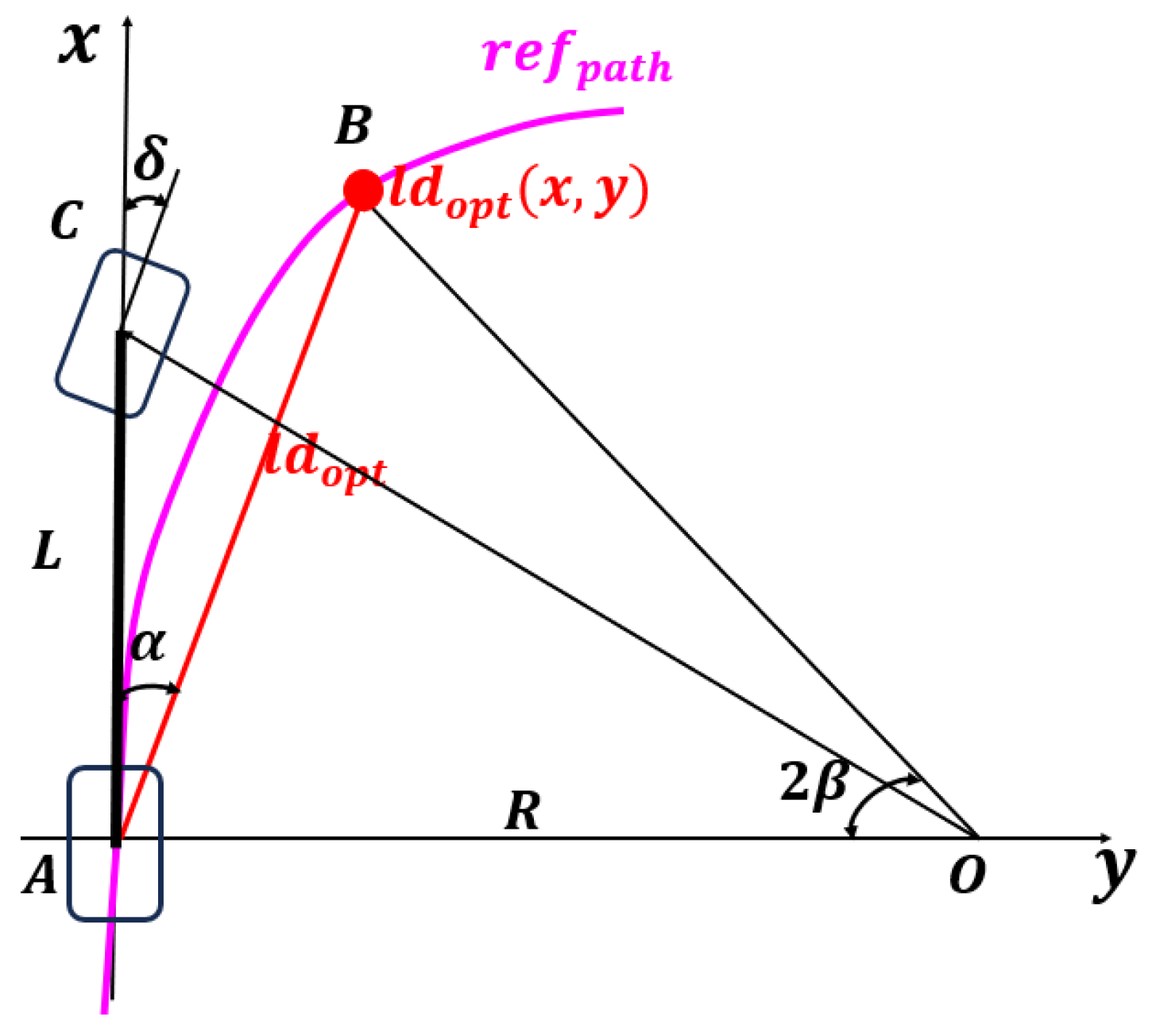
5. Path Tracking Using the PP Method
6. Experiments and Results
6.1. SACPP Network Training
- 1.
- Training scenario 1: Straight driving on a normal road, 1.87 km long, mainly used to learn basic acceleration and deceleration operations.
- 2.
- Training scenario 2: Circular driving on a normal road, 6.366 km long, aimed at mastering basic left and right turn operations.
- 3.
- Training scenario 3: Normal road with a combination of straight lines and arcs, 3.61 km long, aimed at achieving simple straight driving, acceleration, and deceleration, and basic operations such as left and right turns.
- 4.
- Training scenario 4: A simple scenario with different road surfaces, combining straight lines, arcs, and U-turns, 4.02 km long. This scenario helps the controller adapt to disturbances caused by road changes.
- 5.
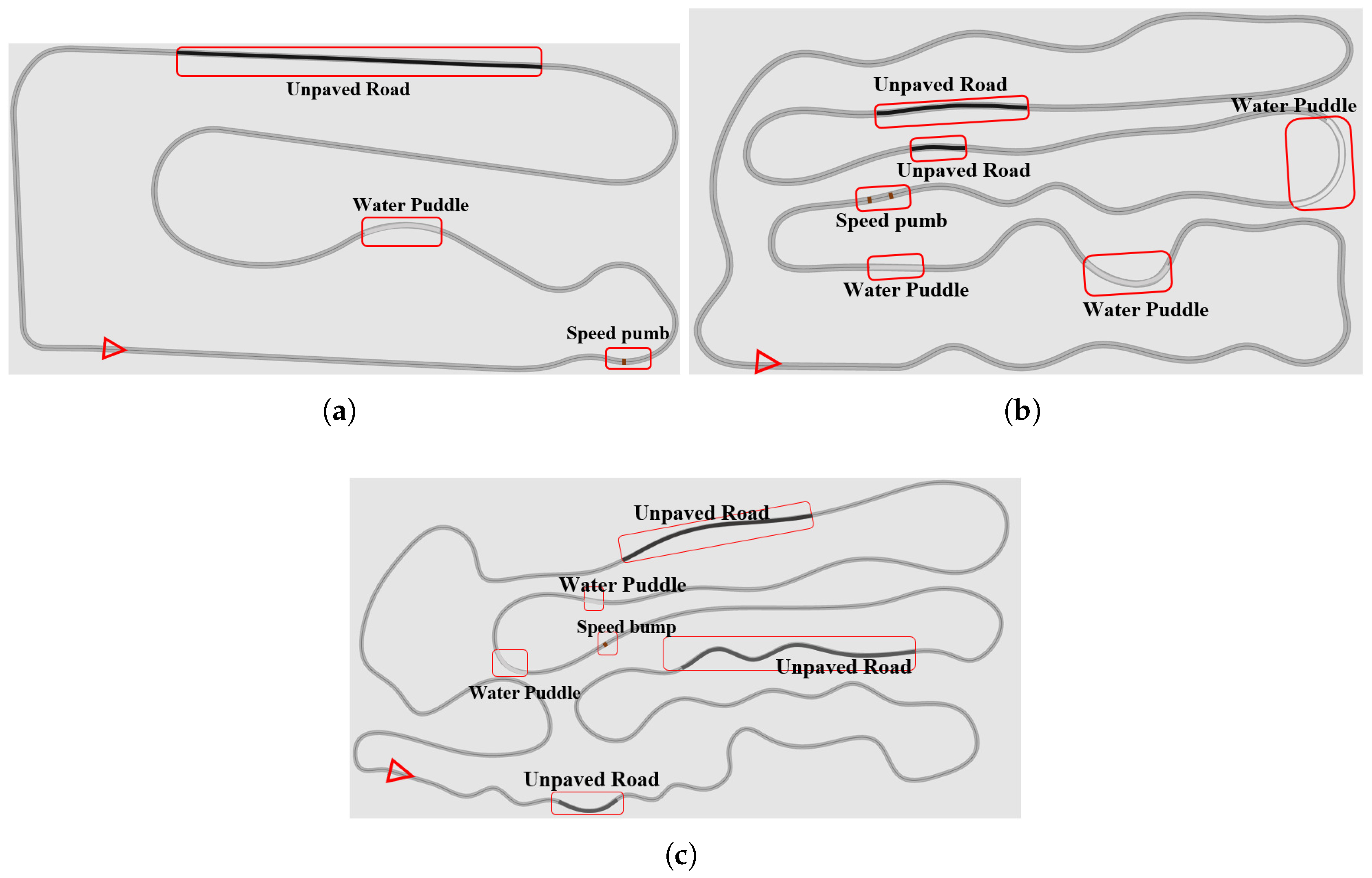
- Training scenario 5: A complex scenario with a variety of road types, including straight lines, arcs, continuous turns, and multiple U-turns, with a length of 5.184 km. Since this scenario involves different road types, continuous turns, and diverse U-turns, it aims to improve the controller’s precise tracking capabilities in complex environments.
- 6.
- Verification scenario 6: This is a complex test scenario (straight line + arc + continuous turns + multiple U-turns) with a length of 7.787 km, covering a variety of road types, continuous curves, and multiple U-turns. This scenario is designed to fully verify the performance of the algorithm in actual applications.
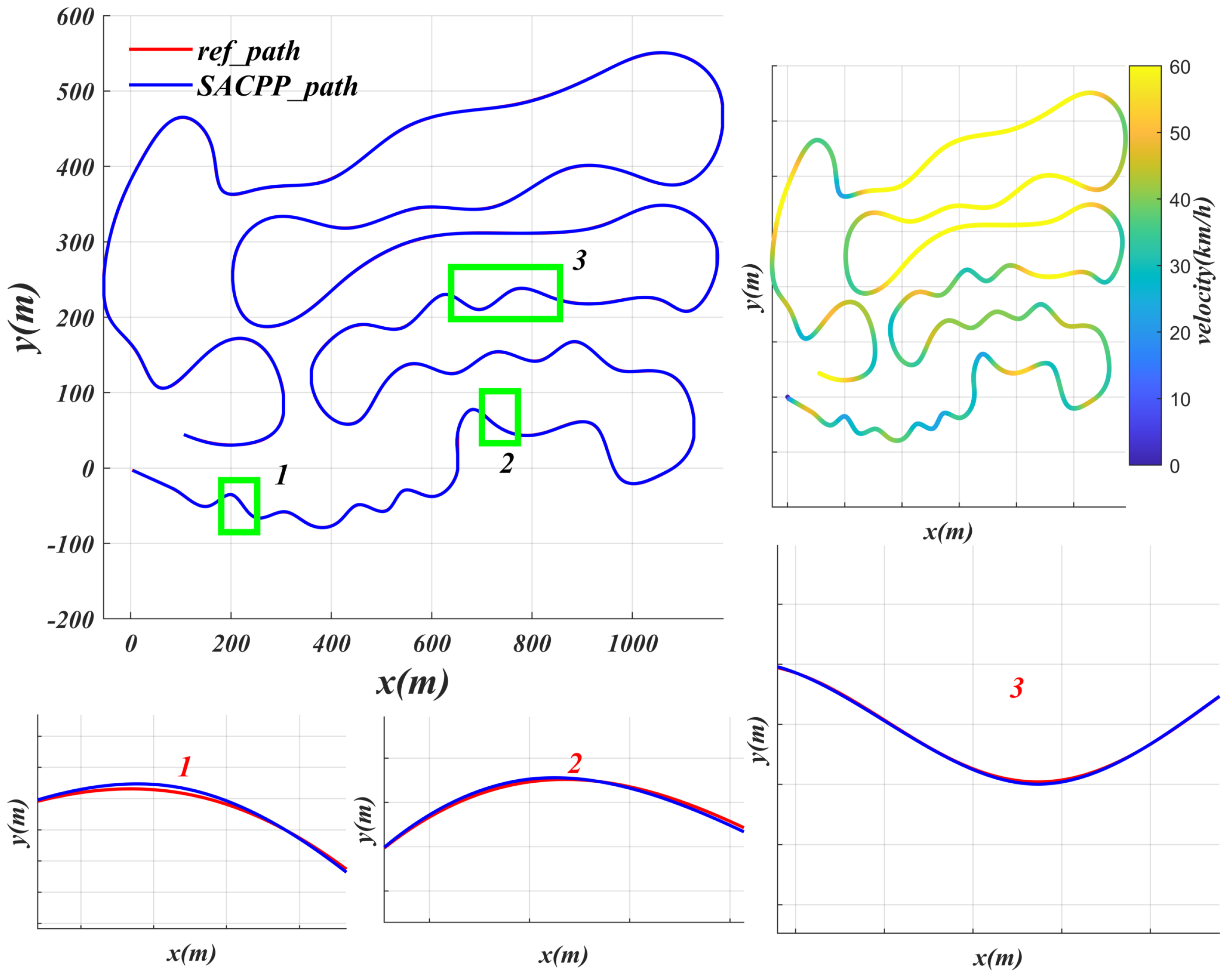
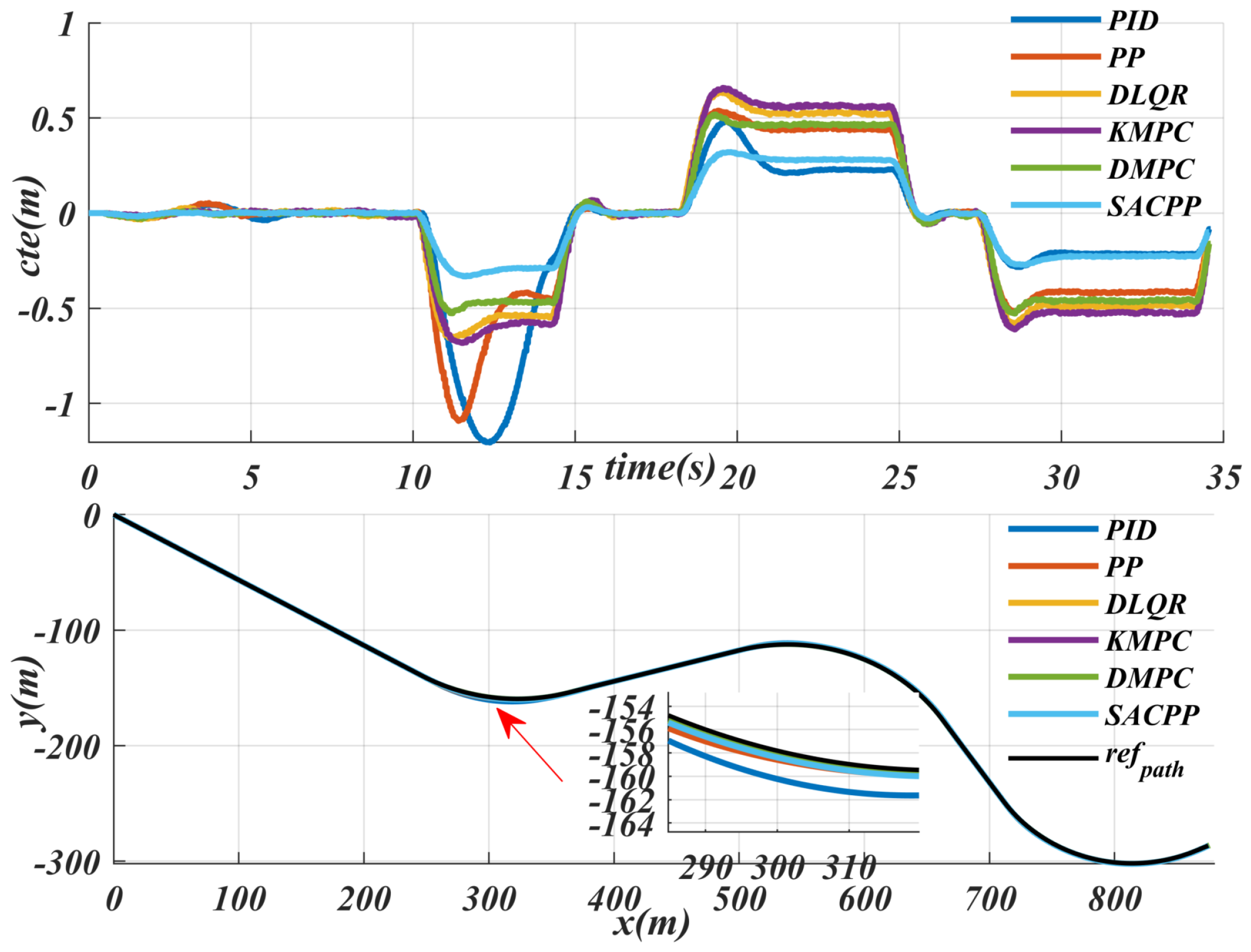
6.2. Generalization Performance Verification
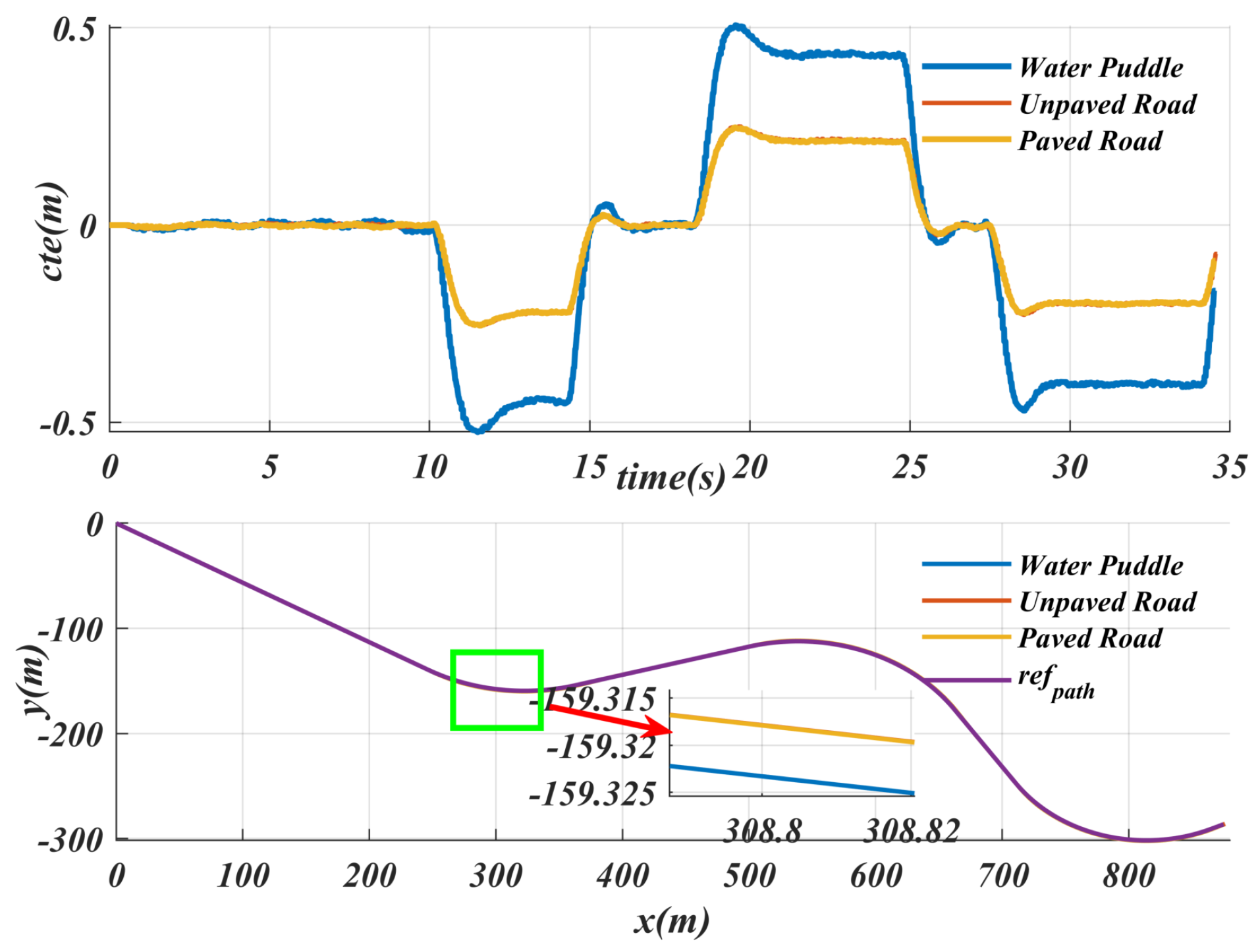
6.3. Uncertainties
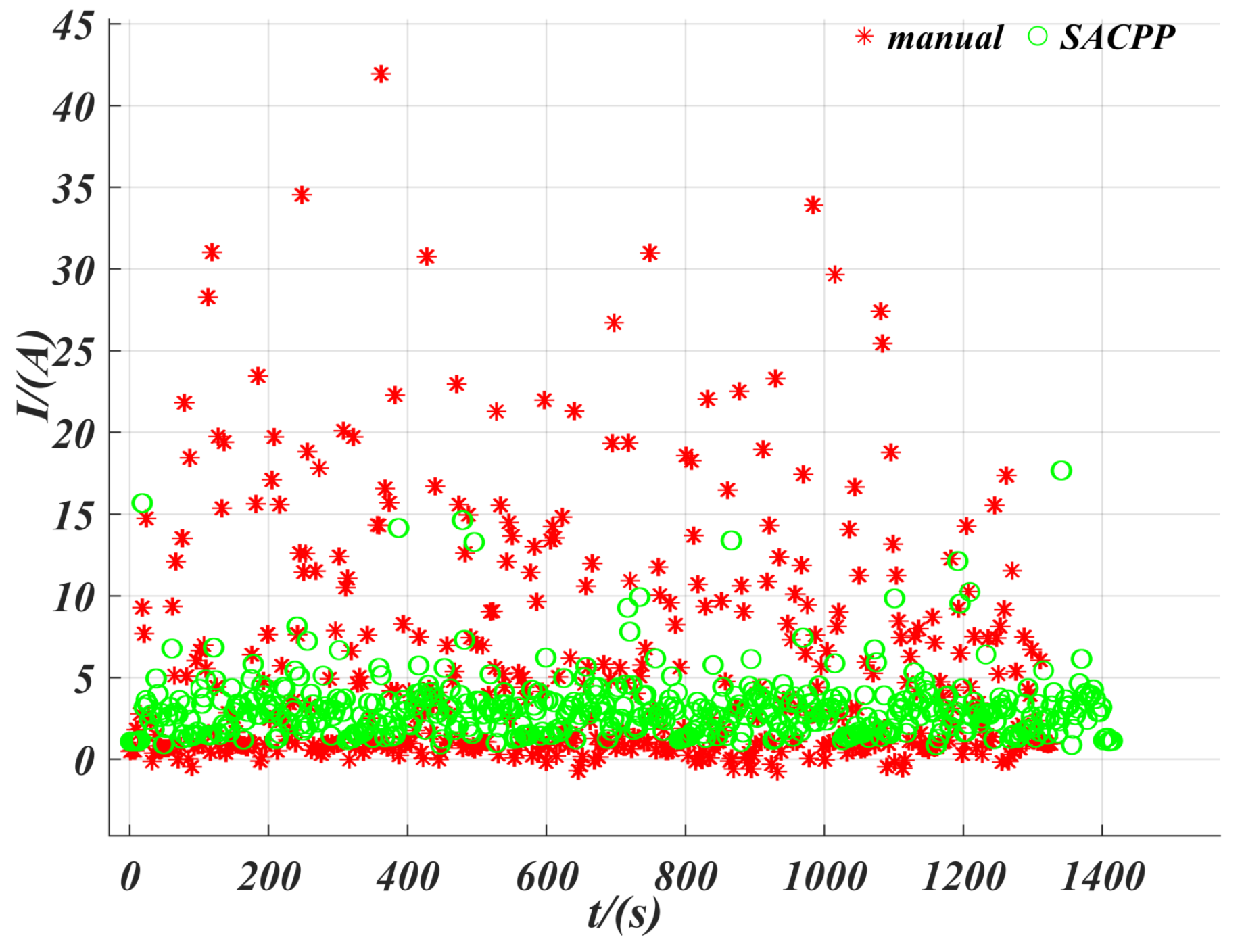
6.4. Energy Consumption
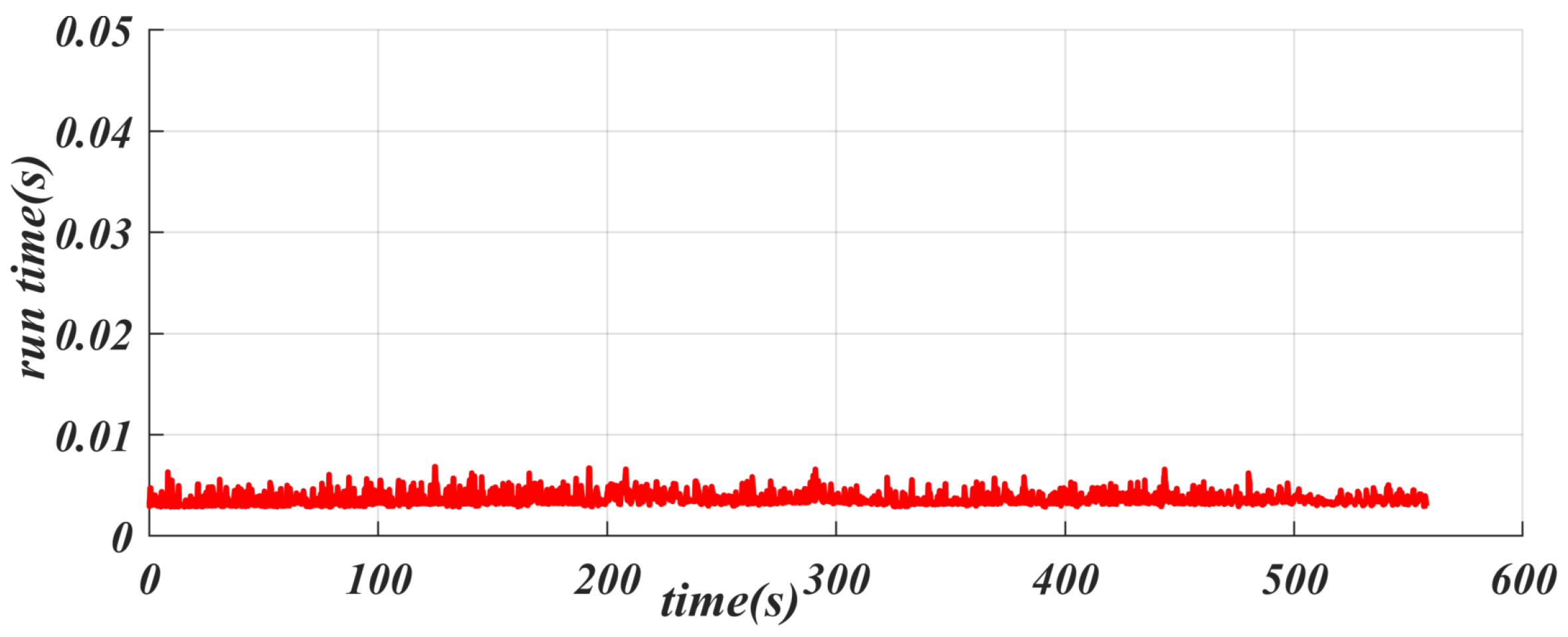
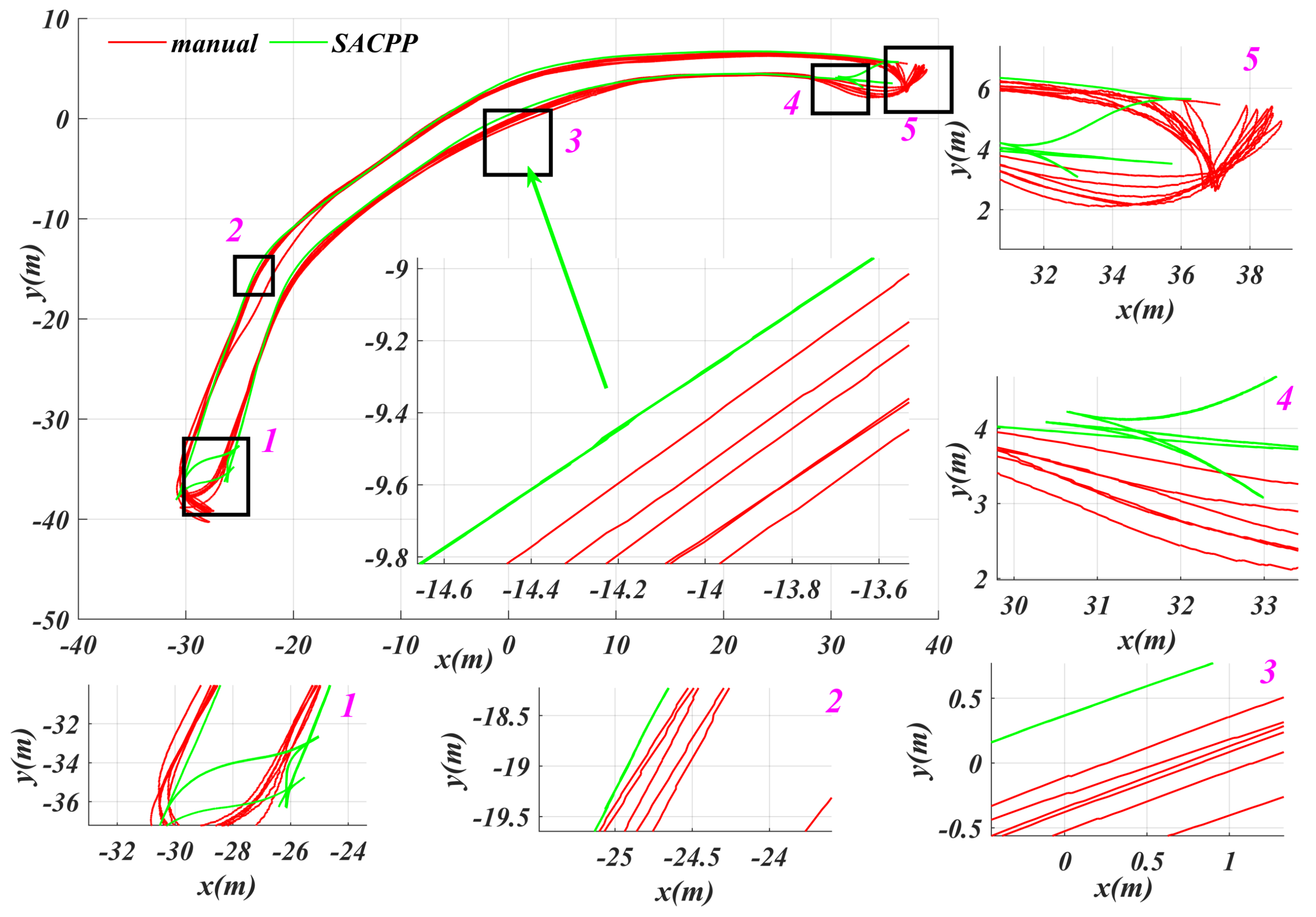
6.5. Testing in the Real Vehicle
7. Conclusions
- 1.
- We will focus on terrain changes (such as mountain roads and different slopes) to further improve the tracking performance of the controller under various terrains.
- 2.
- We will study the impact of different rewards on the stability of the overall controller, and related experiments will be included in subsequent work.
- 3.
- We plan to conduct robustness experiments on the proposed algorithm under different weather conditions in future work. However, due to the difficulties in obtaining relevant data and the challenges associated with actual scene testing, this work is currently difficult to implement. Therefore, we will focus on testing the performance of the algorithm in various weather conditions and on steep slope scenarios.
- 4.
- Subsequent work will integrate various traffic signs and trajectory predictions of surrounding vehicles to generate a driving speed that takes into account traffic information and surrounding vehicle conditions. This will not only help save energy but also improve travel efficiency. In addition, the algorithm can be deployed on multiple vehicles to achieve collaborative path tracking, further enhancing overall travel efficiency.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lv, Y.; Chen, Y.; Chen, Z.; Fan, Y.; Tao, Y.; Zhao, R.; Gao, F. Hybrid Supervised and Reinforcement Learning for Motion-Sickness-Aware Path Tracking in Autonomous Vehicles. Sensors 2025, 25, 3695. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Liu, K.; Gao, F.; Zhao, F. Research on Path Planning and Path Tracking Control of Autonomous Vehicles Based on Improved APF and SMC. Sensors 2023, 23, 7918. [Google Scholar] [CrossRef] [PubMed]
- Han, C.; Yu, Z.; Shi, X.; Fan, J. Dynamic Path Planning for Rapidly Expanding Autonomous Vehicles in Complex Environments. IEEE Sens. J. 2025, 25, 1216–1229. [Google Scholar] [CrossRef]
- Bai, Z.; Pang, H.; He, Z.; Zhao, B.; Wang, T. Path Planning of Autonomous Mobile Robot in Comprehensive Unknown Environment Using Deep Reinforcement Learning. IEEE Internet Things J. 2024, 11, 22153–22166. [Google Scholar] [CrossRef]
- Dong, D.; Ye, H.; Luo, W.; Wen, J.; Huang, D. Collision Avoidance Path Planning and Tracking Control for Autonomous Vehicles Based on Model Predictive Control. Sensors 2024, 24, 5211. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Liu, H.; Wang, H.; Cheng, K.W.E. Energy-Efficient Trajectory Optimization of Autonomous Driving Systems With Personalized Driving Style. IEEE Trans. Ind. Inform. 2025, 21, 1026–1037. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Ai, Z.; Murphey, Y.L.; Zhang, J. Energy Optimal Control of Motor Drive System for Extending Ranges of Electric Vehicles. IEEE Trans. Ind. Electron. 2021, 68, 1728–1738. [Google Scholar] [CrossRef]
- Zhang, Y.; Ai, Z.; Chen, J.; You, T.; Du, C.; Deng, L. Energy-Saving Optimization and Control of Autonomous Electric Vehicles With Considering Multiconstraints. IEEE Trans. Cybern. 2022, 52, 10869–10881. [Google Scholar] [CrossRef] [PubMed]
- Szczepanski, R.; Erwinski, K.; Tejer, M.; Daab, D. Optimal Path Planning Algorithm with Built-In Velocity Profiling for Collaborative Robot. Sensors 2024, 24, 5332. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Liu, H.-T.; Wu, R.-S. Robust H∞ Fault-Tolerant Observer-Based PID Path Tracking Control of Autonomous Ground Vehicle With Control Saturation. IEEE Open J. Veh. Technol. 2024, 5, 298–311. [Google Scholar] [CrossRef]
- Huang, Z.; Li, H.; Li, W.; Liu, J.; Huang, C.; Yang, Z.; Fang, W. A New Trajectory Tracking Algorithm for Autonomous Vehicles Based on Model Predictive Control. Sensors 2021, 21, 7165. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Wu, Z.; Zhao, Y. An Improved Longitudinal Driving Car-Following System Considering the Safe Time Domain Strategy. Sensors 2024, 24, 5202. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.; Yang, K.; Tan, C.; Wang, J.; Yin, G. Enhancing High-Speed Cruising Performance of Autonomous Vehicles Through Integrated Deep Reinforcement Learning Framework. IEEE Trans. Intell. Transp. Syst. 2025, 26, 835–848. [Google Scholar] [CrossRef]
- Xia, Q.; Chen, P.; Xu, G.; Sun, H.; Li, L.; Yu, G. Adaptive Path-Tracking Controller Embedded With Reinforcement Learning and Preview Model for Autonomous Driving. IEEE Trans. Veh. Technol. 2025, 74, 3736–3750. [Google Scholar] [CrossRef]
- Liu, J.; Cui, Y.; Duan, J.; Jiang, Z.; Pan, Z.; Xu, K.; Li, H. Reinforcement Learning-Based High-Speed Path Following Control for Autonomous Vehicles. IEEE Trans. Veh. Technol. 2024, 73, 7603–7615. [Google Scholar] [CrossRef]
- Coelho, D.; Oliveira, M.; Santos, V. RLAD: Reinforcement Learning From Pixels for Autonomous Driving in Urban Environments. IEEE Trans. Autom. Sci. Eng. 2024, 21, 7427–7435. [Google Scholar] [CrossRef]
- Huang, Z.; Sheng, Z.; Qu, Y.; You, J.; Chen, S. VLM-RL: A Unified Vision Language Models and Reinforcement Learning Framework for Safe Autonomous Driving. arXiv 2024, arXiv:2412.15544. Available online: https://arxiv.org/abs/2412.15544 (accessed on 20 December 2024).
- Dang, F.; Chen, D.; Chen, J.; Li, Z. Event-Triggered Model Predictive Control With Deep Reinforcement Learning for Autonomous Driving. IEEE Trans. Intell. Veh. 2024, 9, 459–468. [Google Scholar] [CrossRef]
- Han, B.; Sun, J. Finite Time ESO-Based Line-of-Sight Following Method with Multi-Objective Path Planning Applied on an Autonomous Marine Surface Vehicle. Electronics 2025, 14, 896. [Google Scholar] [CrossRef]
- Sun, L.; Bockman, J.; Sun, C. A Framework for Leveraging Interimage Information in Stereo Images for Enhanced Semantic Segmentation in Autonomous Driving. IEEE Trans. Instrum. Meas. 2023, 72, 1–12. [Google Scholar] [CrossRef]
- Sun, L.; Xia, J.; Xie, H.; Sun, C. EPNet: An Efficient Postprocessing Network for Enhancing Semantic Segmentation in Autonomous Driving. IEEE Trans. Instrum. Meas. 2025, 74, 1–11. [Google Scholar] [CrossRef]
- Liu, H.; Sun, J.; Cheng, K.W.E. A Two-Layer Model Predictive Path-Tracking Control With Curvature Adaptive Method for High-Speed Autonomous Driving. IEEE Access 2023, 11, 89228–89239. [Google Scholar] [CrossRef]
- Olutayo, T.; Champagne, B. Dynamic Conjugate Gradient Unfolding for Symbol Detection in Time-Varying Massive MIMO. IEEE Open J. Veh. Technol. 2025, 5, 792–806. [Google Scholar] [CrossRef]
- Verma, P.; Chaudhary, A. Improving Freedom of Visually Impaired Individuals with Innovative EfficientNet and Unified Spatial-Channel Attention: A Deep Learning-Based Road Surface Detection System. Teh. Glas. 2025, 19, 17–25. [Google Scholar]
- Liu, H.; Sun, J.; Wang, H.; Cheng, K.W.E. Comprehensive Analysis of Adaptive Soft Actor-Critic Reinforcement Learning-Based Control Framework for Autonomous Driving in Varied Scenarios. IEEE Trans. Transp. Electrif. 2025, 11, 3667–3679. [Google Scholar] [CrossRef]
- Schaul, T.; Quan, J.; Antonoglou, I.; Silver, D. Prioritized Experience Replay. In Proceedings of the International Conference on Learning Representations (ICLR), San Juan, Puerto Rico, 25 February 2016. [Google Scholar]
- Jeong, S.; Lee, S.; Lee, H.; Kim, H.K. X-CANIDS: Signal-Aware Explainable Intrusion Detection System for Controller Area Network-Based In-Vehicle Network. IEEE Trans. Veh. Technol. 2024, 73, 3230–3246. [Google Scholar] [CrossRef]




| No | Operational Layer | Output | Connected |
|---|---|---|---|
| 1 | input_layer (InputLayer) | 256, 256, 3 | |
| 2 | conv2d (Conv2D) | 256, 256, 16 | No. 1 |
| 3 | max_pooling2d (MaxPooling2D) | 128, 128, 16 | No. 2 |
| 4 | conv2d_1 (Conv2D) | 128, 128, 32 | No. 3 |
| 5 | max_pooling2d_1 (MaxPooling2D) | 64, 64, 32 | No. 4 |
| 6 | conv2_2 (Conv2D) | 64, 64, 64 | No. 5 |
| 7 | max_pooling2d_2 (MaxPooling2D) | 32, 32, 64 | No. 6 |
| 8 | conv2_3 (Conv2D) | 32, 32, 128 | No. 7 |
| 9 | max_pooling2d_3 (MaxPooling2D) | 16, 16, 128 | No. 8 |
| 10 | conv2_4 (Conv2D) | 16, 16, 256 | No. 9 |
| 11 | conv2d_transpose (Conv2DTranspose) | 32, 32, 128 | No. 10 |
| 12 | concatenate (Concatenate) | 32, 32, 256 | No. 11, 8 |
| 13 | Conv2_5 (Conv2D) | 32, 32, 128 | No. 12 |
| 14 | conv2d_transpose_1 (Conv2DTranspose) | 64, 64, 64 | No. 13 |
| 15 | concatenate_1 (Concatenate) | 64, 64, 128 | No. 14, 6 |
| 16 | conv2_6 (Conv2D) | 64, 64, 64 | No. 15 |
| 17 | conv2d_transpose_2 (Conv2DTranspose) | 128, 128, 32 | No. 16 |
| 18 | concatenate_2 (Concatenate) | 128, 128, 64 | No. 17, 4 |
| 19 | conv2d_7 (Conv2D) | 128, 128, 32 | No. 18 |
| 20 | conv2_9 (Conv2D) | 256, 256, 13 | No. 19 |
| Hyperparameter | Value |
|---|---|
| Learning rate: actor | 0.0003 |
| Learning rate: critic | 0.0003 |
| Learning rate: entropy regularization coefficient | 0.0003 |
| Discount factor | 0.99 |
| Target network update rate | 0.005 |
| Replay buffer | 1,000,000 |
| Entropy regularization coefficient | 0.2 |
| Parameter | Value |
|---|---|
| Vehicle mass (kg) | 600 |
| Wheel radius (m) | 0.3125 |
| Wheel inertia (km/m2) | 0.25 |
| Battery normal voltage (V) | 72 |
| Motor max power (kW) | 84 |
| Motor max torque (Nm) | 280 |
| Uncertainty Parameters | Max (m) | Mean (m) | |
|---|---|---|---|
| Mass | m | 0.220 | 0.099 |
| m | 0.2548 | 0.108 | |
| m | 0.3025 | 0.1235 | |
| Road surface | Water Puddle | 0.5249 | 0.2207 |
| Unpaved | 0.2549 | 0.1089 | |
| Paved | 0.2321 | 0.092 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, B.; Sun, J. Road-Adaptive Precise Path Tracking Based on Reinforcement Learning Method. Sensors 2025, 25, 4533. https://doi.org/10.3390/s25154533
Han B, Sun J. Road-Adaptive Precise Path Tracking Based on Reinforcement Learning Method. Sensors. 2025; 25(15):4533. https://doi.org/10.3390/s25154533
Chicago/Turabian StyleHan, Bingheng, and Jinhong Sun. 2025. "Road-Adaptive Precise Path Tracking Based on Reinforcement Learning Method" Sensors 25, no. 15: 4533. https://doi.org/10.3390/s25154533
APA StyleHan, B., & Sun, J. (2025). Road-Adaptive Precise Path Tracking Based on Reinforcement Learning Method. Sensors, 25(15), 4533. https://doi.org/10.3390/s25154533







