A Comprehensive Review of Artificial Intelligence-Based Algorithms for Predicting the Remaining Useful Life of Equipment
Abstract
1. Introduction
2. Data Acquisition
2.1. Data Classification
2.1.1. Fully Degraded Data
2.1.2. Partially Degraded Data
2.1.3. Fault Time Data
2.2. Equipment Data
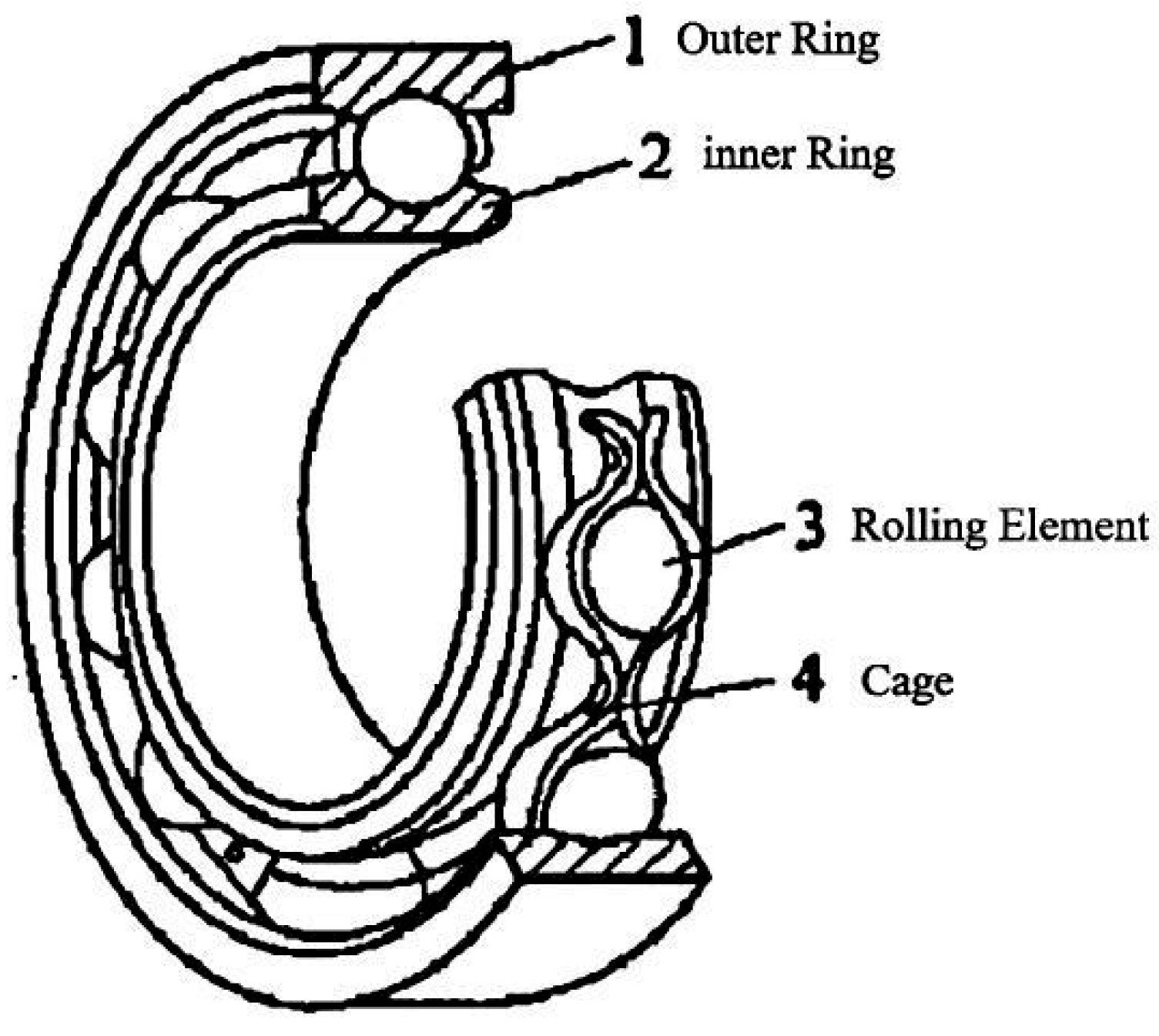
2.2.1. Rolling Bearings
- The resonance effect, which occurs when the mechanical equipment operates;
- The interaction force between parts, caused by the assembly structure of mechanical equipment parts;
- The slight influence of the working environment on its basic structure, such as humidity, pressure, and temperature, which are also related to internal factors, such as the temperature change caused by friction between rolling elements and inner and outer rings.
- 1.
- Forced vibration caused by a machining assembly error or mistake.
- 2.
- Inherent vibration caused by the bearing structure.
- 3.
- Impact vibration caused by mechanical failure.
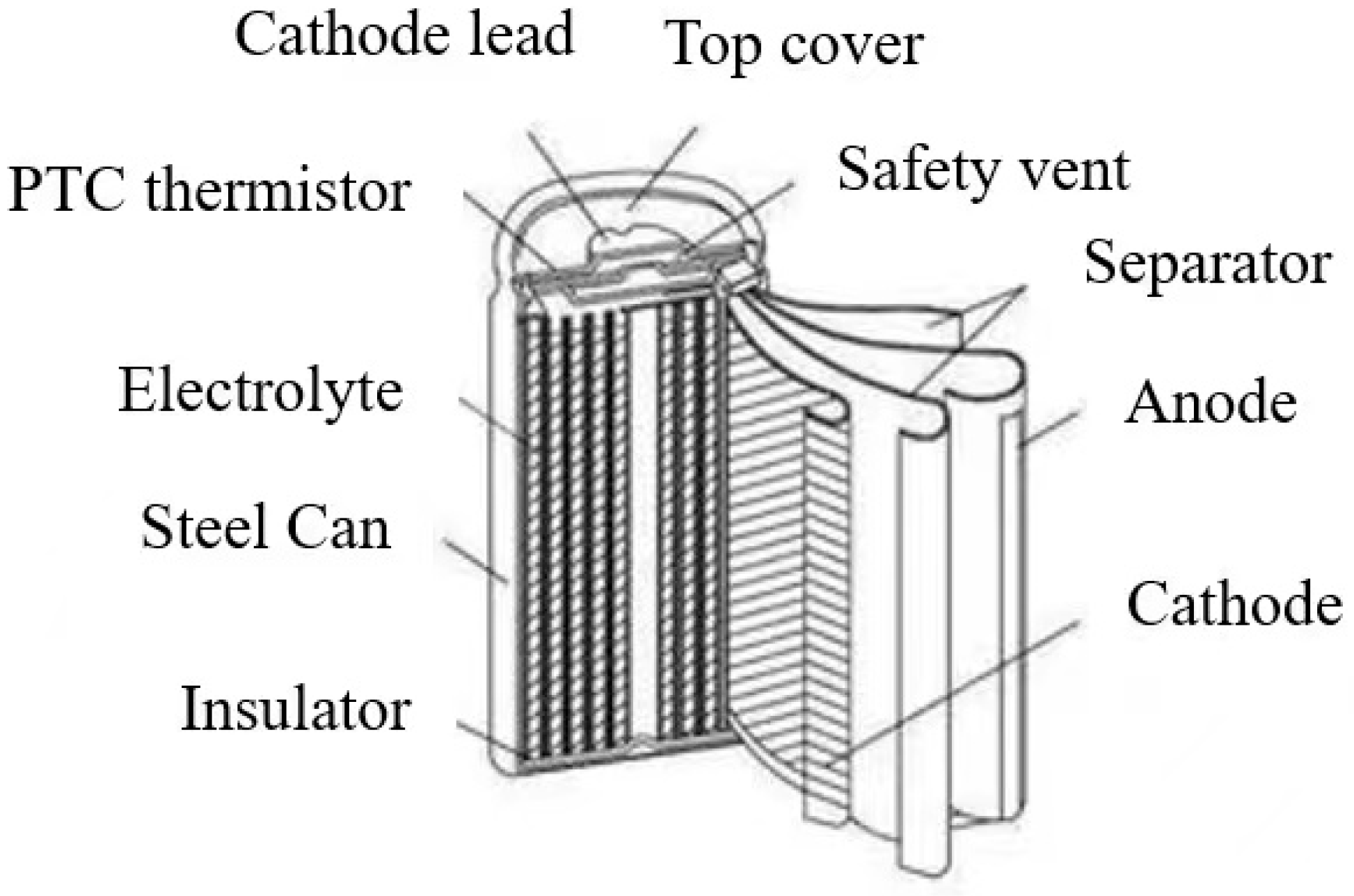
2.2.2. Lithium Batteries
- 1.
- Temperature
- 2.
- External stress
- 3.
- Unreasonable charging and discharging rates
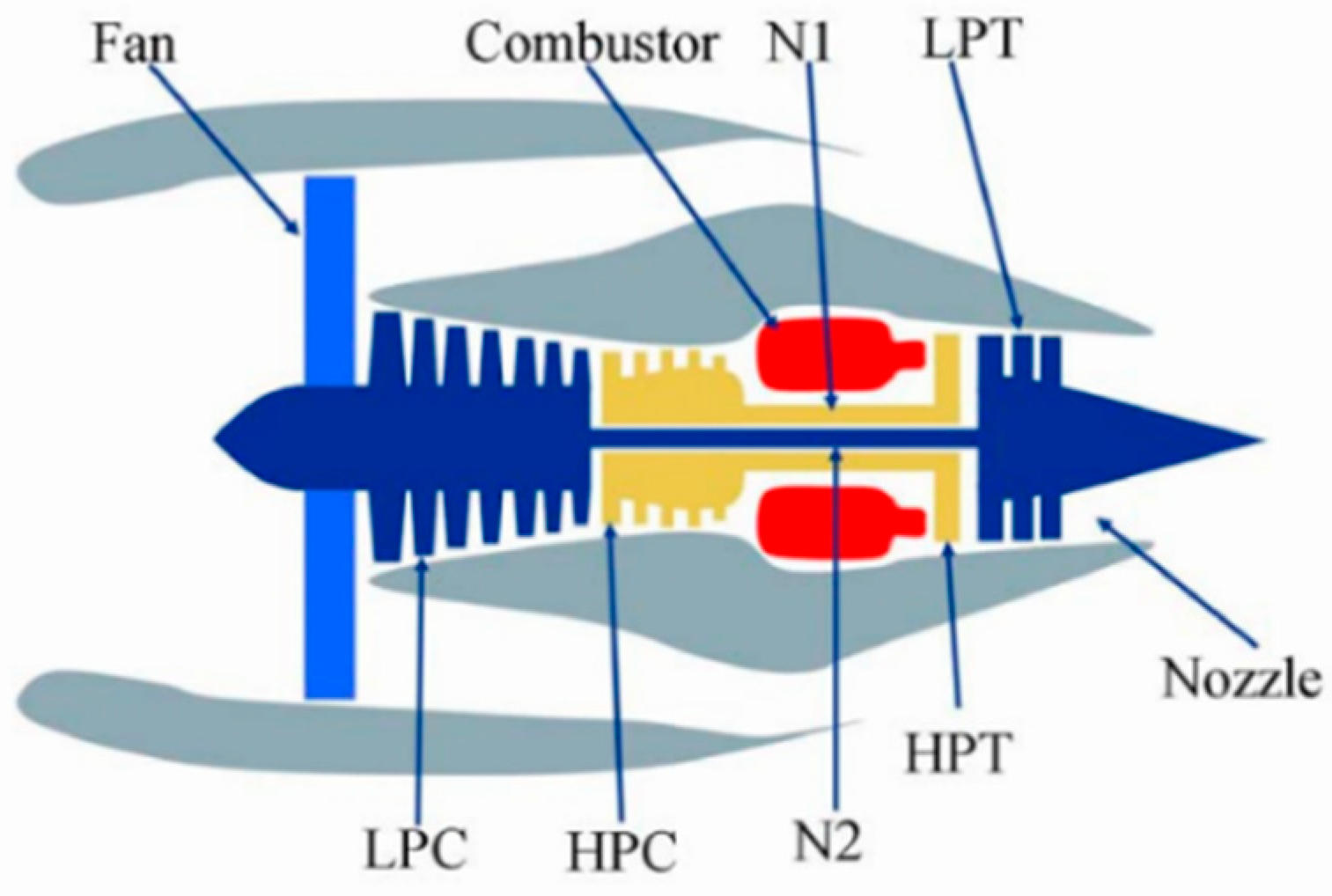
2.2.3. Turbine Engines
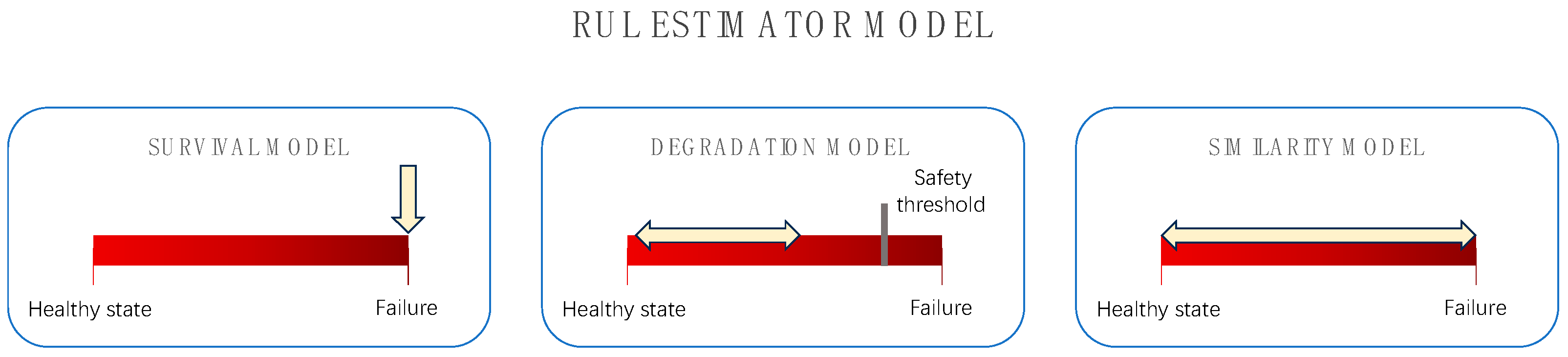
3. Construction of Health Factors
3.1. Direct HI
3.2. Indirect HI
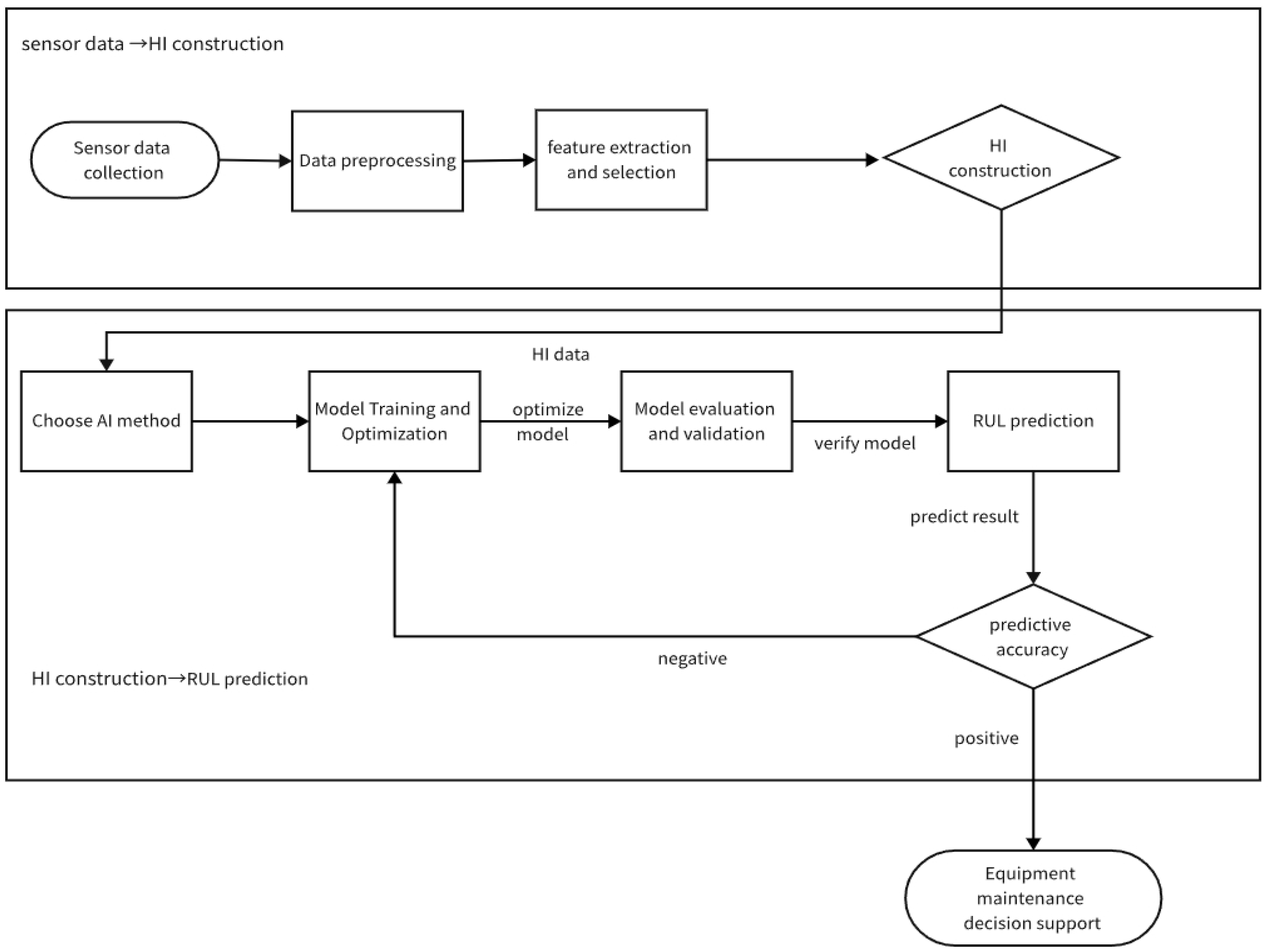
4. RUL Prediction Methods Based on AI
4.1. AI Methods
4.1.1. Artificial Neural Networks
4.1.2. Neuro-Fuzzy Systems
4.1.3. Support Vector Machines and Derived Models
- 1.
- Support vector machines
- 2.
- Support vector regression
- 3.
- Relevance vector machines
4.1.4. Gaussian Process Regression
4.1.5. Hybrid Methods
4.1.6. Discussion on Suitable Attributes for Different Scenarios
Small-Scale Datasets
Noisy Data
Real-Time Applications
4.2. Evaluation Index
- Mean absolute error
- 2.
- Mean absolute percentage error
- 3.
- Root mean square error
5. Case Study
5.1. Dataset Introduction
- 1.
- University of Maryland lithium-ion battery research dataset
- 2.
- NASA lithium-ion battery aging dataset
5.2. Research Introduction
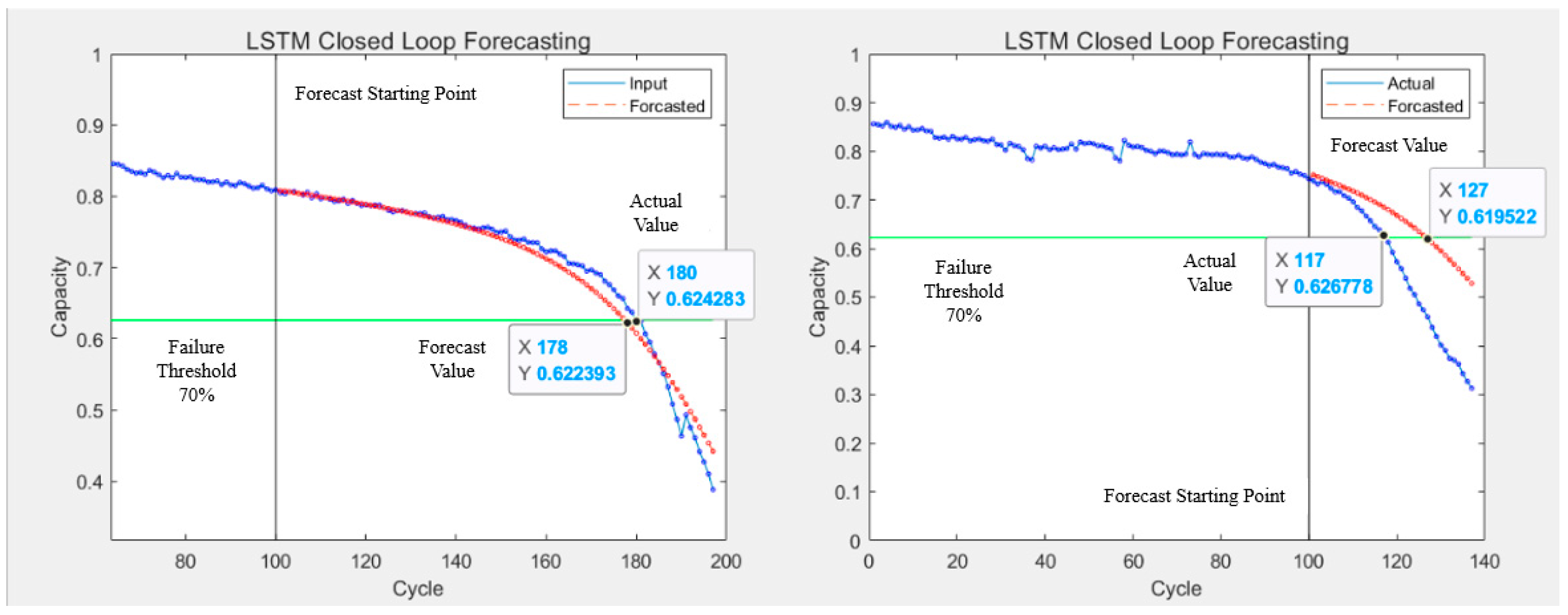
- Based on the battery capacity curve 1, we chose the LSTM algorithm as the prediction method for lithium battery RUL. According to the theoretical basis and model-building method of the LSTM algorithm, we used the battery capacity data in A12 and A3 as a training set to train the model, and we used the capacitance data in A5 and A8 before 100 cycles as a test set for prediction. The prediction starting point was set at 100 cycles.
- Based on battery capacity curve 1, we chose the PF-LSTM fusion method as the prediction method for lithium battery RUL. According to the theoretical basis and model-building method of the PF and LSTM algorithms, we used the same prediction process as in 1.
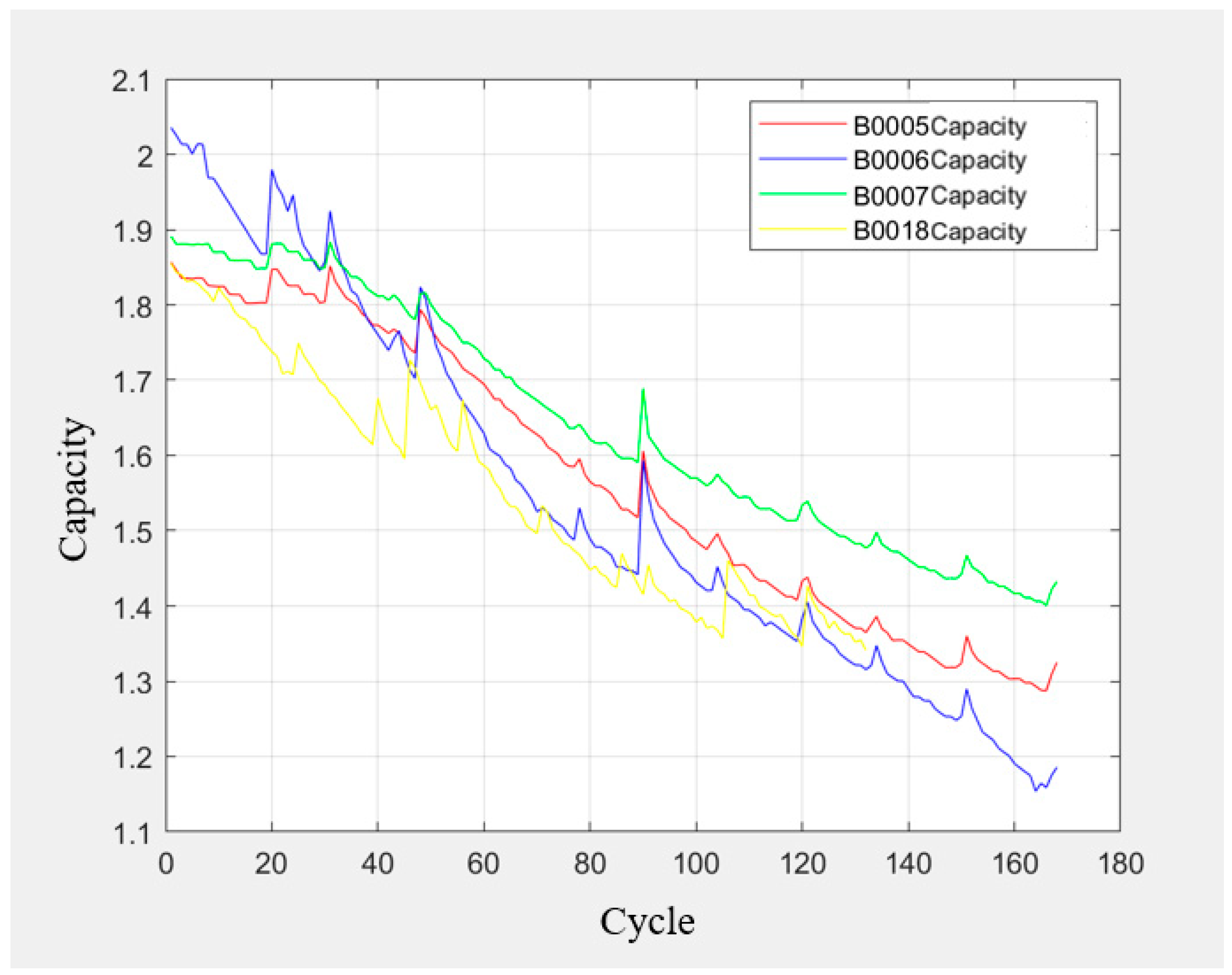
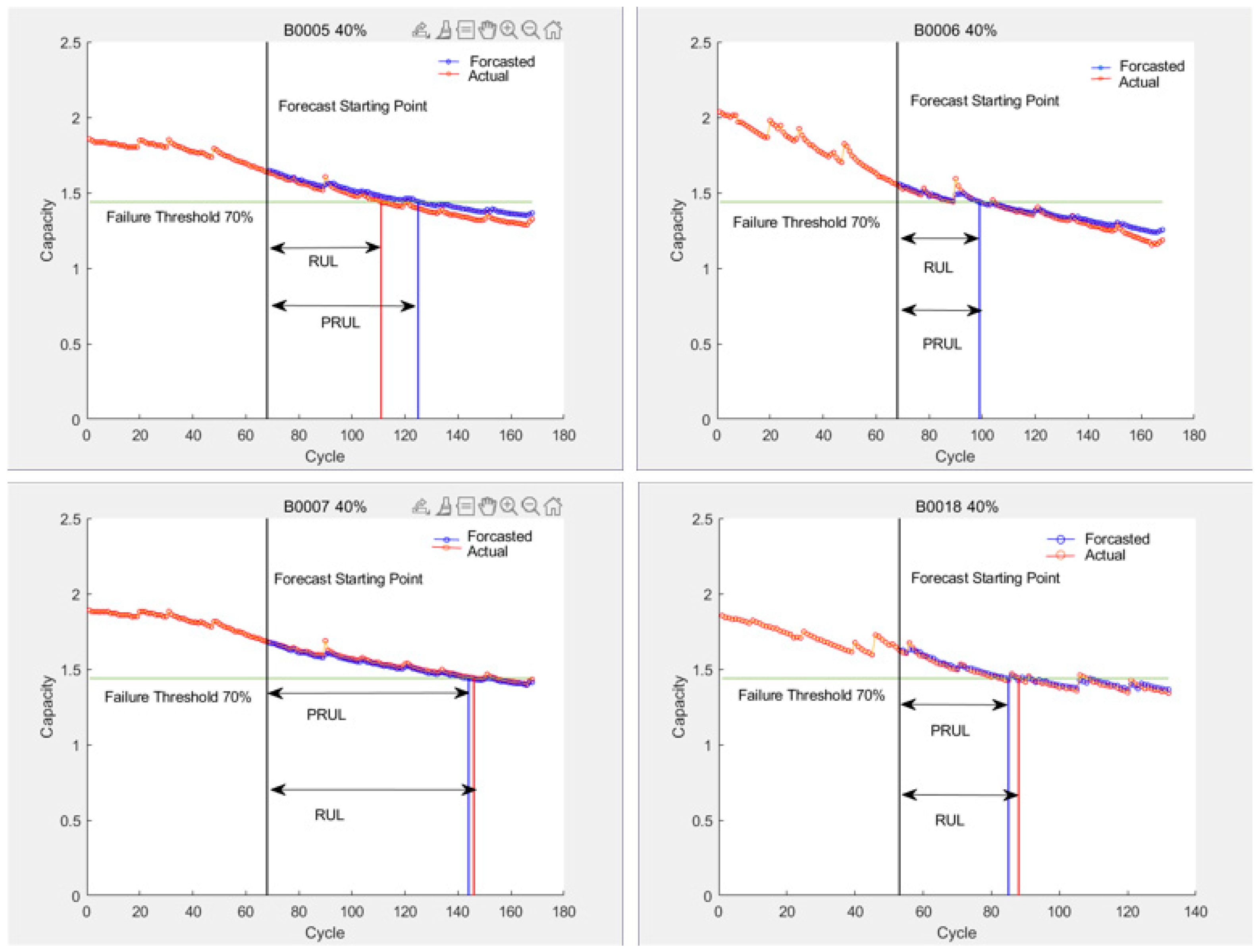
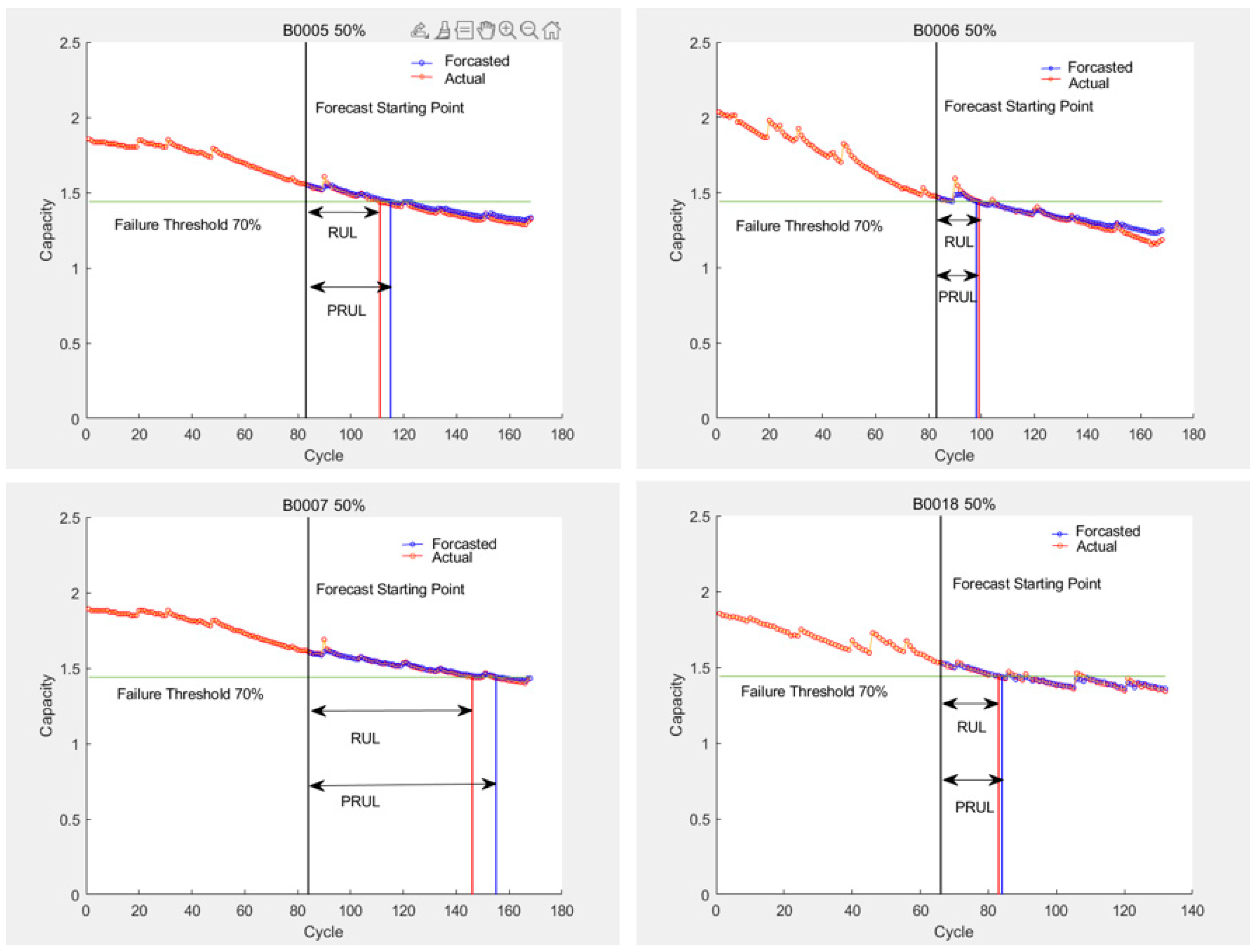
- Based on battery capacity curve 2, we chose the SVR algorithm as the prediction method for lithium battery RUL. According to the feature extraction and SVR algorithm model-building method mentioned in [1], we respectively took 40% and 50% of the constant pressure rise time series and constant pressure drop time series as the X label. We then took the battery capacity at the corresponding cycle times as the Y label, and we used the X and Y labels as inputs for the SVR model training. We used 60% and 50% of the cycle data as test sets for prediction, with the prediction starting points set at 40% and 50% of the total cycles, respectively.
5.3. Experimental Method
5.4. Results Comparison
5.5. Summary
6. Conclusions and Future Challenges
6.1. Conclusions
6.2. Challenges
6.2.1. Domain Adaptation Challenges
6.2.2. AI Model Interpretability Challenges
6.2.3. Uncertainty Quantification Challenges
6.2.4. Integration of Physics-Based Models Challenges
Funding
Conflicts of Interest
References
- Wu, W.; Lu, S. RUL prediction of lithium-ion batteries based on PCA-CEEMDAN and improved support vector regression. J. Power Supply 2023, 1–14. Available online: https://kns.cnki.net/kcms2/detail/12.1420.tm.20230525.1000.002.html (accessed on 3 May 2025).
- Zio, E.; Maio, F.D. A data-driven fuzzy approach for predicting the remaining useful life in dynamic failure scenarios of a nuclear system. Reliab. Eng. Syst. Saf. 2010, 95, 49–57. [Google Scholar] [CrossRef]
- Huang, C.-G.; Huang, H.-Z.; Peng, W.; Huang, T. Improved trajectory similarity-based approach for turbofan engine prognostics. J. Mech. Sci. Technol. 2019, 33, 4877–4890. [Google Scholar] [CrossRef]
- Lyu, J.H.; Ying, R.R.; Lu, N.Y.; Zhang, B.L. Remaining useful life estimation with multiple local similarities. Eng. Appl. Artif. Intell. 2020, 95, 103849. [Google Scholar] [CrossRef]
- Soons, Y.; Dijkman, R.; Jilderda, M.; Duivesteijn, W. Predicting Remaining Useful Life with Similarity-Based Priors. In Proceedings of the 18th International Symposium on Intelligent Data Analysis (IDA), Konstanz, Germany, 27–29 April 2020. [Google Scholar]
- Liu, Y.C.; Hu, X.F.; Zhang, W.J. Remaining useful life prediction based on health index similarity. Reliab. Eng. Syst. Saf. 2019, 185, 502–510. [Google Scholar] [CrossRef]
- Yu, W.N.; Kim, I.Y.; Mechefske, C. Remaining useful life estimation using a bidirectional recurrent neural network based autoencoder scheme. Mech. Syst. Signal Process. 2019, 129, 764–780. [Google Scholar] [CrossRef]
- Gu, M.Y.; Ge, J.Q. Method for residual useful life prediction based on compound similarity. J. Mech. Sci. Technol. 2022, 36, 5959–5969. [Google Scholar] [CrossRef]
- Liu, Z.; Cheng, Y.H.; Wang, P.; Yu, Y.L.; Long, Y.W. A method for remaining useful life prediction of crystal oscillators using the Bayesian approach and extreme learning machine under uncertainty. Neurocomputing 2018, 305, 27–38. [Google Scholar] [CrossRef]
- Hou, M.R.; Pi, D.C.; Li, B.R. Similarity-based deep learning approach for remaining useful life prediction. Measurement 2020, 159, 107788. [Google Scholar] [CrossRef]
- Chen, Z.Z.; Cao, S.C.; Mao, Z.J. Remaining Useful Life Estimation of Aircraft Engines Using a Modified Similarity and Supporting Vector Machine (SVM) Approach. Energies 2018, 11, 28. [Google Scholar] [CrossRef]
- Wang, B.; Lei, Y.G.; Li, N.P.; Li, N.B. A Hybrid Prognostics Approach for Estimating Remaining Useful Life of Rolling Element Bearings. IEEE Trans. Reliab. 2020, 69, 401–412. [Google Scholar] [CrossRef]
- Huang, Y.X.; Lu, Z.Y.; Dai, W.; Zhang, W.F.; Wang, B. Remaining Useful Life Prediction of Cutting Tools Using an Inverse Gaussian Process Model. Appl. Sci. 2021, 11, 5011. [Google Scholar] [CrossRef]
- Wang, H.Y.; Song, W.Q.; Zio, E.; Kudreyko, A.; Zhang, Y.J. Remaining useful life prediction for Lithium-ion batteries using fractional Brownian motion and Fruit-fly Optimization Algorithm. Measurement 2020, 161, 107904. [Google Scholar] [CrossRef]
- Liao, L.X.; Köttig, F. A hybrid framework combining data-driven and model-based methods for system remaining useful life prediction. Appl. Soft Comput. 2016, 44, 191–199. [Google Scholar] [CrossRef]
- Yan, M.M.; Wang, X.G.; Wang, B.X.; Chang, M.X.; Muhammad, I. Bearing remaining useful life prediction using support vector machine and hybrid degradation tracking model. ISA Trans. 2020, 98, 471–482. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Mu, Z.; Sun, C. Remaining Useful Life Prediction for Lithium-Ion Batteries Based on Exponential Model and Particle Filter. IEEE Access 2018, 6, 17729–17740. [Google Scholar] [CrossRef]
- Ding, F.; He, Z.J.; Zi, Y.Y.; Chen, X.F.; Cao, H.R.; Tan, J.Y. Reliability Assessment Based on Equipment Condition Vibration Feature Using Proportional Hazards Model. Chin. J. Mech. Eng. 2009, 45, 89–94. [Google Scholar] [CrossRef]
- Wang, F.; Chen, X.; Dun, B.; Wang, B.; Yan, D.; Zhu, H. Rolling Bearing Reliability Assessment via Kernel Principal Component Analysis and Weibull Proportional Hazard Model. Shock Vib. 2017, 2017, 6184190. [Google Scholar] [CrossRef]
- Xu, H.; Fard, N.; Fang, Y. Time series chain graph for modeling reliability covariates in degradation process. Reliab. Eng. Syst. Saf. 2020, 204, 107207. [Google Scholar] [CrossRef]
- Chu, C.-H.; Lee, C.-J.; Yeh, H.-Y. Developing Deep Survival Model for Remaining Useful Life Estimation Based on Convolutional and Long Short-Term Memory Neural Networks. Wirel. Commun. Mob. Comput. 2020, 2020, 8814658. [Google Scholar] [CrossRef]
- Cui, L.; Wang, X.; Wang, H.; Ma, J. Research on Remaining Useful Life Prediction of Rolling Element Bearings Based on Time-Varying Kalman Filter. IEEE Trans. Instrum. Meas. 2020, 69, 2858–2867. [Google Scholar] [CrossRef]
- Sharma, P.; Bora, B.J.J. A Review of Modern Machine Learning Techniques in the Prediction of Remaining Useful Life of Lithium-Ion Batteries. Batteries 2023, 9, 13. [Google Scholar] [CrossRef]
- Ordonez, C.; Lasheras, F.S.; Roca-Pardinas, J.; de Juez, F.J.C. A hybrid ARIMA-SVM model for the study of the remaining useful life of aircraft engines. J. Comput. Appl. Math. 2019, 346, 184–191. [Google Scholar] [CrossRef]
- Ni, Q.; Ji, J.C.; Feng, K. Data-Driven Prognostic Scheme for Bearings Based on a Novel Health Indicator and Gated Recurrent Unit Network. IEEE Trans. Ind. Inform. 2023, 19, 1301–1311. [Google Scholar] [CrossRef]
- Mao, W.; Chen, J.; Liu, J.; Liang, X. Self-Supervised Deep Domain-Adversarial Regression Adaptation for Online Remaining Useful Life Prediction of Rolling Bearing Under Unknown Working Condition. IEEE Trans. Ind. Inform. 2023, 19, 1227–1237. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, H.; Jin, Y.; Dang, X.; Deng, W. Feature Extraction for Data-Driven Remaining Useful Life Prediction of Rolling Bearings. IEEE Trans. Instrum. Meas. 2021, 70, 3511910. [Google Scholar] [CrossRef]
- Chen, Y.; Peng, G.; Zhu, Z.; Li, S. A novel deep learning method based on attention mechanism for bearing remaining useful life prediction. Appl. Soft Comput. 2020, 86, 105919. [Google Scholar] [CrossRef]
- Ge, M.-F.; Liu, Y.; Jiang, X.; Liu, J. A review on state of health estimations and remaining useful life prognostics of lithium-ion batteries. Measurement 2021, 174, 109057. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Pecht, M.G. Long Short-Term Memory Recurrent Neural Network for Remaining Useful Life Prediction of Lithium-Ion Batteries. IEEE Trans. Veh. Technol. 2018, 67, 5695–5705. [Google Scholar] [CrossRef]
- Lipu, M.H.; Hannan, M.; Hussain, A.; Hoque, M.; Ker, P.J.; Saad, M.; Ayob, A. A review of state of health and remaining useful life estimation methods for lithium-ion battery in electric vehicles: Challenges and recommendations. J. Clean. Prod. 2018, 205, 115–133. [Google Scholar] [CrossRef]
- Ren, L.; Zhao, L.; Hong, S.; Zhao, S.; Wang, H.; Zhang, L. Remaining Useful Life Prediction for Lithium-Ion Battery: A Deep Learning Approach. IEEE Access 2018, 6, 50587–50598. [Google Scholar] [CrossRef]
- Wang, B.; Lei, Y.; Li, N.; Yan, T. Deep separable convolutional network for remaining useful life prediction of machinery. Mech. Syst. Signal Process. 2019, 134, 106330. [Google Scholar] [CrossRef]
- Ellefsen, L.; Bjorlykhaug, E.; Aesoy, V.; Ushakov, S.; Zhang, H. Remaining useful life predictions for turbofan engine degradation using semi-supervised deep architecture. Reliab. Eng. Syst. Saf. 2019, 183, 240–251. [Google Scholar] [CrossRef]
- Miao, H.; Li, B.; Sun, C.; Liu, J. Joint Learning of Degradation Assessment and RUL Prediction for Aeroengines via Dual-Task Deep LSTM Networks. IEEE Trans. Ind. Inform. 2019, 15, 5023–5032. [Google Scholar] [CrossRef]
- Huang, C.-G.; Huang, H.-Z.; Li, Y.-F. A Bidirectional LSTM Prognostics Method Under Multiple Operational Conditions. IEEE Trans. Ind. Electron. 2019, 66, 8792–8802. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, M.; Zhao, R.; Guretno, F.; Yan, R.; Li, X. Machine Remaining Useful Life Prediction via an Attention-Based Deep Learning Approach. IEEE Trans. Ind. Electron. 2021, 68, 2521–2531. [Google Scholar] [CrossRef]
- Ji, D.; Wang, C.; Li, J.H.; Dong, H.L. A review: Data driven-based fault diagnosis and RUL prediction of petroleum machinery and equipment. Syst. Sci. Control Eng. 2021, 9, 724–747. [Google Scholar] [CrossRef]
- Cai, B.; Shao, X.; Liu, Y.; Kong, X.; Wang, H.; Xu, H.; Ge, W. Remaining Useful Life Estimation of Structure Systems Under the Influence of Multiple Causes: Subsea Pipelines as a Case Study. IEEE Trans. Ind. Electron. 2020, 67, 5737–5747. [Google Scholar] [CrossRef]
- Elforjani, M.; Shanbr, S. Prognosis of Bearing Acoustic Emission Signals Using Supervised Machine Learning. IEEE Trans. Ind. Electron. 2018, 65, 5864–5871. [Google Scholar] [CrossRef]
- Ahmad, W.; Khan, S.A.; Kim, J.M. Estimating the remaining useful life of bearings using a neuro-local linear estimator-based method. J. Acoust. Soc. Am. 2017, 141, EL452–EL457. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, W.; Khan, S.A.; Kim, J.M. A Hybrid Prognostics Technique for Rolling Element Bearings Using Adaptive Predictive Models. IEEE Trans. Ind. Electron. 2018, 65, 1577–1584. [Google Scholar] [CrossRef]
- Lei, Y.G.; Li, N.P.; Lin, J. A New Method Based on Stochastic Process Models for Machine Remaining Useful Life Prediction. IEEE Trans. Instrum. Meas. 2016, 65, 2671–2684. [Google Scholar] [CrossRef]
- Li, N.P.; Lei, Y.G.; Lin, J.; Ding, S.X. An Improved Exponential Model for Predicting Remaining Useful Life of Rolling Element Bearings. IEEE Trans. Ind. Electron. 2015, 62, 7762–7773. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Si, X.S.; Hu, C.H. An Age- and State-Dependent Nonlinear Prognostic Model for Degrading Systems. IEEE Trans. Reliab. 2015, 64, 1214–1228. [Google Scholar] [CrossRef]
- Singleton, R.K.; Strangas, E.G.; Aviyente, S. Extended Kalman Filtering for Remaining-Useful-Life Estimation of Bearings. IEEE Trans. Ind. Electron. 2015, 62, 1781–1790. [Google Scholar] [CrossRef]
- Medjaher, K.; Zerhouni, N.; Baklouti, J. Data-driven prognostics based on health indicator construction: Application to PRONOSTIA’s data. In Proceedings of the European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 1451–1456. [Google Scholar]
- Li, H.R.; Wang, Y.K.; Wang, B.; Sun, J.; Li, Y.L. The application of a general mathematical morphological particle as a novel indicator for the performance degradation assessment of a bearing. Mech. Syst. Signal Process. 2017, 82, 490–502. [Google Scholar] [CrossRef]
- Deutsch, J.; He, D. Using Deep Learning-Based Approach to Predict Remaining Useful Life of Rotating Components. IEEE Trans. Syst. Man Cybern.-Syst. 2018, 48, 11–20. [Google Scholar] [CrossRef]
- Loutas, T.H.; Roulias, D.; Georgoulas, G. Remaining Useful Life Estimation in Rolling Bearings Utilizing Data-Driven Probabilistic E-Support Vectors Regression. IEEE Trans. Reliab. 2013, 62, 821–832. [Google Scholar] [CrossRef]
- Gebraeel, N.; Lawley, M.; Liu, R.; Parmeshwaran, V. Residual life, predictions from vibration-based degradation signals: A neural network approach. IEEE Trans. Ind. Electron. 2004, 51, 694–700. [Google Scholar] [CrossRef]
- Gasperin, M.; Juricic, D.; Boskoski, P.; Vizintin, J. Model-based prognostics of gear health using stochastic dynamical models. Mech. Syst. Signal Process. 2011, 25, 537–548. [Google Scholar] [CrossRef]
- Hu, J.F.; Tse, P.W. A Relevance Vector Machine-Based Approach with Application to Oil Sand Pump Prognostics. Sensors 2013, 13, 12663–12686. [Google Scholar] [CrossRef] [PubMed]
- Wen, P.F.; Zhao, S.; Chen, S.W.; Li, Y. A generalized remaining useful life prediction method for complex systems based on composite health indicator. Reliab. Eng. Syst. Saf. 2021, 205, 107241. [Google Scholar] [CrossRef]
- Baraldi, P.; Bonfanti, G.; Zio, E. Differential evolution-based multi-objective optimization for the definition of a health indicator for fault diagnostics and prognostics. Mech. Syst. Signal Process. 2018, 102, 382–400. [Google Scholar] [CrossRef]
- Widodo, A.; Yang, B.S. Application of relevance vector machine and survival probability to machine degradation assessment. Expert Syst. Appl. 2011, 38, 2592–2599. [Google Scholar] [CrossRef]
- Zhao, M.H.; Tang, B.P.; Tan, Q. Bearing remaining useful life estimation based on time-frequency representation and supervised dimensionality reduction. Measurement 2016, 86, 41–55. [Google Scholar] [CrossRef]
- Fang, X.L.; Paynabar, K.; Gebraeel, N. Multistream sensor fusion-based prognostics model for systems with single failure modes. Reliab. Eng. Syst. Saf. 2017, 159, 322–331. [Google Scholar] [CrossRef]
- Fang, X.L.; Gebraeel, N.Z.; Paynabar, K. Scalable prognostic models for large-scale condition monitoring applications. Iise Trans. 2017, 49, 698–710. [Google Scholar] [CrossRef]
- Yang, H.B.; Sun, Z.; Jiang, G.D.; Zhao, F.; Mei, X.S. Remaining useful life prediction for machinery by establishing scaled-corrected health indicators. Measurement 2020, 163, 108035. [Google Scholar] [CrossRef]
- Guo, L.; Lei, Y.G.; Li, N.P.; Yan, T.; Li, N.B. Machinery health indicator construction based on convolutional neural networks considering trend burr. Neurocomputing 2018, 292, 142–150. [Google Scholar] [CrossRef]
- Guo, L.; Li, N.P.; Jia, F.; Lei, Y.G.; Lin, J. A recurrent neural network based health indicator for remaining useful life prediction of bearings. Neurocomputing 2017, 240, 98–109. [Google Scholar] [CrossRef]
- de Beaulieu, M.H.; Jha, M.S.; Garnier, H.; Cerbah, F. Unsupervised Remaining Useful Life Estimation Based on Deep Virtual Health Index Long-range Prediction. In Proceedings of the 11th IFAC Symposium on Fault Detection, Supervision and Safety for Technical Processes-SAFEPROCESS, Pafos, Cyprus, 7–10 June 2022. [Google Scholar]
- Peng, K.X.; Jiao, R.H.; Dong, J.; Pi, Y.T. A deep belief network based health indicator construction and remaining useful life prediction using improved particle filter. Neurocomputing 2019, 361, 19–28. [Google Scholar] [CrossRef]
- Qiu, H.; Lee, J.; Lin, J.; Yu, G. Robust performance degradation assessment methods for enhanced rolling element bearing prognostics. Adv. Eng. Inform. 2003, 17, 127–140. [Google Scholar] [CrossRef]
- Hong, S.; Zhou, Z.; Zio, E.; Hong, K. Condition assessment for the performance degradation of bearing based on a combinatorial feature extraction method. Digit. Signal Process. 2014, 27, 159–166. [Google Scholar] [CrossRef]
- Hong, S.; Zhou, Z.; Zio, E.; Wang, W.B. An adaptive method for health trend prediction of rotating bearings. Digit. Signal Process. 2014, 35, 117–123. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Gontarz, S.; Lin, J.; Radkowski, S.; Dybala, J. A Model-Based Method for Remaining Useful Life Prediction of Machinery. IEEE Trans. Reliab. 2016, 65, 1314–1326. [Google Scholar] [CrossRef]
- Niu, G.; Yang, B.S. Intelligent condition monitoring and prognostics system based on data-fusion strategy. Expert Syst. Appl. 2010, 37, 8831–8840. [Google Scholar] [CrossRef]
- Krenker, J.; Bešter, J.; Kos, A. Introduction to the artificial neural networks. In Artificial Neural Networks—Methodological Advances and Biomedical Applications; IntechOpen: London, UK, 2011; pp. 1–18. [Google Scholar]
- Agatonovic-Kustrin, S.; Beresford, R. Basic concepts of artificial neural network (ANN) modeling and its application in pharmaceutical research. J. Pharm. Biomed. Anal. 2000, 22, 717–727. [Google Scholar] [CrossRef] [PubMed]
- Uhrig, R.E. Introduction to artificial neural network. In Proceedings of the IECON’95-21st Annual Conference on IEEE Industrial Electronics, Orlando, FL, USA, 6–10 November 1995; Volume 1, pp. 33–37. [Google Scholar]
- Ali, J.B.; Chebel-Morello, B.; Saidi, L.; Malinowski, S.; Fnaiech, F. Accurate bearing remaining useful life prediction based on Weibull distribution and artificial neural network. Mech. Syst. Signal Process. 2015, 56–57, 150–172. [Google Scholar] [CrossRef]
- Tian, Z. An artificial neural network method for remaining useful life prediction of equipment subject to condition monitoring. J. Intell. Manuf. 2012, 23, 227–237. [Google Scholar] [CrossRef]
- Xia, M.; Li, T.; Shu, T.; Wan, J.; de Silva, C.W.; Wang, Z. A Two-Stage Approach for the Remaining Useful Life Prediction of Bearings Using Deep Neural Networks. IEEE Trans. Ind. Inform. 2019, 15, 3703–3711. [Google Scholar] [CrossRef]
- Shihabudheen, K.V.; Pillai, G.N. Recent advances in neuro-fuzzy system: A survey. Knowl. Based Syst. 2018, 152, 136–162. [Google Scholar] [CrossRef]
- Nauck, D.; Kruse, R. Handbook of Fuzzy Computation; CRC Press: Boca Raton, FL, USA, 2020; pp. 319–D312. [Google Scholar]
- Nauck, D.; Kruse, R. A neuro-fuzzy method to learn fuzzy classification rules from data. Fuzzy Sets Syst. 1997, 89, 277–288. [Google Scholar] [CrossRef]
- Kar, S.; Das, S.; Ghosh, P.K. Applications of neuro fuzzy systems: A brief review and future outline. Appl. Soft Comput. 2014, 15, 243–259. [Google Scholar] [CrossRef]
- Flexible Neuro-Fuzzy Systems: Structures, Learning and Performance Evaluation—L. Rutkowski (Boston, MA: Kluwer Academic Publishers, 2004, ISBN: 1-402-08042-5) Reviewed by A. E. Gaweda. IEEE Trans. Neural Netw. 2006, 17, 270. [CrossRef]
- Huang, H.-Z.; Wang, H.-K.; Li, Y.-F.; Zhang, L.; Liu, Z. Support vector machine based estimation of remaining useful life: Current research status and future trends. J. Mech. Sci. Technol. 2015, 29, 151–163. [Google Scholar] [CrossRef]
- Shen, F.; Yan, R. A New Intermediate-Domain SVM-Based Transfer Model for Rolling Bearing RUL Prediction. IEEE/ASME Trans. Mechatron. 2022, 27, 1357–1369. [Google Scholar] [CrossRef]
- Tran, V.T.; Pham, H.T.; Yang, B.-S.; Nguyen, T.T. Machine Performance Degradation Assessment and Remaining Useful Life Prediction Using Proportional Hazard Model and SVM. In Proceedings of the Engineering Asset Management and Infrastructure Sustainability: Proceedings of the 5th World Congress on Engineering Asset Management (WCEAM 2010), London, UK, 1 January 2012; pp. 959–970. [Google Scholar] [CrossRef]
- Nieto, P.J.G.; García-Gonzalo, E.; Lasheras, F.S.; de Juez, F.J.C. Hybrid PSO–SVM-based method for forecasting of the remaining useful life for aircraft engines and evaluation of its reliability. Reliab. Eng. Syst. Saf. 2015, 138, 219–231. [Google Scholar] [CrossRef]
- Wang, Y.; Ni, Y.; Lu, S.; Wang, J.; Zhang, X. Remaining Useful Life Prediction of Lithium-Ion Batteries Using Support Vector Regression Optimized by Artificial Bee Colony. IEEE Trans. Veh. Technol. 2019, 68, 9543–9553. [Google Scholar] [CrossRef]
- Hong, W.-C. Electric load forecasting by seasonal recurrent SVR (support vector regression) with chaotic artificial bee colony algorithm. Energy 2011, 36, 5568–5578. [Google Scholar] [CrossRef]
- Chen, Z.; Shi, N.; Ji, Y.; Niu, M.; Wang, Y. Lithium-ion batteries remaining useful life prediction based on BLS-RVM. Energy 2021, 234, 121269. [Google Scholar] [CrossRef]
- Zhang, G.; Liang, W.; She, B.; Tian, F.; Rainieri, C. Rotating Machinery Remaining Useful Life Prediction Scheme Using Deep-Learning-Based Health Indicator and a New RVM. Shock Vib. 2021, 2021, 8815241. [Google Scholar] [CrossRef]
- Wang, J. An Intuitive Tutorial to Gaussian Processes Regression. arXiv 2020. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Z. Remaining Useful Life Prediction of Lithium-Ion Batteries Based on Health Indicator and Gaussian Process Regression Model. IEEE Access 2019, 7, 39474–39484. [Google Scholar] [CrossRef]
- Kang, W.; Xiao, J.; Xiao, M.; Hu, Y.; Zhu, H.; Li, J. Research on Remaining Useful Life Prognostics Based on Fuzzy Evaluation-Gaussian Process Regression Method. IEEE Access 2020, 8, 71965–71973. [Google Scholar] [CrossRef]
- Liu, K.; Shang, Y.; Ouyang, Q.; Widanage, W.D. A Data-Driven Approach with Uncertainty Quantification for Predicting Future Capacities and Remaining Useful Life of Lithium-ion Battery. IEEE Trans. Ind. Electron. 2021, 68, 3170–3180. [Google Scholar] [CrossRef]
- Zhu, R.; Chen, Y.; Peng, W.; Ye, Z.-S. Bayesian deep-learning for RUL prediction: An active learning perspective. Reliab. Eng. Syst. Saf. 2022, 228, 108758. [Google Scholar] [CrossRef]
- Guo, Q.; He, Z.; Wang, Z.; Qiao, S.; Zhu, J.; Chen, J. A Performance Comparison Study on Climate Prediction in Weifang City Using Different Deep Learning Models. Water 2024, 16, 2870. [Google Scholar] [CrossRef]





| Data Type | Data Volume | Applicable Models | Refs. |
|---|---|---|---|
| Full degradation data | Data for the entire degradation process from normal to failure |
| [2,3,4,5,6,7,8,9,10,11] |
| Partial degradation data | Partial data from the normal state to the moment of failure and safety thresholds for failure thresholds |
| [12] [13,14,15,16,17] |
| Moment of failure data | Fault data and some covariates associated with RUL |
| [18,19,20,21] |
| Installations | Rolling Bearings | Lithium-Ion Batteries | Turbofan Engines |
|---|---|---|---|
| Application areas | Service industry Aerospace Heavy industry | New energy industry Electronic equipment Aerospace | Aerospace |
| Common working environment | High temperature and pressure Wet or dry Operating at extreme speeds Overloaded | Long-term continuous operation High charge/discharge frequency Installed in automobiles or airplanes Variable environment | High temperature and pressure Operating at extreme speeds Overloaded |
| Common input features | Vibration frequency Temperature | Voltage Resistance Charge and discharge time Charge and discharge voltage Capacitance | Diverse and full sensor monitoring data |
| Data characteristics | Small fluctuations in change during the normal phase and a clear trend during the degradation phase Data information contains a lot of noise | Many considerations Lower data volume | High volume and complexity of data Different levels of correlation between data |
| Key to forecasting | Denoising Filtering out sensitive features rich in degradation information | Selection of single or multiple judgmental features Sensitivity of model parameters to prevent overfitting and underfitting | Removal of redundant information Filtering features related to RUL Ranking features and constructing RUL labels for different degradation modes |
| Difficulty in forecasting | Phased degradation Mostly requires full-cycle data | Some data difficult to access Data acquisition is easily interfered with Varying environments and operating conditions Complex modeling makes it difficult to ensure accuracy | Data preprocessing Multi-dimensional data feature integration Feature mapping modeling Information gradient vanishing/explosion |
| Refs. | Chen et al. [37], Ji et al. [38], Cai et al. [39] | Ge et al. [29], Zhang et al. [30], Lipu et al. [31], Elforjani et al. [40], Sharma et al. [23] | Wang et al. [33], Ellefsen et al. [34], Miao et al. [35], Huang et al. [36], Ordonez et al. [24] |
| Names | Model Complexity | Scalability | Interpretability | Data Requirements | Features | Refs. |
|---|---|---|---|---|---|---|
| Artificial neural network | Medium–high Increases with more hidden layers and neurons | High Can scale well with large datasets and complex models through distributed training and hardware acceleration | Low Neural networks are often considered “black-box” models and are difficult to interpret | High Requires a large amount of data to train neural networks to avoid overfitting | Ability to model complex nonlinear relationships During training, the connections between the cells are optimized until the prediction error is minimized and the network reaches a specified level of accuracy | [70,71,72,73,74,75] |
| Neuro-fuzzy system | Medium–high Combines neural network and fuzzy system structures, with model complexity depending on the number of layers in the neural network part and the number of fuzzy rules | Medium Can scale with large datasets but may require careful tuning of the neural network part and fuzzy rules | Medium Fuzzy rules provide some interpretability, but the neural network part is harder to interpret | Medium Needs a certain amount of data to train the neural network part and generate fuzzy rules | Fast learning speed Strong self-adjustment ability Low computational complexity | [76,77,78,79,80] |
| Support vector machine | Medium Depends on the number of support vectors and feature dimensions | Medium Can handle large datasets but may require more computational resources and optimization techniques | Medium The model can be interpreted to some extent through support vectors and decision boundaries | Low–medium Performs well on small-scale datasets but can also benefit from large-scale datasets | Excellent generalization ability and mathematical foundation | [16,24,81,82,83,84] |
| Support vector regression | Medium–high Similar to SVM, but regression tasks may require more complex kernel functions and parameter tuning | Medium Similar to SVM, with potential scalability challenges for very large datasets | Medium Similar to SVM, the regression function and related parameters can be used to explain the model | Low–medium Similar to SVM, with good adaptability to small-scale datasets | The ability to transform optimization problems into unconstrained dual problems The ability to map nonlinear data to high-dimensional feature spaces | [85,86] |
| Relevance vector machine | Medium–high Similar to SVM, but may involve more complex optimization processes to determine relevance vectors | Medium Can scale to large datasets but may require significant computational resources | Medium The model can be interpreted to some extent through support vectors and decision boundaries | Low Relevance vector machine works well on small-scale datasets | Can provide the mean and variance of the predicted values Can produce sparser models than SVM | [87,88] |
| Gaussian regression process | High Bayesian non-parametric model based on kernel functions, with a significant increase in computational complexity as the data volume increases | Low Computationally intensive and may struggle with very large datasets due to its Bayesian nature and need for matrix inversion | Medium The mean function and covariance function of the Gaussian process provide a certain level of interpretability | Low Gaussian process regression performs well on small-scale datasets, but the computational cost is high for large-scale datasets | Ability to handle problems with a small sample size Ability to adapt the complexity of the model to avoid overfitting | [89,90,91,92] |
| Hybrid method | High Combines multiple algorithms, with model complexity depending on the number and types of algorithms integrated | Medium–high Depends on the scalability of the individual algorithms integrated and the overall system design | Low–medium The interpretability of hybrid methods depends on the algorithms integrated, and the overall model may be more difficult to interpret | Medium–high Depends on the algorithms integrated, as more data may be required to train each sub-model | Combine the benefits of multiple models Can complement each other’s shortcomings among models | [88,91,93,94] |
| Algorithm | RUL | PRUL | MAE | RMSE | Ea | Er |
|---|---|---|---|---|---|---|
| LSTM (A5) | 80 | 78 | 0.0120 | 0.0168 | 2 | 2.50% |
| LSTM (A8) | 17 | 27 | 0.1070 | 0.1229 | 10 | 58.90% |
| SVR (B0005 40%) | 111 | 125 | 0.0383 | 0.0417 | 14 | 12.61% |
| SVR (B0006 40%) | 99 | 99 | 0.0228 | 0.0325 | 0 | 0% |
| SVR (B0007 40%) | 146 | 144 | 0.0101 | 0.0138 | 2 | 1.37% |
| SVR (B0018 40%) | 88 | 85 | 0.0146 | 0.0162 | 3 | 3.41% |
| SVR (B0005 50%) | 111 | 115 | 0.0184 | 0.0212 | 4 | 3.60% |
| SVR (B0006 50%) | 99 | 98 | 0.0212 | 0.0314 | 1 | 1.01% |
| SVR (B0007 50%) | 146 | 155 | 0.0067 | 0.0114 | 9 | 6.16% |
| SVR (B0018 50%) | 83 | 84 | 0.1031 | 0.0131 | 1 | 1.20% |
| PF-LSTM (A5) | 81 | 80 | 0.0070 | 0.0083 | 1 | 1.23% |
| PF-LSTM (A8) | 17 | 17 | 0.0064 | 0.0078 | 0 | 0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Chen, J.; Chen, S.; Li, P.; Zhang, B.; Wang, M.; Yang, M.; Wang, J.; Zhou, D.; Yun, J. A Comprehensive Review of Artificial Intelligence-Based Algorithms for Predicting the Remaining Useful Life of Equipment. Sensors 2025, 25, 4481. https://doi.org/10.3390/s25144481
Li W, Chen J, Chen S, Li P, Zhang B, Wang M, Yang M, Wang J, Zhou D, Yun J. A Comprehensive Review of Artificial Intelligence-Based Algorithms for Predicting the Remaining Useful Life of Equipment. Sensors. 2025; 25(14):4481. https://doi.org/10.3390/s25144481
Chicago/Turabian StyleLi, Weihao, Jianhua Chen, Sijuan Chen, Peilin Li, Bing Zhang, Ming Wang, Ming Yang, Jipu Wang, Dejian Zhou, and Junsen Yun. 2025. "A Comprehensive Review of Artificial Intelligence-Based Algorithms for Predicting the Remaining Useful Life of Equipment" Sensors 25, no. 14: 4481. https://doi.org/10.3390/s25144481
APA StyleLi, W., Chen, J., Chen, S., Li, P., Zhang, B., Wang, M., Yang, M., Wang, J., Zhou, D., & Yun, J. (2025). A Comprehensive Review of Artificial Intelligence-Based Algorithms for Predicting the Remaining Useful Life of Equipment. Sensors, 25(14), 4481. https://doi.org/10.3390/s25144481






