Comparing the Accuracy of Soil Moisture Estimates Derived from Bulk and Energy-Resolved Gamma Radiation Measurements
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Site
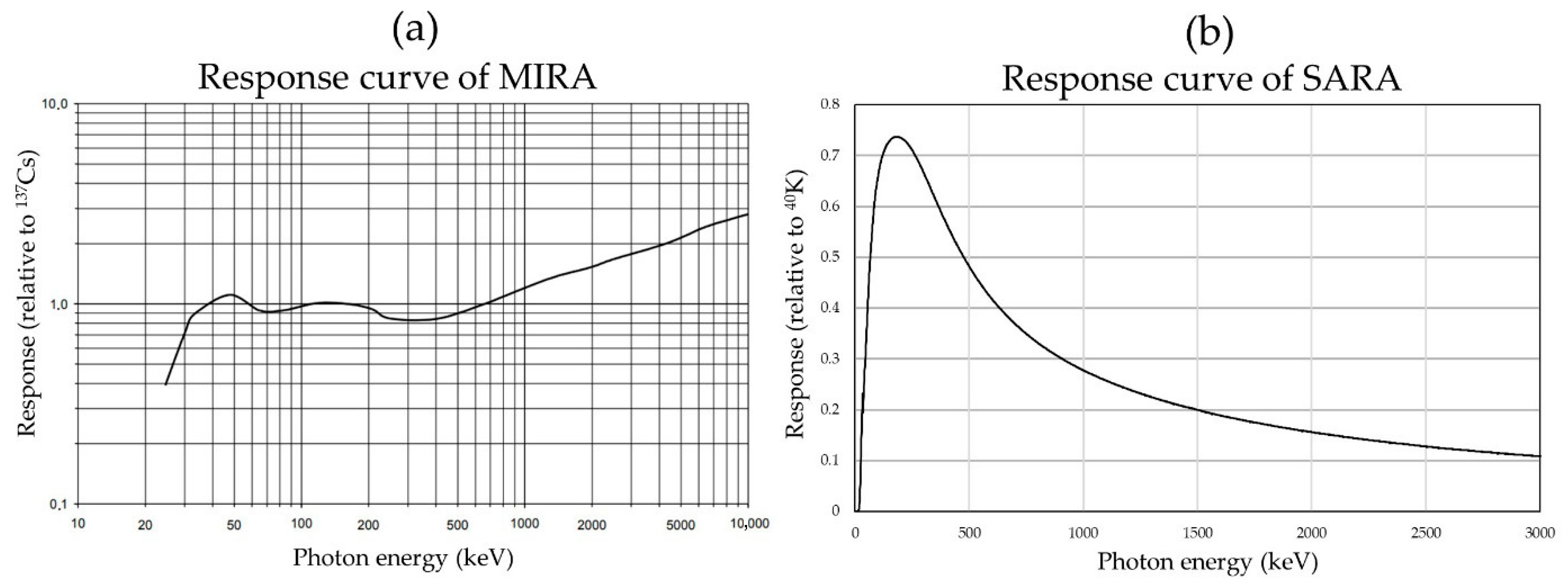
2.2. Experimental Setup
2.3. Data Filtering, Correction and Gap Filling
2.4. Wavelet Analysis
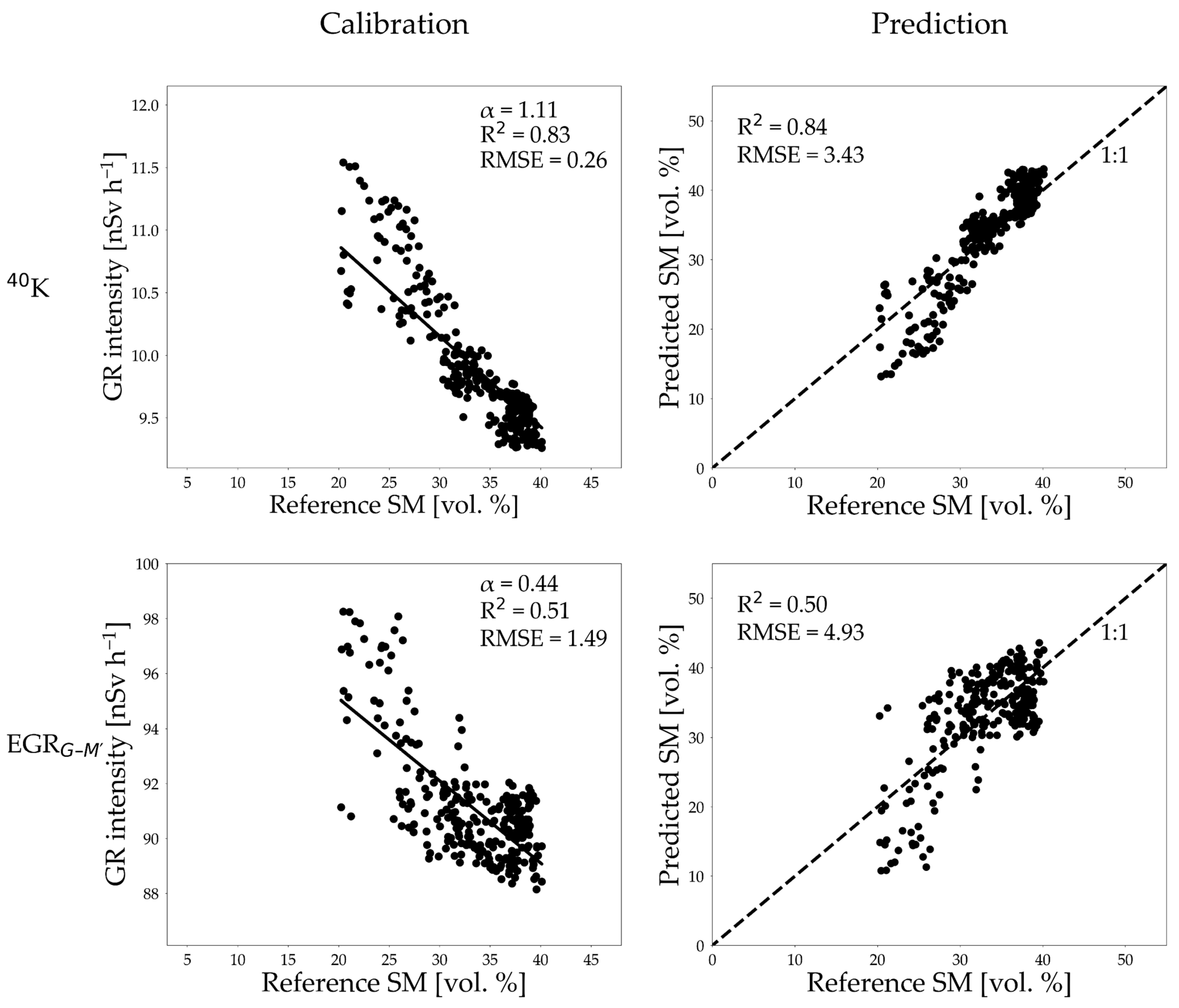
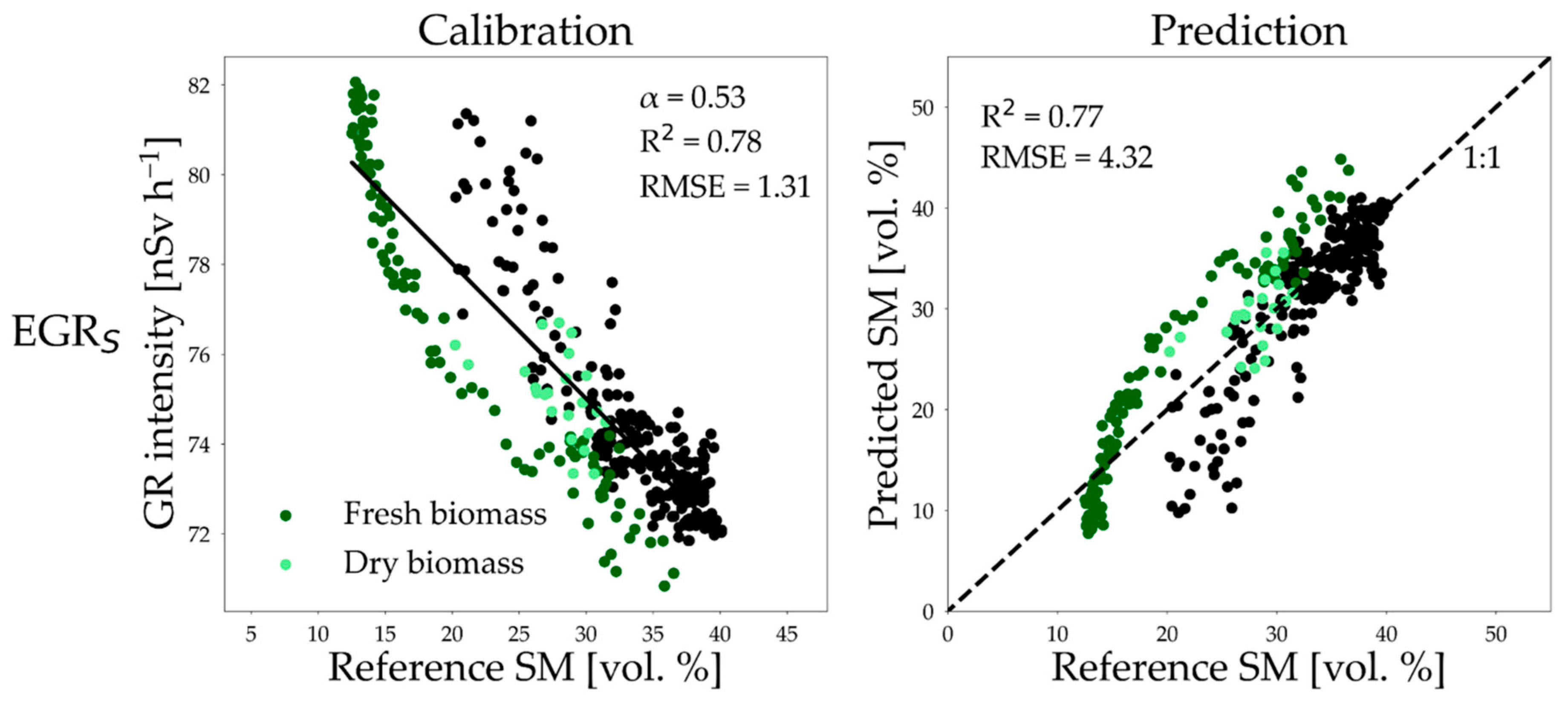
2.5. Soil Moisture Estimation
3. Results and Discussion
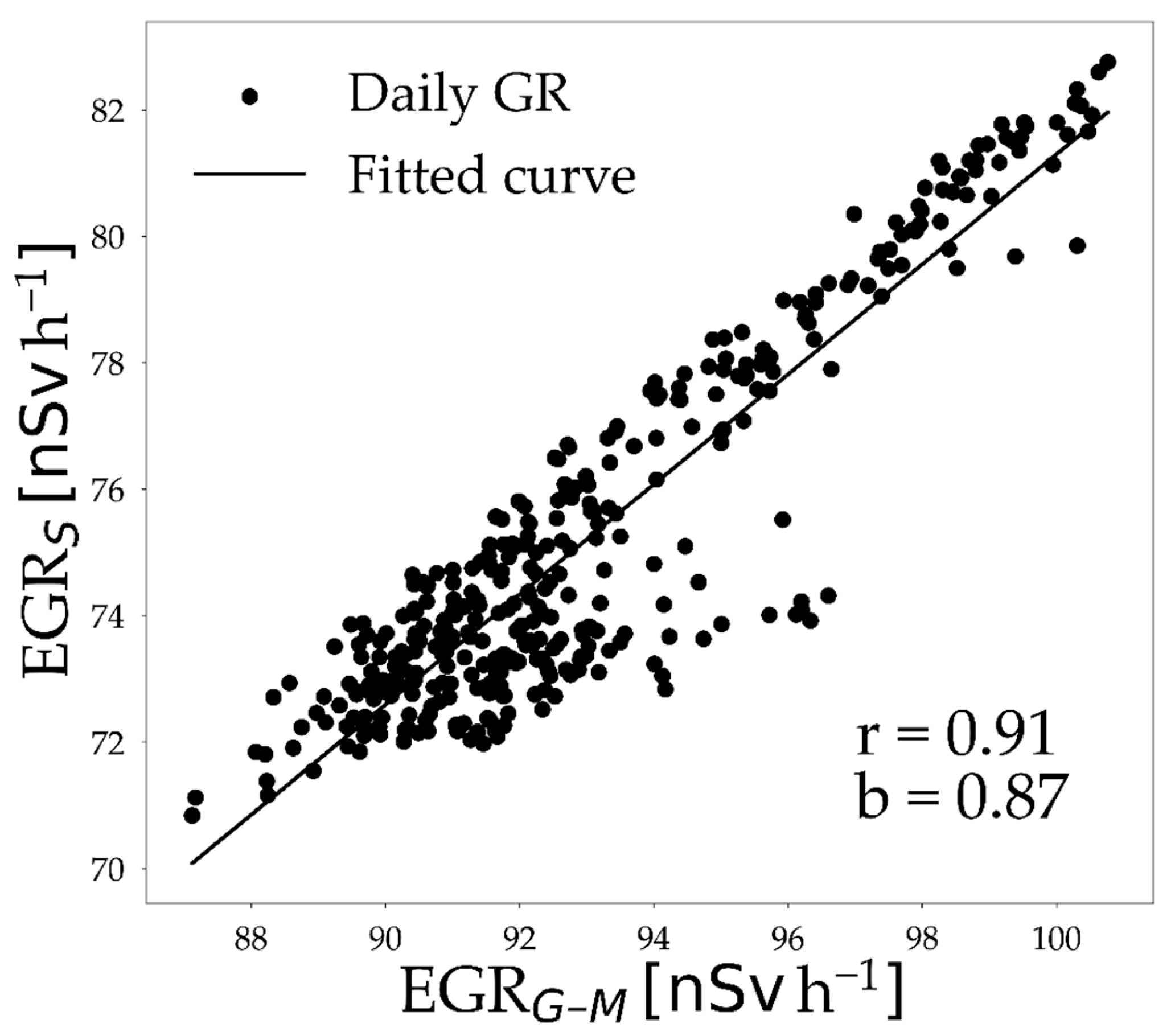
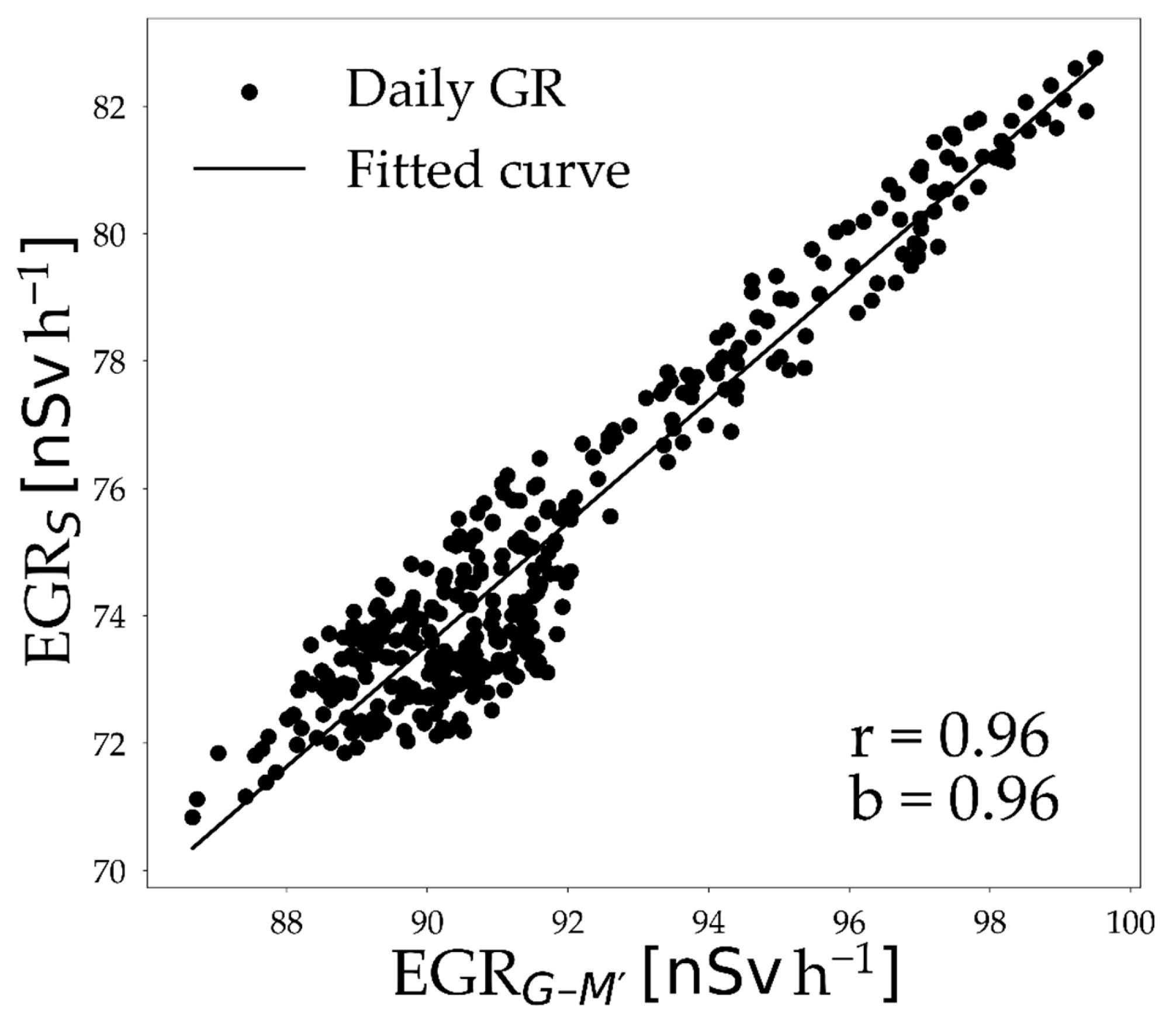
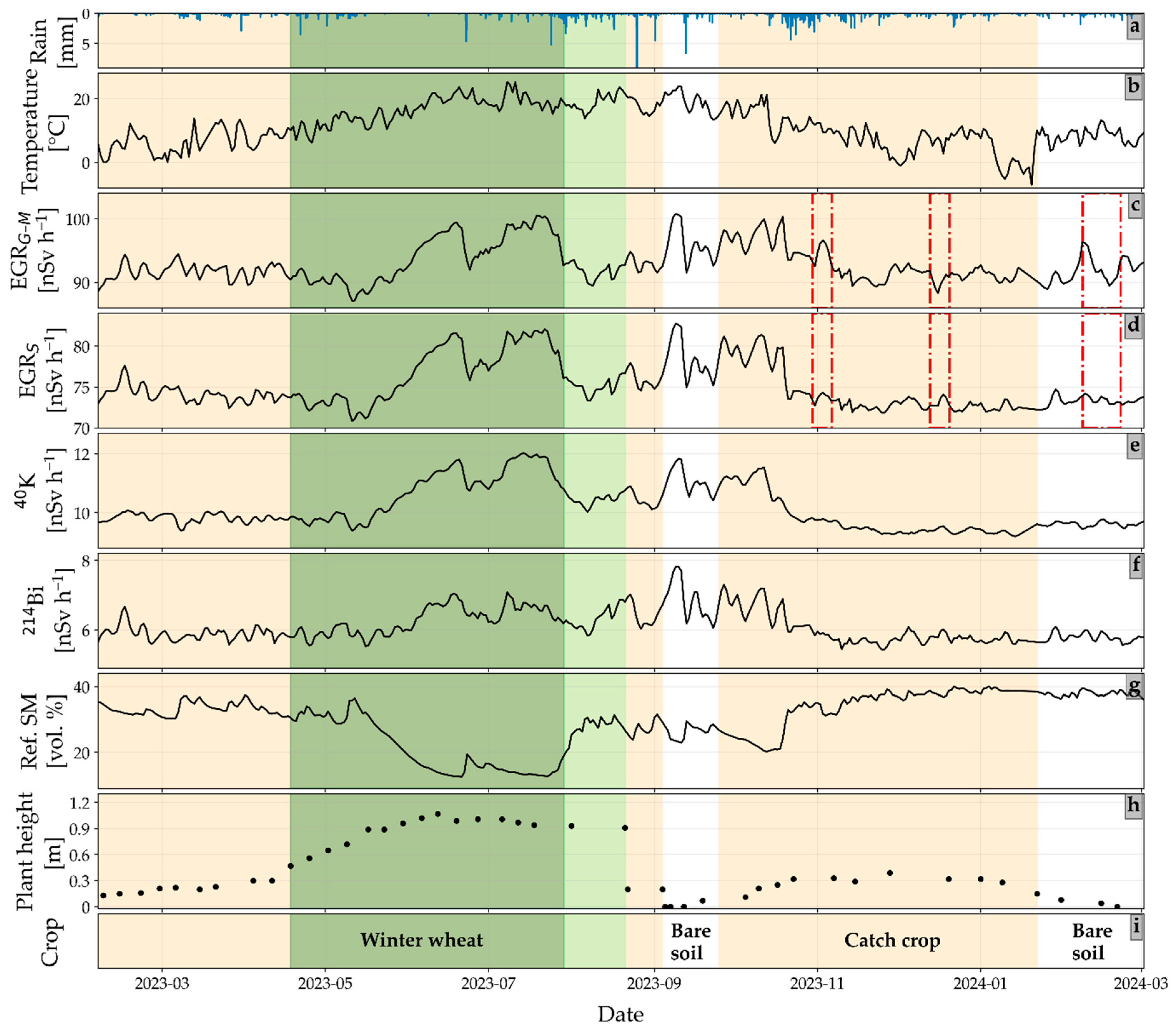
3.1. Analysis of Daily Gamma Radiation (GR) Time Series
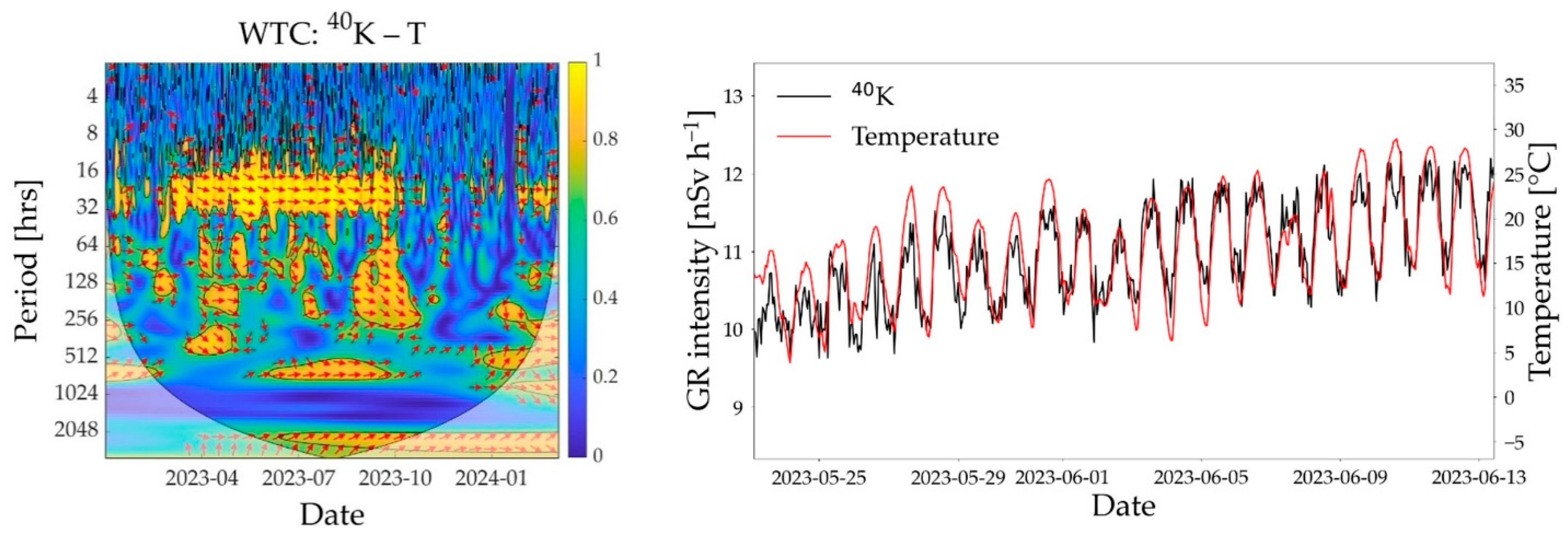
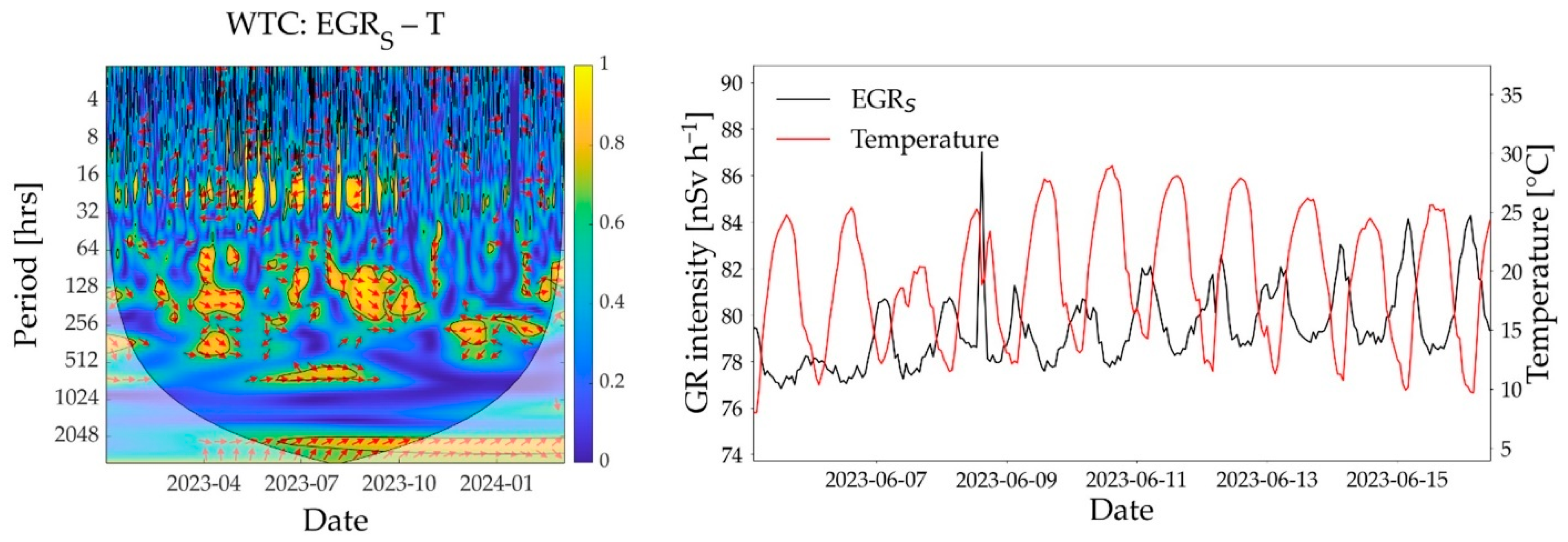
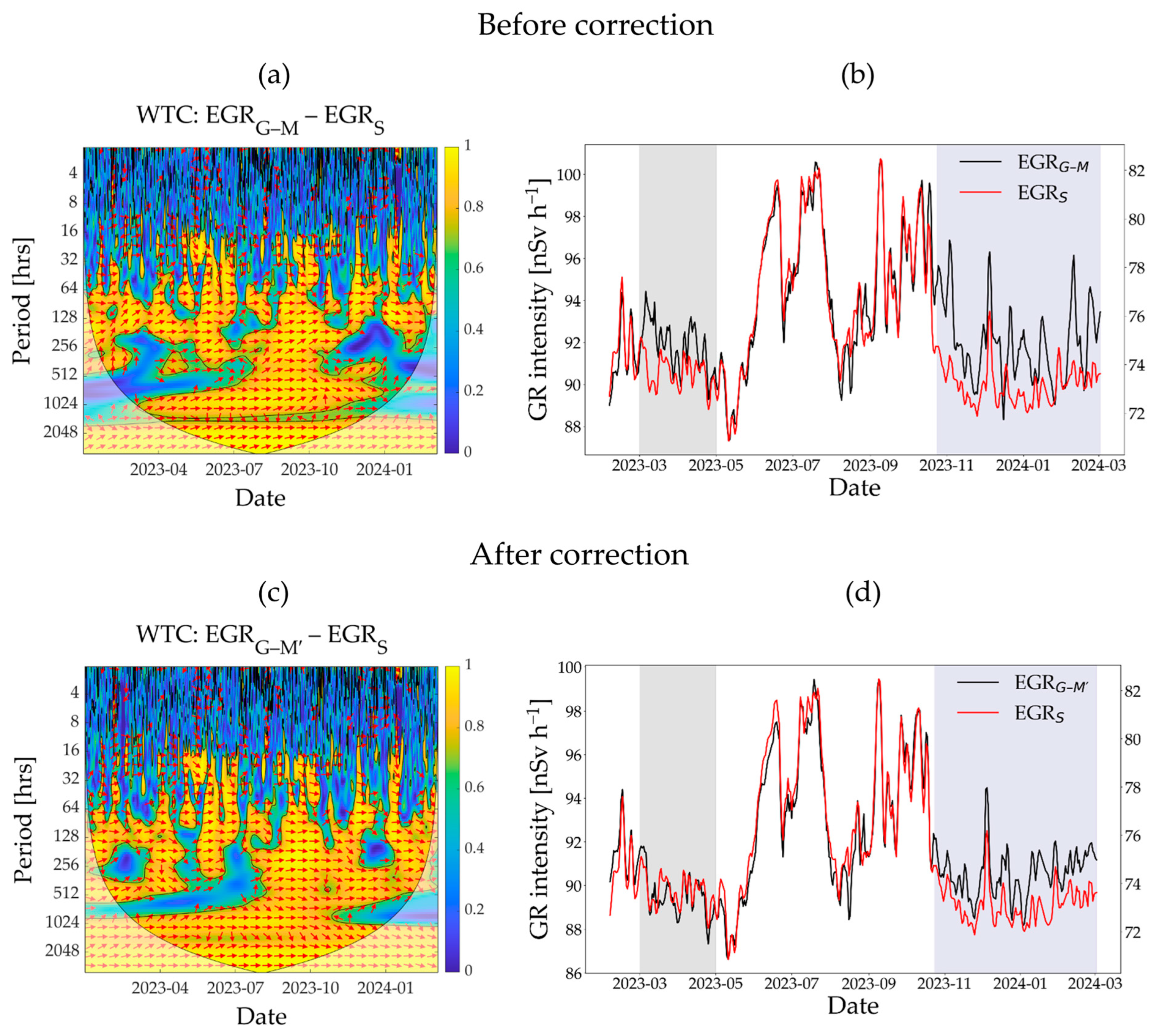
3.2. Wavelet Coherence Analysis
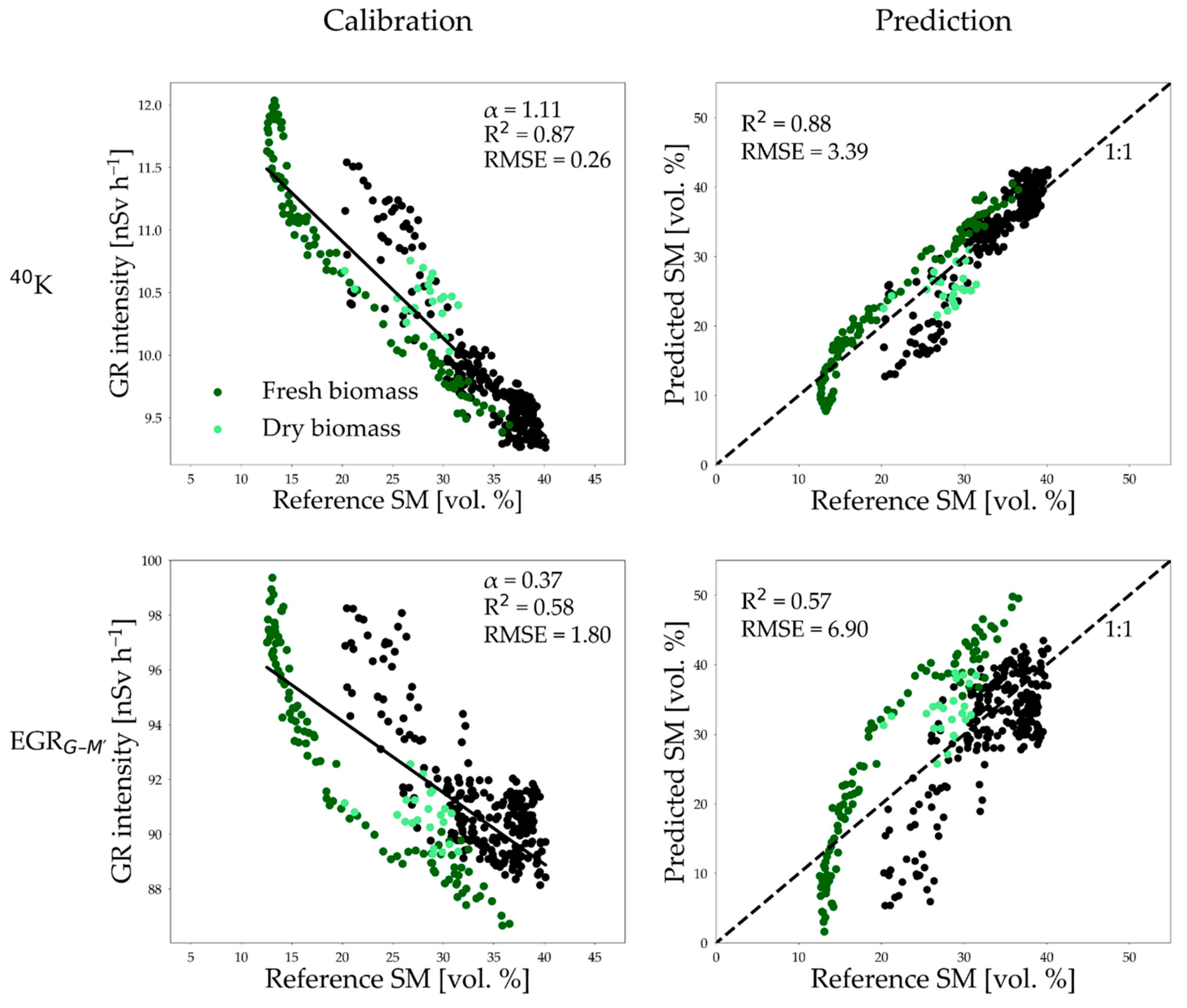
3.3. Influence of Confounding Factors on Soil Moisture Estimation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SM | Soil moisture |
| GR | Gamma radiation |
| SCR | Secondary cosmic radiation |
| EGR | Environmental gamma radiation |
| EGRG–M | Environmental gamma radiation measured by the MIRA detector (Geiger–Mueller) |
| EGRG–M′ | Environmental gamma radiation measured by the MIRA detector after correcting for the short-term SCR variability |
| EGRS | Environmental gamma radiation measured by the SARA detector (spectrometer) |
| 40K GR | Gamma radiation from 40K radionuclide measured by the SARA detector |
| 214Bi GR | Gamma radiation from 214Bi radionuclide measured by the SARA detector |
| WTC | Wavelet transform coherence |
| α | The effective ratio of gamma-ray mass attenuation coefficients for water and solid phases |
Appendix A
References
- Vereecken, H.; Amelung, W.; Bauke, S.L.; Bogena, H.; Brüggemann, N.; Montzka, C.; Vanderborght, J.; Bechtold, M.; Blöschl, G.; Carminati, A.; et al. Soil hydrology in the earth system. Nat. Rev. Earth Environ. 2022, 3, 573–587. [Google Scholar] [CrossRef]
- Kim, J.H.; Jackson, R.B. A global analysis of groundwater recharge for vegetation, climate, and soils. Vadose Zone J. 2012, 11, vzj2011.0021RA. [Google Scholar] [CrossRef]
- Ran, Q.; Wang, J.; Chen, X.; Liu, L.; Li, J.; Ye, S. The relative importance of antecedent soil moisture and precipitation in flood generation in the middle and lower yangtze river basin. Hydrol. Earth Syst. Sci. 2022, 26, 4919–4931. [Google Scholar] [CrossRef]
- Tramblay, Y.; Bouvier, C.; Martin, C.; Didon-Lescot, J.-F.; Todorovik, D.; Domergue, J.-M. Assessment of initial soil moisture conditions for event-based rainfall–runoff modelling. J. Hydrol. 2010, 387, 176–187. [Google Scholar] [CrossRef]
- Lohse, K.A.; Brooks, P.D.; McIntosh, J.C.; Meixner, T.; Huxman, T.E. Interactions between biogeochemistry and hydrologic systems. Annu. Rev. Environ. Resour. 2009, 34, 65–96. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture–climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Bogena, H.R.; Huisman, J.A.; Güntner, A.; Hübner, C.; Kusche, J.; Jonard, F.; Vey, S.; Vereecken, H. Emerging methods for noninvasive sensing of soil moisture dynamics from field to catchment scale: A review. WIREs Water 2015, 2, 635–647. [Google Scholar] [CrossRef]
- Baldoncini, M.; Albéri, M.; Bottardi, C.; Chiarelli, E.; Raptis, K.G.C.; Strati, V.; Mantovani, F. Investigating the potentialities of monte carlo simulation for assessing soil water content via proximal gamma-ray spectroscopy. J. Environ. Radioact. 2018, 192, 105–116. [Google Scholar] [CrossRef] [PubMed]
- van der Veeke, S.; Koomans, R.; Limburg, H. Using a gamma-ray spectrometer for soil moisture monitoring: Development of the gamma soil moisture sensor (gSMS). In Proceedings of the 2020 IEEE International Workshop on Metrology for Agriculture and Forestry (MetroAgriFor), Trento, Italy, 4 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 185–190. [Google Scholar]
- Loijens, H.S. Determination of soil water content from terrestrial gamma radiation measurements. Water Resour. Res. 1980, 16, 565–573. [Google Scholar] [CrossRef]
- Amestoy, J.; Meslin, P.-Y.; Richon, P.; Delpuech, A.; Derrien, S.; Raynal, H.; Pique, É.; Baratoux, D.; Chotard, P.; Van Beek, P.; et al. Effects of environmental factors on the monitoring of environmental radioactivity by airborne gamma-ray spectrometry. J. Environ. Radioact. 2021, 237, 106695. [Google Scholar] [CrossRef] [PubMed]
- Carroll, T.R. Airborne soil moisture measurement using natural terrestrial gamma radiation. Soil Sci. 1981, 132, 358–366. [Google Scholar] [CrossRef]
- van der Veeke, S. UAV-borne radioelement mapping: Towards a guideline and verification methods for geophysical field measurements. Ph.D. Thesis, University of Groningen, Groningen, The Netherlands, 2023. [Google Scholar]
- Beamish, D. Gamma ray attenuation in the soils of Northern Ireland, with special reference to peat. J. Environ. Radioact. 2013, 115, 13–27. [Google Scholar] [CrossRef] [PubMed]
- Becker, S.M.; Franz, T.E.; Morris, T.C.; Mullins, B. Field testing of gamma-spectroscopy method for soil water content estimation in an agricultural field. Sensors 2024, 24, 2223. [Google Scholar] [CrossRef] [PubMed]
- Thompson, I.M.G.; Bøtter-Jensen, L.; Deme, S.; Pernicka, F.; Saéz-Vergara, J.C. (Eds.) Technical Recommendations on Measurements of External Environmental Gamma Radiation Doses; a Report of EURADOS Working Group 12 “Environmental Radiation Monitoring”, European Radiation Dosimetry Group; Radiation protection; Commission of the European Communities: Luxembourg, 1999; ISBN 92-828-7811-2. [Google Scholar]
- Dombrowski, H.; Bleher, M.; De Cort, M.; Dabrowski, R.; Neumaier, S.; Stöohlker, U. Recommendations to harmonize european early warning dosimetry network systems. J. Instrum. 2017, 12, P12024. [Google Scholar] [CrossRef]
- Sangiorgi, M.; Hernández-Ceballos, M.A.; Jackson, K.; Cinelli, G.; Bogucarskis, K.; De Felice, L.; Patrascu, A.; De Cort, M. The European radiological data exchange platform (EURDEP): 25 years of monitoring data exchange. Earth Syst. Sci. Data 2020, 12, 109–118. [Google Scholar] [CrossRef]
- Stöhlker, U.; Bleher, M.; Szegvary, T.; Conen, F. Inter-calibration of gamma dose rate detectors on the European scale. Radioprotection 2009, 44, 777–784. [Google Scholar] [CrossRef][Green Version]
- Stöhlker, U.; Bleher, M.; Doll, H.; Dombrowski, H.; Harms, W.; Hellmann, I.; Luff, R.; Prommer, B.; Seifert, S.; Weiler, F. The German dose rate monitoring network and implemented data harmonization techniques. Radiat. Prot. Dosim. 2019, 183, 405–417. [Google Scholar] [CrossRef] [PubMed]
- Thompson, I.M.G.; Andersen, C.E.; Bøtter-Jensen, L.; Funck, E.; Neumaier, S.; Sáez-Vergara, J.C. An international intercomparison of national network systems used to provide early warning of a nuclear accident having transboundary implications. Radiat. Prot. Dosim. 2000, 92, 89–100. [Google Scholar] [CrossRef]
- Bossew, P.; Cinelli, G.; Hernández-Ceballos, M.; Cernohlawek, N.; Gruber, V.; Dehandschutter, B.; Menneson, F.; Bleher, M.; Stöhlker, U.; Hellmann, I.; et al. Estimating the terrestrial gamma dose rate by decomposition of the ambient dose equivalent rate. J. Environ. Radioact. 2017, 166, 296–308. [Google Scholar] [CrossRef] [PubMed]
- Dombrowski, H.; Wissmann, F. Meteorological influences on the results of area dose rate measurements. Kerntechnik 2008, 73, 113–117. [Google Scholar] [CrossRef]
- Akter, S.; Huisman, J.A.; Bogena, H.R. Estimating Soil moisture from environmental gamma radiation monitoring data. Vadose Zone J. 2024, 23, e20384. [Google Scholar] [CrossRef]
- Bottardi, C.; Albéri, M.; Baldoncini, M.; Chiarelli, E.; Montuschi, M.; Raptis, K.G.C.; Serafini, A.; Strati, V.; Mantovani, F. Rain rate and radon daughters’ activity. Atmos. Environ. 2020, 238, 117728. [Google Scholar] [CrossRef]
- Williams, A.G.; Zahorowski, W.; Chambers, S.; Griffiths, A.; Hacker, J.M.; Element, A.; Werczynski, S. The vertical distribution of radon in clear and cloudy daytime terrestrial boundary layers. J. Atmos. Sci. 2011, 68, 155–174. [Google Scholar] [CrossRef]
- Baldoncini, M.; Albéri, M.; Bottardi, C.; Chiarelli, E.; Raptis, K.G.C.; Strati, V.; Mantovani, F. Biomass water content effect on soil moisture assessment via proximal gamma-ray spectroscopy. Geoderma 2019, 335, 69–77. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Zacharias, S.; Loescher, H.W.; Bogena, H.; Kiese, R.; Schrön, M.; Attinger, S.; Blume, T.; Borchardt, D.; Borg, E.; Bumberger, J.; et al. Fifteen years of integrated terrestrial environmental observatories (TERENO) in Germany: Functions, services, and lessons learned. Earths Future 2024, 12, e2024EF004510. [Google Scholar] [CrossRef]
- Heiskanen, J.; Brümmer, C.; Buchmann, N.; Calfapietra, C.; Chen, H.; Gielen, B.; Gkritzalis, T.; Hammer, S.; Hartman, S.; Herbst, M.; et al. The integrated carbon observation system in Europe. Bull. Am. Meteorol. Soc. 2022, 103, E855–E872. [Google Scholar] [CrossRef]
- Bogena, H.R.; Montzka, C.; Huisman, J.A.; Graf, A.; Schmidt, M.; Stockinger, M.; von Hebel, C.; Hendricks-Franssen, H.J.; van der Kruk, J.; Tappe, W.; et al. The TERENO-Rur hydrological observatory: A multiscale multi-compartment research platform for the advancement of hydrological science. Vadose Zone J. 2018, 17, 1–22. [Google Scholar] [CrossRef]
- Bogena, H.R.; Weuthen, A.; Huisman, J.A. Recent developments in wireless soil moisture sensing to support scientific research and agricultural management. Sensors 2022, 22, 9792. [Google Scholar] [CrossRef] [PubMed]
- Casanovas, R.; Prieto, E.; Salvadó, M. Calculation of the ambient dose equivalent H*(10) from gamma-ray spectra obtained with scintillation detectors. Appl. Radiat. Isot. 2016, 118, 154–159. [Google Scholar] [CrossRef] [PubMed]
- Weigand, S.; Bol, R.; Reichert, B.; Graf, A.; Wiekenkamp, I.; Stockinger, M.; Luecke, A.; Tappe, W.; Bogena, H.; Puetz, T.; et al. Spatiotemporal analysis of dissolved organic carbon and nitrate in waters of a forested catchment using wavelet analysis. Vadose Zone J. 2017, 16, 1–14. [Google Scholar] [CrossRef]
- Robinson, K.-L.; Bogena, H.R.; Wang, Q.; Cammeraat, E.; Bol, R. Effects of deforestation on dissolved organic carbon and nitrate in catchment stream water revealed by wavelet analysis. Front. Water 2022, 4, 1003693. [Google Scholar] [CrossRef]
- Grasty, R.L. Applications of gamma radiation in remote sensing. In Remote Sensing for Environmental Sciences; Ecological Studies; Springer: Berlin/Heidelberg, Germany, 1976; Volume 18, pp. 257–276. ISBN 978-3-642-66236-2. [Google Scholar]
- Løvborg, L. The Calibration of Portable and Airborne Gamma-Ray Spectrometers—Theory, Problems, and Facilities; Danmarks Tekniske Universitet, Risø Nationallaboratoriet for Bæredygtig Energi: Roskilde, Denmark, 1984. [Google Scholar]
- NIST. X-Ray Mass Attenuation Coefficients. Available online: https://physics.nist.gov/PhysRefData/XrayMassCoef/tab4.html (accessed on 28 November 2024).
- Zreda, M.; Shuttleworth, W.J.; Zeng, X.; Zweck, C.; Desilets, D.; Franz, T.; Rosolem, R. COSMOS: The cosmic-ray soil moisture observing system. Hydrol. Earth Syst. Sci. 2012, 16, 4079–4099. [Google Scholar] [CrossRef]
- Greenfield, M.B.; Domondon, A.T.; Okamoto, N.; Watanabe, I. Variation in γ-ray count rates as a monitor of precipitation rates, radon concentrations, and tectonic activity. J. Appl. Phys. 2002, 91, 1628–1633. [Google Scholar] [CrossRef]
- Vinuesa, J.-F.; Basu, S.; Galmarini, S. The Diurnal Evolution of 222Rn and its progeny in the atmospheric boundary layer during the Wangara experiment. Atmos. Chem. Phys. 2007, 7, 5003–5019. [Google Scholar] [CrossRef]
- Neumaier, S.; Dombrowski, H. EURADOS intercomparisons and the harmonisation of environmental radiation monitoring. Radiat. Prot. Dosim. 2014, 160, 297–305. [Google Scholar] [CrossRef] [PubMed]
- Sandness, G.A.; Schweppe, J.E.; Hensley, W.K.; Borgardt, J.D.; Mitchell, A.L. Accurate modeling of the terrestrial gamma-ray background for homeland security applications. In Proceedings of the 2009 IEEE Nuclear Science Symposium Conference Record (NSS/MIC), Orlando, FL, USA, 24 October–1 November 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 126–133. [Google Scholar]
- Fowler, J.W.; Szypryt, P.; Bunker, R.; Edwards, E.R.; Florang, I.F.; Gao, J.; Giachero, A.; Hoogerheide, S.F.; Loer, B.; Mumm, H.P.; et al. Spectroscopic measurements and models of energy deposition in the substrate of quantum circuits by natural ionizing radiation. PRX Quantum 2024, 5, 040323. [Google Scholar] [CrossRef]
- Hayashi, K.; Yasuoka, Y.; Nagahama, H.; Muto, J.; Ishikawa, T.; Omori, Y.; Suzuki, T.; Homma, Y.; Mukai, T. Normal seasonal variations for atmospheric radon concentration: A sinusoidal model. J. Environ. Radioact. 2015, 139, 149–153. [Google Scholar] [CrossRef] [PubMed]
- Yamazawa, H.; Miyazaki, T.; Moriizumi, J.; Iida, T.; Takeda, S.; Nagara, S.; Sato, K.; Tokizawa, T. Radon exhalation from a ground surface during a cold snow season. Int. Congr. Ser. 2005, 1276, 221–222. [Google Scholar] [CrossRef]
- Puchkov, A.V.; Berezina, E.V.; Yakovlev, E.Y.; Hasson, N.R.; Druzhinin, S.V.; Tyshov, A.S.; Ushakova, E.V.; Koshelev, L.S.; Lapikov, P.I. Radon flux density in conditions of permafrost thawing: Simulation experiment. Geogr. Environ. Sustain. 2022, 15, 5–18. [Google Scholar] [CrossRef]
- Yang, J.; Busen, H.; Scherb, H.; Hürkamp, K.; Guo, Q.; Tschiersch, J. Modeling of radon exhalation from soil influenced by environmental parameters. Sci. Total Environ. 2019, 656, 1304–1311. [Google Scholar] [CrossRef] [PubMed]
- Akbar, M.A.; Kenimer, A.L.; Searcy, S.W.; Torbert, H.A. Soil water estimation using electromagnetic induction. Trans. ASAE 2005, 48, 129–135. [Google Scholar] [CrossRef]
- Altdorff, D.; Von Hebel, C.; Borchard, N.; Van Der Kruk, J.; Bogena, H.R.; Vereecken, H.; Huisman, J.A. Potential of catchment-wide soil water content prediction using electromagnetic induction in a forest ecosystem. Environ. Earth Sci. 2017, 76, 111. [Google Scholar] [CrossRef]
- Peng, Z.; Lin, S.; Zhang, B.; Wei, Z.; Liu, L.; Han, N.; Cai, J.; Chen, H. Winter wheat canopy water content monitoring based on spectral transforms and “three-edge” parameters. Agric. Water Manag. 2020, 240, 106306. [Google Scholar] [CrossRef]
- Lee, M.S. Gamma-ray exposure rate monitoring by energy spectra of NaI(Tl) scintillation detectors. J. Radiat. Prot. Res. 2017, 42, 158–165. [Google Scholar] [CrossRef][Green Version]

| Measurements | Mean [nSv h−1] | Maximum [nSv h−1] | Minimum [nSv h−1] | Coefficient of Variation |
|---|---|---|---|---|
| EGRG–M 1 | 92.98 | 100.76 | 87.12 | 0.032 |
| EGRG-M′ 2 | 91.71 | 99.49 | 86.66 | 0.031 |
| EGRS 3 | 75.18 | 82.76 | 70.84 | 0.038 |
| GR from 40K 4 | 10.17 | 12.04 | 9.20 | 0.073 |
| GR from 214Bi 5 | 6.11 | 7.82 | 5.43 | 0.075 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akter, S.; Huisman, J.A.; Bogena, H.R. Comparing the Accuracy of Soil Moisture Estimates Derived from Bulk and Energy-Resolved Gamma Radiation Measurements. Sensors 2025, 25, 4453. https://doi.org/10.3390/s25144453
Akter S, Huisman JA, Bogena HR. Comparing the Accuracy of Soil Moisture Estimates Derived from Bulk and Energy-Resolved Gamma Radiation Measurements. Sensors. 2025; 25(14):4453. https://doi.org/10.3390/s25144453
Chicago/Turabian StyleAkter, Sonia, Johan Alexander Huisman, and Heye Reemt Bogena. 2025. "Comparing the Accuracy of Soil Moisture Estimates Derived from Bulk and Energy-Resolved Gamma Radiation Measurements" Sensors 25, no. 14: 4453. https://doi.org/10.3390/s25144453
APA StyleAkter, S., Huisman, J. A., & Bogena, H. R. (2025). Comparing the Accuracy of Soil Moisture Estimates Derived from Bulk and Energy-Resolved Gamma Radiation Measurements. Sensors, 25(14), 4453. https://doi.org/10.3390/s25144453








