A Rolling Bearing Fault Diagnosis Method Based on Wild Horse Optimizer-Enhanced VMD and Improved GoogLeNet
Abstract
1. Introduction
2. Algorithm
2.1. IWHO-VMD
2.1.1. VMD
- (1)
- Perform Hilbert transform on the modal components to obtain the unilateral spectrum:
- (2)
- Shift the spectrum of each modal component uk (t) to its corresponding baseband:
- (3)
- Estimate the bandwidth through Gaussian smoothing of the demodulated signal and construct the constrained variational model:
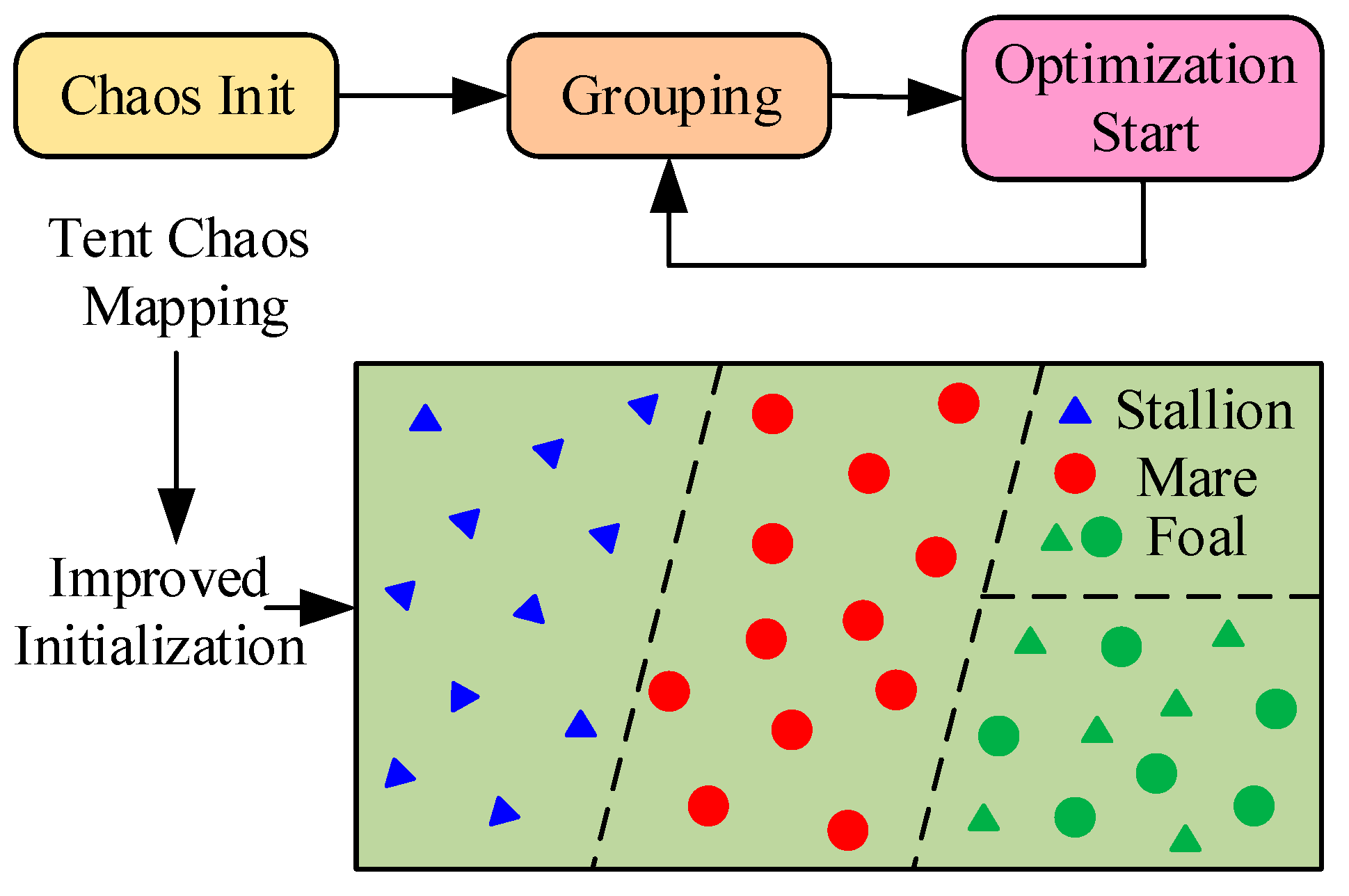
2.1.2. IWHO
2.1.3. VMD Parameter Auto-Tuning Model Based on IWHO
2.2. Kurtosis Criterion and Time–Frequency Feature Extraction
2.3. Improved GoogLeNet Classifier
- (1)
- Replace the n × n size convolution kernel in the Inception block with a convolution combination of 1 × n and n × 1 to reduce the model parameters to adapt to small-scale datasets, while reducing the training time.
- (2)
- The ReLU activation function is replaced by TReLU. By introducing trainable parameters β and γ, the adaptability of the activation function to different data distributions is improved and the convergence speed is accelerated. The formula for the TReLU activation function is
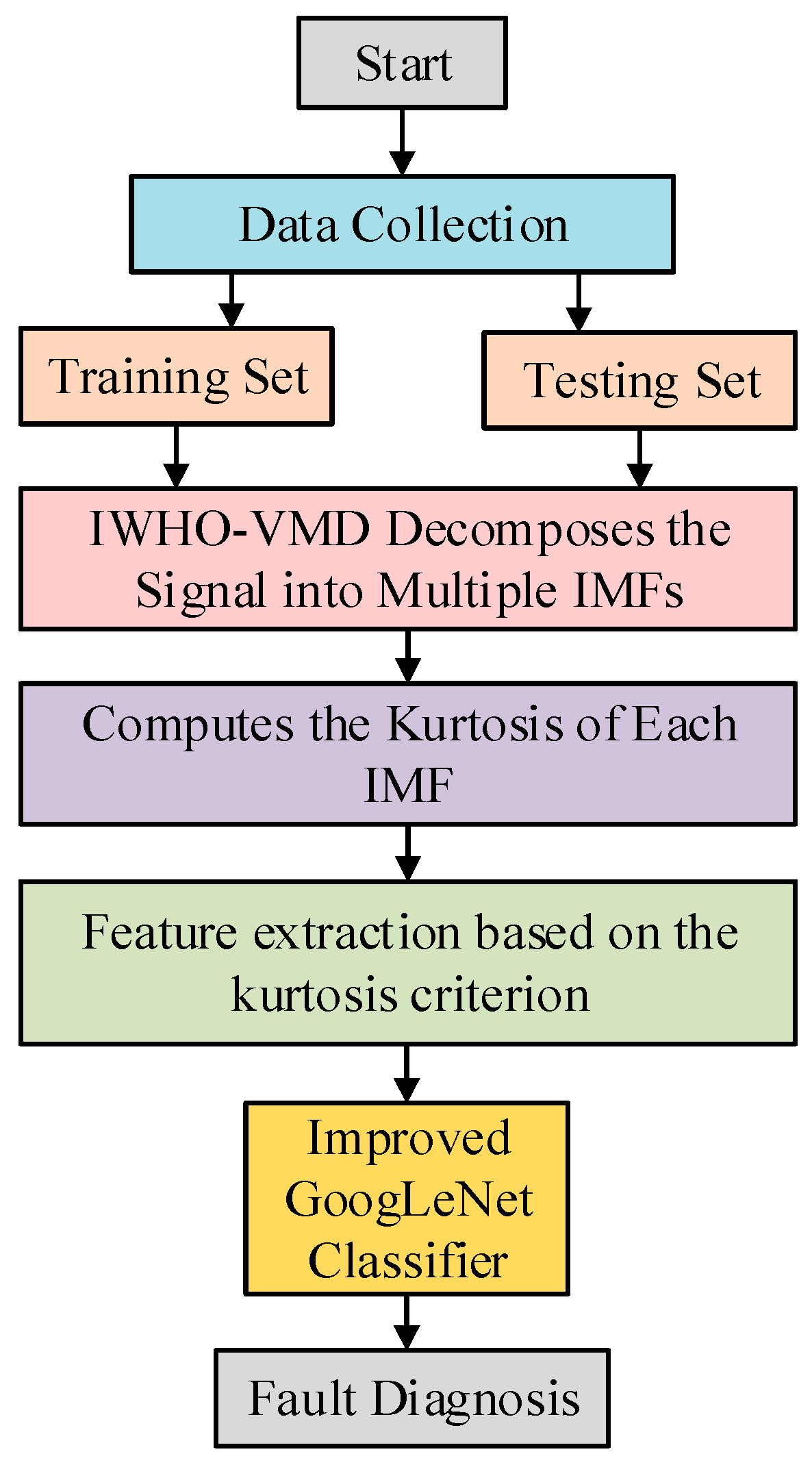
2.4. Proposed Fault Diagnosis Framework
- (1)
- Vibration signals are collected under different machine states using sensors to reflect operational conditions.
- (2)
- The acquired signals are decomposed via IWHO-VMD to obtain Y IMF components, with kurtosis values computed for each IMF.
- (3)
- The top y IMFs with highest kurtosis values are selected based on the kurtosis criterion, followed by time–frequency feature extraction to capture fault characteristics.
- (4)
- Feature vectors are constructed to train an GoogLeNet classifier for fault pattern differentiation. Among them, the dataset of each state is divided into a training set and a test set at a classical ratio of 7:3.
- (5)
- Test samples are input into the trained GoogLeNet classifier for pattern recognition and final classification.
3. Case Study I: CWRU Dataset
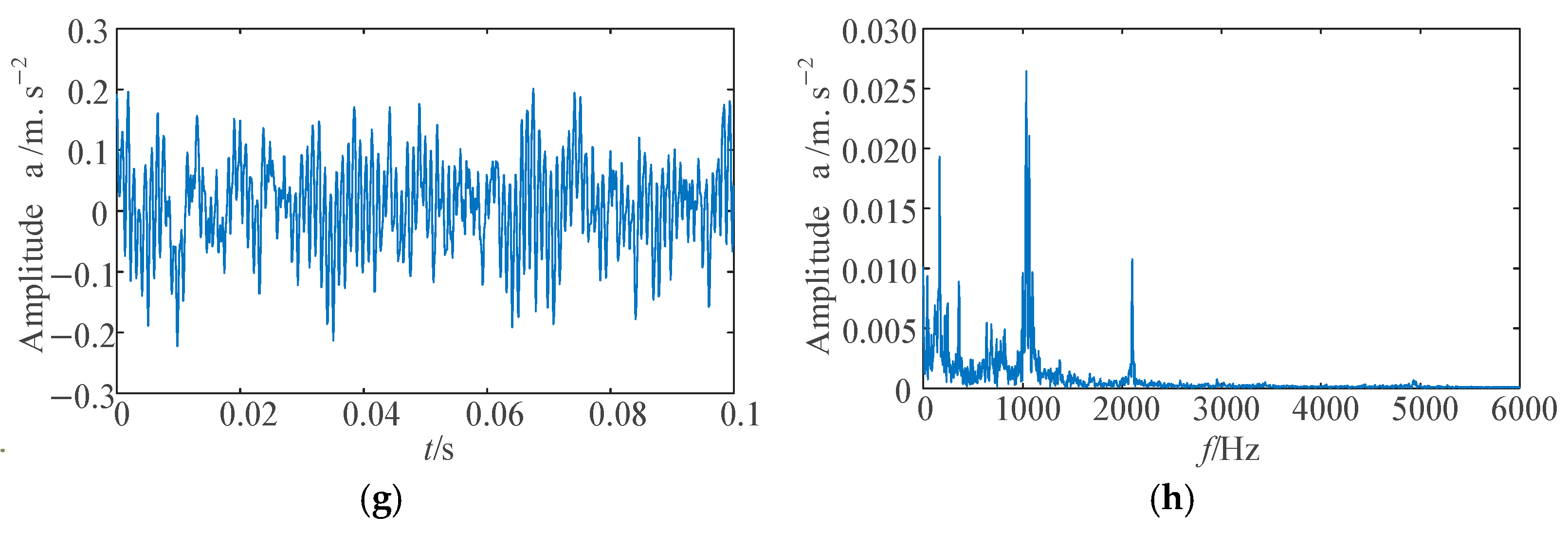
3.1. Data Acquisition for Case Study I
3.2. IWHO Iteration Curves
3.3. IMFs After Enhanced-VMD
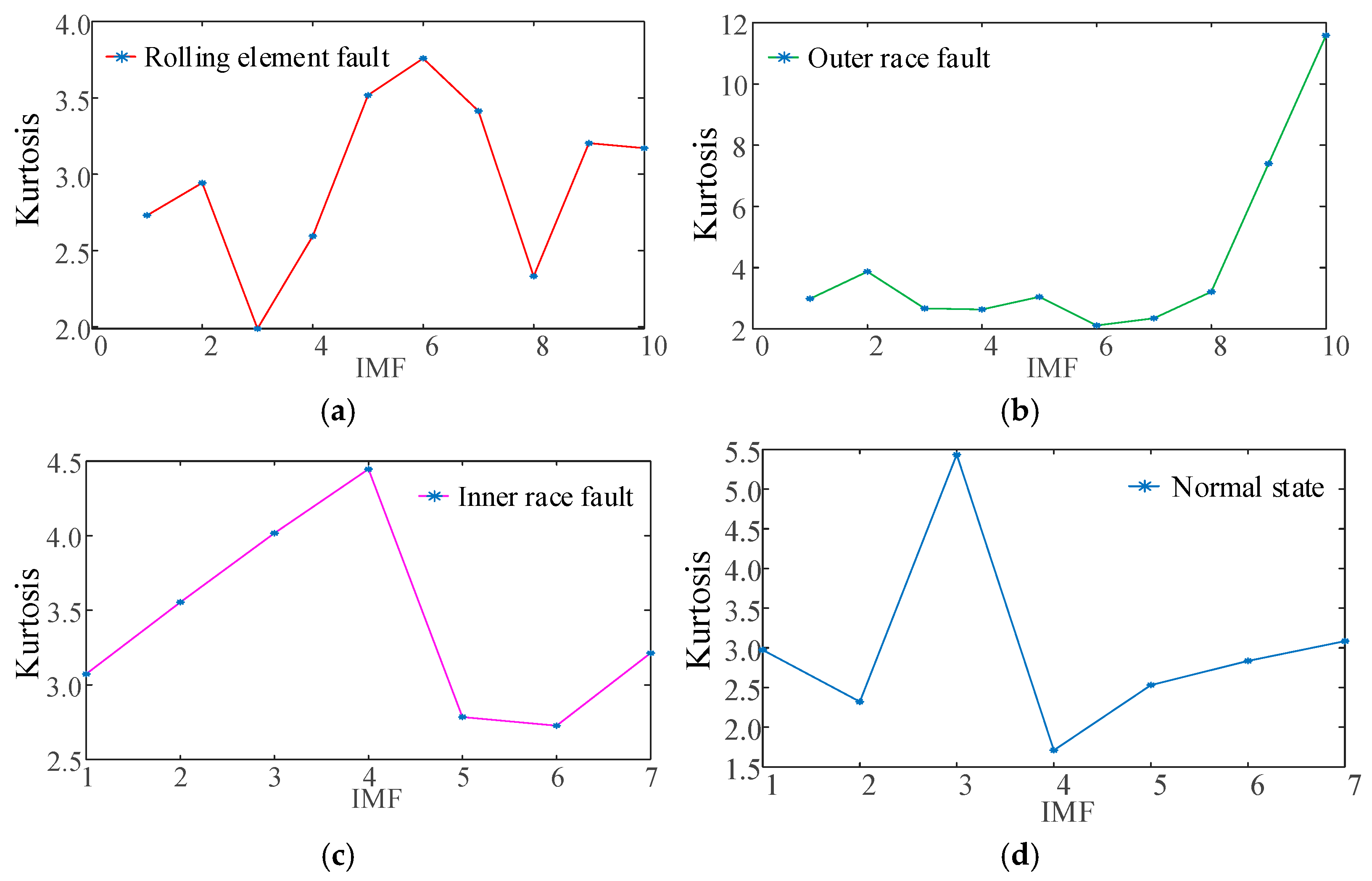
3.4. Kurtosis Criterion Analysis
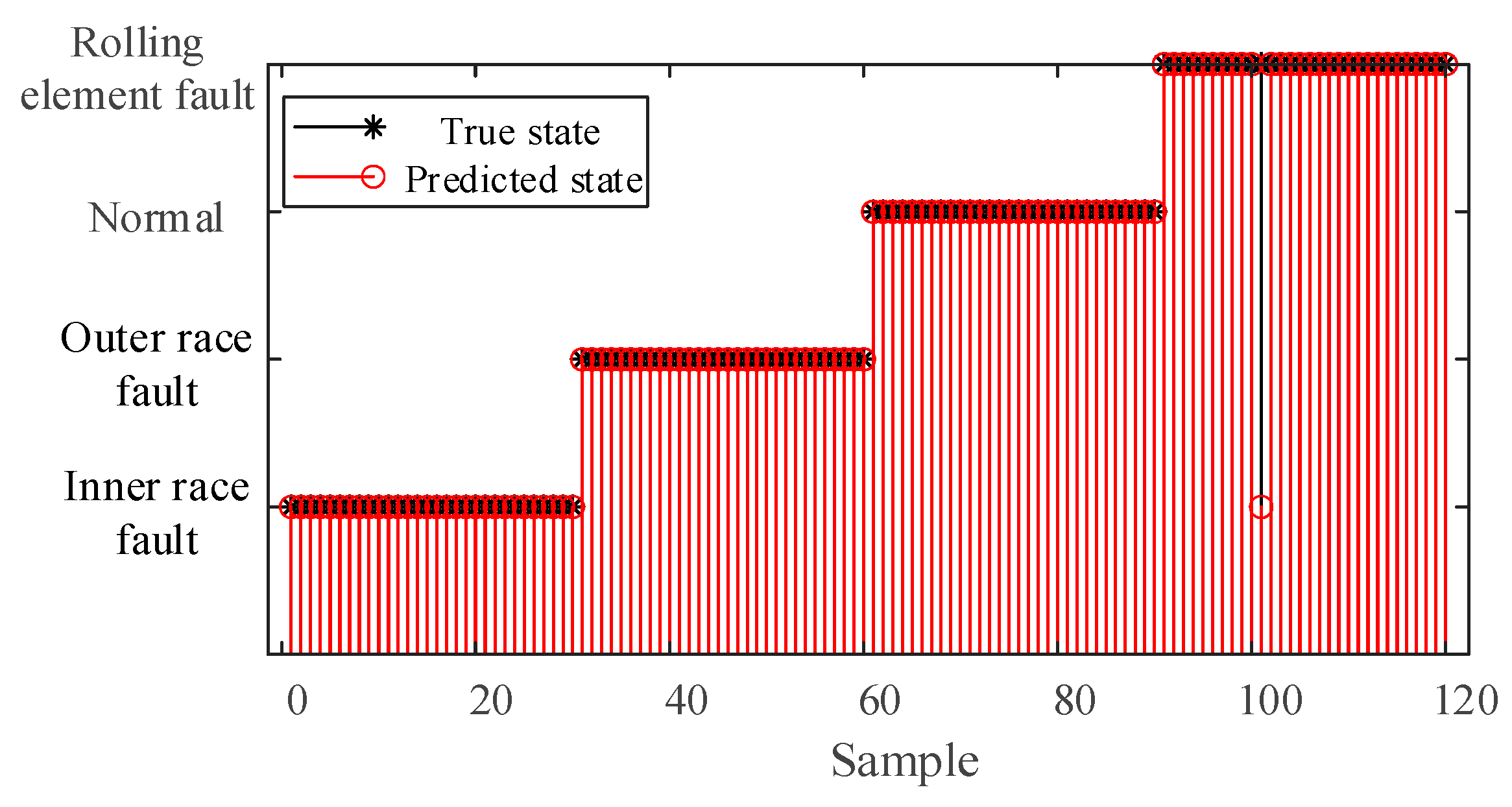
3.5. Fault Diagnosis Results
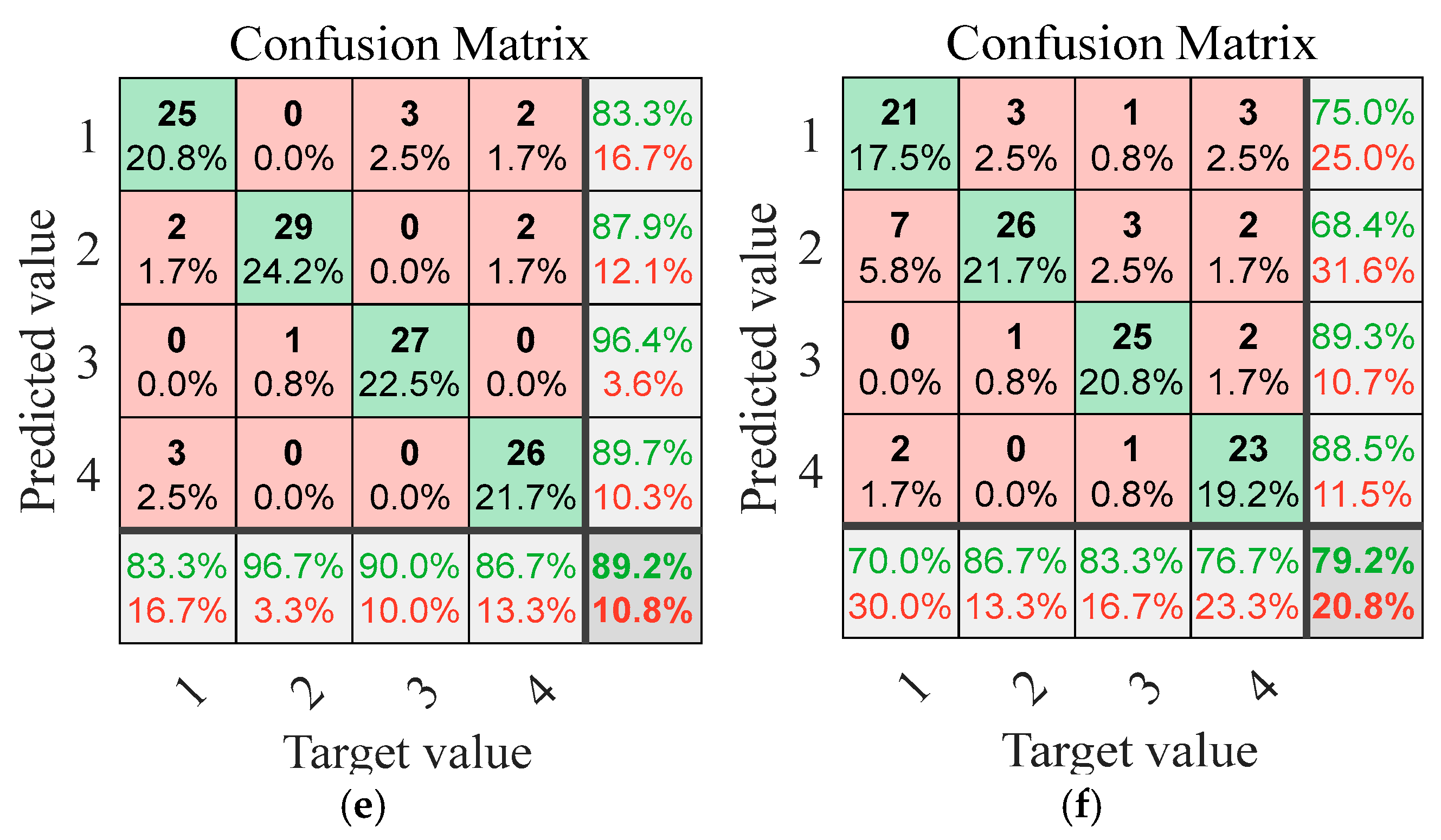
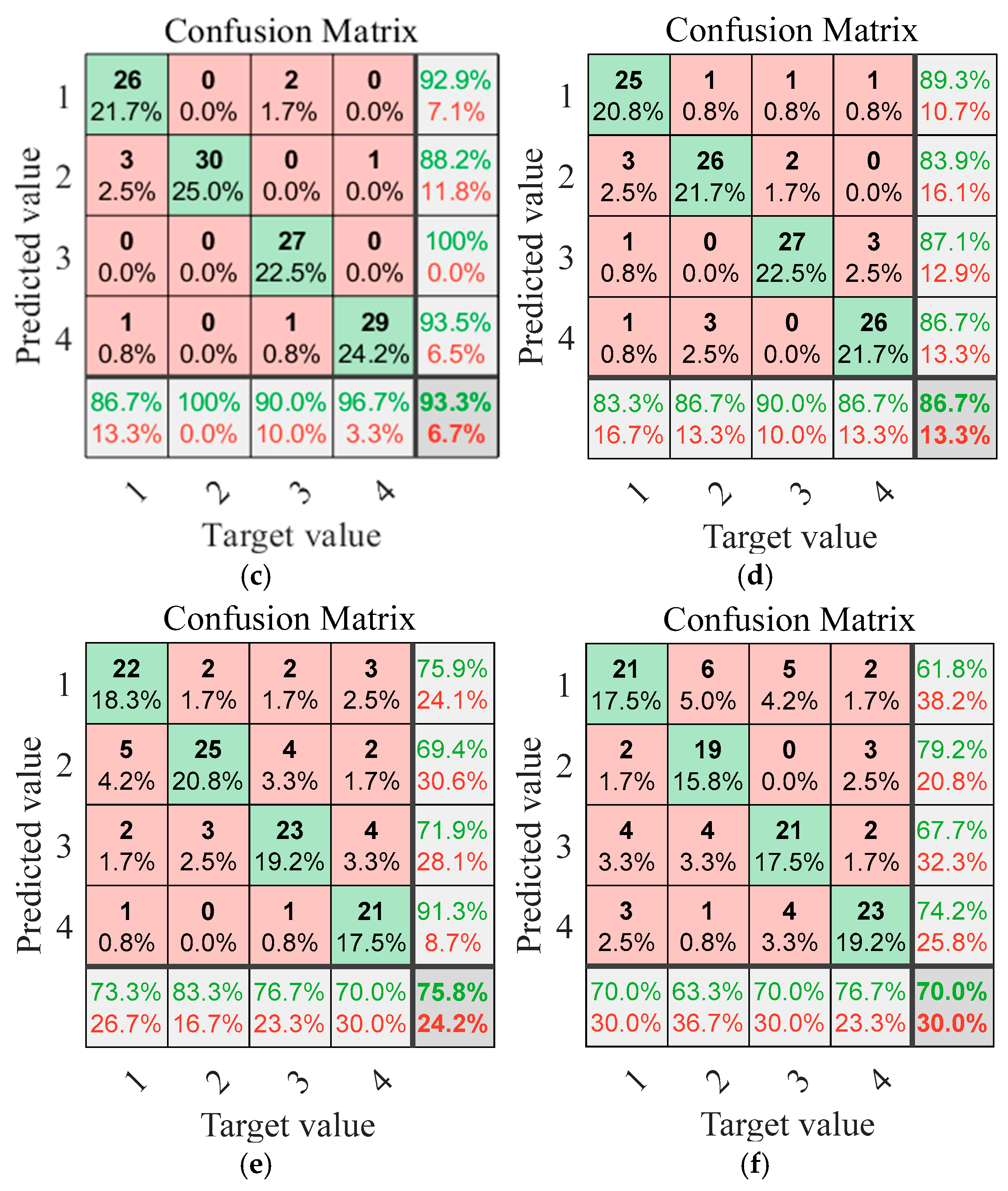
3.6. Performance Comparison of Methods
4. Case Study II: HUST Dataset
4.1. Data Acquisition for Case Study II
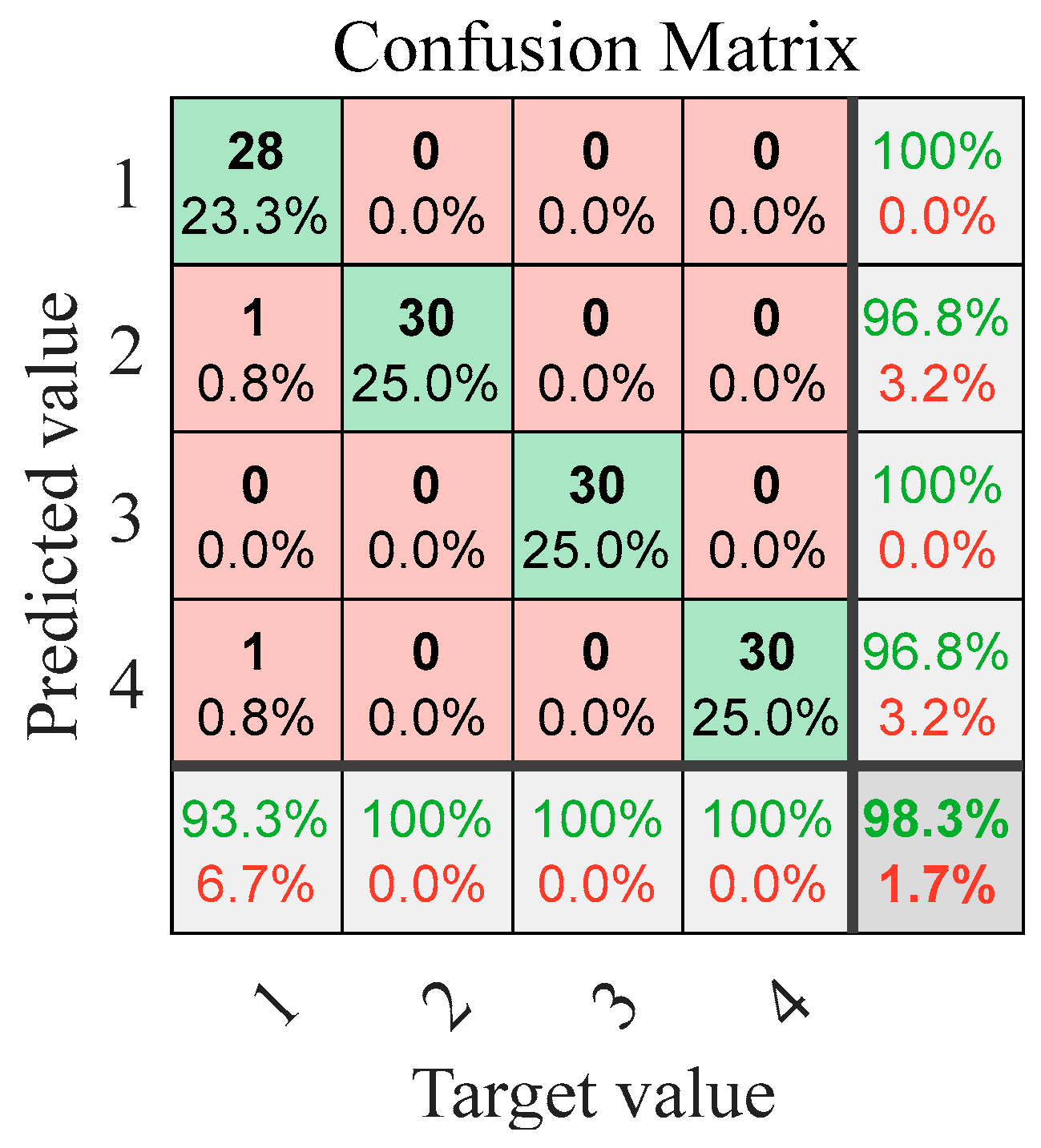
4.2. Fault Diagnosis Results and Performance Comparison of Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Wang, S.; Lei, Y.; Lu, N.; Yang, B.; Li, X.; Li, N. Graph continual learning network: An incremental intelligent diagnosis method of machines for new fault detection. IEEE Trans. Autom. Sci. Eng. 2024, 1–11. [Google Scholar] [CrossRef]
- Sahu, A.R.; Palei, S.K.; Mishra, A. Data-driven fault diagnosis approaches for industrial equipment: A review. Expert Syst. 2024, 41, e13360. [Google Scholar] [CrossRef]
- Shu, Y.D.; Ma, T.C.; Lin, Y.G. Rolling bearing fault diagnosis based on data-level and feature-level information fusion. J. Southeast Univ. (Engl. Ed.) 2024, 40, 396–402. [Google Scholar]
- Li, J.; Luo, W.; Bai, M. Review of research on signal decomposition and fault diagnosis of rolling bearing based on vibration signal. Meas. Sci. Technol. 2024, 35, 092001. [Google Scholar] [CrossRef]
- Maheswari, R.U.; Umamaheswari, R. Trends in non-stationary signal processing techniques applied to vibration analysis of wind turbine drive train—A contemporary survey. Mech. Syst. Signal Process. 2017, 85, 296–311. [Google Scholar] [CrossRef]
- Yan, R.; Shang, Z.; Xu, H.; Wen, J.; Zhao, Z.; Chen, X.; Gao, R.X. Wavelet transform for rotary machine fault diagnosis: 10 years revisited. Mech. Syst. Signal Process. 2023, 200, 110545. [Google Scholar] [CrossRef]
- Sun, Y.; Li, S.; Wang, Z. Bearing fault diagnosis based on EMD and improved Chebyshev distance in SDP image. Measurement 2021, 176, 109100. [Google Scholar] [CrossRef]
- Liang, X.; Luo, Y.; Deng, F.; Li, Y. Investigation on vibration signal characteristics in a centrifugal pump using EMD-LS-MFDFA. Processes 2022, 10, 1169. [Google Scholar] [CrossRef]
- Zhao, Y.; Fan, Y.; Li, H.; Gao, X. Rolling bearing composite fault diagnosis method based on EEMD fusion feature. J. Mech. Sci. Technol. 2022, 36, 4563–4570. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Cui, H.J.; Guan, Y.; Chen, H.Y. Rolling element fault diagnosis based on VMD and sensitivity MCKD. IEEE Access 2021, 9, 120297–120308. [Google Scholar] [CrossRef]
- Hua, Z.; Xiao, Y.C.; Cao, J.D. Misalignment fault prediction of wind turbines based on improved artificial fish swarm algorithm. Entropy 2021, 23, 692. [Google Scholar] [CrossRef] [PubMed]
- Qi, B.; Yang, G.; Guo, D.; Wang, C. EMD and VMD-GWO parallel optimization algorithm to overcome Lidar ranging limitations. Opt. Express 2021, 29, 2855–2873. [Google Scholar] [CrossRef] [PubMed]
- Xiong, J.; Sun, Y.; Sun, J.; Wan, Y.; Yu, G. Sparse temporal data-driven SSA-CNN-LSTM-based fault prediction of electromechanical equipment in rail transit stations. Appl. Sci. 2024, 14, 8156. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F. Wild horse optimizer: A new meta-heuristic algorithm for solving engineering optimization problems. Eng. Comput. 2021, 38, 3025–3056. [Google Scholar] [CrossRef]
- Zheng, R.; Hussien, A.G.; Jia, H.M.; Abualigah, L.; Wang, S.; Wu, D. An improved wild horse optimizer for solving optimization problems. Mathematics 2022, 10, 1311. [Google Scholar] [CrossRef]
- Li, Y.; Yuan, Q.; Han, M.; Cui, R. Hybrid multi-strategy improved wild horse optimizer. Adv. Intell. Syst. 2022, 4, 2200097. [Google Scholar] [CrossRef]
- Wang, S.; Feng, Z. Multi-sensor fusion rolling bearing intelligent fault diagnosis based on VMD and ultra-lightweight GoogLeNet in industrial environments. Digit. Signal Process. 2024, 145, 104306. [Google Scholar] [CrossRef]
- Liu, Y.; He, B.; Liu, F.; Lu, S.; Zhao, Y. Feature fusion using kernel joint approximate diagonalization of eigen-matrices for rolling bearing fault identification. J. Sound Vib. 2016, 385, 389–401. [Google Scholar] [CrossRef]
- Hua, L.; Wu, X.; Liu, T.; Li, S. The methodology of modified frequency band envelope kurtosis for bearing fault diagnosis. IEEE Trans. Ind. Inf. 2022, 19, 2856–2865. [Google Scholar] [CrossRef]
- Bai, Y.; Cheng, W.; Wen, W.; Liu, Y. Application of time-frequency analysis in rotating machinery fault diagnosis. Shock Vib. 2023, 2023, 9878228. [Google Scholar] [CrossRef]
- Wang, Y.; Zou, Y.; Hu, W.; Chen, J.; Xiao, Z. Intelligent fault diagnosis of hydroelectric units based on radar maps and improved GoogleNet by depthwise separate convolution. Meas. Sci. Technol. 2023, 35, 025103. [Google Scholar] [CrossRef]
- Neupane, D.; Seok, J. Bearing fault detection and diagnosis using Case Western Reserve University dataset with deep learning approaches: A review. IEEE Access 2020, 8, 93155–93178. [Google Scholar] [CrossRef]













| Domain | Features |
|---|---|
| Time-domain | Mean, variance, standard deviation, kurtosis, skewness |
| Frequency-domain | Center frequency, mean frequency, power spectrum |
| Time–frequency-domain | Energy entropy |
| Condition | Rolling Element Fault | Outer Race Fault | Inner Race Fault | Normal State |
|---|---|---|---|---|
| Penalty Factor (α) | 3000 | 1000 | 1000 | 1609 |
| Mode Number (K) | 10 | 10 | 7 | 7 |
| Model | VMD-GoogLeNet | PSO-VMD-GoogLeNet | WOA-VMD-GoogLeNet | IWHO-VMD-GoogLeNet |
|---|---|---|---|---|
| Accuracy (%) | 94.17 | 95.83 | 96.67 | 99.17 |
| Time(s) | 104.00 | 322.29 | 863.24 | 558.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Zhao, F.; Song, N.; Liu, Z.; Cao, L. A Rolling Bearing Fault Diagnosis Method Based on Wild Horse Optimizer-Enhanced VMD and Improved GoogLeNet. Sensors 2025, 25, 4421. https://doi.org/10.3390/s25144421
He X, Zhao F, Song N, Liu Z, Cao L. A Rolling Bearing Fault Diagnosis Method Based on Wild Horse Optimizer-Enhanced VMD and Improved GoogLeNet. Sensors. 2025; 25(14):4421. https://doi.org/10.3390/s25144421
Chicago/Turabian StyleHe, Xiaoliang, Feng Zhao, Nianyun Song, Zepeng Liu, and Libing Cao. 2025. "A Rolling Bearing Fault Diagnosis Method Based on Wild Horse Optimizer-Enhanced VMD and Improved GoogLeNet" Sensors 25, no. 14: 4421. https://doi.org/10.3390/s25144421
APA StyleHe, X., Zhao, F., Song, N., Liu, Z., & Cao, L. (2025). A Rolling Bearing Fault Diagnosis Method Based on Wild Horse Optimizer-Enhanced VMD and Improved GoogLeNet. Sensors, 25(14), 4421. https://doi.org/10.3390/s25144421








