Differentiated Embedded Pilot Assisted Automatic Modulation Classification for OTFS System: A Multi-Domain Fusion Approach
Abstract
1. Introduction
- We propose a multi-domain fusion-based AMC approach for OTFS systems by designing a dual-stream CNN architecture that simultaneously incorporates the time-domain and DD-domain features of OTFS signals.
- We develop a differentiated embedded pilot insertion scheme which incorporates modulation-related pilot symbols in DD plane structure to enhance classification accuracy.
- We conduct extensive experiments, and the results demonstrate that the proposed approach can achieve high classification accuracy in high-mobility scenarios and low-signal-to-noise ratio (SNR) conditions and outperform the state-of-the-art approaches.
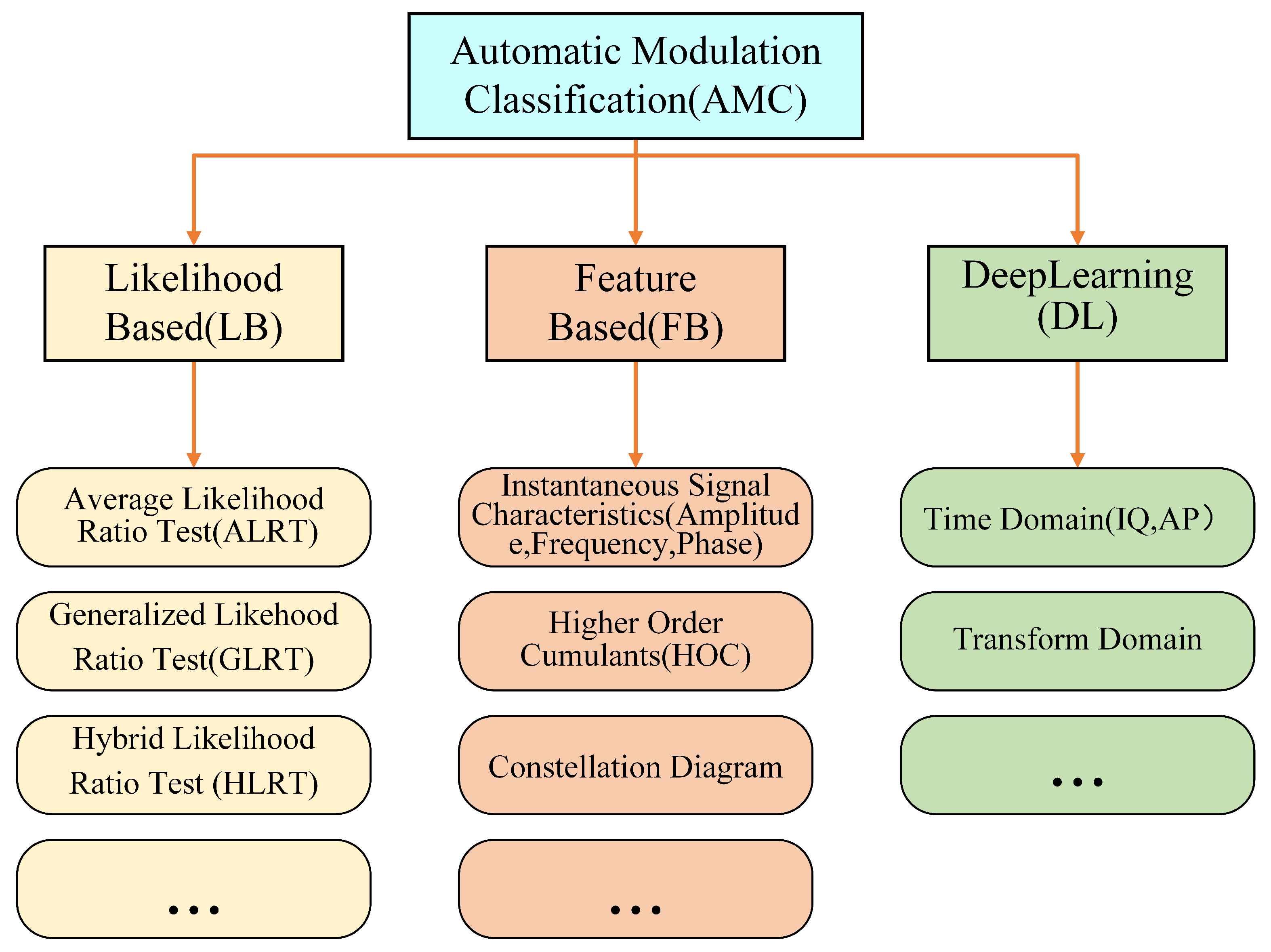
2. Related Work
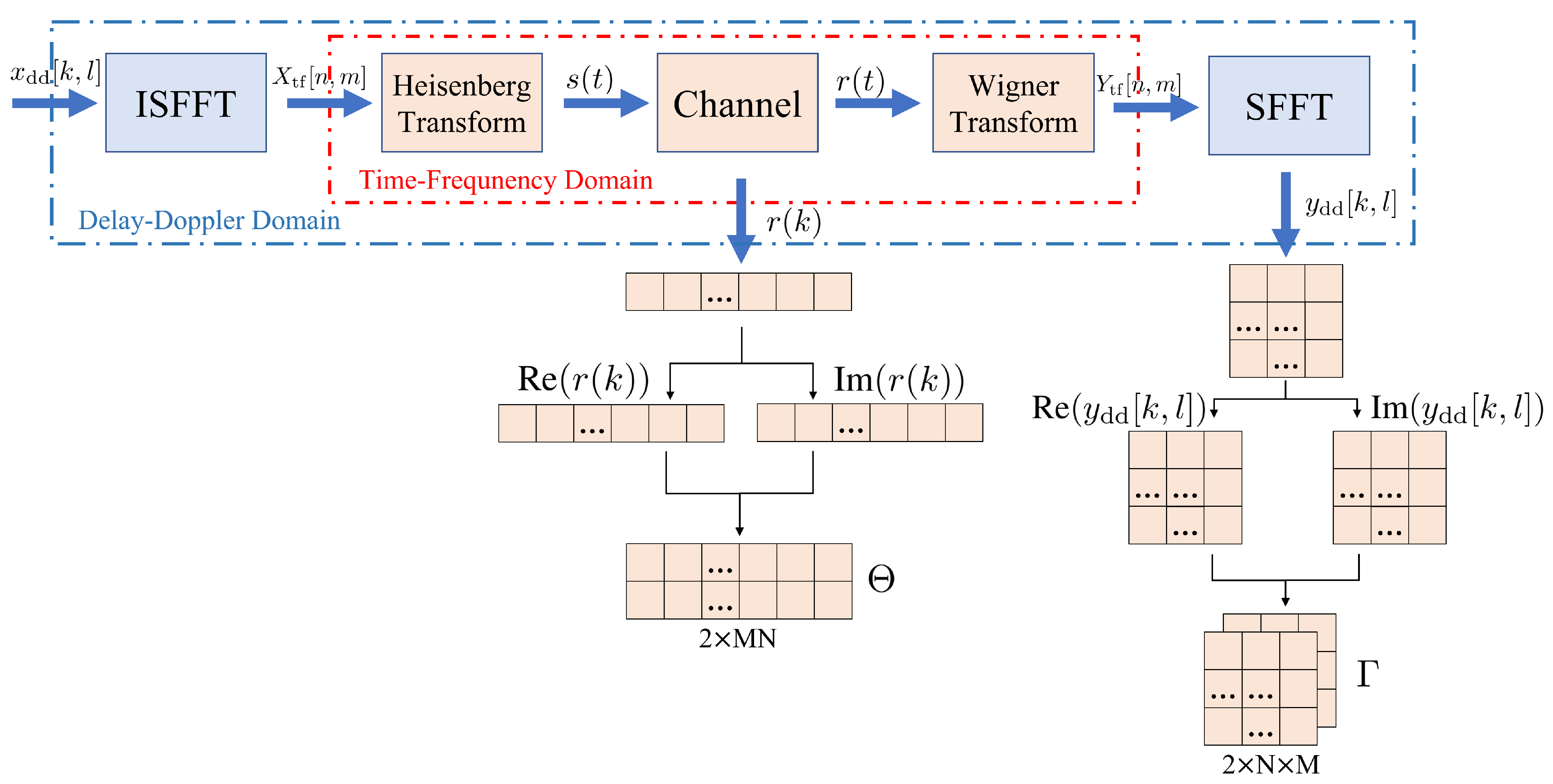
3. System Model
4. Proposed Method
4.1. Differentiated Embedded Pilot Insertion Scheme
4.2. Dataset Design
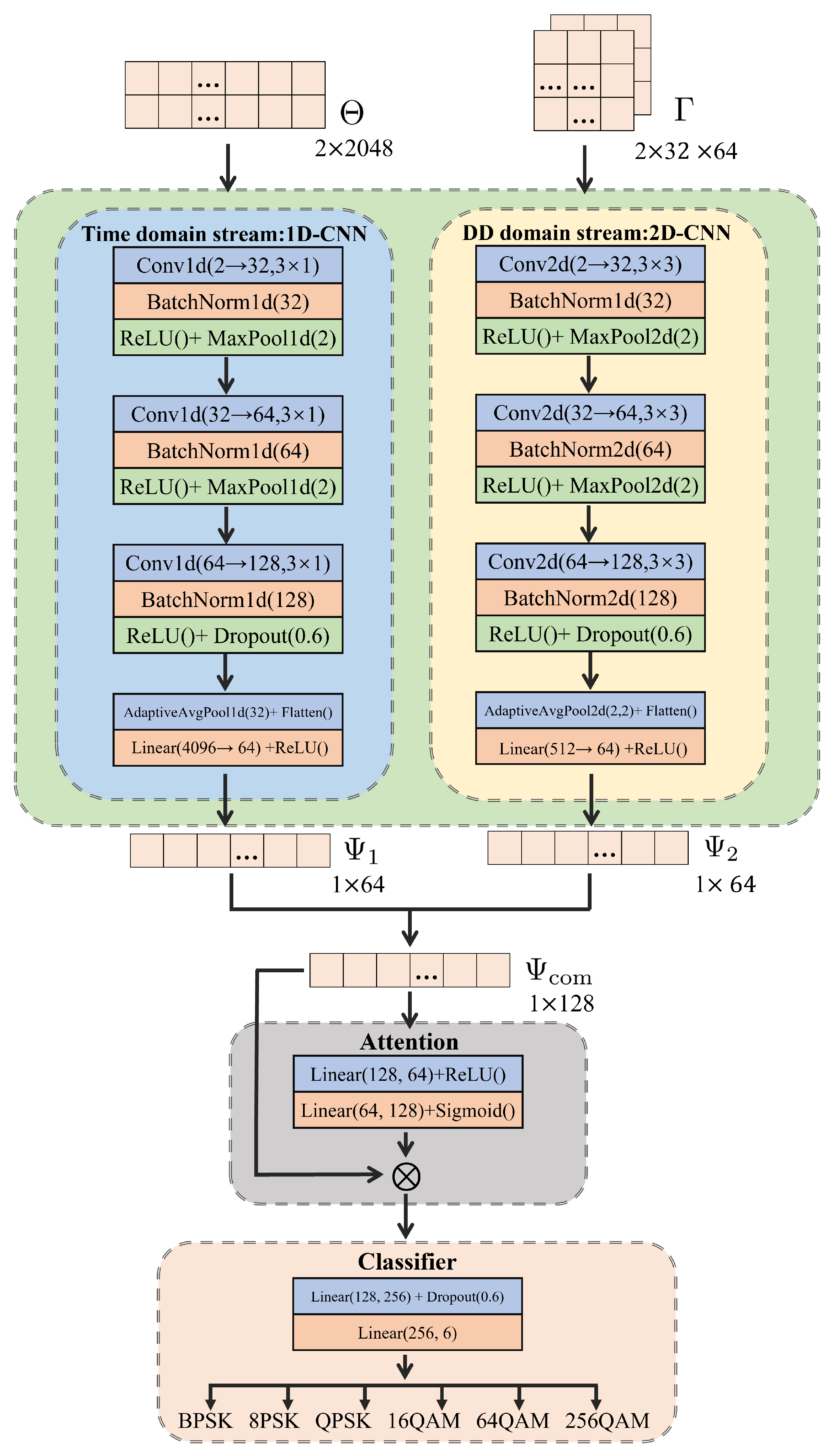
4.3. Dual-Stream Architecture for Multi-Domain Fusion
4.4. Computational Complexity Analysis
5. Numerical Results
5.1. Experimental Settings and Performance Metric
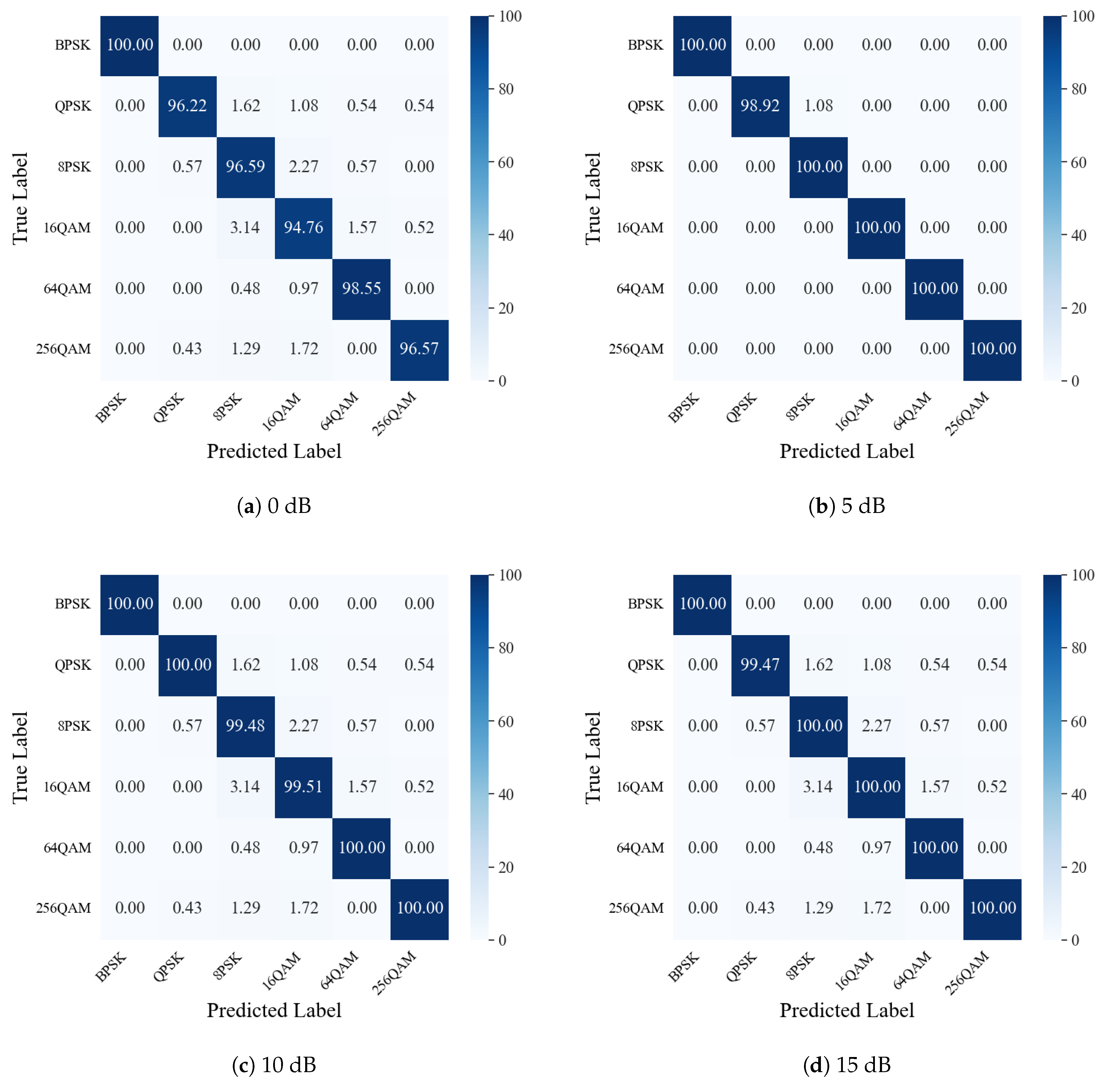
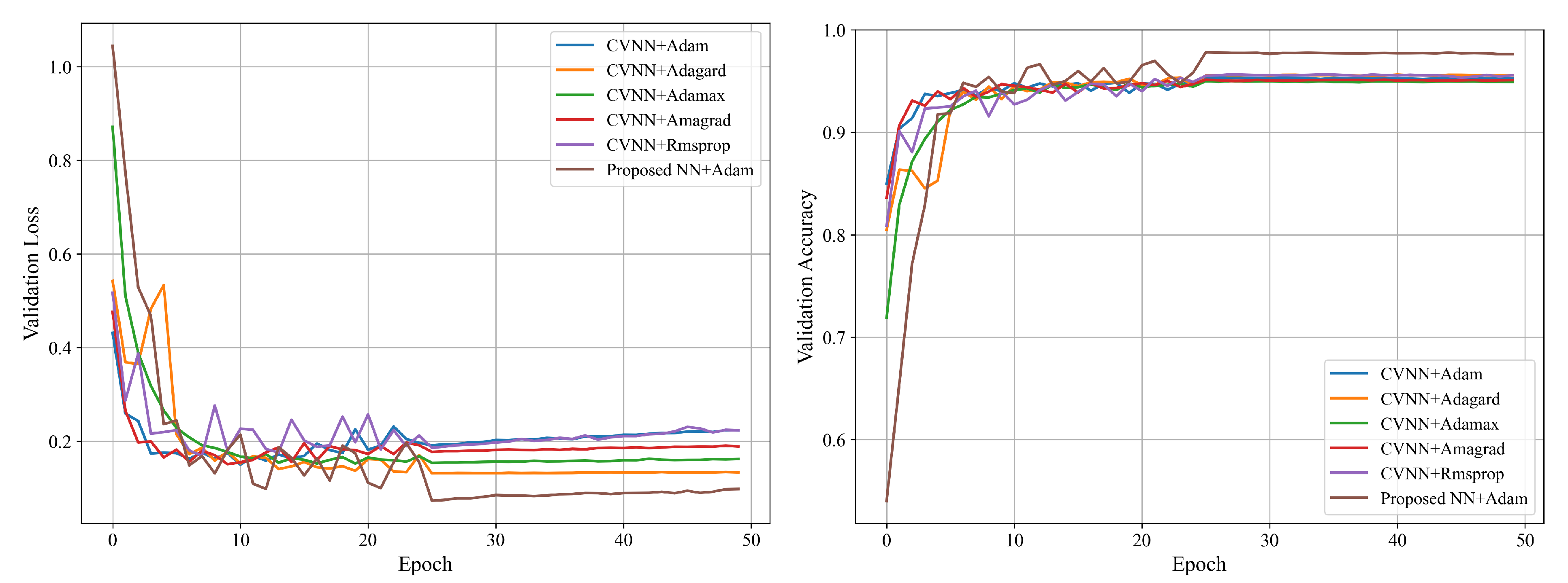
5.2. Performance Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wei, Z.; Yuan, W.; Li, S.; Yuan, J.; Bharatula, G.; Hadani, R.; Hanzo, L. Orthogonal time-frequency space modulation: A promising next-generation waveform. IEEE Wirel. Commun. 2021, 28, 136–144. [Google Scholar] [CrossRef]
- Shen, W.; Dai, L.; An, J.; Fan, P.; Heath, R.W. Channel estimation for orthogonal time frequency space (OTFS) massive MIMO. IEEE Trans. Signal Process. 2019, 67, 4204–4217. [Google Scholar] [CrossRef]
- Hadani, R.; Rakib, S.; Tsatsanis, M.; Monk, A.; Goldsmith, A.J.; Molisch, A.F.; Calderbank, R. Orthogonal time frequency space modulation. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, CA, USA, 19–22 March 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Zhang, Z.; Xiao, Y.; Ma, Z.; Xiao, M.; Ding, Z.; Lei, X.; Karagiannidis, G.K.; Fan, P. 6G wireless networks: Vision, requirements, architecture, and key technologies. IEEE Veh. Technol. Mag. 2019, 14, 28–41. [Google Scholar] [CrossRef]
- Matz, G.; Hlawatsch, F. Time-varying communication channels: Fundamentals, recent developments, and open problems. In Proceedings of the 2006 14th European Signal Processing Conference, Florence, Italy, 4–8 September 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 1–5. [Google Scholar]
- Zhou, X.; Ying, K.; Gao, Z.; Wu, Y.; Xiao, Z.; Chatzinotas, S.; Yuan, J.; Ottersten, B. Active terminal identification, channel estimation, and signal detection for grant-free NOMA-OTFS in LEO satellite Internet-of-Things. IEEE Trans. Wirel. Commun. 2022, 22, 2847–2866. [Google Scholar] [CrossRef]
- Gao, Z.; Zhou, X.; Zhao, J.; Li, J.; Zhu, C.; Hu, C.; Xiao, P.; Chatzinotas, S.; Ng, D.W.K.; Ottersten, B. Grant-free NOMA-OTFS paradigm: Enabling efficient ubiquitous access for LEO satellite Internet-of-Things. IEEE Netw. 2023, 37, 18–26. [Google Scholar] [CrossRef]
- Buzzi, S.; Caire, G.; Colavolpe, G.; D’Andrea, C.; Foggi, T.; Piemontese, A.; Ugolini, A. LEO satellite diversity in 6G non-terrestrial networks: OFDM vs. OTFS. IEEE Commun. Lett. 2023, 27, 3013–3017. [Google Scholar] [CrossRef]
- Linsalata, F.; Albanese, A.; Sciancalepore, V.; Roveda, F.; Magarini, M.; Costa-Perez, X. OTFS-superimposed PRACH-aided localization for UAV safety applications. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Han, R.; Ma, J.; Bai, L. Trajectory planning for OTFS-based UAV communications. China Commun. 2023, 20, 114–124. [Google Scholar] [CrossRef]
- Blazek, T.; Radovic, D. Performance evaluation of OTFS over measured V2V channels at 60 GHz. In Proceedings of the 2020 IEEE MTT-S International Conference on Microwaves for Intelligent Mobility (ICMIM), Linz, Austria, 23 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–4. [Google Scholar]
- Lopez, L.M.W.; Bengtsson, M. Achievable rates of orthogonal time frequency space (OTFS) modulation in high speed railway environments. In Proceedings of the 2022 IEEE 33rd Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Kyoto, Japan, 12–15 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 982–987. [Google Scholar]
- Ma, Y.; Ma, G.; Ai, B.; Fei, D.; Wang, N.; Zhong, Z.; Yuan, J. Characteristics of channel spreading function and performance of OTFS in high-speed railway. IEEE Trans. Wirel. Commun. 2023, 22, 7038–7054. [Google Scholar] [CrossRef]
- Liu, X.; Yang, D.; El Gamal, A. Deep neural network architectures for modulation classification. In Proceedings of the 2017 51st Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 29 October–1 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 915–919. [Google Scholar]
- Wei, W.; Mendel, J.M. Maximum-likelihood classification for digital amplitude-phase modulations. IEEE Trans. Commun. 2000, 48, 189–193. [Google Scholar] [CrossRef]
- Su, W.; Xu, J.L.; Zhou, M. Real-time modulation classification based on maximum likelihood. IEEE Commun. Lett. 2008, 12, 801–803. [Google Scholar] [CrossRef]
- Liedtke, F. Computer simulation of an automatic classification procedure for digitally modulated communication signals with unknown parameters. Signal Process. 1984, 6, 311–323. [Google Scholar] [CrossRef]
- Gardner, W.A.; Spooner, C.M. Cyclic spectral analysis for signal detection and modulation recognition. In Proceedings of the MILCOM 88, 21st Century Military Communications-What’s Possible?’ Conference Record, Military Communications Conference, San Diego, CA, USA, 23–26 October 1988; IEEE: Piscataway, NJ, USA, 1988; pp. 419–424. [Google Scholar]
- Meng, F.; Chen, P.; Wu, L.; Wang, X. Automatic modulation classification: A deep learning enabled approach. IEEE Trans. Veh. Technol. 2018, 67, 10760–10772. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Hermawan, A.P.; Ginanjar, R.R.; Kim, D.S.; Lee, J.M. CNN-based automatic modulation classification for beyond 5G communications. IEEE Commun. Lett. 2020, 24, 1038–1041. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, M.; Yang, J.; Gui, G. Data-driven deep learning for automatic modulation recognition in cognitive radios. IEEE Trans. Veh. Technol. 2019, 68, 4074–4077. [Google Scholar] [CrossRef]
- Chen, Y.; Shao, W.; Liu, J.; Yu, L.; Qian, Z. Automatic modulation classification scheme based on LSTM with random erasing and attention mechanism. IEEE Access 2020, 8, 154290–154300. [Google Scholar] [CrossRef]
- Rajendran, S.; Meert, W.; Giustiniano, D.; Lenders, V.; Pollin, S. Deep learning models for wireless signal classification with distributed low-cost spectrum sensors. IEEE Trans. Cogn. Commun. Netw. 2018, 4, 433–445. [Google Scholar] [CrossRef]
- Zhang, Z.; Luo, H.; Wang, C.; Gan, C.; Xiang, Y. Automatic modulation classification using CNN-LSTM based dual-stream structure. IEEE Trans. Veh. Technol. 2020, 69, 13521–13531. [Google Scholar] [CrossRef]
- West, N.E.; O’shea, T. Deep architectures for modulation recognition. In Proceedings of the 2017 IEEE International Symposium on Dynamic Spectrum Access Networks (DySPAN), Baltimore, MD, USA, 6–9 March 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Wu, Y.; Li, X.; Fang, J. A deep learning approach for modulation recognition via exploiting temporal correlations. In Proceedings of the 2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Kalamata, Greece, 25–28 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Xu, J.; Luo, C.; Parr, G.; Luo, Y. A spatiotemporal multi-channel learning framework for automatic modulation recognition. IEEE Wirel. Commun. Lett. 2020, 9, 1629–1632. [Google Scholar] [CrossRef]
- Li, L.; Zhu, Y.; Zhu, Z. Automatic modulation classification using ResNeXt-GRU with deep feature fusion. IEEE Trans. Instrum. Meas. 2023, 72, 1–10. [Google Scholar] [CrossRef]
- Elsagheer, M.M.; Ramzy, S.M. A hybrid model for automatic modulation classification based on residual neural networks and long short term memory. Alex. Eng. J. 2023, 67, 117–128. [Google Scholar] [CrossRef]
- Wang, X.; Liu, D.; Zhang, Y.; Li, Y.; Wu, S. A spatiotemporal multi-stream learning framework based on attention mechanism for automatic modulation recognition. Digit. Signal Process. 2022, 130, 103703. [Google Scholar] [CrossRef]
- Li, S.; Ding, C.; Xiao, L.; Zhang, X.; Liu, G.; Jiang, T. Expectation propagation aided model driven learning for OTFS signal detection. IEEE Trans. Veh. Technol. 2023, 72, 12407–12412. [Google Scholar] [CrossRef]
- Kumar, A.; Manish; Satija, U. Residual stack-aided hybrid CNN-LSTM-based automatic modulation classification for orthogonal time-frequency space system. IEEE Commun. Lett. 2023, 27, 3255–3259. [Google Scholar] [CrossRef]
- Raviteja, P.; Phan, K.T.; Hong, Y. Embedded pilot-aided channel estimation for OTFS in delay–Doppler channels. IEEE Trans. Veh. Technol. 2019, 68, 4906–4917. [Google Scholar] [CrossRef]
- Guo, L.; Gu, P.; Zou, J.; Liu, G.; Shu, F. DNN-based fractional Doppler channel estimation for OTFS modulation. IEEE Trans. Veh. Technol. 2023, 72, 15062–15067. [Google Scholar] [CrossRef]
- Azzouz, E.; Nandi, A. Procedure for automatic recognition of analogue and digital modulations. IEE Proc.-Commun. 1996, 143, 259–266. [Google Scholar] [CrossRef]
- Kim, K.; Polydoros, A. Digital modulation classification: The BPSK versus QPSK case. In Proceedings of the MILCOM 88, 21st Century Military Communications-What’s Possible?’ Conference Record, Military Communications Conference, San Diego, CA, USA, 23–26 October 1988; IEEE: Piscataway, NJ, USA, 1988; pp. 431–436. [Google Scholar]
- Boiteau, D.; Le Martret, C. A general maximum likelihood framework for modulation classification. In Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP’98 (Cat. No. 98CH36181), Seattle, WA, USA, 15 May 1998; IEEE: Piscataway, NJ, USA, 1998; Volume 4, pp. 2165–2168. [Google Scholar]
- Panagiotou, P.; Anastasopoulos, A.; Polydoros, A. Likelihood ratio tests for modulation classification. In Proceedings of the MILCOM 2000, 21st Century Military Communications, Architectures and Technologies for Information Superiority (Cat. No. 00CH37155), Los Angeles, CA, USA, 22–25 October 2000; IEEE: Piscataway, NJ, USA, 2000; Volume 2, pp. 670–674. [Google Scholar]
- Azzouz, E.E.; Nandi, A.K.; Azzouz, E.E.; Nandi, A.K. Modulation recognition using artificial neural networks. Autom. Modul. Recognit. Commun. Signals 1996, 132–176. [Google Scholar]
- Swami, A.; Sadler, B.M. Hierarchical digital modulation classification using cumulants. IEEE Trans. Commun. 2000, 48, 416–429. [Google Scholar] [CrossRef]
- Kim, K.; Akbar, I.A.; Bae, K.K.; Um, J.S.; Spooner, C.M.; Reed, J.H. Cyclostationary approaches to signal detection and classification in cognitive radio. In Proceedings of the 2007 2nd IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks, Dublin, Ireland, 17–20 April 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 212–215. [Google Scholar]
- Raviteja, P.; Phan, K.T.; Hong, Y.; Viterbo, E. Interference cancellation and iterative detection for orthogonal time frequency space modulation. IEEE Trans. Wirel. Commun. 2018, 17, 6501–6515. [Google Scholar] [CrossRef]
- 3GPP. Physical Channels and Modulation, TS 38.211. Available online: https://www.etsi.org/deliver/etsi_ts/138200_138299/138211/16.02.00_60/ts_138211v160200p.pdf (accessed on 11 July 2025).
- Lee, C.; Hasegawa, H.; Gao, S. Complex-Valued Neural Networks: A Comprehensive Survey. IEEE/CAA J. Autom. Sin. 2022, 9, 1406–1426. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| Delay-Doppler grid size | N = 32, M = 64 |
| Pilot symbol dimensions | 3 × 3 |
| Guard interval lengths | 2 |
| Sampling rate (kHz) | 100 |
| Maximum Doppler shift (Hz) | 1000 |
| Carrier frequency (GHz) | 5 |
| Channel model | Extended vehicular A model (EVA) |
| Modes of modulation | BPSK, QPSK, 8PSK, 16QAM, 64QAM, 256QAM |
| Modulation Type | Pilot Type | Value |
|---|---|---|
| BPSK | Real number | 2 |
| QPSK | Complex number | |
| 8PSK | Phase rotation | |
| 16QAM | Complex number | |
| 64QAM | Complex number | |
| 256QAM | Real number | 2.5 |
| Pilot Symbol Configuration | Average Classification Acc. (%) |
|---|---|
| 3 × 3 differentiated pilot symbols | 97.8 |
| 3 × 3 same pilot symbols | 93.7 |
| 2 × 2 differentiated pilot symbols | 92.8 |
| 2 × 2 same pilot symbols | 92.6 |
| 1 × 1 differentiated pilot symbols | 92.4 |
| 1 × 1 same pilot symbols | 81.2 |
| No pilot symbols | 74.6 |
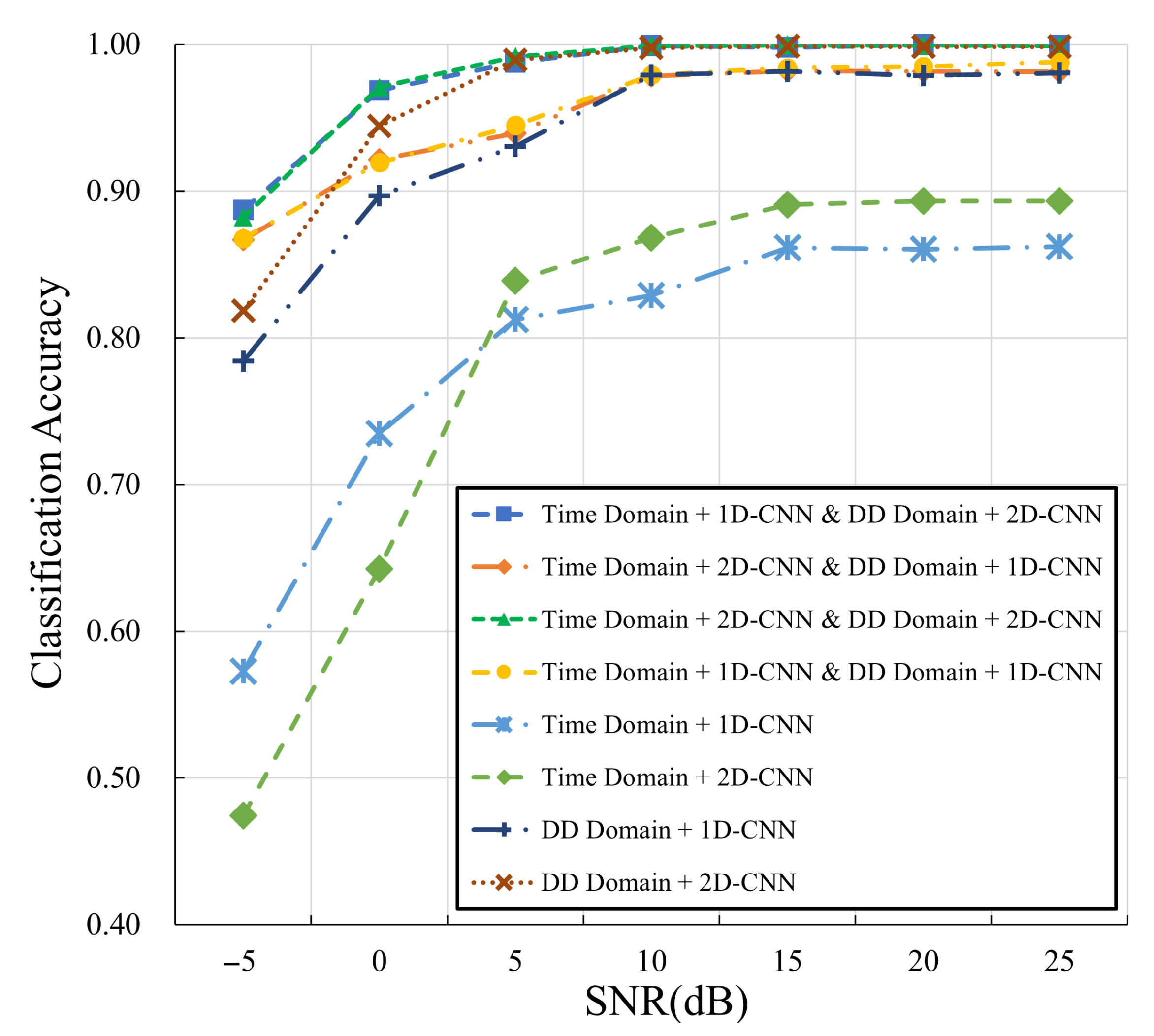
| Parameter | Average Classification Acc. (%) | Parameter | Average Classification Acc. (%) |
|---|---|---|---|
| Time Domain + 1D-CNN & DD Domain + 2D-CNN | 97.8 | Time Domain + 1D-CNN | 79.0 |
| Time Domain + 2D-CNN & DD Domain + 1D-CNN | 95.0 | Time Domain + 2D-CNN | 78.6 |
| Time Domain + 2D-CNN & DD Domain + 2D-CNN | 97.7 | DD Domain + 1D-CNN | 93.3 |
| Time Domain + 1D-CNN & DD Domain + 1D-CNN | 95.3 | DD Domain + 2D-CNN | 96.4 |
| Maximum Doppler Shift (Speed) | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) |
|---|---|---|---|---|
| 400 Hz (86 km/h) | 98.26 | 98.27 | 98.26 | 98.27 |
| 1000 Hz (216 km/h) | 97.81 | 97.81 | 97.81 | 97.81 |
| 1200 Hz (260 km/h) | 97.71 | 97.77 | 97.73 | 97.75 |
| 1400 Hz (302 km/h) | 95.41 | 95.43 | 95.40 | 95.40 |
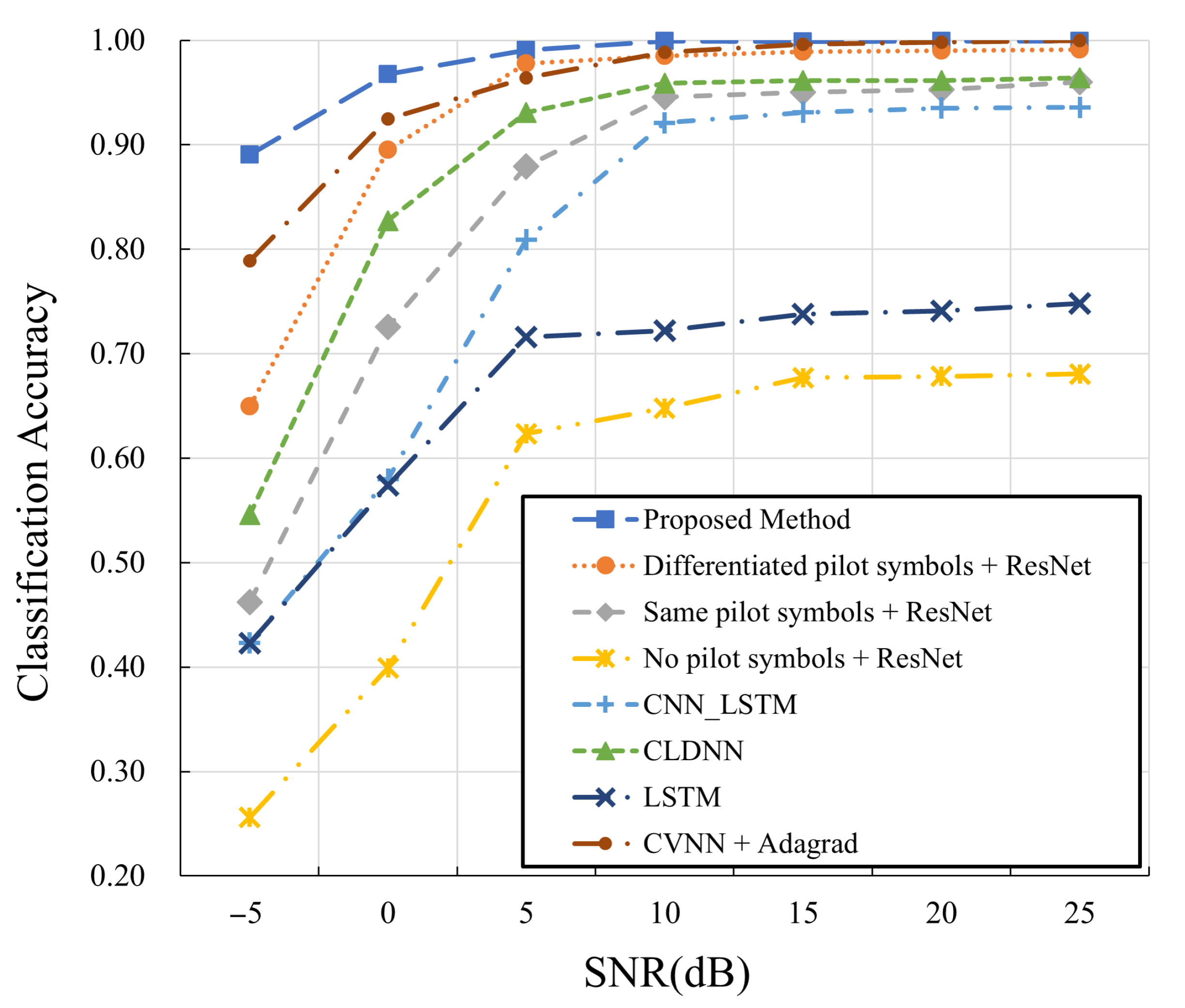
| Model | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) |
|---|---|---|---|---|
| Proposed Method | 97.81 | 97.81 | 97.81 | 97.81 |
| Differentiated pilot symbols + ResNet [14] | 92.50 | 92.57 | 92.52 | 92.54 |
| Same pilot symbols + ResNet [14] | 83.87 | 83.90 | 83.89 | 83.88 |
| no pilot symbols + ResNet [14] | 56.45 | 60.81 | 56.14 | 56.97 |
| CNN_LSTM [33] | 79.09 | 79.06 | 79.14 | 79.09 |
| CLDNN [26] | 87.87 | 88.84 | 87.87 | 87.81 |
| LSTM [24] | 66.60 | 69.30 | 59.50 | 64.00 |
| CVNN + Adagrad [45] | 95.62 | 95.64 | 95.63 | 95.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Zhang, B.; Luo, H.; He, H. Differentiated Embedded Pilot Assisted Automatic Modulation Classification for OTFS System: A Multi-Domain Fusion Approach. Sensors 2025, 25, 4393. https://doi.org/10.3390/s25144393
Liu Z, Zhang B, Luo H, He H. Differentiated Embedded Pilot Assisted Automatic Modulation Classification for OTFS System: A Multi-Domain Fusion Approach. Sensors. 2025; 25(14):4393. https://doi.org/10.3390/s25144393
Chicago/Turabian StyleLiu, Zhenkai, Bibo Zhang, Hao Luo, and Hao He. 2025. "Differentiated Embedded Pilot Assisted Automatic Modulation Classification for OTFS System: A Multi-Domain Fusion Approach" Sensors 25, no. 14: 4393. https://doi.org/10.3390/s25144393
APA StyleLiu, Z., Zhang, B., Luo, H., & He, H. (2025). Differentiated Embedded Pilot Assisted Automatic Modulation Classification for OTFS System: A Multi-Domain Fusion Approach. Sensors, 25(14), 4393. https://doi.org/10.3390/s25144393






