Non-Adiabatically Tapered Optical Fiber Humidity Sensor with High Sensitivity and Temperature Compensation
Abstract
1. Introduction
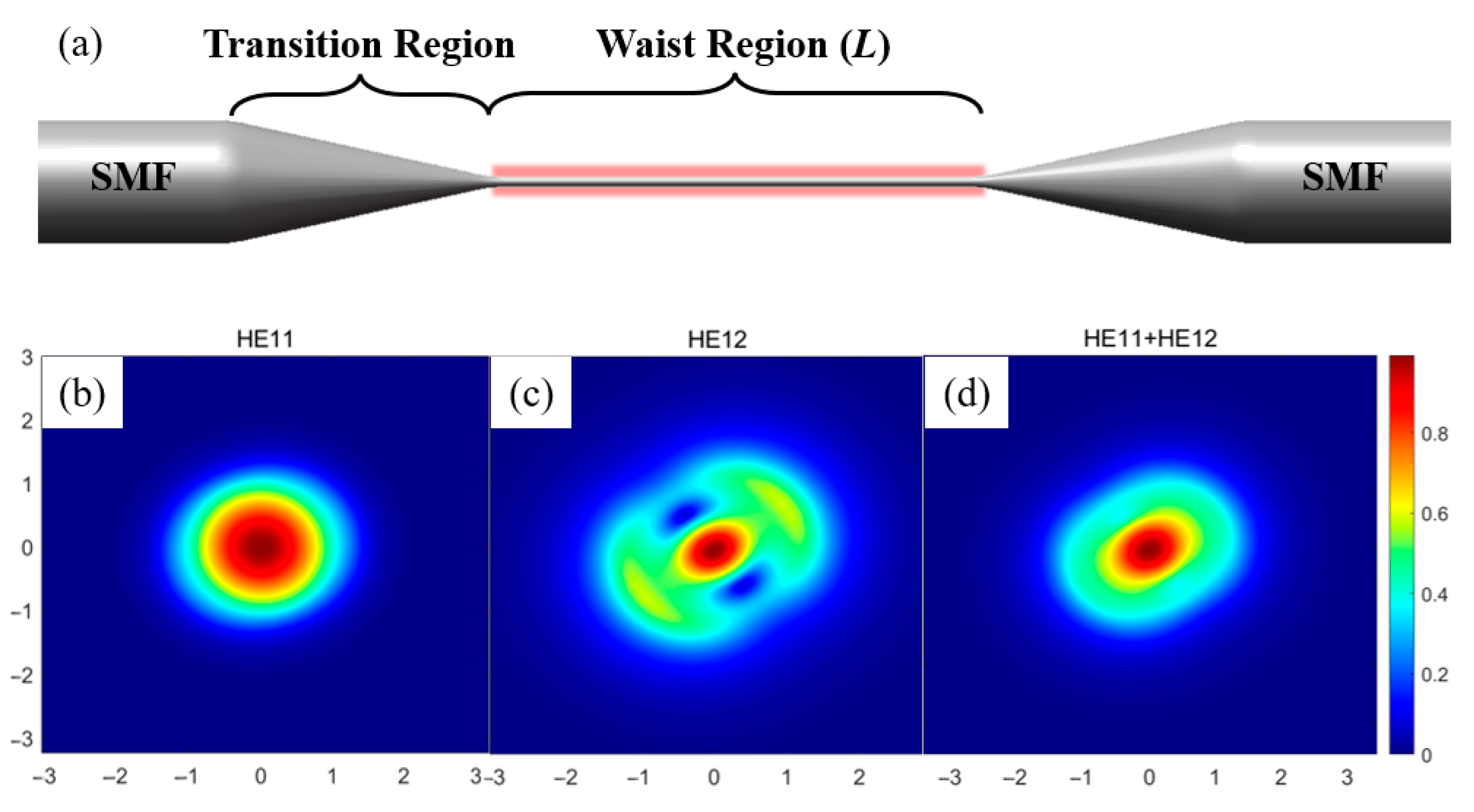
2. Sensing Principle
3. Sensor Fabrication and Test System
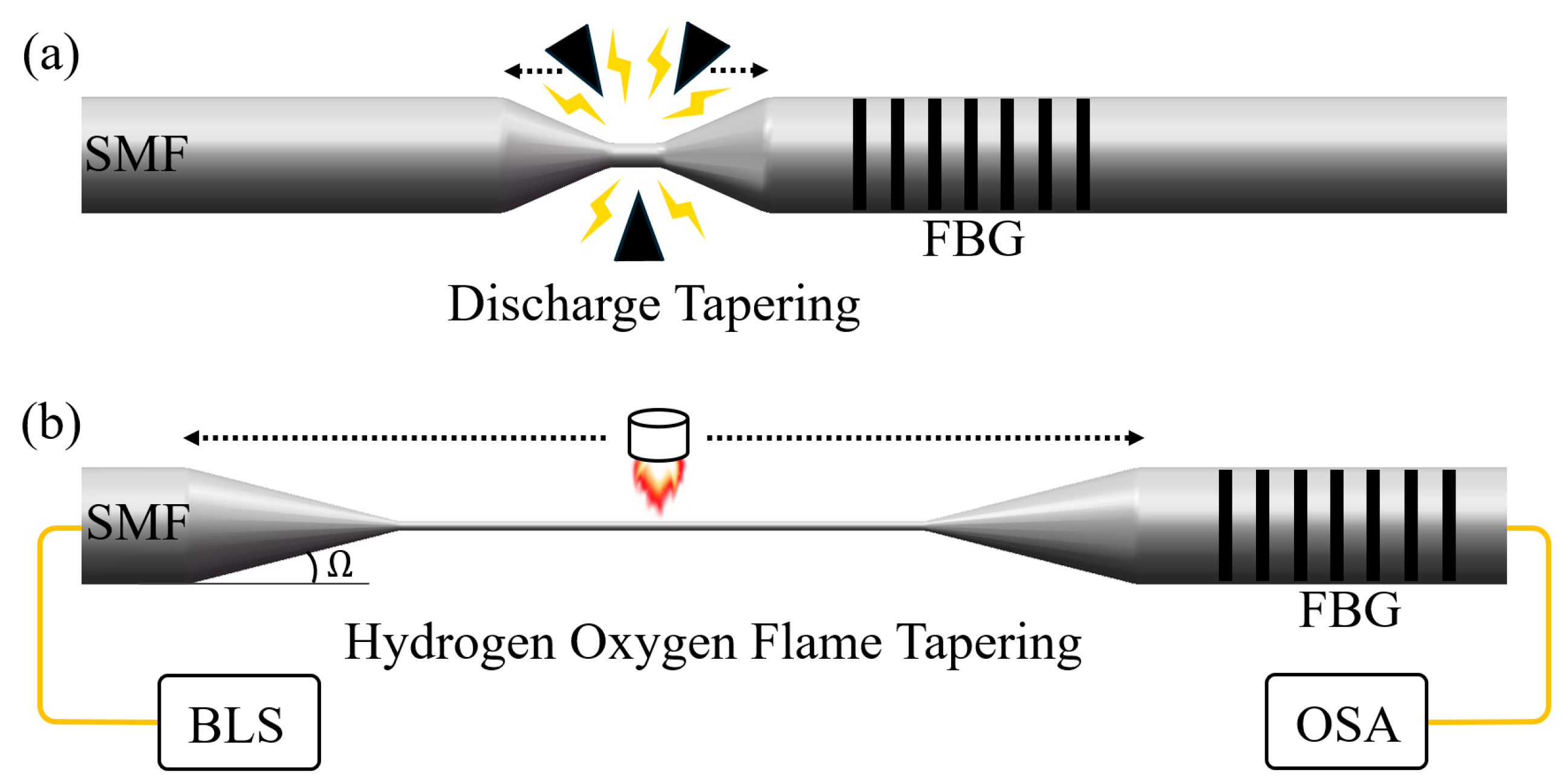
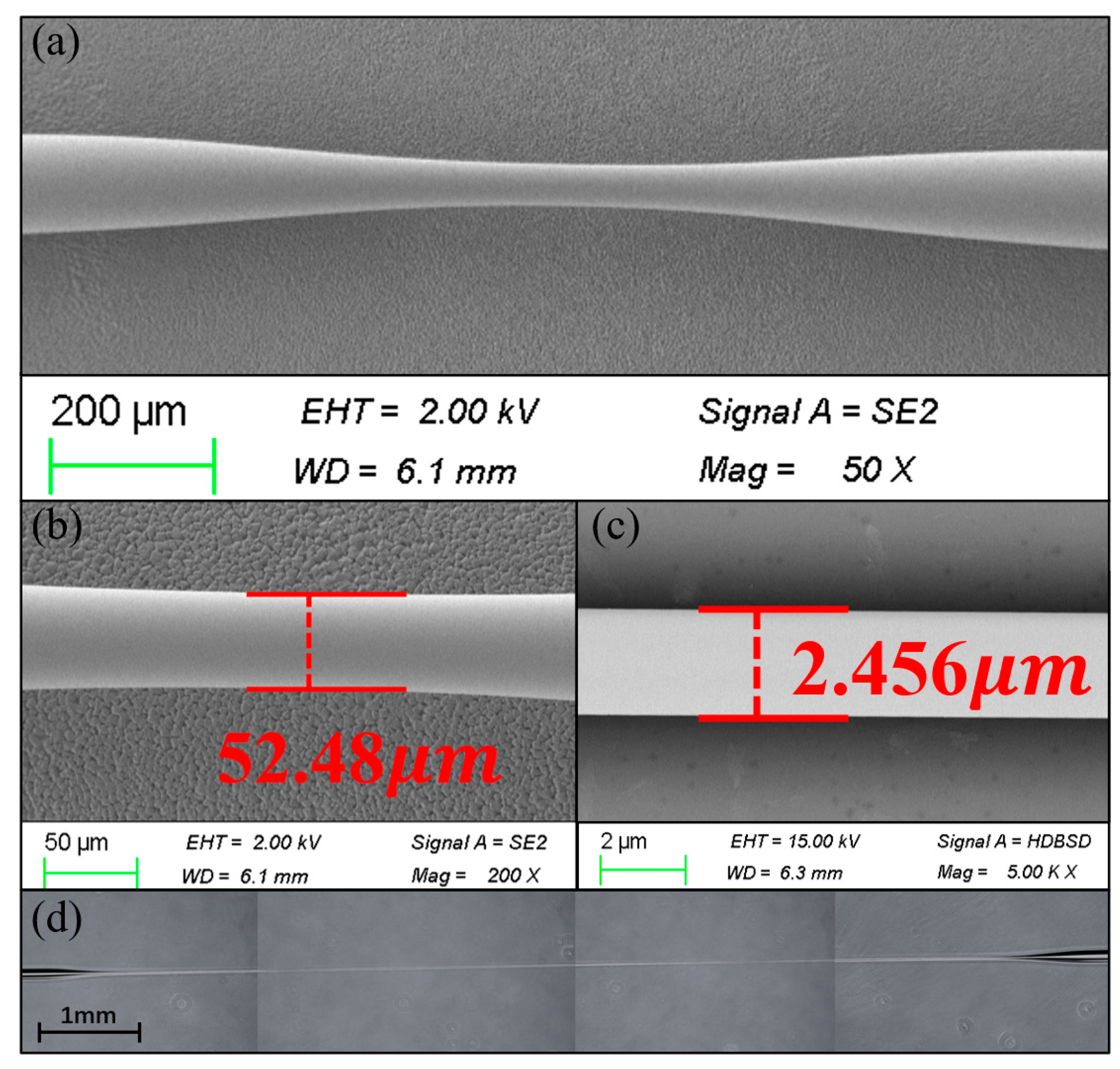
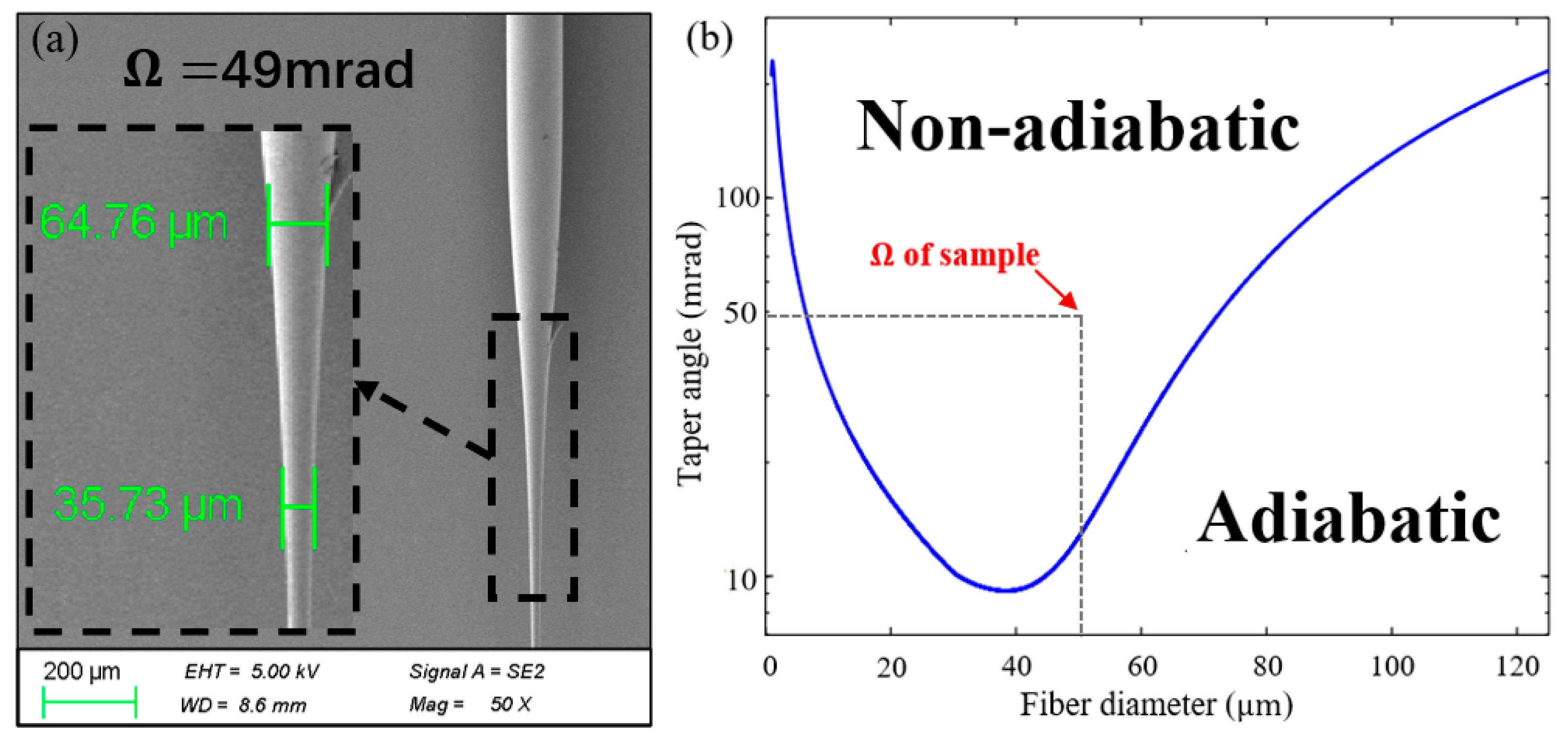
3.1. Fabrication of Cascaded FBG Tapered Fiber Optic Sensor
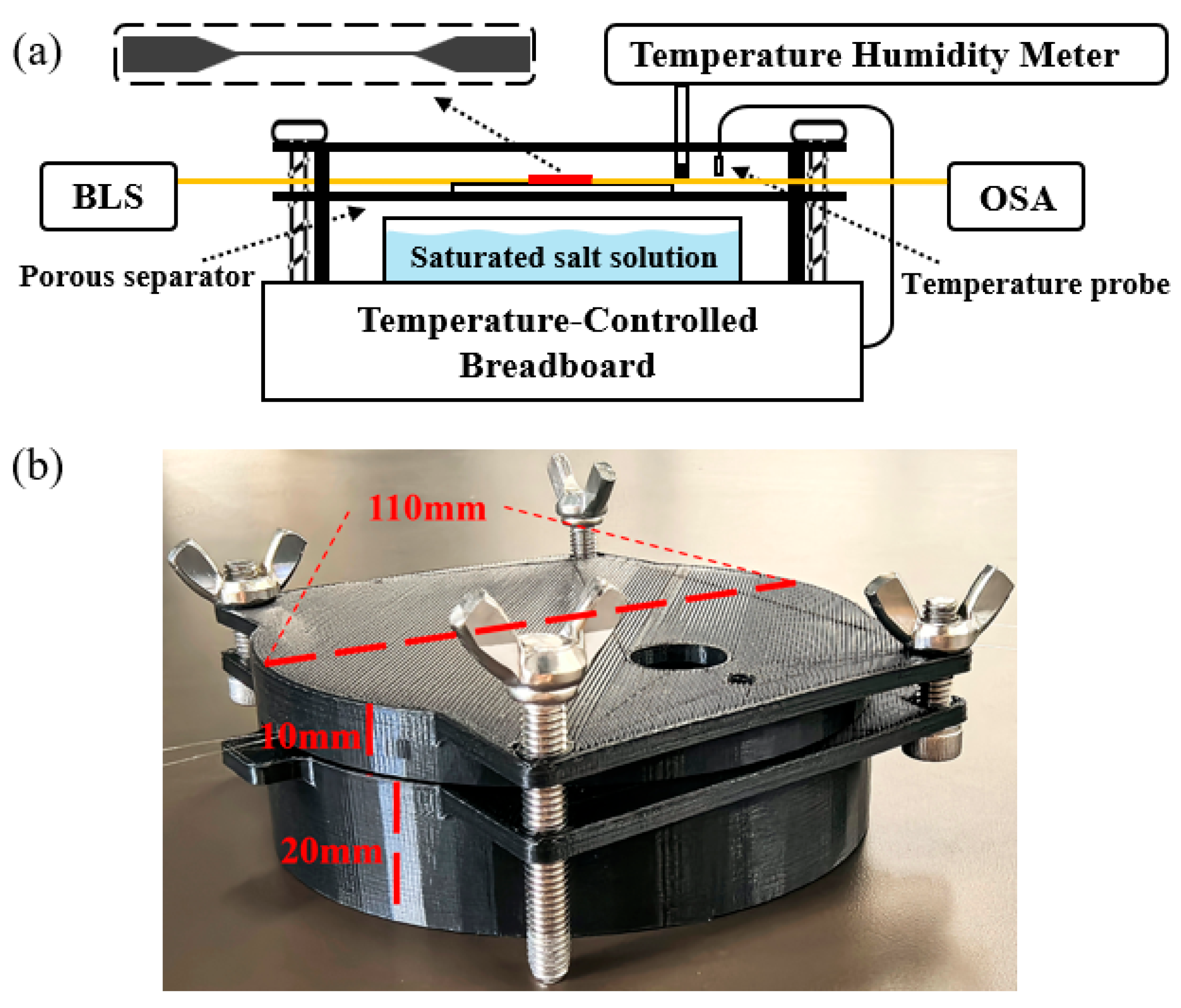
3.2. Temperature and Humidity Testing System
4. Experiment Result and Discussion
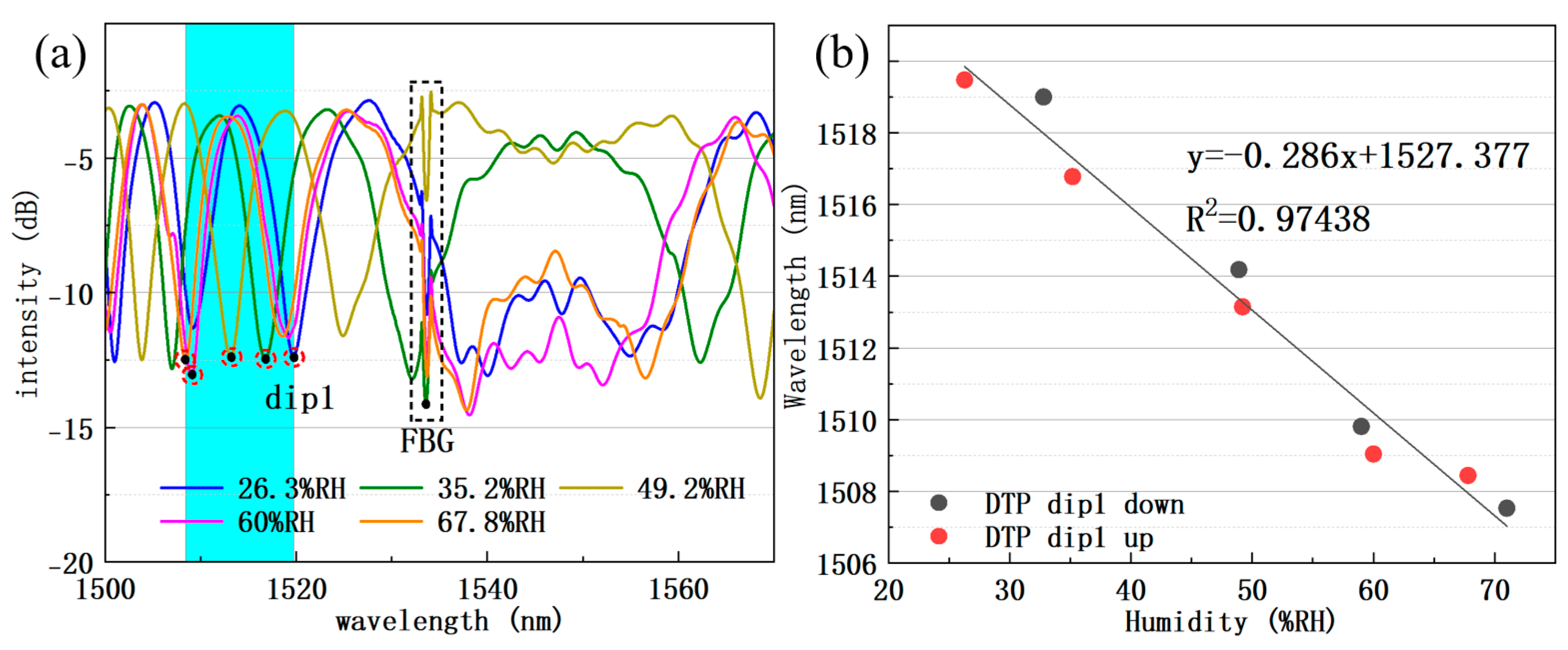
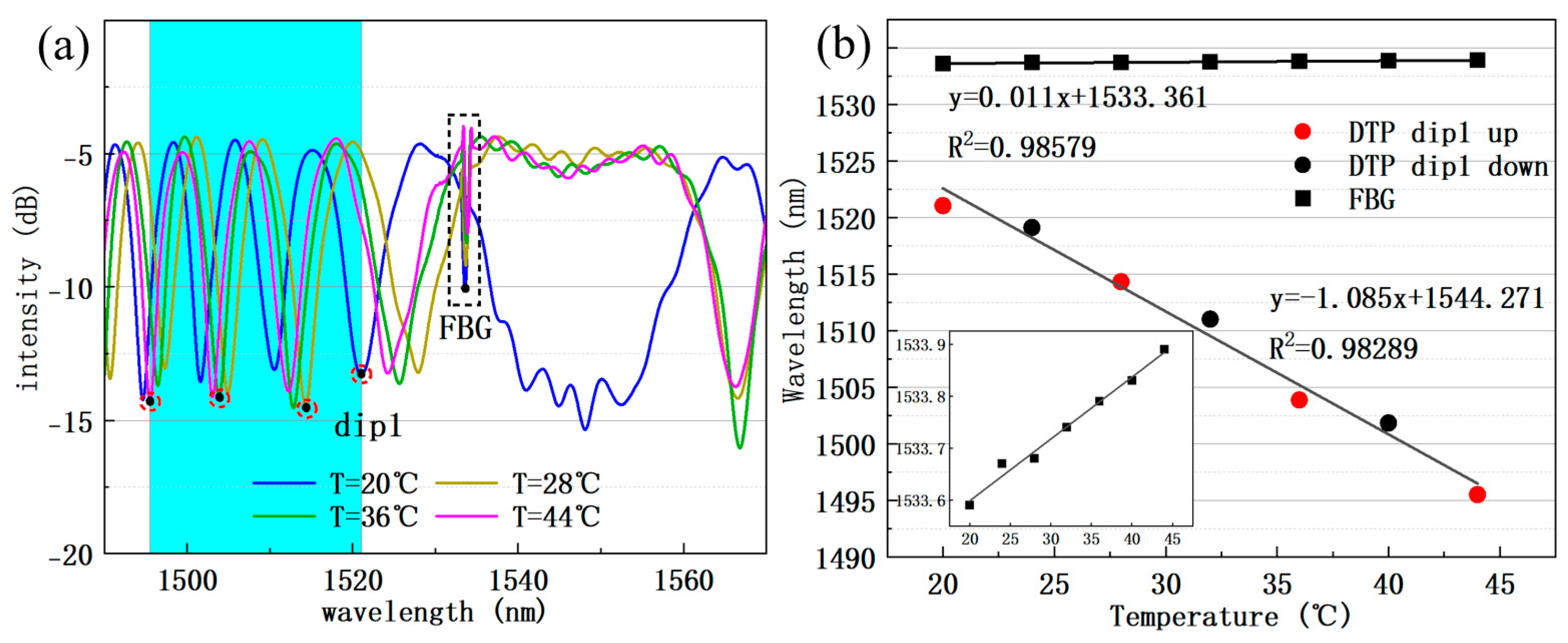
4.1. Humidity and Temperature Dual-Parameter Measurement
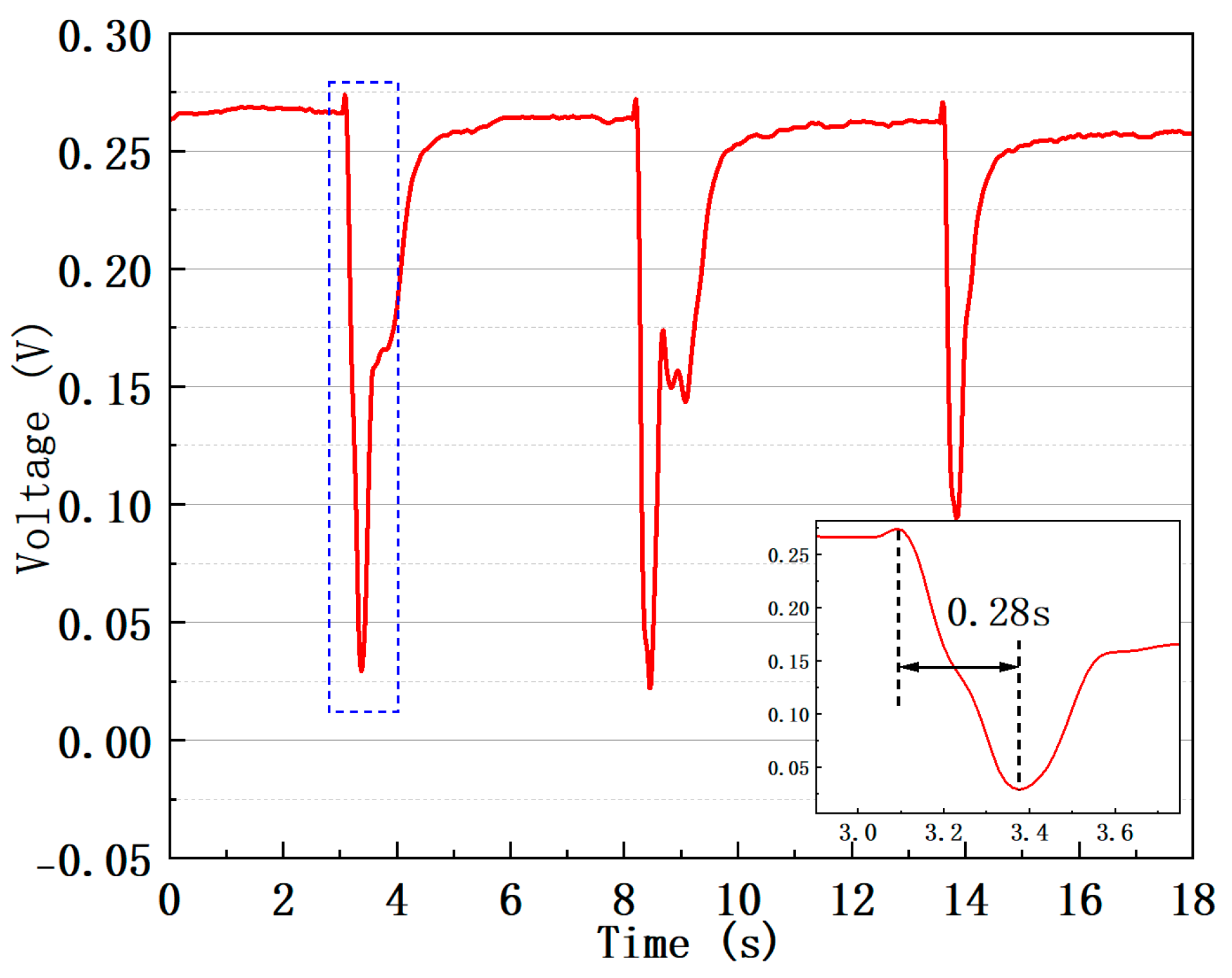
4.2. Stability and Response Time
4.3. Comparison and Discussion
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, C.Y.; Lee, G.B. Humidity sensors: A review. Sens. Lett. 2005, 3, 1–15. [Google Scholar] [CrossRef]
- Kolpakov, S.A.; Gordon, N.T.; Mou, C.B.; Zhou, K.M. Toward a New Generation of Photonic Humidity Sensors. Sensors 2014, 14, 3986–4013. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Li, J.; Guo, L.N.; Tian, M.J.; Meng, F.L. Development of fabrication technique and sensing performance of optical fiber humidity sensors in the most recent decade. Measurement 2023, 215, 112888. [Google Scholar] [CrossRef]
- Zhang, J.X.; Shen, X.Y.; Qian, M.; Xiang, Z.; Hu, X.D. An optical fiber sensor based on polyimide coated fiber Bragg grating for measurement of relative humidity. Opt. Fiber Technol. 2021, 61, 102406. [Google Scholar] [CrossRef]
- Wang, Y.L.; Liu, Y.Q.; Zou, F.; Jiang, C.; Mou, C.B.; Wang, T.Y. Humidity Sensor Based on a Long-Period Fiber Grating Coated with Polymer Composite Film. Sensors 2019, 19, 2263. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Yang, J.D.; Zhang, M.; Li, S.; Liu, Z.H.; Zhang, Y.X.; Zhang, J.Z.; Yuan, L.B. Long-period fiber grating humidity sensor based on spider silks. Sens. Actuators A—Phys. 2022, 342, 113660. [Google Scholar] [CrossRef]
- Zhou, C.; Song, Y.J.; Zhou, Q.; Tian, J.J.; Yao, Y. Ultra-High-Sensitivity Humidity Fiber Sensor Based on Harmonic Vernier Effect in Cascaded FPI. Sensors 2022, 22, 4816. [Google Scholar] [CrossRef]
- Liu, P.Y.; Feng, L.H.; Chen, H.Y.; Li, P.J.; Ma, X.X.; Lv, M. Humidity sensor based on tapered no-core fiber coated with Ti3C2Tx MXene. Ceram. Int. 2024, 50, 23586–23592. [Google Scholar] [CrossRef]
- Liu, Y.; Li, X.S.; You, J.; Peng, Y.F.; Chen, H.B. A controllable humidity sensitivity measurement solution based on a pure FPI fiber tip and the harmonic Vernier effect. Sens. Actuators B—Chem. 2024, 403, 135085. [Google Scholar] [CrossRef]
- Tan, Y.Z.; Sun, L.P.; Jin, L.; Li, J.; Guan, B.O. Temperature-Insensitive Humidity Sensor Based on a Silica Fiber Taper Interferometer. IEEE Photonics Technol. Lett. 2013, 25, 2201–2204. [Google Scholar] [CrossRef]
- Zhang, J.T.; Tong, Z.R.; Zhang, W.H.; Zhao, Y.M.; Liu, Y.X. Research on NCF-PCF-NCF Structure Interference Characteristic for Temperature and Relative Humidity Measurement. IEEE Photonics J. 2021, 13, 7100805. [Google Scholar] [CrossRef]
- Fu, H.W.; Jiang, Y.H.; Ding, J.J.; Zhang, J.L. Low Temperature Cross-Sensitivity Humidity Sensor Based on a U-Shaped Microfiber Interferometer. IEEE Sens. J. 2017, 17, 644–649. [Google Scholar] [CrossRef]
- Sun, L.P.; Li, J.; Jin, L.; Ran, Y.; Guan, B.O. High-birefringence microfiber Sagnac interferometer based humidity sensor. Sens. Actuators B—Chem. 2016, 231, 696–700. [Google Scholar] [CrossRef]
- Xu, K.; Li, H.Y.; Liu, Y.J.; Wang, Y.J.; Tian, J.J.; Wang, L.; Du, J.B.; He, Z.Y.; Song, Q.H. Optical Fiber Humidity Sensor Based on Water Absorption Peak Near 2-μm Waveband. IEEE Photonics J. 2019, 11, 7101308. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, Y.D.; Su, H.Y.; Qi, K.Y.; Zhu, F.X.; Wu, Y.F. Dual-Parameter Fiber-Optics Relative Humidity and Displacement Sensor Based on the Topological Ring Structures. IEEE Sens. J. 2022, 22, 330–337. [Google Scholar] [CrossRef]
- Gao, D.; Ma, G.M.; Qin, W.Q.; Gao, T.Y.; Wang, Y.K.; Wang, Y.; Zhang, Y.A.; Zhou, H.Y. A Relative Humidity Sensor Based on Non-Adiabatic Tapered Optical Fiber for Remote Measurement in Power Cable Tunnel. IEEE Trans. Instrum. Meas. 2022, 71, 9505608. [Google Scholar] [CrossRef]
- Xu, W.Y.; Wu, B.; Wei, Y.L.; Zhang, G.Y.; Zhao, Y.J.; Cui, X.J.; Peng, F.; Yang, J. Axial strain and temperature sensor based on tapered seven-core fiber operating at dispersion turning point. Opt. Laser Technol. 2024, 174, 110656. [Google Scholar] [CrossRef]
- Zhu, C.L.; Tang, C.F.; Huang, S.; Qu, Z.X.; Zhao, Y.; Li, H.P. Cross-Sensitivity-Free Highly Sensitive Torsion and Strain Sensor Based on Concatenated DTP-Customizable Helical Fiber Gratings. IEEE Sens. J. 2023, 23, 27423–27430. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Yang, P.; Wei, W.X.; Jiang, S.C.; Bao, W.G.; Zhu, X.S.; Wu, G.Z.; Chen, D.R. Highly Sensitive Salinity Sensor Based on Virtual Vernier Effect of Micro-Nano Fiber Mode Interferometer. IEEE Sens. J. 2024, 24, 16121–16129. [Google Scholar] [CrossRef]
- Xu, S.Y.; Kang, P.; Hu, Z.J.; Chang, W.J.; Huang, F. Ultrasensitive Optical Fiber Sensors Working at Dispersion Turning Point: Review. Sensors 2023, 23, 1725. [Google Scholar] [CrossRef]
- Zhang, N.M.Y.; Li, K.W.; Zhang, N.; Zheng, Y.; Zhang, T.; Qi, M.; Shum, P.; Wei, L. Highly sensitive gas refractometers based on optical microfiber modal interferometers operating at dispersion turning point. Opt. Express 2018, 26, 29148–29158. [Google Scholar] [CrossRef] [PubMed]
- Ismaeel, R.; Lee, T.; Ding, M.; Belal, M.; Brambilla, G. Optical microfiber passive components. Laser Photonics Rev. 2013, 7, 350–384. [Google Scholar] [CrossRef]
- Fielding, A.J.; Edinger, K.; Davis, C.C. Experimental observation of mode evolution in single-mode tapered optical fibers. J. Light. Technol. 1999, 17, 1649–1656. [Google Scholar] [CrossRef]
- Liu, K.J.; Fan, J.H.; Luo, B.B.; Zou, X.; Wu, D.C.; Zou, X.L.; Shi, S.H.; Guo, Y.F.; Zhao, M.F. Highly sensitive vibration sensor based on the dispersion turning point microfiber Mach-Zehnder interferometer. Opt. Express 2021, 29, 32983–32995. [Google Scholar] [CrossRef] [PubMed]
- Edlén, B. The Refractive Index of Air. Metrologia 1966, 2, 71–80. [Google Scholar] [CrossRef]
- Jones, F.E. The Refractivity of Air. J. Res. Natl. Bur. Stand. 1981, 86, 27–32. [Google Scholar] [CrossRef]
- Pevec, S.; Donlagic, D. Multiparameter fiber-optic sensors: A review. Opt. Eng. 2019, 58, 072009. [Google Scholar] [CrossRef]
- Ravets, S.; Hoffman, J.E.; Kordell, P.R.; Wong-Campos, J.D.; Rolston, S.L.; Orozco, L.A. Intermodal energy transfer in a tapered optical fiber: Optimizing transmission. J. Opt. Soc. Am. A—Opt. Image Sci. Vis. 2013, 30, 2361–2371. [Google Scholar] [CrossRef]
- Qi, Y.F.; Jia, C.; Tang, L.; Zhang, X.; Gong, C.B.; Liu, Y.Y.; Liu, X.Q. Research on temperature and humidity sensing characteristics of cascaded LPFG-FBG. Optik 2019, 188, 19–26. [Google Scholar] [CrossRef]


| Start Speed /s) | Sweep Speed /s) | Waist Length ) | Start Power | Waist Power |
|---|---|---|---|---|
| 50 | 600 | 500 | 400 | 450 |
| Step | Stretching Length ) | Fire Height ) | Stretching Speed /s) | Hydrogen Flow Rate (sccm) | Sweep Speed /s) | Sweep Distance ) |
|---|---|---|---|---|---|---|
| Step1 | 0–4000 | 3.011 | 70 | 180 | / | / |
| Step2 | 4000–10,000 | 3.011 | 90 | 150 | 2000 | 6000 |
| Sensors | Humidity Sensitivity | Range | Cost | Stability | Response Time | Citation |
|---|---|---|---|---|---|---|
| Panda fiber-SI | −0.422 nm/%RH | 25–70%RH | high | 0.024 dB in 1 min | 0.06 s | [13] |
| Tapered microfiber | 0.18 mW/%RH | 28–90%RH | low | 3.66% in 3 h | 0.8 s | [14] |
| Microfiber knot resonator | 0.010 nm%RH | 35–95%RH | low | 0.28 dB in 3 h | 1.55 s | [14] |
| U-shaped-taper-MI | 0.115 nm/%RH | 30–90%RH | low | 0.4% in 3 h | / | [12] |
| NCF-PCF-NCF-taper-MZI | 0.02 nm/%RH | 30–70%RH | high | 2.7% in 2 h | / | [11] |
| DTP-FBG taper | −0.286 nm/%RH | 25–86%RH | low | 0.4% in 40 min | 0.26 s | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Z.; Wang, C.; Tang, Y.; Jiang, S.; Zhong, X.; Zhang, Z.; Dai, R. Non-Adiabatically Tapered Optical Fiber Humidity Sensor with High Sensitivity and Temperature Compensation. Sensors 2025, 25, 4390. https://doi.org/10.3390/s25144390
Liang Z, Wang C, Tang Y, Jiang S, Zhong X, Zhang Z, Dai R. Non-Adiabatically Tapered Optical Fiber Humidity Sensor with High Sensitivity and Temperature Compensation. Sensors. 2025; 25(14):4390. https://doi.org/10.3390/s25144390
Chicago/Turabian StyleLiang, Zijun, Chao Wang, Yaqi Tang, Shoulin Jiang, Xianjie Zhong, Zhe Zhang, and Rui Dai. 2025. "Non-Adiabatically Tapered Optical Fiber Humidity Sensor with High Sensitivity and Temperature Compensation" Sensors 25, no. 14: 4390. https://doi.org/10.3390/s25144390
APA StyleLiang, Z., Wang, C., Tang, Y., Jiang, S., Zhong, X., Zhang, Z., & Dai, R. (2025). Non-Adiabatically Tapered Optical Fiber Humidity Sensor with High Sensitivity and Temperature Compensation. Sensors, 25(14), 4390. https://doi.org/10.3390/s25144390





