Cross-Scale Hypergraph Neural Networks with Inter–Intra Constraints for Mitosis Detection
Abstract
1. Introduction
- Limited training data: In pathological slides, mitotic cells are significantly fewer than normal cells, leading to a severe class imbalance between positive and negative samples in the dataset. Furthermore, since annotation requires expert pathologists, the amount of data available for training is extremely limited. In addition, the structure and morphology of cells vary greatly, and an imbalanced distribution among different types of mitotic figures is very common in datasets. As a result, trained detection models often suffer from high false negative or false positive rates. Moreover, with the increasing complexity and parameter size of current benchmark models, overfitting on mitosis detection tasks has become a frequent issue.
- Subtle features: Mitosis is a complex biological process and pathologists typically rely on nuclear morphology to determine whether a cell is undergoing mitosis. In H&E-stained slides, mitotic nuclei appear as dark blue dots, which are often difficult to distinguish from the background and can easily be confused with apoptotic cells that also appear as dark blue dots. In addition, the morphological differences between various cell types in tissue sections are minimal, and mitotic cells often resemble normal cells in appearance. These factors make the accurate detection of mitotic figures extremely challenging.
- Neglecting cell relationships: In pathological diagnosis, valuable information lies not only in individual cellular features but also in the relationships between surrounding cells. For cells with ambiguous or indistinct features, pathologists often rely on comparisons with neighboring cells to determine whether mitosis is occurring. However, most current models lack the ability to effectively model intercellular context, resulting in the loss of critical diagnostic information.
- Design a Block-Based Mixed Mechanism (BBMM), using parallel convolutional modules to efficiently extract deep information and enrich the gradient flow during training. In the feature fusion phase of the model, use a Bottom–Up mechanism to recover non-abstracted spatial details. These operations enable efficient feature analysis at the inter-level.
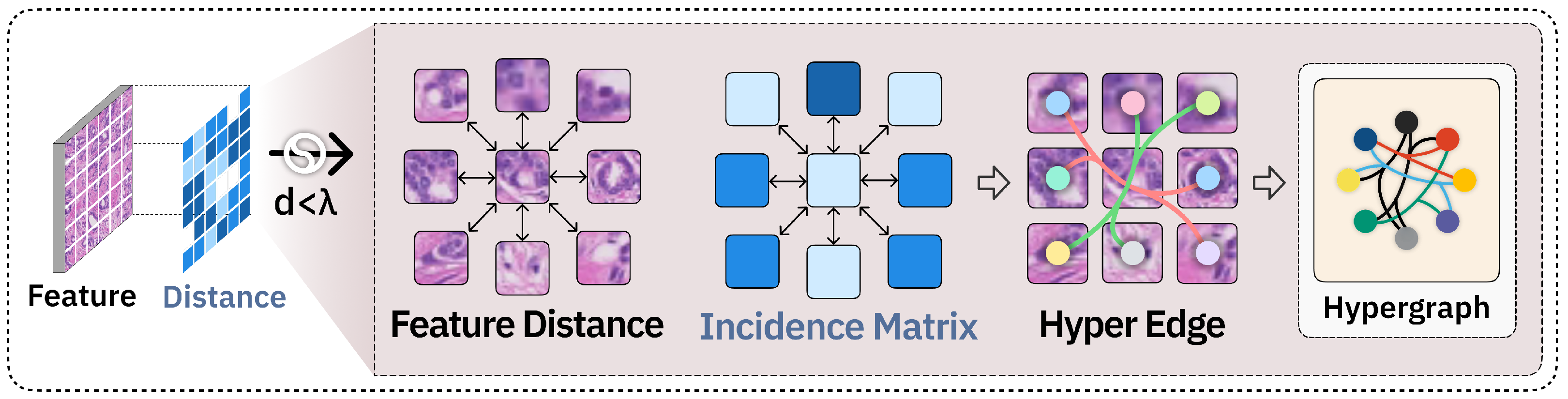
- Thoroughly analyze the shortcomings of existing mitosis detection models and apply the HGNN concept to the cell detection domain, effectively modeling the relationships between individual cells and cell populations. A novel hyperedge convolutional construction is designed to capture the visual features of different cells. These operations facilitate efficient feature analysis at the intra-level.
- Test the model on a public dataset with multiple tumor labels and originating from different staining imaging conditions, achieving favorable results. According to this research, this is the first time the HGNN concept has been applied in the mitosis detection domain.
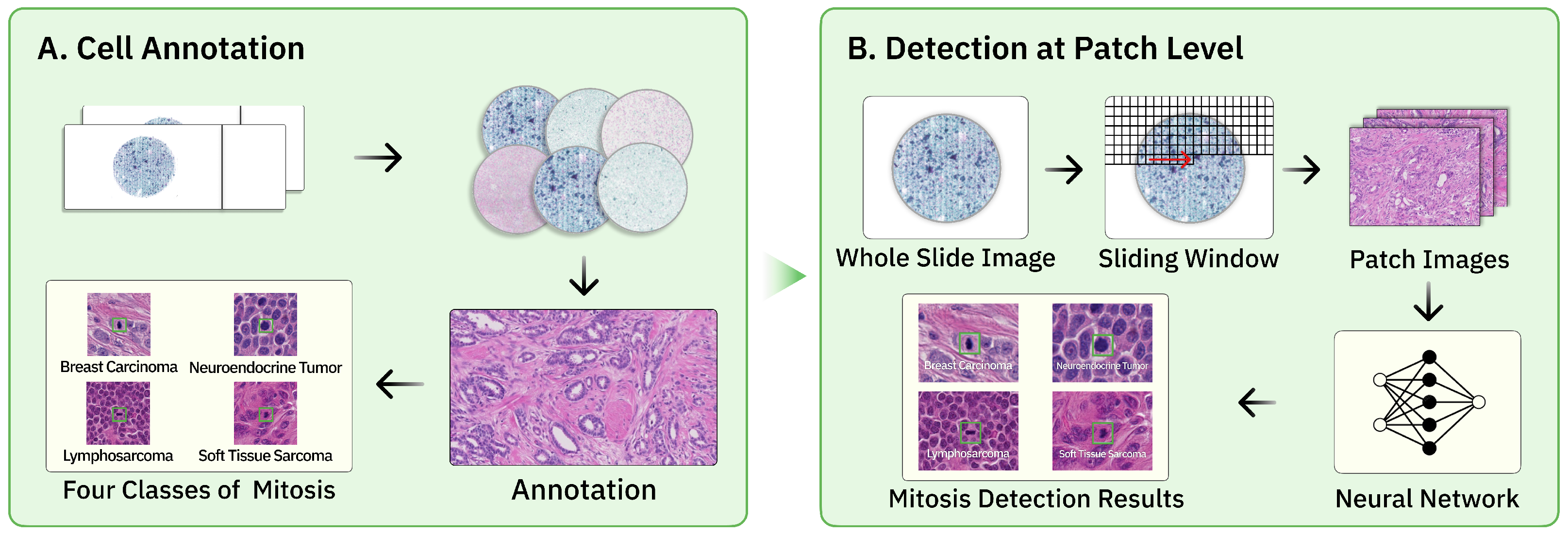
2. Materials and Methods
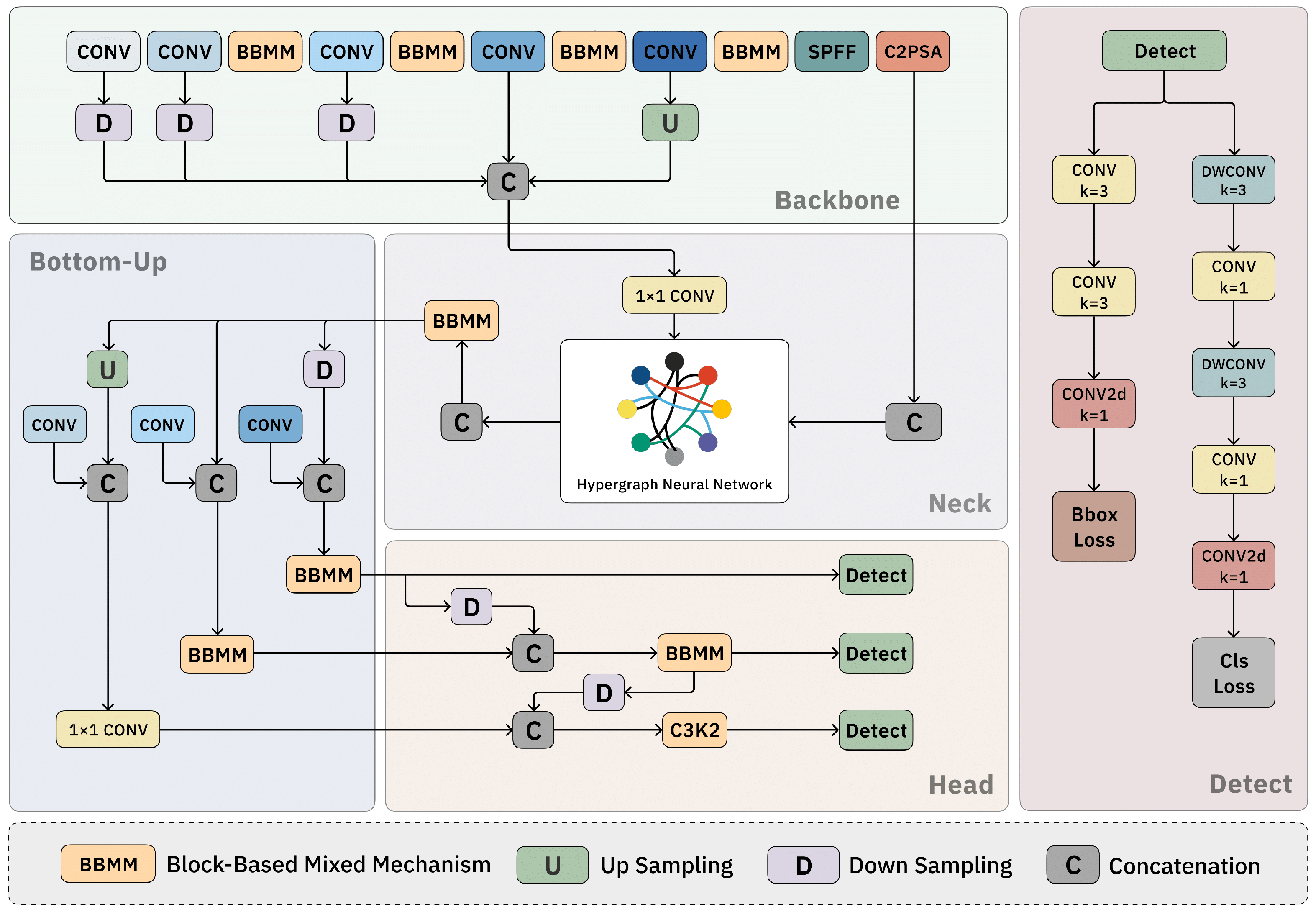
2.1. Overview
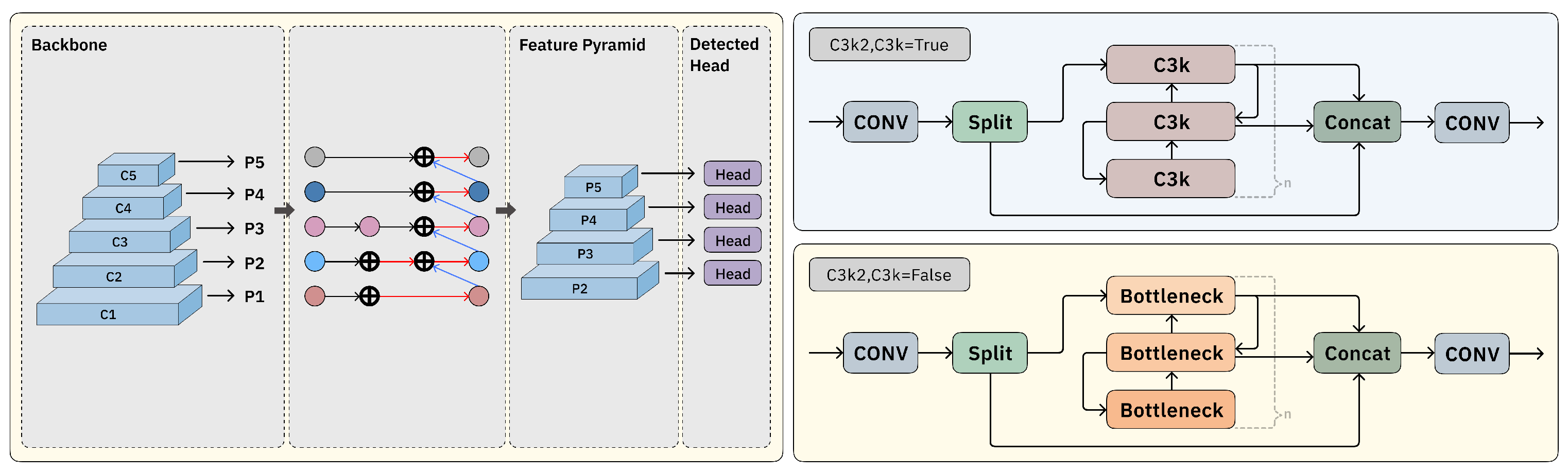
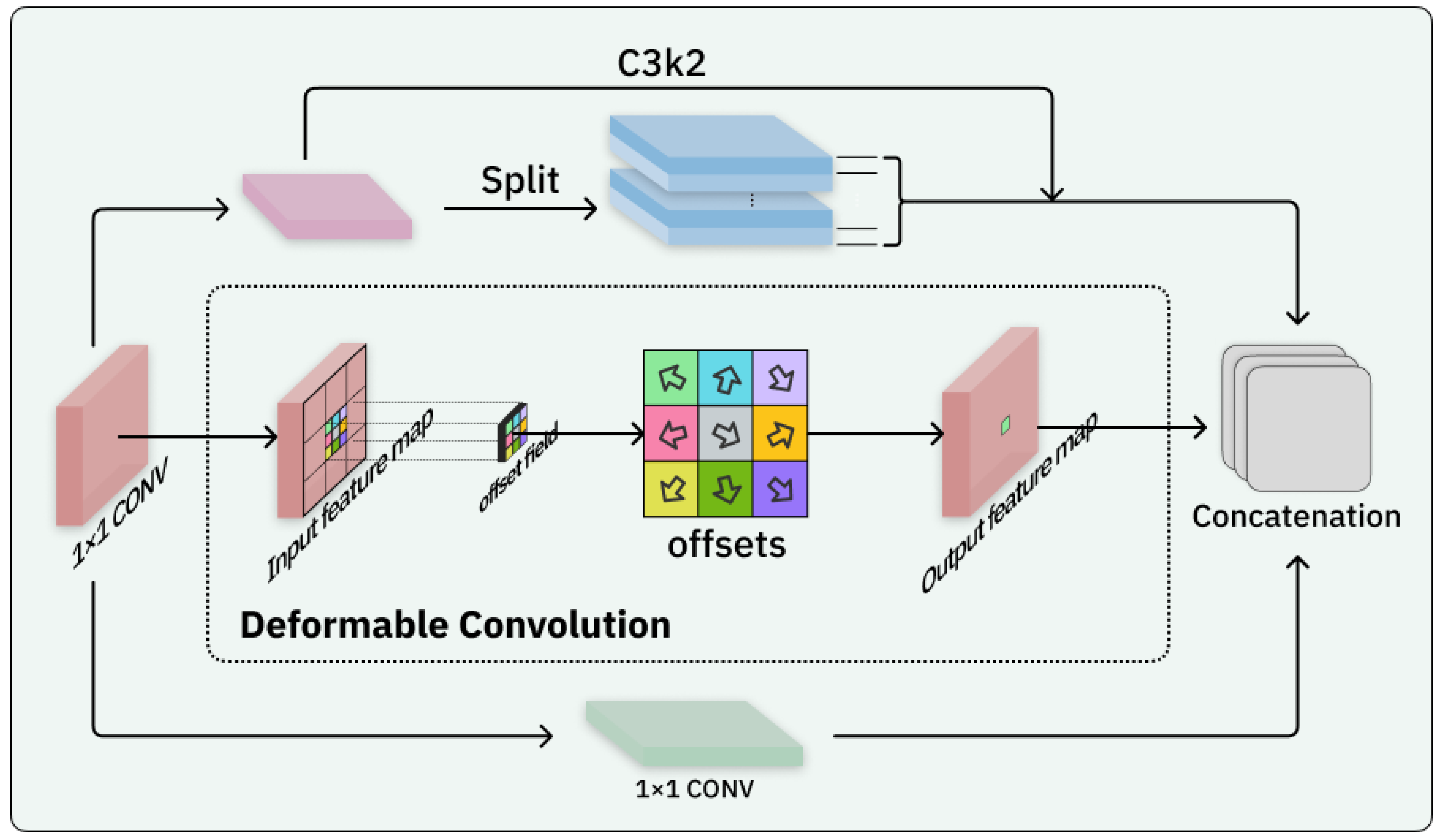
2.2. Block-Based Mixed Mechanism (BBMM)
2.3. Hypergraph Neural Network
2.4. Bottom–Up
3. Experiments and Results
3.1. Datasets
3.2. Implementation Details
3.3. Comparative Analysis
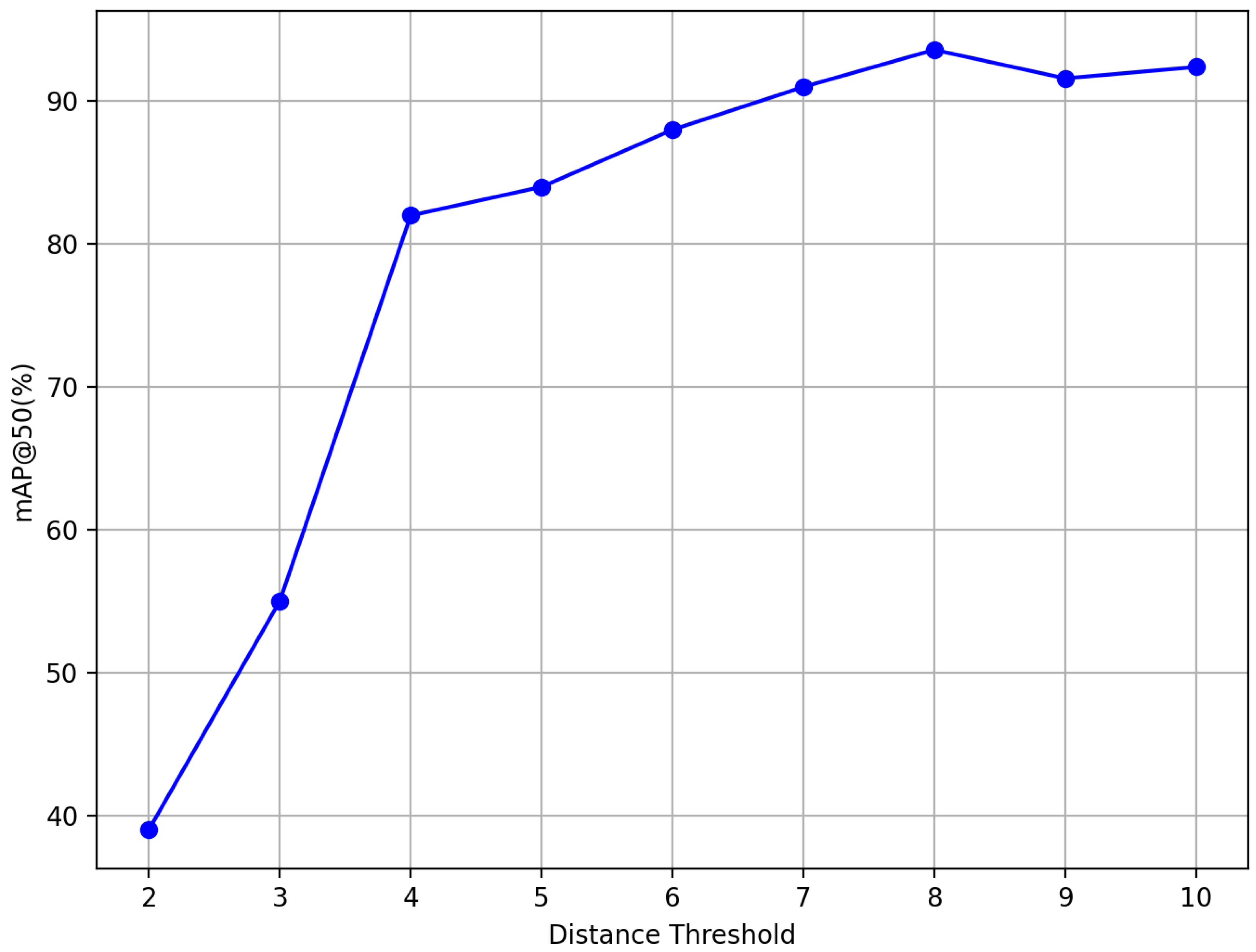
3.4. Ablation Study
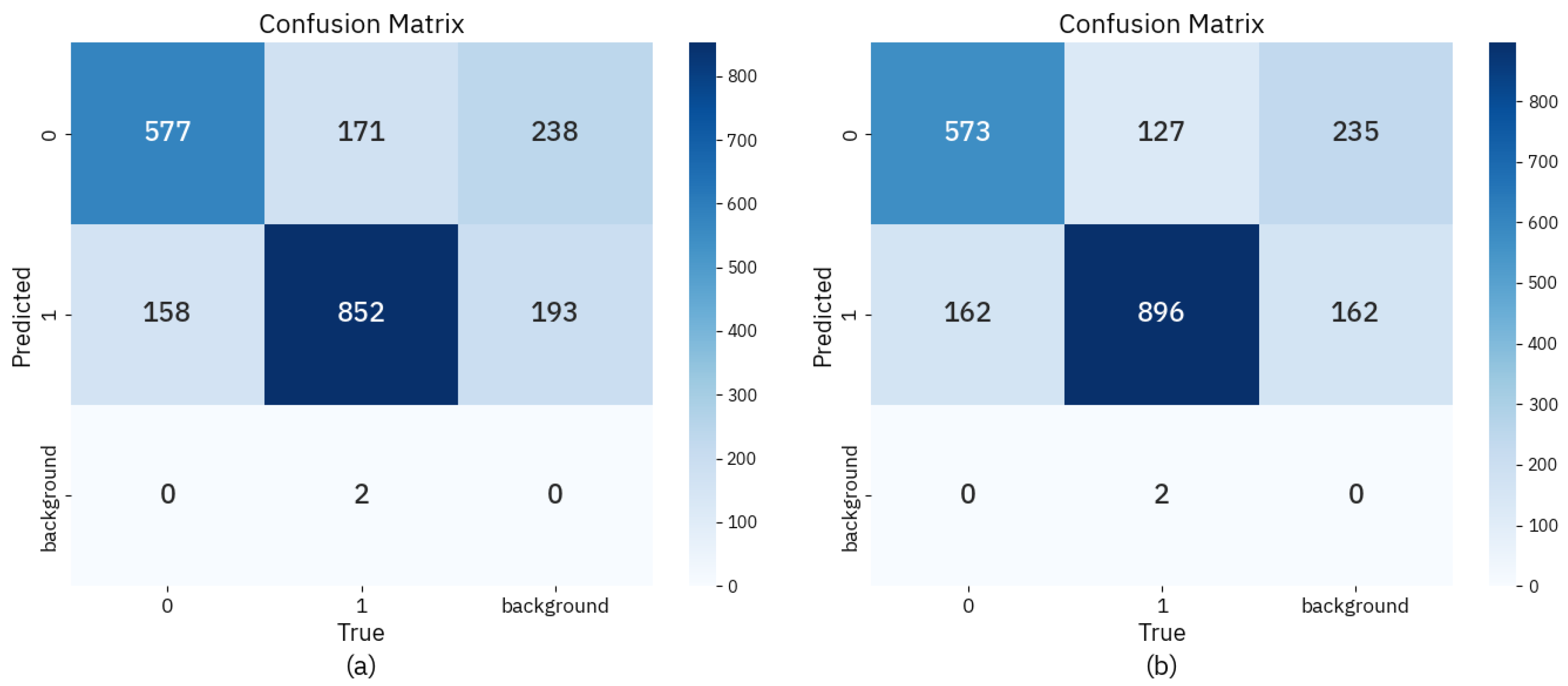
3.5. Visualization Map
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Siegel, R.; Miller, K.; Jemal, A. Cancer statistics, 2018. CA Cancer J. Clin. 2018, 68, 7–30. [Google Scholar] [CrossRef]
- Wang, N.; Liu, S.; Yang, L.; Zhang, X.; Yuan, Y.; Li, H.; Fu, J.J. Interpretation of 2018 global cancer statistical report. J. Esophageal Surg. (Electron. Vers.) 2019, 5, 87–97. [Google Scholar]
- Cree, I.A.; Tan, P.H.; Travis, W.D.; Wesseling, P.; Yagi, Y.; White, V.A.; Lokuhetty, D.; Scolyer, R.A. Counting mitoses: Si (ze) matters! Mod. Pathol. 2021, 34, 1651–1657. [Google Scholar] [CrossRef]
- Avallone, G.; Rasotto, R.; Chambers, J.K.; Miller, A.D.; Behling-Kelly, E.; Monti, P.; Berlato, D.; Valenti, P.; Roccabianca, P. Review of histological grading systems in veterinary medicine. Vet. Pathol. 2021, 58, 809–828. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Jiang, H.; Zhou, Y.; Lin, Y.; Chan, R.C.; Liu, J.; Chen, H. Deep learning for computational cytology: A survey. Med. Image Anal. 2023, 84, 102691. [Google Scholar] [CrossRef] [PubMed]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef]
- Lin, T.-Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2999–3007. [Google Scholar] [CrossRef]
- Cireşan, D.; Giusti, A.; Gambardella, L.M.; Schmidhuber, J. Mitosis detection in breast cancer histology images with deep neural networks. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2013, Proceedings of the 16th International Conference, Nagoya, Japan, 22–26 September 2013; Springer: Berlin/Heidelberg, Germany, 2013; Volume 16, pp. 411–418. [Google Scholar]
- Chen, H.; Dou, Q.; Wang, X.; Qin, J.; Heng, P.-A. Mitosis detection in breast cancer histology images via deep cascaded networks. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, AAAI’16, Phoenix, AZ, USA, 12–17 February 2016; AAAI Press: Washington, DC, USA, 2016; pp. 1160–1166. [Google Scholar]
- Alom, M.Z.; Aspiras, T.; Taha, T.; Bowen, T.; Asari, V. Mitosisnet: End-to-end mitotic cell detection by multi-task learning. IEEE Access 2020, 8, 68695–68710. [Google Scholar] [CrossRef]
- Jahanifar, M.; Shepard, A.; Zamanitajeddin, N.; Bashir, R.S.; Bilal, M.; Khurram, S.A.; Minhas, F.; Rajpoot, N. Stain-robust mitotic figure detection for the mitosis domain generalization challenge. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Strasbourg, France, 27 September–1 October 2021; Springer International Publishing: Cham, Switzerland, 2021; pp. 48–52. [Google Scholar]
- Yang, S.; Luo, F.; Zhang, J.; Wang, X. Sk-Unet model with Fourier domain for mitosis detection. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Strasbourg, France, 27 September–1 October 2021; Springer International Publishing: Cham, Switzerland, 2021; pp. 86–90. [Google Scholar]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The graph neural network model. IEEE Trans. Neural Netw. 2008, 20, 61–80. [Google Scholar] [CrossRef]
- Sun, X.; Xu, C.; Rocha, J.F.; Liu, C.; Hollander-Bodie, B.; Goldman, L.; Krishnaswamy, S.; DiStasio, M.; Perlmutter, M. Hyperedge representations with hypergraph wavelets: Applications to spatial transcriptomics. In Proceedings of the ICASSP 2025—2025 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Hyderabad, India, 6–11 April 2025; IEEE: Piscataway, NJ, USA, 2025; pp. 1–5. [Google Scholar]
- Cai, S.; Huang, W.; Yi, W.; Zhang, B.; Liao, Y.; Wang, Q.; Cai, H.; Chen, L.; Su, W. Survival Analysis of Histopathological Image Based on a Pretrained Hypergraph Model of Spatial Transcriptomics Data. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Marrakesh, Morocco, 7–11 October 2024; Springer Nature: Cham, Switzerland, 2024; pp. 455–466. [Google Scholar]
- Bretto, A. Hypergraph theory. An introduction. In Mathematical Engineering; Springer: Cham, Switzerland, 2013; Volume 1, pp. 209–216. [Google Scholar]
- Feng, Y.; You, H.; Zhang, Z.; Ji, R.; Gao, Y. Hypergraph neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 1 February 2019; Volume 33, pp. 3558–3565. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Bochkovskiy, A.; Wang, C.Y.; Liao, H.Y.M. Yolov4: Optimal speed and accuracy of object detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Jocher, G. Ultralytics YOLOv5. 2020. Available online: https://github.com/ultralytics/yolov5 (accessed on 9 July 2025).
- Li, C.; Li, L.; Geng, Y.; Jiang, H.; Cheng, M.; Zhang, B.; Ke, Z.; Xu, X.; Chu, A.X. YOLOv6 v3.0: A full-scale reloading. arXiv 2023, arXiv:2301.05586. [Google Scholar] [CrossRef]
- Wang, C.-Y.; Bochkovskiy, A.; Liao, H.-Y.M. YOLOv7: Trainable bag-of-freebies sets new state-of-the-art for real-time object detectors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 7464–7475. [Google Scholar]
- Jocher, G.; Chaurasia, A.; Qiu, J. Ultralytics YOLOv8. 2023. Available online: https://github.com/ultralytics/ultralytics (accessed on 9 July 2025).
- Wang, C.Y.; Yeh, I.H.; Mark Liao, H.Y. Yolov9: Learning what you want to learn using programmable gradient information. In European Conference on Computer Vision; Springer Nature: Cham, Switzerland, 2024; pp. 1–21. [Google Scholar]
- Wang, C.; He, W.; Nie, Y.; Guo, J.; Liu, C.; Wang, Y.; Han, K. Gold-YOLO: Efficient object detector via gather-and-distribute mechanism. In Proceedings of the Thirty-Seventh Conference on Neural Information Processing Systems, New Orleans, LA, USA, 10–16 December 2023. [Google Scholar]
- Xu, S.; Wang, X.; Lv, W.; Chang, Q.; Cui, C.; Deng, K.; Wang, G.; Dang, Q.; Wei, S.; Du, Y.; et al. PP-YOLOE: An evolved version of yolo. arXiv 2022, arXiv:2203.16250. [Google Scholar] [CrossRef]
- Nazir, A.; Wani, M.A. You only look once-object detection models: A review. In Proceedings of the 2023 10th International Conference on Computing for Sustainable Global Development (INDIACom), New Delhi, India, 15–17 March 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1088–1095. [Google Scholar]
- Li, J.; Zheng, M.; Dong, D.; Xie, X. PC-CS-YOLO: High-Precision Obstacle Detection for Visually Impaired Safety. Sensors 2025, 25, 534. [Google Scholar] [CrossRef]
- Tian, Y.; Ye, Q.; Doermann, D. Yolov12: Attention-centric real-time object detectors. arXiv 2025, arXiv:2502.12524. [Google Scholar]
- Khanam, R.; Hussain, M. Yolov11: An overview of the key architectural enhancements. arXiv 2024, arXiv:2410.17725. [Google Scholar]
- Xu, S.; Fei, J.; Zhao, G.; Liu, X.; Li, H. CCL-YOLO: Catenary Components Location Based on YOLO and Gather-Distribute Mechanism. IEEE Access 2024, 13, 9064–9072. [Google Scholar] [CrossRef]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 764–773. [Google Scholar]
- Wang, K.; Liew, J.H.; Zou, Y.; Feng, J. Panet: Few-shot image semantic segmentation with prototype alignment. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9197–9206. [Google Scholar]
- Aubreville, M.; Stathonikos, N.; Bertram, C.A.; Klopfleisch, R.; ter Hoeve, N.; Ciompi, F.; Wilm, F.; Marzahl, C.; Donovan, T.A.; Maier, A.; et al. Mitosis domain generalization in histopathology images-the MIDOG challenge. Med. Image Anal. 2023, 84, 102699. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Chen, K.; Wang, J.; Pang, J.; Cao, Y.; Xiong, Y.; Li, X.; Sun, S.; Feng, W.; Liu, Z.; Xu, J.; et al. MMDetection: Open MMLab Detection Toolbox and Benchmark. arXiv 2019, arXiv:1906.07155. [Google Scholar] [CrossRef]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. In Lecture Notes in Computer Science, Proceedings of the Computer Vision—ECCV 2014, Zurich, Switzerland, 6–12 September 2014; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer: Cham, Switzerland, 2014; Volume 8693. [Google Scholar] [CrossRef]
- Raschka, S. An overview of general performance metrics of binary classifier systems. arXiv 2014, arXiv:1410.5330. [Google Scholar]
- Davis, J.; Goadrich, M. The relationship between Precision-Recall and ROC curves. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 233–240. [Google Scholar]
- Sun, P.; Zhang, R.; Jiang, Y.; Kong, T.; Xu, C.; Zhan, W.; Tomizuka, M.; Li, L.; Yuan, Z.; Wang, C.; et al. Sparse r-cnn: End-to-end object detection with learnable proposals. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 14454–14463. [Google Scholar]
- Cai, Z.; Vasconcelos, N. Cascade r-cnn: Delving into high quality object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6154–6162. [Google Scholar]
- Ge, Z. Yolox: Exceeding yolo series in 2021. arXiv 2021, arXiv:2107.08430. [Google Scholar]
- Zhao, Y.; Lv, W.; Xu, S.; Wei, J.; Wang, G.; Dang, Q.; Liu, Y.; Chen, J. Detrs beat yolos on real-time object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 16965–16974. [Google Scholar]
- Litjens, G.; Bandi, P.; Ehteshami Bejnordi, B.; Geessink, O.; Balkenhol, M.; Bult, P.; Halilovic, A.; Hermsen, M.; Van de Loo, R.; Vogels, R.; et al. 1399 H&E-stained sentinel lymph node sections of breast cancer patients: The CAMELYON dataset. GigaScience 2018, 7, giy065. [Google Scholar]
- Yan, K.; Wang, X.; Lu, L.; Summers, R.M. Deeplesion: Automated deep mining, categorization and detection of significant radiology image findings using large-scale clinical lesion annotations. arXiv 2017, arXiv:1710.01766. [Google Scholar]
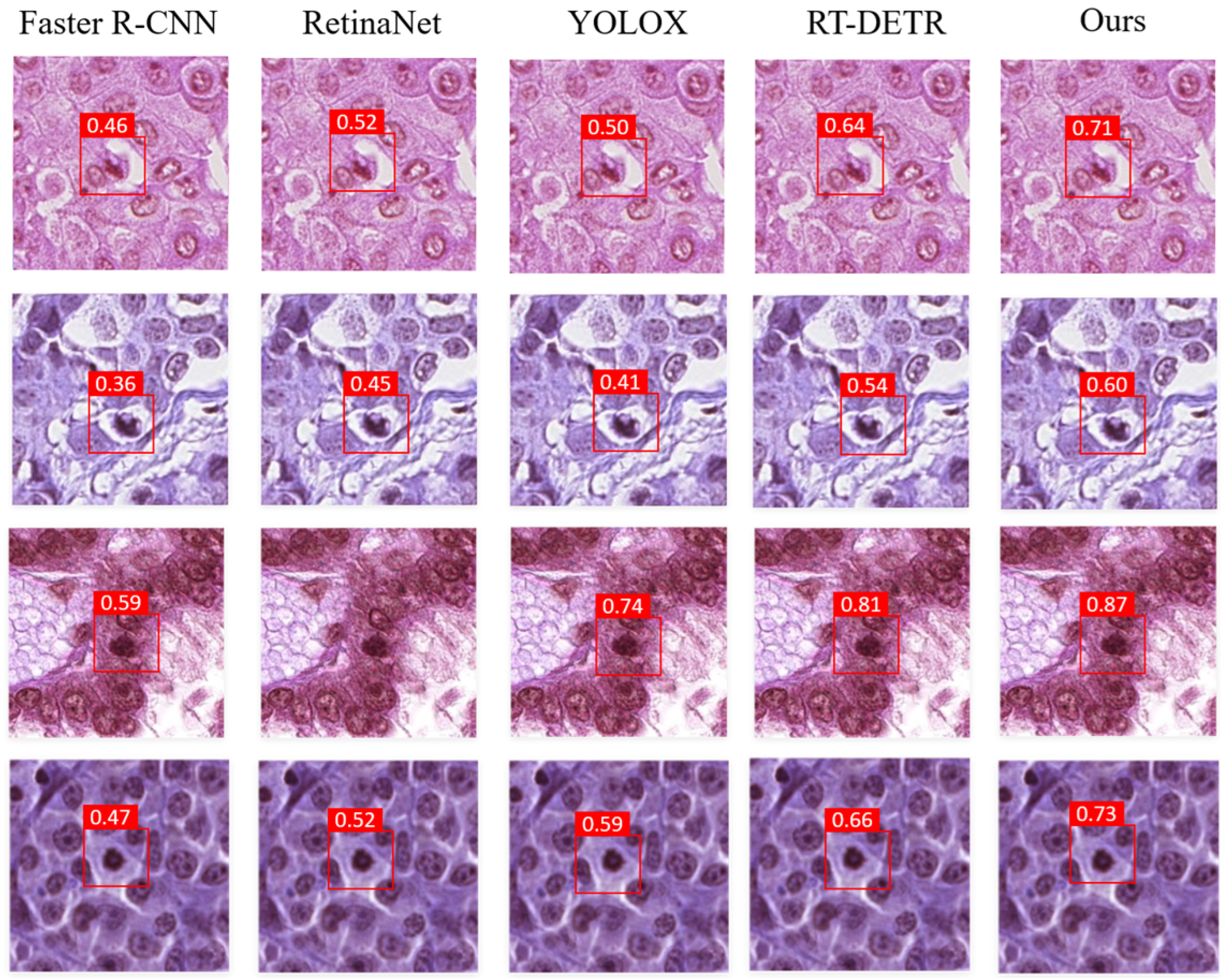
| Model | Precision (%) | Recall (%) | mAP50 (%) | ACC (%) | F1-Score | Paramets (M) | GLOPs (G) |
|---|---|---|---|---|---|---|---|
| Faster R-CNN [7] | 74.5 | 78.2 | 82.0 | 74.6 | 0.763 | 41.3 | 190.1 |
| RetinaNet [8] | 68.2 | 70.5 | 72.3 | 68.2 | 0.693 | 37.9 | 193.8 |
| Sparse R-CNN [42] | 71.4 | 77.1 | 80.9 | 71.4 | 0.741 | 107.3 | 150.7 |
| Cascade R-CNN [43] | 79.3 | 85.1 | 88.4 | 79.3 | 0.821 | 77.3 | 278.4 |
| YOLOX [44] | 73.7 | 78.2 | 86.1 | 73.7 | 0.759 | 47.1 | 115.6 |
| YOLO11 [32] | 77.4 | 81.6 | 87.6 | 77.4 | 0.794 | 25.3 | 86.9 |
| RT-DETR [45] | 80.3 | 84.5 | 87.2 | 80.3 | 0.823 | 42 | 136 |
| Ours | 83.1 | 89.7 | 93.6 | 83.6 | 0.863 | 56.3 | 211 |
| Model | BBMM | HGNN | Precision (%) | Recall (%) | mAP50 (%) |
|---|---|---|---|---|---|
| Baseline [32] | 77.4 | 81.6 | 87.5 | ||
| Baseline + BBMM | ✓ | 80.4 | 86.9 | 88.2 | |
| Baseline + HGNN | ✓ | 79.1 | 87.3 | 90.1 | |
| Ours | ✓ | ✓ | 83.1 | 89.7 | 93.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Dong, D.; Zhan, Y.; Zhu, G.; Zhang, H.; Xie, X.; Yang, L. Cross-Scale Hypergraph Neural Networks with Inter–Intra Constraints for Mitosis Detection. Sensors 2025, 25, 4359. https://doi.org/10.3390/s25144359
Li J, Dong D, Zhan Y, Zhu G, Zhang H, Xie X, Yang L. Cross-Scale Hypergraph Neural Networks with Inter–Intra Constraints for Mitosis Detection. Sensors. 2025; 25(14):4359. https://doi.org/10.3390/s25144359
Chicago/Turabian StyleLi, Jincheng, Danyang Dong, Yihui Zhan, Guanren Zhu, Hengshuo Zhang, Xing Xie, and Lingling Yang. 2025. "Cross-Scale Hypergraph Neural Networks with Inter–Intra Constraints for Mitosis Detection" Sensors 25, no. 14: 4359. https://doi.org/10.3390/s25144359
APA StyleLi, J., Dong, D., Zhan, Y., Zhu, G., Zhang, H., Xie, X., & Yang, L. (2025). Cross-Scale Hypergraph Neural Networks with Inter–Intra Constraints for Mitosis Detection. Sensors, 25(14), 4359. https://doi.org/10.3390/s25144359





