CPG-Based Control of an Octopod Biomimetic Machine Lobster for Mining Applications: Design and Implementation in Challenging Underground Environments
Abstract
1. Introduction
2. Machine Lobster Modeling
2.1. Physical Modeling of Machine Lobster
2.2. Mathematical Modeling of a Machine Lobster
2.3. High Order Fully Driven Dynamic Modeling
2.4. Machine Lobster Gait Design
2.5. Simulation Validation of the Mathematical Parameters of the Machine Lobster
3. Machine Lobster Modeling
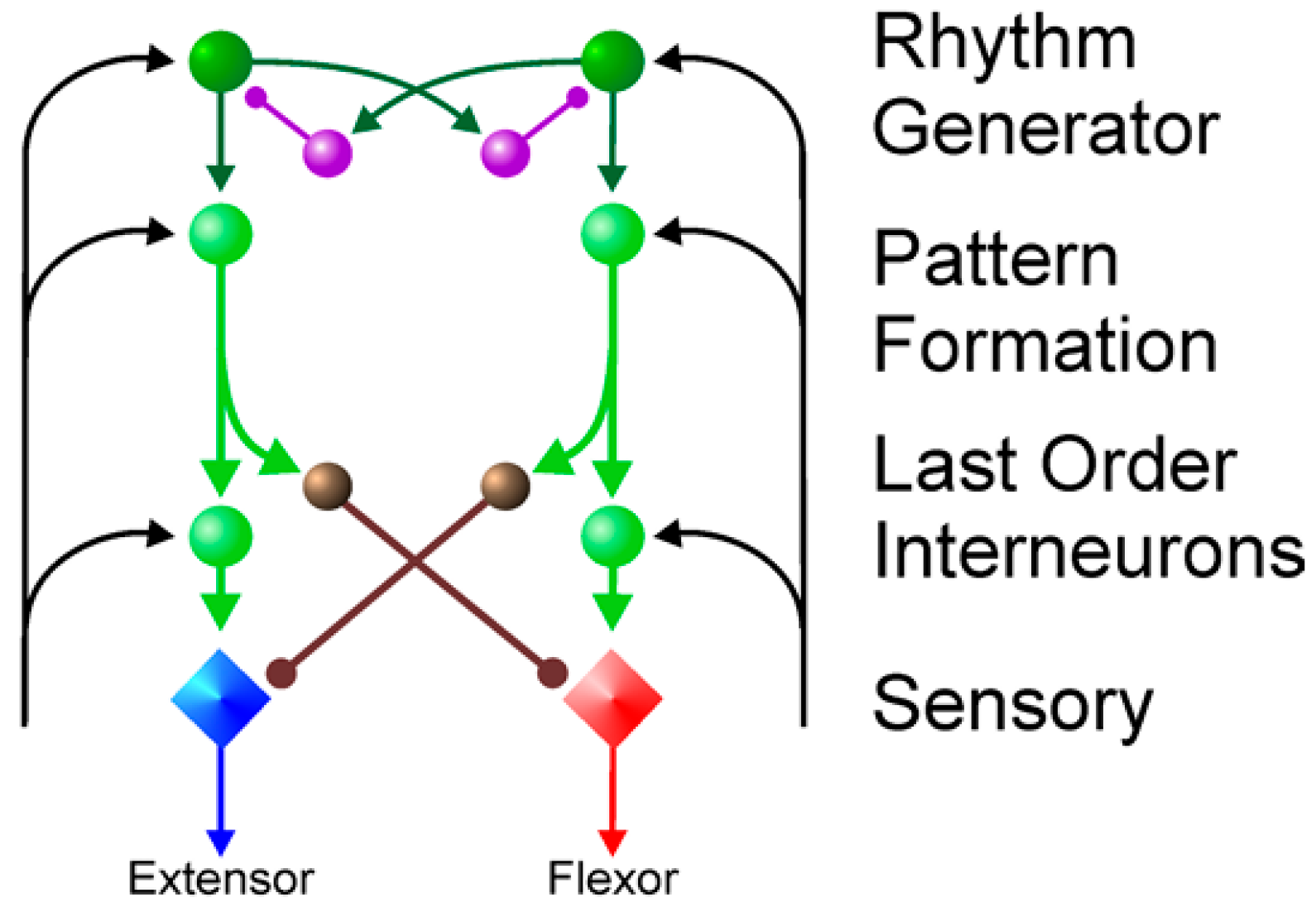
3.1. Selection of Rhythm Generators
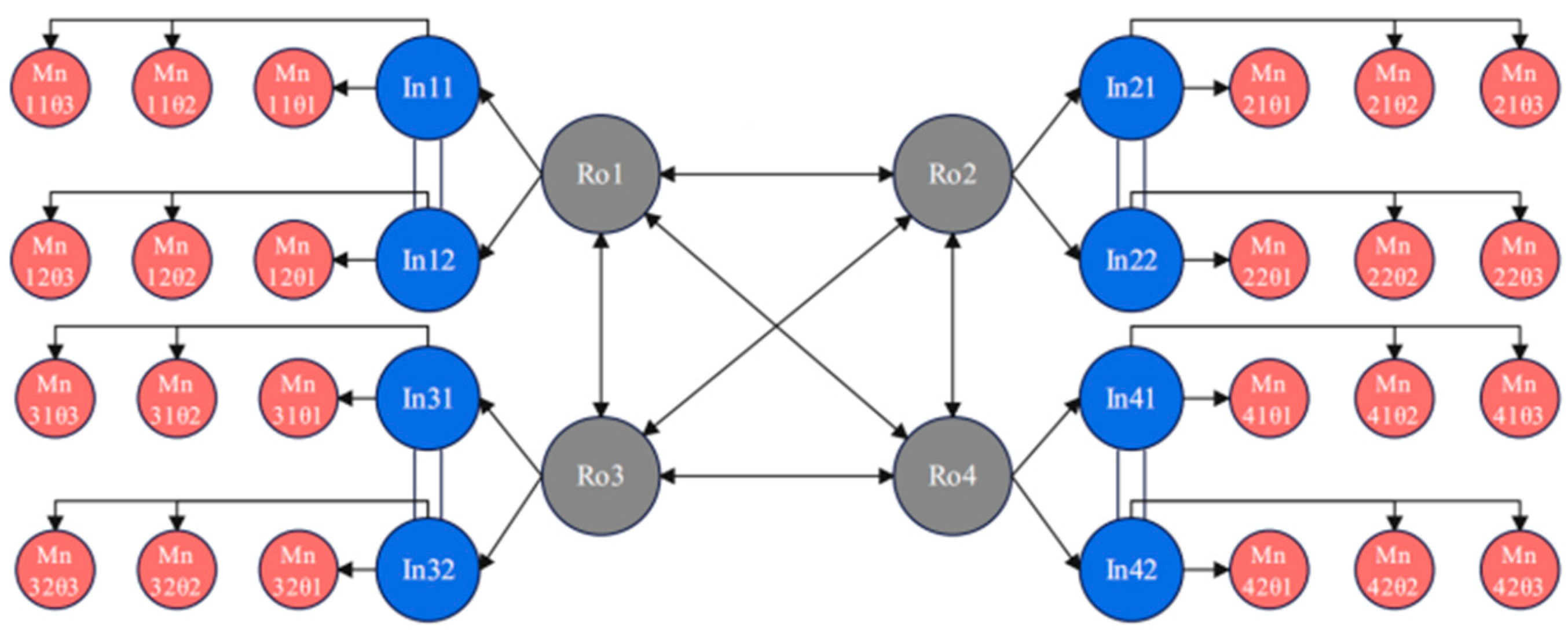
3.2. CPG Control Methods in Machine Lobster
4. Simulation and Analysis of the Machine Lobster CPG Network
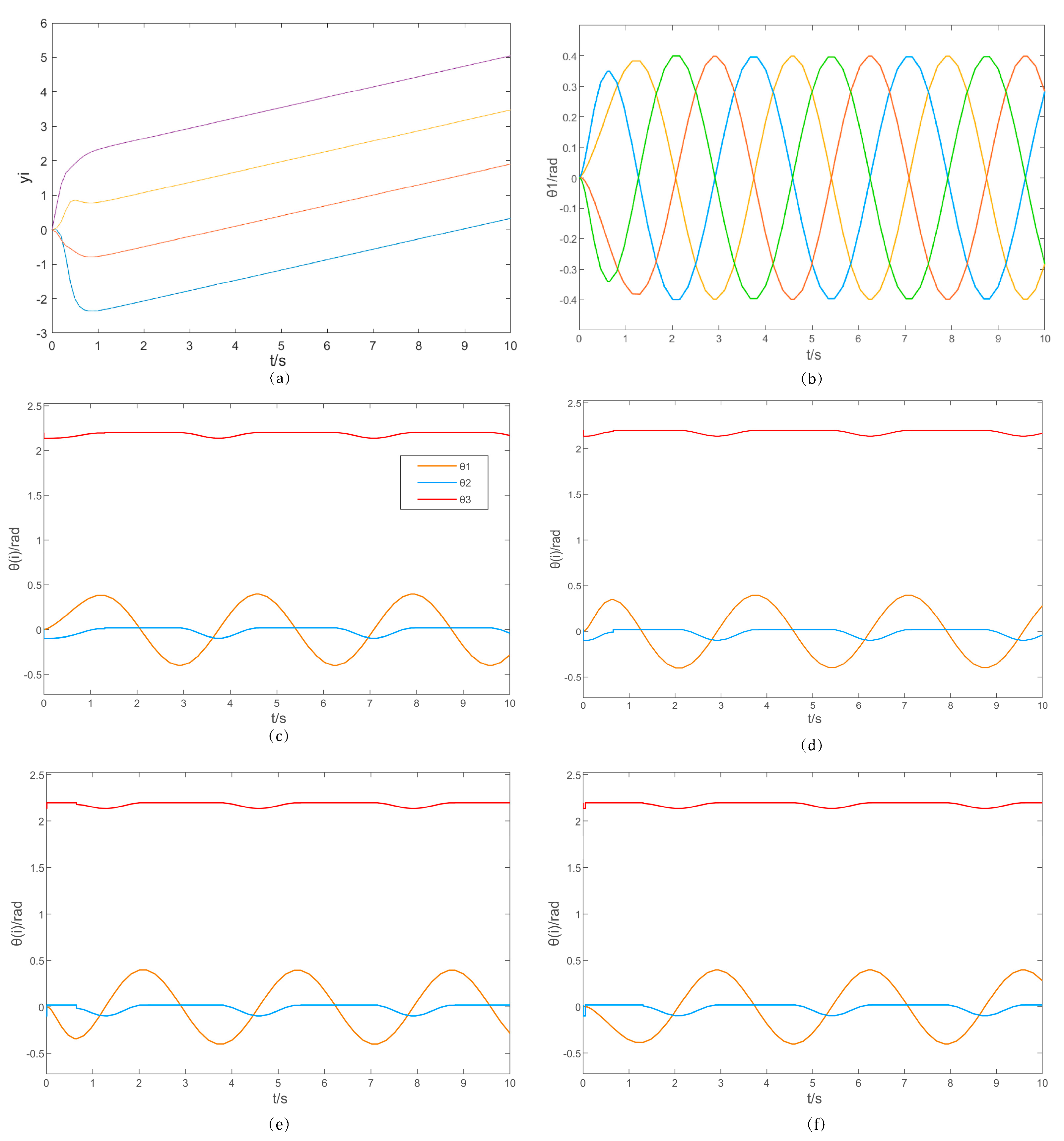
4.1. Machine Lobster Octopod Front-Back Gait Simulation
4.2. Adams Simulation of Machine Lobster Motion
5. Conclusions
- (1)
- The machine lobster must enhance the forward and backward gaits while developing supplementary gaits to fully utilize the octopodal structure and three degrees of freedom of the machine lobster legs. We plan to develop a turning gait using a differential steering mechanism. This involves adjusting the phase difference between the left and right central pattern generator (CPG) networks to generate rotational torque. Additionally, we will incorporate shape memory alloy (SMA)-driven tail deflection and clamp limb assistance to reduce the turning radius. Simultaneously, we aim to enhance the multi-level adaptability of both forward and backward gaits by dynamically adjusting step frequency and joint amplitude based on LiDAR terrain scanning and inertial measurement unit (IMU) attitude feedback. This approach will enable three operational modes: low-speed with high stability, medium-speed cruising, and high-speed breakthroughs.
- (2)
- Refinement of the oscillator mathematical model and adjustment of the central pattern generator (CPG) neural network architecture are necessary to accommodate a broader spectrum of gaits.
- (3)
- The refinement of the oscillator mathematical model and the adjustment of the central pattern generator (CPG) neural network architecture are essential for accommodating a wider range of gaits. Integrating a feedback mechanism into the robotic lobster to adapt its locomotion based on environmental inputs is crucial. We plan to enhance the adaptability of bio-inspired robotic lobsters in complex underground environments, wherein a hierarchical feedback control architecture is proposed. First, real-time perception of terrain slope, ground reaction forces, and obstacle information will be achieved using body inertial measurement units (IMUs), foot force sensors, and laser radars. This will enable dynamic adjustments to the oscillation frequency, phase difference, and joint movement amplitude of the high-level CPG network (e.g., reducing step frequency or adjusting stance duration to prevent overturning based on slope).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sayed, M.E.; Roberts, J.O.; Donaldson, K.; Mahon, S.T.; Iqbal, F.; Li, B.; Stokes, A.A. Modular robots for enabling operations in unstructured extreme environments. Adv. Intell. Syst. 2022, 4, 2000227. [Google Scholar] [CrossRef]
- Gao, Z.; Shi, Q.; Fukuda, T.; Li, C.; Huang, Q. An overview of biomimetic robots with animal behaviors. Neurocomputing 2019, 332, 339–350. [Google Scholar] [CrossRef]
- Liu, J.; Tan, M.; Zhao, X. Legged robots—An overview. Trans. Inst. Meas. Control. 2007, 29, 185–202. [Google Scholar] [CrossRef]
- Raibert, M.H. Legged robots. Commun. ACM 1986, 29, 499–514. [Google Scholar] [CrossRef]
- Raibert, M.H.; Blankespoor, K.; Nelson, G.; Playter, R.; The BigDog Team. BigDog, the rough-terrain quadruped robot. In Proceedings of the 17th IFAC World Congress, Seoul, Republic of Korea, 6–11 July 2008; pp. 10822–10825. [Google Scholar]
- Raibert, M.H. ALPHADOG, the rough-terrain robot. Robotica 2012, 30, 481–492. [Google Scholar]
- Bledt, G.; Powell, M.J.; Katz, B.; Di Carlo, J.; Wensing, P.M.; Kim, S. MIT Cheetah 3: Design and control of a robust, dynamic quadruped robot. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 2245–2252. [Google Scholar]
- Greiner, H.; Shectman, A. Autonomous legged underwater vehicles for near land warfare. Auton. Robot. 1996, 3, 41–48. [Google Scholar]
- Sunspiral, V.; Wheeler, D.W.; Chavez-Clemente, D.; Mittman, D. Development and field testing of the footfall planning system for the ATHLETE robots. J. Field Robot. 2012, 29, 483–505. [Google Scholar] [CrossRef]
- Brembs, B. Operant conditioning in invertebrates. Curr. Opin. Neurobiol. 2003, 13, 710–717. [Google Scholar] [CrossRef]
- Duysens, J.; Forner-Cordero, A. A controller perspective on biological gait control: Reflexes and central pattern generators. Annu. Rev. Control. 2019, 48, 392–400. [Google Scholar] [CrossRef]
- Kimura, H.; Fukuoka, Y.; Cohen, A.H. Biologically inspired adaptive walking of a quadruped robot. Philos. Trans. R. Soc. A 2007, 365, 153–170. [Google Scholar]
- Bellegarda, G.; Ijspeert, A. CPG-RL: Learning central pattern generators for quadruped locomotion. IEEE Robot. Autom. Lett. 2022, 7, 12547–12554. [Google Scholar] [CrossRef]
- Ijspeert, A.J. Decoding the neural mechanisms underlying locomotion using mathematical models and bio-inspired robots. In Robotics Research; Springer: Cham, Switzerland, 2018; pp. 3–12. [Google Scholar]
- Ijspeert, A.J.; Crespi, A.; Ryczko, D.; Cabelguen, J.M. From swimming to walking with a salamander robot driven by a spinal cord model. Science 2007, 315, 1416–1420. [Google Scholar] [CrossRef] [PubMed]
- Grzelczyk, D.; Szymanowska, O.; Awrejcewicz, J. Kinematic and dynamic simulation of an octopod robot controlled by different central pattern generators. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2019, 233, 400–417. [Google Scholar] [CrossRef]
- Grzelczyk, D.; Awrejcewicz, J. Modeling and control of an eight-legged walking robot driven by different gait generators. Int. J. Struct. Stab. Dynamics 2018, 19, 1941009. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, L.; Sun, J.; Fan, S.; Li, G.; Sui, M.; Dai, X.; Li, Y. A Model-Based Control Framework for a Novel Combined Octopod Robot. In Proceedings of the 2024 WRC Symposium on Advanced Robotics and Automation (WRC SARA), Beijing, China, 23 August 2024; IEEE: New York, NY, USA, 2024. [Google Scholar]
- Sun, H.; Wei, C.; Yao, Y.A.; Wu, J. Analysis and experiment of a bioinspired multimode octopod robot. Chin. J. Mech. Eng. 2023, 36, 142. [Google Scholar] [CrossRef]
- Wu, J.; Yang, H.; Li, R.; Ruan, Q.; Yan, S.; Yao, Y.A. Design and analysis of a novel octopod platform with a reconfigurable trunk. Mech. Mach. Theory 2021, 156, 104134. [Google Scholar] [CrossRef]
- Matsuoka, K. Sustained oscillations generated by mutually inhibiting neurons with adaptation. Biol. Cybern. 1985, 52, 367–376. [Google Scholar] [CrossRef] [PubMed]
- Kuramoto, Y.; Yamada, T. Pattern formation in oscillatory chemical reactions. Prog. Theor. Phys. 1976, 56, 724–740. [Google Scholar] [CrossRef][Green Version]
- Kuramoto, Y. Collective synchronization of pulse-coupled oscillators and excitable units. Phys. D Nonlinear Phenom. 1991, 50, 15–30. [Google Scholar] [CrossRef]
- Hopf, E. Abzweigung einer periodischen Lösung von einer stationären Lösung eines differential-systems. Ber. Math.-Phys. Kl. Sächs. Akad. Wiss. Leipz. 1942, 94, 1–22. [Google Scholar]
- Ansariara, M.; Emadi, S.; Adami, V.; Botha, A.E.; Kolahchi, M.R. Signs of memory in a plastic frustrated kuramoto model of neurons. Nonlinear Dyn. 2020, 100, 3685–3694. [Google Scholar] [CrossRef]
- Josephine, D.R.; Jung-Woo, S.; Dhanalakshmi, K.; Choi, S.B. Control aspects of shape memory alloys in robotics applications: A review over the last decade. Sensors 2022, 22, 4860. [Google Scholar] [CrossRef]
- Ayers, J.; Witting, J. Biomimetic approaches to the control of underwater walking machines. Philos. Trans. R. Soc. A 2007, 365, 273–295. [Google Scholar] [CrossRef] [PubMed]
- Biswal, P.; Mohanty, P.K. Development of quadruped walking robots: A review. Ain Shams Eng. J. 2021, 12, 2017–2031. [Google Scholar] [CrossRef]
- Yin, Y.; Gao, F.; Sun, Q.; Tian, Y.; Chen, X. Smart Gait: A gait optimization framework for hexapod robots. Chin. J. Mech. Eng. 2024, 37, 15. [Google Scholar] [CrossRef]
- McCrea, D.A.; Rybak, I.A. Organization of mammalian locomotor rhythm and pattern generation. Brain Res. Rev. 2008, 57, 134–146. [Google Scholar] [CrossRef]
- Wang, W.; Ghosh, B. Kuramoto models, coupled oscillations and laser networks. In Proceedings of the SICE Annual Conference 2007, Takamatsu, Japan, 17–20 September 2007; pp. 130–135. [Google Scholar]
- Wu, X.; Ma, S. Adaptive creeping locomotion of a CPG-controlled snake-like robot to environment change. Auton. Robot. 2010, 28, 283–294. [Google Scholar] [CrossRef]
- Wang, C.; Xie, G.; Yin, X.; Li, L.; Wang, L. CPG-based locomotion control of a quadruped amphibious robot. In Proceedings of the 2012 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Kaohsiung, Taiwan, 11–14 July 2012; pp. 1–6. [Google Scholar]
- Ijspeert, A.J.; Nakanishi, J.; Hoffmann, H.; Pastor, P.; Schaal, S. Dynamical movement primitives: Learning attractor models for motor behaviors. Neural Comput. 2013, 25, 328–373. [Google Scholar] [CrossRef]
- Ijspeert, A.J.; Nakanishi, J.; Schaal, S. Learning control policies for movement imitation and movement recognition. Adv. Neural Inf. Process. Syst. 2001, 14, 1547–1554. [Google Scholar]

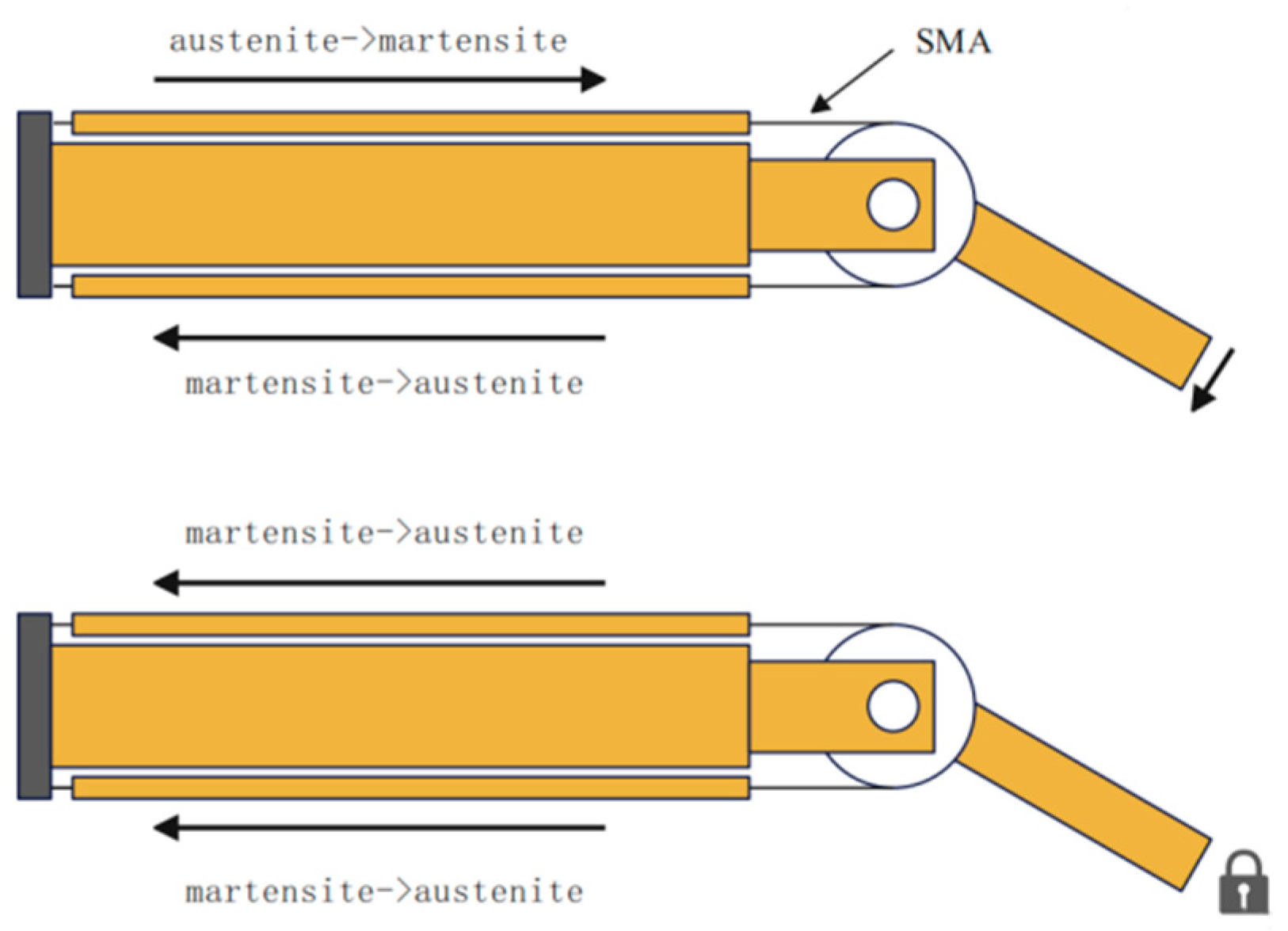
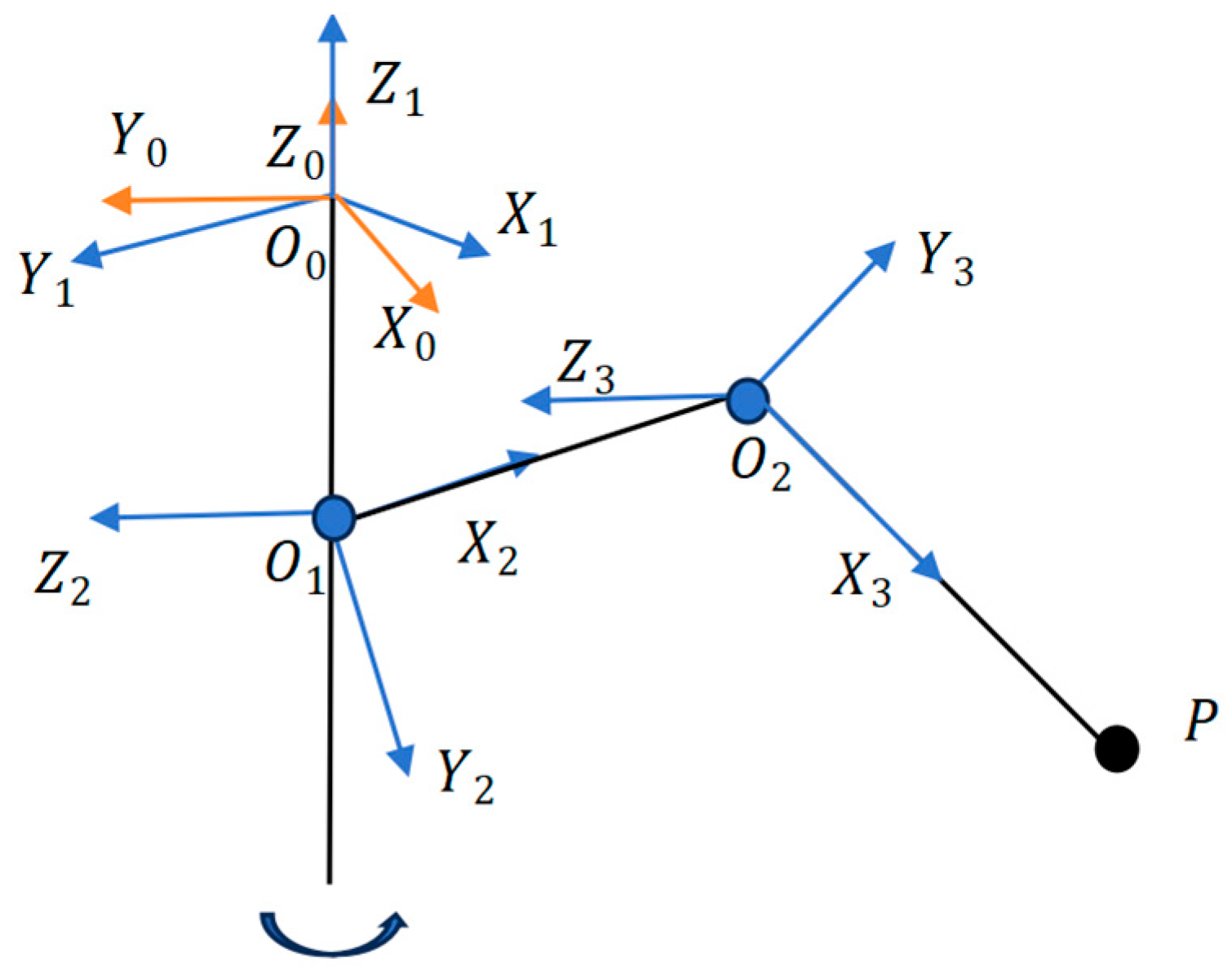
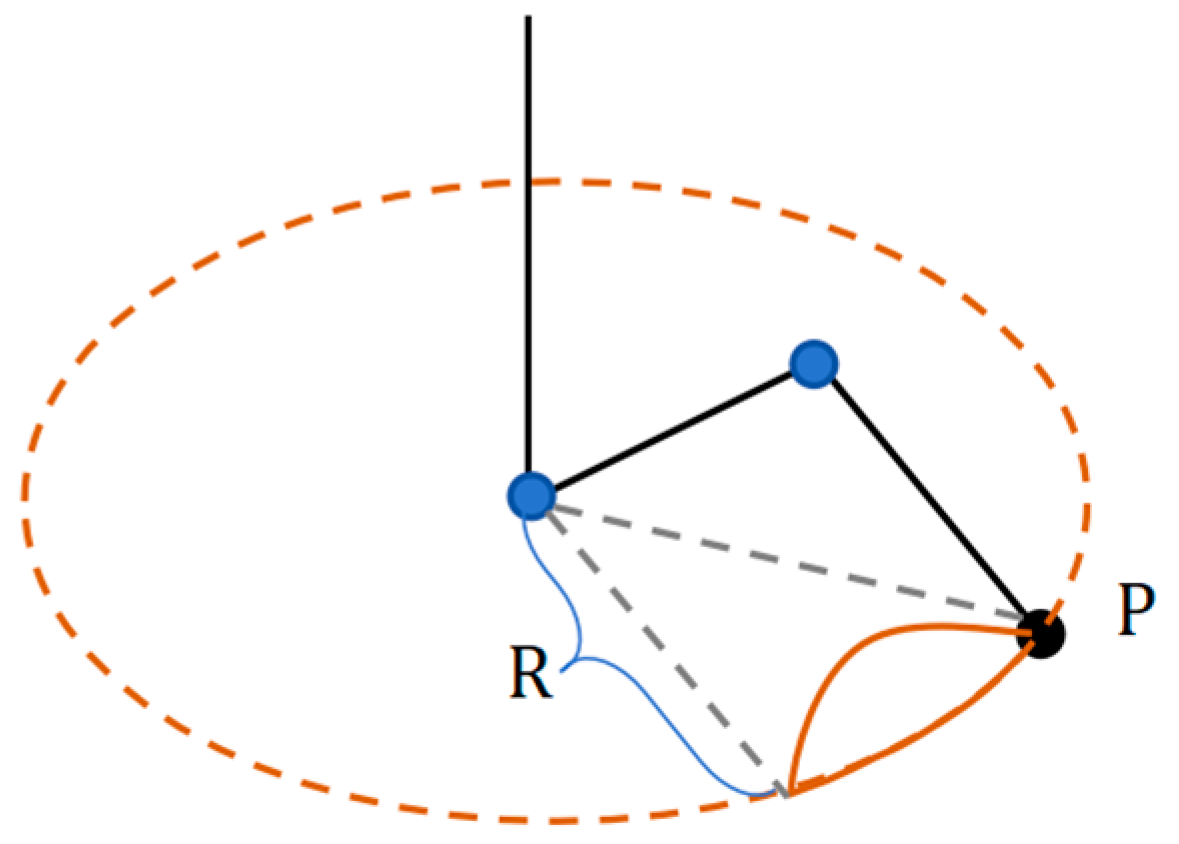
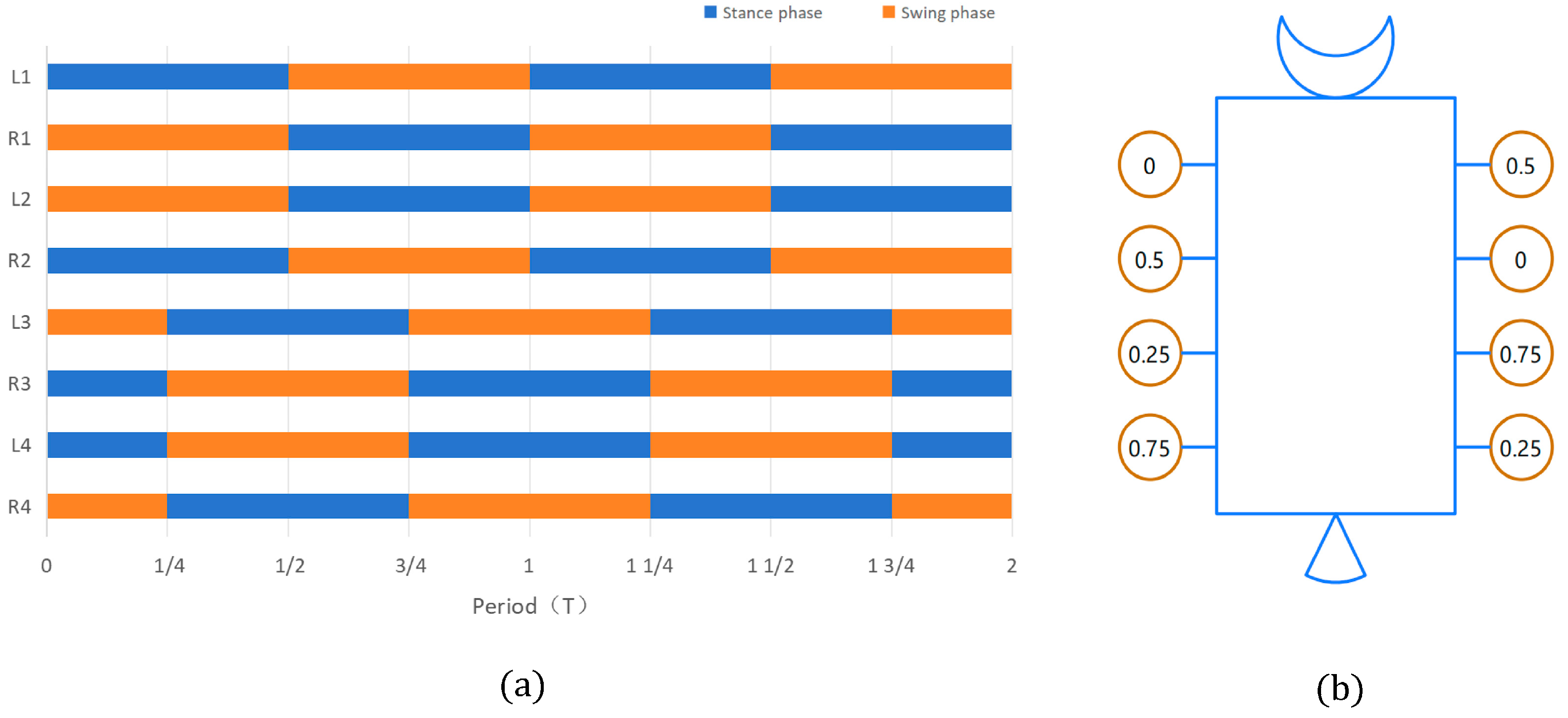




| Rod i | Rod Length | Rotation Angle | Joint Distance | Joint Variable |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | |
| 2 | 0 | |||
| 3 | 0 | 0 |
| Physical Parameter | ||||||
|---|---|---|---|---|---|---|
| Sizes/mm | 300 | 150 | 150 | 75 | 185 | 191.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Zhang, H.; Bao, M.; Yin, B.; Zhang, Y.; Jiang, Z. CPG-Based Control of an Octopod Biomimetic Machine Lobster for Mining Applications: Design and Implementation in Challenging Underground Environments. Sensors 2025, 25, 4331. https://doi.org/10.3390/s25144331
Zhao J, Zhang H, Bao M, Yin B, Zhang Y, Jiang Z. CPG-Based Control of an Octopod Biomimetic Machine Lobster for Mining Applications: Design and Implementation in Challenging Underground Environments. Sensors. 2025; 25(14):4331. https://doi.org/10.3390/s25144331
Chicago/Turabian StyleZhao, Jianwei, Haokun Zhang, Mingsong Bao, Boxiang Yin, Yiteng Zhang, and Zhen Jiang. 2025. "CPG-Based Control of an Octopod Biomimetic Machine Lobster for Mining Applications: Design and Implementation in Challenging Underground Environments" Sensors 25, no. 14: 4331. https://doi.org/10.3390/s25144331
APA StyleZhao, J., Zhang, H., Bao, M., Yin, B., Zhang, Y., & Jiang, Z. (2025). CPG-Based Control of an Octopod Biomimetic Machine Lobster for Mining Applications: Design and Implementation in Challenging Underground Environments. Sensors, 25(14), 4331. https://doi.org/10.3390/s25144331







