Proton Range Measurement Precision in Ionoacoustic Experiments with Wavelet-Based Denoising Algorithm †
Abstract
1. Introduction
2. Materials and Methods
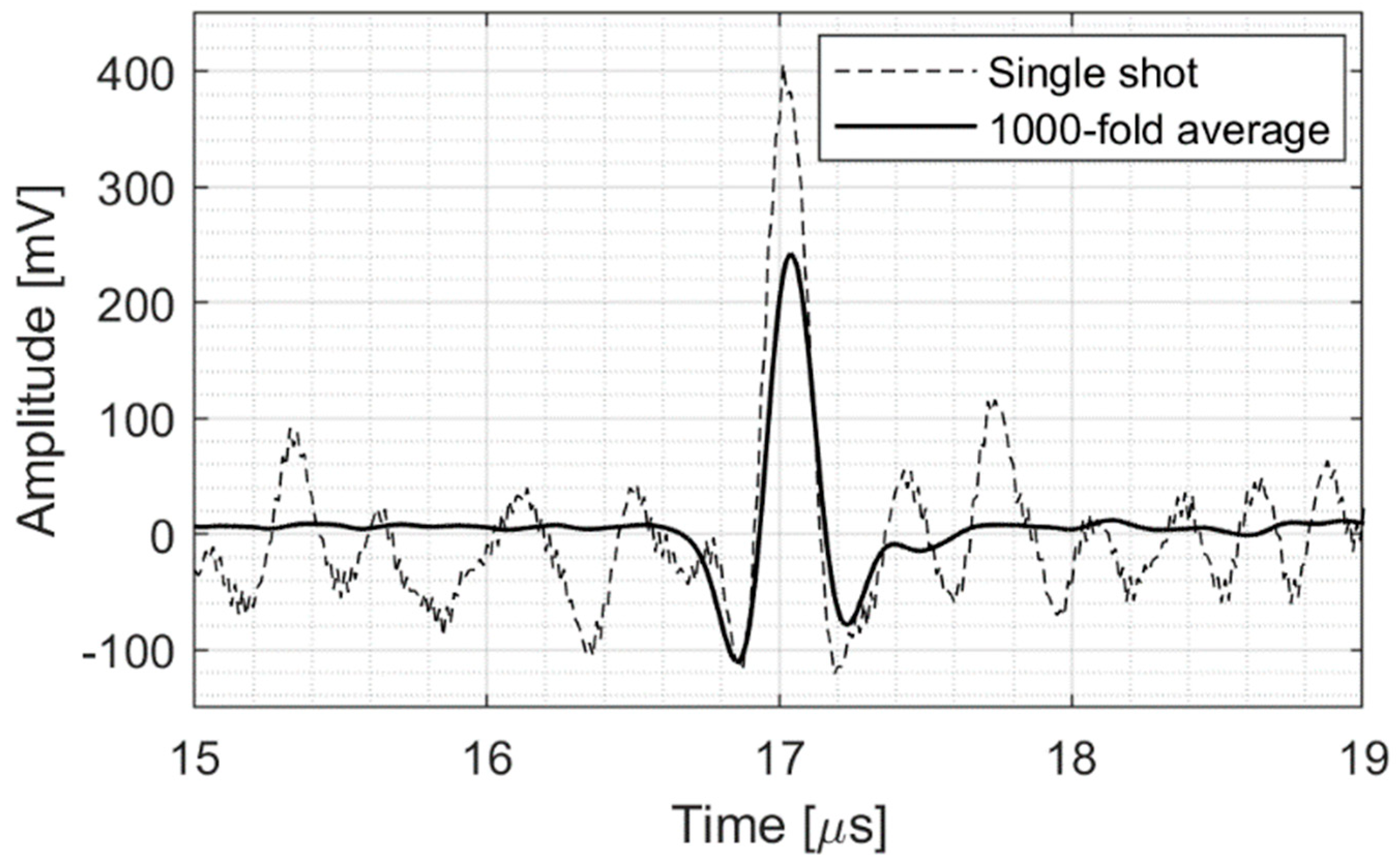
2.1. Ionoacoustic Experimental Setup
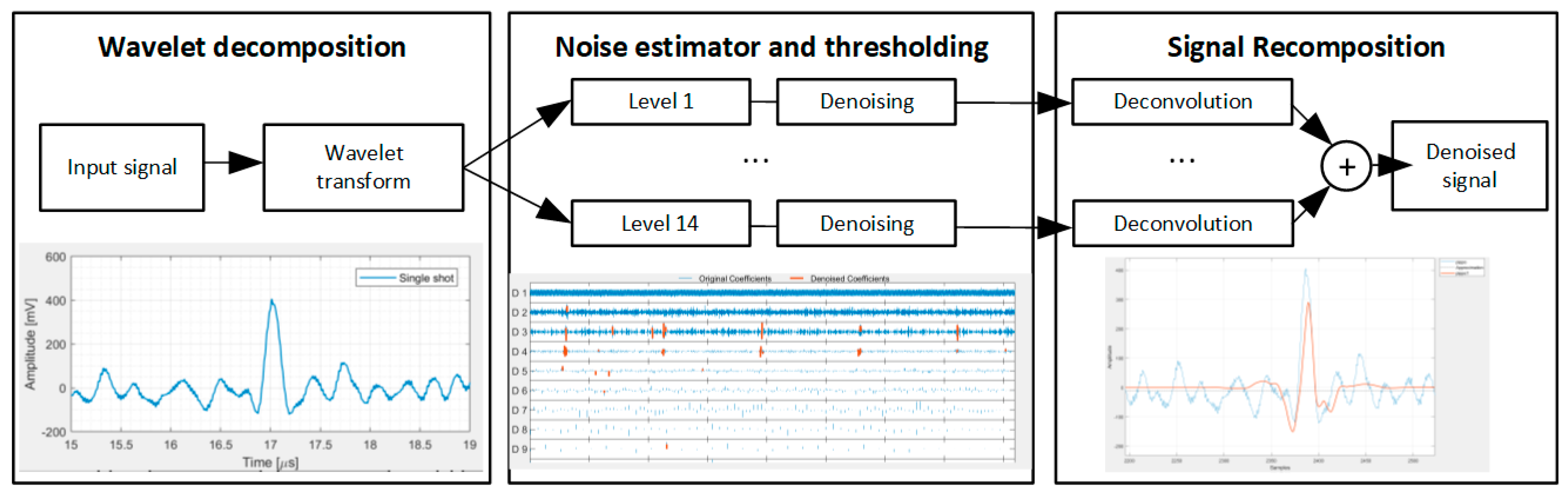
2.2. Wavelet Denoising
3. Experimental Results—20 MeV Pre-Clinical Scenario
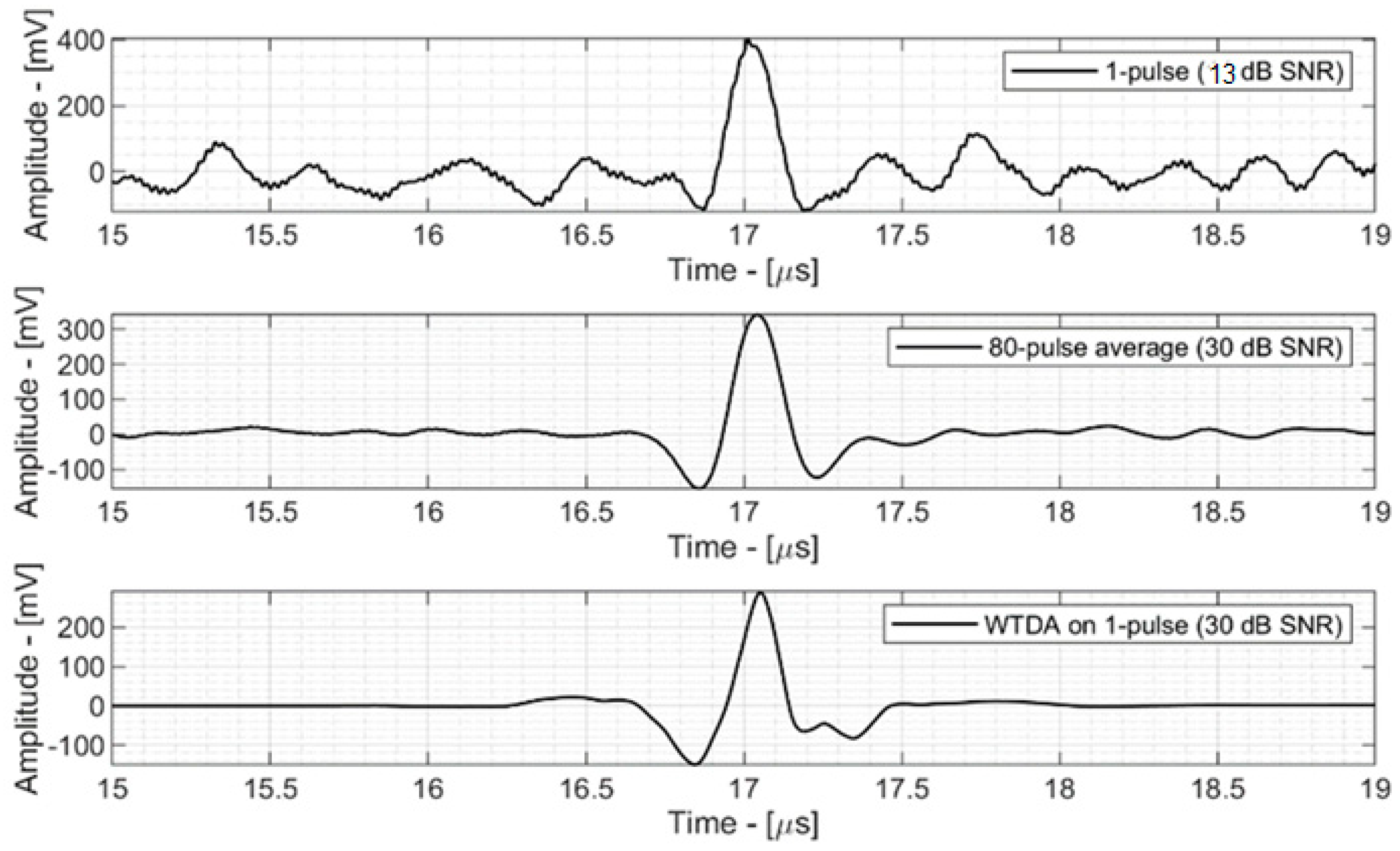
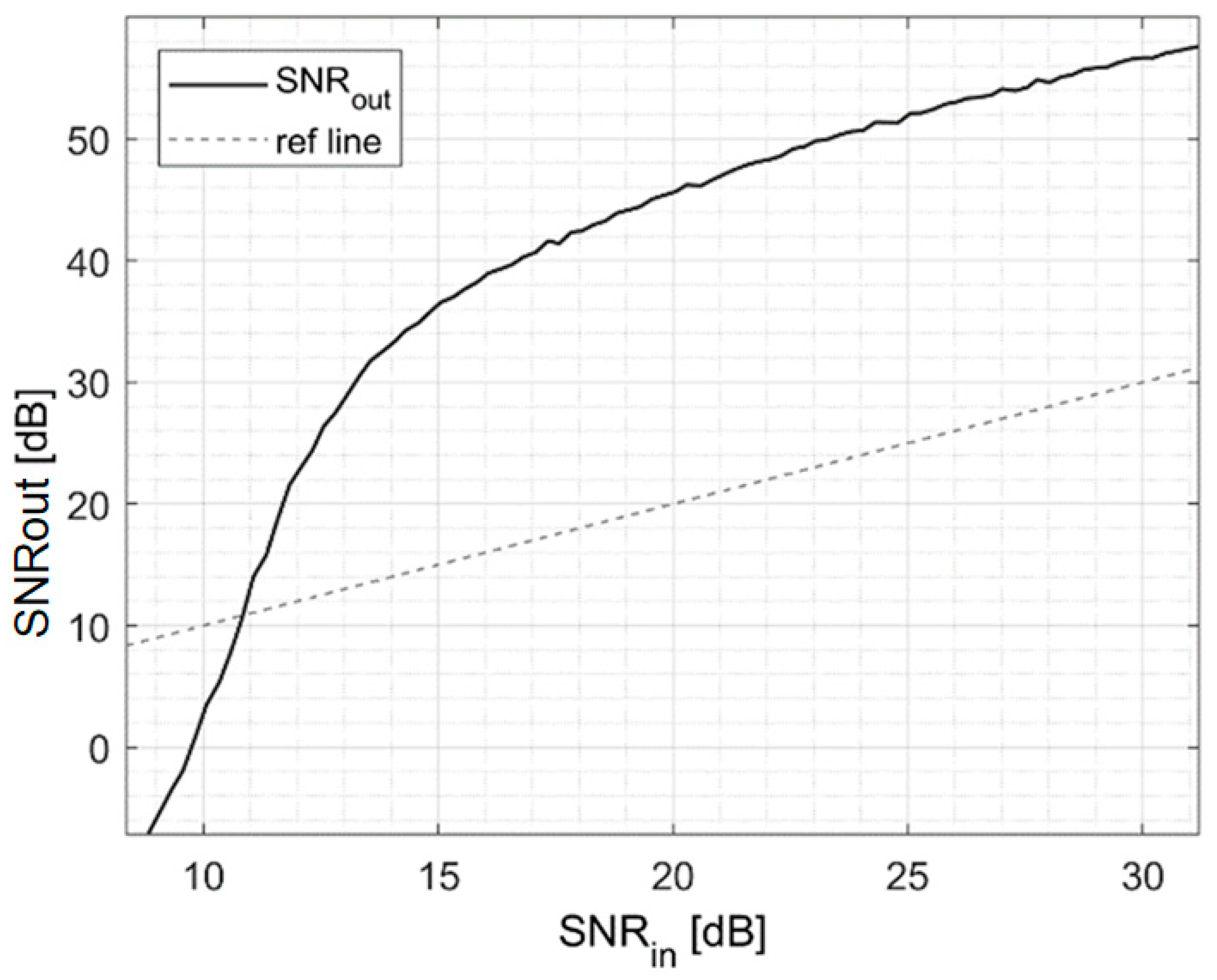
3.1. Signal-to-Noise Ratio Enhancement
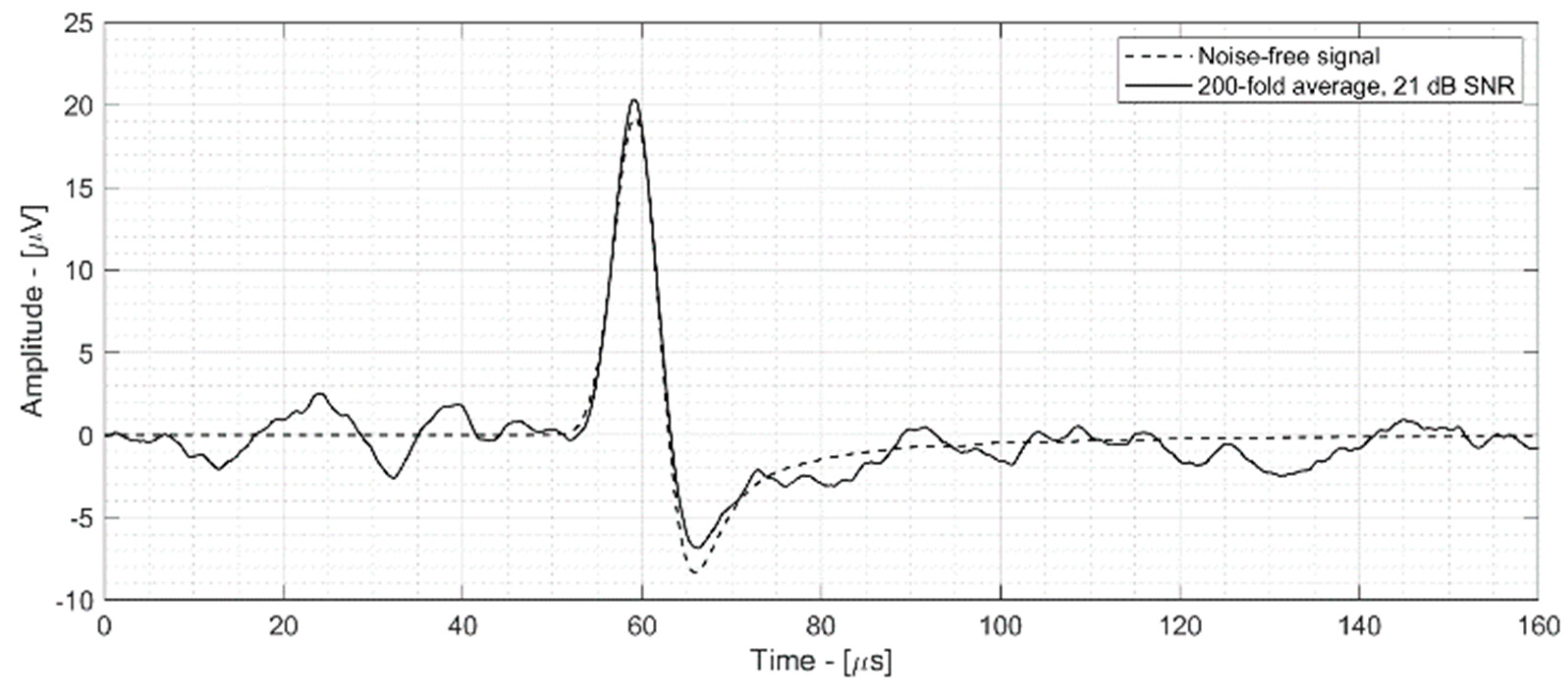
- Figure 5—top shows the 13 dB SNR signal acquired by the ProSD AFE that was used as an input signal for both the WTDA algorithm and an averaging algorithm for reference. This signal was generated by a 0.8 Gy dose deposition.
- Figure 5—middle shows an 80-fold averaged signal (averaging 80 different time-domain signals with 11 dB SNR, acquired during different beam pulses). The SNR has improved to 30 dB according to Equation (1) and the total dose deposition is 64 Gy, 80 times the single-pulse deposition.
- Figure 5—bottom shows the output of the WTDA signal, characterized by the same 30 dB SNR as the 80-fold average signal, but obtained from a single-pulse signal with a total dose deposition of 0.8 Gy.
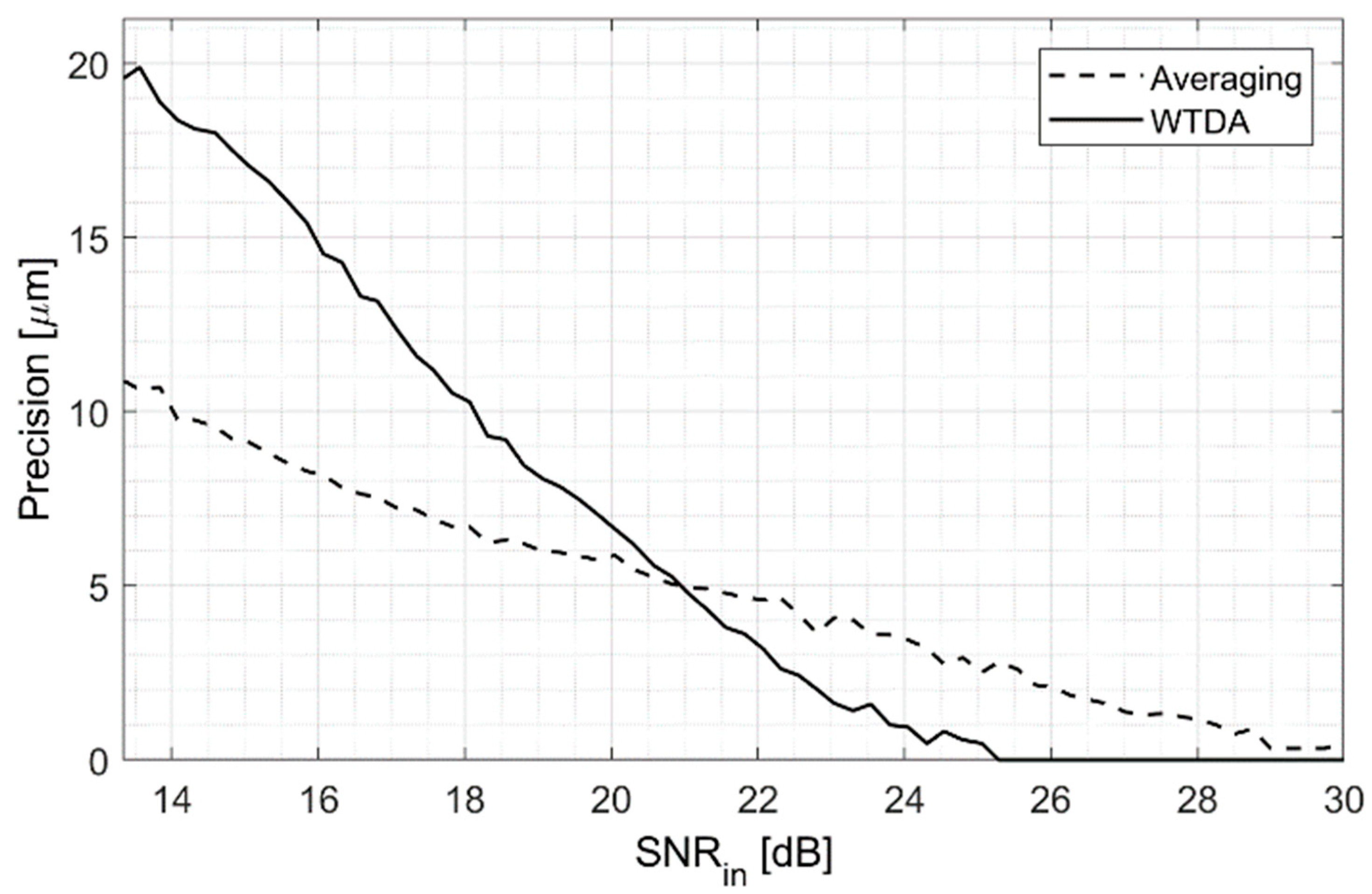
3.2. Measurement Precision Improvement
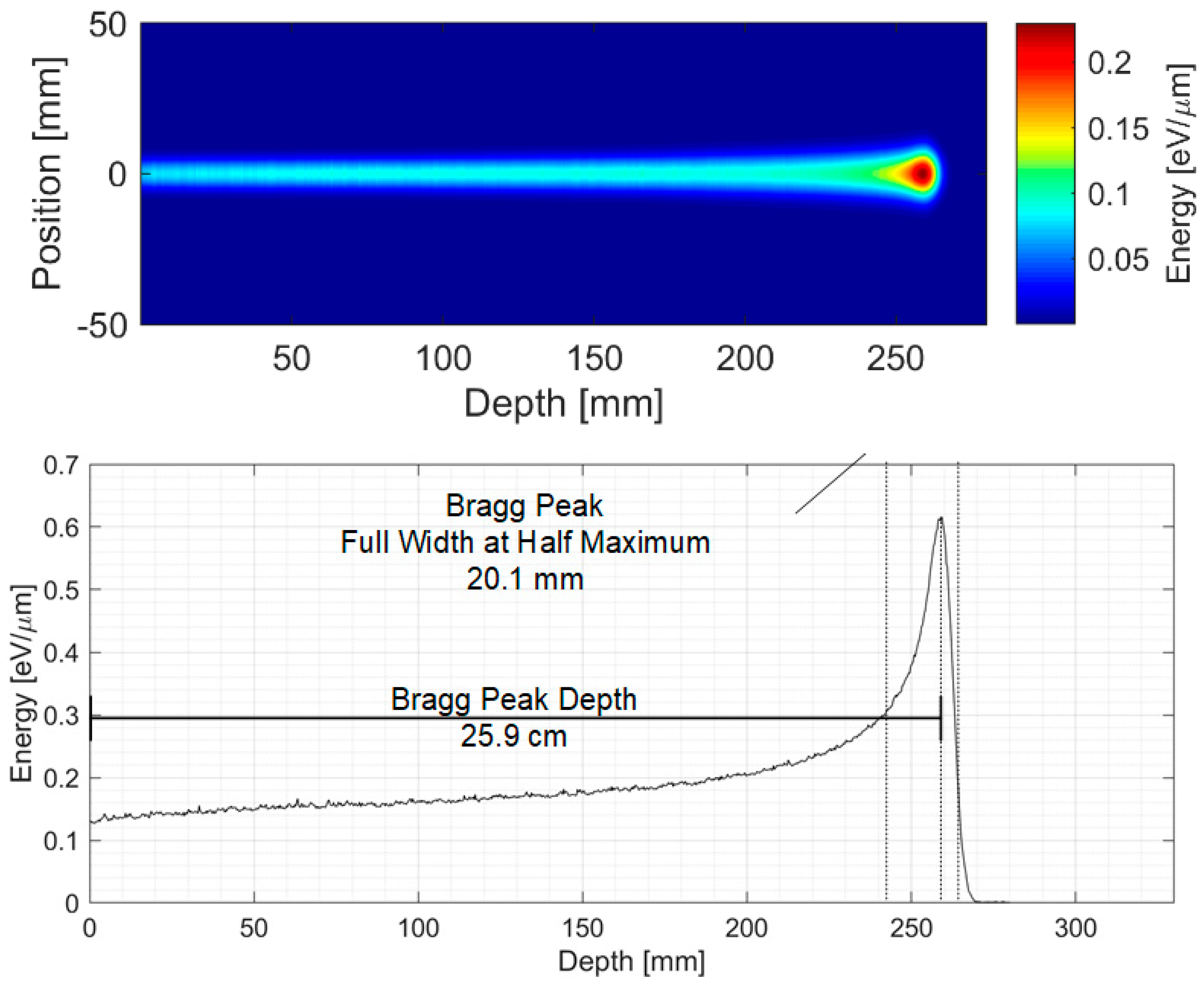
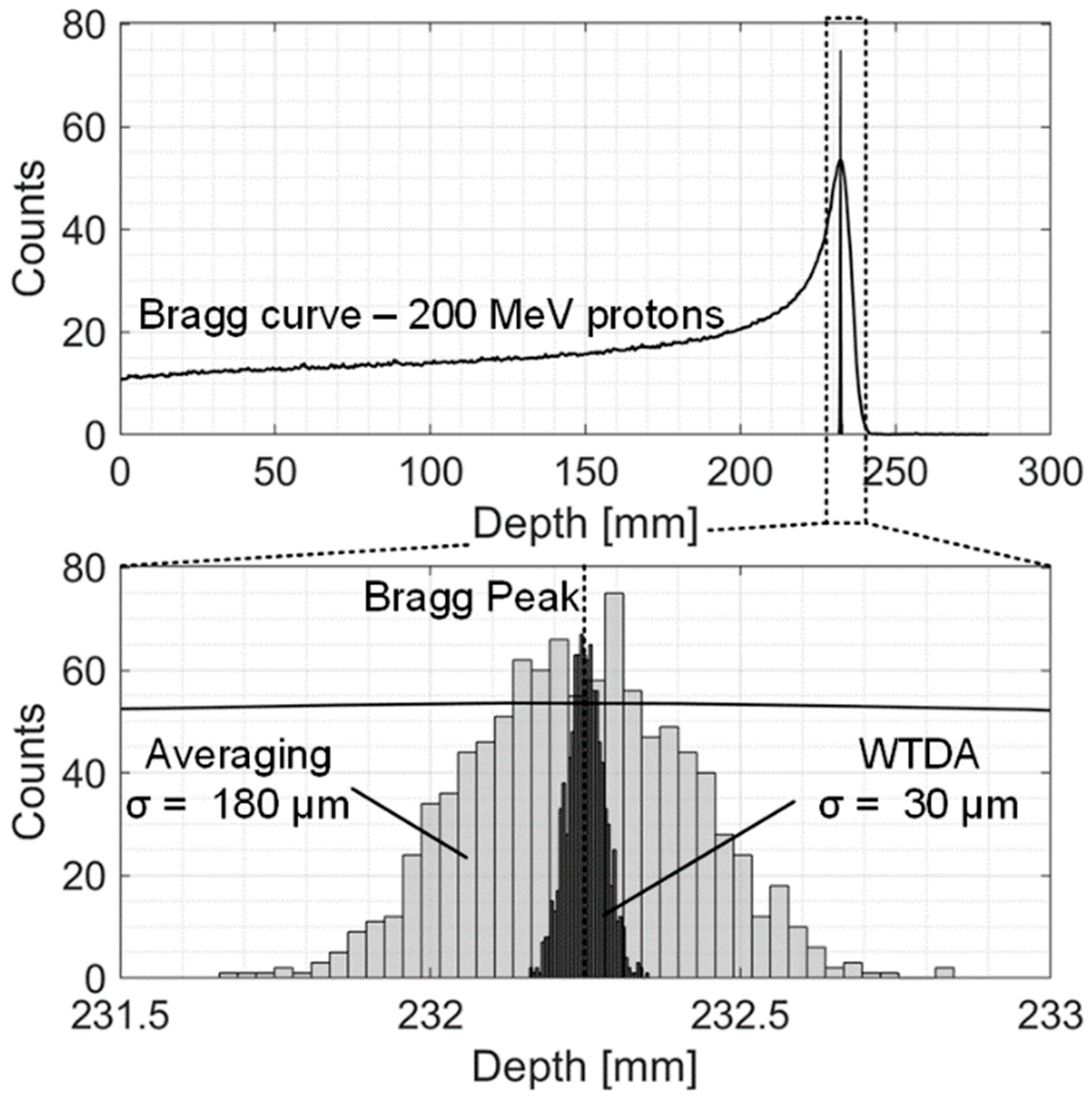
4. Simulation Results—200 MeV Clinical Scenario
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Knoll, G.F. Radiation Sources. In Radiation Detection and Measurement; John Wiley & Sons: Hoboken, NJ, USA, 2000; Chapter 1; pp. 1–28. [Google Scholar]
- Parodi, K.; Polf, J.C. In vivo range verification in particle therapy. Med. Phys. 2018, 45, e1036–e1050. [Google Scholar] [CrossRef]
- Min, C.-H.; Kim, C.H.; Youn, M.-Y.; Kim, J.-W. Prompt gamma measurements for locating the dose falloff region in the proton therapy. Appl. Phys. Lett. 2006, 89, 183517. [Google Scholar] [CrossRef]
- Hueso-González, F.; Rabe, M.; Ruggieri, T.A.; Bortfeld, T.; Verburg, J.M. A full-scale clinical prototype for proton range verification using prompt gamma-ray spectroscopy. Phys. Med. Biol. 2018, 63, 185019. [Google Scholar] [CrossRef] [PubMed]
- Mirandola, A.; Molinelli, S.; Vilches Freixas, G.; Mairani, A.; Gallio, E.; Panizza, D.; Russo, S.; Ciocca, M.; Donetti, M.; Magro, G.; et al. Dosimetric commissioning and quality assurance of scanned ion beams at the Italian National Center for Oncological Hadrontherapy. Radiat. Meas. Phys. 2015, 42, 5287–5300. [Google Scholar] [CrossRef] [PubMed]
- Sulak, L.; Armstrong, T.; Baranger, H.; Bregman, M.; Levi, M.; Mael, D.; Strait, J.; Bowen, T.; Pifer, A.; Polakos, P.; et al. Experimental studies of the acoustic signature of proton beams traversing fluid media. Nucl. Instrum. Methods 1979, 161, 203–217. [Google Scholar] [CrossRef]
- Hayakawa, Y.; Tada, J.; Arai, N.; Hosono, K.; Sato, M.; Wagai, T.; Tsuji, H.; Tsujii, H. Acoustic pulse generated in a patient during treatment by pulsed proton radiation beam. Radiat. Oncol. Investig. 1995, 3, 42–45. [Google Scholar] [CrossRef]
- Assmann, W.; Kellnberger, S.; Reinhardt, S.; Lehrack, S.; Edlich, A.; Thirolf, P.G.; Moser, M.; Dollinger, G.; Omar, M.; Ntziachristos, V.; et al. Ionoacoustic characterization of the proton Bragg peak with sub-millimeter accuracy. Med. Phys. 2015, 42, 567–574. [Google Scholar] [CrossRef]
- Lehrack, S.; Assmann, W.; Bender, M.; Severin, D.; Trautmann, C.; Schreiber, J.; Parodi, K. Ionoacoustic detection of swift heavy ions. Nucl. Instrum. Meth. A 2020, 950, 162935. [Google Scholar] [CrossRef]
- Vallicelli, E.A.; Baschirotto, A.; Lehrack, S.; Assmann, W.; Parodi, K.; Viola, S.; Riccobene, G.; De Matteis, M. 22 dB signal-to-noise ratio real-time proton sound detector for experimental beam range verification. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 68, 3–13. [Google Scholar] [CrossRef]
- Wang, S.; Gonzalez, G.; Sun, L.; Xu, Y.; Pandey, P.; Chen, Y.; Xiang, S. Real-time tracking of the Bragg peak during proton therapy via 3D protoacoustic Imaging in a clinical scenario. npj Imaging 2024, 2, 34. [Google Scholar] [CrossRef]
- Samant, P.; Trevisi, L.M.; Chen, Y.; Zwart, T.; Xiang, L. 3-D Protoacoustic imaging through a planar ultrasound array: A simulation Workflow. IEEE Trans. Radiat. Plasma Med. Sci. 2022, 7, 83–95. [Google Scholar] [CrossRef]
- Yu, Y.; Li, Z.; Zhang, D.; Xing, L.; Peng, H. Simulation studies of time reversal-based protoacoustic reconstruction for range and dose verification in proton therapy. Med. Phys. 2019, 46, 3649–3662. [Google Scholar] [CrossRef]
- Schauer, J.; Wieser, H.-P.; Huang, Y.; Ruser, H.; Lascaud, J.; Würl, M.; Chmyrov, A.; Vidal, M.; Herault, J.; Ntziachristos, V.; et al. Proton beam range verification by means of ionoacoustic measurements at clinically relevant doses using a correlation-based evaluation. Front. Oncol. 2022, 12, 925542. [Google Scholar] [CrossRef] [PubMed]
- Lascaud, J.; Dash, P.; Wieser, H.-P.; Kalunga, R.; Würl, M.; Assmann, W.; Parodi, K. Investigating the accuracy of co-registered ionoacoustic and ultrasound images in pulsed proton beams. Phys. Med. Biol. 2021, 66, 185007. [Google Scholar] [CrossRef] [PubMed]
- Patch, S.K.; Hoff, D.E.M.; Webb, T.B.; Sobotka, L.G.; Zhao, T. Two-stage ionoacoustic range verification leveraging Monte Carlo and acoustic simulations to stably account for tissue inhomogeneity and accelerator–specific time structure–A simulation study. Med. Phys. 2018, 45, 783–793. [Google Scholar] [CrossRef]
- Takayanagi, T.; Uesaka, T.; Nakamura, Y.; Unlu, M.B.; Kuriyama, Y.; Uesugi, T.; Ishi, Y.; Kudo, N.; Kobayashi, M.; Umegaki, K.; et al. On-line range verification for proton beam therapy using spherical ionoacoustic waves with resonant frequency. Sci. Rep. 2020, 10, 20385. [Google Scholar] [CrossRef] [PubMed]
- Lascaud, J.; Dash, P.; Würl, M.; Wieser, H.-P.; Wollant, B.; Kalunga, R.; Assmann, W.; Clevert, D.-A.; Ferrari, A.; Sala, P.; et al. Enhancement of the ionoacoustic effect through ultrasound and photoacoustic contrast agents. Sci. Rep. 2021, 11, 2725. [Google Scholar] [CrossRef]
- Lehrack, S.; Assmann, W.; Bertrand, D.; Henrotin, S.; Herault, J.; Heymans, V.; Stappen, F.V.; Thirolf, P.G.; Vidal, M.; Van de Walle, J.; et al. Submillimeter ionoacoustic range determination for protons in water at a clinical synchrocyclotron. Phys. Med. Biol. 2017, 62, L20. [Google Scholar] [CrossRef]
- De Matteis, M.; Baschirotto, A.; Vallicelli, E.; Zanini, E. Proton-induced thermoacoustic process as Linear-Time-Invariant System. IEEE Trans. Radiat. Plasma Med. Sci. 2021, 6, 336–344. [Google Scholar] [CrossRef]
- Vallicelli, E.A.; De Matteis, M. Analog filters design for improving precision in proton sound detectors. J. Low Power Electron. Appl. 2021, 11, 12. [Google Scholar] [CrossRef]
- Riva, M.; Vallicelli, E.A.; Baschirotto, A.; De Matteis, M. Acoustic analog front end for proton range detection in hadron therapy. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 954–962. [Google Scholar] [CrossRef] [PubMed]
- De Matteis, M.; Galante, N.; Fary, F.; Vallicelli, E.; Baschirotto, A. 64 dB dynamic-range 810 μW 90 MHz fully-differential flipped-source-follower analog filter in 28nm-CMOS. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 3068–3072. [Google Scholar] [CrossRef]
- Vallicelli, E.A.; Turossi, D.; Gelmi, L.; Baù, A.; Bertoni, R.; Fulgione, W.; Quintino, A.; Corcione, M.; Baschirotto, A.; De Matteis, M. A 0.3 nV/√ Hz input-referred-noise analog front-end for radiation-induced thermo-acoustic pulses. Integration 2020, 74, 11–18. [Google Scholar] [CrossRef]
- Mallat, S.G. A Theory for Multiresolution Signal Decomposition: The Wavelet Representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 2, 7. [Google Scholar] [CrossRef]
- Johnstone, I.M.; Silverman, B.W. Empirical Bayes selection of wavelet thresholds. Ann. Stat. 2005, 33, 1700–1752. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.A.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. GEANT4—a simulation toolkit. Nucl. Instrum. Meth. A 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Treeby, B.E.; Cox, B.T. k-Wave: MATLAB toolbox for the simulation and reconstruction of photoacoustic wave fields. J. Biomed. Opt. 2010, 15, 021314. [Google Scholar] [CrossRef]




| Parameter | Symbol | Value |
|---|---|---|
| Particle Energy | E | 20 MeV |
| Current Pulse Time Window | TW | 120 ns |
| Stress confinement | tstress | 220 ns |
| Proton Bunch Number | N | 1 M |
| Beam Diameter | DB | 2 mm |
| Pulse Equivalent Injected Charge | QIN | 0.16 fC |
| Deposited Energy Dose | EDEP | 0.8 Gy |
| BP FWHM | BPFWHM | 0.32 mm |
| Beam Depth Range | R | 4.060 mm |
| BP Volume | BPVOLUME | 0.64 mm3 |
| Sound Speed in Water (22.3 °C) | cw | 1492 m/s |
| Parameter | Value | |
|---|---|---|
| Acoustic Sensor | Pass-band Sensitivity | ~10 µV/Pa |
| Pass-band Frequency Range (− 6 dB) | 2.45–4.95 MHz | |
| Capacitance | 1 nF | |
| Output Noise Power | 5.82 µVRMS | |
| Input Referred Noise | ~580 mPaRMS | |
| LNA | Pass-band Gain | 60–80 dB |
| −3dB lower frequency | 10 kHz | |
| −3dB upper frequency | 4 MHz | |
| Input Referred Noise Voltage | 2.25 µVRMS | |
| Low-Pass Filter | Pass-Band Gain | 0 dB |
| Pole Frequency | 4 MHz | |
| Pole Quality Factor | 0.707 | |
| A-to-D Converter | Sampling Frequency | 80 MHz |
| Number of Bits | 10 | |
| Equivalent Number of Bits (ENOB) | 9.5 |
| Parameter | Assmann et al., 2015 [8] | Vallicelli et al., 2020 [10] | This Work |
|---|---|---|---|
| Proton Energy | 20 MeV | 20 MeV | 20 MeV |
| Detector Features | Commercial Front-end | Dedicated LNA | Dedicated LNA |
| DSP | Averaging | Averaging | WTDA |
| SNR for 1 pulse (0.8 Gy) | 6 dB | 13 dB | 30 dB |
| Dose to achieve 30 dB SNR | 200 Gy | 64 Gy | 0.8 Gy |
| Parameter | Single Pulse [11] | 10-Pulse Average [11] | 20-Pulse Average [11] | 10-Pulse Average + WTDA |
|---|---|---|---|---|
| SNR | 13 dB | 22 dB | 25 dB | 51 dB |
| Dose | 0.8 Gy | 8 Gy | 16 Gy | 8 Gy |
| BP position | 4073 μm | 4073 μm | 4073 μm | 4073 μm |
| Precision | 21 μm | 7.5 μm | 4 μm | 4 μm |
| Relative Error (%) | 0.5 % | 0.2 % | 0.1% | 0.1% |
| Parameter | [10] Averaging | This Work: 500-Pulse Average + WTDA |
|---|---|---|
| Single-pulse SNR | −2 dB | −2 dB |
| 500-pulse SNR | 21 dB | 21 dB |
| Dose per pulse | 35 mGy | 35 mGy |
| Npulse to achieve 30 μm precision | 1770 | 500 |
| Dose to achieve 30 μm precision | 62 Gy | 17 Gy |
| Precision with 17 Gy dose | 180 μm | 30 μm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vallicelli, E.A.; Baschirotto, A.; Stevenazzi, L.; Tambaro, M.; De Matteis, M. Proton Range Measurement Precision in Ionoacoustic Experiments with Wavelet-Based Denoising Algorithm. Sensors 2025, 25, 4247. https://doi.org/10.3390/s25144247
Vallicelli EA, Baschirotto A, Stevenazzi L, Tambaro M, De Matteis M. Proton Range Measurement Precision in Ionoacoustic Experiments with Wavelet-Based Denoising Algorithm. Sensors. 2025; 25(14):4247. https://doi.org/10.3390/s25144247
Chicago/Turabian StyleVallicelli, Elia Arturo, Andrea Baschirotto, Lorenzo Stevenazzi, Mattia Tambaro, and Marcello De Matteis. 2025. "Proton Range Measurement Precision in Ionoacoustic Experiments with Wavelet-Based Denoising Algorithm" Sensors 25, no. 14: 4247. https://doi.org/10.3390/s25144247
APA StyleVallicelli, E. A., Baschirotto, A., Stevenazzi, L., Tambaro, M., & De Matteis, M. (2025). Proton Range Measurement Precision in Ionoacoustic Experiments with Wavelet-Based Denoising Algorithm. Sensors, 25(14), 4247. https://doi.org/10.3390/s25144247








