Multi-Party Verifiably Collaborative Encryption for Biomedical Signals via Singular Spectrum Analysis-Based Chaotic Filter Bank Networks
Abstract
1. Introduction
2. Proposed Cryptosystem
2.1. Decomposition and Reconstruction of Biosensor Signals Based on SSA and Haar Filter Bank
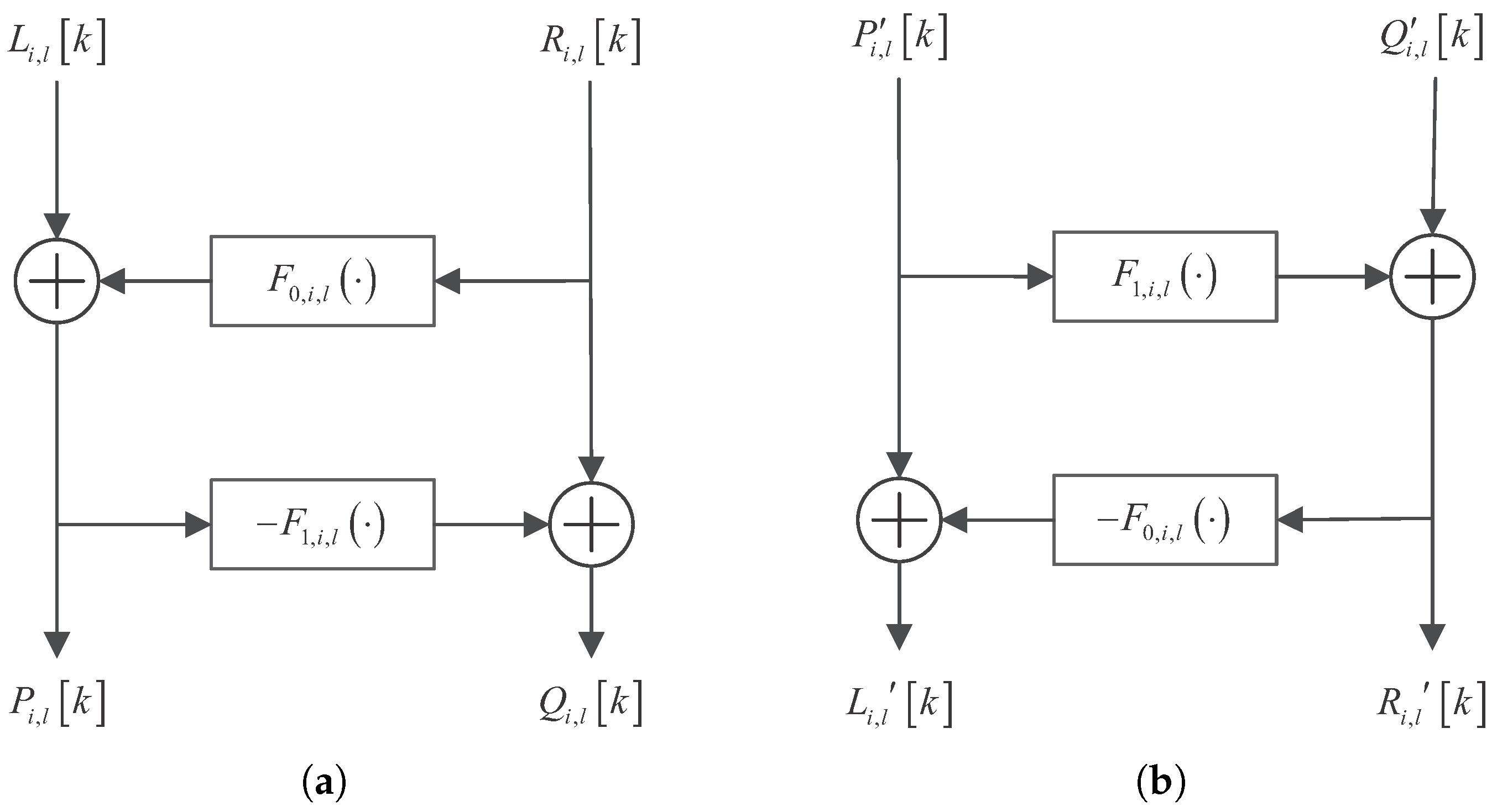
2.2. Dynamics of Nodes in Various Layers of Analysis Network and Synthesis Network
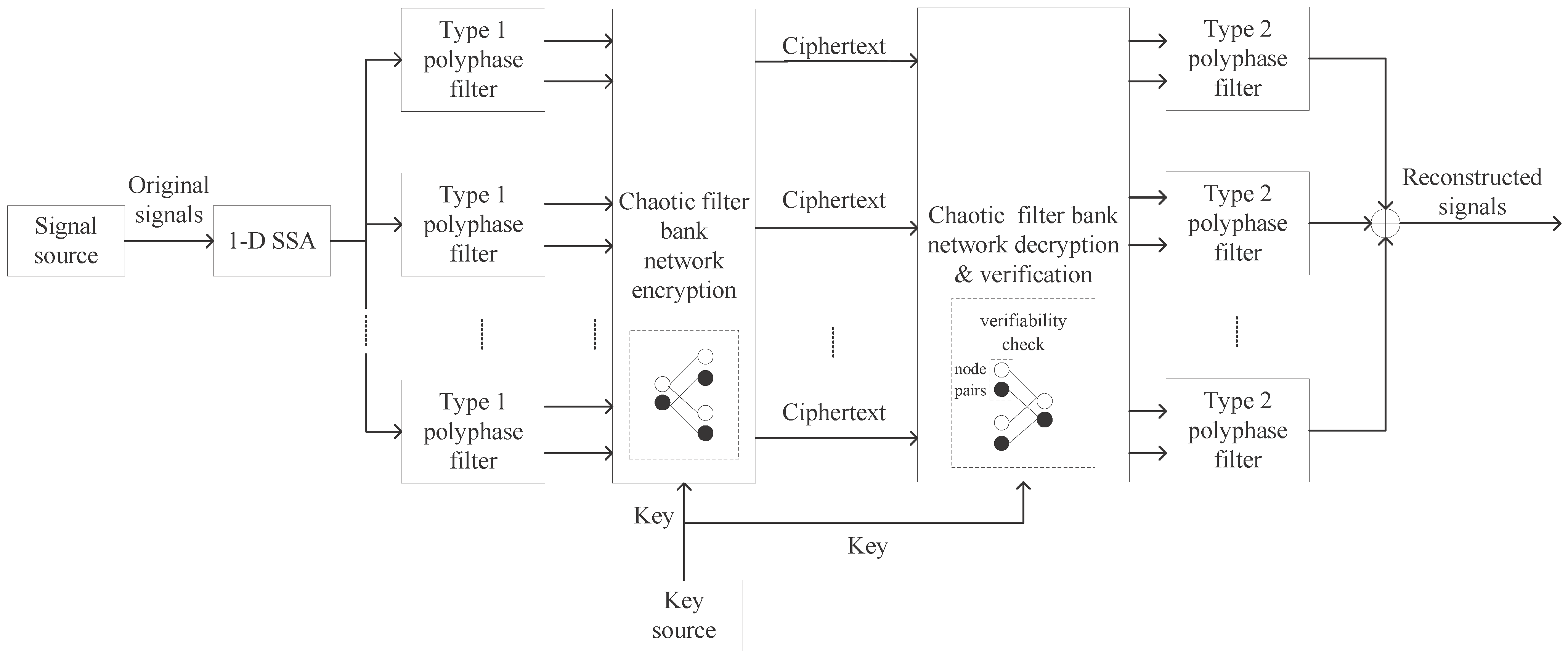
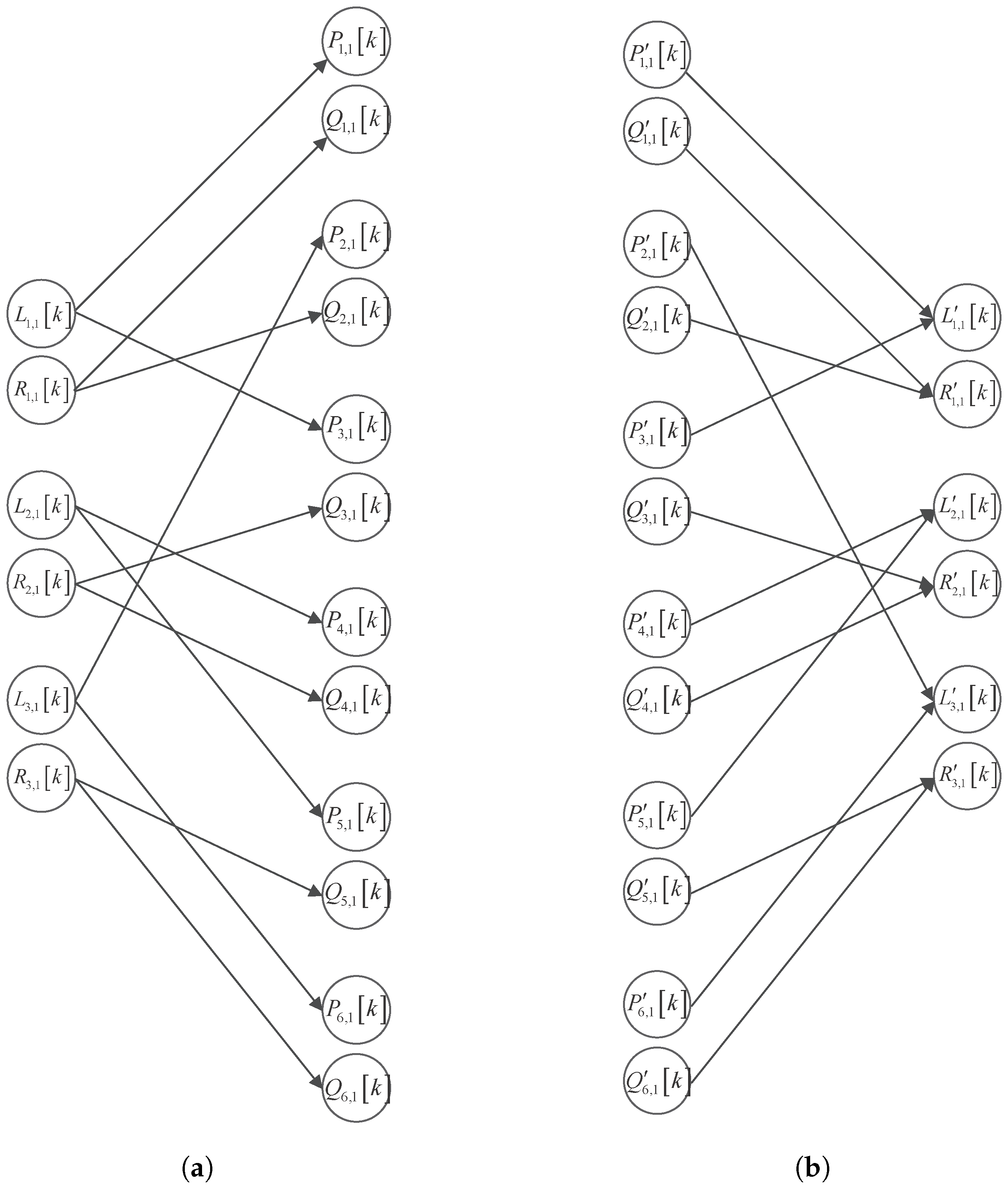
2.3. Multi-Layer Chaotic Network for Performing Multi-Party Verifiable Collaborative Encryption
3. Security Analysis and Computational Complexity
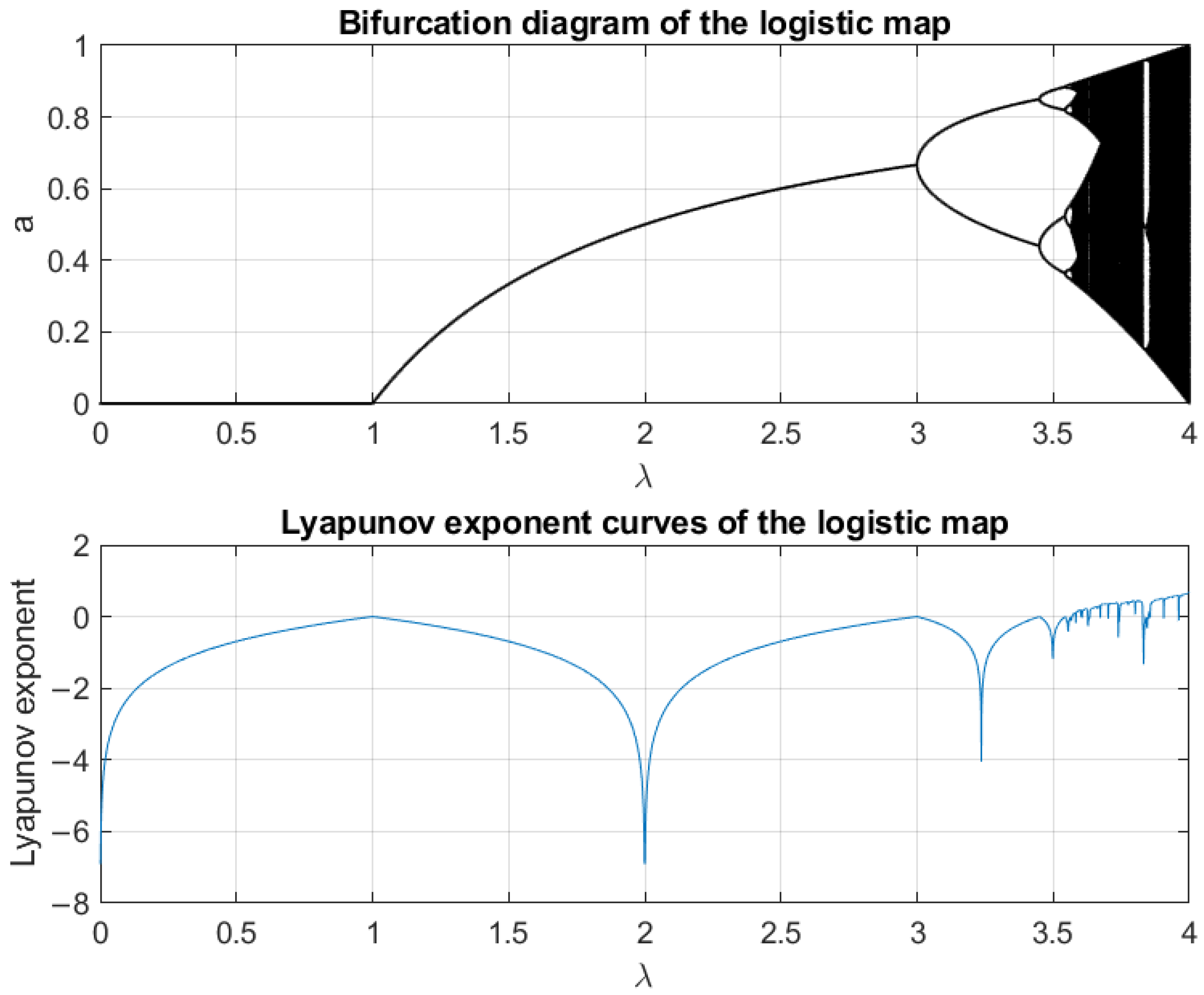
3.1. Dynamic Characteristics of the Logistic Map
3.2. Keyspace Analysis
3.3. Algorithmic Complexity Analysis
4. Computer Numerical Simulation Results
4.1. Data Acquisition
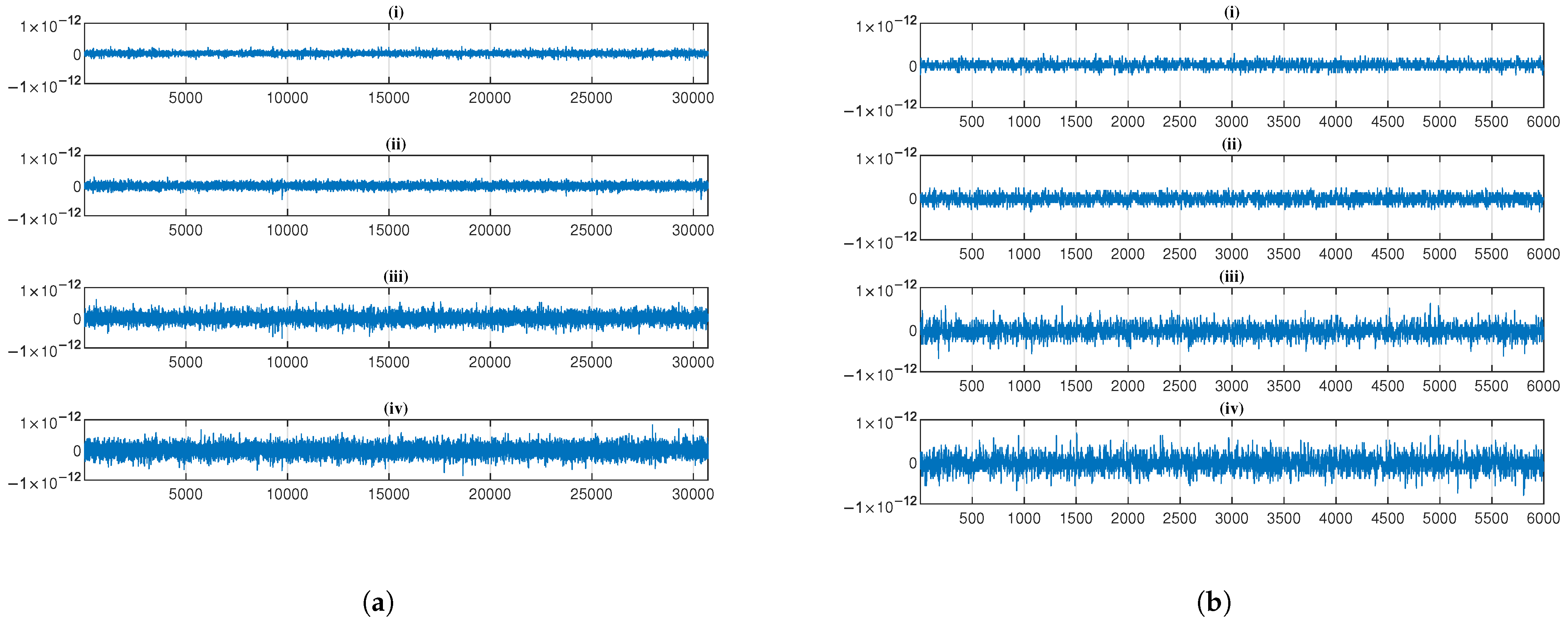
4.2. Reconstruction Error
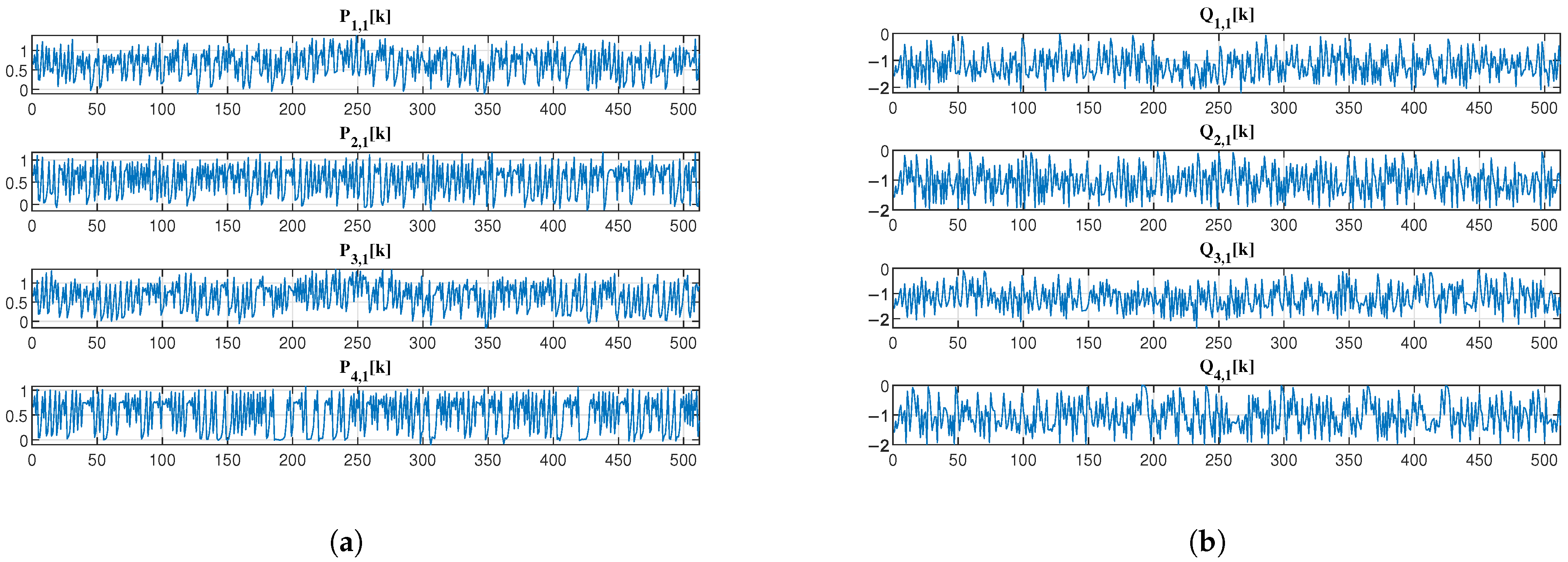
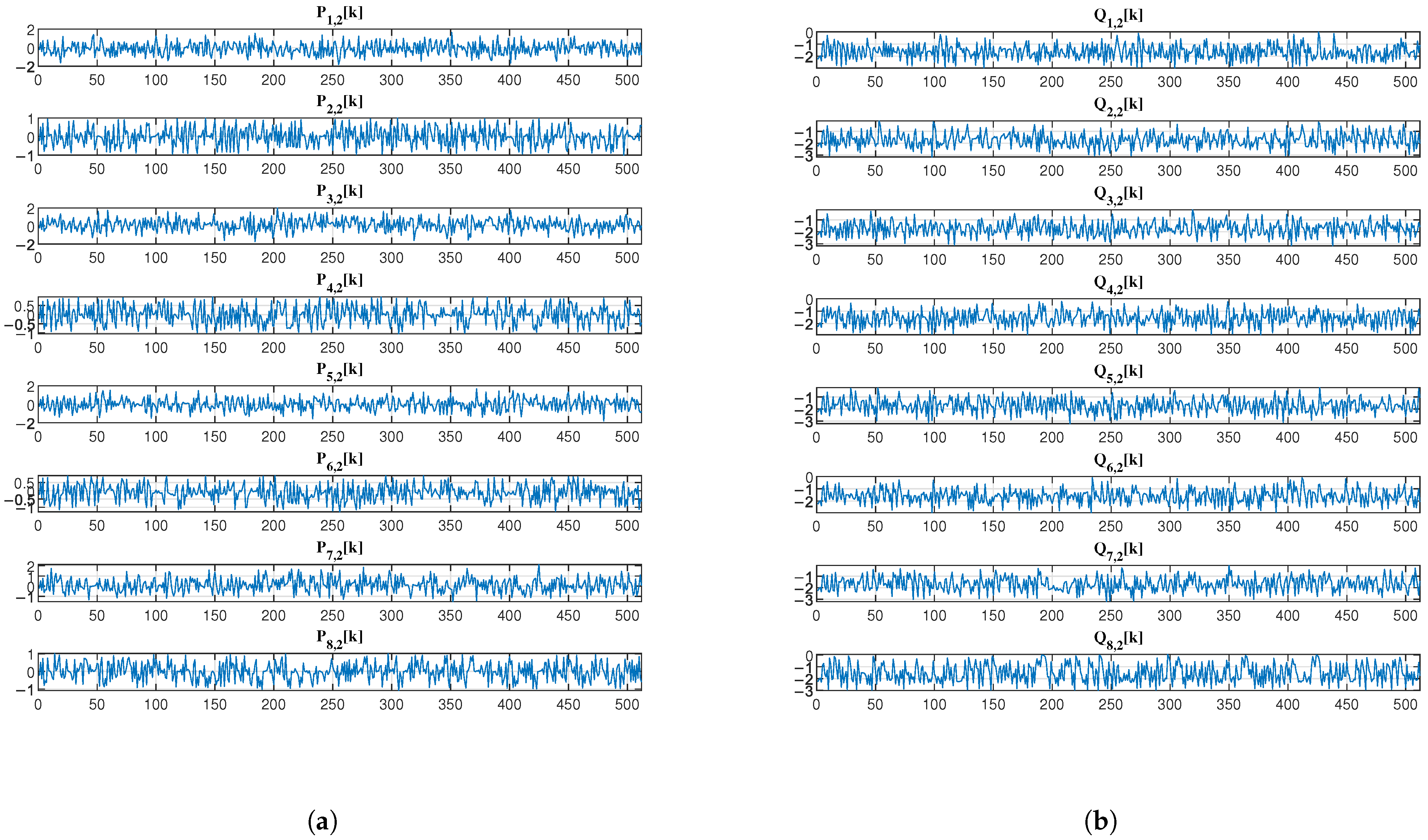
4.3. Signal Processing and Encryption Visualization
4.4. Security Analysis
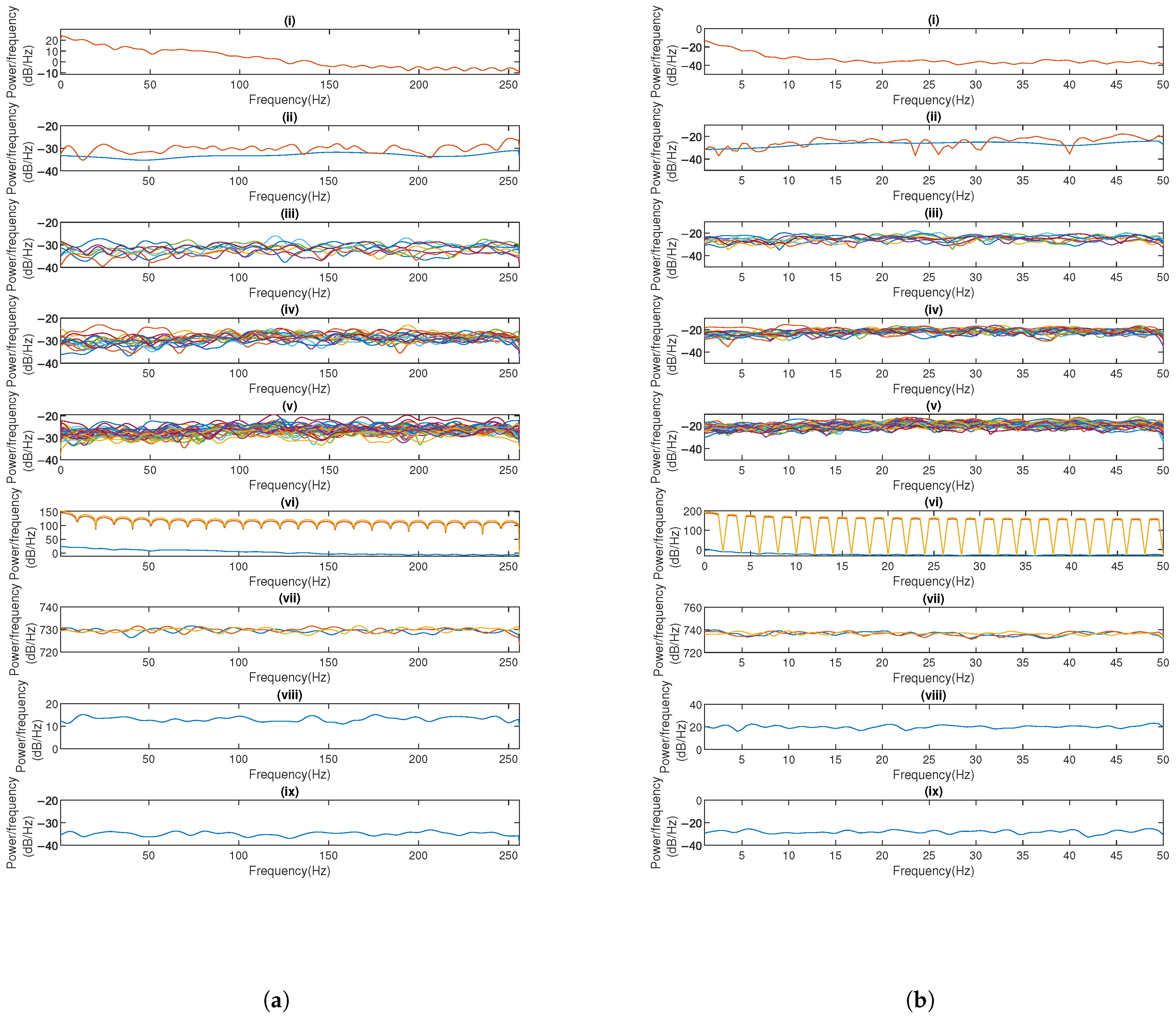
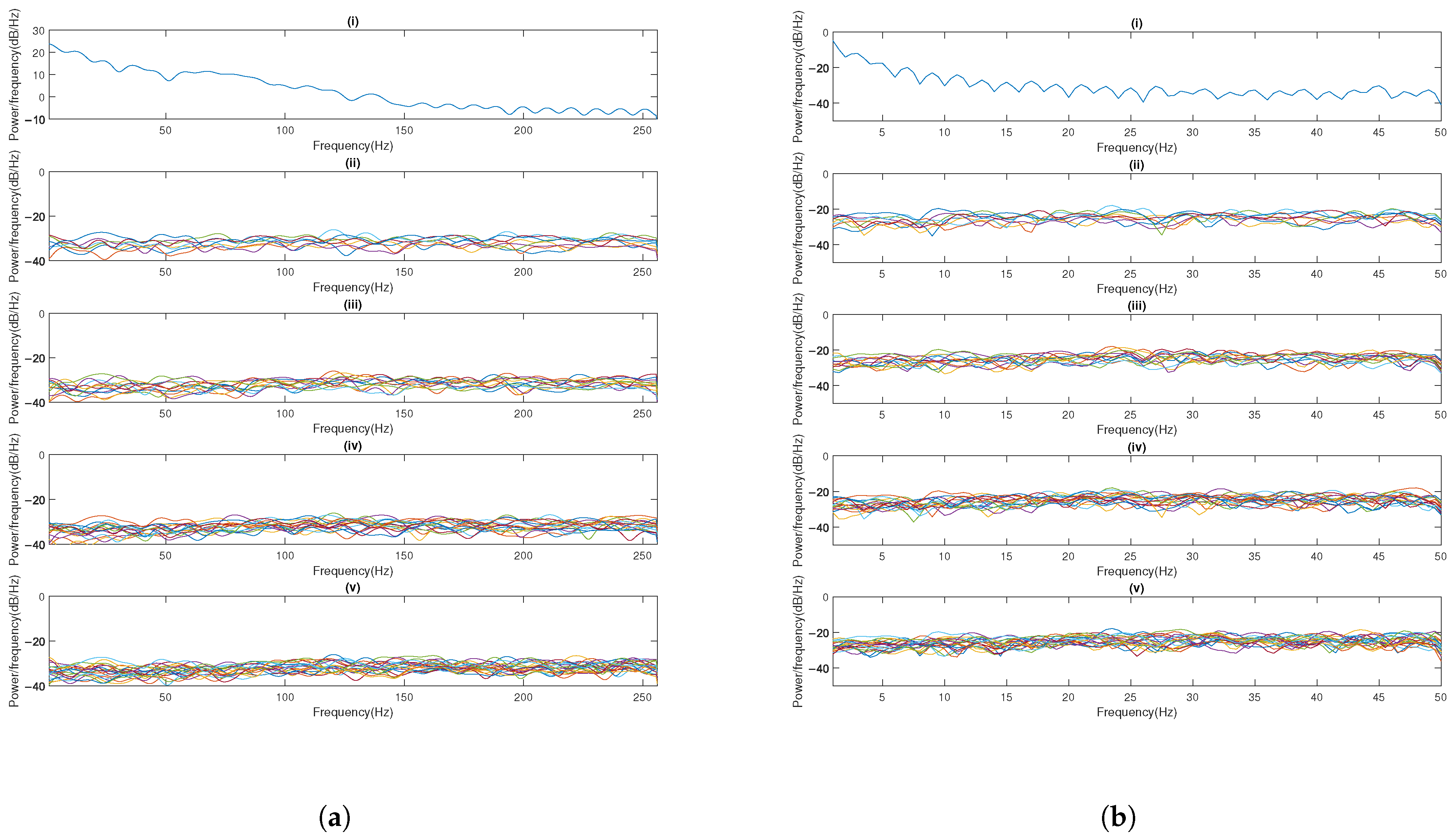
4.4.1. Power Spectral Density Analysis
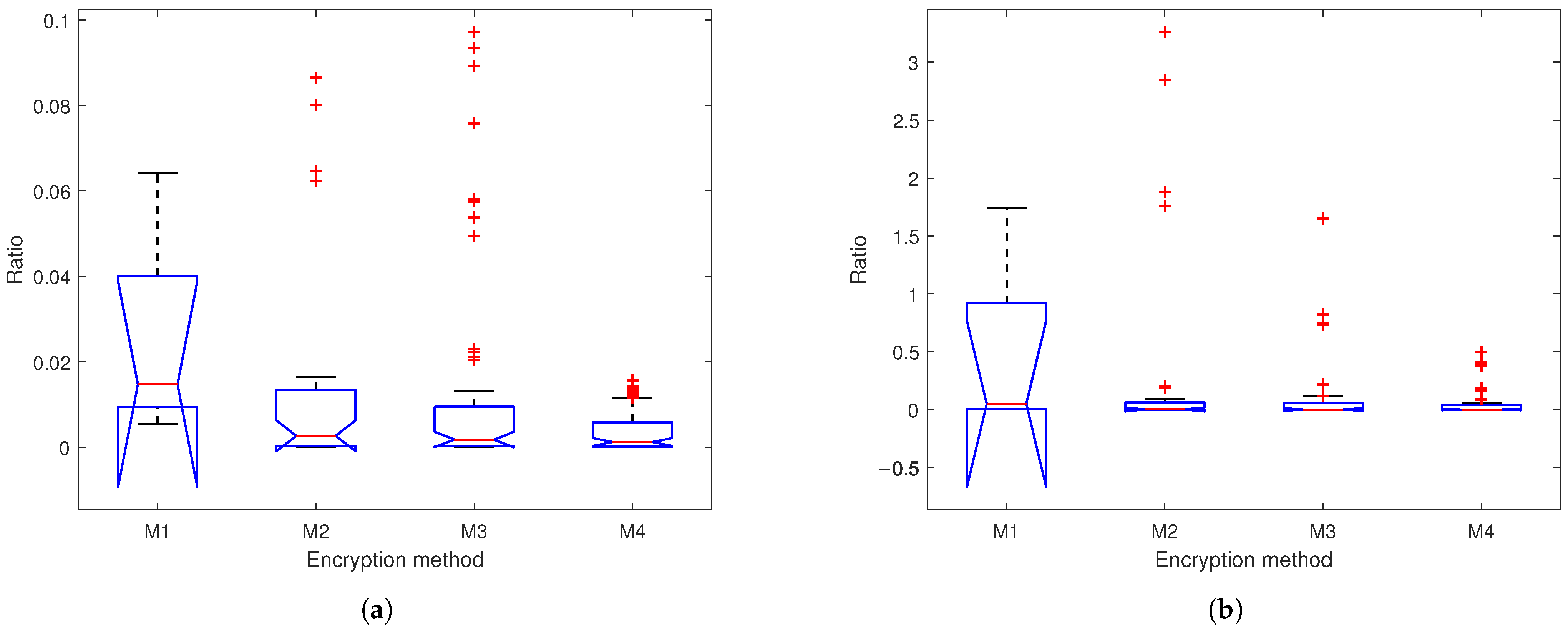
4.4.2. Power Ratio Analysis
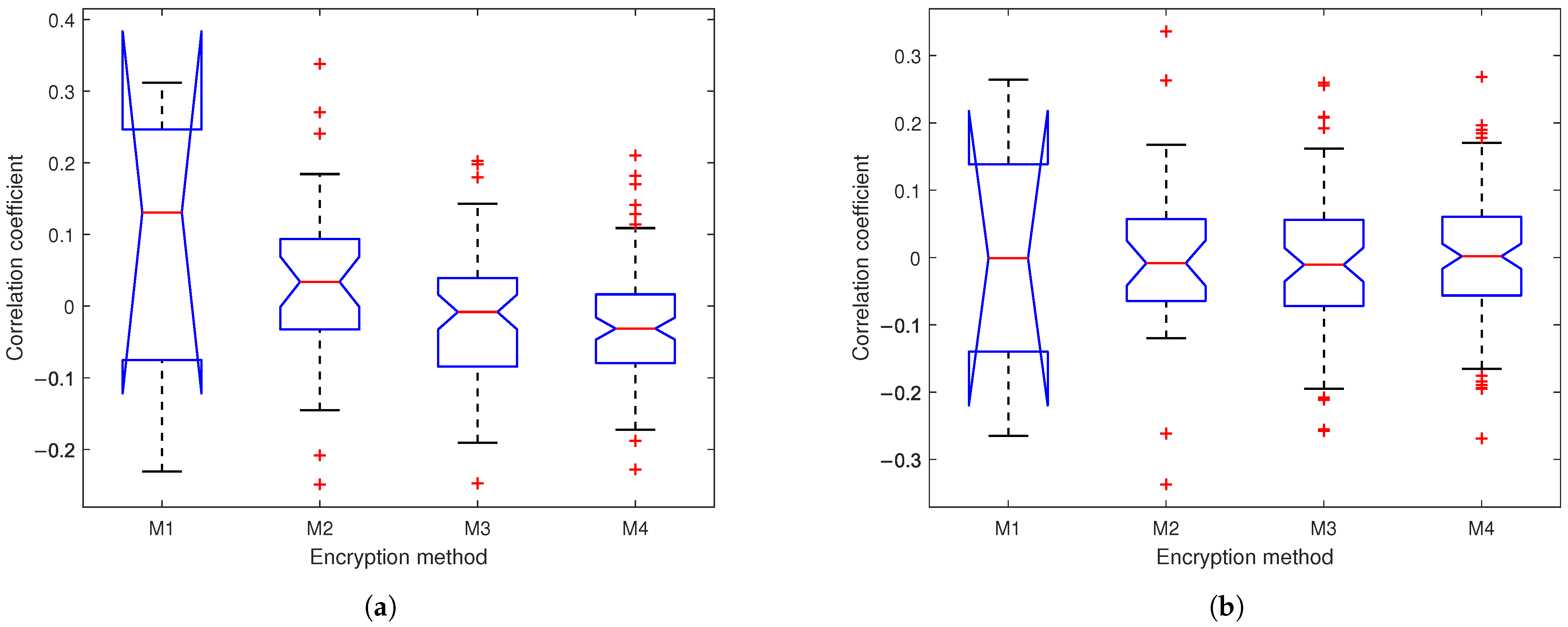
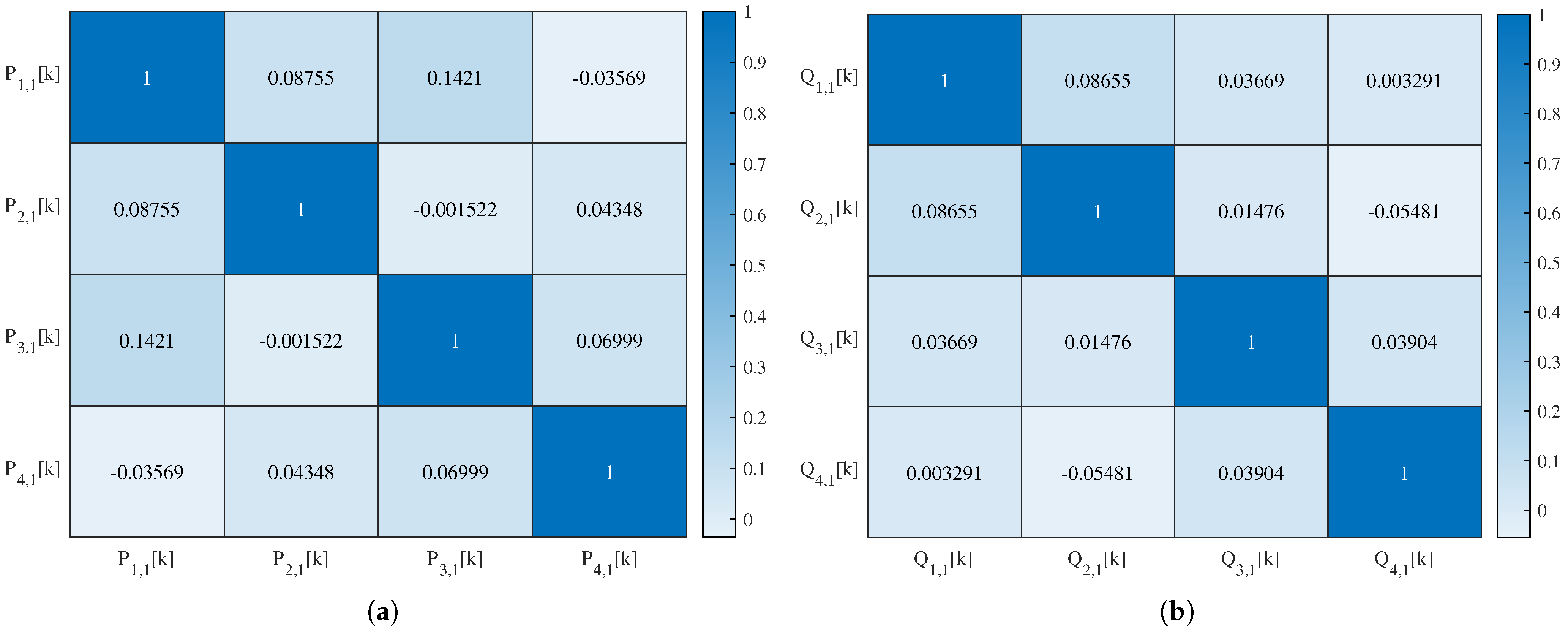
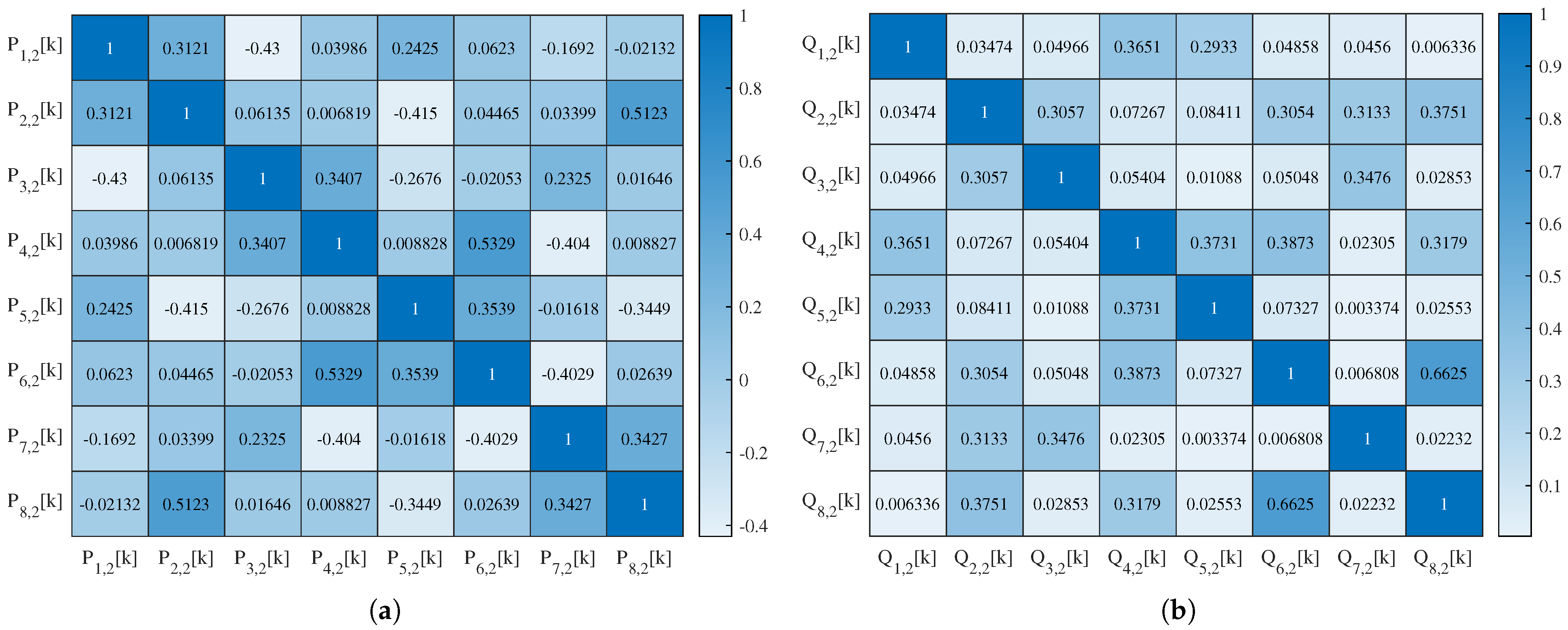
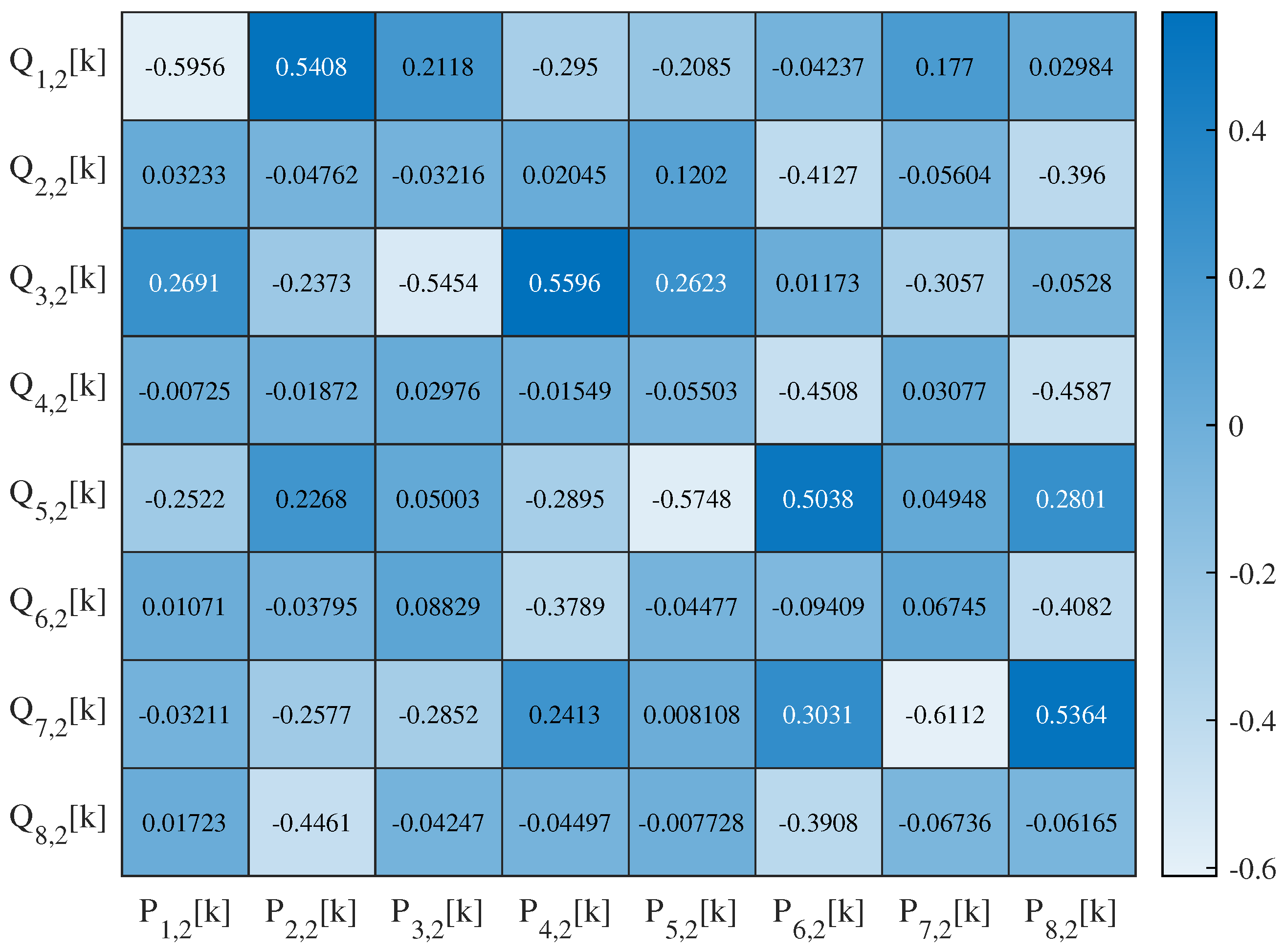
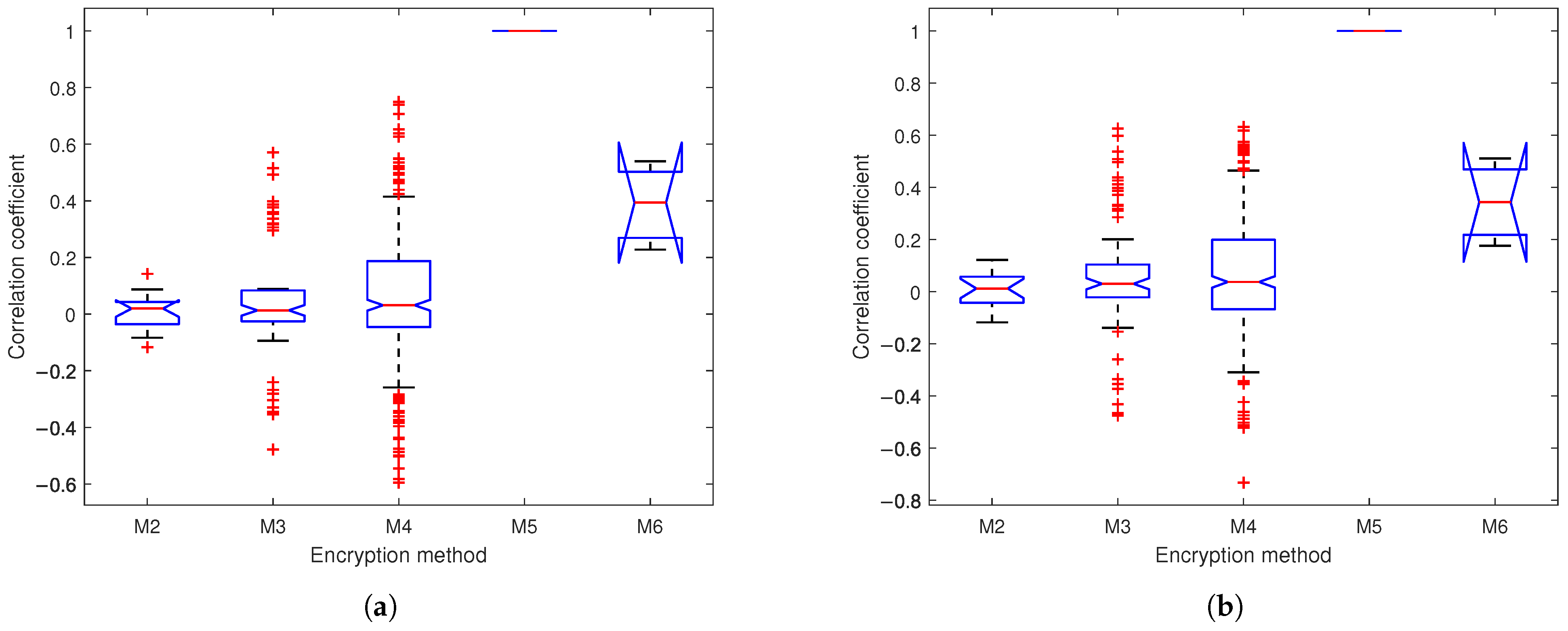
4.4.3. Correlation Analysis
4.5. Verification Performance
4.6. Decryption Error Analysis Under Collaborator Tampering Scenarios
4.7. Encryption and Decryption Efficiency Analysis
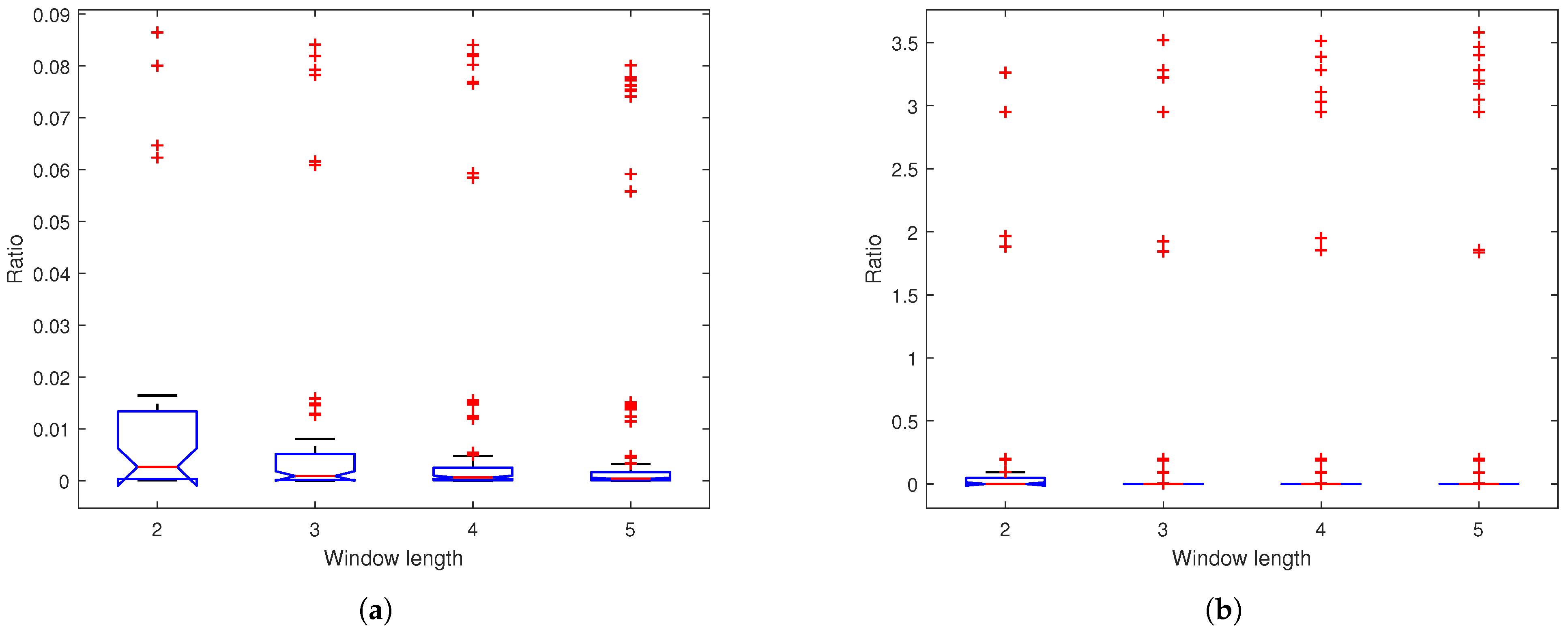
4.8. Performance Across Window Lengths
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jalali, M.S.; Landman, A.; Gordon, W.J. Telemedicine, privacy, and information security in the age of COVID-19. J. Am. Med. Inform. Assoc. 2020, 28, 671–672. [Google Scholar] [CrossRef] [PubMed]
- Lai, J.; Deng, R.H.; Guan, C.; Weng, J. Attribute-Based Encryption With Verifiable Outsourced Decryption. IEEE Trans. Inf. Forensics Secur. 2013, 8, 1343–1354. [Google Scholar]
- Ali, Z.; Imran, M.; Alsulaiman, M.; Zia, T.; Shoaib, M. A zero-watermarking algorithm for privacy protection in biomedical signals. Future Gener. Comput. Syst. 2018, 82, 290–303. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Ling, B.W.-K.; Ho, C.Y.-F.; Tam, P.K.-S. Chaotic filter bank for computer cryptography. Chaos Solitons Fractals 2007, 34, 817–824. [Google Scholar] [CrossRef]
- Wen, D.; Jiao, W.; Li, X.; Wan, X.; Zhou, Y.; Dong, X.; Lan, X.; Han, W. The EEG signals encryption algorithm with K-sine-transform-based coupling chaotic system. Inf. Sci. 2023, 622, 962–984. [Google Scholar] [CrossRef]
- Chen, J.; Ling, B.W.-K.; Feng, P.; Lei, R. Computer cryptography through performing chaotic modulation on intrinsic mode functions with non-dyadic number of encrypted signals. IET Signal Process. 2019, 13, 7–13. [Google Scholar] [CrossRef]
- Soleymani, A.; Nordin, M.J.; Sundararajan, E. A Chaotic Cryptosystem for Images Based on Henon and Arnold Cat Map. Sci. World J. 2014, 2014, 536930. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Zhao, S.; Zhao, M.; Chen, Z.; Gao, C.Z.; Li, H.; Tan, Y.A. Secure multi-party computation: Theory, practice and applications. Inf. Sci. 2019, 476, 357–372. [Google Scholar] [CrossRef]
- Zhou, I.; Tofigh, F.; Piccardi, M.; Abolhasan, M.; Franklin, D.; Lipman, J. Secure multi-party computation for machine learning: A survey. IEEE Access 2024, 12, 53881–53899. [Google Scholar] [CrossRef]
- Yu, Q.; Li, S.; Raviv, N.; Kalan, S.M.M.; Soltanolkotabi, M.; Avestimehr, S.A. Lagrange coded computing: Optimal design for resiliency, security, and privacy. In Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics, Naha, Okinawa, Japan, 16–18 April 2019. [Google Scholar]
- Ben-Or, M.; Goldwasser, S.; Wigderson, A. Completeness theorems for non-cryptographic fault-tolerant distributed computation. In Providing Sound Foundations for Cryptography: On the Work of Shafi Goldwasser and Silvio Micali; Association for Computing Machinery: New York, NY, USA, 2019; pp. 351–371. [Google Scholar]
- Al Badawi, A.; Bates, J.; Bergamaschi, F.; Cousins, D.B.; Erabelli, S.; Genise, N.; Halevi, S.; Hunt, H.; Kim, A.; Lee, Y.; et al. Openfhe: Open-source fully homomorphic encryption library. In Proceedings of the 10th Workshop on Encrypted Computing & Applied Homomorphic Cryptography, Los Angeles, CA, USA, 7 November 2022. [Google Scholar]
- Chillotti, I.; Joye, M.; Ligier, D.; Orfila, J.B.; Tap, S. Concrete: Concrete operates on ciphertexts rapidly by extending tfhe. In Proceedings of the WAHC 2020-8th Workshop on Encrypted Computing & Applied Homomorphic Cryptography, Virtual, 15 December 2020. [Google Scholar]
- Mukherjee, P.; Wichs, D. Two round multiparty computation via multi-key FHE. In Proceedings of the Advances in Cryptology–EUROCRYPT 2016: 35th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Vienna, Austria, 8–12 May 2016. [Google Scholar]
- Kocabas, O.; Soyata, T.; Couderc, J.P.; Aktas, M.; Xia, J.; Huang, M. Assessment of cloud-based health monitoring using homomorphic encryption. In Proceedings of the 2013 IEEE 31st International Conference on Computer Design (ICCD), Asheville, NC, USA, 6–9 October 2013. [Google Scholar]
- Xie, Q.; Jiang, S.; Jiang, L.; Huang, Y.; Zhao, Z.; Khan, S.; Dai, W.; Liu, Z.; Wu, K. Efficiency optimization techniques in privacy-preserving federated learning with homomorphic encryption: A brief survey. IEEE Internet Things 2024, 11, 24569–24580. [Google Scholar] [CrossRef]
- Tamilselvi, P.; Lathika, V.; Jayachitra, S.; Arunkumar, S.; Balasubramani, M.; Kalaichelvi, V. Secure Multi-Party Computation for Collaborative Data Analysis in Network Security. In Proceedings of the 2024 International Conference on Intelligent and Innovative Technologies in Computing, Electrical and Electronics (IITCEE), Bengaluru, India, 24–25 January 2024. [Google Scholar]
- Battah, A.A.; Madine, M.M.; Alzaabi, H.; Yaqoob, I.; Salah, K.; Jayaraman, R. Blockchain-Based Multi-Party Authorization for Accessing IPFS Encrypted Data. IEEE Access 2020, 8, 196813–196825. [Google Scholar] [CrossRef]
- Hidayat, T.; Mahardiko, R. Data encryption algorithm AES by using blockchain technology: A review. BACA J. Dok. Dan Inf. 2021, 42, 19–30. [Google Scholar] [CrossRef]
- Shamir, A. How to share a secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Pournaghi, S.M.; Bayat, M.; Farjami, Y. MedSBA: A novel and secure scheme to share medical data based on blockchain technology and attribute-based encryption. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 4613–4641. [Google Scholar] [CrossRef]
- Cafaro, M.; Pellè, P. Space-Efficient Verifiable Secret Sharing Using Polynomial Interpolation. IEEE Trans. Cloud Comput. 2018, 6, 453–463. [Google Scholar] [CrossRef]
- Soman, A.K.; Vaidyanathan, P.P. On orthonormal wavelets and paraunitary filter banks. IEEE Trans. Signal Process. 1993, 41, 1170–1183. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P. Multirate digital filters, filter banks, polyphase networks, and applications: A tutorial. Proc. IEEE 1990, 78, 56–93. [Google Scholar] [CrossRef]
- Ulam, S.M. On combination of stochastic and deterministic processes. Bull. Am. Math. Soc. 1947, 53, 1120. [Google Scholar]
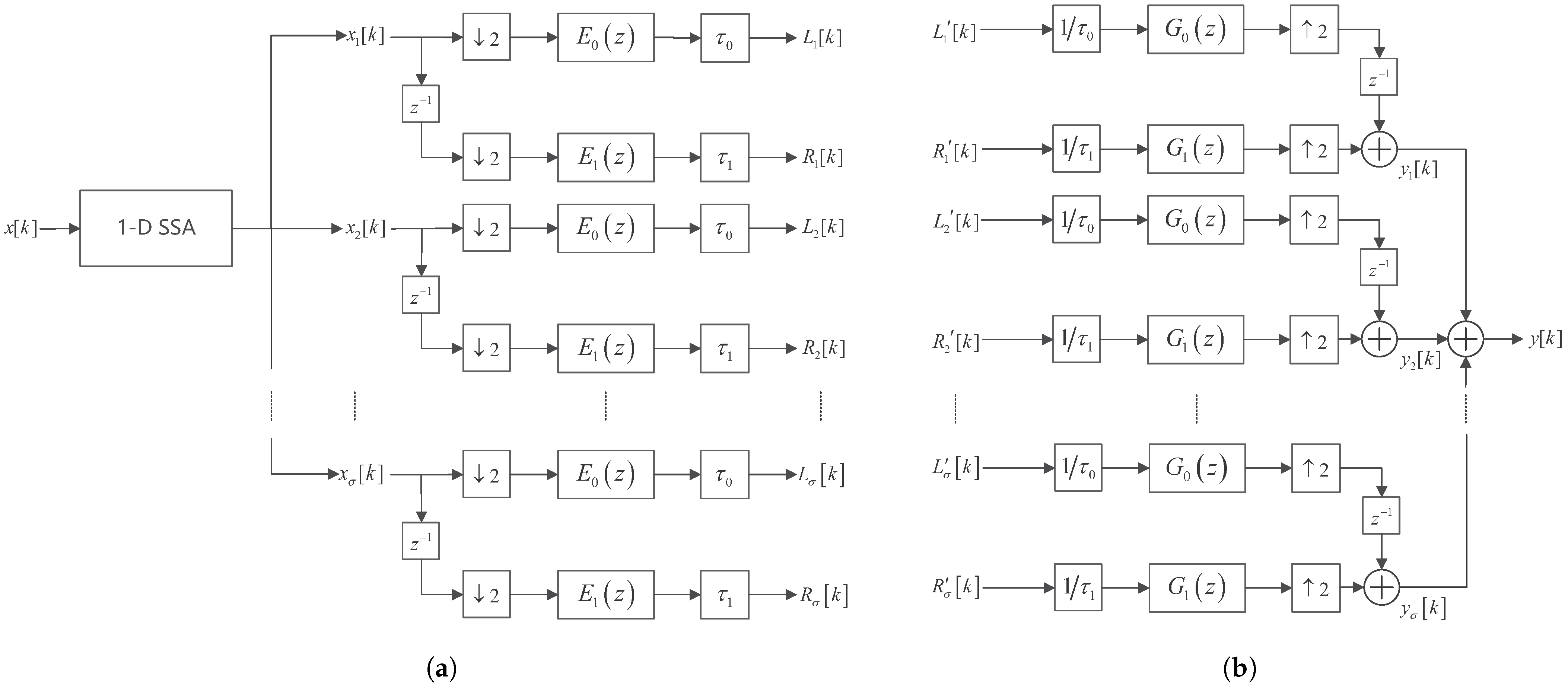



| Signal | EEG | PPG | ||
|---|---|---|---|---|
| Encryption Methods | MSE | PRD | MSE | PRD |
| Logistic chaotic filter bank of [5] | ||||
| Our SSA with 1-layer chaotic network | ||||
| Our SSA with 2-layer chaotic network | ||||
| Our SSA with 3-layer chaotic network | ||||
| Signal | EEG | PPG | ||
|---|---|---|---|---|
| Encryption Methods | Absolute Mean | Variance | Absolute Mean | Variance |
| Logistic chaotic filter bank in [5] | 0.0248 | 0.0005 | 0.4610 | 0.5483 |
| Our SSA with 1-layer chaotic network | 0.0133 | 0.0006 | 0.3255 | 0.6895 |
| Our SSA with 2-layer chaotic network | 0.0124 | 0.0006 | 0.1214 | 0.1095 |
| Our SSA with 3-layer chaotic network | 0.0039 | 0.0000 | 0.0479 | 0.0096 |
| FHE 1 | − | − | − | − |
| Shamir’s scheme | 0.0000 | |||
| Robust BGW variant | ||||
| AES-based blockchain 2 | − | 1.8669 | − | |
| K-sine-transform-based coupling chaotic system 3 | − | 1.0023 | − | |
| Signal | EEG | PPG | ||
|---|---|---|---|---|
| Encryption Methods | Absolute Mean | Variance | Absolute Mean | Variance |
| Logistic chaotic filter bank in [5] | 0.2010 | 0.0401 | 0.1393 | 0.0351 |
| Our SSA with 1-layer chaotic network | 0.0982 | 0.0156 | 0.0850 | 0.0154 |
| Our SSA with 2-layer chaotic network | 0.0756 | 0.0092 | 0.0847 | 0.0125 |
| Our SSA with 3-layer chaotic network | 0.0545 | 0.0046 | 0.0641 | 0.0069 |
| FHE | − | − | − | − |
| Shamir’s scheme | 1 | 0 | 0.9589 | 0 |
| Robust BGW variant | 0.0490 | |||
| AES-based blockchain | − | 0.0285 | − | |
| K-sine-transform-based coupling chaotic system | − | 0.0607 | − | |
| Signal | EEG | PPG | ||
|---|---|---|---|---|
| Paired Decryption Results | MSE | PRD | MSE | PRD |
| Signal | EEG | PPG | ||
|---|---|---|---|---|
| Paired Decryption Results | MSE | PRD | MSE | PRD |
| Signal | EEG | PPG | ||
|---|---|---|---|---|
| Paired Decryption Results | MSE | PRD | MSE | PRD |
| 19.5551 | 1.0225 | |||
| or | 0.0012 | 47.6284 | ||
| or | 0.0012 | 3.0111 | ||
| Signal | EEG | PPG | ||
|---|---|---|---|---|
| Encryption Methods | Encryption Time (s) | Decryption Time (s) | Encryption Time (s) | Decryption Time (s) |
| Logistic chaotic filter bank in [5] | 0.0017 | 0.0017 | 0.0016 | 0.0018 |
| Our SSA with 1-layer chaotic network | 0.0078 | 0.0050 | 0.0083 | 0.0025 |
| Our SSA with 2-layer chaotic network | 0.0098 | 0.0066 | 0.0063 | 0.0015 |
| Our SSA with 3-layer chaotic network | 0.0086 | 0.0011 | 0.0098 | 0.0067 |
| FHE | 0.0966 | 0.0125 | ||
| Shamir’s scheme | 0.0002 | 0.0001 | ||
| Robust BGW variant | 0.0017 | |||
| AES-based blockchain | 0.0006 | 0.0001 | ||
| K-sine-transform-based coupling chaotic system | 0.0079 | 0.0078 | ||
| Signal | EEG | PPG | ||
|---|---|---|---|---|
| Window Length | Absolute Mean | Variance | Absolute Mean | Variance |
| 2 | 0.0982 | 0.0401 | 0.0850 | 0.0154 |
| 3 | 0.0633 | 0.0074 | 0.0726 | 0.0108 |
| 4 | 0.0543 | 0.0055 | 0.0598 | 0.0075 |
| 5 | 0.0480 | 0.0043 | 0.0606 | 0.0065 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; He, J.; Ling, B.W.-K. Multi-Party Verifiably Collaborative Encryption for Biomedical Signals via Singular Spectrum Analysis-Based Chaotic Filter Bank Networks. Sensors 2025, 25, 3823. https://doi.org/10.3390/s25123823
Zhang X, He J, Ling BW-K. Multi-Party Verifiably Collaborative Encryption for Biomedical Signals via Singular Spectrum Analysis-Based Chaotic Filter Bank Networks. Sensors. 2025; 25(12):3823. https://doi.org/10.3390/s25123823
Chicago/Turabian StyleZhang, Xiwen, Jianfeng He, and Bingo Wing-Kuen Ling. 2025. "Multi-Party Verifiably Collaborative Encryption for Biomedical Signals via Singular Spectrum Analysis-Based Chaotic Filter Bank Networks" Sensors 25, no. 12: 3823. https://doi.org/10.3390/s25123823
APA StyleZhang, X., He, J., & Ling, B. W.-K. (2025). Multi-Party Verifiably Collaborative Encryption for Biomedical Signals via Singular Spectrum Analysis-Based Chaotic Filter Bank Networks. Sensors, 25(12), 3823. https://doi.org/10.3390/s25123823







