Detecting Important Features and Predicting Yield from Defects Detected by SEM in Semiconductor Production
Abstract
1. Introduction
1.1. Background of the Study
1.2. Problem Statement and Research Objectives
- (a)
- to find the layers (and types of defect) mostly associated with failures of dice;
- (b)
- to develop a predictive model of the electrical failures (and consequently of the yield of production) starting from the defects detected.
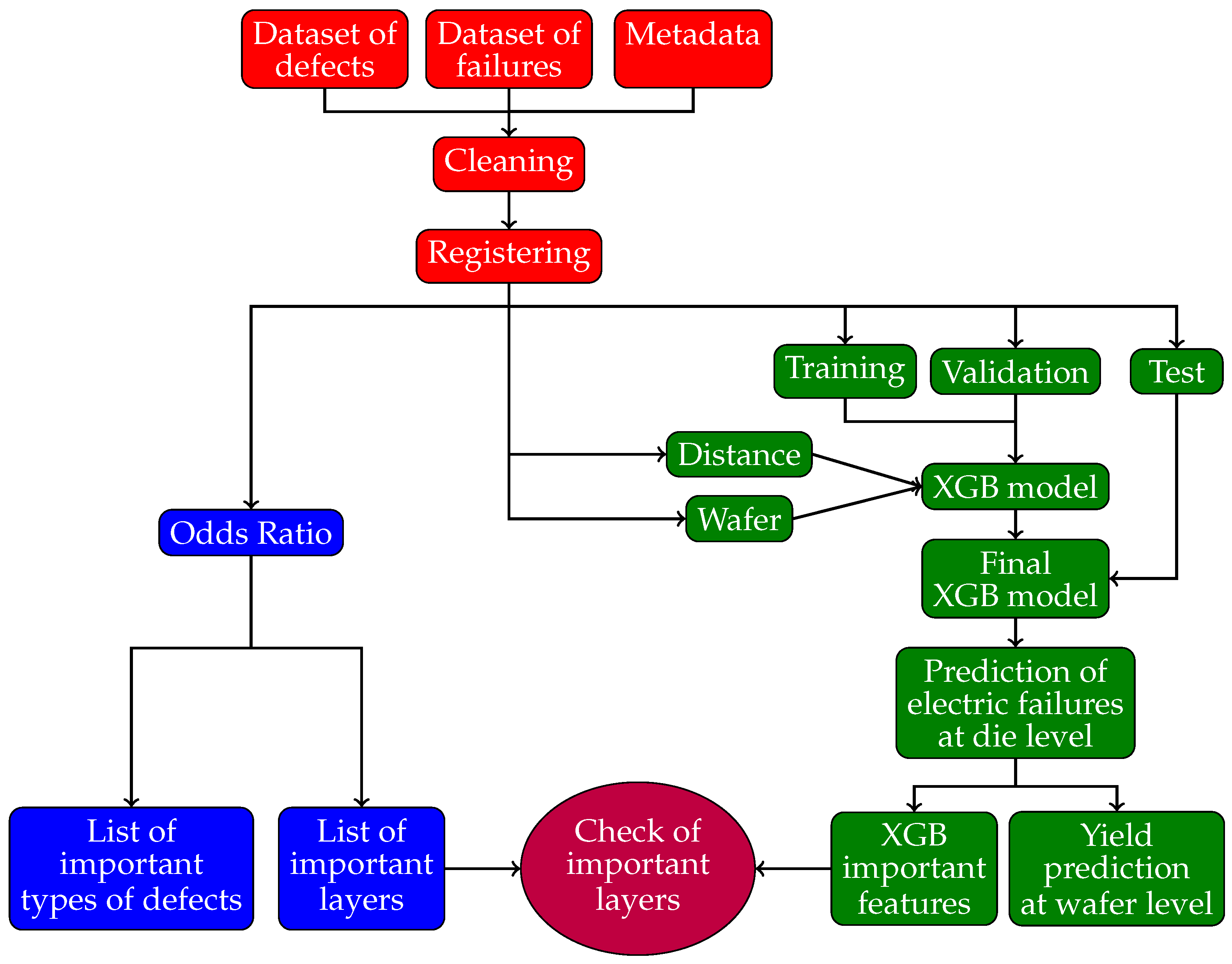
2. Research Process
- (c)
- to develop methodologies maximally noncommittal with respect to the distribution of missing data, potentially working without imputation.
3. Literature Review
4. The Dataset
- The detection of defects on a die is associated with a higher probability of failure in the final electrical test. This increase becomes notably substantial, reaching 250% for the dataset ARES and 110% for the dataset TETIS in comparison to the entire population.
- The criteria employed by STMicroelectronics process engineers for selecting layers at which to inspect wafers prove to be effective. This is evident from the resulting significantly higher rate of electrical failures observed.
- There are causes contributing to electrical failures that extend beyond those discernible through defects detected by the SEM system and the AI tools.
- Defects have not been recognized by the AI tools.
- Defects might not have been inspected at the appropriate layers. Given the low average number of inspected layers for each wafer, as detailed in Table 1, it is plausible that the layers potentially experiencing defects were not adequately inspected.
4.1. Data Collection
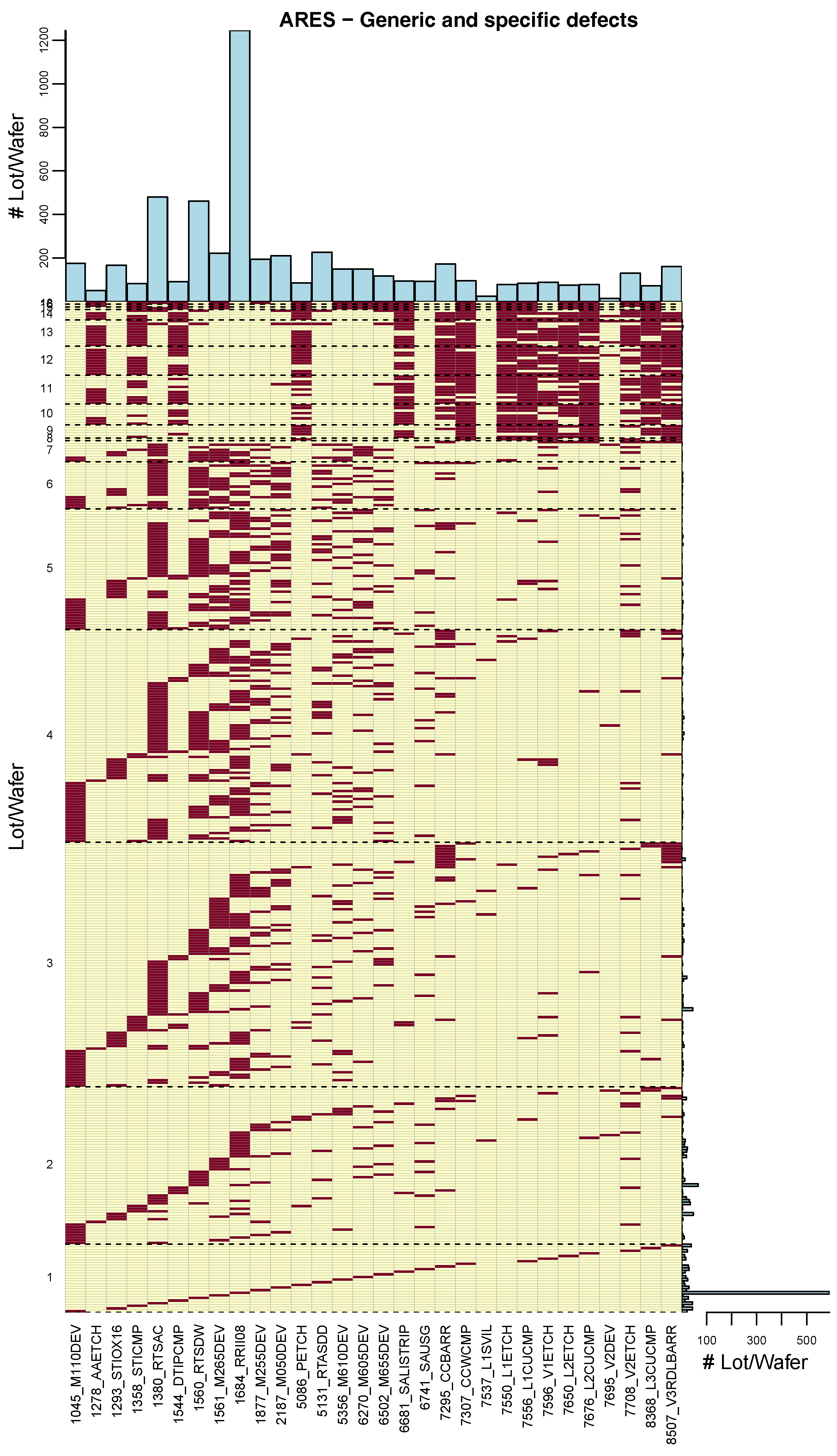
- Defect files (5589 for the dataset ARES), one for each layer and wafer of a lot, including information on defects for each die of the wafer, coordinates of dice on the wafer, and some metadata (lot, wafer, product, etc.).
- Test files (2724 for the dataset ARES), including the outcome of the final electrical tests, coordinates of dice on the wafer, and some metadata, e.g., product, layer, wafer.
- Region files (386 for the dataset ARES), including coordinates of dice on the wafer and a few metadata (e.g., layer).
4.2. Data Preprocessing
4.3. Data: Layer
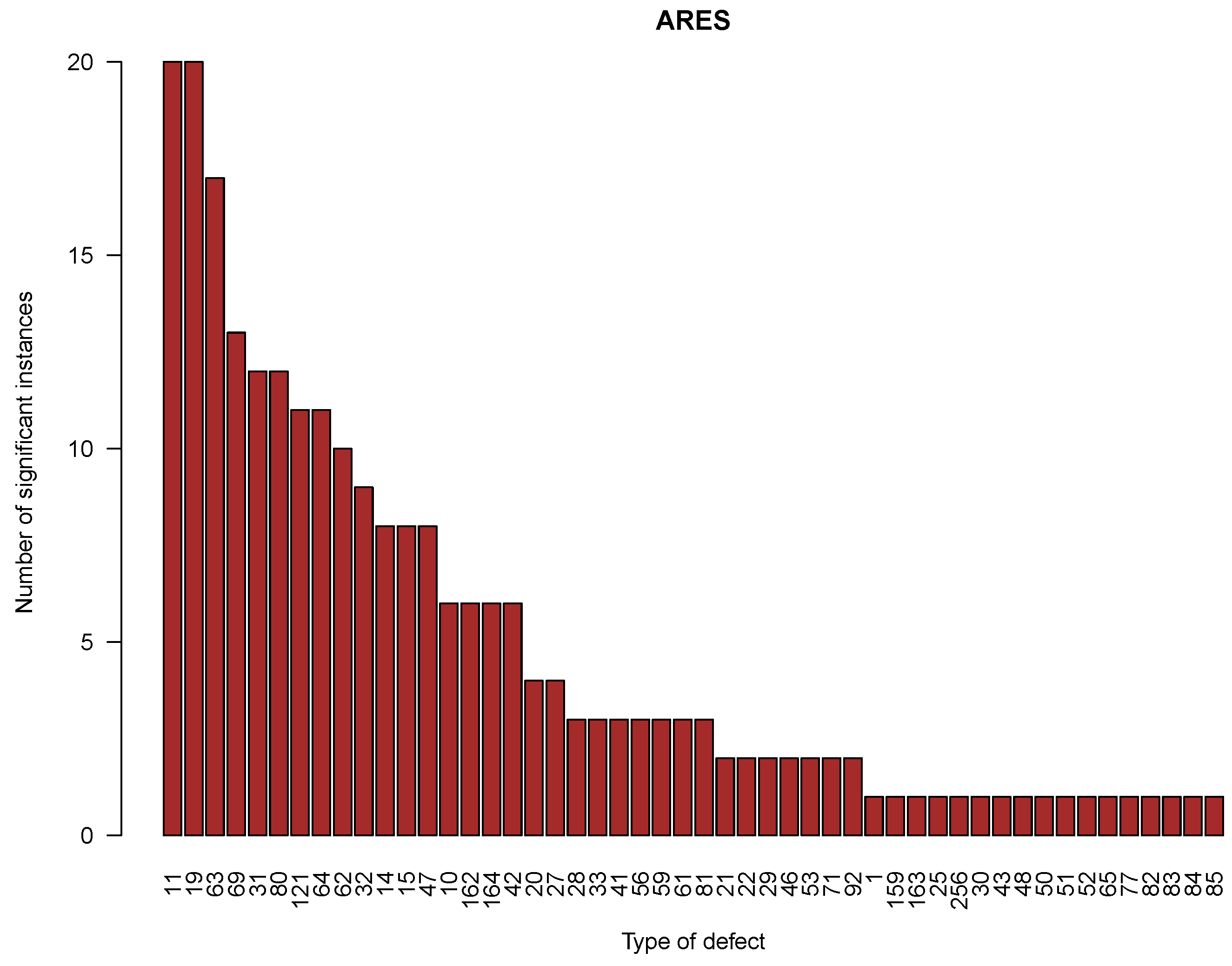
5. Odds Ratio Analysis
- (i)
- The dice with a successful final electrical test that do not exhibit any specific defect (type ) amount to 574,231 dice (91.3% of all inspected ones). Although these dice are not directly informative for identifying factors most predictive of an electrical failure, they serve as a control subset for the analysis. Furthermore, their large number indirectly confirms that defects are a reliable indicator of potential electrical failure; their absence serves as a proxy for functional dice.
- (ii)
- The dice with a failed electrical test and at least one detected specific defect of type amount to 4269, which represents 16.3% of the dice inspected having at least a specific defect of type . In practice, this is the rate of failure of the subset of dice having at least one specific defect of type , which is much higher than the overall rate for the inspected dice (4.2%).
- (iii)
- The dice with a final electrical test that was successful but with at least one specific detected defect (type ) amount to 21,923 (3.5% of the dice inspected). This subset provides information on factors that are not associated with a final electrical failure of dice.
- (iv)
- The electrically failed dice without any detected defect of any type constitute a group of 28,772 dice (4.6% of inspected dice). These are particularly challenging because there is no direct information on factors related to a final electrical failure. The failure rate within this subset is 4.8%, which is lower than the rate in the entire inspected set. The possible causes for this behavior have already been discussed in Section 4.2.
6. Prediction of Electrical Failures
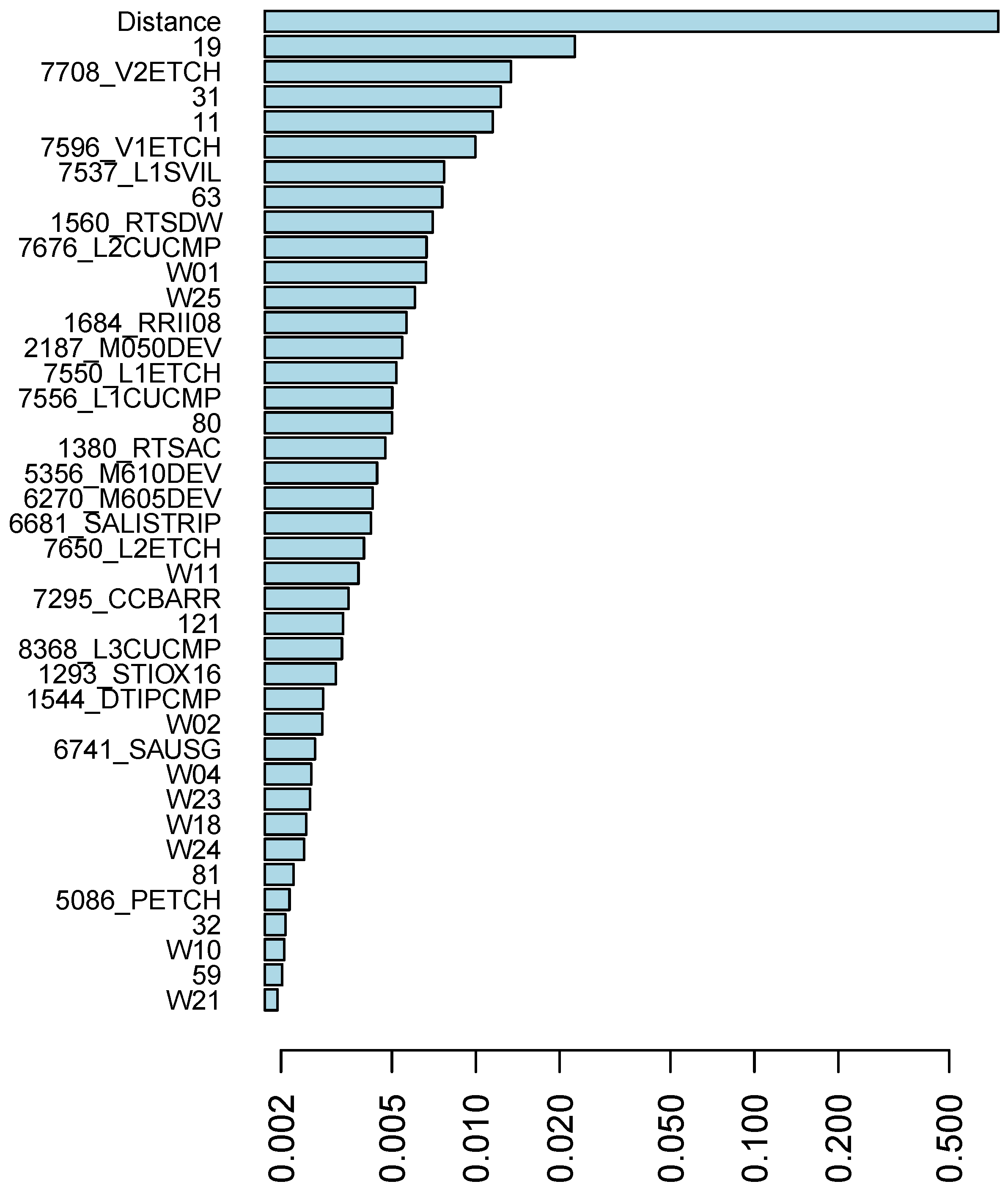
6.1. Predictor Variables
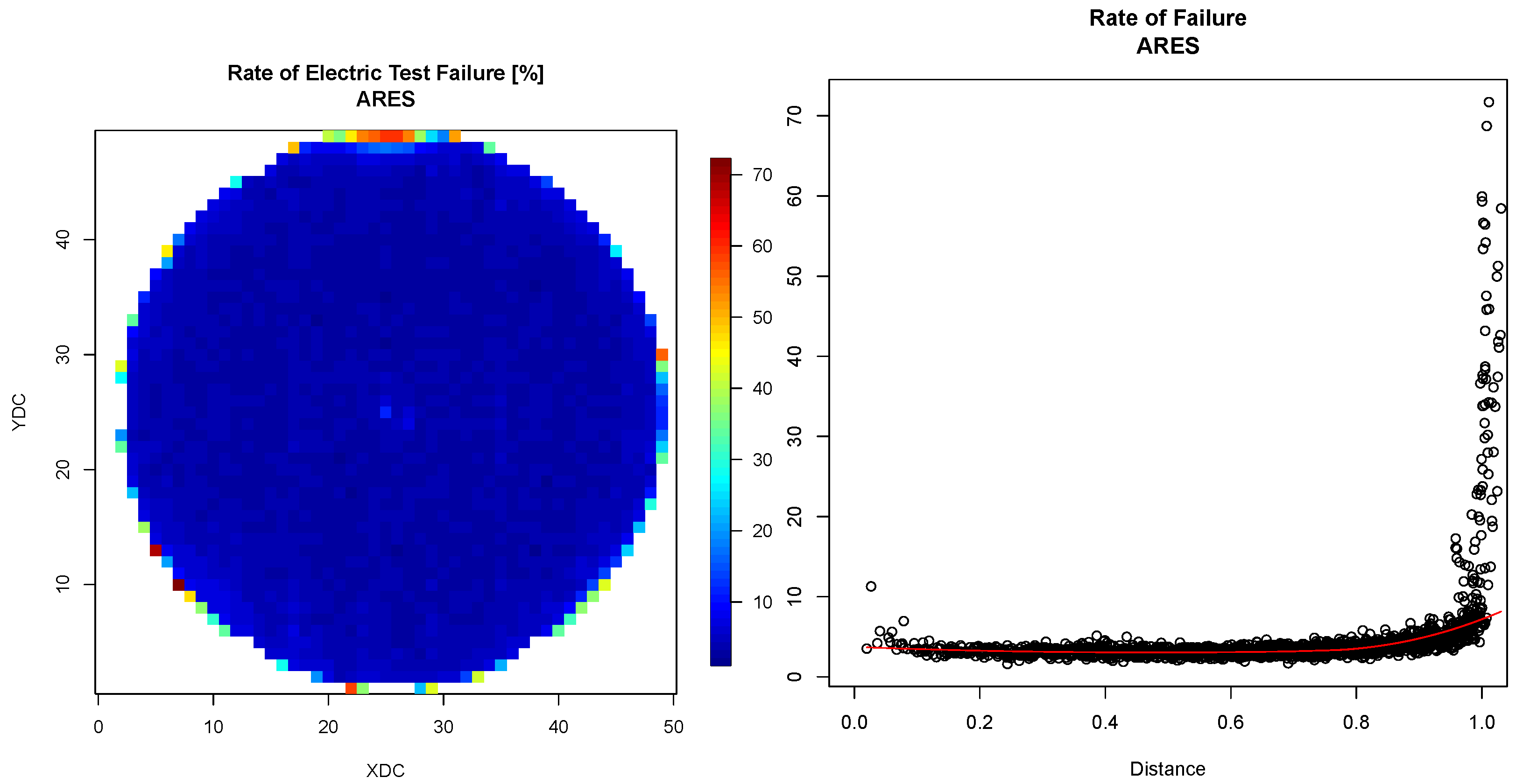
6.1.1. Wafer Slot
6.1.2. Location of Dice on the Wafer
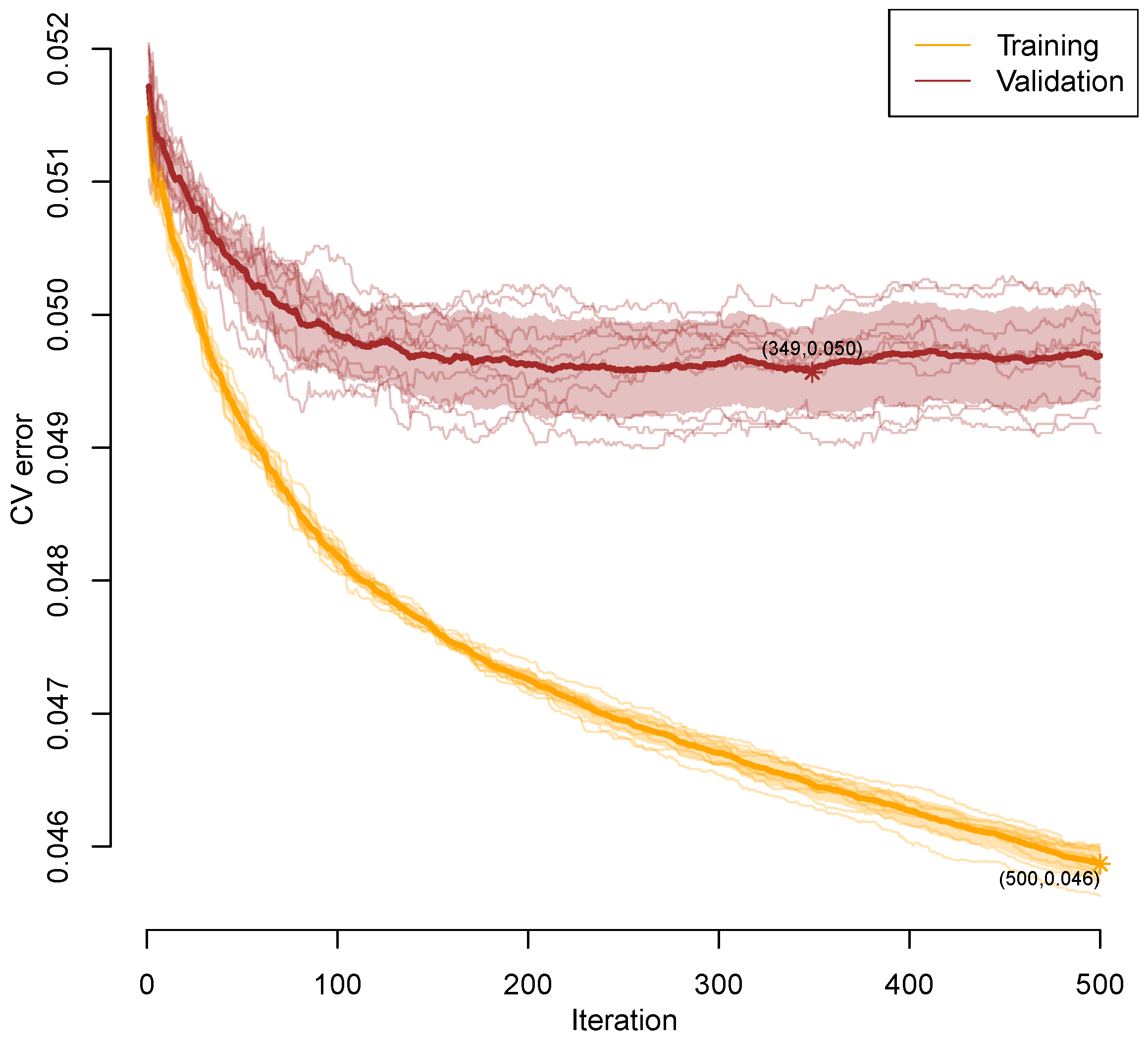
6.2. The Prediction Model—No Interaction Layer-Type of Defect
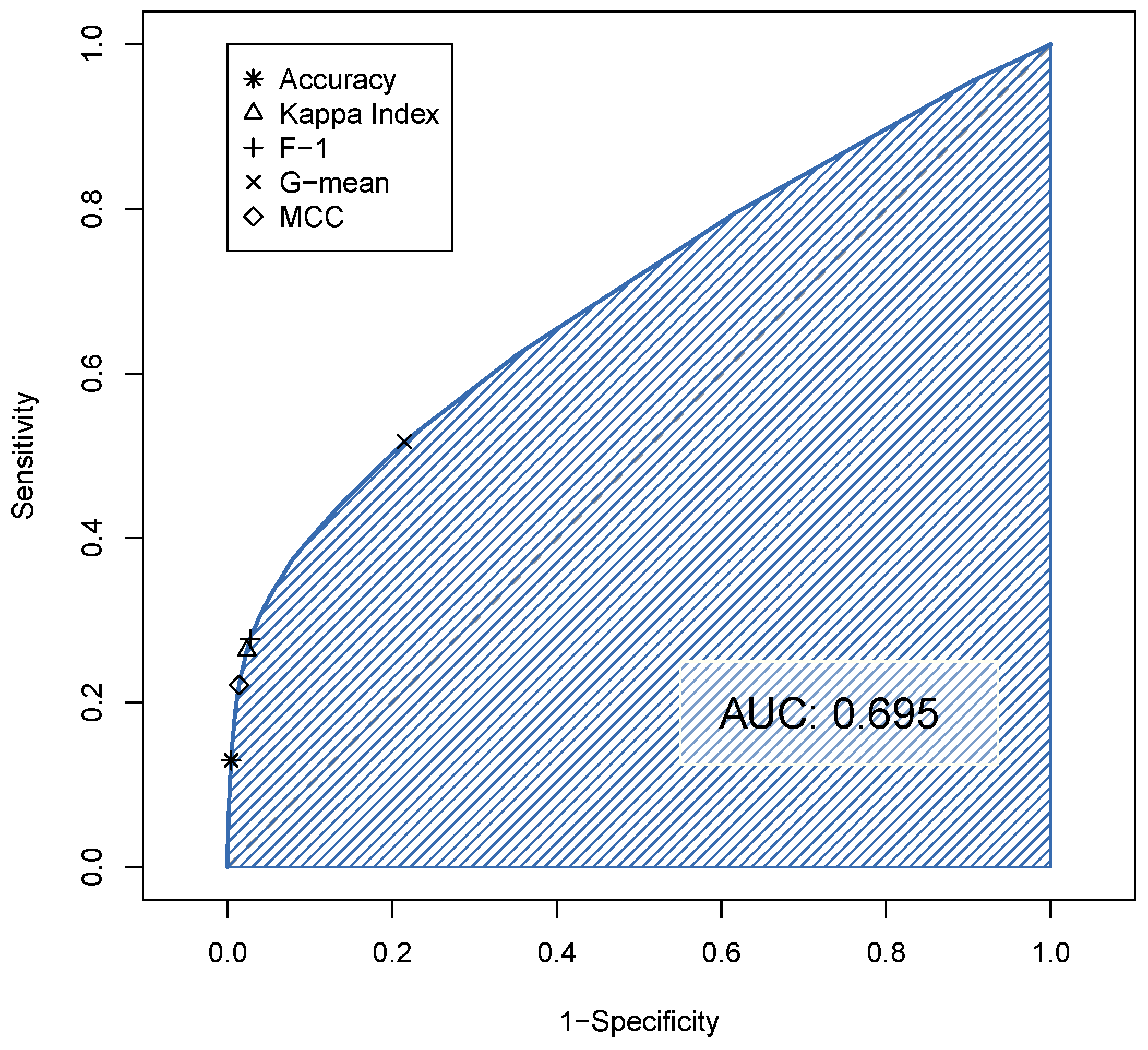
- Total accuracy [54]:
- Sensitivity and Specificity [54]:
- The Cohen kappa statistic (), a chance-corrected accuracy measure [55]:Criticism has been expressed in the literature regarding its use [56]. Also note that for a random model based only on the sample size of the classes. Therefore, negative values are possible, indicating a model that is worse than random.
- F-1 score, the harmonic mean between Precision and Recall [54], also suitable for unbalanced datasets:
- Matthews Correlation Coefficient (MCC) [58].In contrast to F-1, MCC and G-mean are symmetric indicators—their value does not change if one swaps Positives and Negatives. Recent literature [59] asserts that MCC is superior to several alternatives.
6.3. Prediction Model—With Interaction Layer-Type of Defect
6.4. Prediction Model—Yield of a Wafer
7. Discussion
7.1. Odds Ratio
7.2. Prediction
- (i)
- the low number of inspected layers (1.2 and 1.4 per wafer in the average for the datasets TETIS and ARES, respectively, when specific defects are investigated), equivalently the high fraction of missing layer data (95.3% and 96.6% for the datasets ARES and TETIS, respectively);
- (ii)
- the high fraction of electrically failed dice without any specific detected defect (see Section 4), which the model predicts as functional;
- (iii)
- the limited amount of lots and wafers, which also decreases the power of the statistical tests of this study.
8. Conclusions
8.1. Summary and Contribution
8.2. Limitations and Future Work
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| AUC | Area Under Curve |
| False Negative | |
| False Positive | |
| GB | Gradient Boosting |
| MAR | Missing At Random |
| MCAR | Missing Completely At Random |
| MCC | Matthews Correlation Coefficient |
| ROC | Receiving Operating Characteristic |
| SEM | Scanning Electron Microscope |
| True Negative | |
| True Positive | |
| XGB | eXtreme Gradient Boosting |
References
- Deloitte. 2025 Global Semiconductor Industry Outlook. 2025. Available online: https://www2.deloitte.com/us/en/insights/industry/technology/technology-media-telecom-outlooks/semiconductor-industry-outlook.html (accessed on 25 May 2025).
- Lee, T.E.; Kim, H.J.; Yu, T.S. Semiconductor manufacturing automation. In Springer Handbook of Automation; Nof, S.Y., Ed.; Springer International Publishing: Cham, Switzerland, 2023; pp. 841–863. [Google Scholar] [CrossRef]
- Zhai, W.; Han, Q.; Chen, L.; Shi, X. Explainable AutoML (xAutoML) with adaptive modeling for yield enhancement in semiconductor smart manufacturing. In Proceedings of the 2024 2nd International Conference on Artificial Intelligence and Automation Control (AIAC), Guangzhou, China, 20–22 December 2024; pp. 162–171. [Google Scholar] [CrossRef]
- Frascaroli, J.; Tonini, M.; Colombo, S.; Livellara, L.; Mariani, L.; Targa, P.; Fumagalli, R.; Samu, V.; Nagy, M.; Molnár, G.; et al. Automatic defect detection in epitaxial layers by micro photoluminescence imaging. IEEE Trans. Semicond. Manuf. 2022, 35, 540–545. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A Gradient Boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A comparative analysis of Gradient Boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Ren, L.; Wang, T.; Sekhari Seklouli, A.; Zhang, H.; Bouras, A. A review on missing values for main challenges and methods. Inf. Syst. 2023, 119, 102268. [Google Scholar] [CrossRef]
- Emmanuel, T.; Maupong, T.; Mpoeleng, D.; Semong, T.; Mphago, B.; Tabona, O. A survey on missing data in Machine Learning. J. Big Data 2021, 8, 140. [Google Scholar] [CrossRef]
- Madley-Dowd, P.; Hughes, R.; Tilling, K.; Heron, J. The proportion of missing data should not be used to guide decisions on multiple imputation. J. Clin. Epidemiol. 2019, 110, 63–73. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.H.; Huber, J.C., Jr. Evaluation of multiple imputation with large proportions of missing data: How much is too much? Iran. J. Public Health 2021, 50, 1372–1380. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Savalei, V. Three sample estimates of fraction of missing information from full information Maximum Likelihood. Front. Psychol. 2021, 12, 667802. [Google Scholar] [CrossRef]
- Lee, D.H.; Yang, J.K.; Lee, C.H.; Kim, K.J. A data-driven approach to selection of critical process steps in the semiconductor manufacturing process considering missing and imbalanced data. J. Manuf. Syst. 2019, 52, 146–156. [Google Scholar] [CrossRef]
- Park, S.; Lee, K.; Jeong, D.E.; Ko, H.K.; Lee, J. Bayesian nonparametric classification for incomplete data with a high missing rate: An application to semiconductor manufacturing data. IEEE Trans. Semicond. Manuf. 2023, 36, 170–179. [Google Scholar] [CrossRef]
- Shukla, N. An elegantly simple approach for wafer feature extraction and defect pattern recognition. In Proceedings of the 2023 International Semiconductor Conference (CAS), Sinaia, Romania, 11–13 October 2023; pp. 231–234. [Google Scholar] [CrossRef]
- Li, K.S.M.; Jiang, X.H.; Chen, L.L.Y.; Wang, S.J.; Huang, A.Y.A.; Chen, J.E.; Liang, H.C.; Hsu, C.L. Wafer defect pattern labeling and recognition using semi-supervised learning. IEEE Trans. Semicond. Manuf. 2022, 35, 291–299. [Google Scholar] [CrossRef]
- Li, K.S.M.; Chen, L.L.Y.; Liao, P.Y.Y.; Wang, S.J.; Huang, A.Y.A.; Chou, L.; Tsai, N.C.Y.; Cheng, K.C.C.; Han, G.C.H.; Lee, C.S.; et al. Wafer scratch pattern reconstruction for high diagnosis accuracy and yield optimization. IEEE Trans. Semicond. Manuf. 2022, 35, 272–281. [Google Scholar] [CrossRef]
- Yuan-Fu, Y. A Deep Learning model for identification of defect patterns in semiconductor wafer map. In Proceedings of the 2019 30th Annual SEMI Advanced Semiconductor Manufacturing Conference (ASMC), New York, NY, USA, 6–9 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Shim, J.; Kang, S.; Cho, S. Active learning of Nonvolutional Neural Network for cost-effective wafer map pattern classification. IEEE Trans. Semicond. Manuf. 2020, 33, 258–266. [Google Scholar] [CrossRef]
- Alawieh, M.B.; Boning, D.; Pan, D.Z. Wafer map defect patterns classification using deep selective learning. In Proceedings of the 2020 57th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 20–24 July 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Kang, S. Rotation-invariant wafer map pattern classification with convolutional Neural Networks. IEEE Access 2020, 8, 170650–170658. [Google Scholar] [CrossRef]
- Kong, Y.; Ni, D. A semi-supervised and incremental modeling framework for wafer map classification. IEEE Trans. Semicond. Manuf. 2020, 33, 62–71. [Google Scholar] [CrossRef]
- Song, D.; Liu, B.; Li, Y. Based on end-to-end object detection algorithm with transformers for detecting wafer maps. In Proceedings of the 2022 International Conference on Computer Network, Electronic and Automation (ICCNEA), Xi’an, China, 23–25 September 2022; pp. 297–302. [Google Scholar] [CrossRef]
- Junayed, M.; Reza, T.T.; Islam, M.S. Enhancing defect recognition: Convolutional Neural Networks for silicon wafer map analysis. In Proceedings of the 2024 3rd International Conference on Advancement in Electrical and Electronic Engineering (ICAEEE), Gazipur, Bangladesh, 24–26 February 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Shen, P.C.; Lu, M.X.; Lee, C.Y. Spatio-temporal anomaly detection for substrate strip bin map in semiconductor assembly process. IEEE Robot. Autom. Lett. 2022, 7, 9493–9500. [Google Scholar] [CrossRef]
- Jen, E.; Ting, Y.; Chen, B.; Jan, C.; Huang, L.; Lin, C.; Wu, M.; Feng, A.; Wen, C.; Chen, H.; et al. Using BERT pre-trained image transformers to identify potential parametric wafer map defects. In Proceedings of the 2024 35th Annual SEMI Advanced Semiconductor Manufacturing Conference (ASMC), Albany, NY, USA, 13–16 May 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Mishra, A.; Shaik, M.E.; Lingamoorthy, A.; Kumar, S.; Das, A.; Kandasamy, N.; Touba, N.A. WaferCap: Open classification of wafer map patterns using Deep Capsule Network. In Proceedings of the 2024 IEEE 42nd VLSI Test Symposium (VTS), Tempe, AZ, USA, 22–24 April 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Yu, J. Fault detection using principal components-based Gaussian Mixture Model for semiconductor manufacturing processes. IEEE Trans. Semicond. Manuf. 2011, 24, 432–444. [Google Scholar] [CrossRef]
- Baly, R.; Hajj, H. Wafer classification using Support Vector Machines. IEEE Trans. Semicond. Manuf. 2012, 25, 373–383. [Google Scholar] [CrossRef]
- Stich, P.; Wahl, M.; Czerner, P.; Weber, C.; Fathi, M. Yield prediction in semiconductor manufacturing using an AI-based cascading classification system. In Proceedings of the 2020 IEEE International Conference on Electro Information Technology (EIT), Chicago, IL, USA, 31 July–1 August 2020; pp. 609–614. [Google Scholar] [CrossRef]
- Fan, A.; Huang, Y.; Xu, F.; Bom, S. Soft-sensing regression model: From sensor to wafer metrology forecasting. Sensors 2023, 23, 8363. [Google Scholar] [CrossRef]
- Lee, Y.; Roh, Y. An expandable yield prediction framework using explainable Artificial Intelligence for semiconductor manufacturing. Appl. Sci. 2023, 13, 2660. [Google Scholar] [CrossRef]
- Han, Q.; Xia, Y.; Shi, X.; Zeng, Z. AutoML with focal loss for defect diagnosis and prognosis in smart manufacturing. In Proceedings of the 2023 IEEE International Conference on Cybernetics and Intelligent Systems (CIS) and IEEE Conference on Robotics, Automation and Mechatronics (RAM), Penang, Malaysia, 9–12 June 2023; pp. 180–185. [Google Scholar] [CrossRef]
- Park, H.J.; Koo, Y.S.; Yang, H.Y.; Han, Y.S.; Nam, C.S. Study on data preprocessing for Machine Learning based on semiconductor manufacturing processes. Sensors 2024, 24, 5461. [Google Scholar] [CrossRef] [PubMed]
- Jiang, D.; Lin, W.; Raghavan, N. A novel framework for semiconductor manufacturing final test yield classification using Machine Learning techniques. IEEE Access 2020, 8, 197885–197895. [Google Scholar] [CrossRef]
- Vankayalapati, R.K.; Yasmeen, Z.; Bansal, A.; Dileep, V.; Abhireddy, N. Advanced fault detection in semiconductor manufacturing processes using improved AdaBoost RT model. In Proceedings of the 2024 9th International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 16–18 December 2024; pp. 467–472. [Google Scholar] [CrossRef]
- Chu, S.L.; Su, E.; Ho, C.C. Transfer learning-based defect detection system on wafer surfaces. IEEE Trans. Semicond. Manuf. 2025, 38, 154–167. [Google Scholar] [CrossRef]
- Yeh, C.H.; Chen, C.H.; Wu, F.C.; Chen, K.Y.C. Validation and evaluation for defect-kill-rate and yield estimation models in semiconductor manufacturing. Int. J. Prod. Res. 2007, 45, 829–844. [Google Scholar] [CrossRef]
- Nutsch, A.; Oechsner, R.; Schoepka, U.; Pfitzner, L. Yield model for estimation of yield impact of semiconductor manufacturing equipment. In Proceedings of the 2010 International Symposium on Semiconductor Manufacturing (ISSM), Tokyo, Japan, 18–20 October 2010; pp. 1–4. [Google Scholar]
- Kang, S.; Cho, S.; An, D.; Rim, J. Using wafer map features to better predict die-level failures in final test. IEEE Trans. Semicond. Manuf. 2015, 28, 431–437. [Google Scholar] [CrossRef]
- Kong, Y.; Ni, D. A practical yield prediction approach using inline defect metrology data for system-on-chip integrated circuits. In Proceedings of the 2017 13th IEEE Conference on Automation Science and Engineering (CASE), Xi’an, China, 20–23 August 2017; pp. 744–749. [Google Scholar] [CrossRef]
- Lenhard, P.; Kovalenko, A.; Lenhard, R. Integrated circuit die level yield prediction using Deep Learning. In Proceedings of the 2022 33rd Annual SEMI Advanced Semiconductor Manufacturing Conference (ASMC), New York, NY, USA, 2–5 May 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Baron, M.; Yashchin, E.; Takken, A. Introduction to wafer tomography: Likelihood-based prediction of integrated-circuit yield. In Artificial Intelligence, Big Data and Data Science in Statistics: Challenges and Solutions in Environmetrics, the Natural Sciences and Technology; Steland, A., Tsui, K.L., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 227–252. [Google Scholar] [CrossRef]
- Baron, M.; Takken, A.; Yashchin, E.; Lanzerotti, M. Factorial Analysis and Forecasting of Integrated-Circuit Yield. Research Report RC23386 (W0410-131). IBM. 2004. Available online: https://dominoweb.draco.res.ibm.com/4464e3eff3607a7b85256f35006729db.html (accessed on 25 May 2025).
- Baron, M.; Takken, A.; Yashchin, E.; Lanzerotti, M. Modeling and forecasting of defect-limited yield in semiconductor manufacturing. IEEE Trans. Semicond. Manuf. 2008, 21, 614–624. [Google Scholar] [CrossRef]
- Nurani, R.; Akella, R.; Strojwas, A. In-line defect sampling methodology in yield management: An integrated framework. IEEE Trans. Semicond. Manuf. 1996, 9, 506–517. [Google Scholar] [CrossRef]
- Rothman, K.J. Epidemiology: An Introduction, 2nd ed.; Oxford University Press: New York, NY, USA, 2012; Available online: https://books.google.com.sg/books?id=tKs7adtH-_IC&printsec=frontcover#v=onepage&q&f=false (accessed on 25 May 2025).
- Rothman, K.J.; Greenland, S.; Lash, T.L. Modern Epidemiology, 3rd ed.; Wolters Kluwer Health/Lippincott Williams & Wilkins Philadelphia: Philadelphia, PA, USA, 2008. [Google Scholar]
- Benjamini, Y.; Hochberg, Y. Controlling the False Discovery Rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B (Methodol.) 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Calabrese, R. Optimal cut-off for rare events and unbalanced misclassification costs. J. Appl. Stat. 2014, 41, 1678–1693. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Measuring performance in classification models. In Applied Predictive Modeling; Springer: New York, NY, USA, 2013; pp. 247–273. [Google Scholar] [CrossRef]
- Vanacore, A.; Pellegrino, M.S.; Ciardiello, A. Fair evaluation of classifier predictive performance based on binary confusion matrix. Comput. Stat. 2022, 39, 363–383. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The Matthews Correlation Coefficient (MCC) is more informative than Cohen’s Kappa and Brier score in binary classification assessment. IEEE Access 2021, 9, 78368–78381. [Google Scholar] [CrossRef]
- Foody, G.M. Explaining the unsuitability of the kappa coefficient in the assessment and comparison of the accuracy of thematic maps obtained by image classification. Remote Sens. Environ. 2020, 239, 111630. [Google Scholar] [CrossRef]
- Cios, K.J.; Swiniarski, R.W.; Pedrycz, W.; Kurgan, L.A. Data Mining: A Knowledge Discovery Approach, 1st ed.; Springer: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Matthews, B.W. Comparison of the predicted and observed secondary structure of T4 phage lysozyme. Biochim. Biophys. Acta (BBA)-Protein Struct. 1975, 405, 442–451. [Google Scholar] [CrossRef]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 6. [Google Scholar] [CrossRef]
- Boldini, D.; Friedrich, L.; Kuhn, D.; Sieber, S.A. Tuning Gradient Boosting for imbalanced bioassay modelling with custom loss functions. J. Cheminform. 2022, 14, 80. [Google Scholar] [CrossRef]
- Luo, J.; Yuan, Y.; Xu, S. Improving GBDT performance on imbalanced datasets: An empirical study of class-balanced loss functions. Neurocomputing 2025, 634, 129896. [Google Scholar] [CrossRef]





| ARES | TETIS | |
|---|---|---|
| Number of lots | 126 | 120 |
| Total number of wafers | 2242 | 2028 |
| Number of dice | 4,075,773 | 2,283,223 |
| Number of dice per wafer | 1818 | 1126 |
| Number of types of defects | 72 | 75 |
| Number of defects detected | 1,002,480 (1 defects every four dice in the average) | 448,571 (1 defect every five dice in the average) |
| Number of defects of type | 974,092 (97.1% of all defects) | 428,590 (95.5% of all defects) |
| Number of defects of type | 28,888 (2.9% of all defects) | 19,981 (4.4% of all defects) |
| Number of layers | 30 | 35 |
| Average number of inspected layers per wafer | 2.4 | 2.3 |
| Average number of layers per wafer inspected for specific defects (type | 1.4 | 1.2 |
| Inspected dice (type ) | 629,195 (15.4% of total dice) | 368,148 (16.1% of total dice) |
| Inspected dice with at least one defect (type ) | 26,192 (4.2% of inspected dice) | 18,699 (5.1% of inspected dice) |
| Inspected faulty dice (type ) | 33,041 (5.3% of investigated dice–failure rate) | 34,021 (9.2% of investigated dice–failure rate) |
| Inspected faulty dice with at least one defect (type ) | 4269 (0.7% of inspected dice; failure rate with respect to inspected dice with at least one defect (type ): 16.3%) | 3557 (1.0% of inspected dice; failure rate with respect to inspected dice with at least one defect (type ): 19.0%) |
| Inspected faulty dice with no defect (type ) | 28,772 (4.6% of inspected dice; failure rate with respect to inspected dice without defects (type ): 4.8%) | 30,464 (8.3% of inspected dice; failure rate with respect to inspected dice without defects (type ): 8.7%) |
| Inspected functional dice with at least one defect (type ) | 21,923 (3.5% of inspected dice) | 15,142 (4.1% of inspected dice) |
| Inspected functional dice with no defect (type ) | 574,231 (91.3% of inspected dice) | 318,985 (86.6% of inspected dice) |
| Inspected dice with at least one defect (type ) | 836,294 (20.5% of inspected dice) | 338,127 (14.8% of inspected dice) |
| Inspected faulty dice (type ) | 191,942 (4.7% of investigated dice–failure rate) | 207,524 (9.1% of investigated dice–failure rate) |
| Inspected faulty dice with at least one defect (type ) | 56,536 (1.4% of inspected dice; failure rate with respect to inspected dice with at least one defect (type ): 6.8%) | 44,760 (2.0% of inspected dice; failure rate with respect to inspected dice with at least one defect (type ): 13.2%) |
| Inspected faulty dice with no defect (type ) | 135,406 (3.3% of inspected dice; failure rate with respect to inspected dice without defects (type ): 4.2%) | 162,764 (7.1% of inspected dice; failure rate with respect to inspected dice without defects (type ): 8.3%) |
| Inspected functional dice with at least one defect (type ) | 779,758 (19.1% of inspected dice) | 293,367 (12.8% of inspected dice) |
| Inspected functional dice with no defect (type ) | 310,4073 (76.2% of inspected dice) | 1,782,332 (78.1% of inspected dice) |
| Outcome Failed Die () | Outcome Functional Die () | |
|---|---|---|
| Number of dice with defects detected of a certain type or at a certain layer () | ||
| Number of dice with no defects detected of a certain type or layer ( |
| Layer | Number of Dice | Failure Defects | No Failure Defects | Failure No Defects | No Failure No Defects | Failure Rate (All Dice) | Failure Rate (with Defects) | Odds Ratio | p-Value (Adjusted) |
|---|---|---|---|---|---|---|---|---|---|
| 1358_STICMP | 10,896 | 98 | 175 | 525 | 10,098 | 0.057 | 0.359 | 10.772 | 0 |
| 7550_L1ETCH | 16,335 | 160 | 291 | 644 | 15,240 | 0.049 | 0.355 | 13.011 | 0 |
| 5356_M610DEV | 14,536 | 134 | 275 | 746 | 13,381 | 0.061 | 0.328 | 8.742 | 0 |
| 7676_L2CUCMP | 23,595 | 221 | 481 | 1293 | 21,600 | 0.064 | 0.315 | 7.677 | 0 |
| 6502_M655DEV | 9085 | 72 | 172 | 417 | 8424 | 0.054 | 0.295 | 8.461 | 0 |
| 8368_L3CUCMP | 32,778 | 257 | 701 | 1500 | 30,320 | 0.054 | 0.268 | 7.412 | 0 |
| 7650_L2ETCH | 23,556 | 187 | 515 | 1005 | 21,849 | 0.051 | 0.266 | 7.896 | 0 |
| 7295_CCBARR | 58,080 | 404 | 1493 | 2551 | 53,632 | 0.051 | 0.213 | 5.69 | 0 |
| 7556_L1CUCMP | 67,155 | 429 | 1733 | 2805 | 62,188 | 0.048 | 0.198 | 5.489 | 0 |
| 1380_RTSAC | 23,621 | 106 | 456 | 1125 | 21,934 | 0.052 | 0.189 | 4.537 | 0 |
| 1684_RRII08 | 47,216 | 166 | 716 | 2412 | 43,922 | 0.055 | 0.188 | 4.225 | 0 |
| 7596_V1ETCH | 72,480 | 538 | 2449 | 3363 | 66,130 | 0.054 | 0.180 | 4.321 | 0 |
| 6741_SAUSG | 21,804 | 119 | 548 | 1045 | 20,092 | 0.053 | 0.178 | 4.179 | 0 |
| 7695_V2DEV | 12,684 | 82 | 415 | 492 | 11,695 | 0.045 | 0.165 | 4.702 | 0 |
| 5086_PETCH | 27,180 | 149 | 830 | 1186 | 25,015 | 0.049 | 0.152 | 3.789 | 0 |
| 6270_M605DEV | 39,974 | 176 | 1019 | 1913 | 36,866 | 0.052 | 0.147 | 3.331 | 0 |
| 6681_SALISTRIP | 27,180 | 148 | 861 | 1437 | 24,734 | 0.058 | 0.147 | 2.961 | 0 |
| 1544_DTIPCMP | 47,112 | 218 | 1283 | 1946 | 43,665 | 0.046 | 0.145 | 3.815 | 0 |
| 1560_RTSDW | 36,340 | 141 | 894 | 1936 | 33,369 | 0.057 | 0.136 | 2.721 | 0 |
| 2187_M050DEV | 56,327 | 203 | 1296 | 2765 | 52,063 | 0.053 | 0.135 | 2.951 | 0 |
| 7708_V2ETCH | 139,524 | 726 | 4654 | 6582 | 127,562 | 0.052 | 0.135 | 3.024 | 0 |
| 1278_AAETCH | 5436 | 36 | 153 | 213 | 5034 | 0.046 | 0.190 | 5.574 | 1.20 × 10−13 |
| 7537_L1SVIL | 3610 | 16 | 13 | 322 | 3259 | 0.094 | 0.552 | 12.409 | 7.60 × 10−10 |
| 1877_M255DEV | 7268 | 17 | 38 | 358 | 6855 | 0.052 | 0.309 | 8.604 | 1.40 × 10−9 |
| 1293_STIOX16 | 3634 | 30 | 107 | 232 | 3265 | 0.072 | 0.219 | 3.957 | 2.40 × 10−8 |
| 7307_CCWCMP | 3624 | 16 | 58 | 134 | 3416 | 0.041 | 0.216 | 7.07 | 3.70 × 10−8 |
| 5131_RTASDD | 1817 | 11 | 38 | 62 | 1706 | 0.04 | 0.224 | 8.014 | 2.20 × 10−6 |
| 1045_M110DEV | 9085 | 16 | 83 | 371 | 8615 | 0.043 | 0.162 | 4.511 | 4.90 × 10−6 |
| 1561_M265DEV | 10,902 | 23 | 208 | 521 | 10,150 | 0.05 | 0.100 | 2.167 | 0.002 |
| 8507_V3RDLBARR | 30,855 | 64 | 963 | 1504 | 28,324 | 0.051 | 0.062 | 1.254 | 0.095 |
| Type of Defect | Number of Dice | Failure Defects | No Failure Defects | Failure No Defects | No Failure No Defects | Failure Rate (All Dice) | Failure Rate (with Defects) | Odds Ratio | p-Value (Adjusted) |
|---|---|---|---|---|---|---|---|---|---|
| 256 | 62,9195 | 1 | 0 | 33,040 | 596,154 | 0.053 | 1 | – | – |
| 48 | 629,195 | 1 | 0 | 33,040 | 596,154 | 0.053 | 1 | – | – |
| 51 | 629,195 | 1 | 0 | 33,040 | 596,154 | 0.053 | 1 | – | – |
| 52 | 629,195 | 1 | 0 | 33,040 | 596,154 | 0.053 | 1 | – | – |
| 65 | 629,195 | 1 | 0 | 33,040 | 596,154 | 0.053 | 1 | – | – |
| 62 | 629,195 | 58 | 19 | 32,983 | 596,135 | 0.053 | 0.753 | 54.852 | 0 |
| 47 | 629,195 | 106 | 64 | 32,935 | 596,090 | 0.053 | 0.624 | 29.945 | 0 |
| 15 | 629,195 | 37 | 29 | 33,004 | 596,125 | 0.053 | 0.561 | 23.016 | 0 |
| 63 | 629,195 | 340 | 332 | 32,701 | 595,822 | 0.053 | 0.506 | 18.659 | 0 |
| 121 | 629,195 | 58 | 58 | 32,983 | 596,096 | 0.053 | 0.5 | 18.073 | 0 |
| 164 | 629,195 | 27 | 30 | 33,014 | 596,124 | 0.053 | 0.474 | 16.261 | 0 |
| 31 | 629,195 | 195 | 250 | 32,846 | 595,904 | 0.053 | 0.438 | 14.154 | 0 |
| 69 | 629,195 | 129 | 199 | 32,912 | 595,955 | 0.053 | 0.393 | 11.743 | 0 |
| 64 | 629,195 | 61 | 105 | 32,980 | 596,049 | 0.053 | 0.367 | 10.511 | 0 |
| 53 | 629,195 | 160 | 325 | 32,881 | 595,829 | 0.053 | 0.33 | 8.926 | 0 |
| 10 | 629,195 | 33 | 68 | 33,008 | 596,086 | 0.053 | 0.327 | 8.786 | 0 |
| 80 | 629,195 | 352 | 728 | 32,689 | 595,426 | 0.053 | 0.326 | 8.809 | 0 |
| 14 | 629,195 | 103 | 230 | 32,938 | 595,924 | 0.053 | 0.309 | 8.109 | 0 |
| 19 | 629,195 | 505 | 1292 | 32,536 | 594,862 | 0.053 | 0.281 | 7.148 | 0 |
| 59 | 629,195 | 163 | 508 | 32,878 | 595,646 | 0.053 | 0.243 | 5.817 | 0 |
| 11 | 629,195 | 1235 | 3943 | 31,806 | 592,211 | 0.053 | 0.239 | 5.832 | 0 |
| 27 | 629,195 | 69 | 320 | 32,972 | 595,834 | 0.053 | 0.177 | 3.904 | 0 |
| 81 | 629,195 | 134 | 832 | 32,907 | 595,322 | 0.053 | 0.139 | 2.917 | 0 |
| 33 | 629,195 | 240 | 2185 | 32,801 | 593,969 | 0.053 | 0.099 | 1.99 | 0 |
| 32 | 629,195 | 290 | 2738 | 32,751 | 593,416 | 0.053 | 0.096 | 1.92 | 0 |
| 61 | 629,195 | 12 | 1 | 33,029 | 596,153 | 0.053 | 0.923 | 191.472 | 1.30 × 10−14 |
| 162 | 629,195 | 14 | 5 | 33,027 | 596,149 | 0.053 | 0.737 | 49.526 | 2.70 × 10−14 |
| 29 | 629,195 | 17 | 14 | 33,024 | 596,140 | 0.053 | 0.548 | 21.875 | 5.50 × 10−14 |
| 1 | 629,195 | 16 | 14 | 33,025 | 596,140 | 0.053 | 0.533 | 20.6 | 5.50 × 10−13 |
| 163 | 629,195 | 13 | 8 | 33,028 | 596,146 | 0.053 | 0.619 | 29.106 | 6.90 × 10−12 |
| 21 | 629,195 | 24 | 68 | 33,017 | 596,086 | 0.053 | 0.261 | 6.4 | 1.10 × 10−10 |
| 41 | 629,195 | 53 | 324 | 32,988 | 595,830 | 0.053 | 0.141 | 2.962 | 2.60 × 10−10 |
| 42 | 629,195 | 214 | 2430 | 32,827 | 593,724 | 0.053 | 0.081 | 1.594 | 1.80 × 10−9 |
| 28 | 629,195 | 10 | 8 | 33,031 | 596,146 | 0.053 | 0.556 | 22.47 | 9.00 × 10−9 |
| 85 | 629,195 | 7 | 2 | 33,034 | 596,152 | 0.053 | 0.778 | 59.946 | 6.50 × 10−8 |
| 82 | 629,195 | 31 | 189 | 33,010 | 595,965 | 0.053 | 0.141 | 2.974 | 1.40 × 10−6 |
| 56 | 629,195 | 173 | 2074 | 32,868 | 594,080 | 0.053 | 0.077 | 1.509 | 1.60 × 10−6 |
| 83 | 629,195 | 28 | 162 | 33,013 | 595,992 | 0.053 | 0.147 | 3.136 | 1.80 × 10−6 |
| 50 | 629,195 | 10 | 20 | 33,031 | 596,134 | 0.053 | 0.333 | 9.097 | 3.10 × 10−6 |
| 20 | 629,195 | 9 | 24 | 33,032 | 596,130 | 0.053 | 0.273 | 6.844 | 6.30 × 10−5 |
| 46 | 629,195 | 65 | 773 | 32,976 | 595,381 | 0.053 | 0.078 | 1.522 | 0.003 |
| 36 | 629,195 | 44 | 1178 | 32,997 | 594,976 | 0.053 | 0.036 | 0.676 | 0.01 |
| 71 | 629,195 | 3 | 5 | 33,038 | 596,149 | 0.053 | 0.375 | 11.045 | 0.01 |
| 22 | 629,195 | 6 | 27 | 33,035 | 596,127 | 0.053 | 0.182 | 4.094 | 0.011 |
| 77 | 629,195 | 3 | 6 | 33,038 | 596,148 | 0.053 | 0.333 | 9.251 | 0.014 |
| 92 | 629,195 | 2 | 2 | 33,039 | 596,152 | 0.053 | 0.5 | 18.044 | 0.021 |
| 84 | 629,195 | 10 | 79 | 33,031 | 596,075 | 0.053 | 0.112 | 2.317 | 0.032 |
| 115 | 629,195 | 2 | 4 | 33,039 | 596,150 | 0.053 | 0.333 | 9.351 | 0.047 |
| 999 | 629,195 | 7 | 53 | 33,034 | 596,101 | 0.053 | 0.117 | 2.431 | 0.06 |
| 43 | 629,195 | 22 | 252 | 33,019 | 595,902 | 0.053 | 0.08 | 1.586 | 0.061 |
| 159 | 629,195 | 24 | 293 | 33,017 | 595,861 | 0.053 | 0.076 | 1.488 | 0.089 |
| 30 | 629,195 | 1 | 1 | 33,040 | 596,153 | 0.053 | 0.5 | 18.043 | 0.118 |
| 25 | 629,195 | 10 | 104 | 33,031 | 596,050 | 0.053 | 0.088 | 1.761 | 0.127 |
| 72 | 629,195 | 1 | 3 | 33,040 | 596,151 | 0.053 | 0.25 | 6.552 | 0.222 |
| 95 | 629,195 | 1 | 3 | 33,040 | 596,151 | 0.053 | 0.25 | 6.552 | 0.222 |
| 37 | 629,195 | 47 | 756 | 32,994 | 595,398 | 0.053 | 0.059 | 1.126 | 0.457 |
| 136 | 629,195 | 2 | 61 | 33,039 | 596,093 | 0.053 | 0.032 | 0.636 | 0.51 |
| 40 | 629,195 | 1 | 31 | 33,040 | 596,123 | 0.053 | 0.031 | 0.664 | 0.672 |
| 0 | 4,075,773 | 56,536 | 779,758 | 135,406 | 3,104,073 | 0.047 | 0.068 | 1.662 | 0 |
| Predictor | Type | ARES | TETIS |
|---|---|---|---|
| Number of defects at each layer | Continuous a | 30 | 35 |
| Number of defects for each type | Continuous a | 72 | 75 |
| Number of defects at each layer for each type | Continuous a | 2160 | 2625 |
| Wafer slot | Categorical | 25 b | 25 b |
| Distance | Continuous | 1 (range [0, 1]) | 1 (range [0, 1]) |
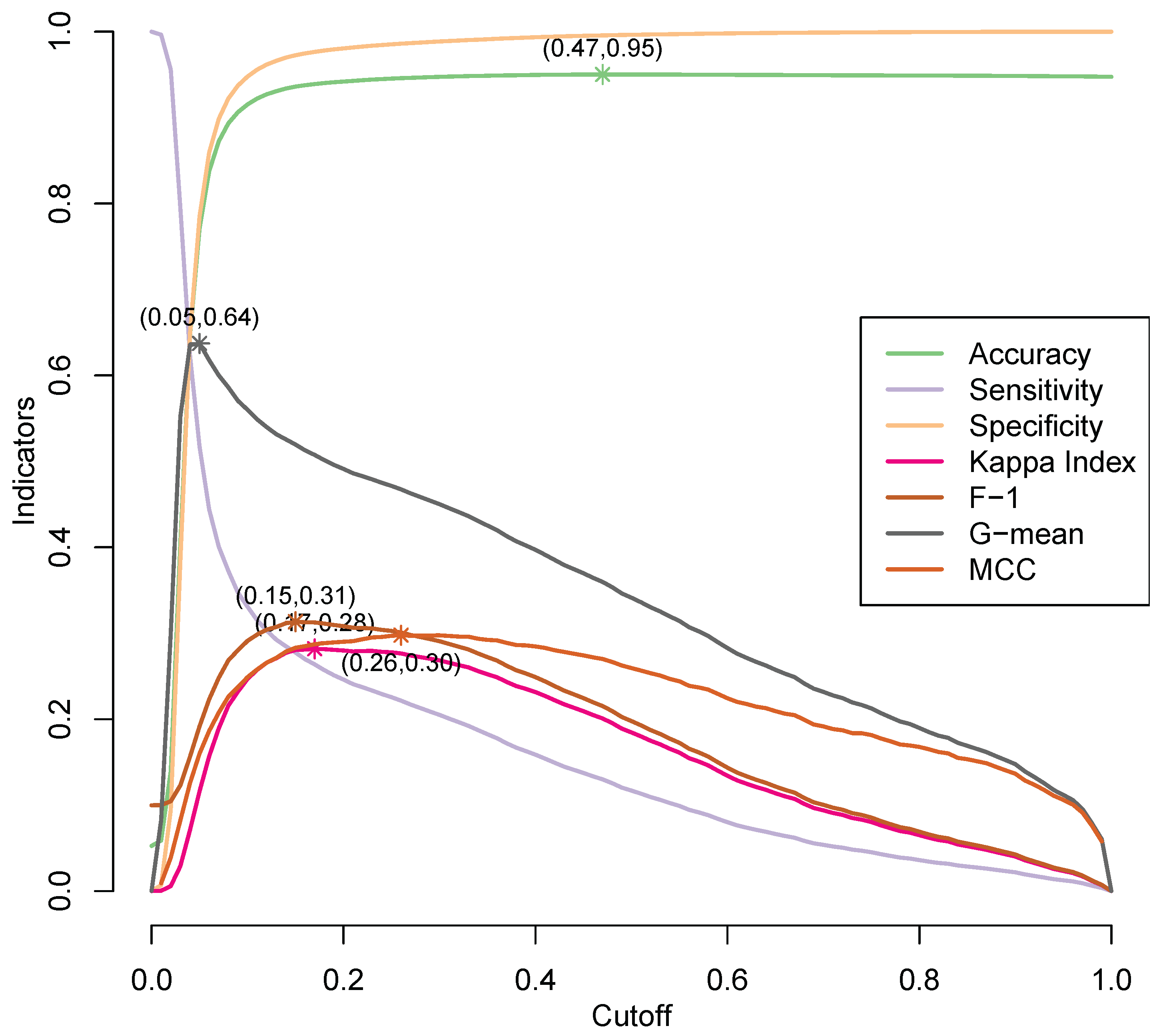
| Indicator | Cutoff | Sensitivity | Specificity | Accuracy | Coefficient | F-1 | G-Mean | MCC |
|---|---|---|---|---|---|---|---|---|
| Accuracy | 0.47 | 0.130 | 0.996 | 0.950 | 0.200 | 0.215 | 0.340 | 0.270 |
| coefficient | 0.17 | 0.264 | 0.977 | 0.939 | 0.282 | 0.313 | 0.507 | 0.287 |
| F-1 | 0.15 | 0.278 | 0.973 | 0.936 | 0.281 | 0.313 | 0.520 | 0.283 |
| G-mean | 0.05 | 0.517 | 0.785 | 0.771 | 0.116 | 0.192 | 0.637 | 0.160 |
| MCC | 0.26 | 0.222 | 0.973 | 0.936 | 0.281 | 0.301 | 0.467 | 0.298 |
| Model | Dataset ARES | Dataset TETIS | ||
|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | |
| Rate of failure | 0.053 | 0.092 | ||
| Without interaction | 0.023 | 0.018 | 0.056 | 0.045 |
| With interaction | 0.024 | 0.018 | 0.056 | 0.045 |
| Reference | 0.019 | 0.014 | 0.033 | 0.025 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amato, U.; Antoniadis, A.; De Feis, I.; Doinychko, A.; Gijbels, I.; La Magna, A.; Pagano, D.; Piccinini, F.; Selvan Suviseshamuthu, E.; Severgnini, C.; et al. Detecting Important Features and Predicting Yield from Defects Detected by SEM in Semiconductor Production. Sensors 2025, 25, 4218. https://doi.org/10.3390/s25134218
Amato U, Antoniadis A, De Feis I, Doinychko A, Gijbels I, La Magna A, Pagano D, Piccinini F, Selvan Suviseshamuthu E, Severgnini C, et al. Detecting Important Features and Predicting Yield from Defects Detected by SEM in Semiconductor Production. Sensors. 2025; 25(13):4218. https://doi.org/10.3390/s25134218
Chicago/Turabian StyleAmato, Umberto, Anestis Antoniadis, Italia De Feis, Anastasiia Doinychko, Irène Gijbels, Antonino La Magna, Daniele Pagano, Francesco Piccinini, Easter Selvan Suviseshamuthu, Carlo Severgnini, and et al. 2025. "Detecting Important Features and Predicting Yield from Defects Detected by SEM in Semiconductor Production" Sensors 25, no. 13: 4218. https://doi.org/10.3390/s25134218
APA StyleAmato, U., Antoniadis, A., De Feis, I., Doinychko, A., Gijbels, I., La Magna, A., Pagano, D., Piccinini, F., Selvan Suviseshamuthu, E., Severgnini, C., Torres, A., & Vasquez, P. (2025). Detecting Important Features and Predicting Yield from Defects Detected by SEM in Semiconductor Production. Sensors, 25(13), 4218. https://doi.org/10.3390/s25134218








