Motor Fault Diagnosis Under Strong Background Noise Based on Parameter-Optimized Feature Mode Decomposition and Spatial–Temporal Features Fusion
Abstract
1. Introduction
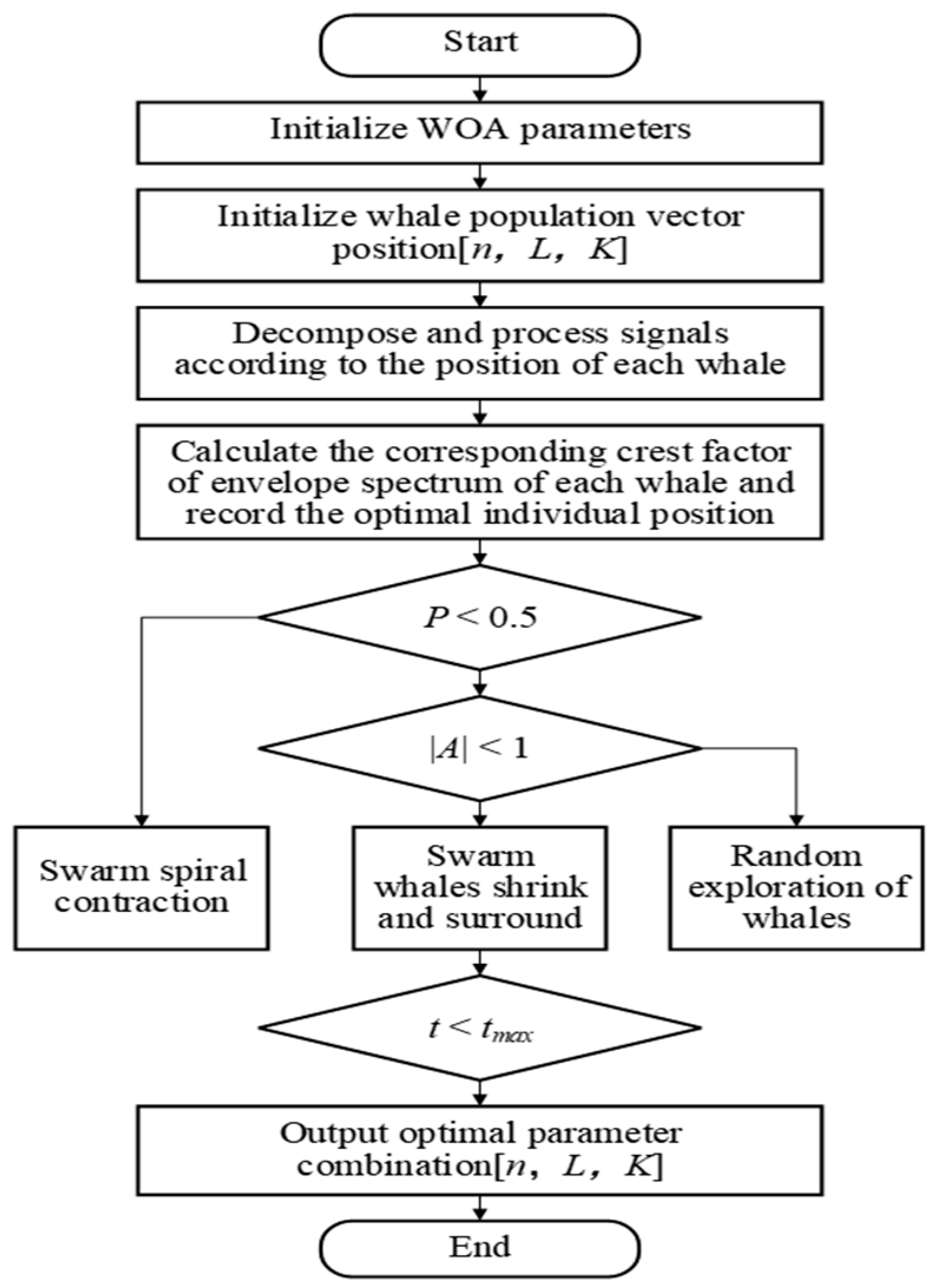
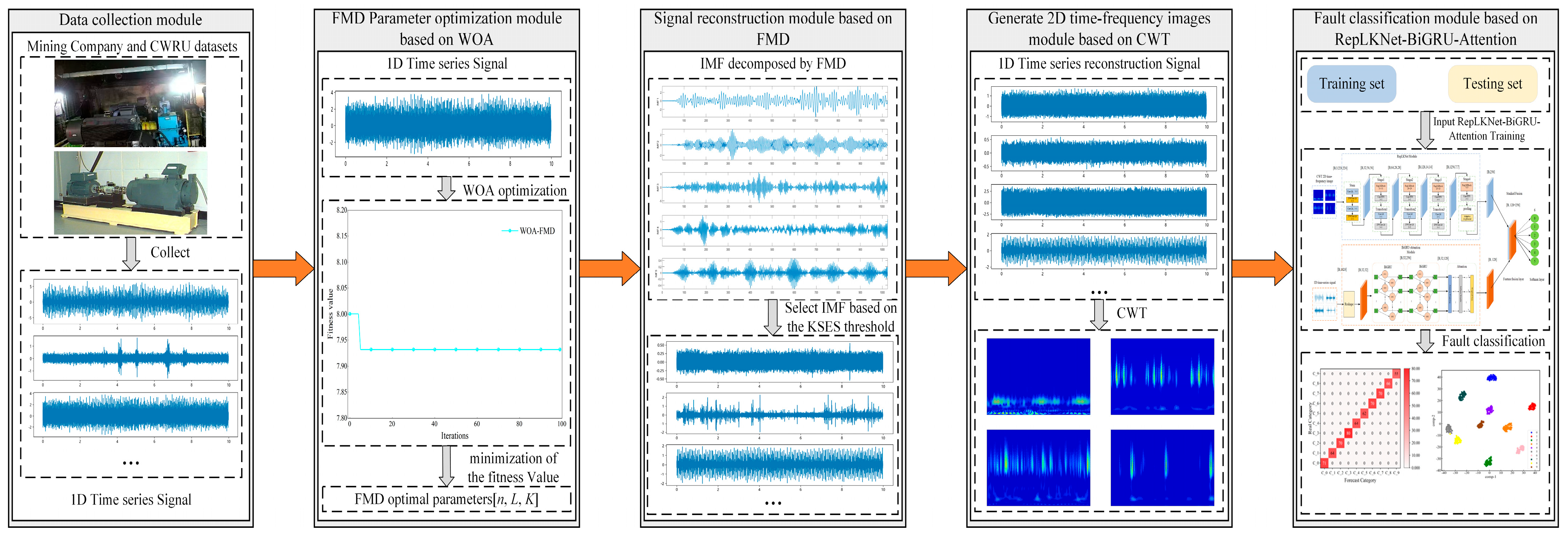
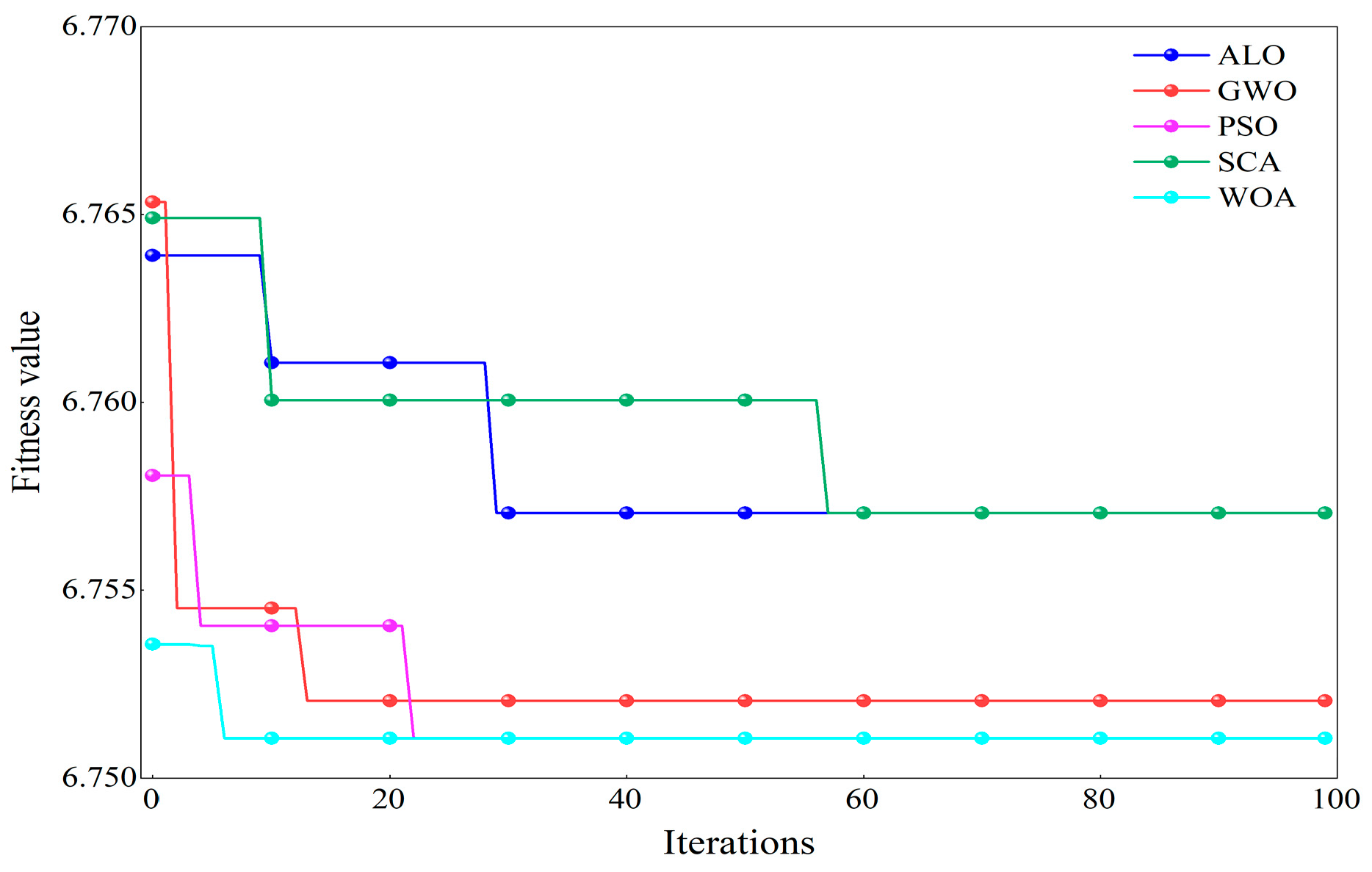
- Data decomposition stage: Aiming at the lack of parameter adaptability of FMD, which leads to insufficient signal decomposition performance, the WOA optimization algorithm is introduced to perform the adaptive optimization of three key parameters [n, L, K], which solves the problem of the error caused by relying on the subjective experience of parameter selection and effectively removes the stochastic noise components in the signal.
- Signal reconstruction stage: To address the issue of the inaccurate selection of dominant IMFs, the average KSES value of all IMFs was used as a threshold to filter out IMFs with prominent fault features. The raw vibration signal was then reconstructed, effectively removing irrelevant noise components such as white noise and mechanical vibration noise, thereby minimizing their impact on the subsequent model diagnosis results.
- Fault Mode Recognition: To overcome the drawback of single-data-type models in comprehensively capturing signal characteristics, this study introduces the RepLKNet-BiGRU-Attention dual-channel architecture. Continuous wavelet transform (CWT) is employed to create time–frequency images, which are subsequently input into the RepLKNet component for extracting intricate spatial features within the signal. Concurrently, the one-dimensional signal is fed into the BiGRU-Attention component to capture its temporal dependencies. This mechanism of multi-feature fusion allows for the concurrent extraction of both temporal dynamics and spatial patterns from input signals, thereby notably enhancing the representation of fault features and boosting the overall performance of the model.
- Experimental Validation: To evaluate the performance of the method, experiments were carried out on a noise-added CWRU bearing fault dataset and actual operating data from mining motors. The results show that the method substantially improves motor fault diagnosis performance under strong background noise.
2. Theoretical Methodology
2.1. Signal Decomposition and Reconstruction Based on WOA-FMD
2.1.1. FMD
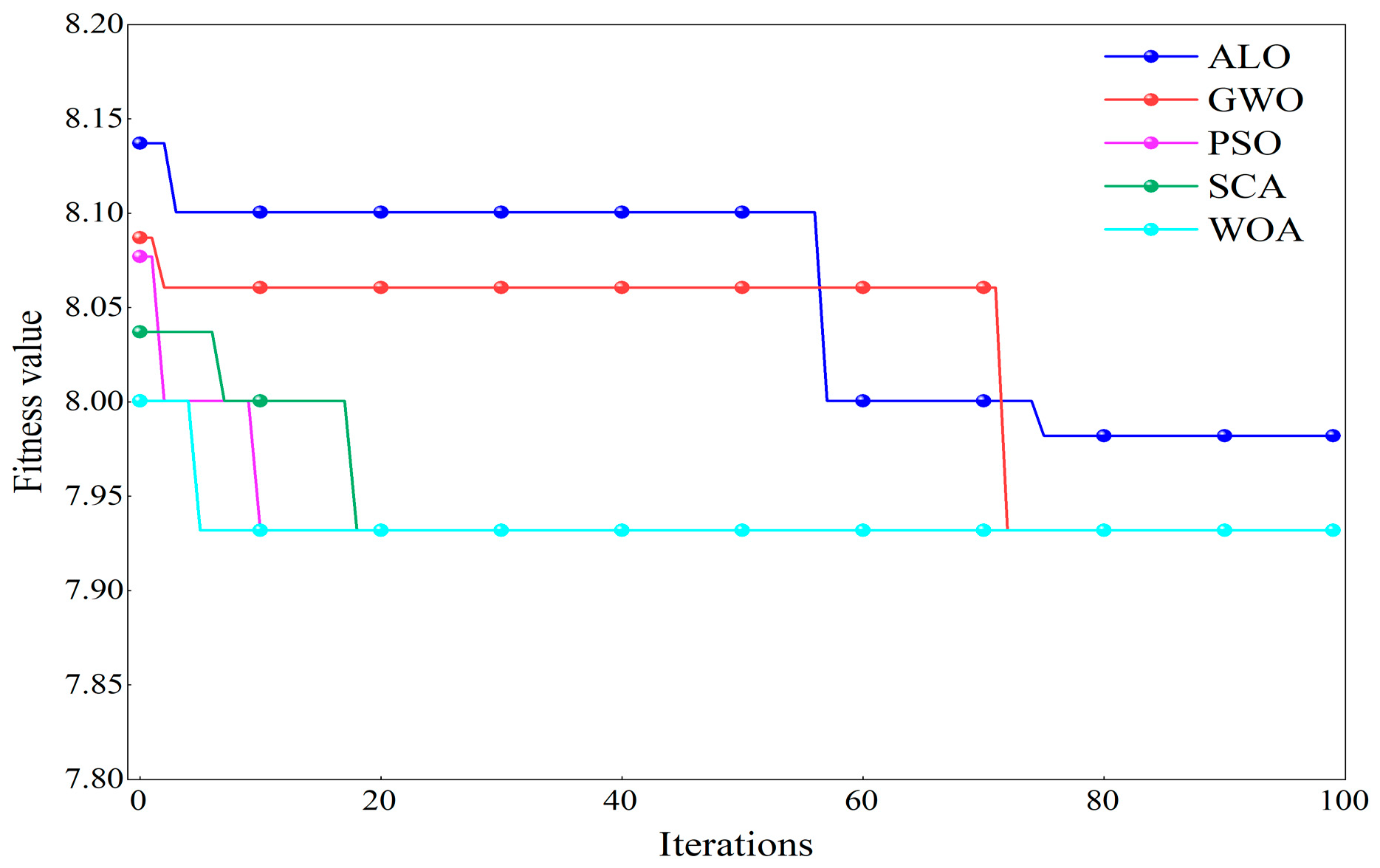
2.1.2. WOA-Based Parameter Optimization for FMD
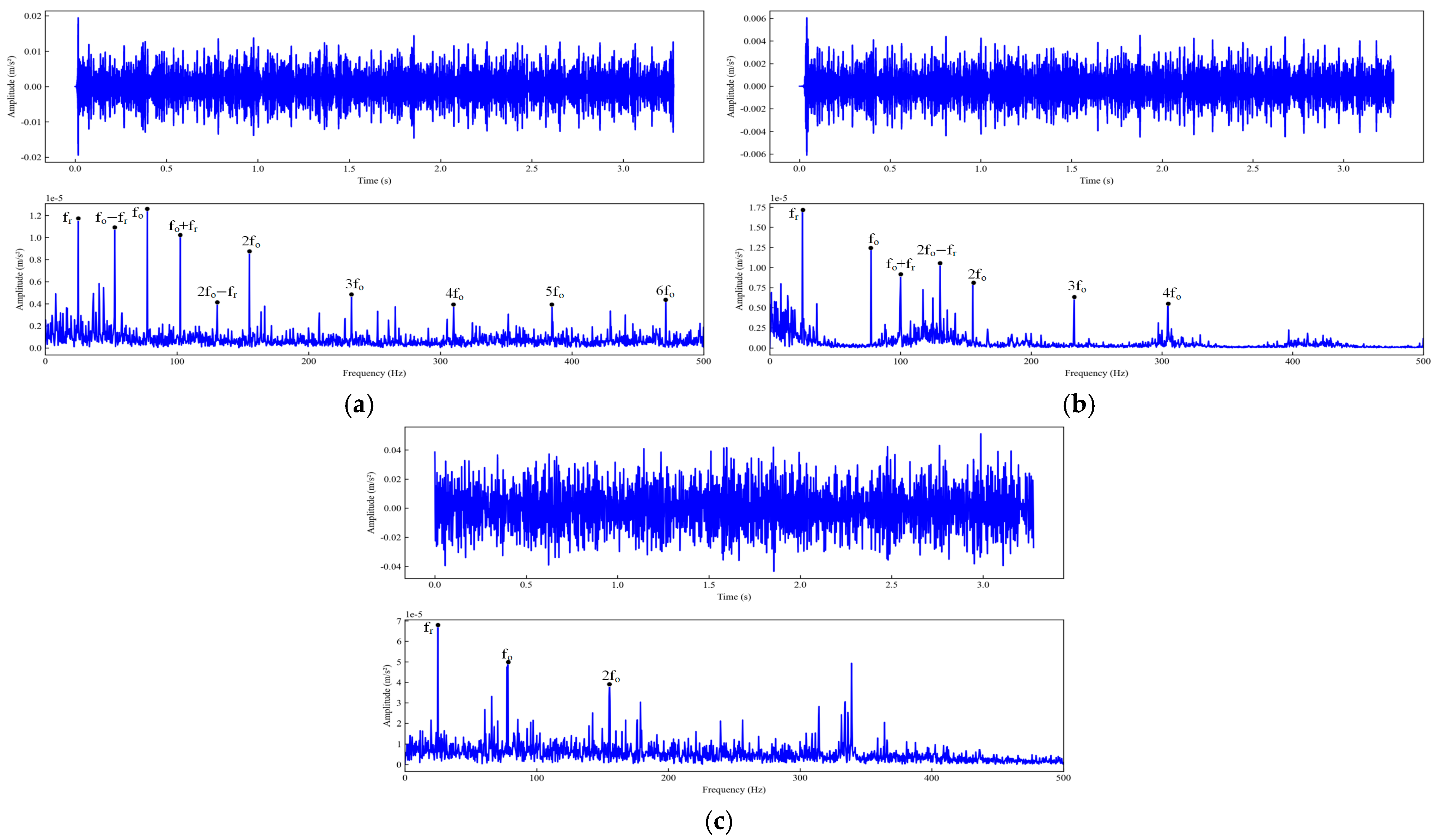
2.1.3. Vibration Signal Reconstruction Based on Kurtosis of Squared Envelope Spectrum
- Calculate the squared envelope of w according to Equation (8), where i is an imaginary unit and Hilbert (w) denotes the Hilbert transform of w.
- 2.
- Calculate the squared envelope spectrum of w according to Equation (9), where DFT[·] denotes the discrete Fourier transform of the SE(w).
- 3.
- Calculate the KSES value of w according to Equation (10), where E[·] denotes the mathematical expectation to find the long-term average.
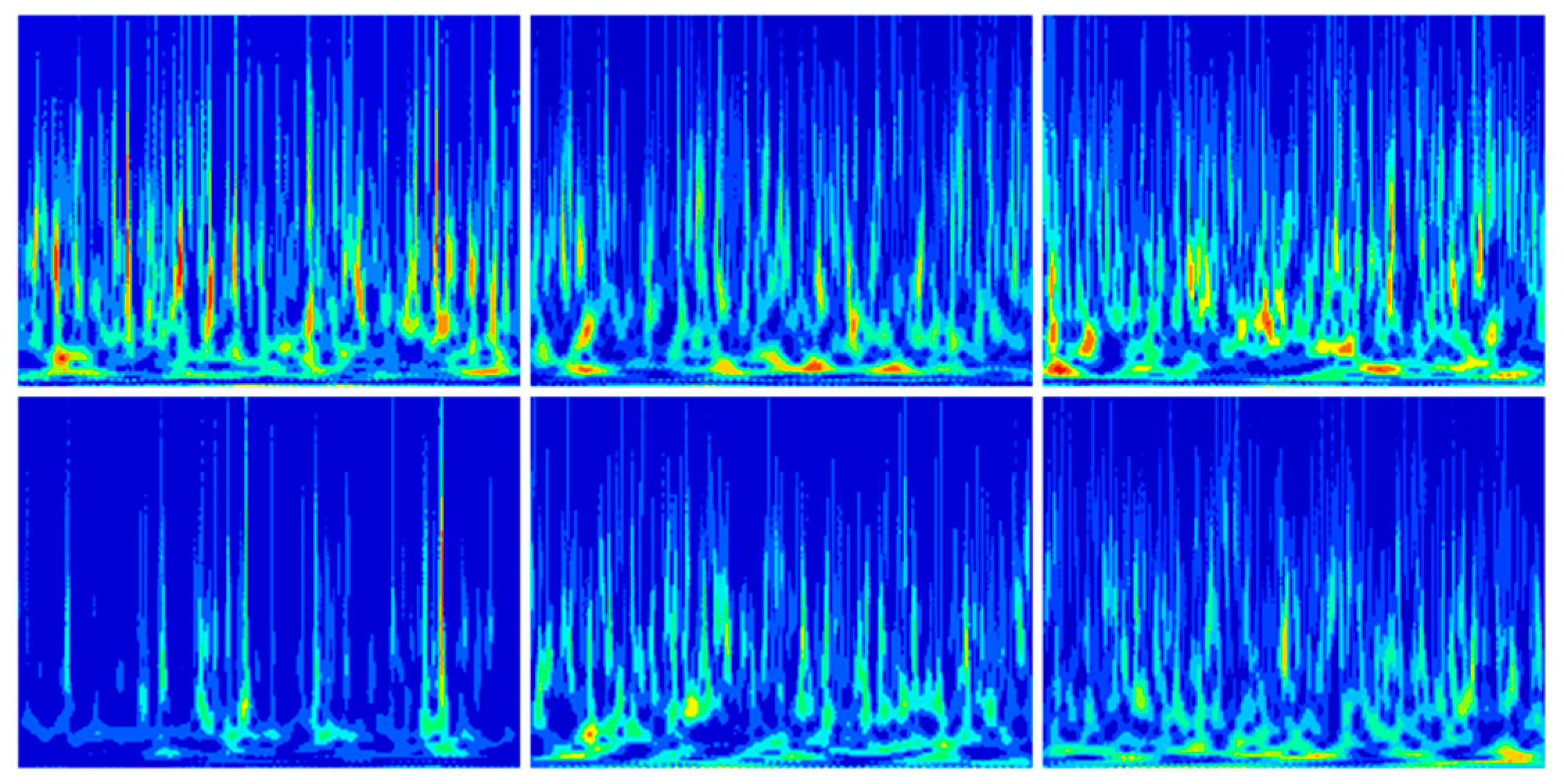
2.2. 2D Time–Frequency Image Generation Based on CWT
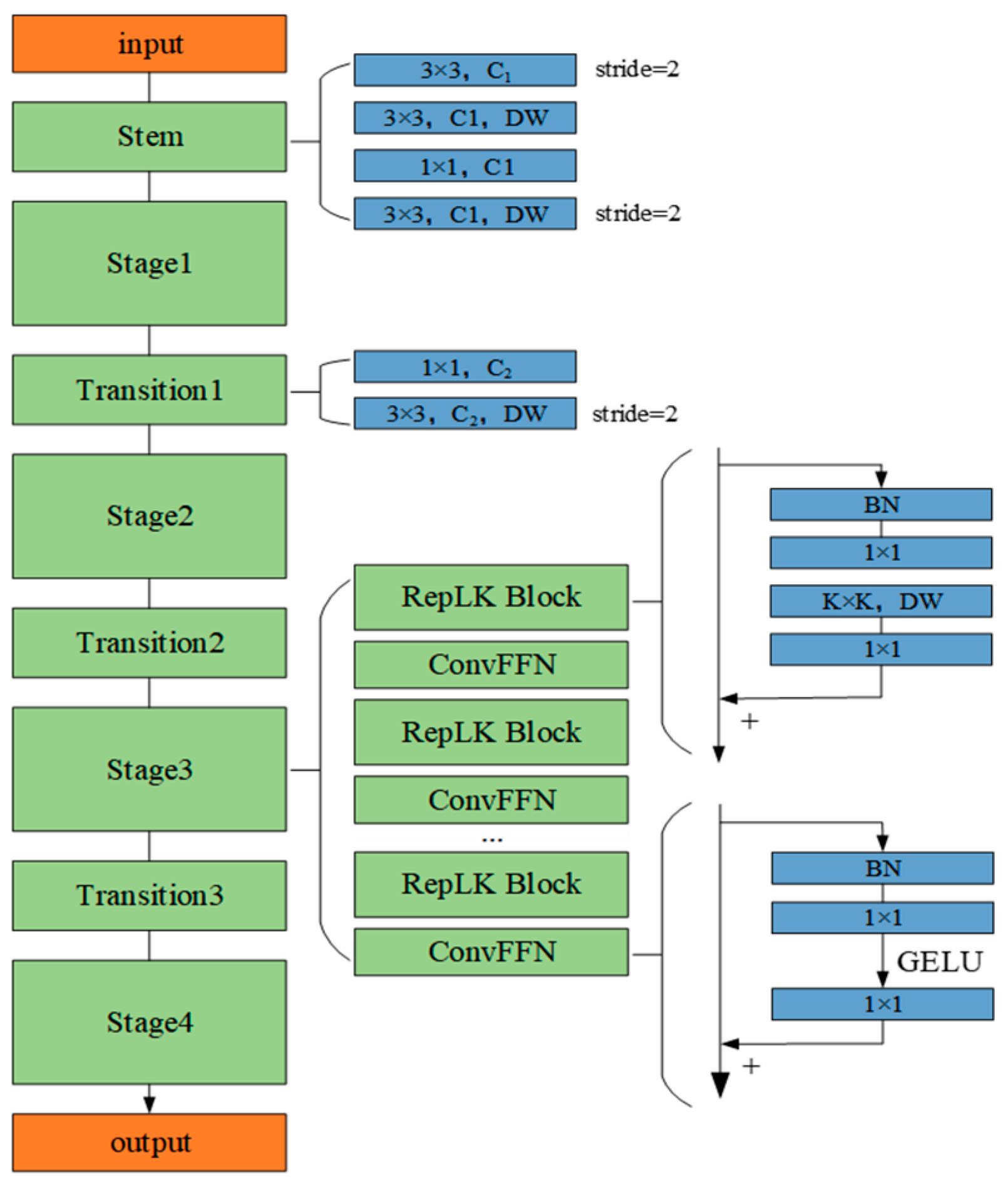
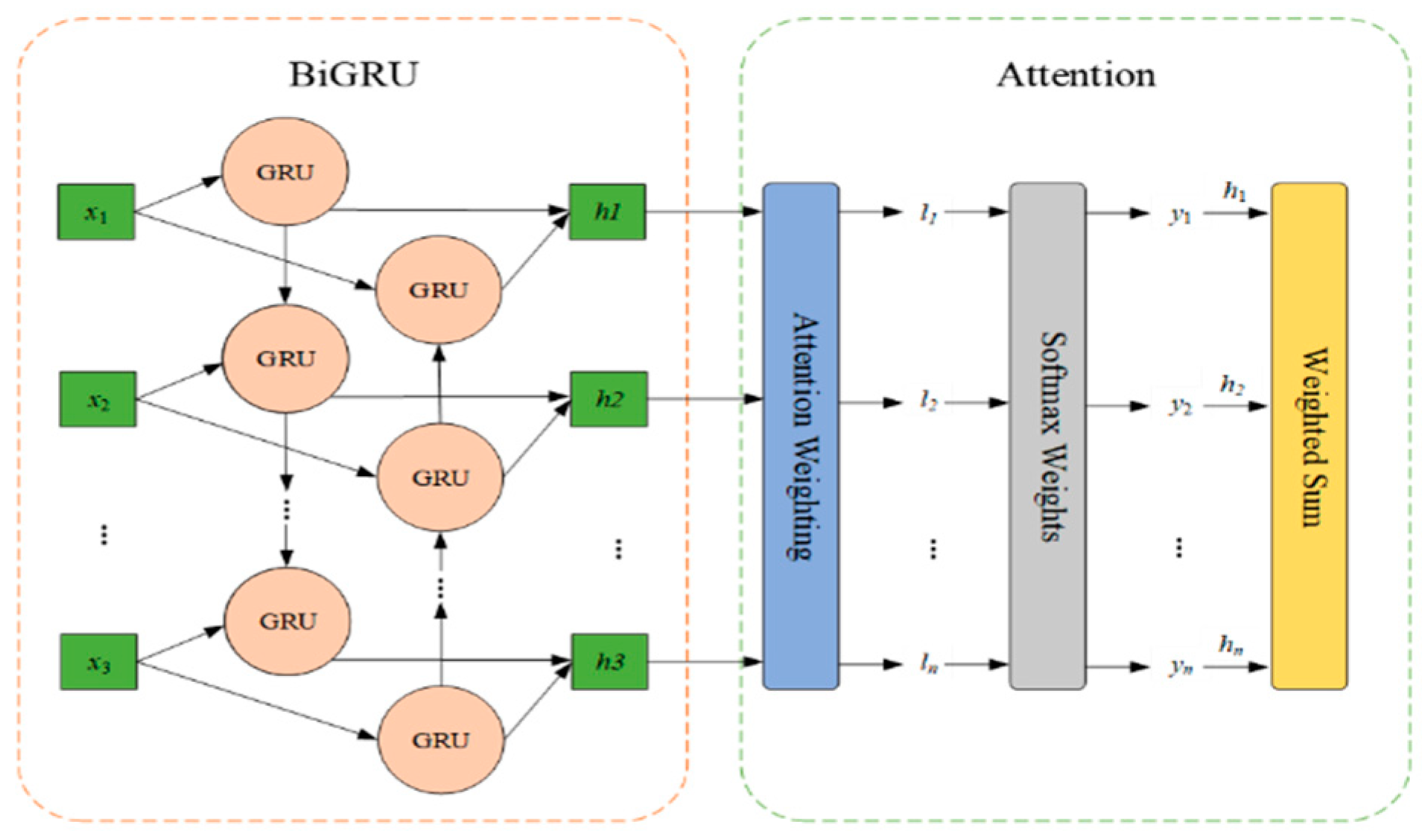
2.3. Dual-Channel Fault Identification Model Based on RepLKNet-BiGRU-Attention
2.3.1. RepLKNet Module
2.3.2. BiGRU-Attention Module
3. Fault Diagnosis Framework of This Study
4. Experimentation and Analysis
4.1. Case 1: Public Dataset
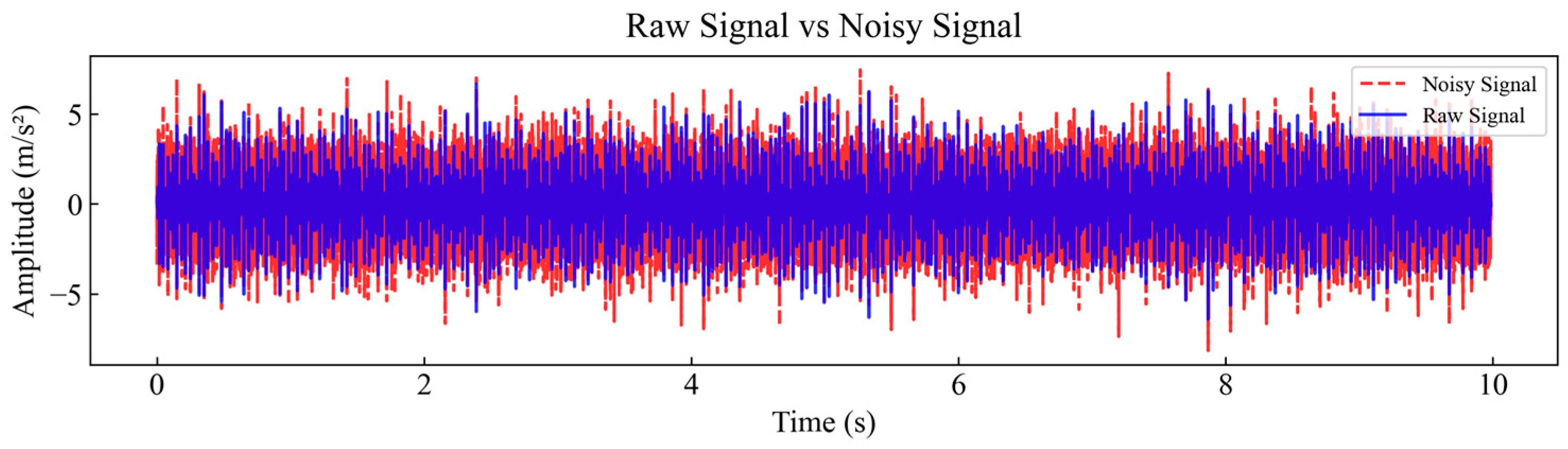
4.1.1. Experimental Data Sources
4.1.2. Signal Decomposition and Reconstruction Based on WOA-FMD
4.1.3. Dual-Channel Fault Identification Model Based on RepLKNet-BiGRU-Attention
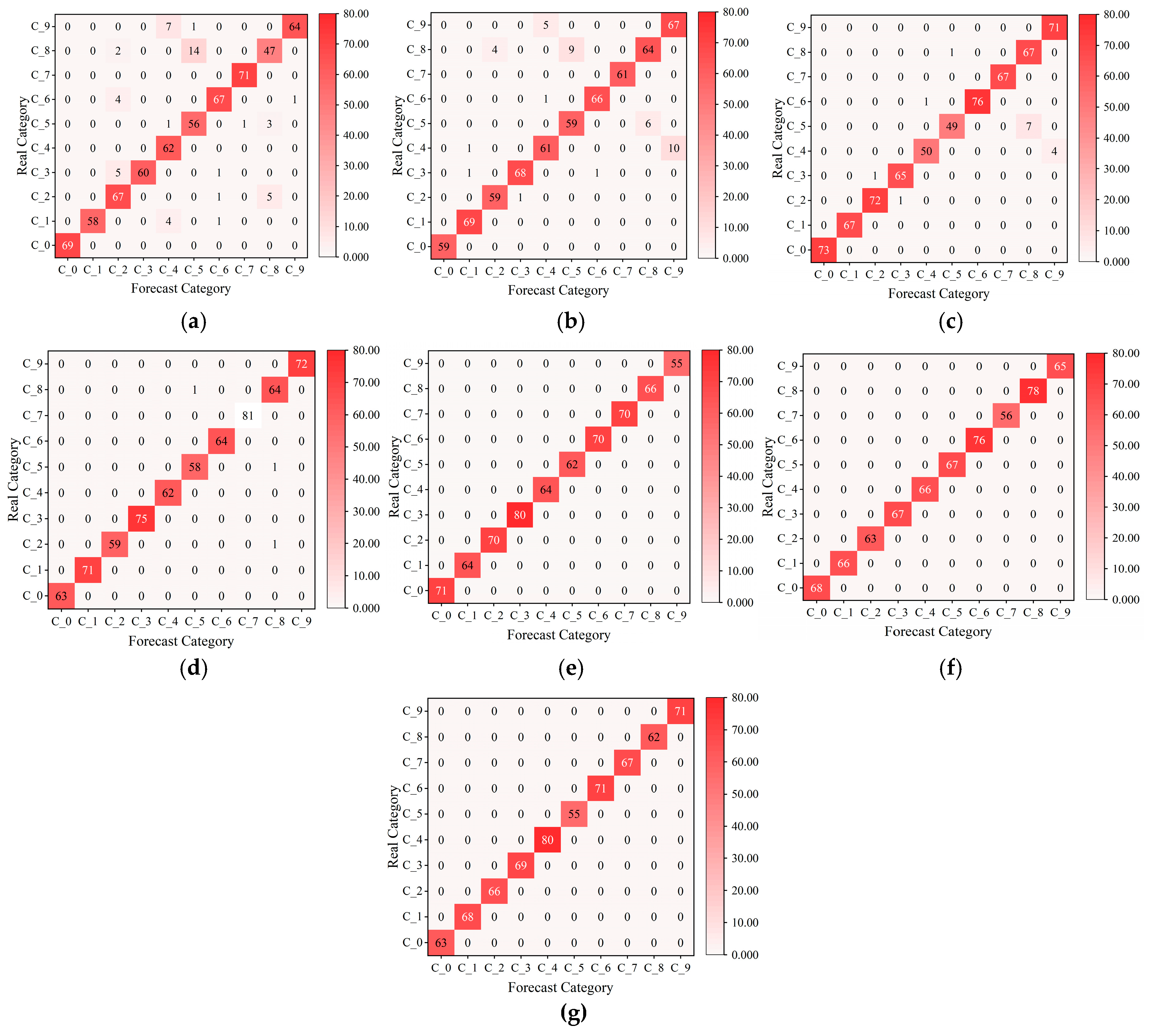
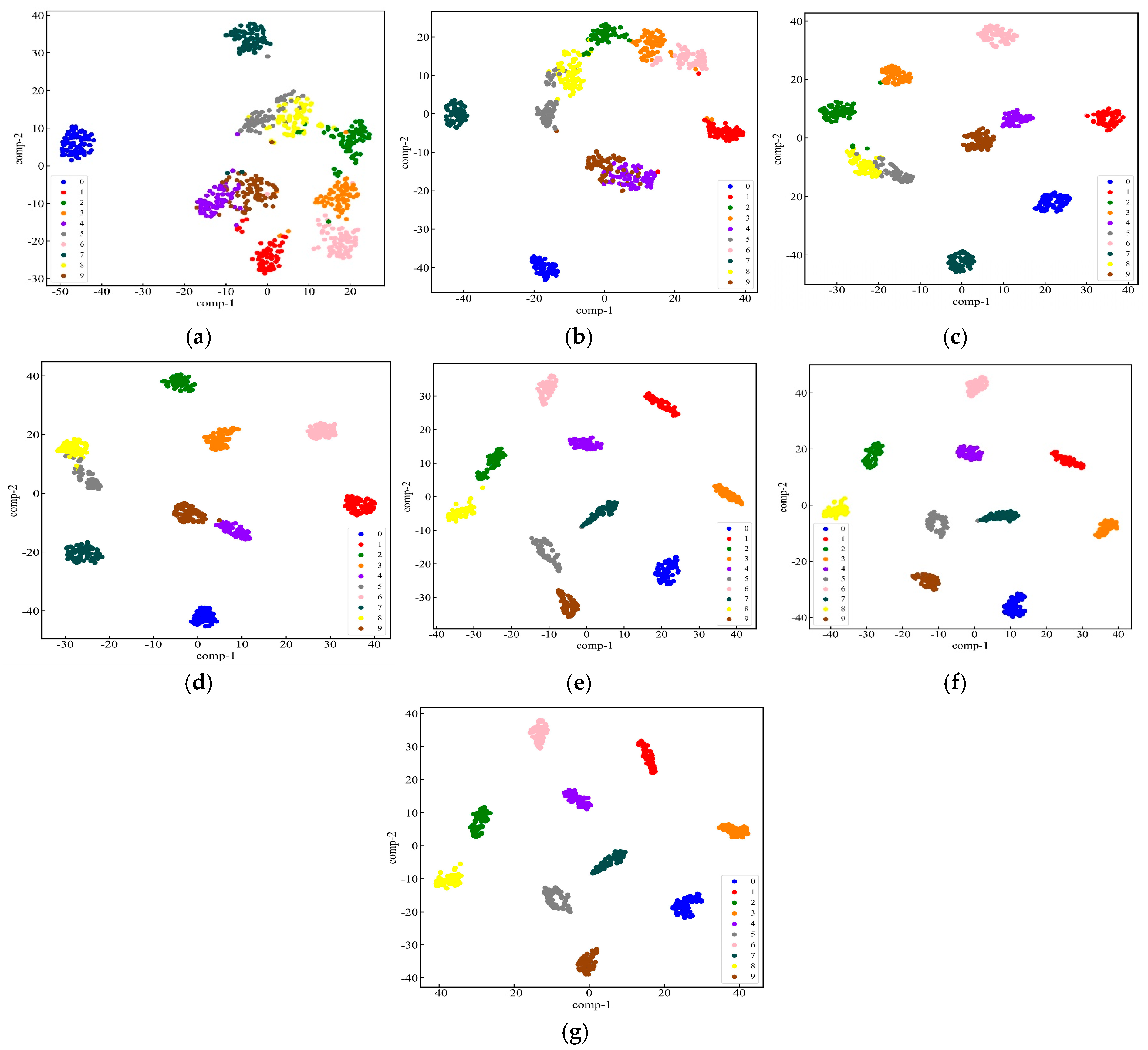
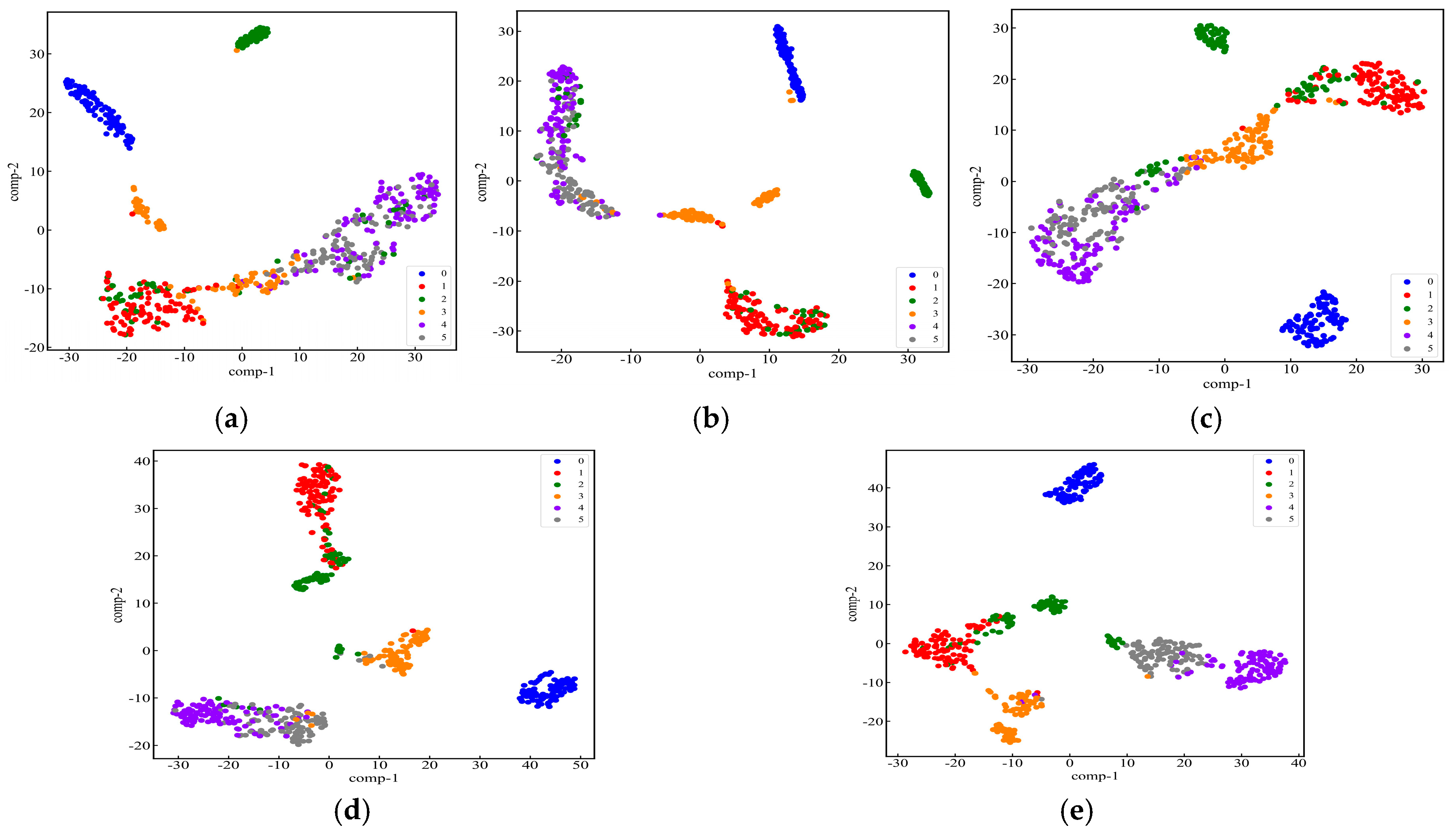
4.1.4. Analysis of Experimental Results
4.2. Case 2: Actual Operational Data
4.2.1. Experimental Data Sources
4.2.2. Signal Decomposition and Reconstruction Based on WOA-FMD
4.2.3. Dual-Channel Fault Identification Model Based on RepLKNet-BiGRU-Attention
4.2.4. Analysis of Experimental Results
5. Conclusions
- The core parameters of the FMD were adaptively optimized using the WOA, and the KSES value was used as an index to select the dominant IMF components for signal reconstruction. This method can successfully remove irrelevant noise components in the signal and make the fault features more obvious. The core parameters of the FMD were adaptively optimized using the WOA, with the KSES value serving as an index to select the dominant IMF components for signal reconstruction. This method effectively removes irrelevant noise components from the signal, thereby enhancing the visibility of fault features.
- Fault identification was performed using the RepLKNet-BiGRU-Attention dual-channel deep learning network model. The CWT image preserves the spatial features of the signal, while the one-dimensional signal retains time-dependent features. The RepLKNet-BiGRU-Attention dual-channel model simultaneously extracts multiscale features of the signal for fusion, thereby enhancing the fault recognition accuracy.
- By combining WOA-FMD with RepLKNet-BiGRU-Attention, a high-performance fault diagnosis method for mining motors was developed.
- In this study, an experimental analysis was carried out using a noise-processed CWRU bearing dataset and various types of fault data under the actual operation of enterprise mining motors. The results show that, compared with the VMD and FMD methods without parameter optimization, the feature extraction method proposed in this paper can effectively extract the fault characteristic frequencies and their corresponding higher harmonics. Moreover, the introduced fault recognition method demonstrated higher accuracy than the other four methods. These results indicate that the proposed method has significant advantages in the fault diagnosis of mining motors under strong background noise.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lei, Y.; Lin, J.; He, Z.; Zuo, M.J. A review on empirical mode decomposition in fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2013, 35, 108–126. [Google Scholar] [CrossRef]
- Xue, X.; Zhou, J.; Xu, Y.; Zhu, W.; Li, C. An adaptively fast ensemble empirical mode decomposition method and its applications to rolling element bearing fault diagnosis. Mech. Syst. Signal Process. 2015, 62, 444–459. [Google Scholar] [CrossRef]
- Lei, Y.; He, Z.; Zi, Y. EEMD method and WNN for fault diagnosis of locomotive roller bearings. Expert. Syst. Appl. 2011, 38, 7334–7341. [Google Scholar] [CrossRef]
- Wang, X.; Yao, Y.; Gao, C. Wasserstein Distance—EEMD Enhanced Multi-Head Graph Attention Network for Rolling Bearing Fault Diagnosis Under Different Working Conditions. Eksploat. I Niezawodn.-Maint. Reliab. 2024, 26, 184037. [Google Scholar] [CrossRef]
- Tian, Y.; Ma, J.; Lu, C.; Wang, Z. Rolling bearing fault diagnosis under variable conditions using LMD-SVD and extreme learning machine. Mech. Mach. Theory 2015, 90, 175–186. [Google Scholar] [CrossRef]
- Liu, W.Y.; Gao, Q.W.; Ye, G.; Ma, R.; Lu, X.N.; Han, J.G. A novel wind turbine bearing fault diagnosis method based on Integral Extension LMD. Measurement 2015, 74, 70–77. [Google Scholar] [CrossRef]
- Zheng, J.; Cheng, J.; Yang, Y. A rolling bearing fault diagnosis approach based on LCD and fuzzy entropy. Mech. Mach. Theory 2013, 70, 441–453. [Google Scholar] [CrossRef]
- Liu, F.; Wang, H.; Li, W.; Zhang, F.; Zhang, L.; Jiang, M.; Sui, Q. Fault diagnosis of rolling bearing combining improved AWSGMD-CP and ACO-ELM model. Measurement 2023, 209, 112531. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, M.; Lin, J. Identification of mechanical compound-fault based on the improved parameter-adaptive variational mode decomposition. ISA Trans. 2019, 84, 82–95. [Google Scholar] [CrossRef]
- Ge, H.; Wang, C.; Guo, A.; Zhang, C.; Zhao, Z.; Yang, M. Wear state identification of ball screw meta action unit based on parameter optimization VMD and improved Bilstm. Eksploat. I Niezawodn.-Maint. Reliab. 2024, 26, 191461. [Google Scholar] [CrossRef]
- Li, J.; Liu, Z.; Qiu, M.; Niu, K. Fault diagnosis model of rolling bearing based on parameter adaptive VMD algorithm and Sparrow Search Algorithm-Based PNN. Eksploat. I Niezawodn.-Maint. Reliab. 2023, 25, 163547. [Google Scholar] [CrossRef]
- Miao, Y.; Zhang, B.; Li, C.; Lin, J.; Zhang, D. Feature Mode Decomposition: New Decomposition Theory for Rotating Machinery Fault Diagnosis. IEE Trans. Ind. Electron. 2023, 70, 1949–1960. [Google Scholar] [CrossRef]
- Li, C.; Zhou, J.; Wu, X.; Liu, T. Adaptive feature mode decomposition method for bearing fault diagnosis under strong noise. Proc. Inst. Mech. Eng. Part. C-J. Mech. Eng. Sci. 2025, 239, 508–519. [Google Scholar] [CrossRef]
- Jia, G.; Meng, Y. Study on Fault Feature Extraction of Rolling Bearing Based on Improved WOA-FMD Algorithm. Shock. Vib. 2023, 2023, 5097144. [Google Scholar] [CrossRef]
- Yan, X.; Jia, M. Bearing fault diagnosis via a parameter-optimized feature mode decomposition. Measurement 2022, 203, 112016. [Google Scholar] [CrossRef]
- Yan, X.; Yan, W.-J.; Xu, Y.; Yuen, K.-V. Machinery multi-sensor fault diagnosis based on adaptive multivariate feature mode decomposition and multi-attention fusion residual convolutional neural network. Mech. Syst. Signal Process. 2023, 202, 110664. [Google Scholar] [CrossRef]
- Abdeljaber, O.; Sassi, S.; Avci, O.; Kiranyaz, S.; Ibrahim, A.A.; Gabbouj, M. Fault Detection and Severity Identification of Ball Bearings by Online Condition Monitoring. IEE Trans. Ind. Electron. 2019, 66, 8136–8147. [Google Scholar] [CrossRef]
- Johny, K.; Pai, M.L.; Adarsh, S. A multivariate EMD-LSTM model aided with Time Dependent Intrinsic Cross-Correlation for monthly rainfall prediction. Appl. Soft Comput. 2022, 123, 108941. [Google Scholar] [CrossRef]
- Wang, L.-H.; Zhao, X.-P.; Wu, J.-X.; Xie, Y.-Y.; Zhang, Y.-H. Motor Fault Diagnosis Based on Short-time Fourier Transform and Convolutional Neural Network. Chin. J. Mech. Eng. 2017, 30, 1357–1368. [Google Scholar] [CrossRef]
- Gu, J.; Peng, Y.; Lu, H.; Chang, X.; Chen, G. A novel fault diagnosis method of rotating machinery via VMD, CWT and improved CNN. Measurement 2022, 200, 111635. [Google Scholar] [CrossRef]
- Wang, Z.; Dong, Y.; Liu, W.; Ma, Z. A Novel Fault Diagnosis Approach for Chillers Based on 1-D Convolutional Neural Network and Gated Recurrent Unit. Sensors 2020, 20, 2458. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Yuan, Y.; Zhao, F. Intelligent Compound Fault Diagnosis of Roller Bearings Based on Deep Graph Convolutional Network. Sensors 2023, 23, 8489. [Google Scholar] [CrossRef]
- Lv, J.; Xiao, Q.; Zhai, X.; Shi, W. A high-performance rolling bearing fault diagnosis method based on adaptive feature mode decomposition and Transformer. Appl. Acoust. 2024, 224, 110156. [Google Scholar] [CrossRef]
- Zhong, T.; Qin, C.; Shi, G.; Zhang, Z.; Tao, J.; Liu, C. A residual denoising and multiscale attention-based weighted domain adaptation network for tunnel boring machine main bearing fault diagnosis. Sci. China-Technol. Sci. 2024, 67, 2594–2618. [Google Scholar] [CrossRef]
- He, C.; Zhong, T.; Feng, C.Y.; Qin, C.J.; Zheng, B.; Shi, X.; Liu, C.L. Adaptive and cross-attention Vision Transformer-based transfer network for elevator fault diagnosis toward unbalanced samples. Struct. Health Monit.-Int. J. 2025. [Google Scholar] [CrossRef]
- Li, O.; Lei, J.B.; Qin, C.J.; Zhang, Z.N.; Tao, J.F.; Liu, C.L. A novel multi-channel CNN-LSTM and transformer-based network for diesel engine misfire diagnosis under different noise conditions. Sci. China-Technol. Sci. 2024, 67, 2965–2967. [Google Scholar] [CrossRef]
- Bin, T.; Chen, Z.; Chao, Y.; Hanyu, H. Power frequency magnetic anomaly signal denoising algorithm based on PSO-VMD. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2024, 52, 47–51+64. [Google Scholar]
- Zhu, H.; Fang, T. Compound fault diagnosis of rolling bearings with few-shot based on DCGAN-RepLKNet. Meas. Sci. Technol. 2024, 35, 066105. [Google Scholar] [CrossRef]












| Fault Diameter (mm) | Fault Type | Labels |
|---|---|---|
| No fault | No fault | 0 |
| 0.1778 | Inner ring fault | 1 |
| 0.1778 | Rolling element fault | 2 |
| 0.1778 | Outer ring fault | 3 |
| 0.3556 | Inner ring fault | 4 |
| 0.3556 | Rolling element fault | 5 |
| 0.3556 | Outer ring fault | 6 |
| 0.5334 | Inner ring fault | 7 |
| 0.5334 | Rolling element fault | 8 |
| 0.5334 | Outer ring fault | 9 |
| Number | Decomposition Number | KSES Value | Mean Value | Dominant IMF |
|---|---|---|---|---|
| 0 | 10 | 9.6, 14.1, 11.1, 4.6, 12.3, 8.0, 6.6, 6.1, 8.0, 5.7 | 8.6 | 1, 2, 3, 5 |
| 1 | 9 | 13.6, 7.0, 9.2, 5.2, 11.8, 9.3, 5.8, 7.5, 6.9 | 8.5 | 1, 3, 5, 6 |
| 2 | 6 | 9.7, 8.5, 8.7, 11.4, 16.0, 6.9 | 10.2 | 4, 5 |
| 3 | 7 | 5.8, 9.6, 11.7, 15.1, 7.9, 7.4, 6.4 | 9.1 | 2, 3, 4 |
| 4 | 5 | 9.9, 9.3, 10.4, 9.3, 11.0 | 10.0 | 3, 5 |
| 5 | 8 | 6.6, 9.7, 12.5, 10.0, 13.1, 11.1, 8.6, 9.7 | 10.2 | 3, 5, 6 |
| 6 | 7 | 11.9, 9.8, 10.1, 15.5, 8.7, 6.8, 8.9 | 10.2 | 1, 4 |
| 7 | 4 | 10.2, 6.2, 5.6, 11.9 | 8.5 | 1, 4 |
| 8 | 8 | 6.2, 8.6, 7.2, 10.3, 13.5, 7.4, 7.6, 6.8 | 8.5 | 2, 4, 5 |
| 9 | 6 | 8.3, 6.7, 38.4, 7.8, 7.2, 10.8 | 13.2 | 3 |
| Models | Input Data Type | Core Structure | Feature Extraction Capability |
|---|---|---|---|
| BiGRU-Attention | 1D time-series signal | BiGRU + Attention mechanism | Captures only timing dependencies, lacks spatial feature modeling. |
| ResNet-18 | 2D time–frequency image | Residual convolutional network | Strong local spatial features, but easy to ignore temporal dynamic information. |
| RepLKNet | 2D time–frequency image | Large convolution kernel | Large sensory fields capture long-range spatial features but not temporal features. |
| Transformer | 1D time-series signal | Self-attention mechanism | Global timing dependence modeling, but with high computational overhead and insensitivity to local shock characteristics. |
| Proposed method | 1D signal + 2D image | Fusion of spatial and temporal features | Extracting large-scale spatial features while capturing bidirectional temporal dependencies. |
| Method | Data Preprocessing | Parameter Optimization Mechanism |
|---|---|---|
| RepLKNet-BiGRU-Attention | None | None |
| VMD-RepLKNet-BiGRU-Attention | VMD Decomposition + KSES Reconstruction | Fixed parameters (empirically dependent) |
| FMD-RepLKNet-BiGRU-Attention | FMD Decomposition + KSES Reconstruction | Fixed parameters (empirically dependent) |
| Proposed method | WOA-FMD Decomposition + KSES Reconstruction | WOA Adaptive Optimization Dynamic Search for Optimal [n, L, K] |
| Fault Type | Labels |
|---|---|
| No fault | 0 |
| Bearing rolling element fault | 1 |
| Bearing retainer fault | 2 |
| Bearing outer ring fault | 3 |
| Shaft misalignment fault | 4 |
| Shaft imbalance fault | 5 |
| Number | Decomposition Number | KSES Value | Mean Value | Dominant IMF |
|---|---|---|---|---|
| 0 | 6 | 5.5, 11.0, 17.3, 5.3, 14.2, 6.5 | 10.0 | 2, 3, 5 |
| 1 | 10 | 10.8, 6.4, 9.3, 7.9, 2.9, 6.6, 6.4, 14.9, 3.9, 11.5 | 8.1 | 1, 3, 8, 10 |
| 2 | 3 | 19.3, 9.7, 7.4 | 12.1 | 1 |
| 3 | 6 | 4.4, 8.9, 7.8, 6.1, 6.6, 18.0 | 8.6 | 6 |
| 4 | 7 | 5.2, 7.7, 4.8, 6.5, 7.7, 7.4, 18.2 | 8.2 | 7 |
| 5 | 8 | 5.6, 10.9, 10.1, 17.1, 6.5, 17.4, 10.0, 7.8 | 10.7 | 2, 4, 6 |
| Models | Accuracy (Mean ± Std) | F1-Score (Mean ± Std) |
|---|---|---|
| BiGRU-Attention | 0.7206 ± 0.022 | 0.7136 ± 0.019 |
| ResNet-18 | 0.8125 ± 0.017 | 0.8053 ± 0.018 |
| RepLKNet | 0.8493 ± 0.014 | 0.8465 ± 0.012 |
| Transformer | 0.8787 ± 0.011 | 0.8792 ± 0.010 |
| Proposed method | 0.9393 ± 0.007 | 0.9390 ± 0.005 |
| Method | Accuracy (Mean ± Std) | F1-Score (Mean ± Std) |
|---|---|---|
| RepLKNet-BiGRU-Attention | 0.7463 ± 0.021 | 0.7385 ± 0.019 |
| VMD-RepLKNet-BiGRU-Attention | 0.8235 ± 0.015 | 0.8243 ± 0.017 |
| FMD-RepLKNet-BiGRU- Attention | 0.8658 ± 0.012 | 0.8664 ± 0.014 |
| Proposed method | 0.9393 ± 0.007 | 0.9390 ± 0.005 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Yuan, Y.; Shen, F.; Chen, C. Motor Fault Diagnosis Under Strong Background Noise Based on Parameter-Optimized Feature Mode Decomposition and Spatial–Temporal Features Fusion. Sensors 2025, 25, 4168. https://doi.org/10.3390/s25134168
Wang J, Yuan Y, Shen F, Chen C. Motor Fault Diagnosis Under Strong Background Noise Based on Parameter-Optimized Feature Mode Decomposition and Spatial–Temporal Features Fusion. Sensors. 2025; 25(13):4168. https://doi.org/10.3390/s25134168
Chicago/Turabian StyleWang, Jingcan, Yiping Yuan, Fangqi Shen, and Caifeng Chen. 2025. "Motor Fault Diagnosis Under Strong Background Noise Based on Parameter-Optimized Feature Mode Decomposition and Spatial–Temporal Features Fusion" Sensors 25, no. 13: 4168. https://doi.org/10.3390/s25134168
APA StyleWang, J., Yuan, Y., Shen, F., & Chen, C. (2025). Motor Fault Diagnosis Under Strong Background Noise Based on Parameter-Optimized Feature Mode Decomposition and Spatial–Temporal Features Fusion. Sensors, 25(13), 4168. https://doi.org/10.3390/s25134168






