Research on Soft-Sensing Method Based on Adam-FCNN Inversion in Pichia pastoris Fermentation
Abstract
1. Introduction
2. Methods
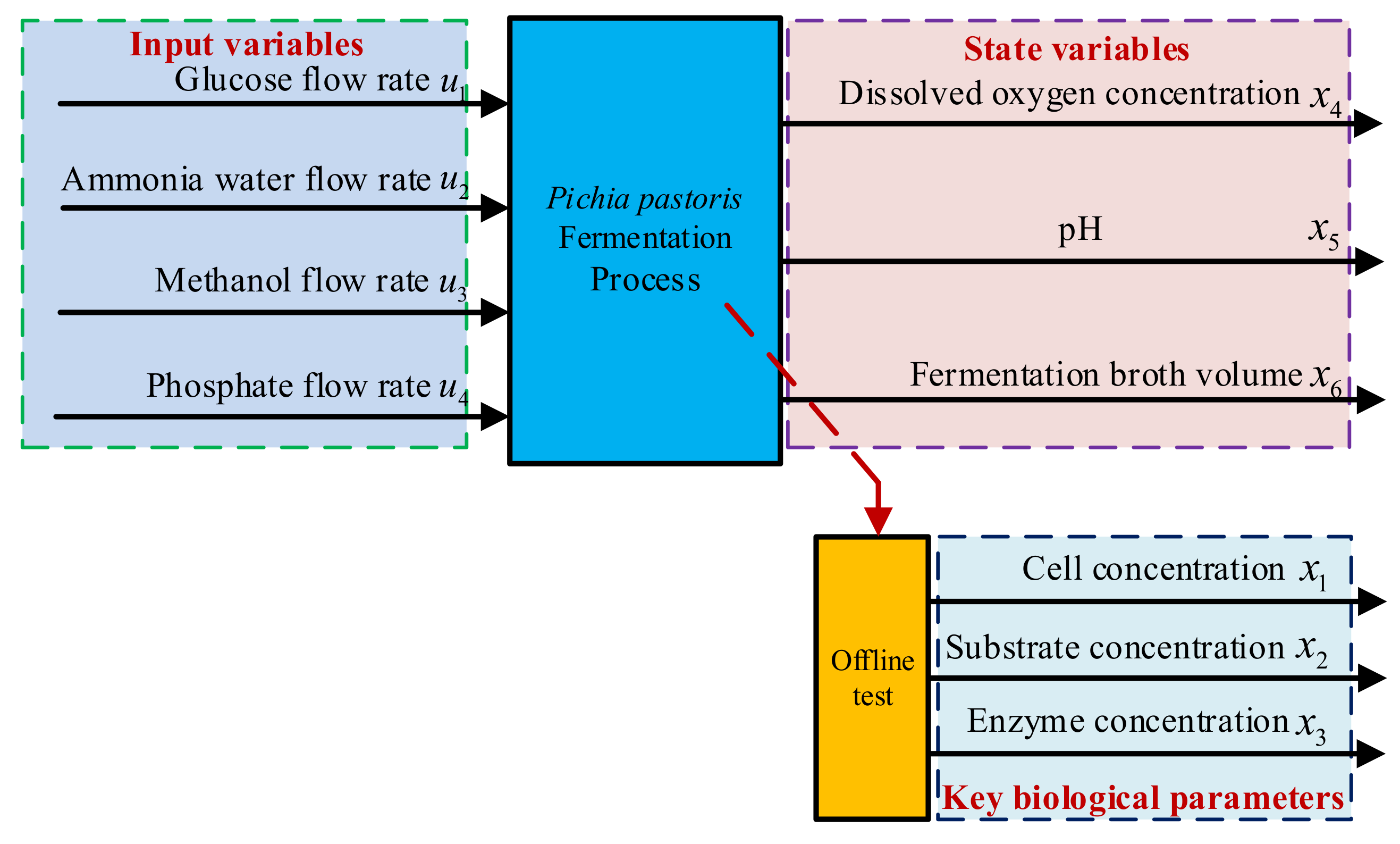
2.1. Non-Deterministic Mechanism Model of the Fermentation Process
2.1.1. Volume Change Equation
2.1.2. Cell Growth Kinetics Equation
2.1.3. Substrate Consumption Equation
2.1.4. Enzyme Production Dynamics
2.1.5. Dissolved Oxygen Dynamics
2.1.6. pH Dynamic
2.1.7. “Grey-Box” Dynamic Model
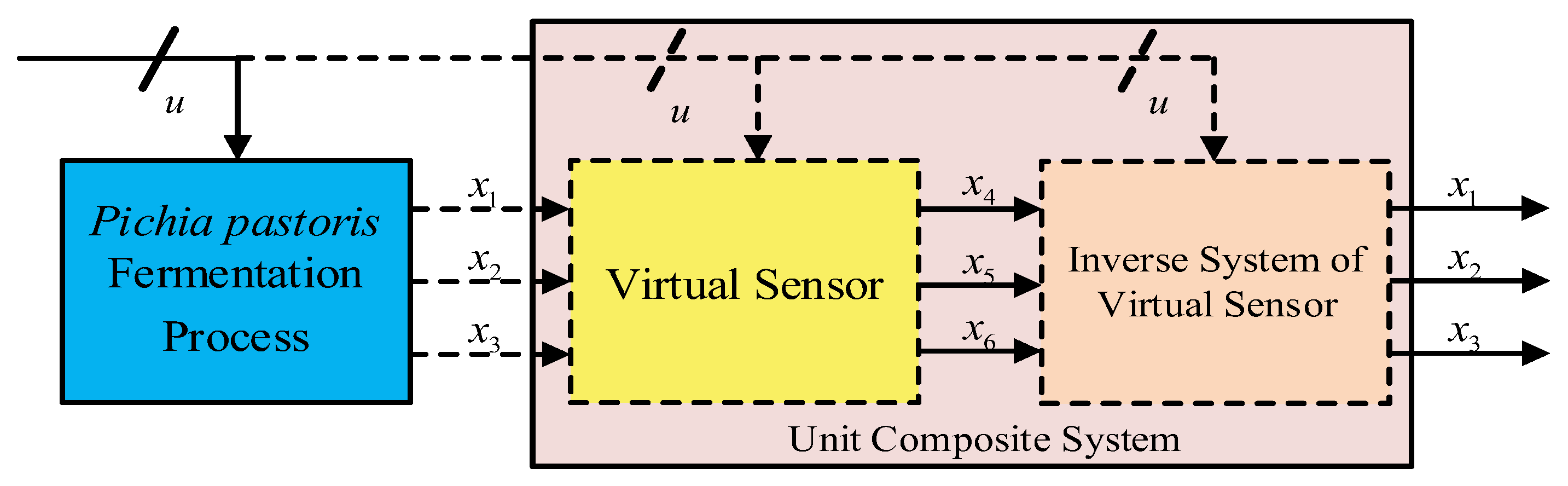
2.2. Reversibility Analysis
- Solve the inverse model of the virtual subsystem;
- Combine the model with the virtual subsystem to form a complete system that works as a dynamic compensator;
- Reconstruct the inputs of the virtual sensor based on the outputs of this complete system.
2.3. Improved FCNN
3. Adam-FCNN Inversion-Based Soft-Sensing
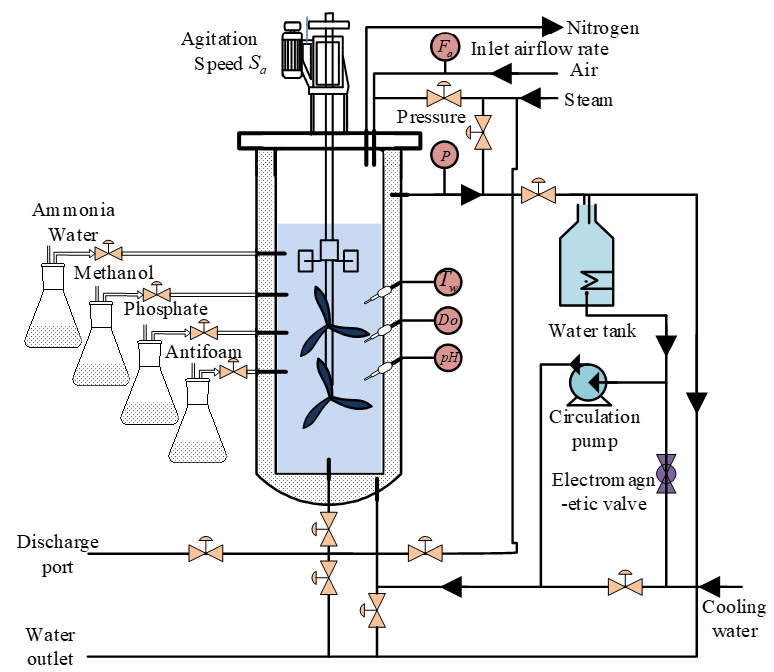
3.1. Data Collection
- Microbial Cultivation: The GS115 strain was cultured on YPD agar plates at 30 °C for 48 h. A single colony was inoculated into BMGY liquid medium and cultivated at 30 °C and 250 rpm for 24 h. The culture was sequentially transferred to a 5 L seed bioreactor, followed by a 50 L secondary seed bioreactor (inoculation volume: 5–10%). When the cell density in the secondary bioreactor reached OD600 = 120 ± 15, the culture was transferred to the main fermentation tank.
- Sterilization: The air pipeline was sterilized at 130 °C for 40 min across three cycles. The bioreactor was sterilized with saturated steam at 0.15 MPa for 30 min. After cooling, sterilized culture medium was introduced into the tank.
- Data Collection and Sample Processing: Auxiliary variables (dissolved oxygen Do, fermentation broth volume, pH, ammonia flow rate, methanol flow rate, antifoaming agent flow rate, and phosphate flow rate) were recorded every 4 h. Meanwhile, methanol consumption was documented, 5 mL fermentation samples were centrifuged (8000 rpm, 10 min), and Pichia pastoris concentration was measured offline via the wet weight method. Supernatants were filtered through 0.22 μm membranes and analyzed for inulinase concentration using HPLC (Agilent 1260, Santa Clara, CN, USA) with a detection limit of 0.01 g/L.
- Batch Cultivation Phase: Pichia pastoris is cultured in mineral medium under batch conditions to accumulate biomass.
- Glycerol Fed-Batch Accumulation Phase: A glycerol-supplemented feeding medium is gradually added to further increase Pichia pastoris concentration, preparing for the subsequent high-density induction phase.
- Methanol Induction Phase: A methanol-supplemented feeding medium is slowly introduced while maintaining the methanol concentration at about 1%. During this phase, Pichia pastoris begins synthesizing inulinase.
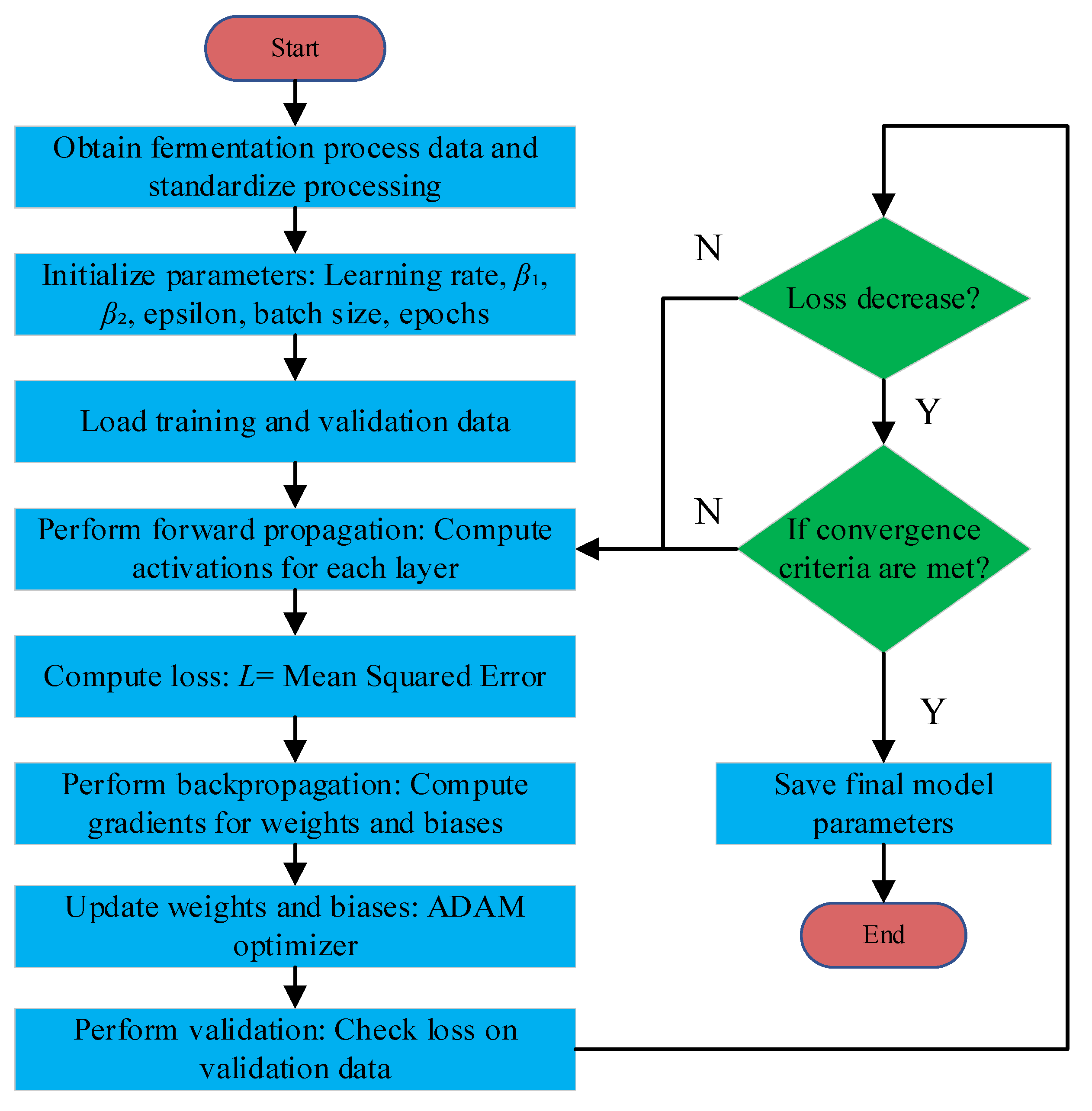
3.2. Model Training and Online Correction
3.3. Adam-FCNN Inversion Soft-Sensing Model
- (1)
- If , the input data are processed using a moving average filter. Specifically, the input data over a defined period are averaged aswhere represents the sampling interval, is the real-time sampled data, denotes historical data points, is the preprocessed data, is the preprocessed data from the previous step, and is a predefined threshold.
- (2)
- If , the current input is temporarily set to , followed by reprocessing using the moving average algorithm to mitigate abrupt fluctuations.
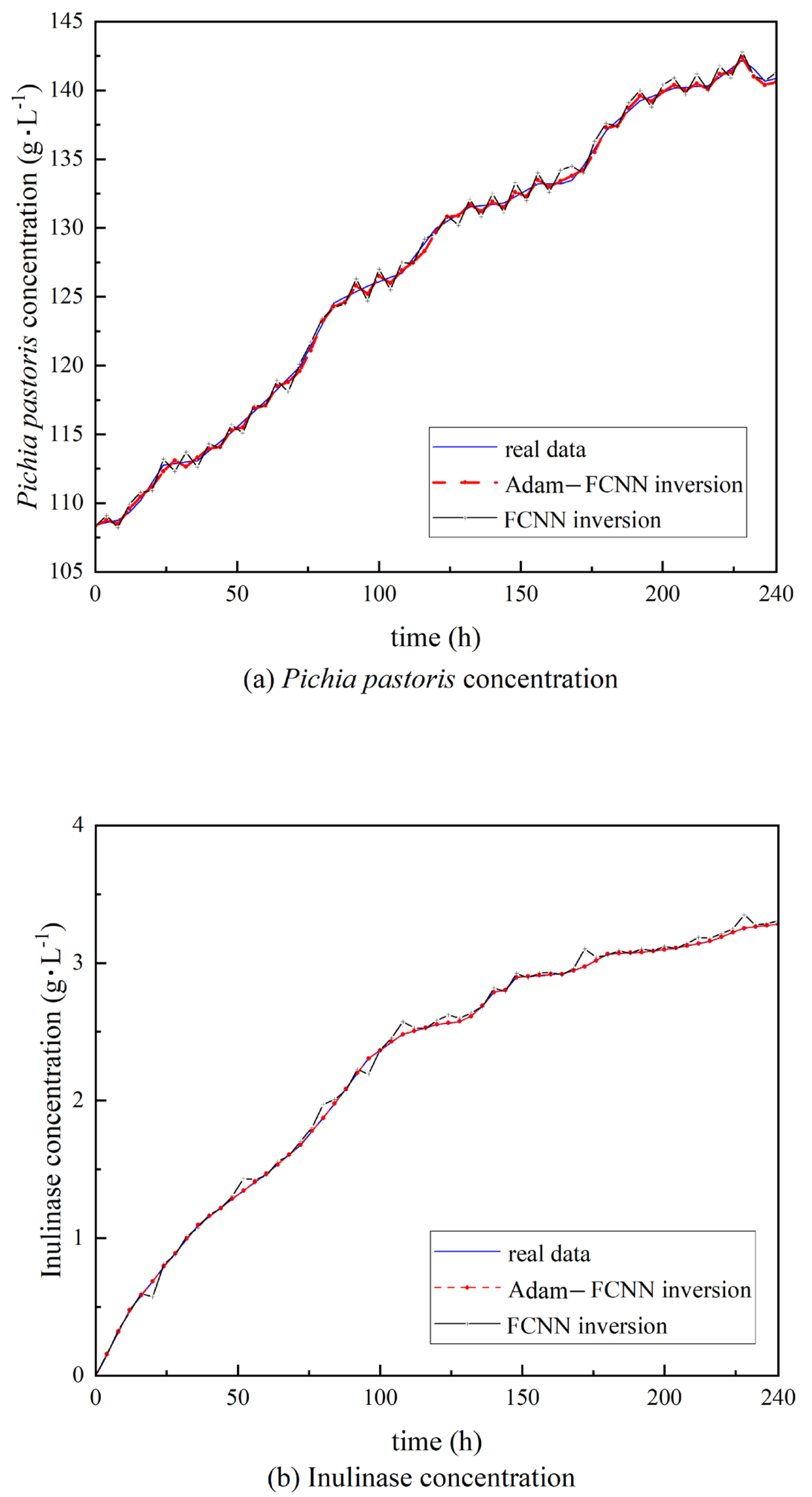
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Sun, Y.; Li, J. Advances in the application of Pichia pastoris in industrial biotechnology. Biotechnol. J. 2023, 18, 803–820. [Google Scholar] [CrossRef]
- Vijaya Krishna, V.S.; Pappa, N.; Vasantha Rani, S.P.J. Deep Learning based Soft Sensor for Bioprocess Application. In Proceedings of the 2021 IEEE Second International Conference on Control, Measurement and Instrumentation (CMI), Kolkata, India, 8–10 January 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Zhou, L.; Hu, R.; Sun, Z. Improving fermentation efficiency through advanced modeling. Ind. Biotechnol. 2022, 39, 321–330. [Google Scholar] [CrossRef]
- Dai, X.Z.; Wang, W.C.; Ding, Y.H.; Sun, Z.Y. “Assumed inherent sensor” inversion-based ANN dynamic soft-sensing method and its application in erythromycin fermentation process. Comput. Chem. Eng. 2006, 30, 1203–1225. [Google Scholar] [CrossRef]
- Feng, R.; Shen, W.; Shao, H. A Soft Sensor Modeling Approach Using Support Vector Machines. In Proceedings of the 2003 American Control Conference (ACC), Denver, CO, USA, 4–6 June 2003; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Zeng, D.W.; Zhu, Y.F.; Zhou, M.H.; Kondo, A.; Hasunuma, T.; Zhao, X.Q. Fermentation Design and Process Optimization Strategy Based on Machine Learning. BioDesign Res. 2025, 7, 100002. [Google Scholar] [CrossRef]
- Zhang, H.; Ma, Y.; Sun, L. The limitations of gradient-based optimization in dynamic systems. In Advances in Bioengineering Systems; Springer: Berlin, Germany, 2022; pp. 145–156. [Google Scholar] [CrossRef]
- Zhang, B.; Rahmat Samii, Y. Adaptive Moment (Adam) Estimation Optimization Applied to AVM-FEM for Rapid Convergence. In Proceedings of the 2021 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting (APS/URSI), Singapore, 4–10 December 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Dragoi, E.N.; Curteanu, S.; Galaction, A.I.; Cascaval, D. Optimization Methodology Based on Neural Networks and Self-Adaptive Differential Evolution Algorithm Applied to an Aerobic Fermentation Process. Appl. Soft Comput. 2013, 13, 222–238. [Google Scholar] [CrossRef]
- Abualigah, L. Enhancing Real-Time Data Analysis through Advanced Machine Learning and Data Analytics Algorithms. Int. J. Online Biomed. Eng. 2025, 21, 4–25. [Google Scholar] [CrossRef]
- D’Anjou, M.C.; Daugulis, A.J. A model-based feeding strategy for fed-batch fermentation of recombinant Pichia pastoris. Biotechnol. Technol. 1997, 11, 865–868. [Google Scholar] [CrossRef]
- Zhang, W.; Hywood Potter, K.J.; Plantz, B.A.; Schlegel, V.L.; Smith, L.A.; Meagher, M.M. Pichia pastoris fermentation with mixed-feeds of glycerol and methanol: Growth kinetics and production improvement. J. Ind. Microbiol. Biotechnol. 2003, 30, 210–215. [Google Scholar] [CrossRef]
- Carly, F.; Niu, H.; Delvigne, F.; Fickers, P. Influence of methanol/sorbitol co-feeding rate on pAOX1 induction in a Pichia pastoris Mut+ strain in bioreactor with limited oxygen transfer rate. J. Ind. Microbiol. Biotechnol. 2016, 43, 517–523. [Google Scholar] [CrossRef]
- Canales, C.; Altamirano, C.; Berrios, J. The growth of Pichia pastoris Mut+ on methanol–glycerol mixtures fit to interactive dual-limited kinetics: Model development and application to optimized fed-batch operation for heterologous protein production. Bioprocess Biosyst. Eng. 2018, 41, 1827–1838. [Google Scholar] [CrossRef]
- Parashar, D.; Satyanarayana, T. Production of bacterial and yeast inulinases in Pichia pastoris and their applications. Appl. Microbiol. Biotechnol. 2016, 100, 8939–8958. [Google Scholar] [CrossRef]
- Liang, J.; Yuan, J. Oxygen transfer model in recombinant Pichia pastoris and its application in biomass estimation. Biotechnol. Lett. 2007, 29, 27–35. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Inan, M.; Meagher, M.M. Fermentation strategies for recombinant protein expression in the methylotrophic yeast Pichia pastoris. Biotechnol. Bioprocess Eng. 2000, 5, 275–287. [Google Scholar] [CrossRef]
- Cos, O.; Ramón, R.; Montesinos, J.L.; Valero, F. Operational strategies, monitoring, and control of heterologous protein production in the methylotrophic yeast Pichia pastoris under different promoters: A review. Microb. Cell Factories 2006, 5, 17. [Google Scholar] [CrossRef]
- González-Herbón, R.; González-Mateos, G.; Rodríguez-Ossorio, J.R.; Prada, M.A.; Morán, A.; Alonso, S.; Fuertes, J.J.; Domínguez, M. Assessment and deployment of a LSTM-based virtual sensor in an industrial process control loop. Neural Comput. Appl. 2024, 37, 10507–10519. [Google Scholar] [CrossRef]
- Singh, M.G.; Titli, A. Systems: Decomposition, Optimisation and Control; Pergamon Press: Oxford, UK, 1978; pp. 123–145. [Google Scholar]
- Ahmad, M.; Hirz, M.; Pichler, H.; Schwab, H. Pichia pastoris: A promising host for the production of recombinant proteins. J. Biotechnol. 2014, 170, 5301–5317. [Google Scholar]
- Kůrková, V.; Neruda, R.; Kárný, M. Limitations of Shallow Networks. In Recent Trends in Learning from Data; Springer: Cham, Switzerland, 2020; pp. 129–154. [Google Scholar] [CrossRef]
- Kong, Z.; Mollaali, A.; Moya, C.; Lu, N.; Lin, G. B-LSTM-MIONet: Bayesian LSTM-based Neural Operators for Learning the Response of Complex Dynamical Systems to Length-Variant Multiple Input Functions. arXiv 2023, arXiv:2311.16519. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: https://www.deeplearningbook.org/ (accessed on 18 November 2016).
- Menet, N.; Hersche, M.; Karunaratne, G.; Benini, L.; Sebastian, A.; Rahimi, A. MIMONets: Multiple-Input-Multiple-Output Neural Networks Exploiting Computation in Superposition. arXiv 2023, arXiv:2312.02829. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Ruder, S. An Overview of Gradient Descent Optimization Algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Luo, L.; Xiong, Y.; Liu, Y.; Sun, X. Adaptive Gradient Methods with Dynamic Bound of Learning Rate. arXiv 2019, arXiv:1902.09843. [Google Scholar]
- De, S.; Mukherjee, A.; Ullah, E. Convergence Guarantees for RMSProp and Adam in Non-Convex Optimization and an Empirical Comparison to Nesterov Acceleration. arXiv 2018, arXiv:1807.06766. [Google Scholar]
- Zaznov, I.; Badii, A.; Kunkel, J.; Dufour, A. AdamZ: An Enhanced Optimisation Method for Neural Network Training. arXiv 2024, arXiv:2411.15375. [Google Scholar]
- Bock, S.; Goppold, J.; Weiß, M. An Improvement of the Convergence Proof of the Adam-Optimizer. arXiv 2018, arXiv:1804.10587. [Google Scholar]
- Reddi, S.J.; Kale, S.; Kumar, S. On the Convergence of Adam and Beyond. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Kaya, U.; Gopireddy, S.; Urbanetz, N.; Kreitmayer, D.; Gutheil, E.; Nopens, I.; Verwaeren, J. Quantifying the hydrodynamic stress for bioprocesses. Biotechnol. Prog. 2023, 39, e3367. [Google Scholar] [CrossRef]
- Zhu, S.; Xu, H.; Liu, Y.; Hong, Y.; Yang, H.; Zhou, C.; Tao, L. Computational advances in biosynthetic gene cluster discovery and prediction. Biotechnol. Adv. 2025, 79, 108632. [Google Scholar] [CrossRef]
- StepHen, G.; Carlos, A.; Duran, V.; Jankauskas, K.; Lovett, D.; Farid, S.S.; Lennox, B. Modern day monitoring and control challenges outlined on an industrial-scale benchmark fermentation process. Comput. Chem. Eng. 2019, 130, 106471. [Google Scholar] [CrossRef]
- Jiang, Y.; Yin, S.; Dong, J.; Kaynak, O. A Review on Soft Sensors for Monitoring, Control, and Optimization of Industrial Processes. IEEE Sens. J. 2021, 21, 12868–12881. [Google Scholar] [CrossRef]
- Patrick, R.; Thomas, V.; Sikvia, P.; Jordan, M.; Perilleux, A.; Souquet, J.; Bielser, J.M.; Herwig, C.; Villiger, T.K. Maduramycin, a novel glycosylation modulator for mammalian fed-batch and steady-state perfusion processes. J. Biotechnol. 2024, 383, 73–75. [Google Scholar] [CrossRef]



| Environmental Parameter | Unit | Measuring Method |
|---|---|---|
| Agitation Speed | rpm | Rotational Speed Sensor |
| Fermentation Temperature | °C | Temperature Sensor |
| Inlet Airflow Rate | L/min | Flowmeter |
| Dissolved Oxygen Do | % | Dissolved Oxygen Analyzer |
| Fermentation Liquid Volume | L | Differential Pressure Sensor |
| Ammonia Water Flow Rate | L/min | Flow Velocity Sensor |
| Methanol Flow Rate | L/min | Flow Velocity Sensor |
| Antifoaming Agent Flow Rate | L/min | Flow Velocity Sensor |
| Phosphate Flow Rate | L/min | Flow Velocity Sensor |
| Pressure in Tank | Mpa | Diaphragm Pressure Gauge |
| Fermentation Time | h | Timer |
| pH Value of Fermentation Liquid | - | pH Electrode |
| Dataset | MSE (FCNN Inversion) | MSE (Adam-FCNN Inversion) |
|---|---|---|
| Training | 0.5127 | 0.0315 |
| Testing | 0.4981 | 0.0371 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Ma, W.; Jiang, H.; Huang, S. Research on Soft-Sensing Method Based on Adam-FCNN Inversion in Pichia pastoris Fermentation. Sensors 2025, 25, 4105. https://doi.org/10.3390/s25134105
Wang B, Ma W, Jiang H, Huang S. Research on Soft-Sensing Method Based on Adam-FCNN Inversion in Pichia pastoris Fermentation. Sensors. 2025; 25(13):4105. https://doi.org/10.3390/s25134105
Chicago/Turabian StyleWang, Bo, Wenyu Ma, Hui Jiang, and Shaowen Huang. 2025. "Research on Soft-Sensing Method Based on Adam-FCNN Inversion in Pichia pastoris Fermentation" Sensors 25, no. 13: 4105. https://doi.org/10.3390/s25134105
APA StyleWang, B., Ma, W., Jiang, H., & Huang, S. (2025). Research on Soft-Sensing Method Based on Adam-FCNN Inversion in Pichia pastoris Fermentation. Sensors, 25(13), 4105. https://doi.org/10.3390/s25134105







