Anomaly Detection Method for Hydropower Units Based on KSQDC-ADEAD Under Complex Operating Conditions
Abstract
1. Introduction
- (1)
- KSQDC Condition Identification Algorithm: A novel two-stage learning paradigm that synergistically combines K-means clustering’s initialization capability with quadratic discriminant analysis’s nonlinear boundary construction. This integration enables precise identification of complex nonlinear condition boundaries and accurate classification of hydroelectric unit operational states.
- (2)
- ADEAD Ensemble Anomaly Detection Algorithm: An adaptive density-aware ensemble framework comprising five complementary sub-models: base isolation forest, extended isolation forest, local density estimation, local outlier factor, and cluster-based scoring. The algorithm enhances detection accuracy and robustness through dynamic inter-model collaboration and adaptive weight fusion strategies.
- (3)
- Integrated Condition-Adaptive Framework: A comprehensive end-to-end system that automates the entire pipeline from data preprocessing and condition identification to anomaly detection. The framework achieves performance optimization through feedback mechanisms and provides a systematic solution for hydroelectric unit health monitoring and predictive maintenance.
2. Related Works
2.1. K-Means
2.2. Quadratic Discriminant Clustering (QDC)
2.3. Isolation Forest
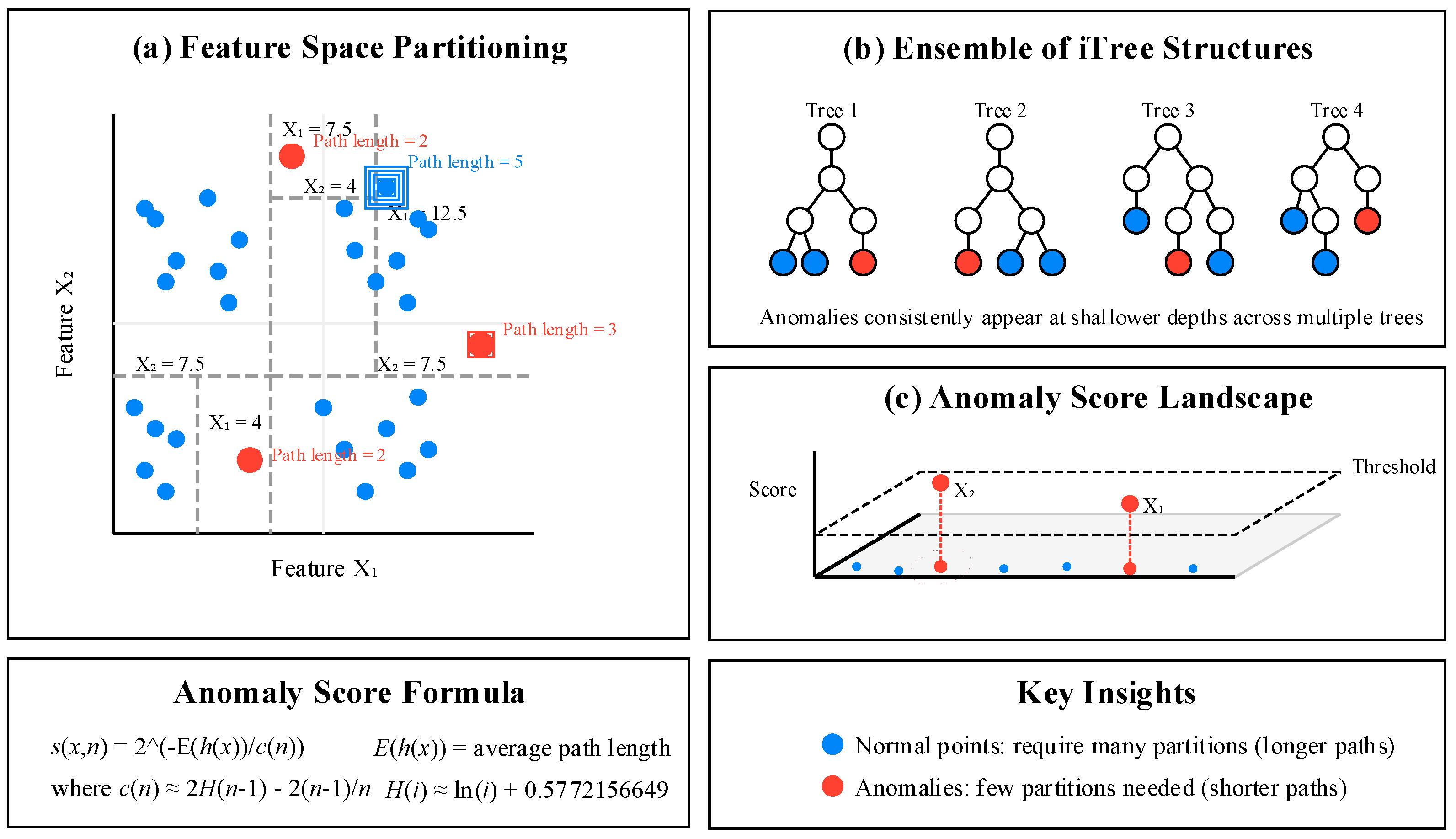
3. The Proposed Method
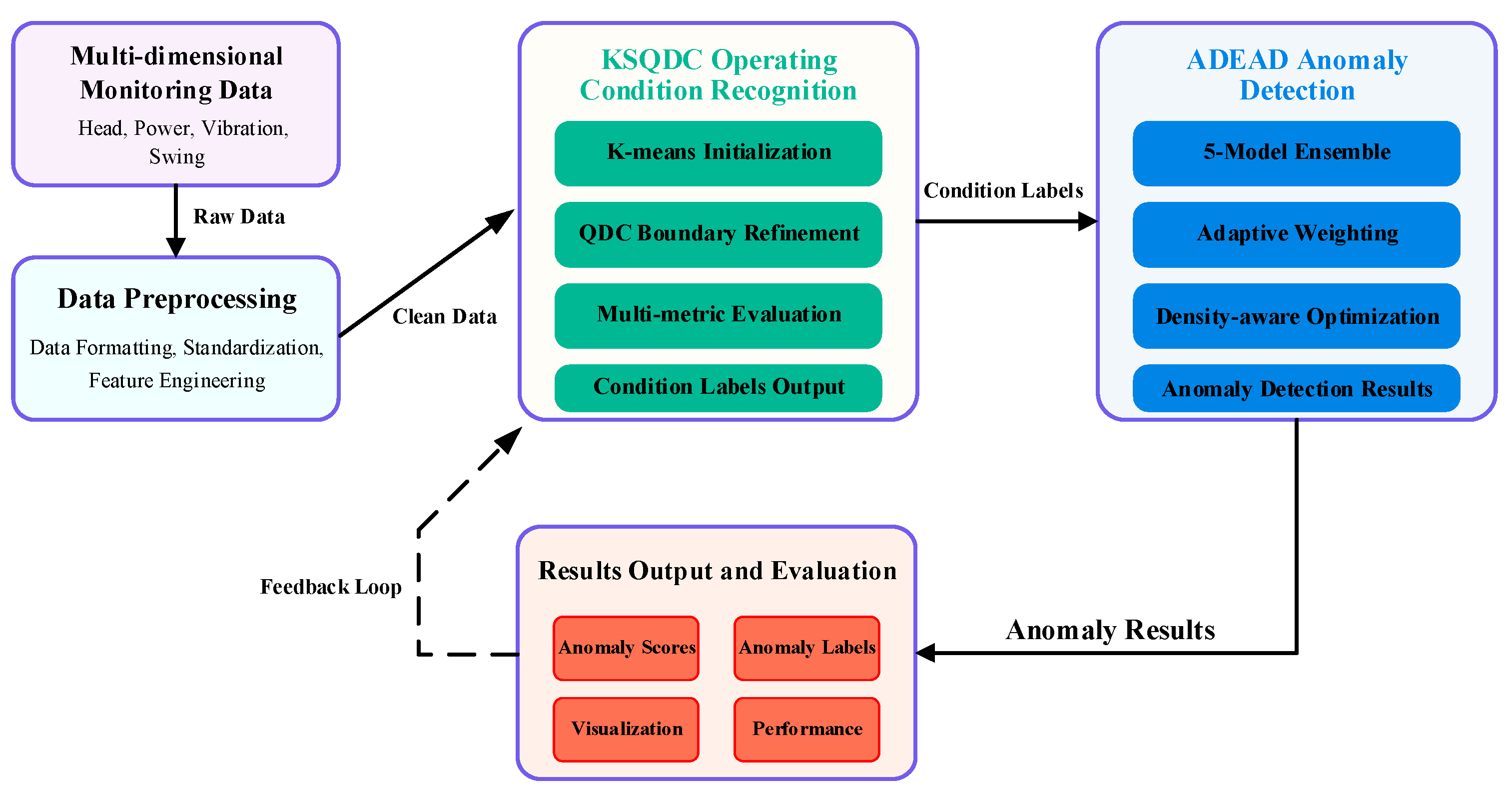
3.1. KSQDC-ADEAD Integrated Anomaly Detection Method
| Algorithm 1: KSQDC-ADEAD integrated framework | |
| Input: | Multi-dimensional monitoring data , maximum clusters |
| Output: | Operating condition labels , anomaly scores , anomaly labels A |
| 1. | Data preprocessing: StandardScaler(x) |
| 2. | For to do |
| 3. | Compute multi-metric evaluation: |
| 4. | End for |
| 5. | Optimal cluster determination: |
| 6. | K-means initialization: |
| 7. | For to do |
| 8. | |
| 9. | |
| 10. | |
| 11. | End for |
| 12. | QDA boundary refinement: For to do |
| 13. | |
| 14. | |
| 15. | End for |
| 16. | For do |
| 17. | |
| 18. | ADEAD sub-model initialization: |
| 19. | BaseIsolationForest () |
| 20. | ExtendedIsolationForest |
| 21. | LocalDensityEstimation |
| 22. | LocalOutlierFactor |
| 23. | ClusterBasedScoring |
| 24. | For to 5 do |
| 25. | . decision function() |
| 26. | |
| 27. | End for |
| 28. | Adaptive weight calculation: |
| 29. | |
| 30. | |
| 31. | Score fusion: |
| 32. | Boundary optimization using silhouette coefficient: |
| 33. | |
| 34. | If for anomaly or for normal then exchange labels |
| 35. | Update |
| 36. | End for |
| 37. | Return Operating condition labels , anomaly scores , anomaly labels |
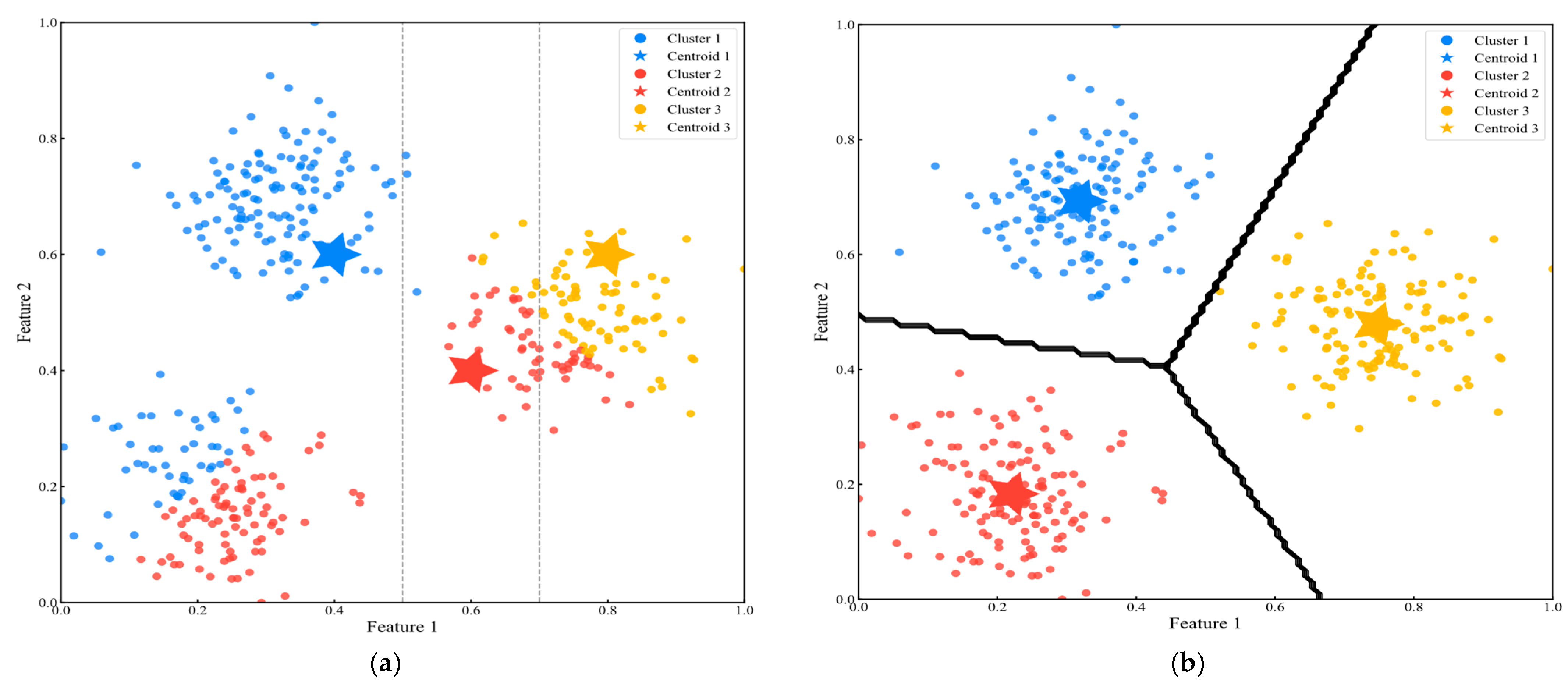
3.2. K-Means Seeded Quadratic Discriminant Clustering (KSQDC)
3.2.1. Non-Linear Decision Boundary Construction
3.2.2. Adaptive Determination of Optimal Number of Classes
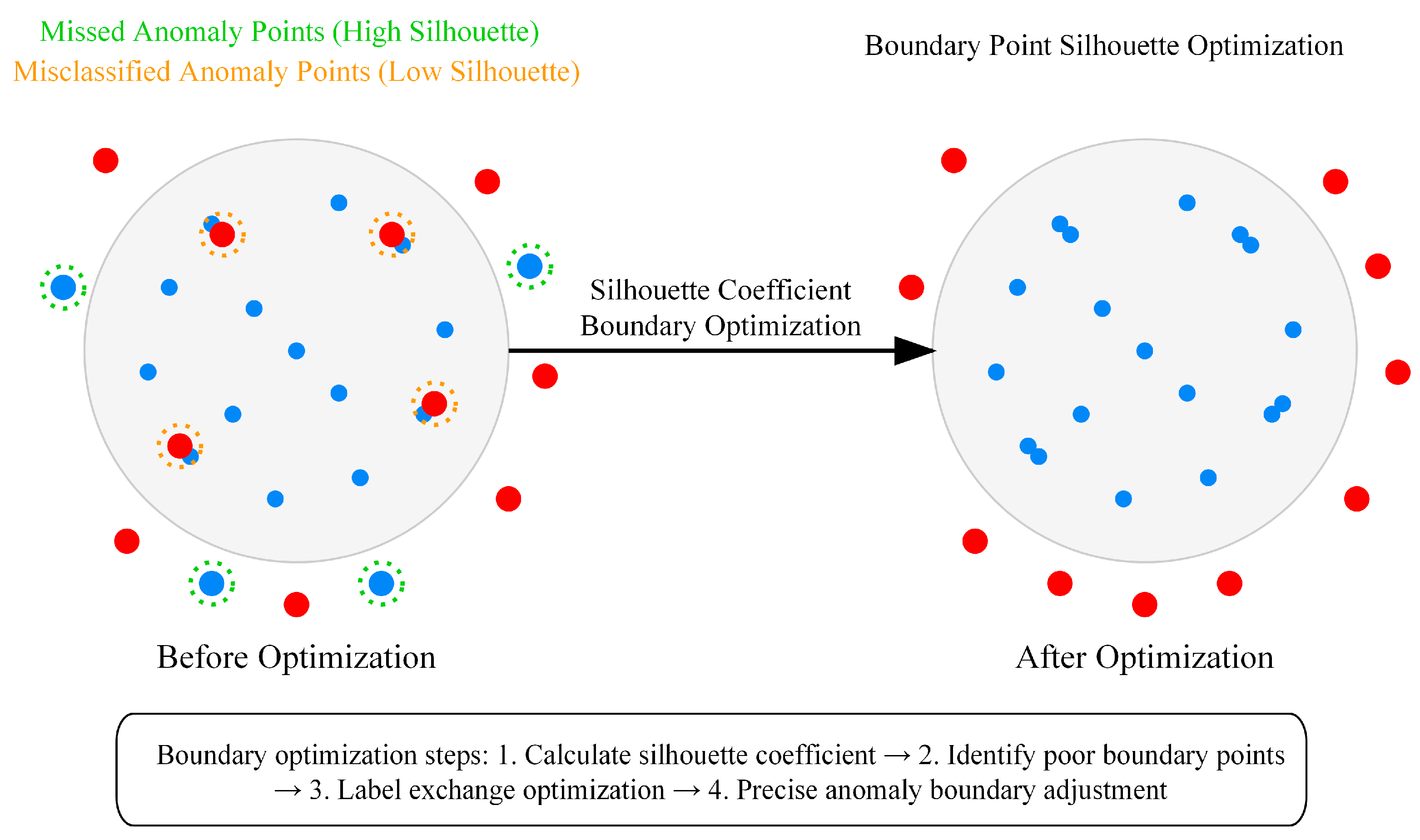
3.3. Adaptive Density-Aware Ensemble Anomaly Detection Algorithm (ADEAD)
3.3.1. Multi-Model Ensemble Architecture for Anomaly Detection
3.3.2. Density-Adaptive Anomaly Optimization Strategy
4. Experimental Study
4.1. Data Description
4.2. Experimental Design
4.2.1. Experimental Methods
4.2.2. Parameter Configuration
4.3. Experimental Results
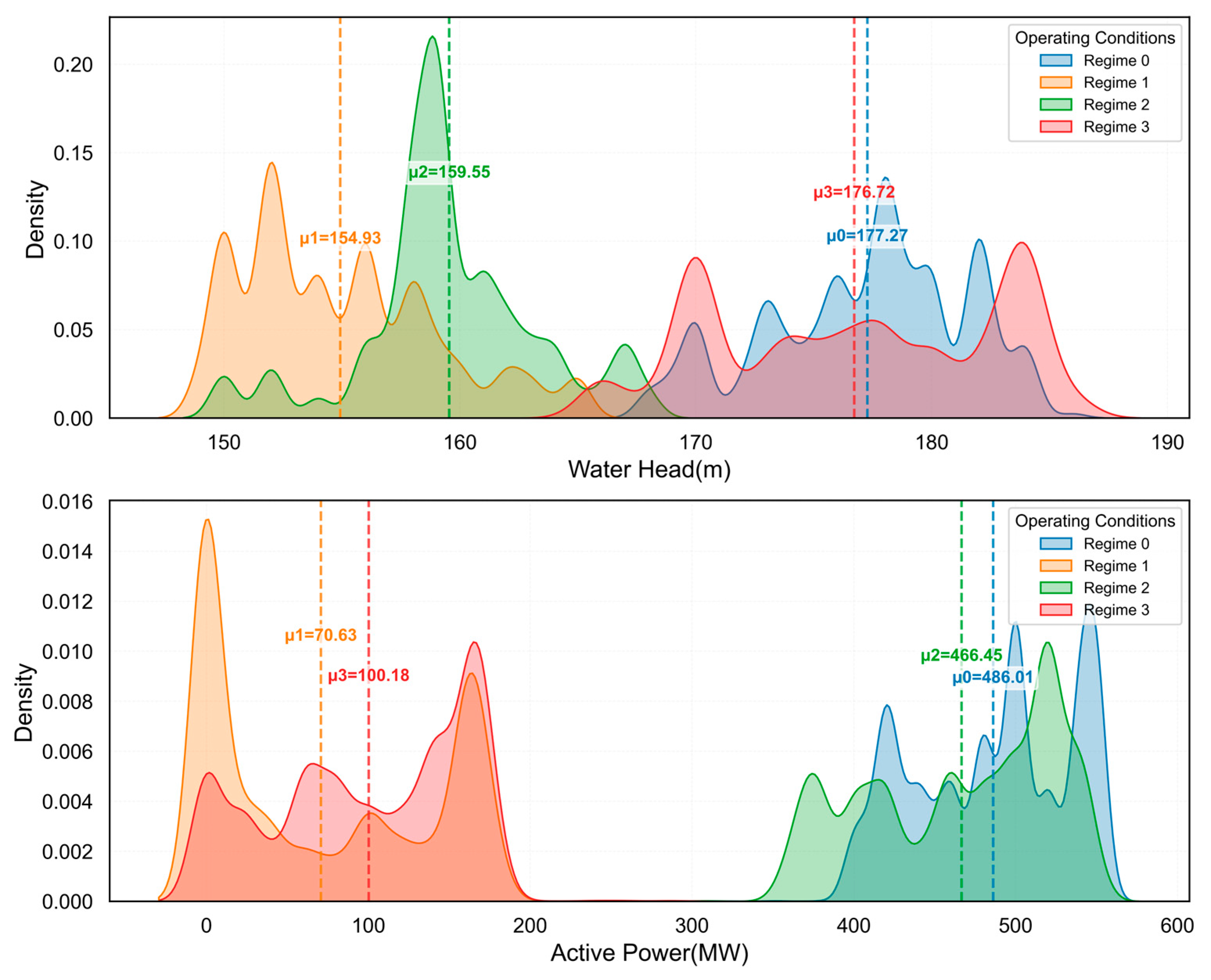
4.3.1. Analysis of Operating Condition Recognition Results
4.3.2. Comparison of Different Operating Condition Recognition Methods
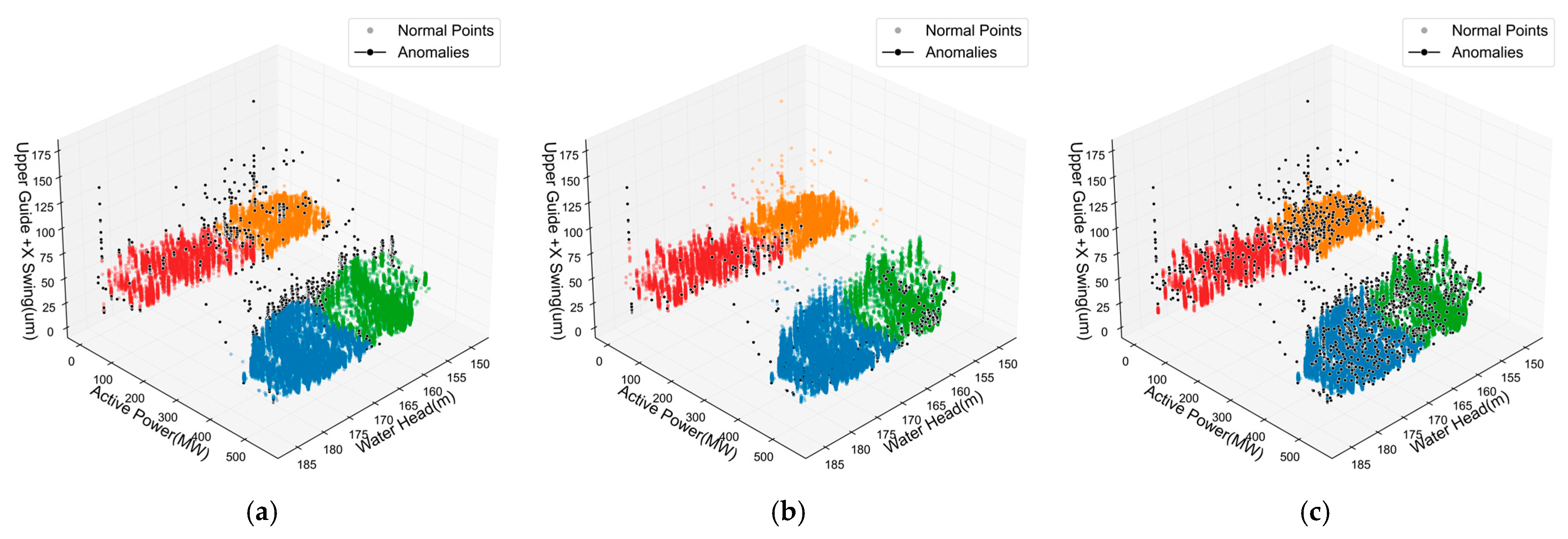
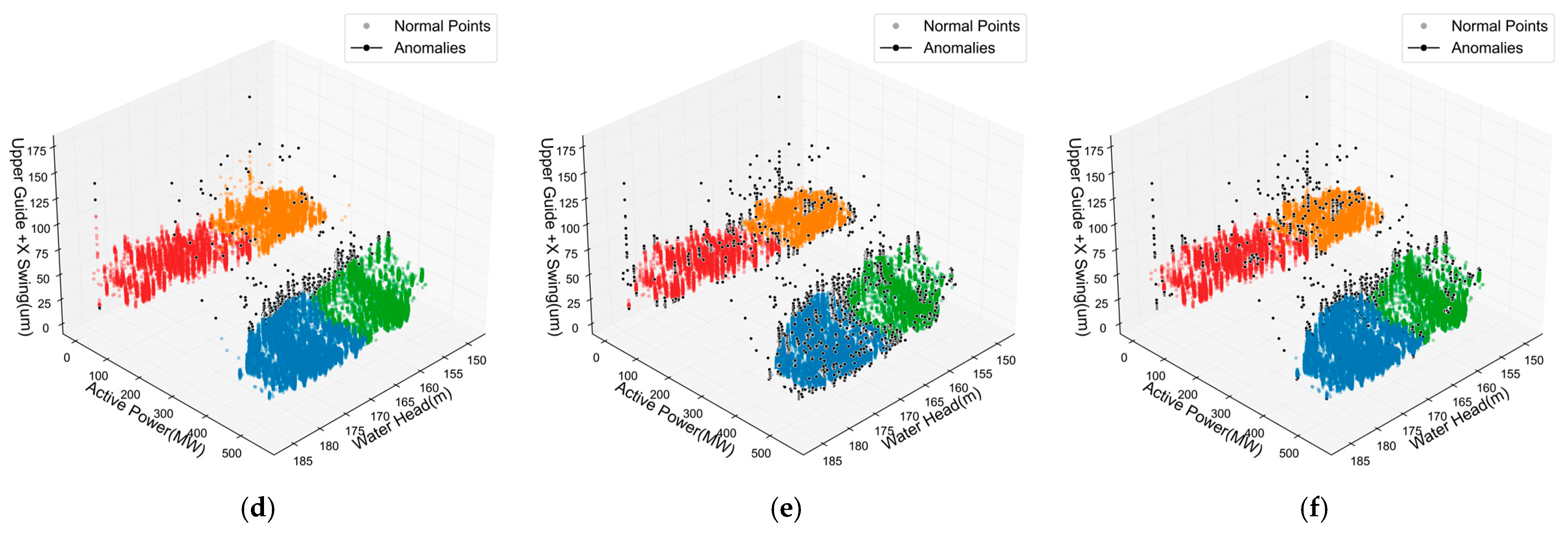
4.3.3. Analysis of Anomaly Detection Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Yuan, W.; Duan, G.; Wang, B.; Liu, H. Detection of abnormal sound of hydroelectric unit based on combination of deep convolutional neural network and Gaussian mixture model. Water Resour. Power 2023, 41, 188–191. [Google Scholar]
- Liu, Y.; Garg, S.; Nie, J.; Zhang, Y.; Xiong, Z.; Kang, J.; Hossain, M.S. Deep anomaly detection for time-series data in industrial IoT: A communication-efficient on-device federated learning approach. IEEE Internet Things J. 2021, 8, 6348–6358. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, Z.; Yuan, Z.; Deng, F. Review on identification and cleaning of abnormal wind power data for wind farms. Power Syst. Technol. 2023, 47, 2367–2380. [Google Scholar]
- Wang, C.; Wei, C. Characteristics of outliers in wind speed-power operation data of wind turbines and its cleaning method. Trans. China Electrotech. Soc. 2018, 33, 3353–3361. [Google Scholar]
- Song, S.; Fan, M. Design of big data anomaly detection model based on random forest algorithm. J. Jilin Univ. 2023, 53, 2659–2665. [Google Scholar]
- Wang, Y.; Infield, D.G.; Stephen, B.; Galloway, S.J. Copula-based model for wind turbine power curve outlier rejection. Wind Energy 2014, 17, 1677–1688. [Google Scholar] [CrossRef]
- Hu, Y.; Qiao, Y. Wind power data cleaning method based on confidence equivalent boundary model. Autom. Electr. Power Syst. 2018, 42, 18–23. [Google Scholar]
- Mo, H.; He, K.; Zhao, X.; Wang, S.; Xu, X.; Wen, H. Abnormal noise analysis method of hydropower units based on isolated forest. China Meas. Test 2025, 51, 162–168. [Google Scholar]
- Wang, K.; Wang, S.; Xiong, X.; Li, A.; Qiu, X.; Wang, B. A dynamic interval coverage method for detecting abnormal vibration of hydroelectric units. J. Hydraul. Eng. 2025, 56, 599–610. [Google Scholar]
- Guha, S.; Mishra, N.; Roy, G.; Schrijvers, O. Robust random cut forest based anomaly detection on streams. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 16–23 July 2016; PMLR: New York, NY, USA, 2016; pp. 2712–2721. [Google Scholar]
- Chen, L.; Tao, T.; Zhang, L.; Lu, B.; Hang, Z. Electric power remote monitor anomaly detection with a density-based data stream clustering algorithm. Autom. Control Intell. Syst. 2015, 3, 71–75. [Google Scholar] [CrossRef]
- Zhang, G.; Wen, L.; Wu, M.; Liu, T.; Zheng, K.; Huang, F.; Yuan, P. Anomaly detection of transformer loss data based on a robust random cut forest. J. East China Norm. Univ. (Nat. Sci.) 2021, 6, 135–146. [Google Scholar][Green Version]
- Yassin, W.; Udzir, N.I.; Muda, Z.; Sulaiman, N. Anomaly-based intrusion detection through k-means clustering and naives bayes classification. In Proceedings of the 4th International Conference on Computing and Informatics, Kuching, Malaysia, 28–30 August 2013; IEEE: Kuala Lumpur, Malaysia, 2013; pp. 298–303. [Google Scholar]
- San, M.; Wan, F.; Zhao, S.; Wu, Q.; Quan, T.; Hu, J. Anomaly detection technology of hydropower unit based on full head three-dimensional historical data. Hydropower Stn. Mech. Electr. Technol. 2025, 48, 85–89. [Google Scholar][Green Version]
- Duan, R.; Zhou, J.; Cai, Y.; Wang, T.; Duan, L. Construction method of state index for hydroelectric generating unit with variable working condition based on low quality data. Water Power 2022, 40, 183–187. [Google Scholar][Green Version]
- Tan, Z.; Ji, L.; Jing, X.; Wang, P.; Tian, H. Data cleaning method for state monitoring of hydroelectric unit based on KD-Tree and DBSCAN. China Rural Water Hydropower 2024, 3, 250–254. [Google Scholar][Green Version]
- Du, W.; Huang, D.; Ji, H. Abnormal monitoring and alarming method of hydroelectric generating unit equipment based on least square support vector machine. Electr. Technol. Econ. 2024, 12, 77–80. [Google Scholar][Green Version]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Ahmed, M.; Seraj, R.; Islam, S.M.S. The k-means algorithm: A comprehensive survey and performance evaluation. Electronics 2020, 9, 1295. [Google Scholar] [CrossRef]
- Guo, Y.; Hastie, T.; Tibshirani, R. Regularized discriminant analysis and its application in microarrays. Biostatistics 2007, 8, 86–100. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; IEEE: Pisa, Italy, 2008; pp. 413–422. [Google Scholar]
- Hariri, S.; Kind, M.C.; Brunner, R.J. Extended isolation forest. IEEE Trans. Knowl. Data Eng. 2019, 32, 2343–2353. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Caliński, T.; Harabasz, J. A dendrite method for cluster analysis. Commun. Stat. Theory Methods 1974, 3, 1–27. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A cluster separation measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, 1, 224–227. [Google Scholar] [CrossRef]
- Ketchen, D.J.; Shook, C.L. The application of cluster analysis in strategic management research: An analysis and critique. Strateg. Manag. J. 1996, 17, 441–458. [Google Scholar] [CrossRef]
- Berrar, D. Bayes’ theorem and naive Bayes classifier. In Encyclopedia of Bioinformatics and Computational Biology: ABC of Bioinformatics; Elsevier: Amsterdam, The Netherlands, 2018; pp. 403–412. [Google Scholar]
- McLachlan, G.J.; Lee, S.X.; Rathnayake, S.I. Finite mixture models. Annu. Rev. Stat. Appl. 2019, 6, 355–378. [Google Scholar] [CrossRef]
- Ghahramani, Z. An introduction to hidden Markov models and Bayesian networks. Int. J. Pattern Recognit. Artif. Intell. 2001, 15, 9–42. [Google Scholar] [CrossRef]
- Murtagh, F.; Contreras, P. Algorithms for hierarchical clustering: An overview. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2012, 2, 86–97. [Google Scholar] [CrossRef]
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. ACM SIGMOD Rec. 2000, 29, 93–104. [Google Scholar] [CrossRef]
- Schubert, E.; Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. DBSCAN revisited, revisited: Why and how you should (still) use DBSCAN. ACM Trans. Database Syst. 2017, 42, 1–21. [Google Scholar] [CrossRef]
- Ruff, L.; Vandermeulen, R.; Goernitz, N.; Deecke, L.; Siddiqui, S.A.; Binder, A.; Müller, E.; Kloft, M. Deep one-class classification. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; PMLR: Stockholm, Sweden, 2018; pp. 4393–4402. [Google Scholar]



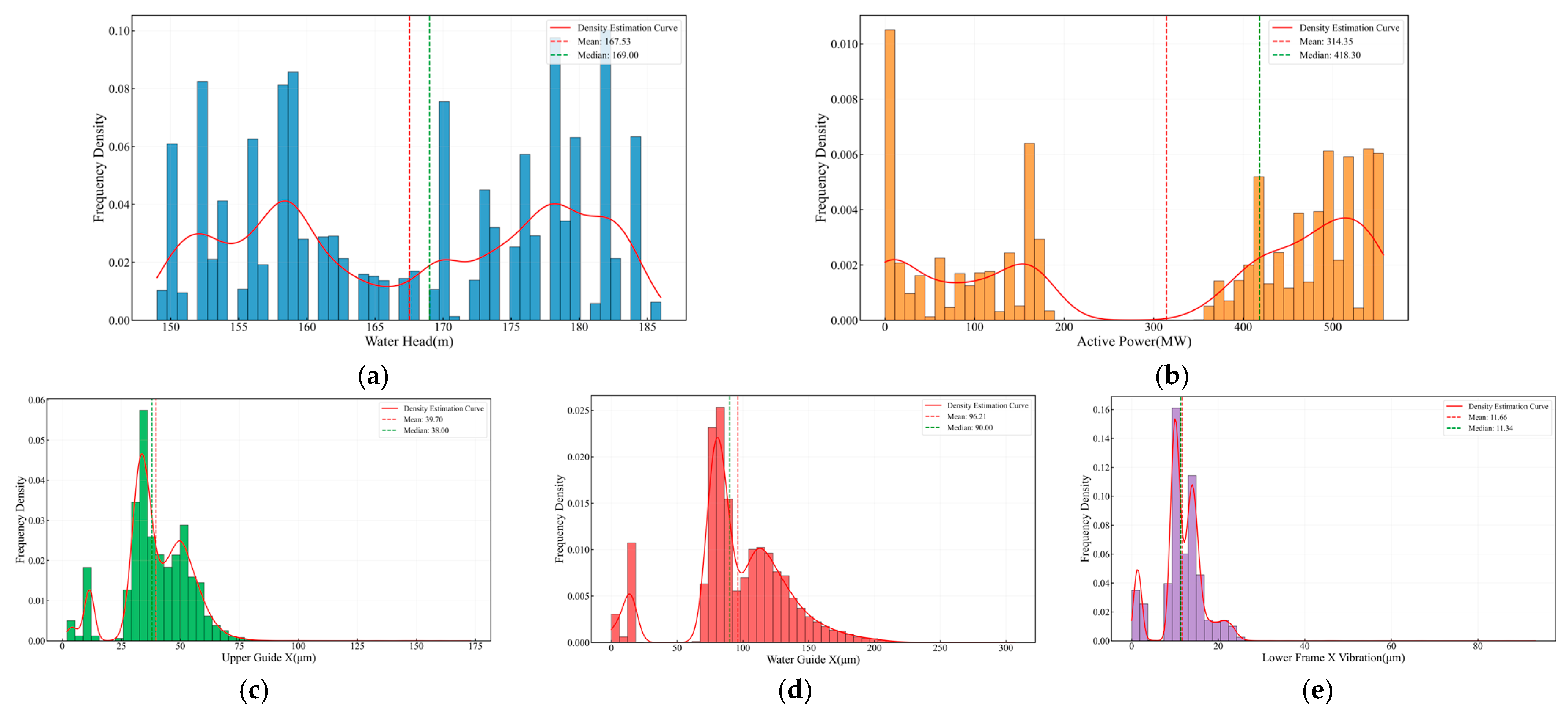



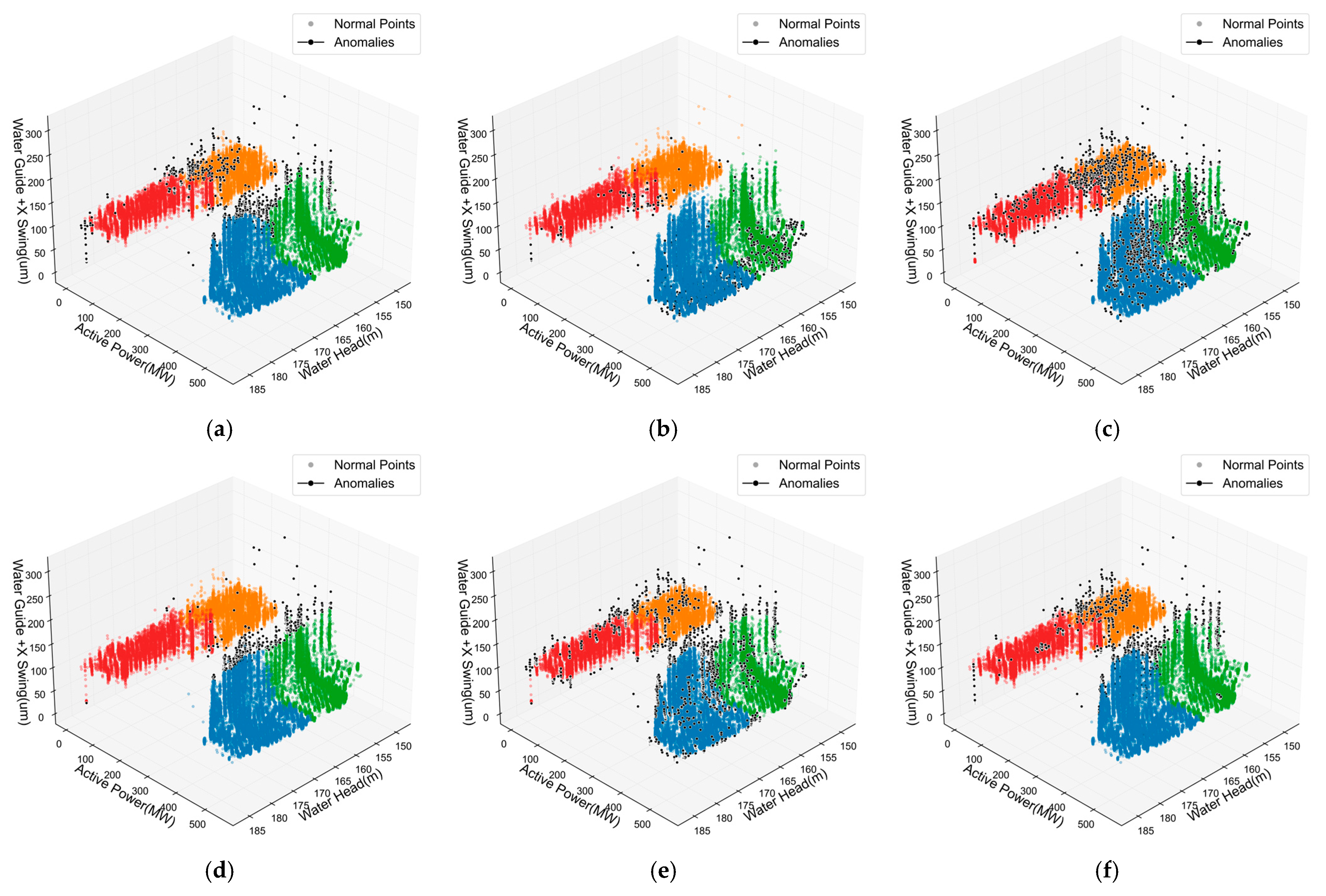
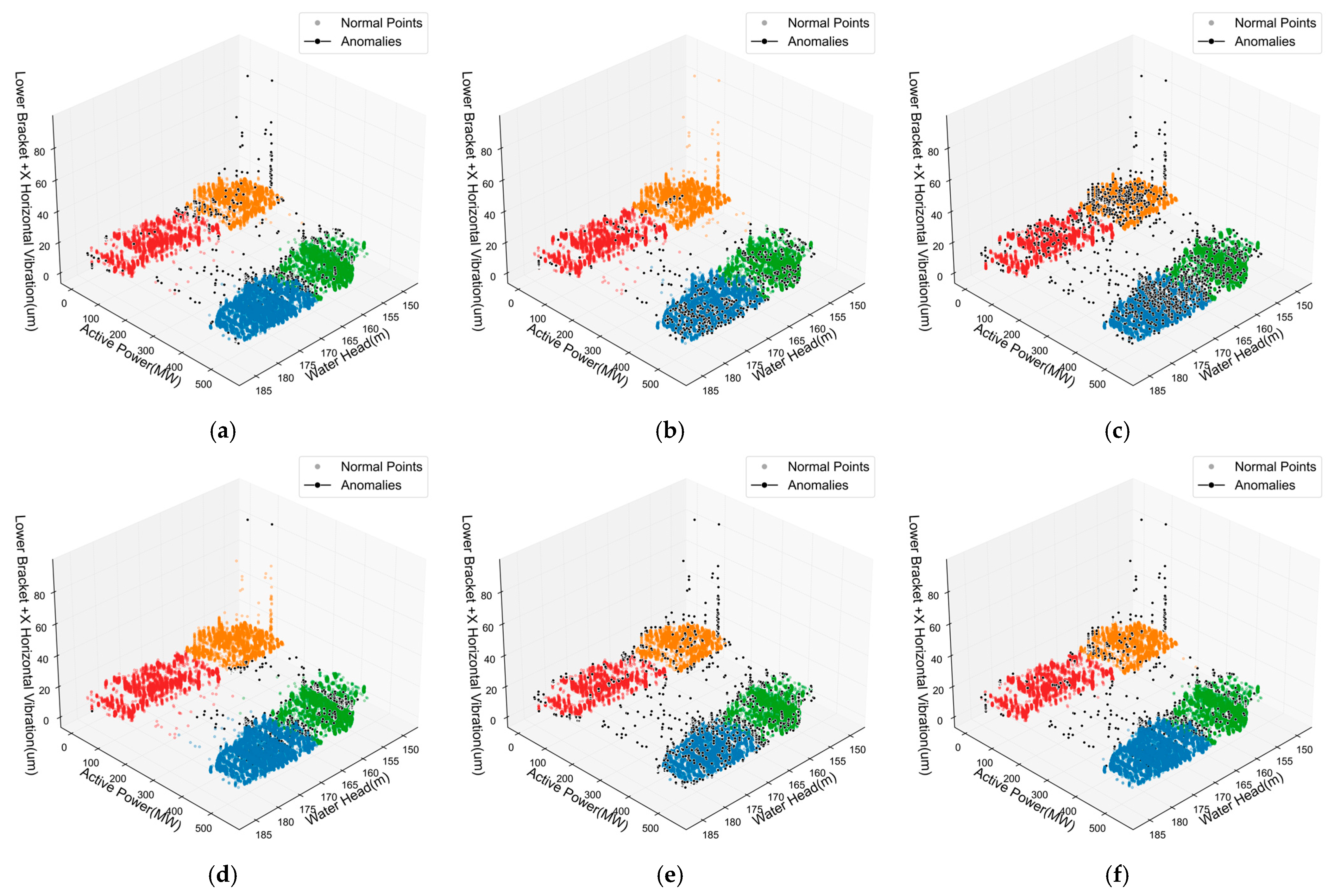
| Parameter | Value |
|---|---|
| Turbine type | Mixed-flow |
| Rated capacity | 550 MW |
| Design water head | 165 m |
| Operating head range | 135–190 m |
| Rated speed | 125 r/min |
| Commissioning date | Late 1990s |
| Parameter Category | Key Metrics | Measurement Points | Value Range | Sampling Interval |
|---|---|---|---|---|
| Water pressure | Gross and net head | 2 | 150–185 m | 10 min |
| Power output | Active power | 1 | 0–500 MW | 10 min |
| Vibration | Multi-directional at 22 sites | 22 | Highly variable | 10 min |
| Shaft displacement | Whirling at guide and thrust bearings (upper guide, lower guide, thrust) | 6 | 0–175 μm | 10 min |
| Total | — | 31 | — | 10 min |
| Stage | Full Method Name | Abbreviation | Fundamental Principle |
|---|---|---|---|
| Operating condition recognition | Gaussian Naive Bayes | GNB | Classification method based on conditional probability and feature independence assumptions |
| Gaussian Mixture Model | GMM | Data distribution modeling using weighted combinations of multiple Gaussian distributions | |
| Hidden Markov Model | HMM | Time-series data analysis through hidden state transition probability modeling | |
| K-means Clustering | KM | Clustering method minimizing the sum of squared distances from samples to cluster centers | |
| Hierarchical Clustering | HC | Clustering method that builds a hierarchy of clusters using linkage criteria | |
| K-means Seeded Quadratic Discriminant Analysis | KSQDC | Hybrid method combining K-means clustering and quadratic discriminant analysis | |
| Anomaly detection | Isolation Forest | iForest | Isolation of sample points through random decision tree construction |
| Local Outlier Factor | LOF | Anomaly identification based on local density deviation | |
| Density-Based Spatial Clustering | DBSCAN | Anomaly detection through identification of high- and low-density regions | |
| Elliptic Envelope | EE | Identification of distribution edge anomalies by fitting minimum volume ellipsoids | |
| One-Class Support Vector Machine | OCSVM | Separation of normal samples from anomalies using hyperspheres | |
| Adaptive Density Ensemble | ADEAD | Integration of multiple basic anomaly detectors with adaptive weight adjustment |
| Operating Condition | Sample Count | Proportion (%) | Water Head Mean (m) | Head Standard Deviation (m) | Active Power Mean (MW) | Active Power Standard Deviation (MW) | Compactness |
|---|---|---|---|---|---|---|---|
| 0 | 22,191 | 36.36% | 177.29 | 4.15 | 486.90 | 47.55 | 465.12 |
| 1 | 16,404 | 26.88% | 154.61 | 3.76 | 67.84 | 68.21 | 426.48 |
| 2 | 12,805 | 20.98% | 159.58 | 3.81 | 465.04 | 57.10 | 287.53 |
| 3 | 9631 | 15.78% | 176.08 | 6.31 | 103.42 | 59.39 | 233.39 |
| Method | IC | CDB | SC | Total Time/s |
|---|---|---|---|---|
| GNB | 353.13 | 0.96 | 0.62 | 38.48 |
| GMM | 71,512.02 | 0.94 | 0.53 | 37.88 |
| HMM | 239.90 | 0.89 | 0.32 | 36.15 |
| KM | 351.48 | 0.96 | 0.63 | 36.58 |
| HC | 384.15 | 0.96 | 0.60 | 37.90 |
| KSQDC | 354.45 | 0.98 | 0.64 | 36.29 |
| Method | SC | Anomaly Count | Anomaly Ratio | Density Ratio | Efficiency Score | Separation | Comprehensive_Score | Total Time/s |
|---|---|---|---|---|---|---|---|---|
| iForest | 0.19 | 1182 | 2.00% | 17.23% | 8.37 | 2.72 | 0.25 | 0.43 |
| LOF | 0.11 | 1171 | 1.98% | 69.37% | 21.01 | 2.48 | 0.21 | 1.22 |
| DBSCAN | 0.08 | 1367 | 2.31% | 16.20% | 8.87 | 2.44 | 0.18 | 1.37 |
| EE | 0.19 | 1184 | 2.00% | 17.04% | 0.44 | 2.74 | 0.25 | 10.95 |
| OCSVM | 0.16 | 2681 | 4.54% | 26.99% | 3.44 | 2.57 | 0.23 | 7.39 |
| ADEAD | 0.28 | 1184 | 2.00% | 28.33% | 0.88 | 3.02 | 0.30 | 6.29 |
| Method | SC | Anomaly Count | Anomaly Ratio | Density Ratio | Efficiency Score | Separation | Comprehensive_Score | Total Time/s |
|---|---|---|---|---|---|---|---|---|
| iForest | 0.20 | 1174 | 2.00% | 23.33% | 8.49 | 2.78 | 0.26 | 0.35 |
| LOF | 0.12 | 1155 | 1.97% | 60.49% | 20.46 | 2.47 | 0.21 | 1.09 |
| DBSCAN | 0.06 | 1291 | 2.20% | 19.75% | 7.37 | 2.36 | 0.17 | 1.27 |
| EE | 0.20 | 1176 | 2.00% | 24.08% | 0.45 | 2.76 | 0.25 | 5.87 |
| OCSVM | 0.18 | 2939 | 5.00% | 40.02% | 3.88 | 2.65 | 0.24 | 6.02 |
| ADEAD | 0.34 | 1176 | 2.00% | 40.22% | 1.09 | 3.30 | 0.34 | 5.60 |
| Method | SC | Anomaly Count | Anomaly Ratio | Density Ratio | Efficiency Score | Separation | Comprehensive_Score | Total Time/s |
|---|---|---|---|---|---|---|---|---|
| iForest | 0.15 | 1210 | 2.00% | 17.22% | 8.69 | 2.56 | 0.22 | 0.42 |
| LOF | 0.10 | 1208 | 2.00% | 57.77% | 18.72 | 2.40 | 0.20 | 1.07 |
| DBSCAN | 0.07 | 1594 | 2.64% | 15.86% | 9.82 | 2.42 | 0.18 | 1.34 |
| EE | 0.11 | 1210 | 2.00% | 31.49% | 1.13 | 2.46 | 0.20 | 6.42 |
| OCSVM | 0.09 | 2331 | 3.86% | 23.97% | 2.79 | 2.40 | 0.19 | 7.32 |
| ADEAD | 0.16 | 1210 | 2.00% | 16.93% | 0.43 | 2.63 | 0.23 | 6.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, T.; Zhao, X.; Shi, Y.; Jing, X.; Lei, W.; Guo, J.; Meng, Y.; Zhang, Z. Anomaly Detection Method for Hydropower Units Based on KSQDC-ADEAD Under Complex Operating Conditions. Sensors 2025, 25, 4093. https://doi.org/10.3390/s25134093
Yi T, Zhao X, Shi Y, Jing X, Lei W, Guo J, Meng Y, Zhang Z. Anomaly Detection Method for Hydropower Units Based on KSQDC-ADEAD Under Complex Operating Conditions. Sensors. 2025; 25(13):4093. https://doi.org/10.3390/s25134093
Chicago/Turabian StyleYi, Tongqiang, Xiaowu Zhao, Yongjie Shi, Xiangnan Jing, Wenyang Lei, Jiang Guo, Yang Meng, and Zhengyu Zhang. 2025. "Anomaly Detection Method for Hydropower Units Based on KSQDC-ADEAD Under Complex Operating Conditions" Sensors 25, no. 13: 4093. https://doi.org/10.3390/s25134093
APA StyleYi, T., Zhao, X., Shi, Y., Jing, X., Lei, W., Guo, J., Meng, Y., & Zhang, Z. (2025). Anomaly Detection Method for Hydropower Units Based on KSQDC-ADEAD Under Complex Operating Conditions. Sensors, 25(13), 4093. https://doi.org/10.3390/s25134093







