Rolling Based on Multi-Source Time–Frequency Feature Fusion with a Wavelet-Convolution, Channel-Attention-Residual Network-Bearing Fault Diagnosis Method
Abstract
1. Introduction
- (A)
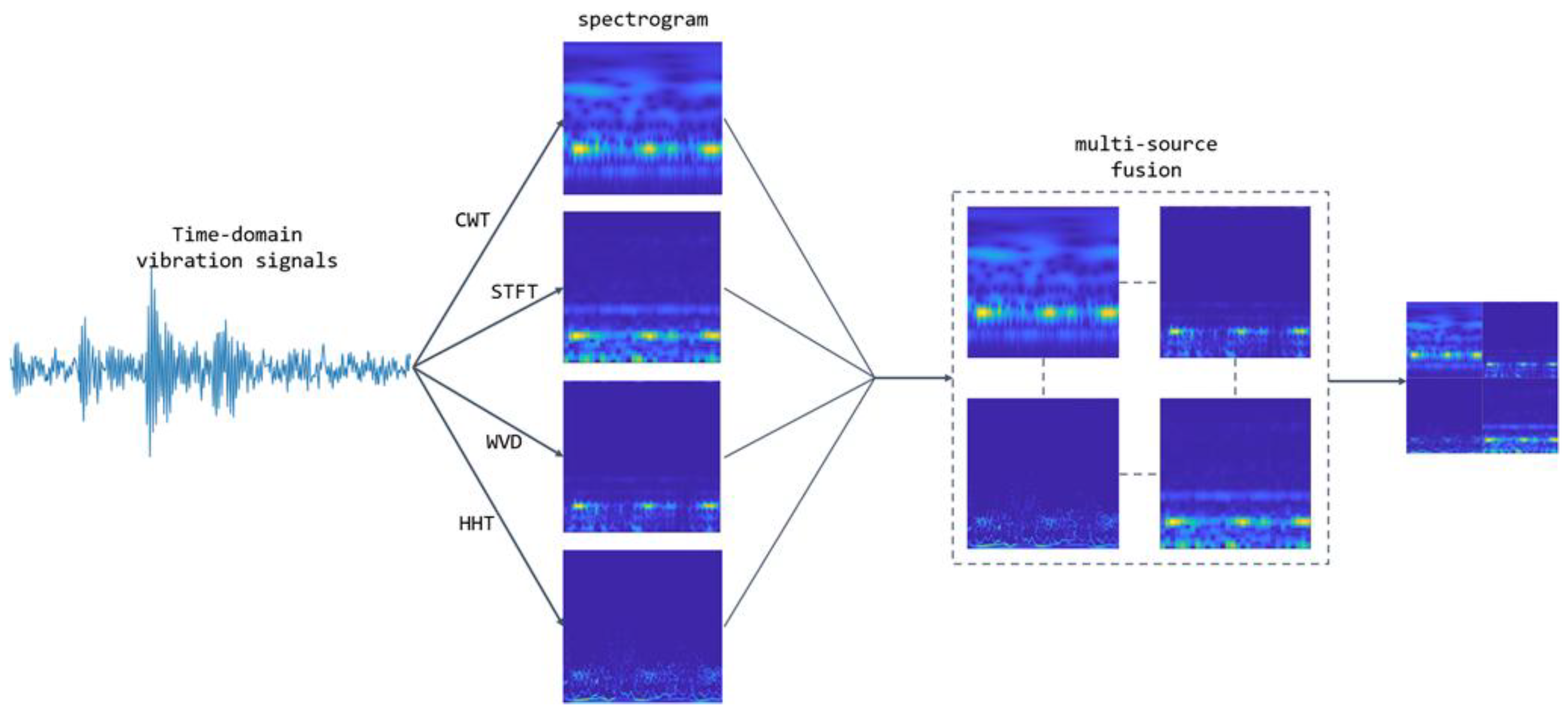
- Four types of time–frequency maps—namely, continuous wavelet transform (CWT), short-time Fourier transform (STFT), Hilbert–Huang transform (HHT), and Wigner–Ville distribution (WVD)—are fused and used as input features. This integration fully leverages the global stability of STFT, the multi-scale characteristics of CWT, the adaptive decomposition capability of HHT, and the high-resolution advantage of WVD, thereby enhancing the fault feature detection rate through feature complementarity.
- (B)
- WaveCAResNet, a lightweight network, was designed with the introduction of the wavelet convolution layer (WTConv), as well as the channel-attention-weighted residual (CAWR), and based on EMA, weighted residual efficient multi-scale attention (WREMA) was designed. WaveCAResNet effectively integrates wavelet convolution, CAWR, and WREMA, and constructs a lightweight, efficient bearing fault diagnosis network, which effectively solves the deficiencies of the above methods.
2. Proposed Method for Fault Diagnosis in Bearings
2.1. Data Pre-Processing
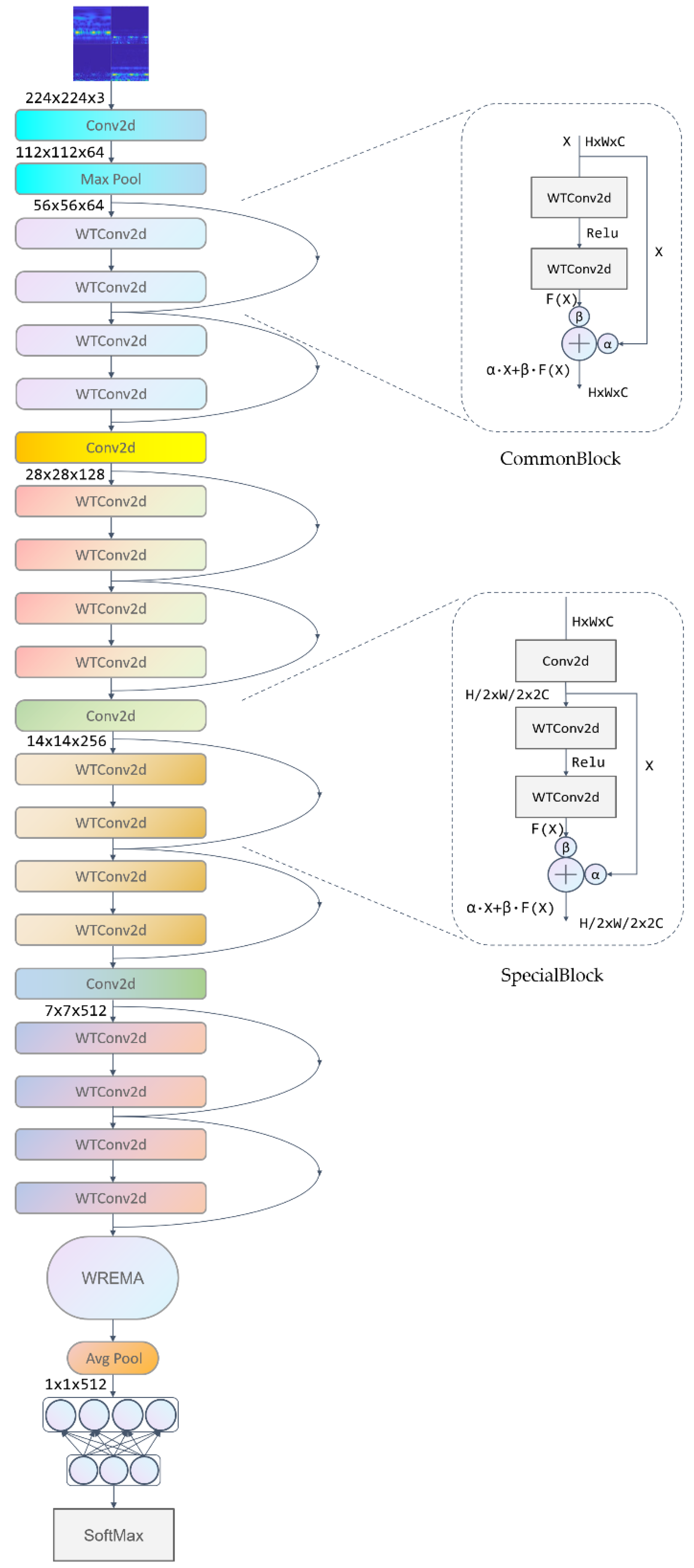
2.2. A Lightweight Model WaveCAResNet
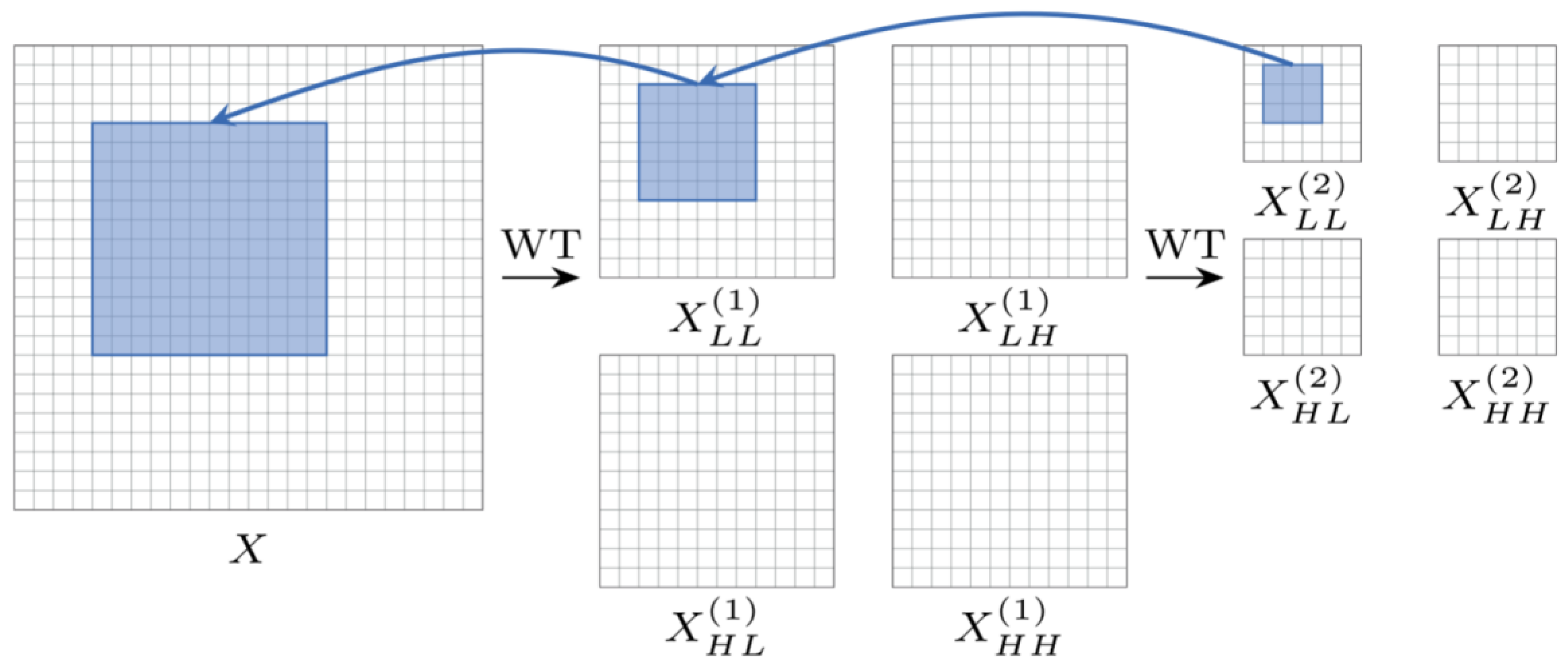
2.2.1. Wavelet Convolution Layer
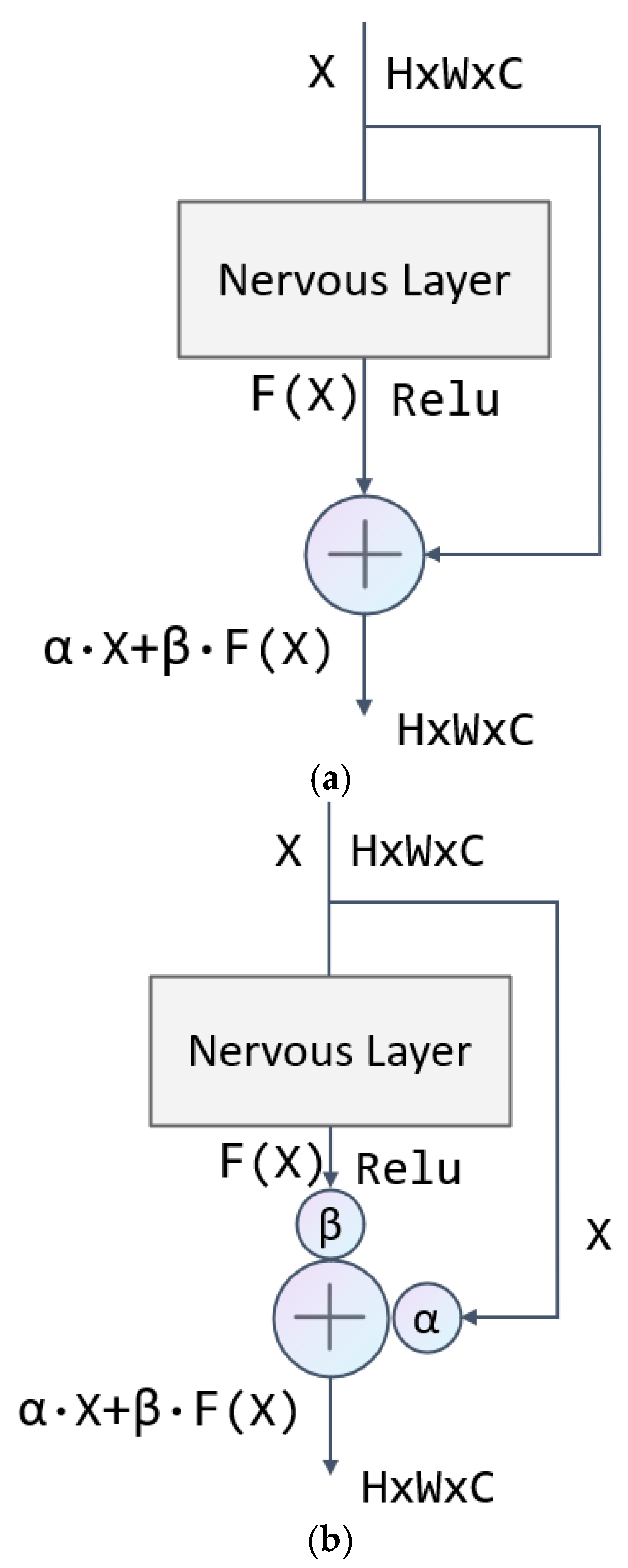
2.2.2. Channel-Attention-Weighted Residual (CAWR)
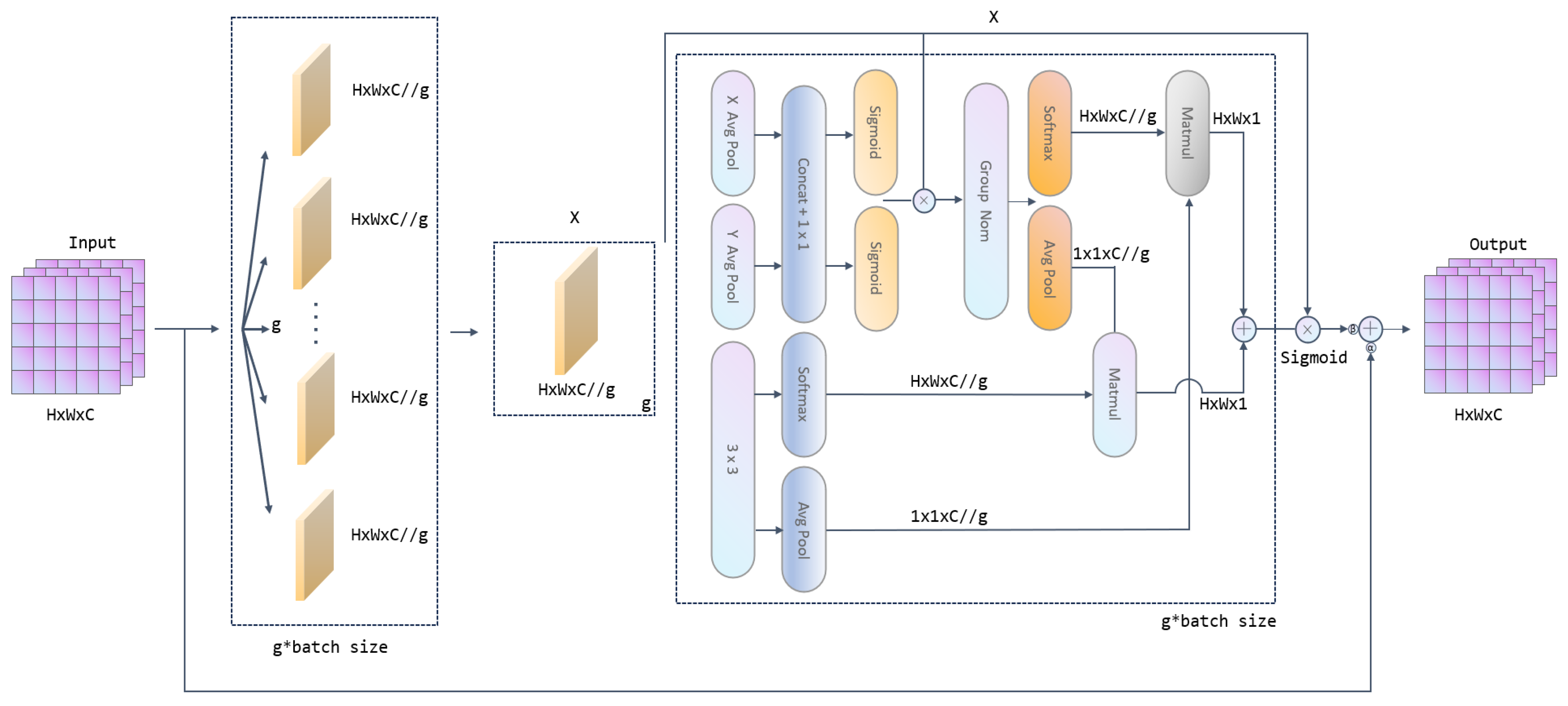
2.2.3. Weighted Residual Efficient Multi-Scale Attention (WREMA)
2.2.4. Overall Model Architecture
3. Experimental Results and Evaluation
3.1. Experimental Settings and Data Sources
3.2. Assessment of Indicators
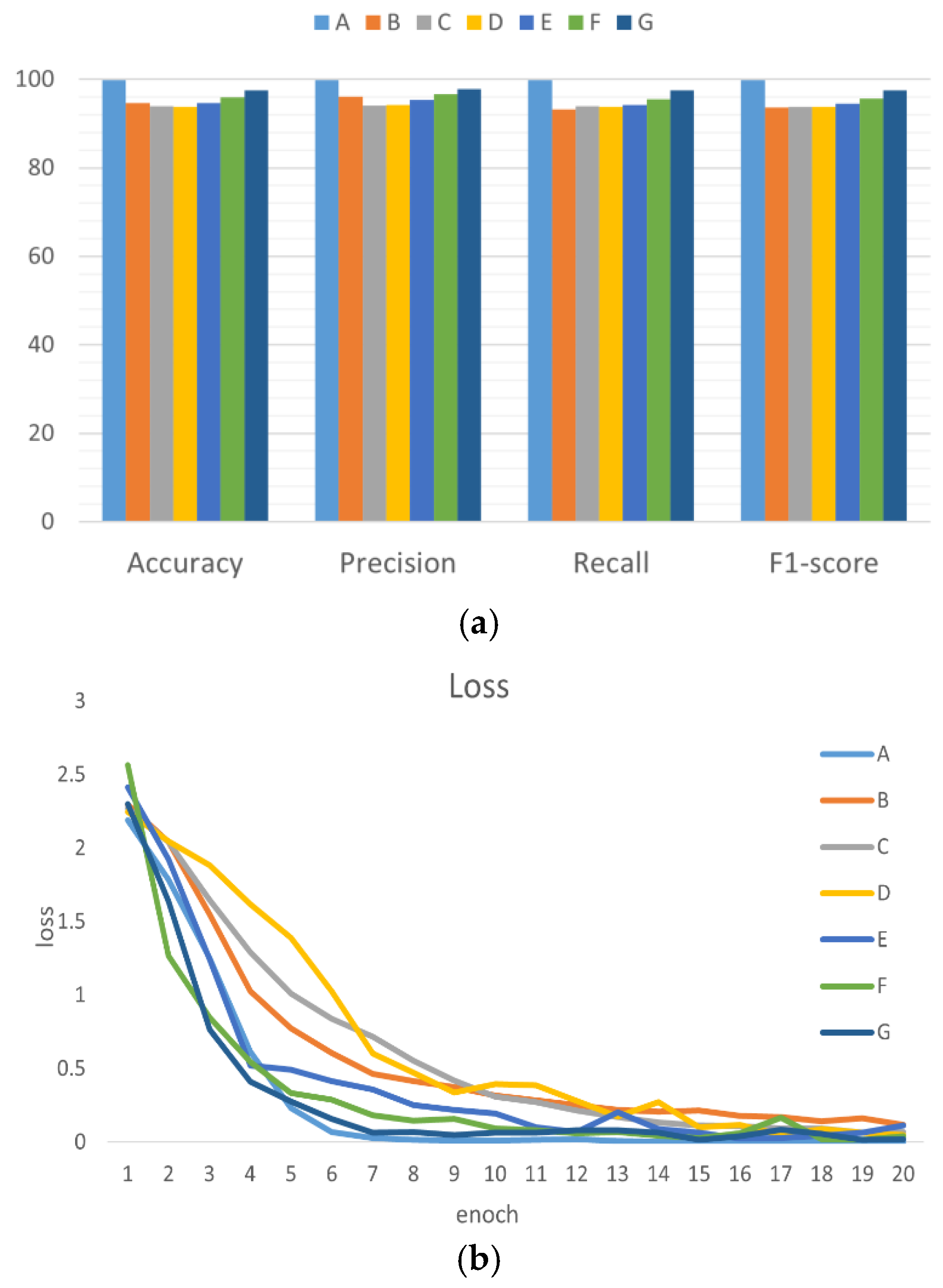
3.3. Experimental Results on the CWRU Dataset
3.3.1. Comparative Experiments
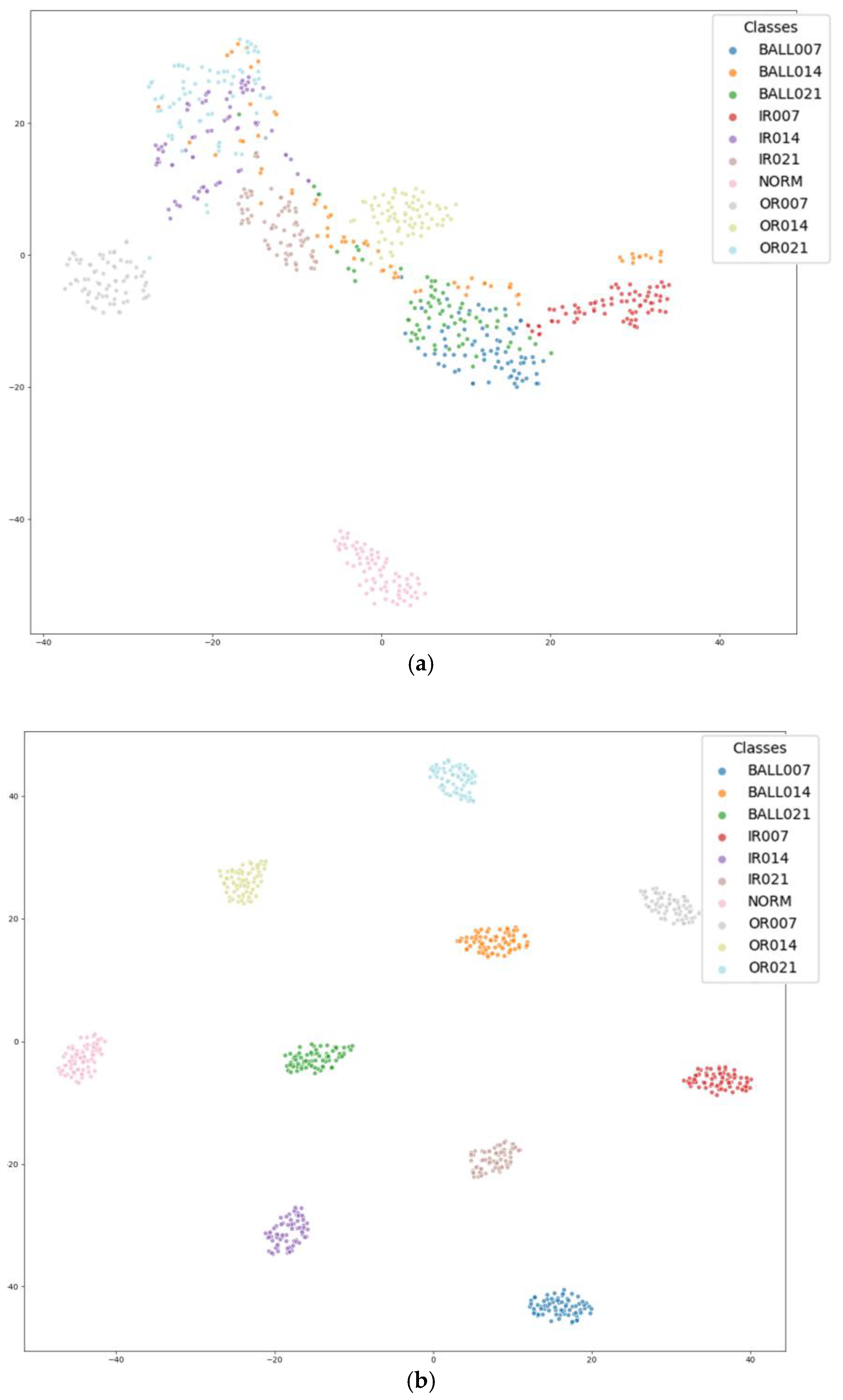
3.3.2. Visualization of Model Results
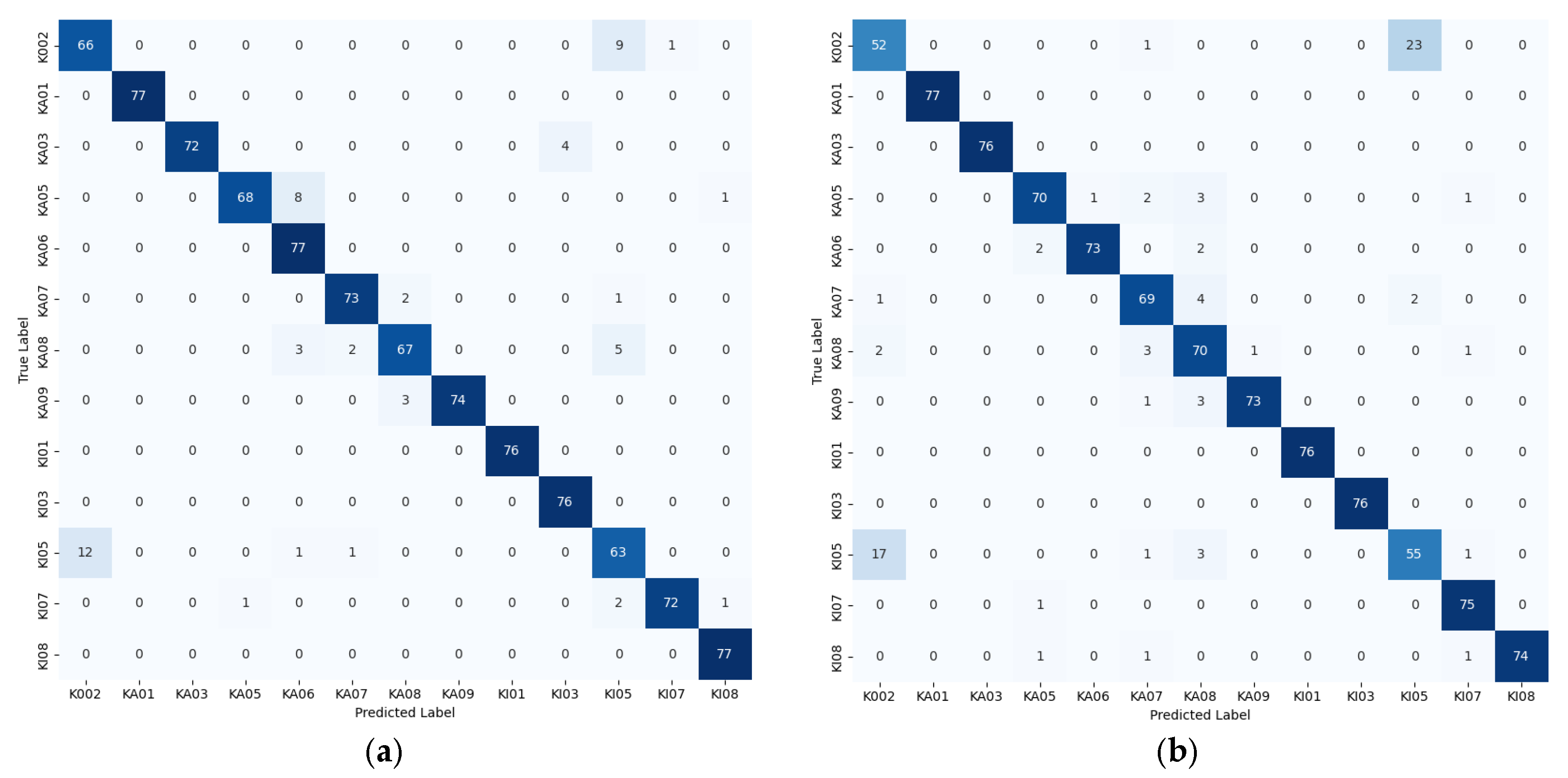
3.4. Experimental Results on the Paderborn Dataset
3.4.1. Comparative Experiments of Time-Frequency Analysis Methods
- Four single time–frequency representation analysis methods (CWT, STFT, HHT, WVD);
- Channel-overlay time–frequency map method (generated by superimposing time–frequency map derived from three analytical techniques—CWT, STFT, and WVD—onto corresponding RGB channels);
- The spatially fused time–frequency map method is introduced in this study.
- The experimental groupings are detailed in Table 6.
| Time–Frequency Analysis Methods | Groups |
|---|---|
| CWT | A |
| STFT | B |
| HHT | C |
| WVD | D |
| Channel-overlay time–frequency map method | E |
| fused time–frequency map method | F |
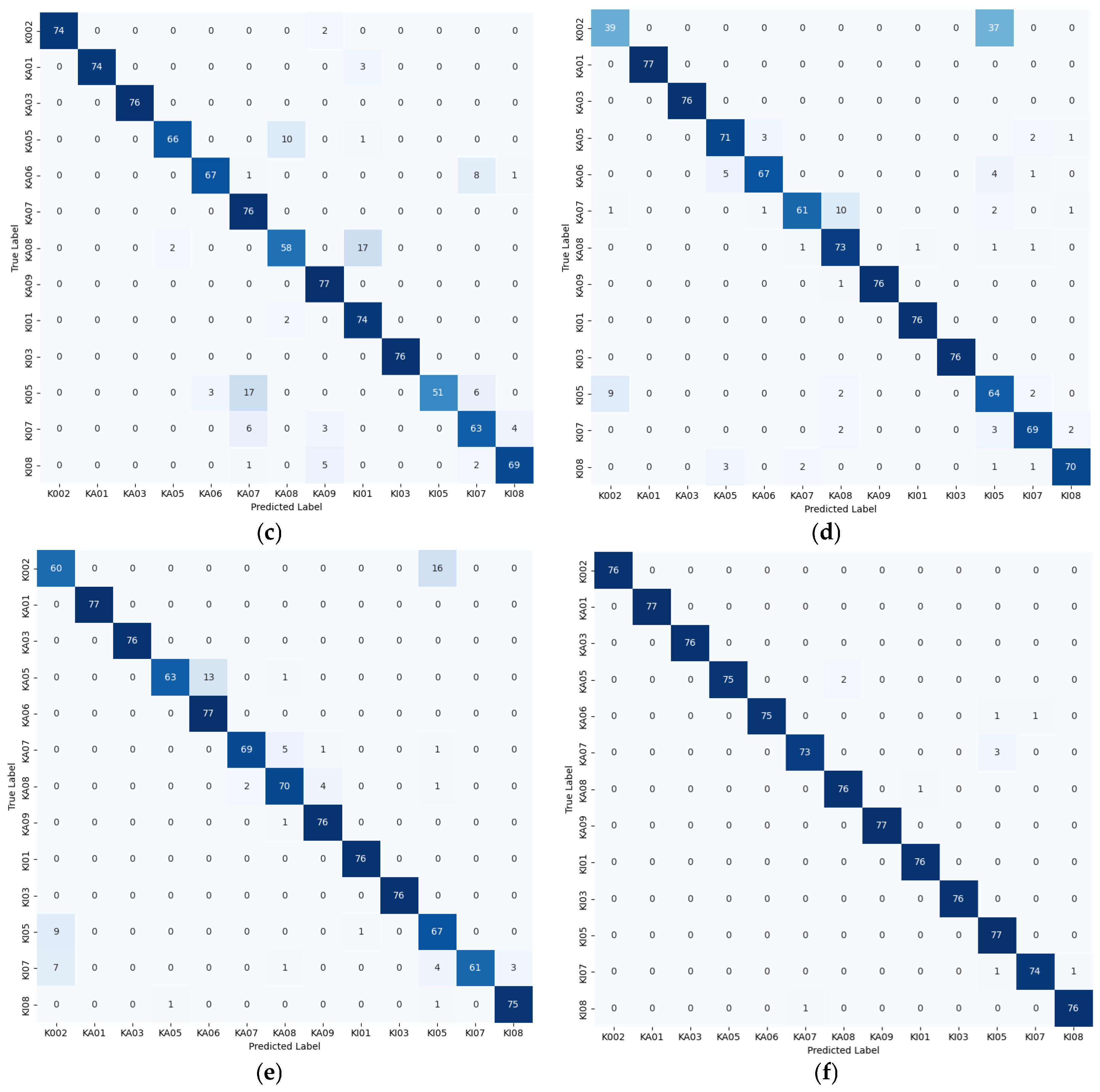
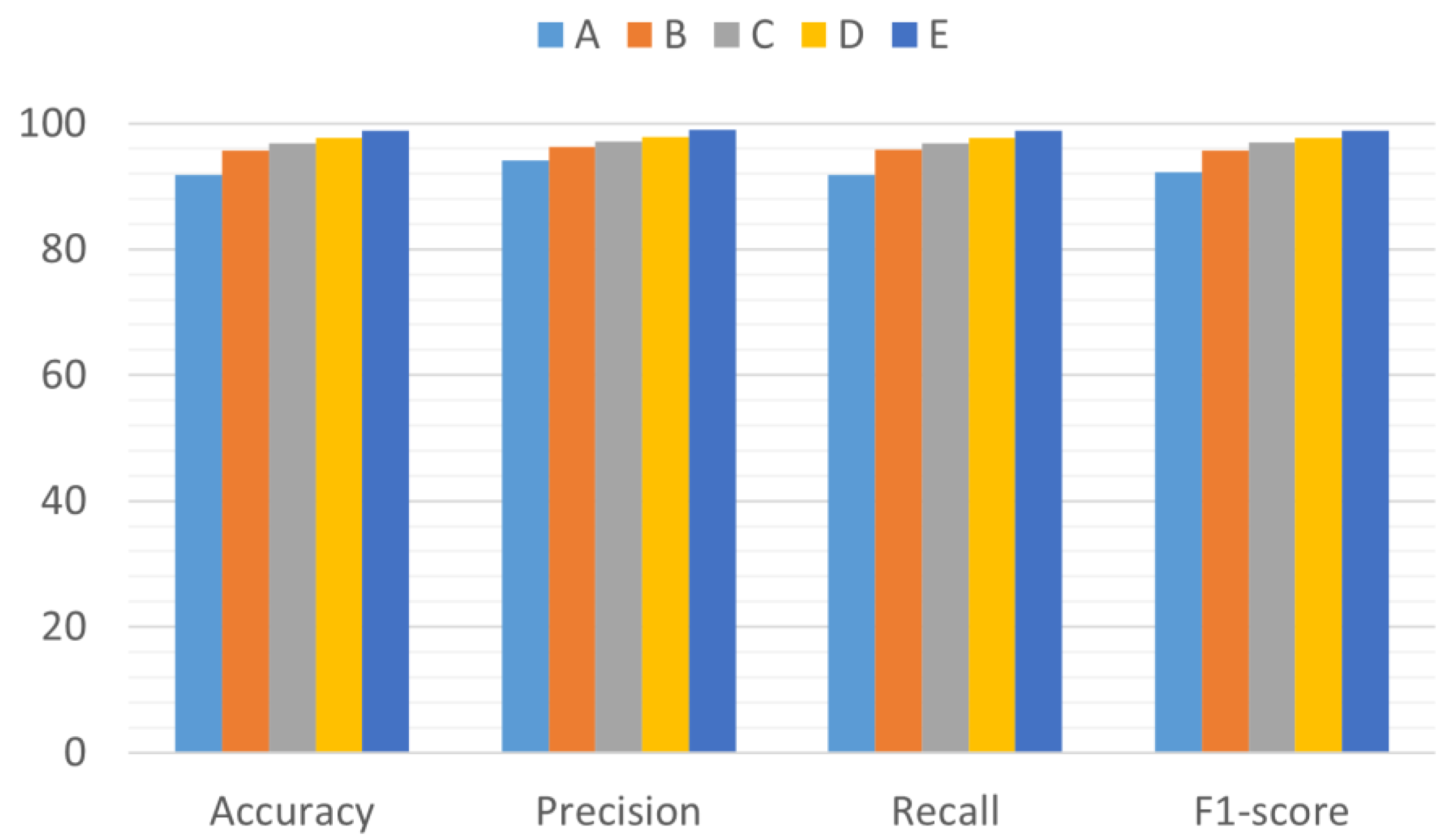
3.4.2. Ablation Experiments
3.4.3. Model Performance in Noisy Environments
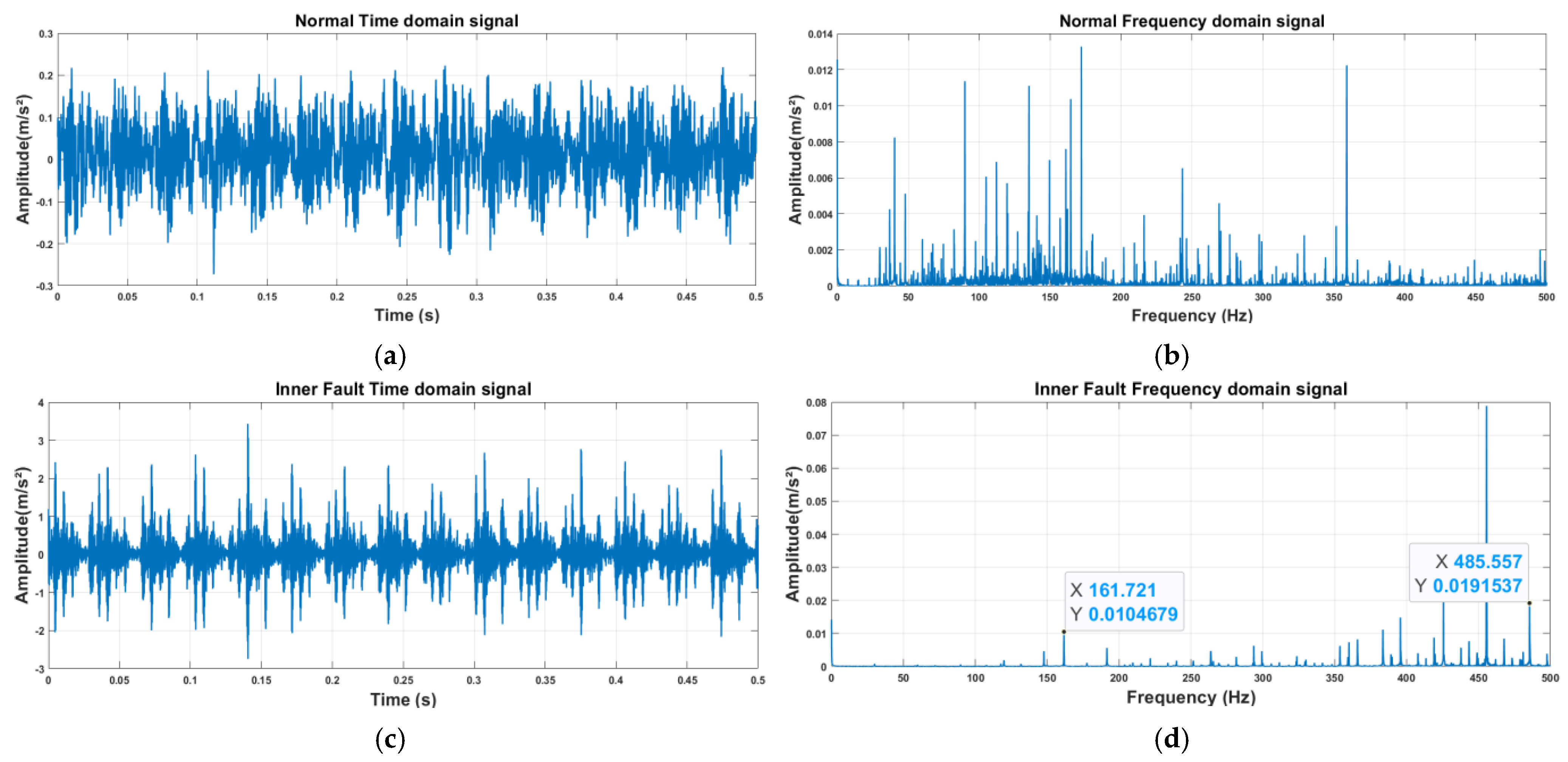
3.4.4. Verification of Frequency Response of Fault Characteristics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CWT | continuous wavelet transform |
| STFT | Short Time Fourier Transform |
| HHT | Hilbert-Huang Transform |
| WVD | Wigner-Ville distribution |
| CNN | convolutional neural network |
| ReLU | rectified linear unit |
References
- Tchakoua, P.; Wamkeue, R.; Ouhrouche, M.; Slaoui-Hasnaoui, F.; Tameghe, T.; Ekemb, G. Wind Turbine Condition Monitoring: State-of-the-Art Review, New Trends, and Future Challenges. Energies 2014, 7, 2595–2630. [Google Scholar] [CrossRef]
- A New Unsupervised Health Index Estimation Method for Bearing Early Fault Detection Based on Gaussian Mixture Model. Eng. Appl. Artif. Intell. 2024, 128, 107562. [CrossRef]
- Gabor, D. Theory of Communication. Part 1: The Analysis of Information. J. Inst. Electr. Eng. III Radio Commun. Eng. 1946, 93, 429–441. [Google Scholar] [CrossRef]
- Feng, Z.; Liang, M.; Chu, F. Recent Advances in Time–Frequency Analysis Methods for Machinery Fault Diagnosis: A Review with Application Examples. Mech. Syst. Signal Process. 2013, 38, 165–205. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Ville, J. Theorie et Application Dela Notion de Signal Analysis. Cables Transm. 1948, 2, 61–74. [Google Scholar]
- Sharma, R.R.; Pachori, R.B. Improved Eigenvalue Decomposition-Based Approach for Reducing Cross-Terms in Wigner–Ville Distribution. Circuits Syst. Signal Process. 2018, 37, 3330–3350. [Google Scholar] [CrossRef]
- Li, S.; Li, Q.; Li, K.; Gao, X. Intelligent Rolling Bearing Fault Diagnosis Based on Vibration Signal Transformer Neural Network. In Proceedings of the 35th Chinese Process Control Conference, Yichang, China, 25 July 2024; p. 77. [Google Scholar]
- Yu, D.; Fu, H.; Song, Y.; Xie, W.; Xie, Z. Deep Transfer Learning Rolling Bearing Fault Diagnosis Method Based on Convolutional Neural Network Feature Fusion. Meas. Sci. Technol. 2023, 35, 15013. [Google Scholar] [CrossRef]
- Siddique, M.F.; Saleem, F.; Umar, M.; Kim, C.H.; Kim, J.-M. A Hybrid Deep Learning Approach for Bearing Fault Diagnosis Using Continuous Wavelet Transform and Attention-Enhanced Spatiotemporal Feature Extraction. Sensors 2025, 25, 2712. [Google Scholar] [CrossRef]
- Li, B.; Chow, M.-Y.; Tipsuwan, Y.; Hung, J.C. Neural-Network-Based Motor Rolling Bearing Fault Diagnosis. IEEE Trans. Ind. Electron. 2000, 47, 1060–1069. [Google Scholar] [CrossRef]
- Ruan, D.; Wang, J.; Yan, J.; Gühmann, C. CNN Parameter Design Based on Fault Signal Analysis and Its Application in Bearing Fault Diagnosis. Adv. Eng. Inf. 2023, 55, 101877. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, B.; Gao, D. Bearing Fault Diagnosis Base on Multi-Scale CNN and LSTM Model. J. Intell. Manuf. 2021, 32, 971–987. [Google Scholar] [CrossRef]
- Gao, D.; Zhu, Y.; Ren, Z.; Yan, K.; Kang, W. A Novel Weak Fault Diagnosis Method for Rolling Bearings Based on LSTM Considering Quasi-Periodicity. Knowl. Based Syst. 2021, 231, 107413. [Google Scholar] [CrossRef]
- Wang, H.; Wu, X.; Huang, Z.; Xing, E.P. High-Frequency Component Helps Explain the Generalization of Convolutional Neural Networks. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 8681–8691. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Ding, Y.; Jia, M.; Miao, Q.; Cao, Y. A Novel Time–Frequency Transformer Based on Self–Attention Mechanism and Its Application in Fault Diagnosis of Rolling Bearings. Mech. Syst. Signal Process. 2022, 168, 108616. [Google Scholar] [CrossRef]
- Jin, Y.; Hou, L.; Chen, Y. A New Rotating Machinery Fault Diagnosis Method Based on the Time Series Transformer. arXiv 2021, arXiv:2108.12562. [Google Scholar]
- Wang, H.; Xu, J.; Yan, R.; Gao, R.X. A New Intelligent Bearing Fault Diagnosis Method Using SDP Representation and SE-CNN. IEEE Trans. Instrum. Meas. 2020, 69, 2377–2389. [Google Scholar] [CrossRef]
- Lin, T.; Zhu, Y.; Ren, Z.; Huang, K.; Gao, D. CCFT: The Convolution and Cross-Fusion Transformer for Fault Diagnosis of Bearings. IEEE/ASME Trans. Mechatron. 2024, 29, 2161–2172. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, X.; Han, J.; Ding, G. Scaling up Your Kernels to 31 × 31: Revisiting Large Kernel Design in CNNs. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 11953–11965. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Guo, Y.; Yao, A.; Chen, Y. Dynamic Network Surgery for Efficient DNNs. In Proceedings of the Advances in Neural Information Processing Systems 29, Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Misra, D.; Nalamada, T.; Arasanipalai, A.U.; Hou, Q. Rotate to Attend: Convolutional Triplet Attention Module. arXiv 2020, arXiv:2010.03045. [Google Scholar]
- Finder, S.E.; Amoyal, R.; Treister, E.; Freifeld, O. Wavelet Convolutions for Large Receptive Fields. In Proceedings of the Computer Vision—ECCV 2024, Milan, Italy, 29 September–4 October 2024; Leonardis, A., Ricci, E., Roth, S., Russakovsky, O., Sattler, T., Varol, G., Eds.; Springer Nature: Cham, Switzerland, 2025; pp. 363–380. [Google Scholar]
- Ouyang, D.; He, S.; Zhang, G.; Luo, M.; Guo, H.; Zhan, J.; Huang, Z. Efficient Multi-Scale Attention Module with Cross-Spatial Learning. In Proceedings of the ICASSP 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhosed Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar]
- Loparo, K.A. Bearing Vibration Data Set. Available online: https://engineering.case.edu/bearingdatacenter/download-data-file (accessed on 24 January 2025).
- Lessmeier, C.; Kimotho, J.K.; Zimmer, D.; Sextro, W. Condition Monitoring of Bearing Damage in Electromechanical Drive Systems by Using Motor Current Signals of Electric Motors: A Benchmark Data Set for Data-Driven Classification. PHM Soc. Eur. Conf. 2016, 3, 3–12. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.-C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- Tan, M.; Le, Q. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image Is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2021, arXiv:2010.11929. [Google Scholar]
- Liu, Z.; Mao, H.; Wu, C.-Y.; Feichtenhofer, C.; Darrell, T.; Xie, S. A ConvNet for the 2020s. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 9992–10002. [Google Scholar]
- Smith, W.A.; Randall, R.B. Rolling Element Bearing Diagnostics Using the Case Western Reserve University Data: A Benchmark Study. Mech. Syst. Signal Process. 2015, 64, 100–131. [Google Scholar] [CrossRef]





| Parameter Category | CWRU Dataset | Paderborn Dataset |
|---|---|---|
| Motor parameters | Motor type: 1.5 kW (2HP) induction motor | Drive motor: Haning synchronous motor (425 W, 3000 RPM, 1.35 Nm) Motor type: 1.5 kW (2HP) induction motor |
| Speed range: 1730–1797 RPM | Load motor: Siemens synchronous servo motor (1.7 kW, 3000 RPM, 6 Nm) | |
| Bearing parameters | Model: SKF 6205-2RS | Model: Ball Bearing 6203 |
| Inner diameter: 25 mm | Inner diameter: 30 mm | |
| outer diameter: 52 mm | outer diameter: 55 mm | |
| Number of rolling elements: 9 | Number of rolling elements: 12 |
| Block | Layers | Training Settings | Hyperparameterization | Settings | Quantities |
|---|---|---|---|---|---|
| - | Conv2d | Epoch = 20 Batch Size = 32 Learning Rate = 0.001 Loss Function = CrossEntropyLoss Optimizer = Adam | kernel | 7 × 7 | 1 |
| Stride | 2 | ||||
| Padding | 3 | ||||
| channels | 64 | ||||
| CommonBlock | WTConv2d | kernel | 3 × 3 | [2, 1, 1, 1] | |
| Stride | 1 | ||||
| number | 2 | ||||
| SpecialBlock | Conv2d | kernel | 1 × 1 | [0, 1, 1, 1] | |
| Stride | 2 | ||||
| channels | [128, 256, 512] | ||||
| number | 1 | ||||
| WTConv2d | kernel | 3 × 3 | |||
| Stride | 1 | ||||
| number | 2 | ||||
| CAWR | Linear | dimensionality reduction ratio | 16 | 9 | |
| WREMA | GroupNorm | Number of groups | 8 | 1 |
| Bearing Condition | Failure Size/Inch | Labels |
|---|---|---|
| normal | - | NORM |
| inner-ring failures | 0.007 | IN007 |
| 0.014 | IR014 | |
| 0.021 | IR021 | |
| outer-ring failures | 0.007 | OR007 |
| 0.014 | OR014 | |
| 0.021 | OR021 | |
| ball failures | 0.007 | BALL007 |
| 0.014 | BALL014 | |
| 0.021 | BALL021 |
| Model | Size (MB) | Quantity of Participants (M) | FLOPs (G) | Groups |
|---|---|---|---|---|
| WaveCAResNet | 4.7 | 1.07 | 0.2 | A |
| AlexNet | 55.7 | 14.6 | 0.28 | B |
| MobileNet-V2 | 8.7 | 2.24 | 0.33 | C |
| EfficientNet-b0 | 15.6 | 4.02 | 0.41 | D |
| ViT-Base | 327.4 | 85.81 | 16.86 | E |
| ConvNeXt-T | 104.2 | 27.83 | 4.45 | F |
| SwinT | 105.3 | 27.53 | 4.37 | G |
| Bearing Condition | Extent of Damage (Level) | Damage Method | Labels |
|---|---|---|---|
| normal | - | - | K002 |
| outer-ring failures | 1 | EDM | KA01 |
| 2 | electric engraver | KA03 | |
| 1 | electric engraver | KA05 | |
| 2 | electric engraver | KA06 | |
| 1 | drilling | KA07 | |
| 2 | drilling | KA08 | |
| 2 | drilling | KA09 | |
| inner-ring failures | 1 | EDM | KI01 |
| 1 | electric engraver | KI03 | |
| 1 | electric engraver | KI05 | |
| 2 | electric engraver | KI07 | |
| 2 | electric engraver | KI08 |
| Model | Groups |
|---|---|
| ResNet-18 | A |
| WTResNet | B |
| WT-EMA-ResNet | C |
| WT-WREMA-ResNet | D |
| WaveCAResNet | E |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, T.; Wang, Z.; Qiu, L.; Li, H.; Wang, Z. Rolling Based on Multi-Source Time–Frequency Feature Fusion with a Wavelet-Convolution, Channel-Attention-Residual Network-Bearing Fault Diagnosis Method. Sensors 2025, 25, 4091. https://doi.org/10.3390/s25134091
Feng T, Wang Z, Qiu L, Li H, Wang Z. Rolling Based on Multi-Source Time–Frequency Feature Fusion with a Wavelet-Convolution, Channel-Attention-Residual Network-Bearing Fault Diagnosis Method. Sensors. 2025; 25(13):4091. https://doi.org/10.3390/s25134091
Chicago/Turabian StyleFeng, Tongshuhao, Zhuoran Wang, Lipeng Qiu, Hongkun Li, and Zhen Wang. 2025. "Rolling Based on Multi-Source Time–Frequency Feature Fusion with a Wavelet-Convolution, Channel-Attention-Residual Network-Bearing Fault Diagnosis Method" Sensors 25, no. 13: 4091. https://doi.org/10.3390/s25134091
APA StyleFeng, T., Wang, Z., Qiu, L., Li, H., & Wang, Z. (2025). Rolling Based on Multi-Source Time–Frequency Feature Fusion with a Wavelet-Convolution, Channel-Attention-Residual Network-Bearing Fault Diagnosis Method. Sensors, 25(13), 4091. https://doi.org/10.3390/s25134091






