Single-Image Super-Resolution via Cascaded Non-Local Mean Network and Dual-Path Multi-Branch Fusion
Abstract
1. Introduction
- We introduce a novel PSNLM module, inspired by the traditional NLM algorithm, which effectively captures fine-grained long-range dependencies by combining the strengths of NLM and self-attention mechanisms;
- We design an ADMFB that enhances both scale diversity and feature discriminability by simultaneously extracting and fusing hierarchical features through parallel attention pathways;
- We integrate a PSNLM and ADMFB into a CNN framework, achieving competitive performance on standard benchmarks, demonstrating the effectiveness of our hybrid design.
2. Related Work
2.1. Traditional Methods
2.2. Deep Learning-Based Super-Resolution Methods
2.2.1. CNN-Based Methods
2.2.2. Transformer-Based Methods
2.2.3. Hybrid CNN–Transformer Methods
3. Methods
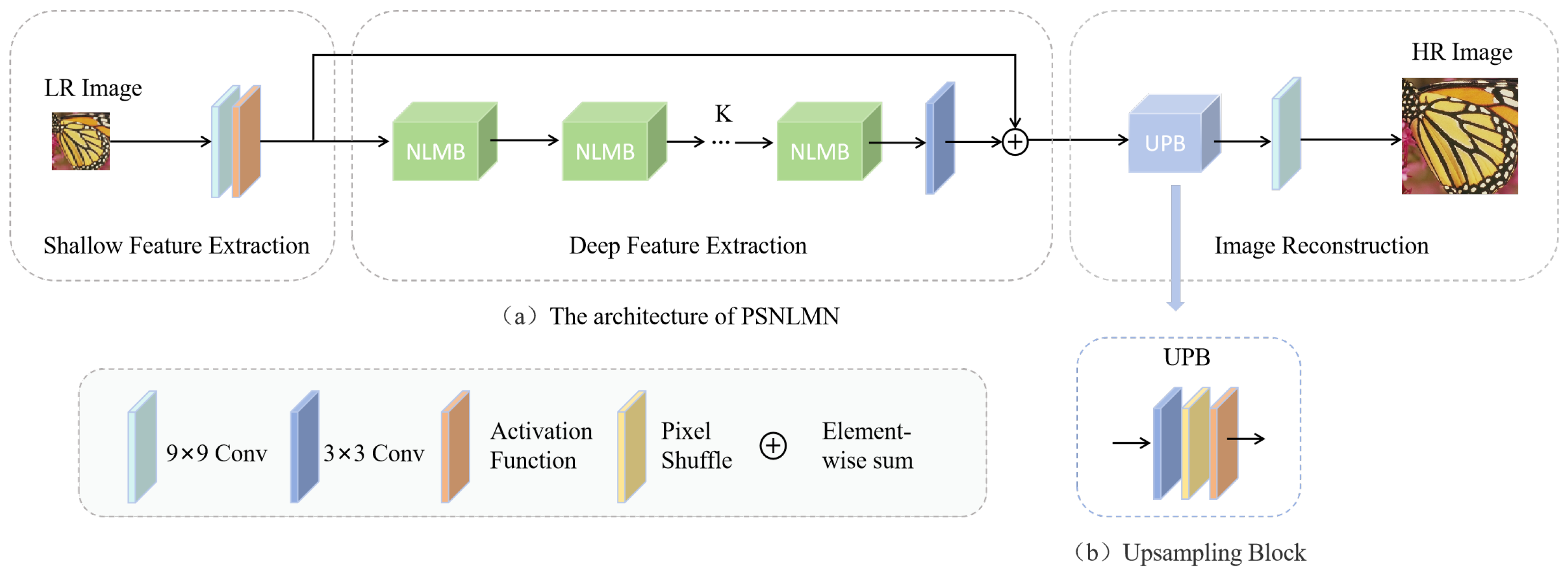
3.1. Network Structure
3.2. The Non-Local Multi-Branch Module (NLMB)
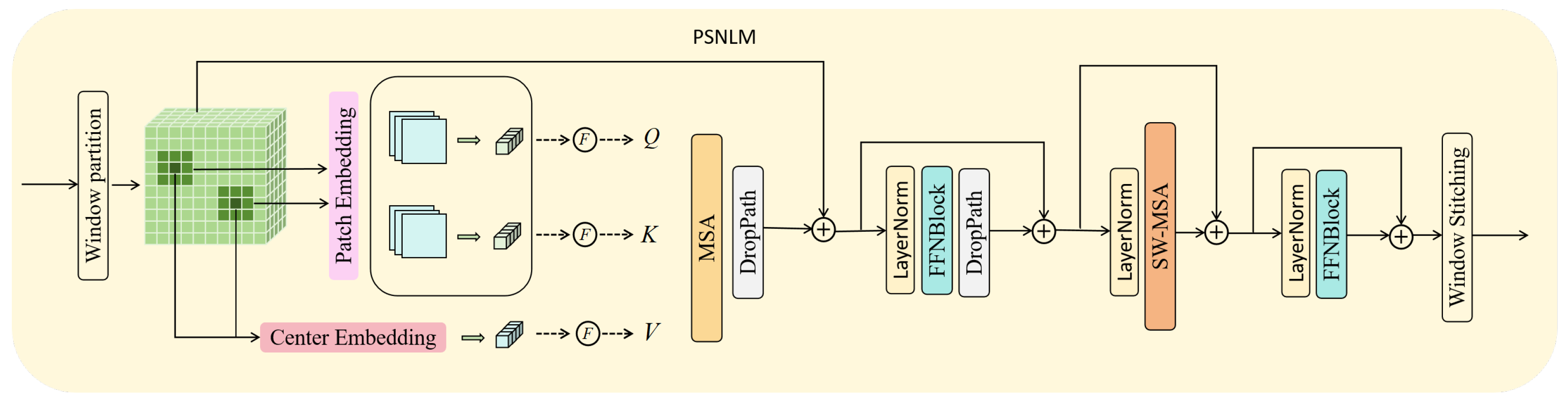
3.3. Pixel-Wise Self-Attention-Based Non-Local Mean Module (PSNLM)
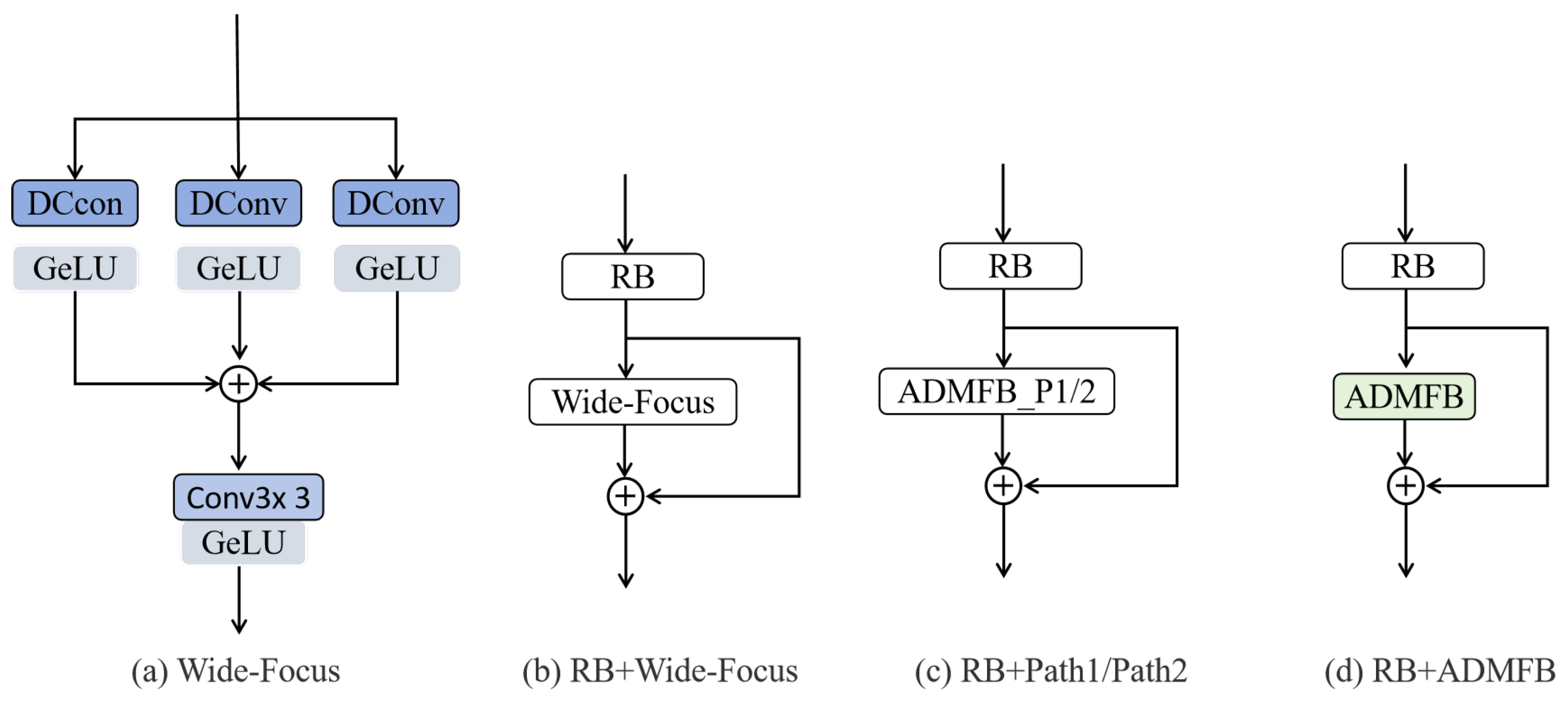
3.4. Adaptive Dual-Path Multi-Branch Fusion Block (ADMFB)
4. Experiments
4.1. Experimental Settings
4.2. Ablation Studies
4.2.1. Ablation Study of Module PSNLM
4.2.2. Ablation Study of Module ADMFB
4.2.3. Ablation Study on the Combined Modules
4.3. Performance Evaluation
4.3.1. Quantitative Results Analysis
4.3.2. Qualitative Results Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Sixou, B.; Peyrin, F. A review of the deep learning methods for medical images super resolution problems. IRBM 2021, 42, 120–133. [Google Scholar] [CrossRef]
- Dong, R.; Zhang, L.; Fu, H. RRSGAN: Reference-based super-resolution for remote sensing image. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5601117. [Google Scholar] [CrossRef]
- Shan, T.; Wang, J.; Chen, F.; Szenher, P.; Englot, B. Simulation-based lidar super-resolution for ground vehicles. Robot. Auton. Syst. 2020, 134, 103647. [Google Scholar] [CrossRef]
- Anwar, S.; Khan, S.; Barnes, N. A deep journey into super-resolution: A survey. Acm Comput. Surv. CSUR 2020, 53, 1–34. [Google Scholar] [CrossRef]
- Xu, X.; Ma, Y.; Sun, W. Towards real scene super-resolution with raw images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 1723–1731. [Google Scholar]
- Holst, G.C. Electro-Optical Imaging System Performance; SPIE Press Monograph; SPIE Press: Bellingham, WA, USA, 2008; Volume PM187. [Google Scholar]
- Sze, V.; Chen, Y.H.; Emer, J.; Suleiman, A.; Zhang, Z. Hardware for machine learning: Challenges and opportunities. In Proceedings of the 2017 IEEE Custom Integrated Circuits Conference (CICC), Austin, TX, USA, 30 April–3 May 2017; pp. 1–8. [Google Scholar]
- Wang, Y.; Bashir, S.M.A.; Khan, M.; Ullah, Q.; Wang, R.; Song, Y.; Guo, Z.; Niu, Y. Remote sensing image super-resolution and object detection: Benchmark and state of the art. Expert Syst. Appl. 2022, 197, 116793. [Google Scholar] [CrossRef]
- Wang, L.; Li, D.; Zhu, Y.; Tian, L.; Shan, Y. Dual super-resolution learning for semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR 2020), Seattle, WA, USA, 14–19 June 2020; pp. 3774–3783. [Google Scholar]
- Kim, K.I.; Kwon, Y. Single-image super-resolution using sparse regression and natural image prior. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1127–1133. [Google Scholar] [PubMed]
- Dong, W.; Zhang, L.; Shi, G.; Wu, X. Image deblurring and super-resolution by adaptive sparse domain selection and adaptive regularization. IEEE Trans. Image Process. 2011, 20, 1838–1857. [Google Scholar] [CrossRef] [PubMed]
- Yue, L.; Shen, H.; Li, J.; Yuan, Q.; Zhang, H.; Zhang, L. Image super-resolution: The techniques, applications, and future. Signal Process. 2016, 128, 389–408. [Google Scholar] [CrossRef]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image super-resolution via sparse representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Tai, Y.; Yang, J.; Liu, X.; Xu, C. Memnet: A persistent memory network for image restoration. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 4539–4547. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Zhang, K.; Zuo, W.; Zhang, L. Learning a single convolutional super-resolution network for multiple degradations. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3262–3271. [Google Scholar]
- Ahn, N.; Kang, B.; Sohn, K.A. Fast, accurate, and lightweight super-resolution with cascading residual network. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; pp. 252–268. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; pp. 286–301. [Google Scholar]
- Hui, Z.; Gao, X.; Yang, Y.; Wang, X. Lightweight image super-resolution with information multi-distillation network. In Proceedings of the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019; pp. 2024–2032. [Google Scholar]
- Sun, L.; Pan, J.; Tang, J. Shufflemixer: An efficient convnet for image super-resolution. Adv. Neural Inf. Process. Syst. 2022, 35, 17314–17326. [Google Scholar]
- Ji, J.; Zhong, B.; Wu, Q.; Ma, K.K. A channel-wise multi-scale network for single image super-resolution. IEEE Signal Process. Lett. 2024, 31, 805–809. [Google Scholar] [CrossRef]
- Ke, G.; Lo, S.L.; Zou, H.; Liu, Y.F.; Chen, Z.Q.; Wang, J.K. CSINet: A Cross-Scale Interaction Network for Lightweight Image Super-Resolution. Sensors 2024, 24, 1135. [Google Scholar] [CrossRef] [PubMed]
- Dosovitskiy, A. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]
- Liang, J.; Cao, J.; Sun, G.; Zhang, K.; Van Gool, L.; Timofte, R. Swinir: Image restoration using swin transformer. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision Workshops (ICCVW), Montreal, BC, Canada, 11–17 October 2021; pp. 1833–1844. [Google Scholar]
- Tragakis, A.; Kaul, C.; Murray-Smith, R.; Husmeier, D. The fully convolutional transformer for medical image segmentation. In Proceedings of the 2023 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV 2023), Waikoloa, HI, USA, 2–7 January 2023; pp. 3660–3669. [Google Scholar]
- Choi, H.; Lee, J.; Yang, J. N-gram in swin transformers for efficient lightweight image super-resolution. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR 2023), Vancouver, BC, Canada, 18–22 June 2023; pp. 2071–2081. [Google Scholar]
- Liu, Y.; Xue, J.; Li, D.; Zhang, W.; Chiew, T.K.; Xu, Z. Image recognition based on lightweight convolutional neural network: Recent advances. Image Vis. Comput. 2024, 146, 105037. [Google Scholar] [CrossRef]
- Yang, F.; Yang, H.; Fu, J.; Lu, H.; Guo, B. Learning texture transformer network for image super-resolution. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR 2020), Seattle, WA, USA, 14–19 June 2020; pp. 5791–5800. [Google Scholar]
- Lu, Z.; Li, J.; Liu, H.; Huang, C.; Zhang, L.; Zeng, T. Transformer for single image super-resolution. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), New Orleans, LA, USA, 19–20 June 2022; pp. 457–466. [Google Scholar]
- Gao, G.; Wang, Z.; Li, J.; Li, W.; Yu, Y.; Zeng, T. Lightweight Bimodal Network for Single-Image Super-Resolution via Symmetric CNN and Recursive Transformer. In Proceedings of the 31st International Joint Conference on Artificial Intelligence, Vienna, Austria, 23–29 July 2022; pp. 913–919. [Google Scholar]
- Keys, R. Cubic convolution interpolation for digital image processing. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 1153–1160. [Google Scholar] [CrossRef]
- Duchon, C.E. Lanczos filtering in one and two dimensions. J. Appl. Meteorol. 1962–1982 1979, 18, 1016–1022. [Google Scholar] [CrossRef]
- Siu, W.C.; Hung, K.W. Review of image interpolation and super-resolution. In Proceedings of the 2012 Asia Pacific Signal and Information Processing Association Annual Summit and Conference, Hollywood, CA, USA, 3–6 December 2012; pp. 1–10. [Google Scholar]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Hoi, S.C. Deep learning for image super-resolution: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 3365–3387. [Google Scholar] [CrossRef] [PubMed]
- Timofte, R.; De Smet, V.; Van Gool, L. Anchored neighborhood regression for fast example-based super-resolution. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 1920–1927. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Tai, Y.; Yang, J.; Liu, X. Image super-resolution via deep recursive residual network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3147–3155. [Google Scholar]
- Chen, H.; Wang, Y.; Guo, T.; Xu, C.; Deng, Y.; Liu, Z.; Ma, S.; Xu, C.; Xu, C.; Gao, W. Pre-trained image processing transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 12299–12310. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. In Proceedings of the 13th European Conference, Zurich, Switzerland, 6–12 September 2014; pp. 740–755. [Google Scholar]
- Bevilacqua, M.; Roumy, A.; Guillemot, C.; Alberi-Morel, M.L. Low-complexity single-image super-resolution based on nonnegative neighbor embedding. In Proceedings of the British Machine Vision Conference, Guildford, UK, 3–7 September 2012; pp. 135.1–135.10. [Google Scholar]
- Zeyde, R.; Elad, M.; Protter, M. On single image scale-up using sparse-representations. In Proceedings of the 7th International Conference, Avignon, France, 24–30 June 2010; pp. 711–730. [Google Scholar]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proceedings of the Eighth IEEE International Conference on Computer Vision, ICCV 2001, Vancouver, BC, Canada, 7–14 July 2001; Volume 2, pp. 416–423. [Google Scholar]
- Huang, J.B.; Singh, A.; Ahuja, N. Single image super-resolution from transformed self-exemplars. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Boston, MA, USA, 7–12 June 2015; pp. 5197–5206. [Google Scholar]
- Liu, J.; Tang, J.; Wu, G. Residual feature distillation network for lightweight image super-resolution. In Proceedings of the Computer Vision—ECCV 2020 Workshops, Glasgow, UK, 23–28 August 2020; pp. 41–55. [Google Scholar]
- Sun, L.; Dong, J.; Tang, J.; Pan, J. Spatially-adaptive feature modulation for efficient image super-resolution. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops (ICCVW), Paris, France, 2–6 October 2023; pp. 13190–13199. [Google Scholar]
- Li, Z.; Liu, Y.; Chen, X.; Cai, H.; Gu, J.; Qiao, Y.; Dong, C. Blueprint separable residual network for efficient image super-resolution. In Proceedings of the Computer Vision and Pattern Recognition, New Orleans, LO, USA, 18–24 June 2022; pp. 833–843. [Google Scholar]





| Model | RB | NLMB_PL | NLMB_P | Set5 | Set14 | BSD100 | Urban100 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | ||||
| Base_Model | ✓ | ✗ | ✗ | 31.607 | 0.8984 | 27.942 | 0.8029 | 27.419 | 0.7502 | 25.670 | 0.7870 |
| Model_PSNLM_L | ✗ | ✓ | ✗ | 31.929 | 0.9024 | 28.217 | 0.8086 | 27.561 | 0.7549 | 26.098 | 0.7994 |
| Model_PSNLM | ✗ | ✗ | ✓ | 32.021 | 0.9036 | 28.250 | 0.8098 | 27.613 | 0.7563 | 26.161 | 0.8021 |
| Model | RB | Wide-Focus | Path1 | Path2 | Set5 | Set14 | BSD100 | Urban100 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | |||||
| Base_Model_WF | ✓ | ✓ | ✗ | ✗ | 31.794 | 0.9010 | 28.030 | 0.8050 | 27.406 | 0.7535 | 25.803 | 0.7947 |
| Base_Model_P1 | ✓ | ✗ | ✓ | ✗ | 31.835 | 0.9011 | 28.102 | 0.8065 | 27.476 | 0.7539 | 25.897 | 0.7951 |
| Base_Model_P2 | ✓ | ✗ | ✗ | ✓ | 31.898 | 0.9014 | 28.175 | 0.8068 | 27.515 | 0.7541 | 25.937 | 0.7956 |
| Model_ADMFB | ✓ | ✗ | ✓ | ✓ | 31.962 | 0.9026 | 28.213 | 0.8077 | 27.598 | 0.7560 | 26.084 | 0.7989 |
| Model | Num_branch | NLMB_P | Path1 | Path2 | Set5 | Set14 | BSD100 | Urban100 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | |||||
| Model_PSNLM | 3 | ✓ | ✗ | ✗ | 32.021 | 0.9036 | 28.250 | 0.8098 | 27.613 | 0.7563 | 26.161 | 0.8021 |
| Model_ADMFB | 3 | ✗ | ✓ | ✓ | 31.962 | 0.9026 | 28.213 | 0.8077 | 27.598 | 0.7561 | 26.084 | 0.7989 |
| PSNLMN_2 | 2 | ✓ | ✓ | ✓ | 32.024 | 0.9031 | 28.271 | 0.8088 | 27.573 | 0.7552 | 26.04 | 0.7986 |
| PSNLMN_4 | 3 | ✓ | ✓ | ✓ | 32.132 | 0.9037 | 28.542 | 0.8108 | 27.643 | 0.7568 | 26.237 | 0.8029 |
| PSNLMN_3 | 4 | ✓ | ✓ | ✓ | 32.144 | 0.9039 | 28.572 | 0.8110 | 27.650 | 0.7571 | 26.243 | 0.8030 |
| Method | Scale | Set5 | Set14 | BSD100 | Urban100 |
|---|---|---|---|---|---|
| PSNR/SSIM | PSNR/SSIM | PSNR/SSIM | PSNR/SSIM | ||
| MemNet [15] | 37.78/0.9597 | 33.28/0.9142 | 32.08/0.8978 | 31.31/0.9195 | |
| SRMDNF [17] | 37.79/0.960 | 33.32/0.915 | 32.05/0.898 | 31.33/0.920 | |
| CARN [18] | 37.76/0.9590 | 33.52/0.9166 | 32.09/0.8978 | 31.92/0.9256 | |
| IMDN [20] | 38.00/0.9605 | 33.63/0.9177 | 32.19/0.8996 | 32.17/0.9283 | |
| RFDN-L [49] | 38.08/0.9606 | 33.67/0.9190 | 32.18/0.8996 | 32.24/0.9290 | |
| ShuffleMixer [21] | 38.01/0.9606 | 33.63/0.9180 | 32.17/0.8995 | 31.89/0.9257 | |
| ESRT [31] | 38.03/0.9600 | 33.75/0.9184 | 32.25/0.9001 | 32.58/0.9318 | |
| LBNet [32] | 38.05/0.9607 | 33.65/0.9177 | 32.16/0.8994 | 32.30/0.9291 | |
| SAFMN [50] | 38.00/0.9605 | 33.54/0.9177 | 32.16/0.8995 | 31.84/0.9256 | |
| BSRN [51] | 38.10/0.9610 | 33.74/0.9193 | 32.24/0.9006 | 32.34/0.9303 | |
| NGswin [28] | 38.05/0.9610 | 33.79/0.9199 | 32.27/0.9008 | 32.53/0.9324 | |
| PSNLMN(our) | 38.06/0.9654 | 34.27/0.9349 | 32.31/0.9119 | 32.55/0.9447 | |
| MemNet [15] | 34.09/0.9248 | 30.00/0.8350 | 28.96/0.8001 | 27.56/0.8376 | |
| SRMDNF [17] | 34.12/0.925 | 30.04/0.837 | 28.97/0.803 | 27.57/0.840 | |
| CARN [18] | 34.29/0.9255 | 30.29/0.8407 | 29.06/0.8034 | 28.06/0.8493 | |
| IMDN [20] | 34.36/0.9270 | 30.32/0.8417 | 29.09/0.8046 | 28.17/0.8519 | |
| RFDN-L [49] | 34.47/0.9280 | 30.35/0.8421 | 29.11/0.8053 | 28.32/0.8547 | |
| ShuffleMixer [21] | 34.40/0.9272 | 30.37/0.8423 | 29.12/0.8051 | 28.08/0.8498 | |
| ESRT [31] | 34.42/0.9268 | 30.43/0.8433 | 29.15/0.8063 | 28.46/0.8574 | |
| LBNet [32] | 34.47/0.9277 | 30.38/0.8417 | 29.13/0.8061 | 28.42/0.8559 | |
| SAFMN [50] | 34.34/0.9267 | 30.33/0.8418 | 29.08/0.8048 | 27.95/0.8474 | |
| BSRN [51] | 34.46/0.9277 | 30.47/0.8449 | 29.18/0.8068 | 28.39/0.8567 | |
| NGswin [28] | 34.52/0.9282 | 30.53/0.8456 | 29.19/0.8078 | 28.52/0.8603 | |
| PSNLMN(our) | 34.56/0.9369 | 30.60/0.8689 | 29.23/0.8266 | 28.71/0.8740 | |
| MemNet [15] | 31.74/0.8893 | 28.26/0.7723 | 27.40/0.7281 | 25.50/0.7630 | |
| SRMDNF [17] | 31.96/0.893 | 28.35/0.777 | 27.49/0.734 | 25.68/0.773 | |
| CARN [18] | 32.13/0.8937 | 28.60/0.7806 | 27.58/0.7349 | 26.07/0.7837 | |
| IMDN [20] | 32.21/0.8948 | 28.58/0.7811 | 27.56/0.7353 | 26.04/0.7838 | |
| RFDN-L [49] | 32.28/0.8957 | 28.61/0.7818 | 27.58/0.7363 | 26.20/0.7883 | |
| ShuffleMixer [21] | 32.21/0.8953 | 28.66/0.7827 | 27.61/0.7366 | 26.08/0.7835 | |
| ESRT [31] | 32.19/0.8947 | 28.69/0.7833 | 27.69/0.7379 | 26.39/0.7962 | |
| LBNet [32] | 32.29/0.8960 | 28.68/0.7832 | 27.62/0.7382 | 26.27/0.7906 | |
| SAFMN [50] | 32.18/0.8948 | 28.60/0.7813 | 27.58/0.7359 | 25.97/0.7809 | |
| BSRN [51] | 32.35/0.8966 | 28.73/0.7847 | 27.65/0.7387 | 26.27/0.7908 | |
| NGswin [28] | 32.33/0.8963 | 28.78/0.7859 | 27.66/0.7396 | 26.45/0.7963 | |
| PSNLMN(our) | 32.33/0.9059 | 28.74/0.8132 | 27.70/0.7597 | 26.56/0.8133 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Wang, Y. Single-Image Super-Resolution via Cascaded Non-Local Mean Network and Dual-Path Multi-Branch Fusion. Sensors 2025, 25, 4044. https://doi.org/10.3390/s25134044
Xu Y, Wang Y. Single-Image Super-Resolution via Cascaded Non-Local Mean Network and Dual-Path Multi-Branch Fusion. Sensors. 2025; 25(13):4044. https://doi.org/10.3390/s25134044
Chicago/Turabian StyleXu, Yu, and Yi Wang. 2025. "Single-Image Super-Resolution via Cascaded Non-Local Mean Network and Dual-Path Multi-Branch Fusion" Sensors 25, no. 13: 4044. https://doi.org/10.3390/s25134044
APA StyleXu, Y., & Wang, Y. (2025). Single-Image Super-Resolution via Cascaded Non-Local Mean Network and Dual-Path Multi-Branch Fusion. Sensors, 25(13), 4044. https://doi.org/10.3390/s25134044




