Design of Space Target Surveillance Constellation Based on Simulation Comparison Method
Abstract
1. Introduction
- Collision Avoidance: Through precise orbital prediction mechanisms, STS triggers real-time satellite evasion maneuvers to effectively prevent collision accidents.
- Satellite Maintenance Support: By leveraging advanced technologies such as thermal imaging and radio frequency (RF) monitoring, STS conducts health monitoring of high-value aerospace assets like communication satellites and meteorological satellites, providing critical technical support for satellite operation and maintenance.
- Space Sustainability Promotion: By continuously tracking the distribution and movement patterns of space debris, STS provides accurate target lists for space debris cataloging and active removal operations, strongly advancing the sustainable development of the space environment.
- Space Military Security Safeguard: Through dynamic tracking and feature recognition of adversarial spacecraft, STS delivers real-time intelligence support to command centers, serving as a core capability for maintaining space military security.
2. Related Research
3. Analysis of the Requirements of Space Target Surveillance
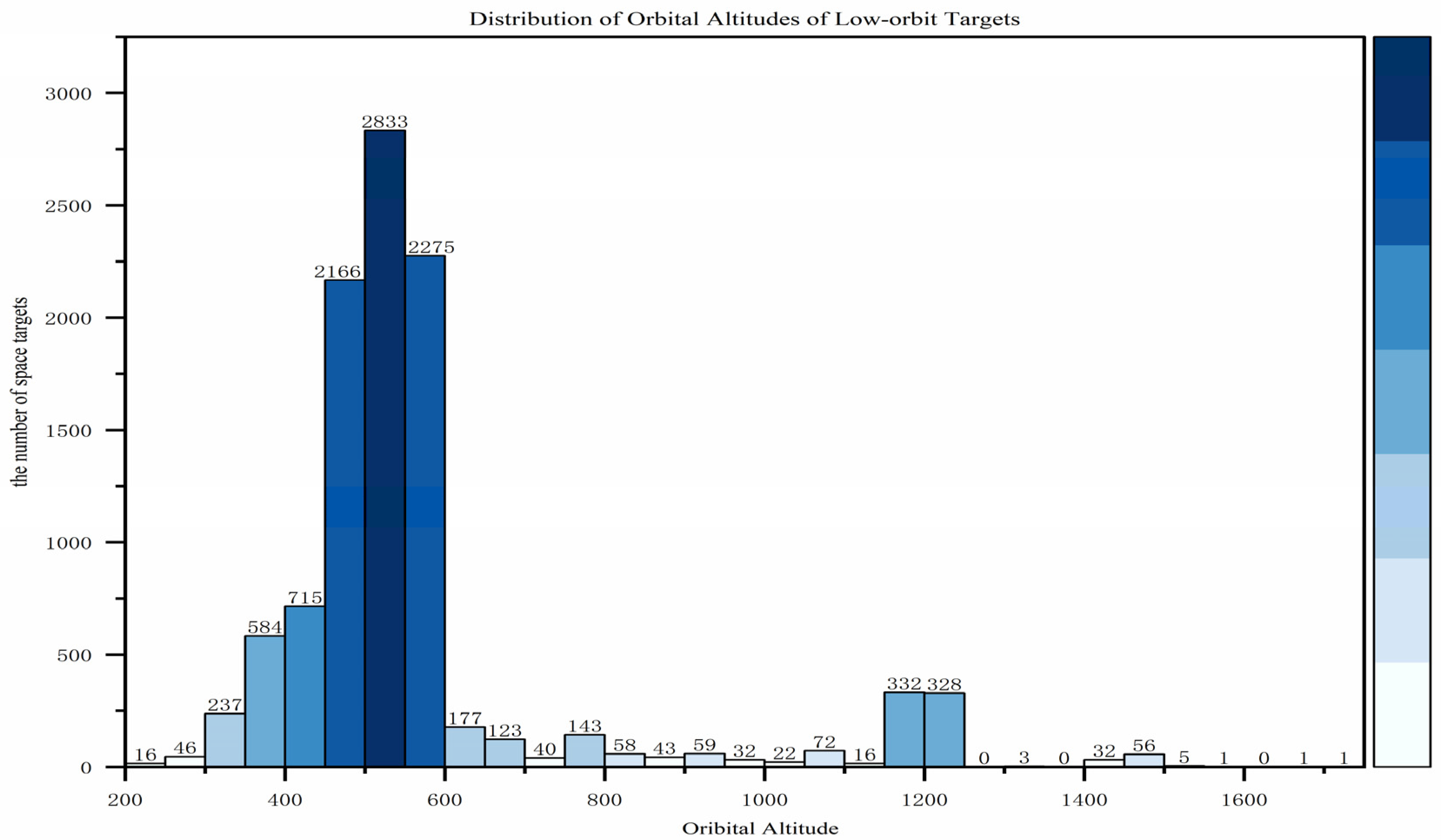
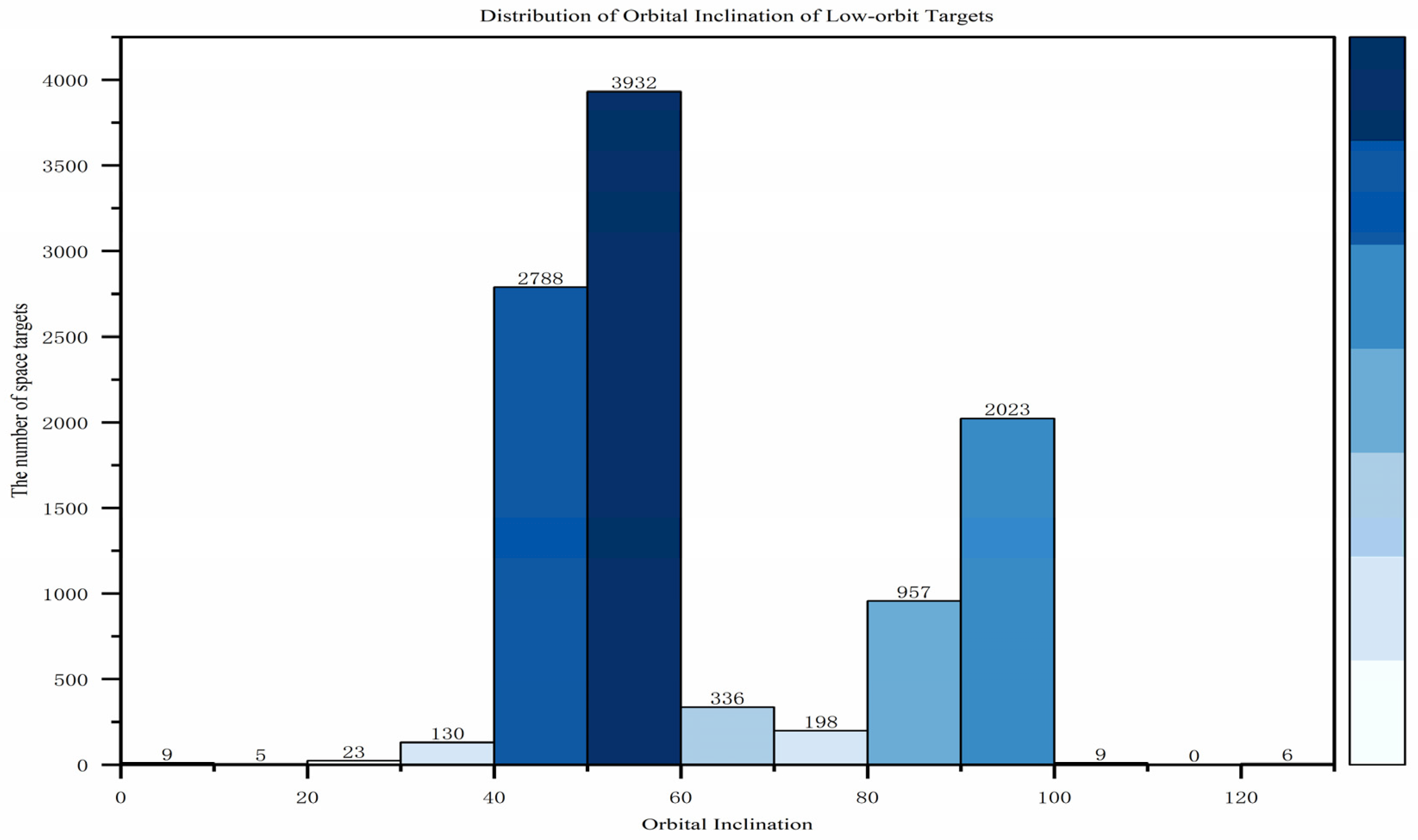
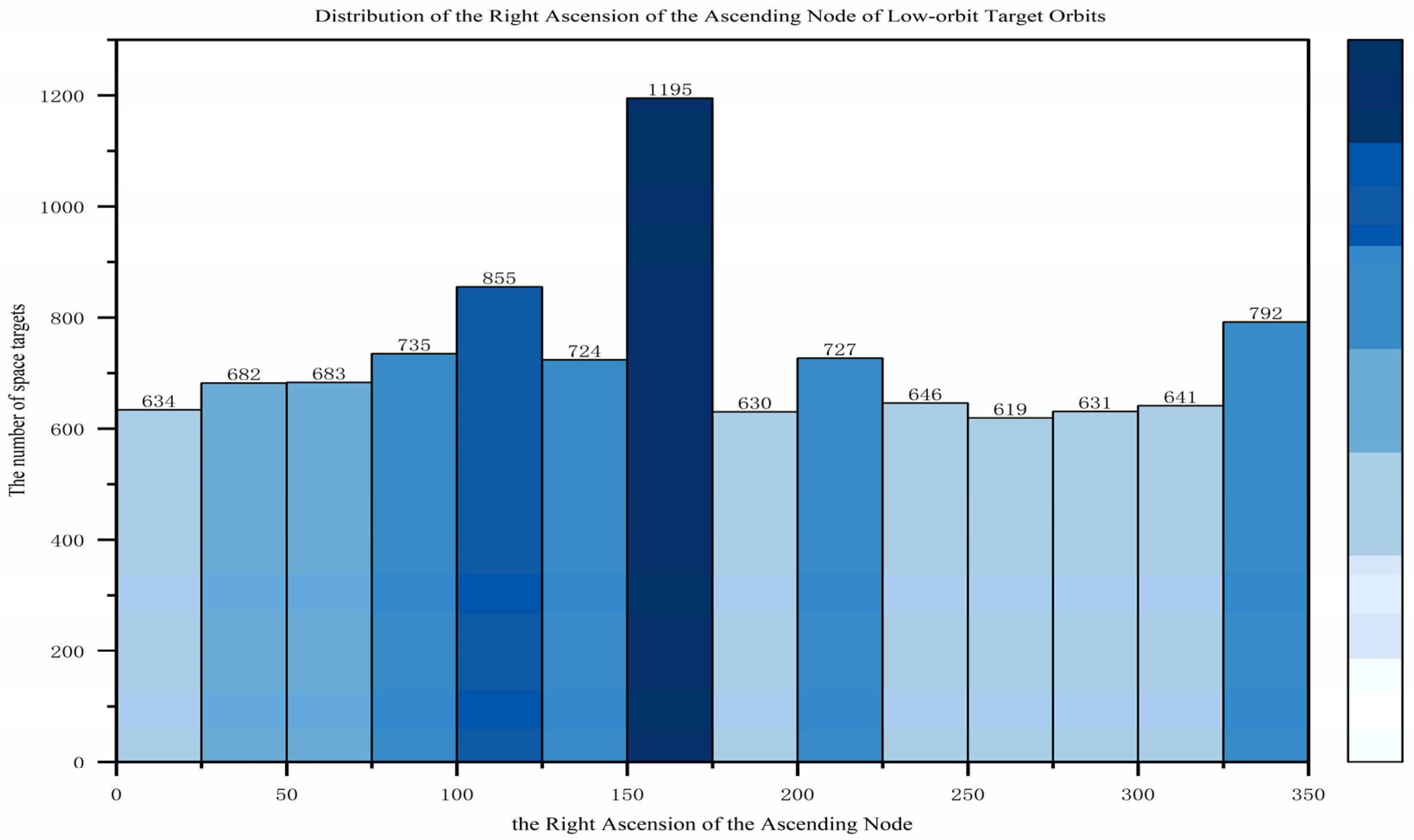
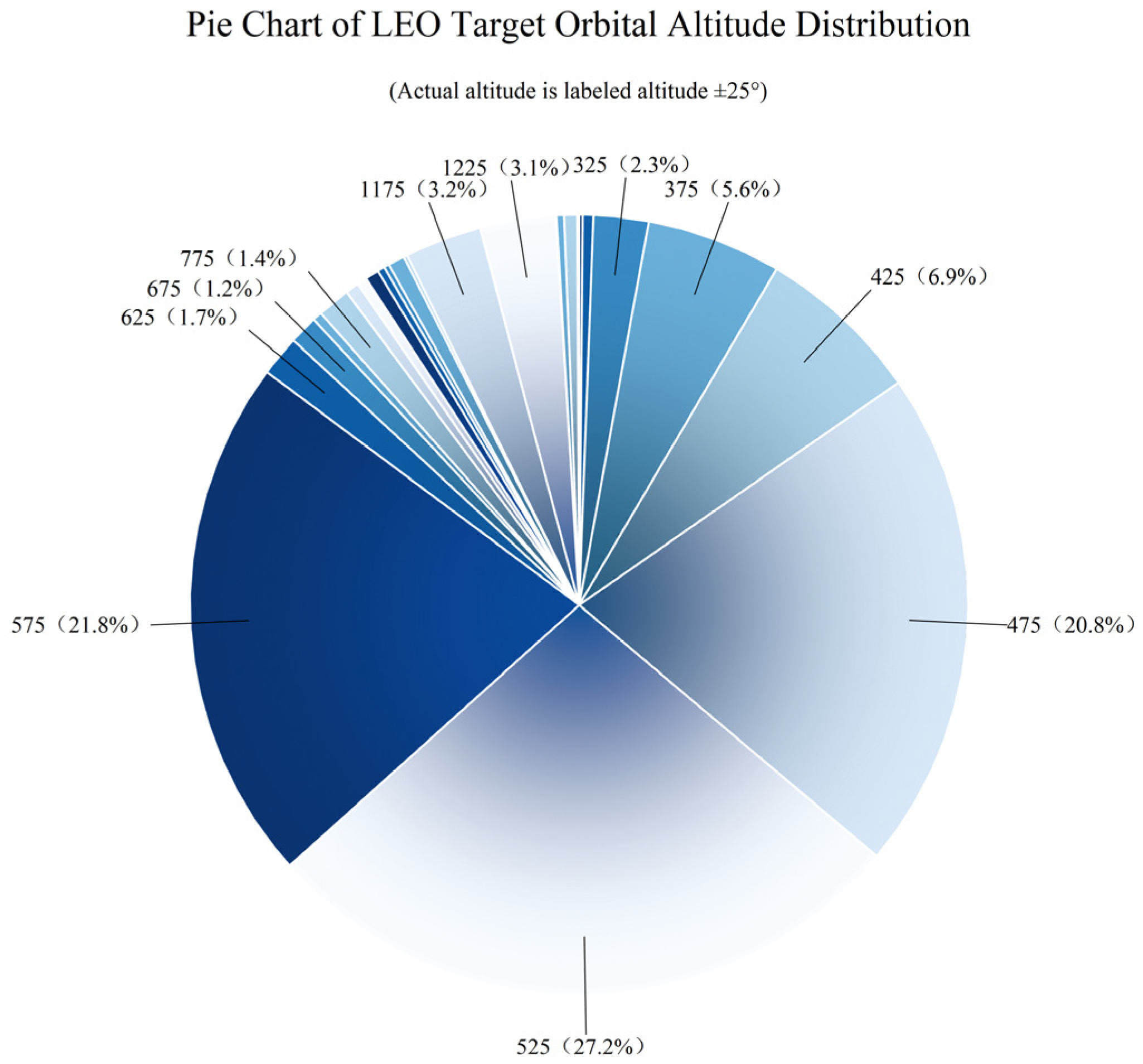
3.1. Surveillance Target Characteristics
- Semi-major axis (a): The length of the major axis of the orbital ellipse.
- Eccentricity (e): A parameter characterizing the deviation of the orbit from a circular shape.
- Inclination (i): The angle between the orbital plane and the Earth’s equatorial plane.
- Right ascension of the ascending node (Ω): The angle between the Earth’s vernal equinox direction and the ascending node (the point where the satellite crosses the equatorial plane from south to north).
- Argument of perigee (ω): The angle between the ascending node and the perigee (the point closest to Earth in the orbit).
- True anomaly (ν): The angle between the perigee and the satellite’s current position, measured at the Earth’s center.
3.2. Surveillance Task Requirements
- Revisit Interval
- Observability Rate
- Coverage Ratio
3.3. Analysis of Constraints
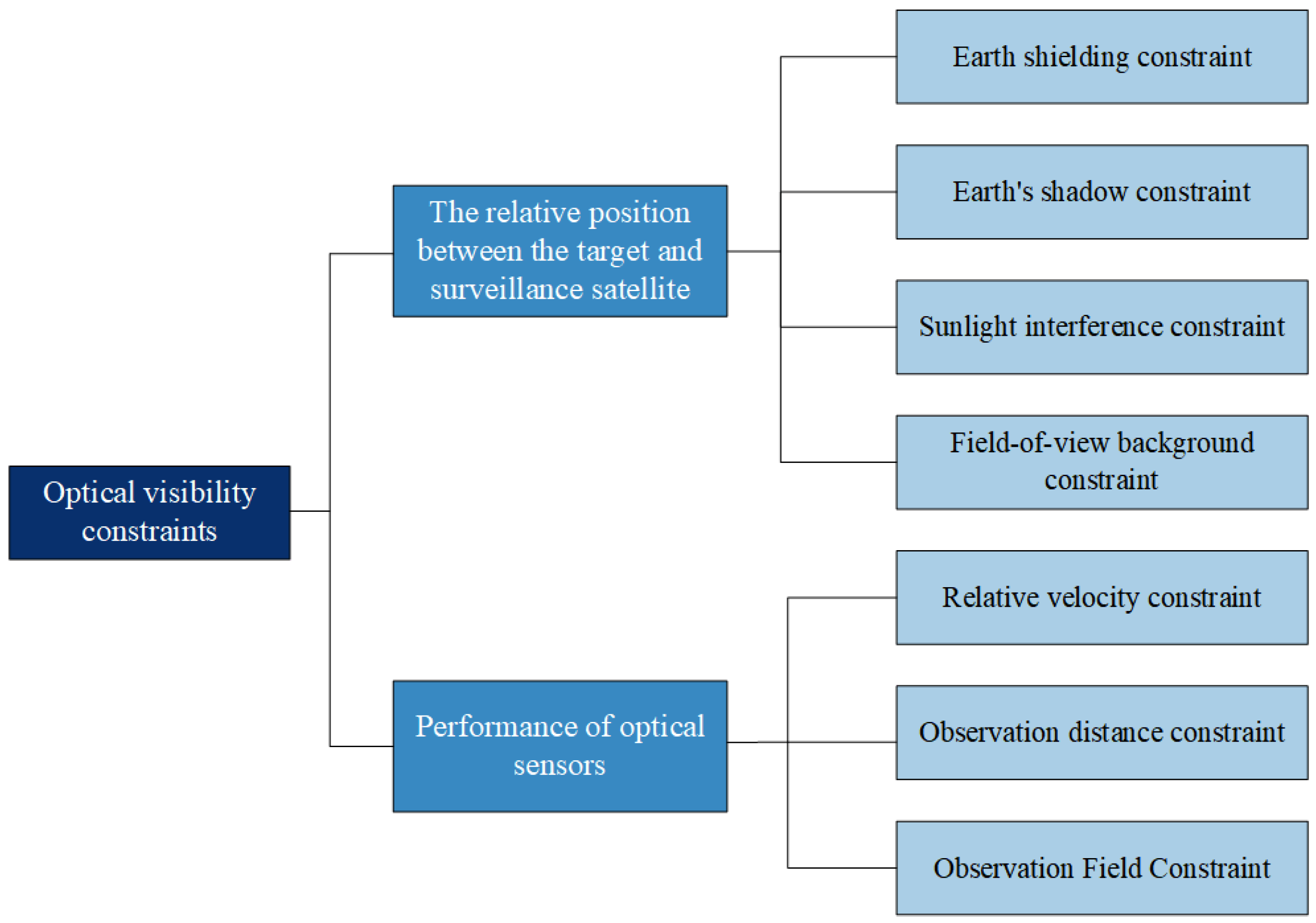
3.3.1. Optical Visibility Constraints
- Earth shielding constraint
- Earth’s shadow constraint
- Sunlight interference constraint
- Field-of-view background constraint
- Relative velocity constraint
- Observation distance constraint
- Observation Field Constraint
3.3.2. Arc Segment Validity Constraint
4. Simulation Experiments and Result Analysis
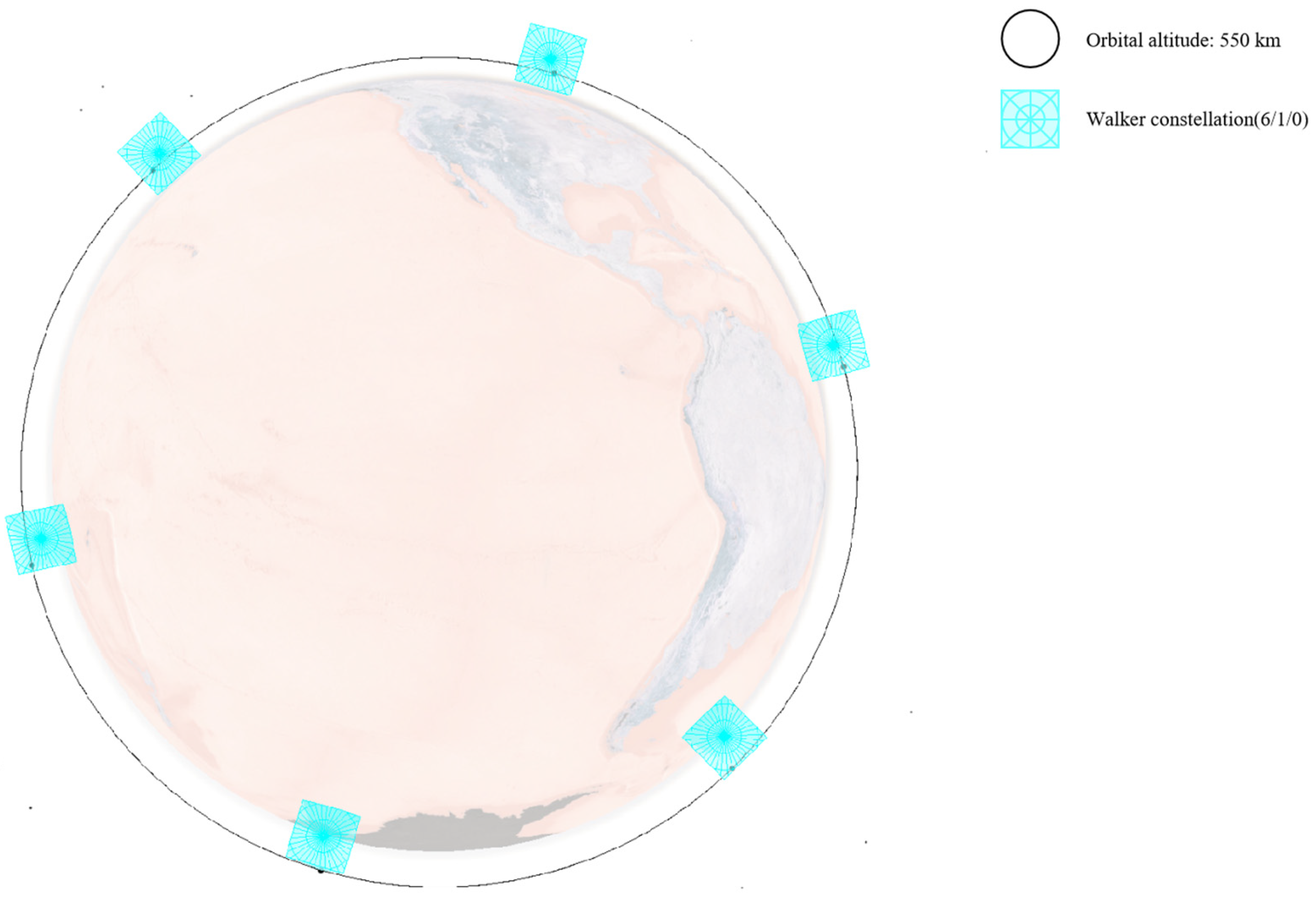
4.1. Constellation Schemes
4.2. Simulation Process
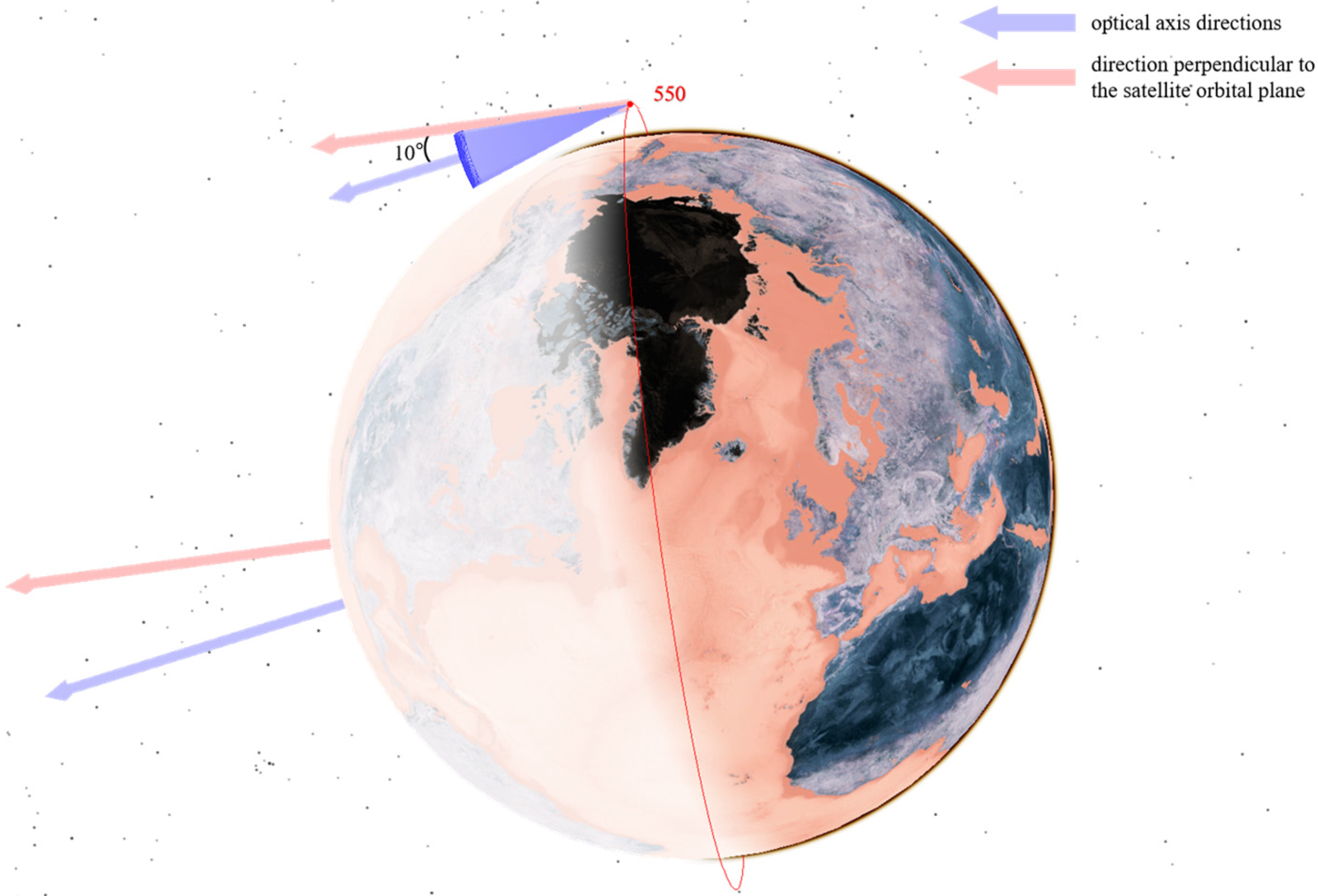
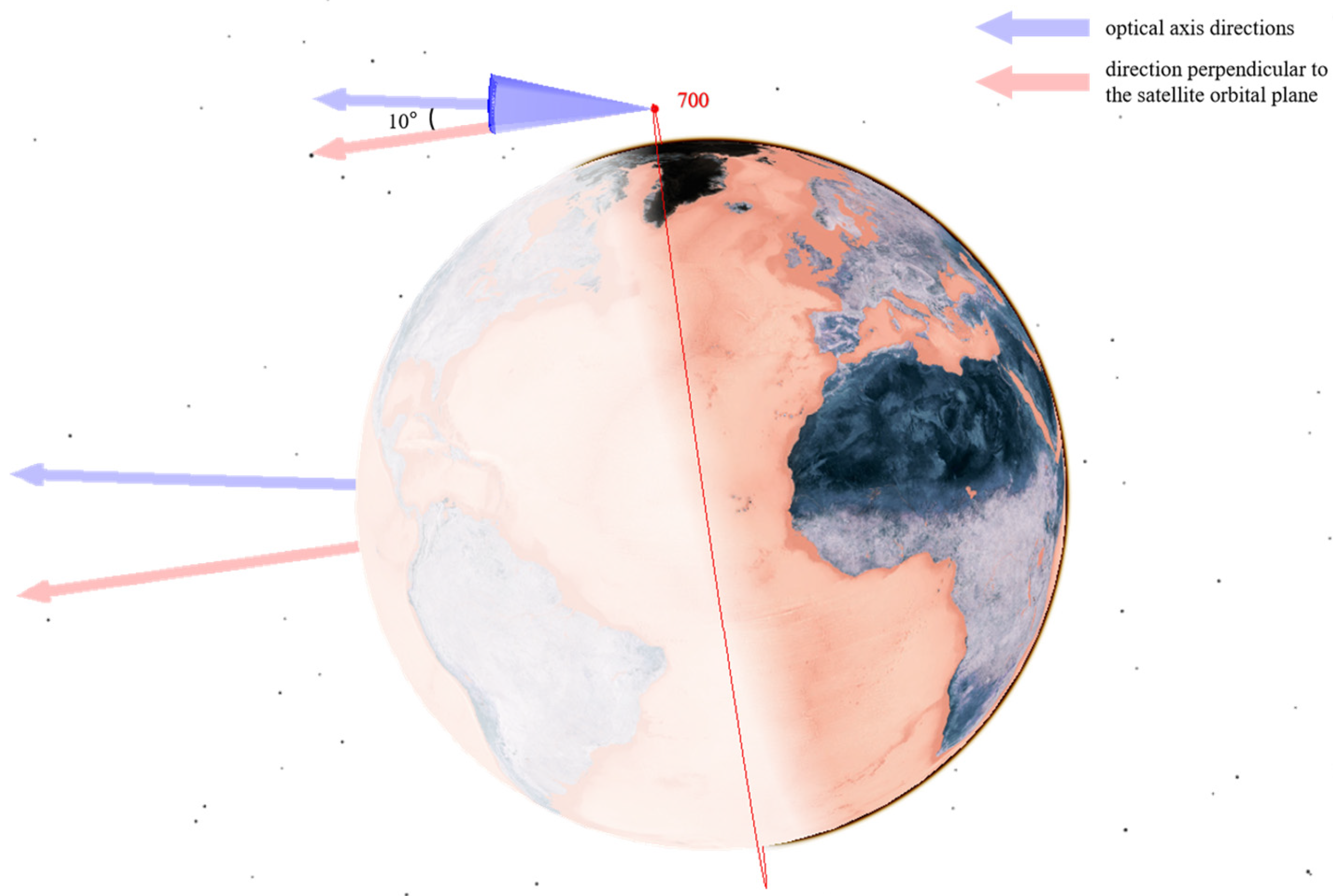
- In the CON.1 constellation, the optical axis of each satellite is deflected by 10° toward the Earth’s center.
- For the CON.2 constellation, the satellite at 550 km altitude features a 10° optical axis deflection toward the Earth’s center, whereas the satellite at 700 km altitude has a 10° deflection away from the Earth’s center.
- In the CON.3 constellation, the 550 km altitude satellite exhibits a 10° optical axis deflection toward the Earth’s center, and the 1600 km altitude satellite has a 15° deflection in the same direction.
4.3. Performance Analysis
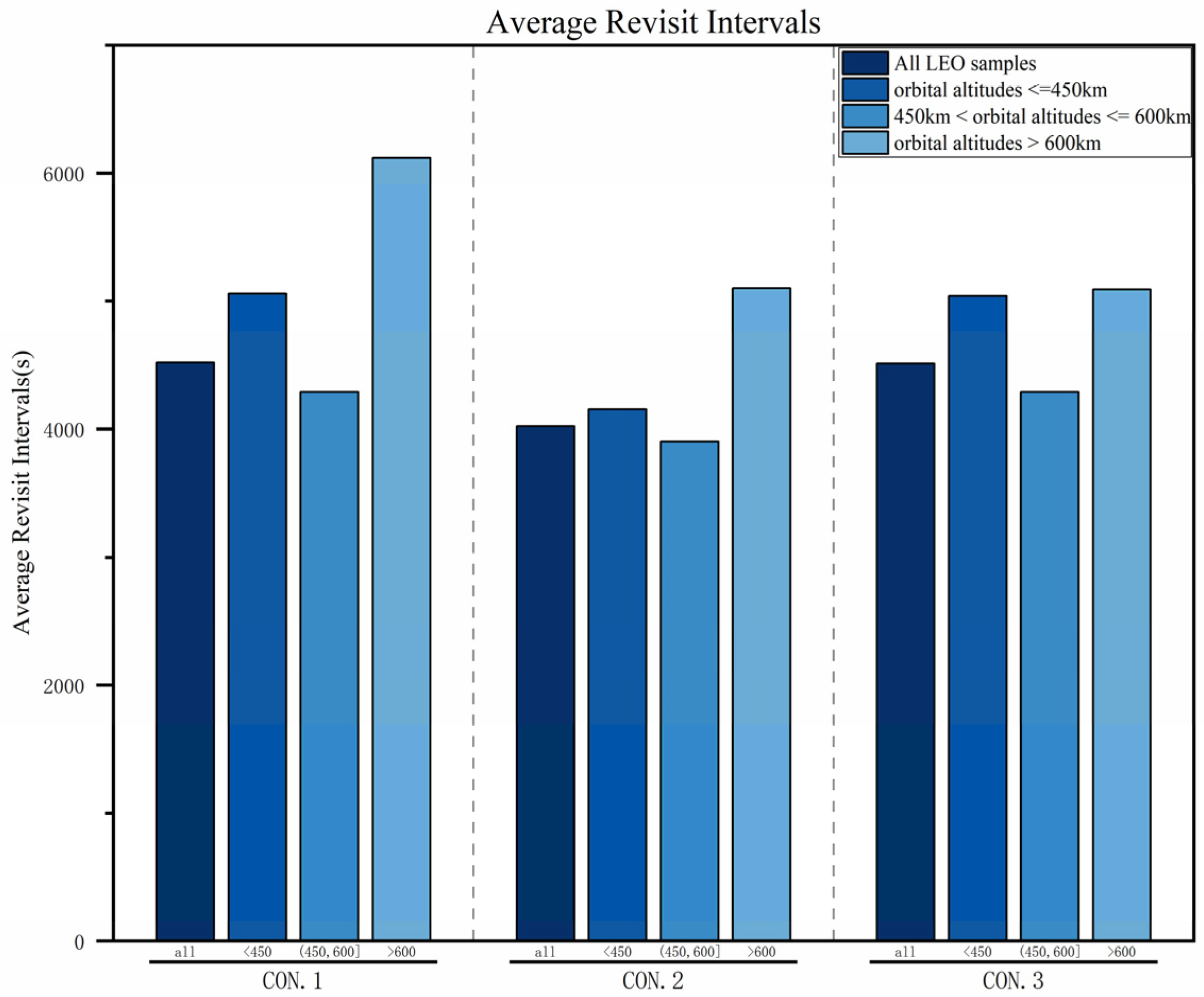
4.3.1. Average Revisit Intervals
4.3.2. Average Observability Rates
4.3.3. Coverage Ratios
5. Conclusions
- Optimize payloads for a wider FOV and a longer observation range.
- Integrate space-based and ground-based systems for multi-source surveillance, leveraging their combined advantages.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gong, J.G.; Ning, Y.; Lv, N. Development and implications of U.S. high-Earth-orbit space situational awareness technology. Space Control. Technol. Appl. 2021, 47, 1–7. [Google Scholar] [CrossRef]
- Tang, Z.Y.; Huang, X.F.; Cai, Z.B. Development status and implications of overseas space-based space object surveillance systems. Aerosp. Electron. Countermeas. 2015, 31, 24–26. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Z.; Ye, H.; Zhang, G. Analysis and development trends of foreign space situational awareness capabilities (invited paper). Prog. Laser Optoelectron. 2024, 61, 66–83. [Google Scholar] [CrossRef]
- Wang, D.J.; Wu, G.Q.; Han, L.; Jing, Y.X.; Liu, C.H.; Shang, X.Y. Analysis and research on the observation mode of the US GSSAP satellite. Space Control Technol. Appl. 2022, 48, 22–28. [Google Scholar] [CrossRef]
- Wang, G.; Zuo, P.; Hong, T.; Zhang, G. Review of low Earth orbit satellite constellation design methods. In Proceedings of the 18th Annual Satellite Communication Academic Conference, Beijing, China, 12 August 2022; pp. 61–66. [Google Scholar]
- Zhang, C.; Zhu, Z.F. Design of space-based situational awareness constellation configuration. Comput. Simul. 2023, 40, 93–98, 107. [Google Scholar] [CrossRef]
- Du, J.; Chen, J.; Li, B.; Sang, J. Tentative Design of SBSS Constellations for LEO Debris Catalog Maintenance. Acta Astronaut. 2019, 155, 379–388. [Google Scholar] [CrossRef]
- Ye, J.; Zhang, Y.; Zhang, K.P.; Lu, S.Z.; Wang, H.B. Design of high-orbit optical observation constellation configuration and coverage analysis. Space Control Technol. Appl. 2023, 49, 64–73. [Google Scholar] [CrossRef]
- Huo, G. Research on the Coordinated Observation and Orbit Determination Technology of Space-Based Surveillance Constellations. Master’s Thesis, Harbin Institute of Technology, Harbin, China, May 2023. [Google Scholar]
- Yang, L.; Lu, Y.; Liu, L. Advances in theories and technologies for space target cataloging and orbit determination. Space Debris Res. 2023, 23, 56–63. [Google Scholar] [CrossRef]
- Liu, L. Research on the Initial Orbit Determination of Space Target Direction Finding Based on Space-Based Surveillance. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2010. [Google Scholar]
- Zhang, Z.Y.; Sang, J.Z.; Chen, J.Y. Application of neural networks in the problem of determining initial orbits for very short arcs. Surv. Mapp. Geogr. Inf. 2022, 47, 16–19. [Google Scholar] [CrossRef]
- Lei, X.X. Research on the initial orbital relationship of space debris with a short angle and arc. J. Geod. 2021, 50, 283. [Google Scholar]





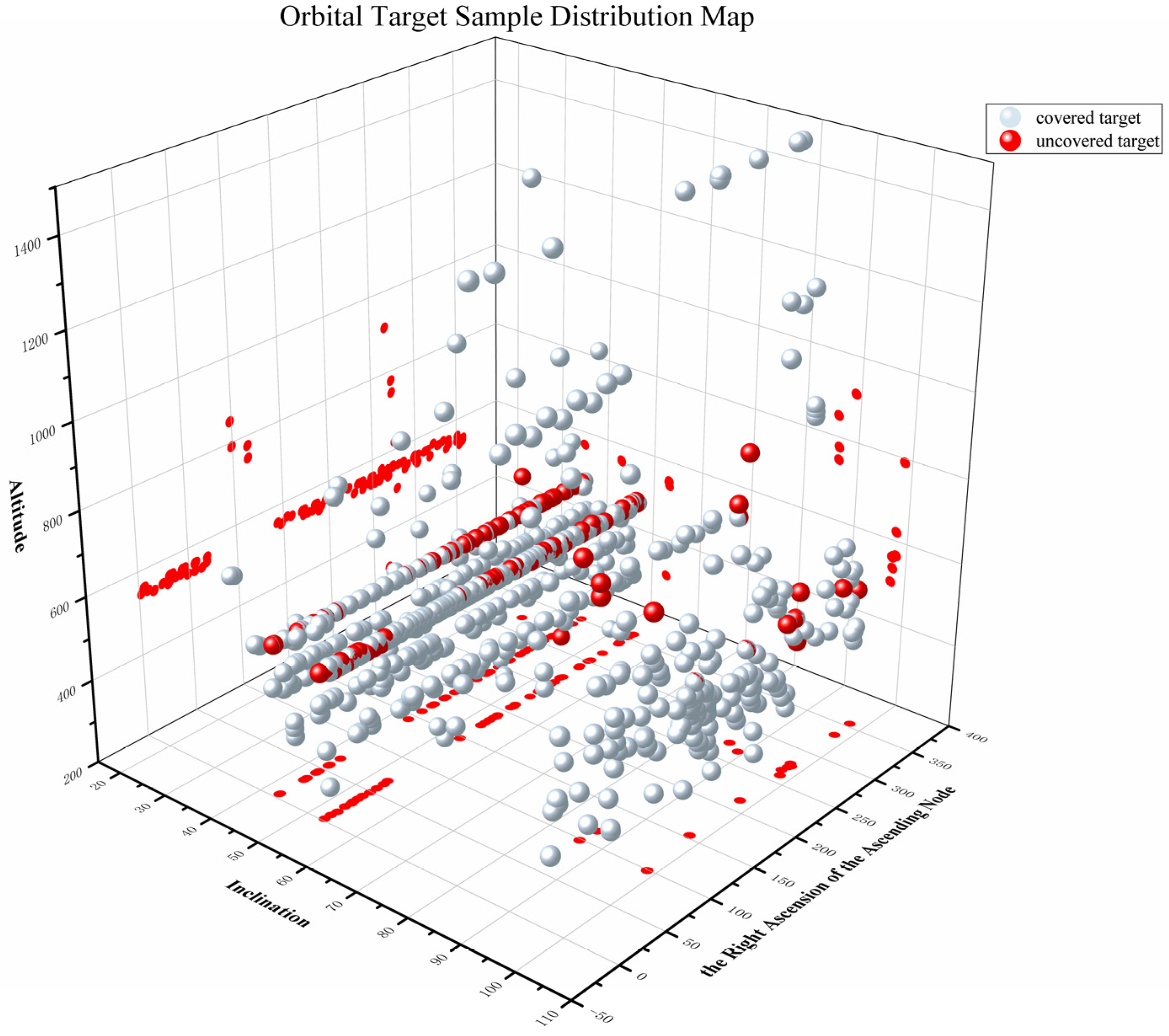
| Target Type | Grouping Criteria | Percentage of All Targets(%) |
|---|---|---|
| LEO | a < 8378 km | 92.90 |
| MEO | 8378 km < a < 27,378 km | 1.14 |
| HEO | 27,378 km < a < 42,078 km | 0.70 |
| GEO | a > 42,078 km and i < 15° | 4.98 |
| IGSO | a > 42,078 km and i > 15° | 0.28 |
| Layer Serial Number (h) | Stratification Criterion | Total Quantity of the hth Layer (Nh) | Percentage of LEO Targets(%) |
|---|---|---|---|
| 1 | i < 40° | 167 | 1.61 |
| 2 | 40° <= i < 60 | 6720 | 64.51 |
| 3 | 60° <= i < 90° | 1491 | 14.31 |
| 4 | 90° <= i | 2039 | 19.57 |
| Target Type | Minimum Observation Arc Length (Single Satellite)(s) | Minimum Observation Arc Length (Double Satellites)(s) |
|---|---|---|
| LEO | 400 | 40 |
| GEO | 1700 | 450 |
| Constellation | Orbital Inclination (°) | Orbital Altitude (km) | T | P | F | Orbital Type |
|---|---|---|---|---|---|---|
| CON.1 | 97.6 | 550 | 6 | 1 | 0 | Sun-synchronous dawn-dusk orbit |
| CON.2 | 97.6 | 550 | 6 | 1 | 0 | Sun-synchronous dawn-dusk orbit |
| 98.2 | 700 | 3 | 1 | 0 | Sun-synchronous dawn-dusk orbit | |
| CON.3 | 97.6 | 550 | 6 | 1 | 0 | Sun-synchronous dawn-dusk orbit |
| 102.51 | 1600 | 6 | 1 | 0 | Sun-synchronous dawn-dusk orbit |
| Payload | Distance (km) | Imaging Resolution | Aperture (mm) | Lateral Relative Velocity (km/s) | Field of View (°) | Angular Resolution (″) |
|---|---|---|---|---|---|---|
| CCD/CMOS | 300 | 4096 × 4096 | 120 | 3 | 9 × 9 | 8.8 |
| Constellation | Simulation Targets | Average Revisit Interval (s) | Average Observability Rate (%) | Coverage Ratio (%) |
|---|---|---|---|---|
| CON.1 | All LEO target samples | 4522.37 | 1.84 | 81.90 |
| orbital altitude < 450 km | 5057.14 | 2.20 | 96.18 | |
| orbital altitude between 450 and 600 km | 4290.40 | 1.77 | 81.95 | |
| orbital altitude > 600 km | 6117.76 | 2.28 | 33.56 | |
| CON.2 | All LEO target samples | 4022.99 | 2.18 | 86.27 |
| orbital altitude < 450 km | 4157.13 | 2.56 | 96.82 | |
| orbital altitude between 450 and 600 km | 3901.40 | 2.12 | 91.82 | |
| orbital altitude > 600 km | 5100.86 | 2.49 | 46.58 | |
| CON.3 | All LEO target samples | 4512.63 | 1.84 | 83.50 |
| orbital altitude < 450 km | 5040.86 | 2.20 | 97.45 | |
| orbital altitude between 450 and 600 km | 4290.40 | 1.77 | 81.95 | |
| orbital altitude > 600 km | 5091.60 | 2.12 | 74.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Q.; Liu, D.; Dong, Z. Design of Space Target Surveillance Constellation Based on Simulation Comparison Method. Sensors 2025, 25, 3977. https://doi.org/10.3390/s25133977
Hu Q, Liu D, Dong Z. Design of Space Target Surveillance Constellation Based on Simulation Comparison Method. Sensors. 2025; 25(13):3977. https://doi.org/10.3390/s25133977
Chicago/Turabian StyleHu, Qinying, Desheng Liu, and Ziwei Dong. 2025. "Design of Space Target Surveillance Constellation Based on Simulation Comparison Method" Sensors 25, no. 13: 3977. https://doi.org/10.3390/s25133977
APA StyleHu, Q., Liu, D., & Dong, Z. (2025). Design of Space Target Surveillance Constellation Based on Simulation Comparison Method. Sensors, 25(13), 3977. https://doi.org/10.3390/s25133977






