Distance Measurement and Data Analysis for Civil Aviation at 1000 Frames per Second Using Single-Photon Detection Technology
Abstract
1. Introduction
2. Principle of Single-Photon Laser Radar Distance Measurement
- Dead Time Mitigation: By implementing active quenching circuits and parallel readout architectures, the SPAD reset time can be reduced.
- Algorithm-Hardware Co-design: Replace the standard histogram-based processing with sparse event-driven algorithms.
3. Civil Aviation Thousand Frame Distance Measurement
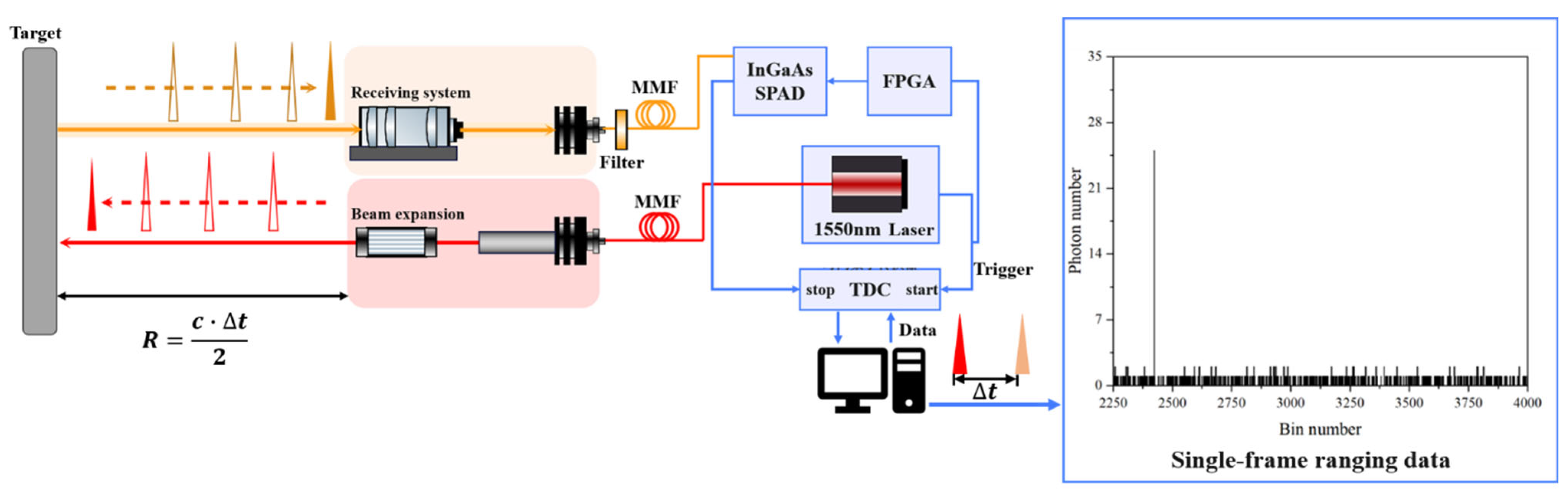
3.1. Distance Measurement Experiment
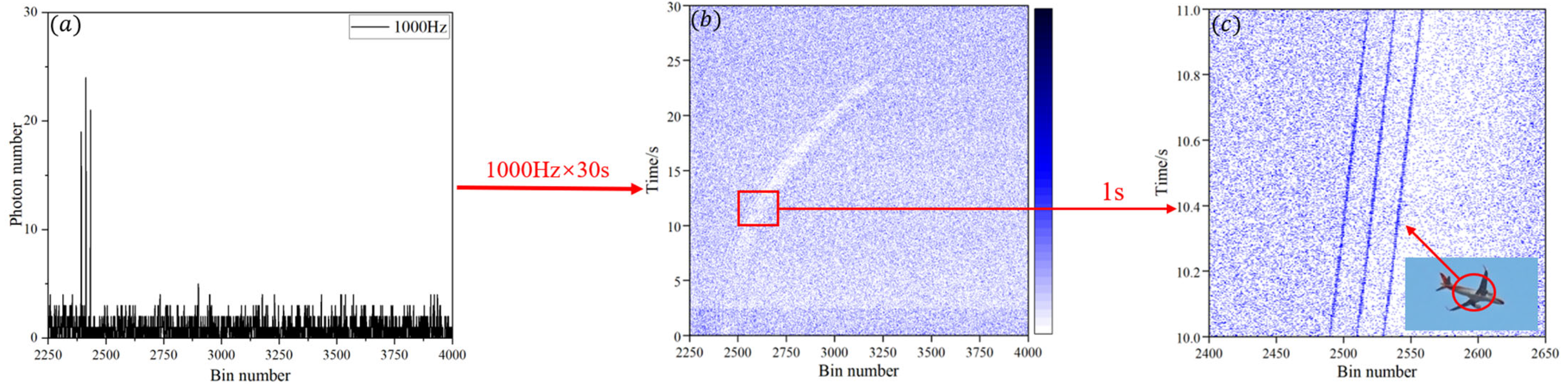
3.2. Noise-Filtering Algorithm
4. Analysis of Distance Measurement Results
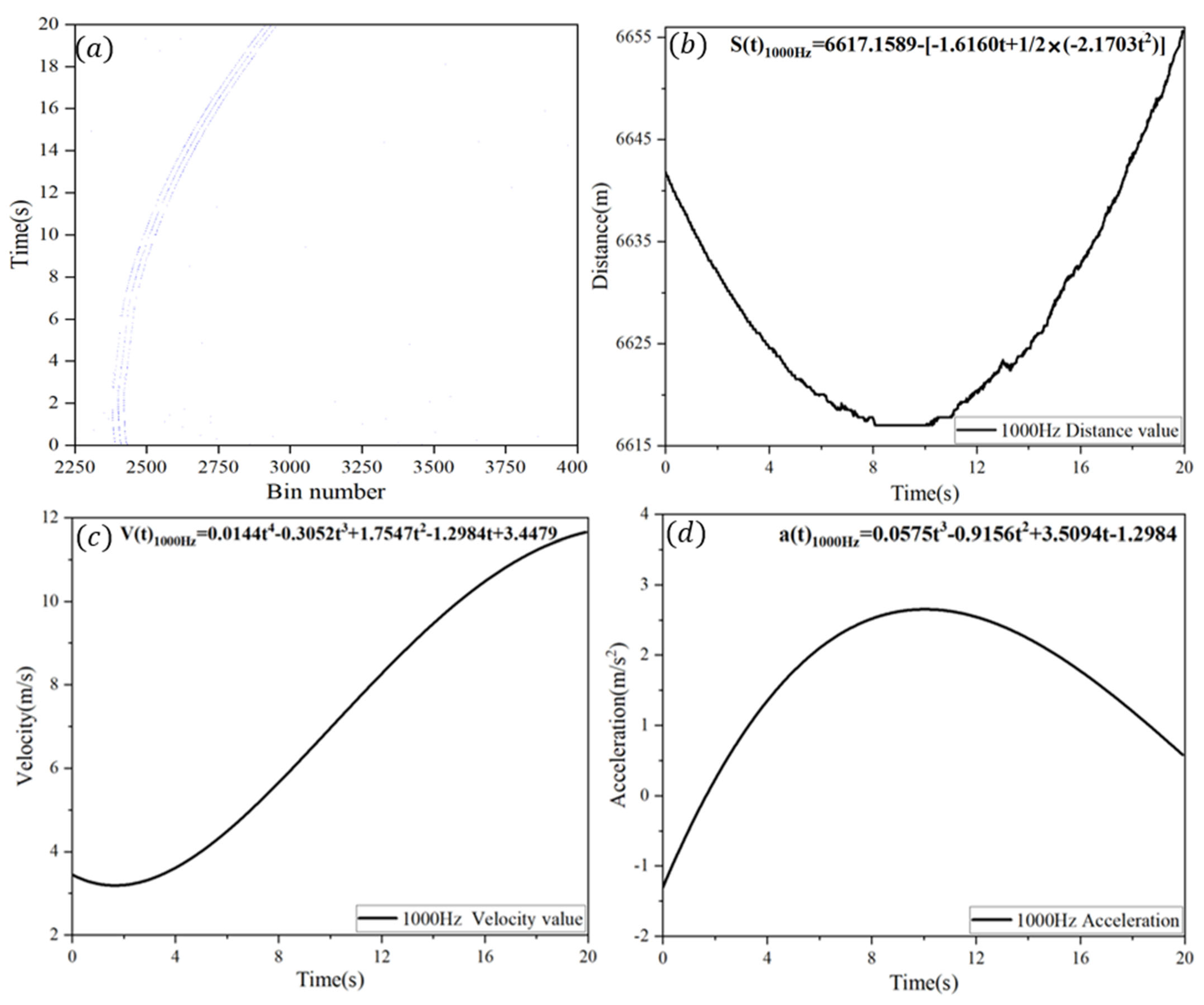
4.1. Data Processing
4.2. The Impact of Frame Rate on Distance Measurement Precision
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tahk, M.-J.; Song, K.-R.; Kim, T.-H.; Lee, C.-H. A New Guidance Algorithm Against High-Speed Maneuvering Target. Int. J. Aeronaut. Space Sci. 2021, 22, 1170–1182. [Google Scholar] [CrossRef]
- Raman, A.; Shekhar, D.; Kumar, N. Sub-Micron Semiconductor Devices: Design and Applications; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Nakamura, M.; Abe, T.; Ueno, M.; Yamazaki, A.; Ando, H.; Futaguchi, M.; Sato, M.; Iwagami, N.; Hashimoto, G.L.; Hirata, N.; et al. Absolute calibration of brightness temperature of the Venus disk observed by the Longwave Infrared Camera onboard Akatsuki. Earth Planets Space 2017, 69, 141. [Google Scholar] [CrossRef]
- Li, G.; Shi, K.; Liu, X.; Chen, Z.; Chen, N. The research about high-dynamic and low-gray target image differential capture technology based on laser active detection. EURASIP J. Image Video Process. 2018, 2018, 78. [Google Scholar] [CrossRef]
- Chan, S.C.A.; Lam, Y.E.; Tsia, K. Pixel Super-Resolution of Time-Stretch Imaging by an Equivalent-Time Sampling Concept; The University of Hong Kong: Hong Kong, China, 2016. [Google Scholar]
- Liu, B.; Yu, Y.; Jiang, S. Review of Advances in LiDAR Detection and 3D Imaging. Guangdian Gongcheng/Opto-Electron. Eng. 2019, 46, 2019–2065. [Google Scholar]
- Önder, A.; Goit, J.P. The effect of coastal terrain on nearshore offshore wind farms: A large-eddy simulation study. J. Renew. Sustain. Energy 2022, 14, 043304. [Google Scholar] [CrossRef]
- Abshire, J.B.; Cohen, S.C.; Degnan, J.J.; Bufton, J.L.; Garvin, J.B. The Geoscience Laser Altimetry/Ranging System. IEEE Trans. Geosci. Remote Sens. 1987, GE-25, 581–592. [Google Scholar] [CrossRef]
- Jia, B.; Cao, G.; Lv, Q.; Zhang, X. Dual station visualization measuring method of LRCS. In Proc. SPIE 10153, Advanced Laser Manufacturing Technology; SPIE: Bellingham, WA, USA, 19 October 2016; Volume 1015308. [Google Scholar]
- Jung, K.T.; Jee, I.G. VA-LOAM: Visual Assist LiDAR Odometry and Mapping for Accurate Autonomous Navigation. Sensors 2024, 24, 3831. [Google Scholar] [CrossRef] [PubMed]
- Landes, T.; Lecomte, V.; Macher, H. Combination of thermal infrared images and laserscanning data for 3D thermal point cloud generation on buildings and trees. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 48, 129–136. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, J.; Li, J.; Yan, M. Multiview infrared target detection and localization. Opt. Eng. 2019, 58, 113104. [Google Scholar] [CrossRef]
- Goyal, V.K.; Venkatraman, D.; Wong, F.N.C.; Zappa, F.; Shin, D.; Xu, F.; Shapiro, J.H.; Villa, F.; Lussana, R. Photon-efficient imaging with a single-photon camera. Nat. Commun. 2016, 7, 12046. [Google Scholar] [CrossRef]
- Holst, G.C. CCD Arrays, Cameras, and Displays; JCD Publishing: Oviedo, FL, USA, 1998. [Google Scholar]
- Cova, S.; Lovati, P.; Lacaita, A.; Zappa, F. Counting, timing, and tracking with a single-photon germanium detector. Opt. Lett. 1996, 21, 59–61. [Google Scholar] [CrossRef]
- Lin, Z.; Shangguan, M.; Cao, F.; Yang, Z.; Qiu, Y.; Weng, Z. Underwater Single-Photon Lidar Equipped with High-Sampling-Rate Multi-Channel Data Acquisition System. Remote Sens. 2023, 15, 5216. [Google Scholar] [CrossRef]
- Gerrits, T.; Migdall, A.; Bienfang, J.C.; Lehman, J.; Nam, S.W.; Splett, J.; Vayshenker, I.; Wang, J. Calibration of free-space and fiber-coupled single-photon detectors. Metrologia 2020, 57, 015002. [Google Scholar] [CrossRef]
- Massa, J.S. Laser depth measurement based on time-correlated single-photon counting. Opt. Lett. 1997, 22, 543–545. [Google Scholar] [CrossRef] [PubMed]
- Massa, J.S. Time-of-flight optical ranging system based on time-correlated single-photon counting. Appl. Opt. 1998, 37, 7298–7304. [Google Scholar] [CrossRef]
- Bayer, M.M.; Torun, R.; Li, X.; Velazco, J.E.; Boyraz, O. Simultaneous ranging and velocimetry with multi-tone continuous wave lidar. Opt. Express 2020, 28, 17241–17252. [Google Scholar] [CrossRef]
- Xu, C.; Xia, L.; Wu, C.; Huang, H. Moving target detection based on velocity compensation methods in a coherent continuous wave lidar. J. Eng. 2019, 2019, 7065–7068. [Google Scholar] [CrossRef]
- Peng, C.-Z.; Jin, W.; Li, Z.-P.; Li, Y.-H.; Pan, J.-W.; Huang, X.; Wang, B.; Yu, C.; Zhang, Q.; Xu, F.; et al. Single-photon computational 3D imaging at 45 km. Photonics Res. 2020, 8, 1532–1540. [Google Scholar] [CrossRef]
- Wang, L.; Han, S.; Xia, W.; Lei, J. Adaptive aperture for Geiger mode avalanche photodiode flash ladar systems. Rev. Sci. Instrum. 2018, 89, 023105. [Google Scholar] [CrossRef]
- McCarthy, A.; Ren, X.; Della Frera, A.; Gemmell, N.R.; Krichel, N.J.; Scarcella, C.; Ruggeri, A.; Tosi, A.; Buller, G.S. Kilometer-range depth imaging at 1550 nm wavelength using an InGaAs/InP single-photon avalanche diode detector. Opt. Express 2013, 21, 22098–22113. [Google Scholar] [CrossRef]
- Markfort, A.; Baranov, A.; Conneely, T.M.; Duran, A.; Lapington, J.; Milnes, J.; Moore, W.; Mudrov, A.; Tyukin, I. Investigating machine learning solutions for a 256 channel TCSPC camera with sub-70 ps single photon timing per channel at data rates >10 Gbps. J. Instrum. 2022, 17, C07023. [Google Scholar] [CrossRef]
- Milstein, A.B.; Jiang, L.A.; Luu, J.X.; Hines, E.L.; Schultz, K.I. Acquisition algorithm for direct-detection ladars with Geiger-mode avalanche photodiodes. Appl. Opt. 2008, 47, 296–311. [Google Scholar] [CrossRef] [PubMed]
- Henriksson, M.; Tolt, G.; Grönwall, C. Peak detection approaches for time-correlated single-photon counting three-dimensional lidar systems. Opt. Eng. 2018, 57, 031306. [Google Scholar] [CrossRef]
- Zhao, X.; He, W.; Chen, Q.; Zhang, L.; Wu, M.; Chen, R. Enhancing LiDAR performance using threshold photon-number-resolving detection. Opt. Express 2024, 32, 2574–2589. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, J.; Hua, K.; Wang, H.; Zhang, Q.; Li, Z.; Liu, B. Target Tracking and Ranging Based on Single Photon Detection. Photonics 2021, 8, 278. [Google Scholar] [CrossRef]
- Alem, N.; Pellen, F.; Le Brun, G.; Le Jeune, B. Radiofrequency modulator for marine lidar radar systems featuring compact and agile extra-cavity architecture using a polarimetric effect. Appl. Opt. 2022, 61, 3671–3678. [Google Scholar] [CrossRef]
- Trunk, G.; Brockett, S. Range and velocity ambiguity resolution. In Proceedings of the Record of the 1993 IEEE National Radar Conference, Lynnfield, MA, USA, 20–22 April 1993; pp. 146–149. [Google Scholar]
- Du, B.; Pang, C.; Wu, D.; Li, Z.; Peng, H.; Tao, Y.; Wu, E.; Wu, G. High-speed photon-counting laser ranging for broad range of distances. Sci. Rep. 2018, 8, 4198. [Google Scholar] [CrossRef]
- Feng, B.; Gao, H.; Yang, Y.; Ren, F.; Lu, T. Multi-target CFAR detector based on compressed sensing radar system. Int. J. Electron. 2024, 111, 975–988. [Google Scholar] [CrossRef]
- Bai, X.; Wang, D.; Liu, X. Multi-fold high-order cumulants based CFAR detector for radar weak target detection. Digit. Signal Process. 2023, 139, 104076. [Google Scholar] [CrossRef]




| Detection Time | Original Data SNR (dB) | Target Location | Sun Location | Noise Reduction Parameters | SNR of Filtered Data (dB) | |||
|---|---|---|---|---|---|---|---|---|
| Azimuth | Elevation | Azimuth | Elevation | |||||
| 07:30 | 17.31 | 97°02′26″ | 34°07′12″ | 79°59′24″ | 19°08′24″ | 9 | 3 | 23.65 |
| 08:30 | 16.56 | 107°19′30″ | 41°02′15″ | 96°46′40″ | 29°46′48″ | 8 | 3 | 21.77 |
| 09:30 | 13.23 | 104°12′03″ | 47°06′26″ | 116°7′48″ | 39°11′24″ | 10 | 3 | 21.86 |
| 10:30 | 9.84 | 107°22′12″ | 53°15′11″ | 134°24′26″ | 47°42′06″ | 9 | 2 | 10.33 |
| 11:30 | 4.66 | 89°01′18″ | 41°15′38″ | 153°37′48″ | 53°15′36″ | 15 | 4 | 6.31 |
| 12:30 | 5.81 | 101°27′46″ | 56°12′36″ | 173°06′02″ | 56°21′26″ | 12 | 3 | 8.62 |
| 13:30 | 6.31 | 109°10′48″ | 54°39′36″ | 192°15′36″ | 56°53′24″ | 9 | 2 | 10.68 |
| 14:30 | 5.21 | 107°06′15″ | 49°12′36″ | 221°07′02″ | 56°04′48″ | 7 | 3 | 16.31 |
| 15:30 | 8.67 | 105°31′36″ | 53°22′48″ | 227°43′48″ | 52°09′36″ | 9 | 3 | 13.86 |
| 16:30 | 13.83 | 104°15′08″ | 46°02′21″ | 247°25′12″ | 47°01′12″ | 8 | 2 | 19.86 |
| 17:30 | 21.92 | 112°25′17″ | 40°18′13″ | 266°48′21″ | 40°46′36″ | 7 | 2 | 26.32 |
| 18:30 | 21.63 | 102°18′35″ | 47°38′15″ | 286°47′24″ | 29°29′24″ | 6 | 2 | 28.36 |
| 19:30 | 22.33 | 105°33′06″ | 52°48′06″ | 305°19′55″ | 17°05′31″ | 5 | 3 | 27.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, Y.; Pang, X.; Wang, H.; Zhao, J.; Yang, S.; Li, Y.; Xu, G.; Cai, L.; Liu, Z.; Wang, X.; et al. Distance Measurement and Data Analysis for Civil Aviation at 1000 Frames per Second Using Single-Photon Detection Technology. Sensors 2025, 25, 3918. https://doi.org/10.3390/s25133918
Shan Y, Pang X, Wang H, Zhao J, Yang S, Li Y, Xu G, Cai L, Liu Z, Wang X, et al. Distance Measurement and Data Analysis for Civil Aviation at 1000 Frames per Second Using Single-Photon Detection Technology. Sensors. 2025; 25(13):3918. https://doi.org/10.3390/s25133918
Chicago/Turabian StyleShan, Yiming, Xinyu Pang, Huan Wang, Jitong Zhao, Shuai Yang, Yunlong Li, Guicheng Xu, Lihua Cai, Zhenyu Liu, Xiaoming Wang, and et al. 2025. "Distance Measurement and Data Analysis for Civil Aviation at 1000 Frames per Second Using Single-Photon Detection Technology" Sensors 25, no. 13: 3918. https://doi.org/10.3390/s25133918
APA StyleShan, Y., Pang, X., Wang, H., Zhao, J., Yang, S., Li, Y., Xu, G., Cai, L., Liu, Z., Wang, X., & Yu, Y. (2025). Distance Measurement and Data Analysis for Civil Aviation at 1000 Frames per Second Using Single-Photon Detection Technology. Sensors, 25(13), 3918. https://doi.org/10.3390/s25133918




