Utilizing GCN-Based Deep Learning for Road Extraction from Remote Sensing Images
Abstract
1. Introduction
- High-dimensional features are extracted using CNNs, with ResNeXt—characterized by its unique group convolution structure—serving as the primary architecture. This enhances both the model’s accuracy and its feature extraction capabilities while maintaining a constant parameter count.
- A hybrid loss function is formulated by integrating the stability of binary cross-entropy loss with the optimization prowess of the Dice loss function, effectively addressing the imbalance between background and road features in the images.
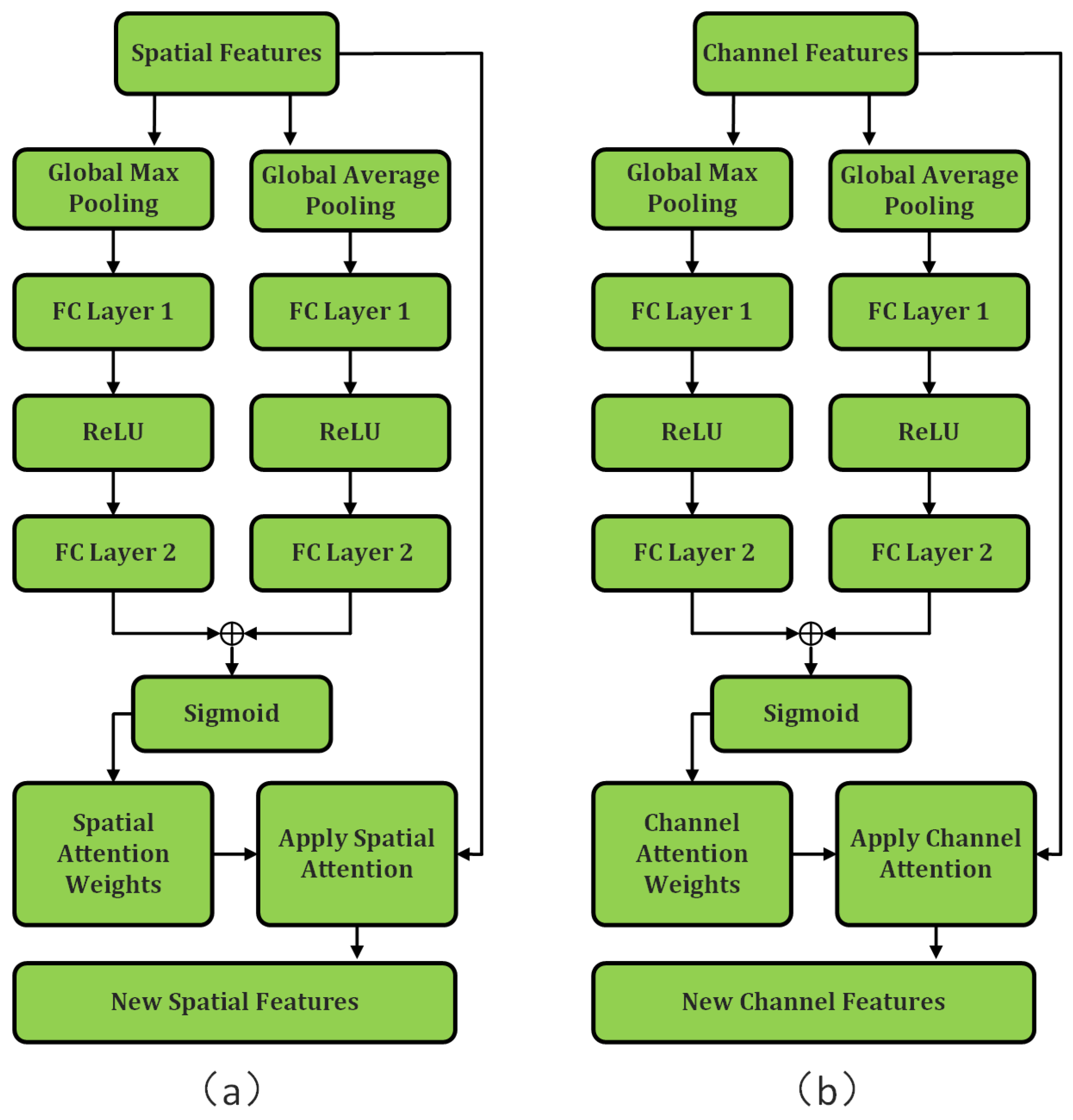
- A feature separation module within the encoder incorporates AMs, facilitating separate extraction of spatial and channel features. Spatial attention is applied during the extraction of spatial features, and channel attention during channel feature extraction, with dynamic weighting of each feature.
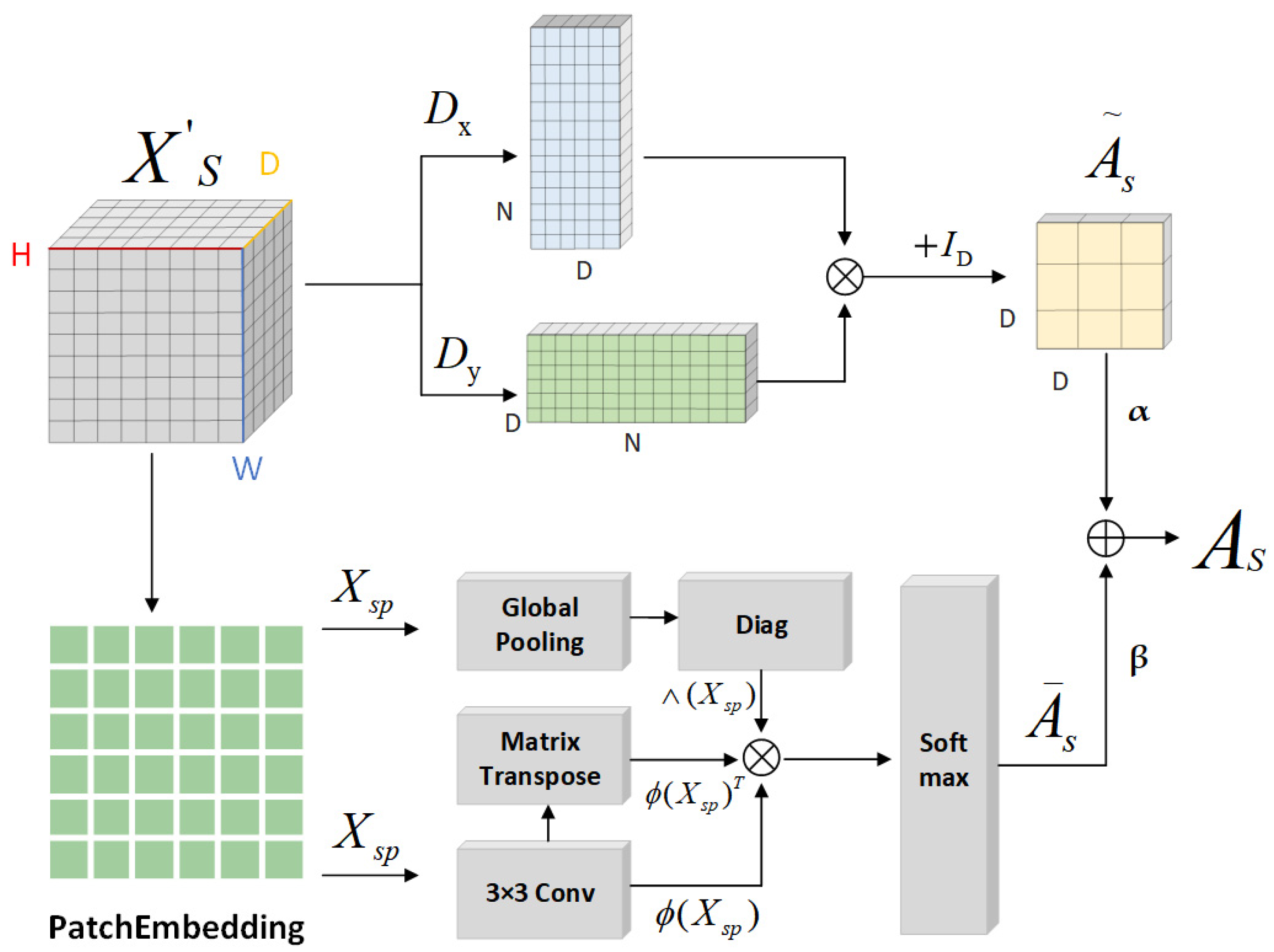
- We have reengineered the adjacency matrix construction within the graph convolution process of the encoder. By merging data from the similarity matrix with the adjacency matrix, constructed using gradient operators, we establish a novel adjacency matrix for graph convolution. This matrix furnishes enriched structural information about the graph, thereby enabling the GCN to consider both structural and feature similarities between nodes concurrently.
2. Materials and Methods
2.1. Dataset
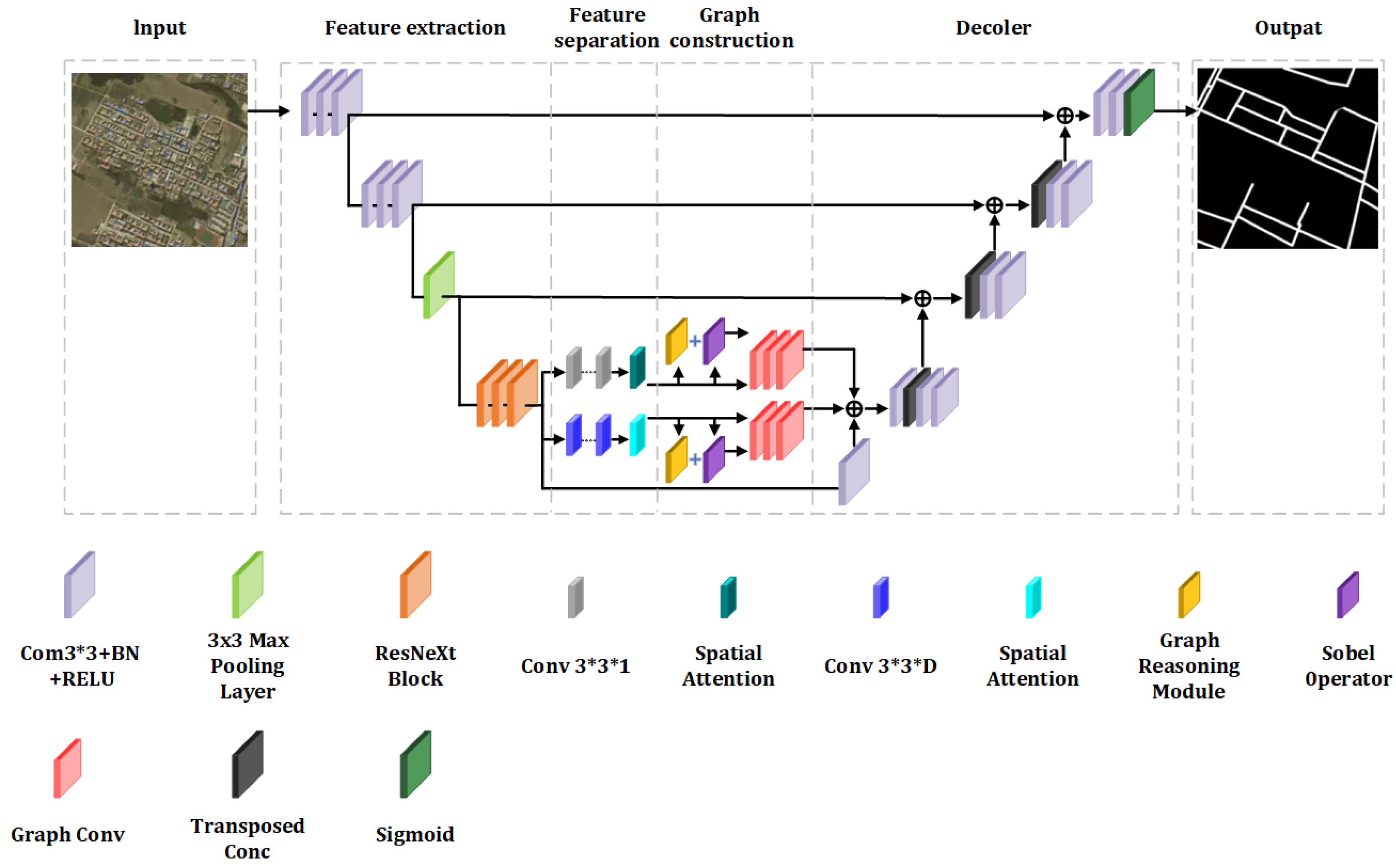
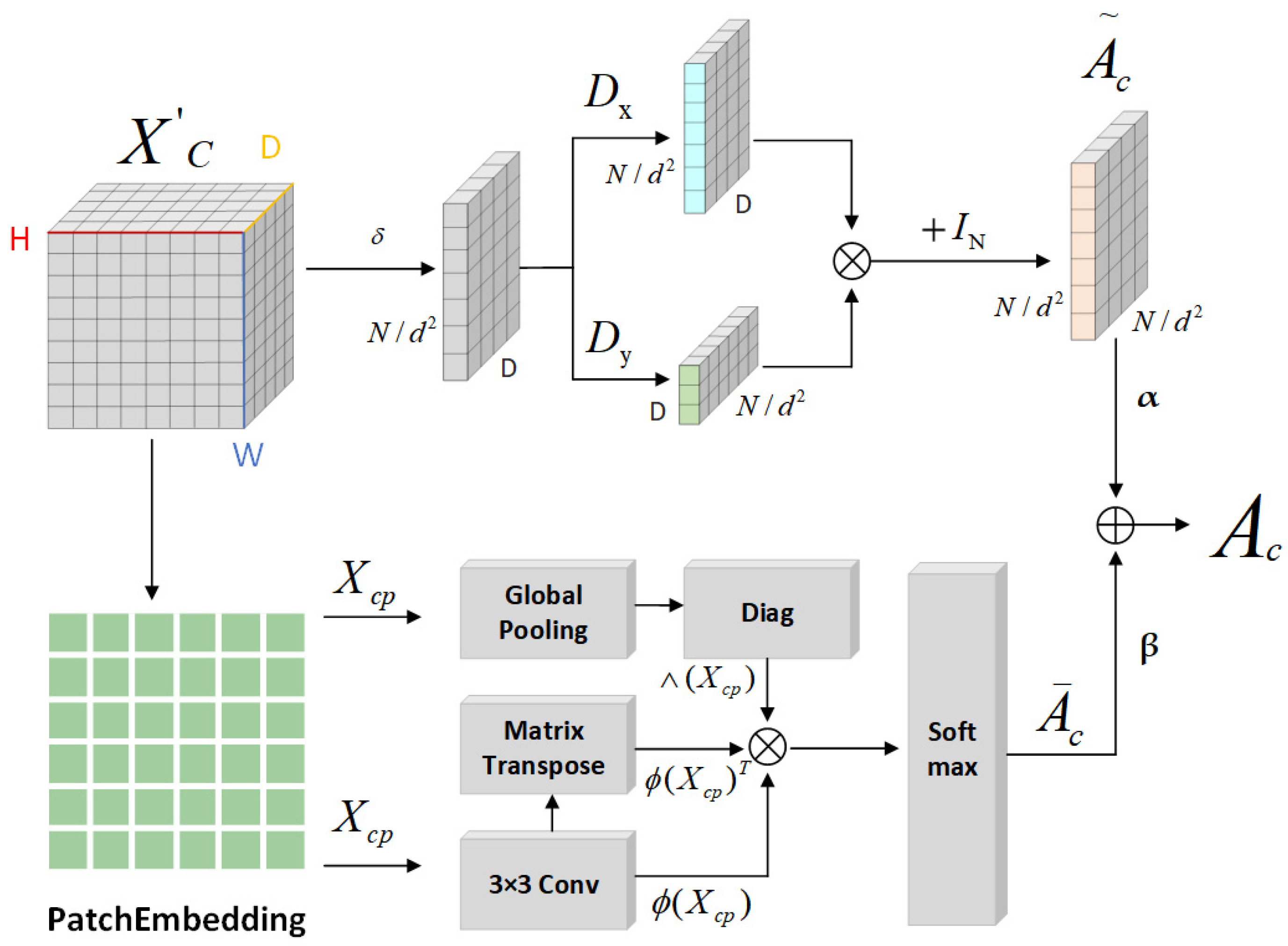
2.2. Structural Overview
- Feature Extraction: In contrast to the conventional three-channel RGB information, the extraction of high-dimensional features offers a more comprehensive dataset. The ResNeXt architecture is employed to perform this function, capturing an extensive range of data.
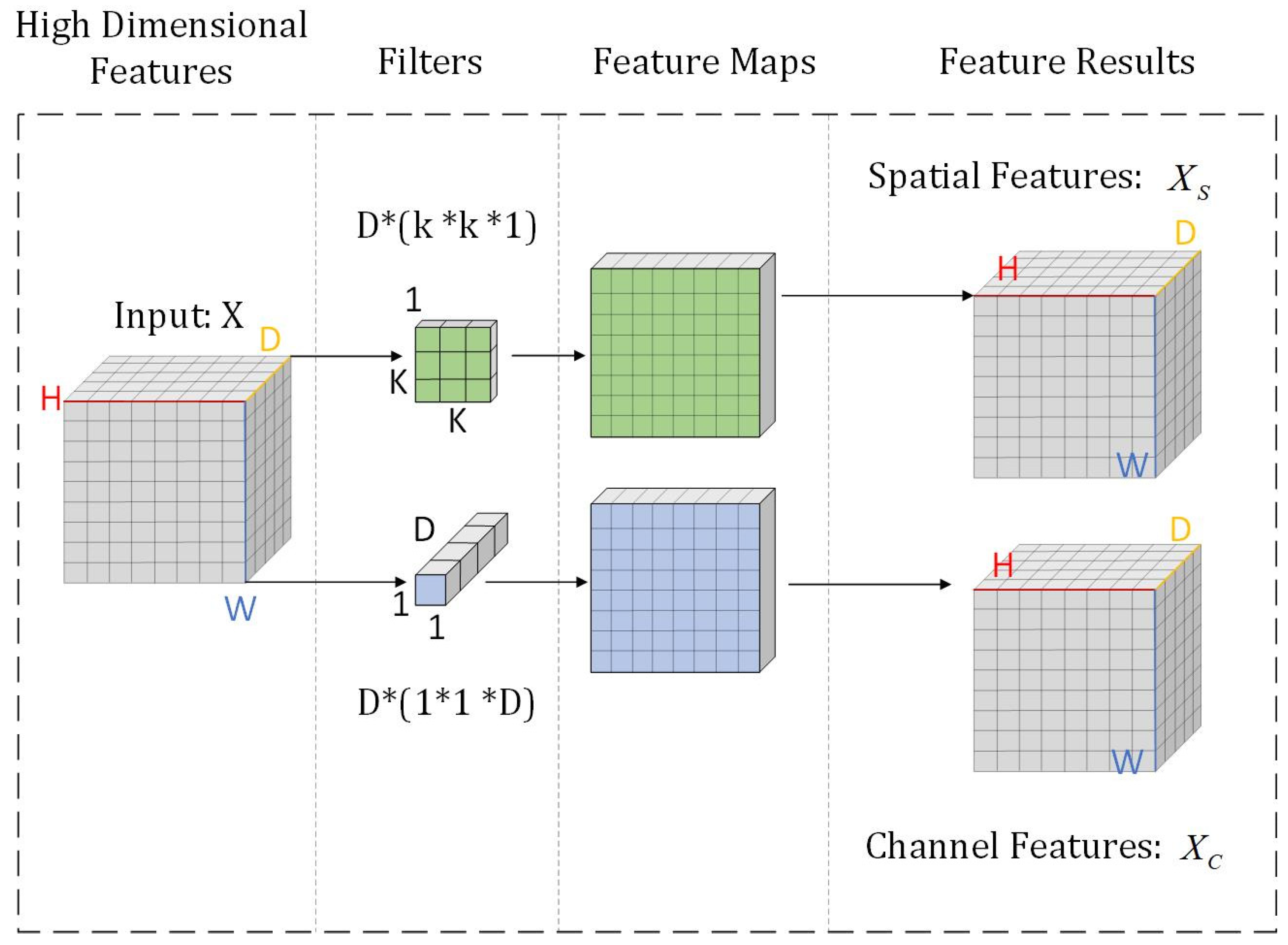
- Feature Separation: Given that spatial and channel features occupy distinct dimensions, their separate extraction facilitates enhanced representational capability. An AM is incorporated to variably weight these features, utilizing split depthwise separable convolutions in conjunction with the AM to precisely delineate both spatial and channel features.
- Graph Construction: The model incorporates two distinct GCNs to assimilate the global contextual information of the spatial and channel features within the FR-SGCN framework. Initially, a similarity matrix is generated through feature-based graph reasoning, which, when merged with an adjacency matrix derived from gradient operators, forms a new adjacency matrix. Subsequent feature propagation through the GCNs allows for the integration of all features, denoting this sequence as the encoder module.
- Decoder: Following the GCNs, the model employs transpose convolutions and convolution layers for upsampling, which restores the resolution of the feature map. The fusion of features at various levels is achieved by integrating corresponding features from the encoder module at each stage. The model concludes with convolution layers and a Sigmoid classifier that delineates roads from the background on a pixel-wise basis, effectively categorizing the output into two channels.
2.2.1. Feature Extraction Module
2.2.2. Feature Separation Module
2.2.3. Graph Construction
2.2.4. Decoder
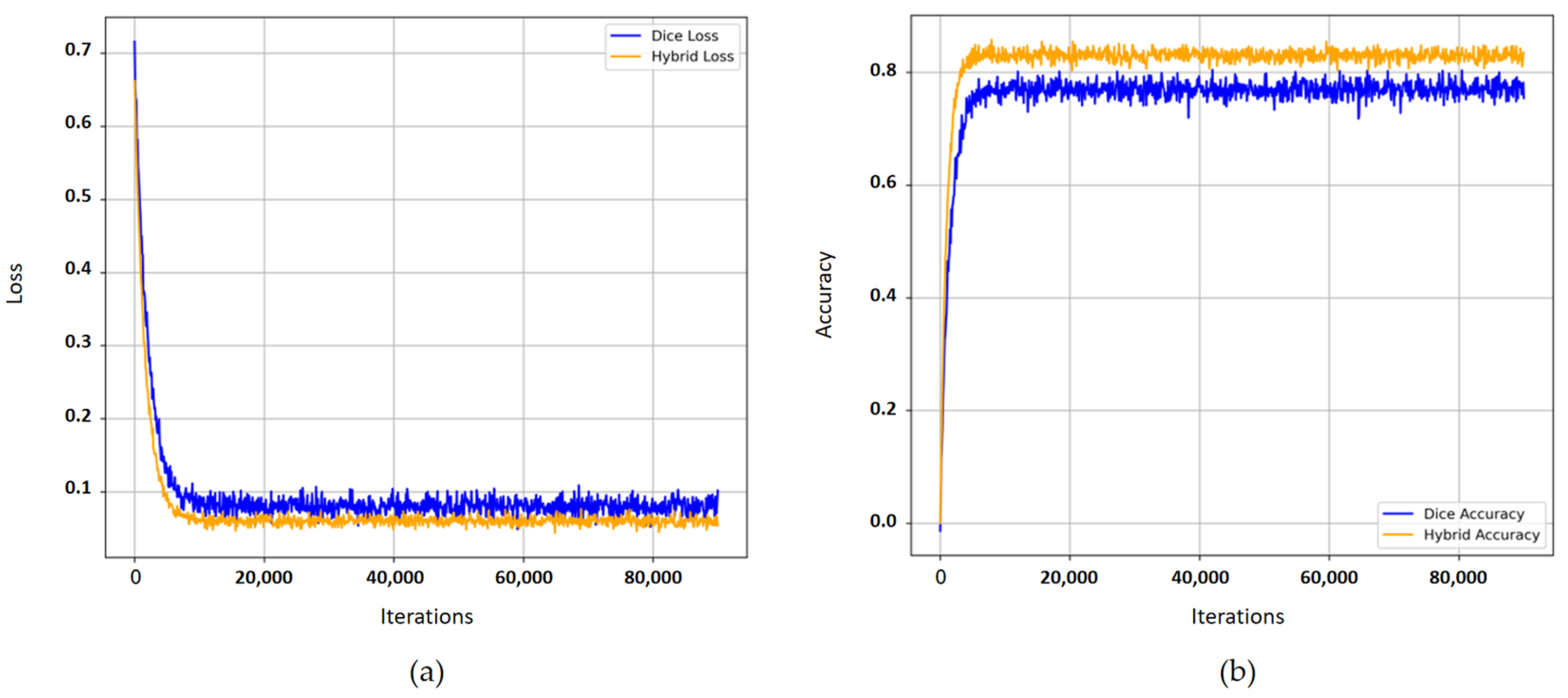
2.2.5. Hybrid Loss Function
3. Experimental Results and Analysis
3.1. Evaluation Metrics
3.2. Experimental Setup
3.3. Model Comparison Experiments
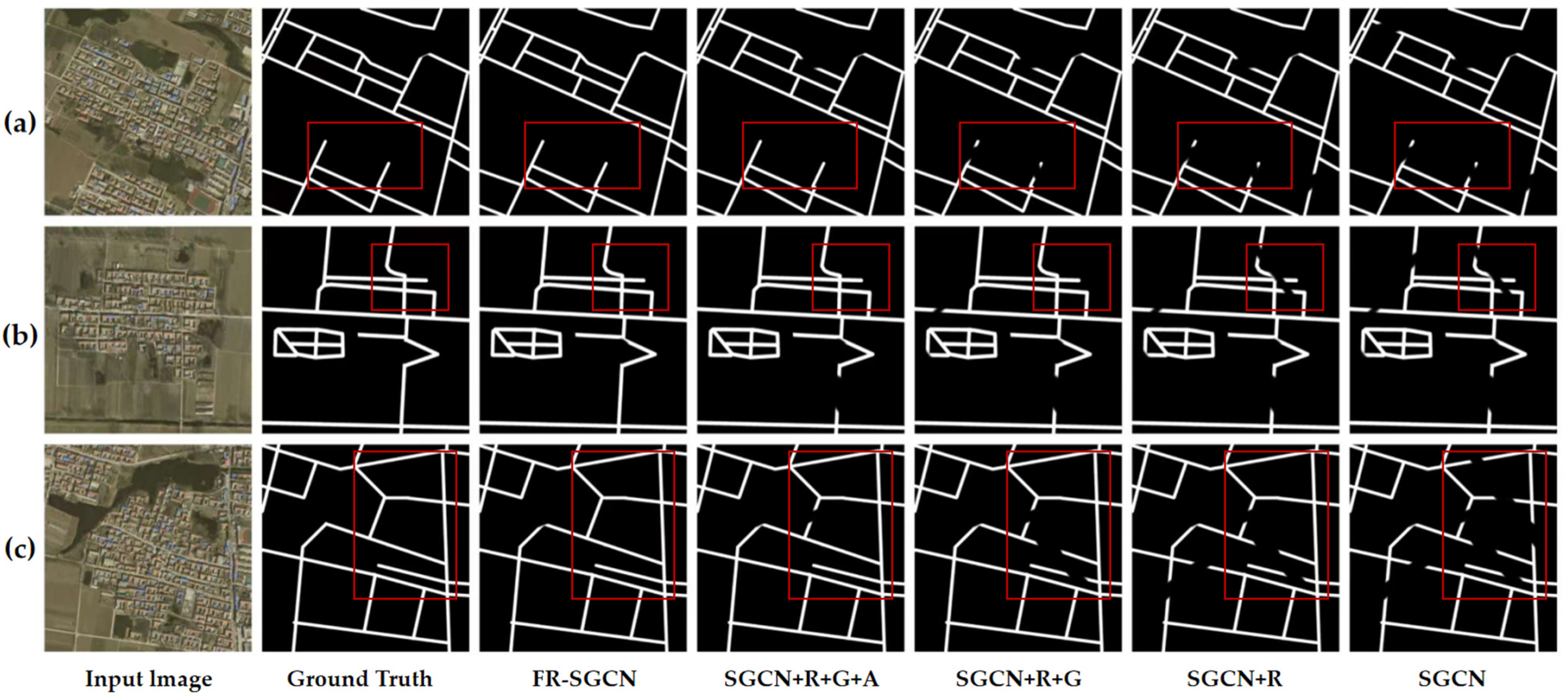
3.4. Ablation Experiments
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bong, D.B.L.; Lai, K.C.; Joseph, A.A. Automatic road network recognition and extraction for urban planning. World Acad. Sci. Eng. Technol. Int. J. Civil Environ. Struct. Construct. Archit. Eng. 2009, 3, 206–212. [Google Scholar]
- Manandhar, P.; Marpu, P.R.; Aung, Z. Deep learning approach to update road network using VGI data. In Proceedings of the 2018 International Conference on Signal Processing and Information Security (ICSPIS), Dubai, United Arab Emirates, 7–8 November 2018; pp. 1–4. [Google Scholar]
- Manandhar, P.; Marpu, P.R.; Aung, Z.; Melgani, F. Towards automatic extraction and updating of VGI-based road networks using deep learning. Remote Sens. 2019, 11, 1012. [Google Scholar] [CrossRef]
- Chang, C.-K.; Siagian, C.; Itti, L. Mobile robot vision navigation based on road segmentation and boundary extraction algorithms. J. Vis. 2012, 12, 200. [Google Scholar] [CrossRef]
- Ghaziani, M.; Mohamadi, Y.; Koku, A.B. Extraction of unstructured roads from satellite images using binary image segmen-tation. In Proceedings of the 2013 21st Signal Processing and Communications Applications Conference, Haspolat, Turkey, 24–26 April 2013; pp. 1–4. [Google Scholar]
- Sirmacek, B.; Unsalan, C. Road network extraction using edge detection and spatial voting. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 3113–3116. [Google Scholar]
- Mnih, V.; Hinton, G.E. Learning to detect roads in high-resolution aerial images. In Proceedings of the 11th European Conference on Computer Vision, Berlin, Germany, 5–11 September 2010; pp. 210–223. [Google Scholar] [CrossRef]
- Alshehhi, R.; Marpu, P.R.; Woon, W.L.; Dalla Mura, M. Simultaneous extraction of roads and buildings in remote sensing imagery with convolutional neural networks. ISPRS J. Photogramm. Remote Sens. 2017, 130, 139–149. [Google Scholar] [CrossRef]
- Liu, R.; Miao, Q.; Song, J.; Quan, Y.; Li, Y.; Xu, P.; Dai, J. Multiscale road centerlines extraction from highresolution aerial imagery. Neurocomputing 2019, 329, 384–396. [Google Scholar] [CrossRef]
- Li, P.; Zang, Y.; Wang, C.; Li, J.; Cheng, M.; Luo, L.; Yu, Y. Road network extraction via deep learning and line integral convolution. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 June 2016; pp. 1599–1602. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Varia, N.; Dokania, A.; Senthilnath, J. DeepExt: A Convolution Neural Network for Road Extraction using RGB images captured by UAV. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018; pp. 1890–1895. [Google Scholar]
- Panboonyuen, T.; Jitkajornwanich, K.; Lawawirojwong, S.; Srestasathiern, P.; Vateekul, P. Road Segmentation of Remotely-Sensed Images Using Deep Convolutional Neural Networks with Landscape Metrics and Conditional Random Fields. Remote Sens. 2017, 9, 680. [Google Scholar] [CrossRef]
- Mei, J.; Li, R.-J.; Gao, W.; Cheng, M.-M. CoANet: Connectivity Attention Network for Road Extraction From Satellite Imagery. IEEE Trans. Image Process. 2021, 30, 8540–8552. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhang, Y.; Wang, L.; Zhong, Y.; Guan, Q.; Lu, X.; Zhang, L.; Li, D. A global context-aware and batch-independent network for road extraction from VHR satellite imagery. ISPRS J. Photogramm. Remote Sens. 2021, 175, 353–365. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, J.; Zhang, L.; Liu, X.; Qiao, H. Bi-HRNet: A Road Extraction Framework from Satellite Imagery Based on Node Heatmap and Bidirectional Connectivity. Remote Sens. 2022, 14, 1732. [Google Scholar] [CrossRef]
- Luo, Z.; Zhou, K.; Tan, Y.; Wang, X.; Zhu, R.; Zhang, L. AD-RoadNet: An Auxiliary-Decoding Road Extraction Network Improving Connectivity While Preserving Multiscale Road Details. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 8049–8062. [Google Scholar] [CrossRef]
- Lin, S.; Yao, X.; Liu, X.; Wang, S.; Chen, H.-M.; Ding, L.; Zhang, J.; Chen, G.; Mei, Q. MS-AGAN: Road Extraction via Multi-Scale Information Fusion and Asymmetric Generative Adversarial Networks from High-Resolution Remote Sensing Images under Complex Backgrounds. Remote Sens. 2023, 15, 3367. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, X.; Wei, Y.; Zhang, L. Road Topology Extraction From Satellite Imagery by Joint Learning of Nodes and Their Connectivity. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5602613. [Google Scholar] [CrossRef]
- Liu, W.; Gao, S.; Zhang, C.; Yang, B. RoadCT: A Hybrid CNN-Transformer Network for Road Extraction From Satellite Imagery. IEEE Geosci. Remote Sens. Lett. 2024, 21, 2501805. [Google Scholar] [CrossRef]
- Zhu, X.; Huang, X.; Cao, W.; Yang, X.; Zhou, Y.; Wang, S. Road Extraction from Remote Sensing Imagery with Spatial Attention Based on Swin Transformer. Remote Sens. 2024, 16, 1183. [Google Scholar] [CrossRef]
- Zhou, G.; Chen, W.; Gui, Q.; Li, X.; Wang, L. Split depth-wise separable graphconvolution network for road extraction in complex environments from high-resolution remote-sensing images. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5614115. [Google Scholar] [CrossRef]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual Attention Network for Scene Segmentation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 3146–3154. [Google Scholar]
- Li, J.; Liu, Y.; Zhang, Y.; Zhang, Y. Cascaded Attention DenseUNet (CADUNet) for Road Extraction from Very-High-Resolution Images. ISPRS Int. J. Geo-Inf. 2021, 10, 329. [Google Scholar] [CrossRef]
- Xu, K.; Huang, H.; Deng, P.; Li, Y. Deep Feature Aggregation Framework Driven by Graph Convolutional Network for Scene Classification in Remote Sensing. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 5751–5765. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated residual transformations for deep neural networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1492–1500. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- Tao, C.; Qi, J.; Li, Y.; Wang, H.; Li, H. Spatial information inference net: Road extraction using road-specific contextual information. ISPRS J. Photogramm. Remote Sens. 2019, 158, 155–166. [Google Scholar] [CrossRef]
- Chen, R.; Hu, Y.; Wu, T.; Peng, L. Spatial Attention Network for Road Extraction. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 1841–1844. [Google Scholar] [CrossRef]
- Meng, Q.; Zhou, D.; Zhang, X.; Yang, Z.; Chen, Z. Road Extraction from Remote Sensing Images via Channel Attention and Multilayer Axial Transformer. IEEE Geosci. Remote Sens. Lett. 2024, 21, 5504705. [Google Scholar] [CrossRef]
- Liu, G.; Shan, Z.; Meng, Y.; Akbar, T.A.; Ye, S. RDPGNet: A road extraction network with dual-view information perception based on GCN. J. King Saud Univ. Comput. Inf. Sci. 2024, 36, 102009. [Google Scholar] [CrossRef]
- Shi, Y.; Li, Q.; Zhu, X.X. Building segmentation through a gated graph convolutional neural network with deep structured feature embedding. ISPRS J. Photogramm. Remote Sens. 2020, 159, 184–197. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Chen, Y.; Zhao, D.; Chen, J. Graph-FCN for image semantic segmentation. In Proceedings of the 16th International Symposium on Neural Networks, ISNN 2019, Moscow, Russia, 10–12 July 2019; pp. 97–105. [Google Scholar]
- Zhang, X.; Zhang, C.K.; Li, H.M.; Luo, Z. A road extraction method based on high resolution remote sensing image. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLII-3/W10, 671–676. [Google Scholar] [CrossRef]
- Liu, Q.; Kampffmeyer, M.; Jenssen, R.; Salberg, A.-B. Selfconstructing graph convolutional networks for semantic labeling. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 1801–1804. [Google Scholar]
- Guobin, C.; Sun, Z.; Zhang, L. Road Identification Algorithm for Remote Sensing Images Based on Wavelet Transform and Recursive Operator. IEEE Access 2020, 8, 141824–141837. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E. Pattern Classification and Scene Analysis; Wiley: New York, NY, USA, 1973. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Shan, B.; Fang, Y. A Cross Entropy Based Deep Neural Network Model for Road Extraction from Satellite Images. Entropy 2020, 22, 535. [Google Scholar] [CrossRef] [PubMed]
- Milletari, F.; Navab, N.; Ahmadi, S.-A. V-Net: Fully convolutional neural networks for volumetric medical image segmentation. arXiv 2016, arXiv:1606.04797. [Google Scholar]


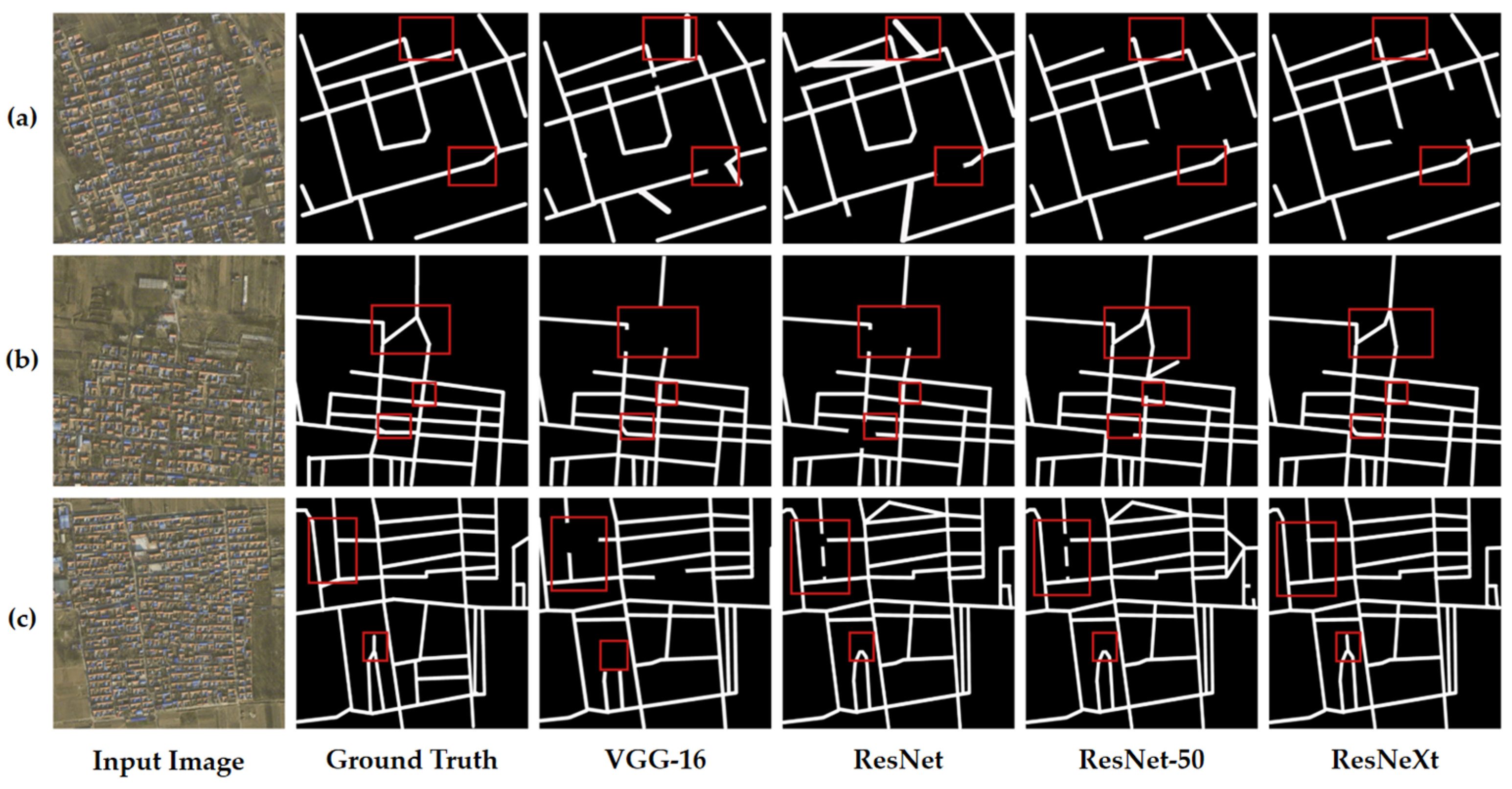
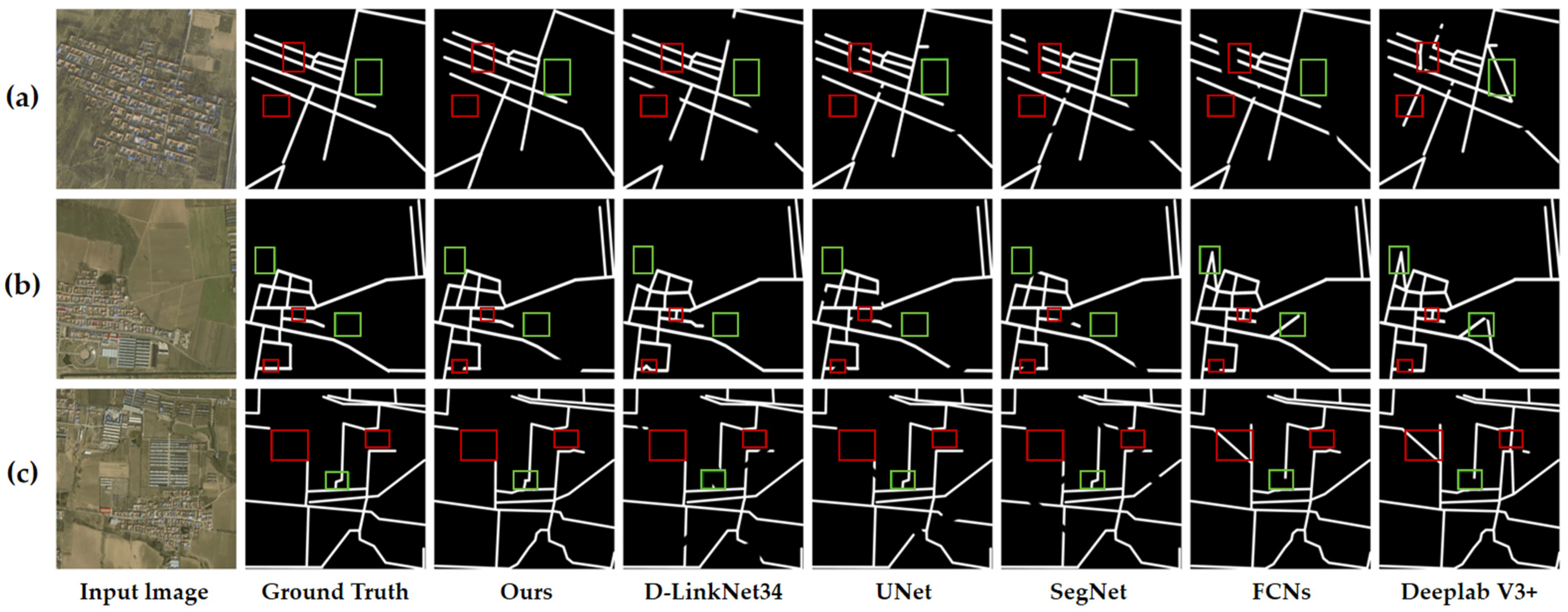
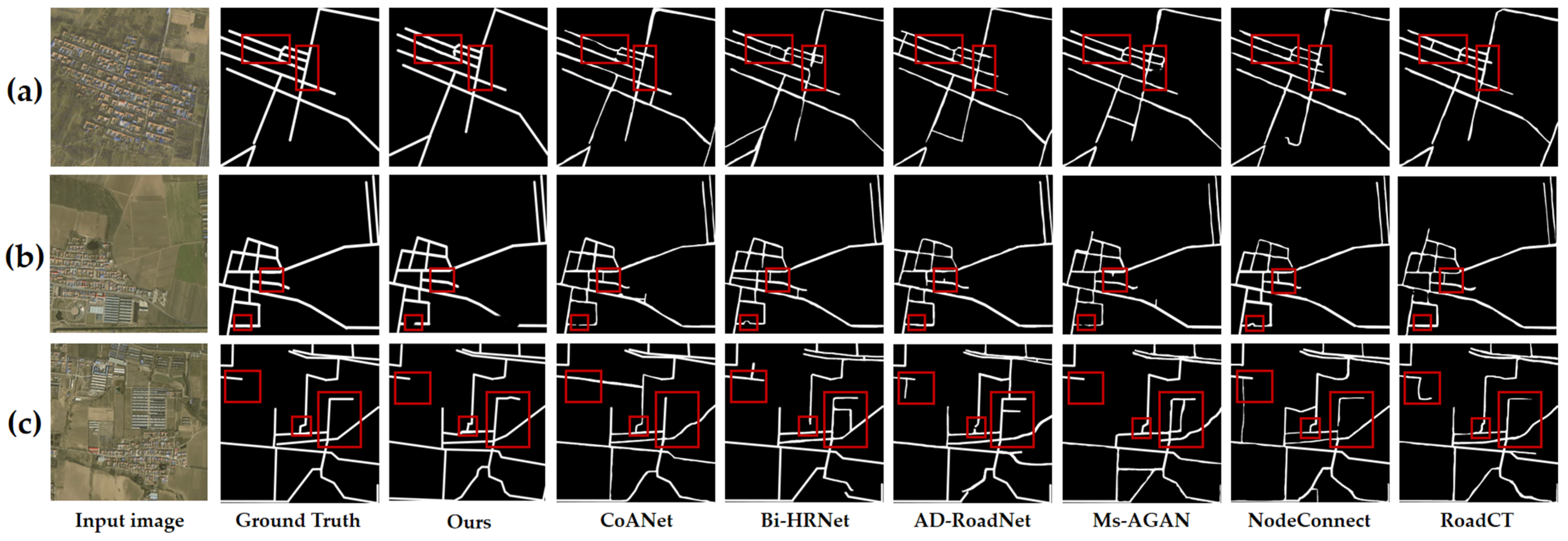

| Backbone | Precision | Recall | F1-Score |
|---|---|---|---|
| VGG-16 | 84.88% | 70.2% | 76.85% |
| ResNet | 85.26% | 75.2% | 79.91% |
| ResNet-50 | 85.78% | 77.3% | 81.94% |
| ResNeXt | 86.69% | 78.2% | 82.22% |
| Method | Precision | Recall | F1-Score |
|---|---|---|---|
| UNet | 82.59% | 63.21% | 71.61% |
| SegNet | 77.93% | 55.25% | 64.66% |
| FCNs | 78.51% | 68.21% | 73.00% |
| Deeplab V3+ | 73.53% | 46.56% | 57.02% |
| D-LinkNet34 | 88.32% | 45.69% | 60.22% |
| CoANet | 83.89% | 79.10% | 81.42% |
| Bi-HRNet | 83.88% | 69.50% | 76.02% |
| AD-RoadNet | 83.37% | 79.11% | 81.18% |
| Ms-AGAN | 75.66% | 78.46% | 77.03% |
| NodeConnect | 83.34% | 80.38% | 81.83% |
| RoadCT | 83.23% | 80.92% | 82.06% |
| Ours | 86.69% | 78.20% | 82.23% |
| Method | Precision (Mean ± Std) | Recall (Mean ± Std) | F1-Score (Mean ± Std) | p-Value |
|---|---|---|---|---|
| CoANet | 82.89% ± 0.45% | 79.10% ± 0.50% | 80.95% ± 0.47% | 0.00012 * |
| Bi-HRNet | 82.88% ± 0.40% | 77.50% ± 0.60% | 80.10% ± 0.50% | 0.00002 * |
| AD-RoadNet | 84.37% ± 0.35% | 80.11% ± 0.55% | 82.18% ± 0.45% | 0.02660 * |
| Ms-AGAN | 82.66% ± 0.50% | 79.46% ± 0.48% | 81.03% ± 0.49% | 0.00021 * |
| NodeConnect | 84.34% ± 0.42% | 81.38% ± 0.52% | 82.83% ± 0.47% | 0.88280 |
| RoadCT | 83.23% ± 0.38% | 80.32% ± 0.50% | 81.75% ± 0.44% | 0.00240 * |
| Ours | 83.89% ± 0.30% | 81.87% ± 0.40% | 82.87% ± 0.35% |
| Method | Precision (Mean ± Std) | Recall (Mean ± Std) | F1-Score (Mean ± Std) | p-Value |
|---|---|---|---|---|
| SGCN | 80.94% ± 0.40% | 73.41% ± 0.45% | 76.99% ± 0.38% | 0.00012 * |
| SGCN + R | 81.55% ± 0.43% | 75.49% ± 0.44% | 78.40% ± 0.41% | 0.00002 * |
| SGCN + R + G | 83.29% ± 0.39% | 76.97% ± 0.47% | 80.01% ± 0.43% | 0.02831 * |
| SGCN + R + G + A | 84.37% ± 0.37% | 77.82% ± 0.40% | 80.96% ± 0.39% | 0.00240 * |
| SGCN + R + G + A + H (FR-SGCN) | 86.69% ± 0.32% | 78.20% ± 0.34% | 82.22% ± 0.33% |
| Method | Precision (Mean ± Std) | Recall (Mean ± Std) | F1-Score (Mean ± Std) | p-Value | Parameters (M) | Inference Speed (FPS) |
|---|---|---|---|---|---|---|
| Transformer | 85.52% ± 0.35% | 77.15% ± 0.40% | 81.21% ± 0.30% | 0.00036 * | 48.7 | 12.3 |
| Swin Transformer | 86.72% ± 0.30% | 77.83% ± 0.35% | 82.20% ± 0.25% | 0.78201 | 36.5 | 18.7 |
| Ours | 86.69% ± 0.25% | 78.20% ± 0.30% | 82.22% ± 0.20% | 12.4 | 32.5 |
| Method | Precision (Mean ± Std) | Recall (Mean ± Std) | F1-Score (Mean ± Std) | p-Value |
|---|---|---|---|---|
| Dice Loss | 85.71% ± 0.25% | 77.89% ± 0.30% | 81.52% ± 0.20% | 0.00025 * |
| Hybrid Loss | 86.69% ± 0.20% | 78.20% ± 0.25% | 82.22% ± 0.15% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Zhao, J.; Luo, W.; Guo, B.; An, Z.; Xu, Y. Utilizing GCN-Based Deep Learning for Road Extraction from Remote Sensing Images. Sensors 2025, 25, 3915. https://doi.org/10.3390/s25133915
Jiang Y, Zhao J, Luo W, Guo B, An Z, Xu Y. Utilizing GCN-Based Deep Learning for Road Extraction from Remote Sensing Images. Sensors. 2025; 25(13):3915. https://doi.org/10.3390/s25133915
Chicago/Turabian StyleJiang, Yu, Jiasen Zhao, Wei Luo, Bincheng Guo, Zhulin An, and Yongjun Xu. 2025. "Utilizing GCN-Based Deep Learning for Road Extraction from Remote Sensing Images" Sensors 25, no. 13: 3915. https://doi.org/10.3390/s25133915
APA StyleJiang, Y., Zhao, J., Luo, W., Guo, B., An, Z., & Xu, Y. (2025). Utilizing GCN-Based Deep Learning for Road Extraction from Remote Sensing Images. Sensors, 25(13), 3915. https://doi.org/10.3390/s25133915






