Intelligent Robust Control Design with Closed-Loop Voltage Sensing for UPS Inverters in IoT Devices
Abstract
1. Introduction
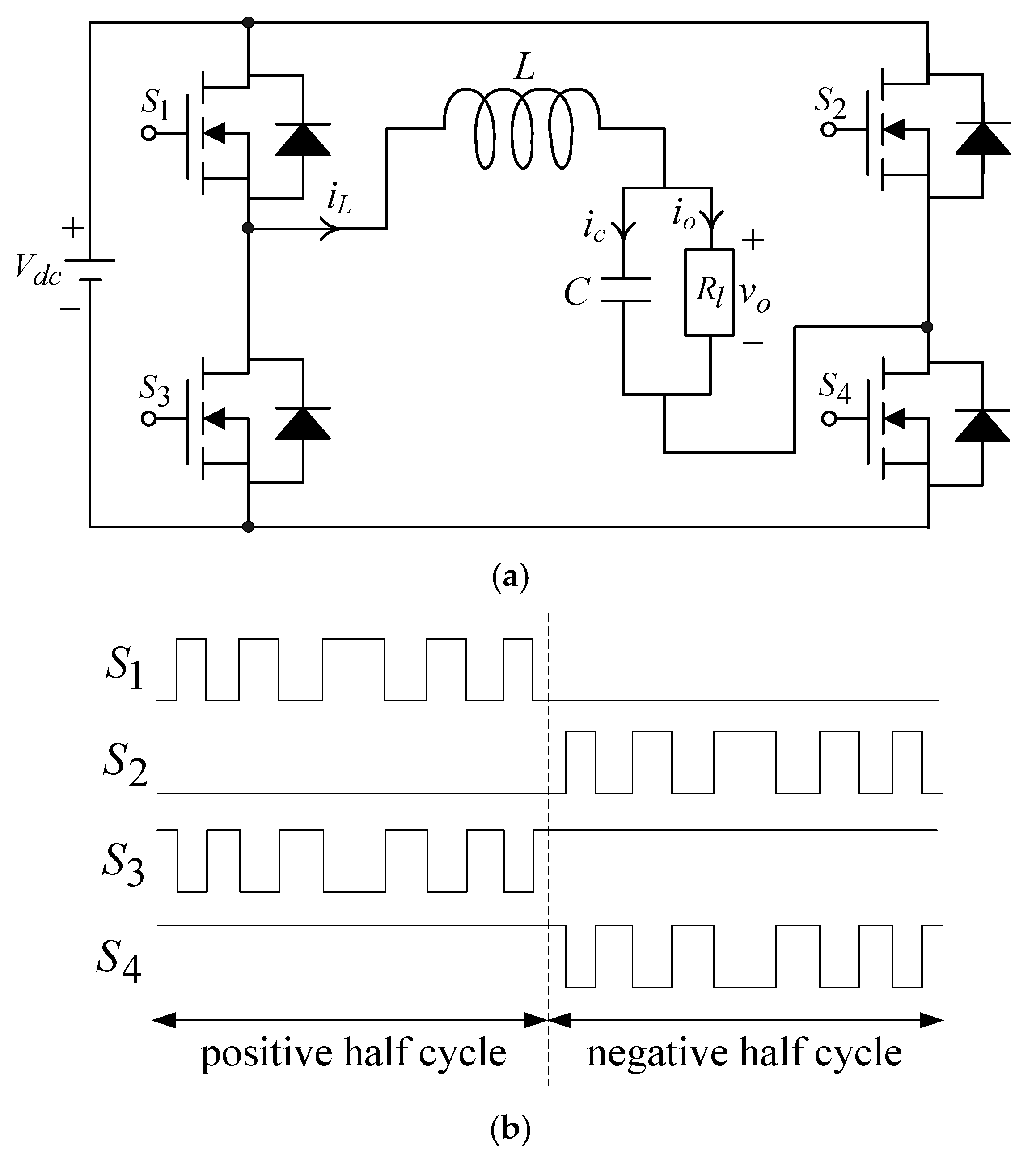
2. Dynamic Modeling of the UPS Inverter
3. Control Design
- Step 1: An -item sequence containing non-negative values is expressed as follows:
- Step 2: By allowing to be a first-order accumulated generated operation (1-AGO) sequence for , one obtains the following:where , .
- Step 3: The first-order non-homogeneous differential gray model based on the can be built as follows:where denotes the developed coefficient of the model, and stands for the gray action.
- Step 4: With the inverse AGO, the predicted expression for the primitive sequence yields the following:
| Algorithm 1. Pseudocode of the whole method |
| Define all system parameters based on (1). Initialize all width, center, and weight vectors in the RBFNN. For k = 1:N Define the reference sine wave. Compute the measured output sine wave from (1). Compute the error of the state. Choose the sliding surface as given in (3) and the sliding-mode approximation rule as described in (4). Compute the control law from the FVSSMC with (5). Sample the measured output sine wave. Execute MGM steps 1 to 4 to predict output by using (8) to (17). Input predict sample data using (17) into input layer of RBFNN. Compute the width and center from (21) and (22). Update weight vectors to get RBFNN output from (23). End for |
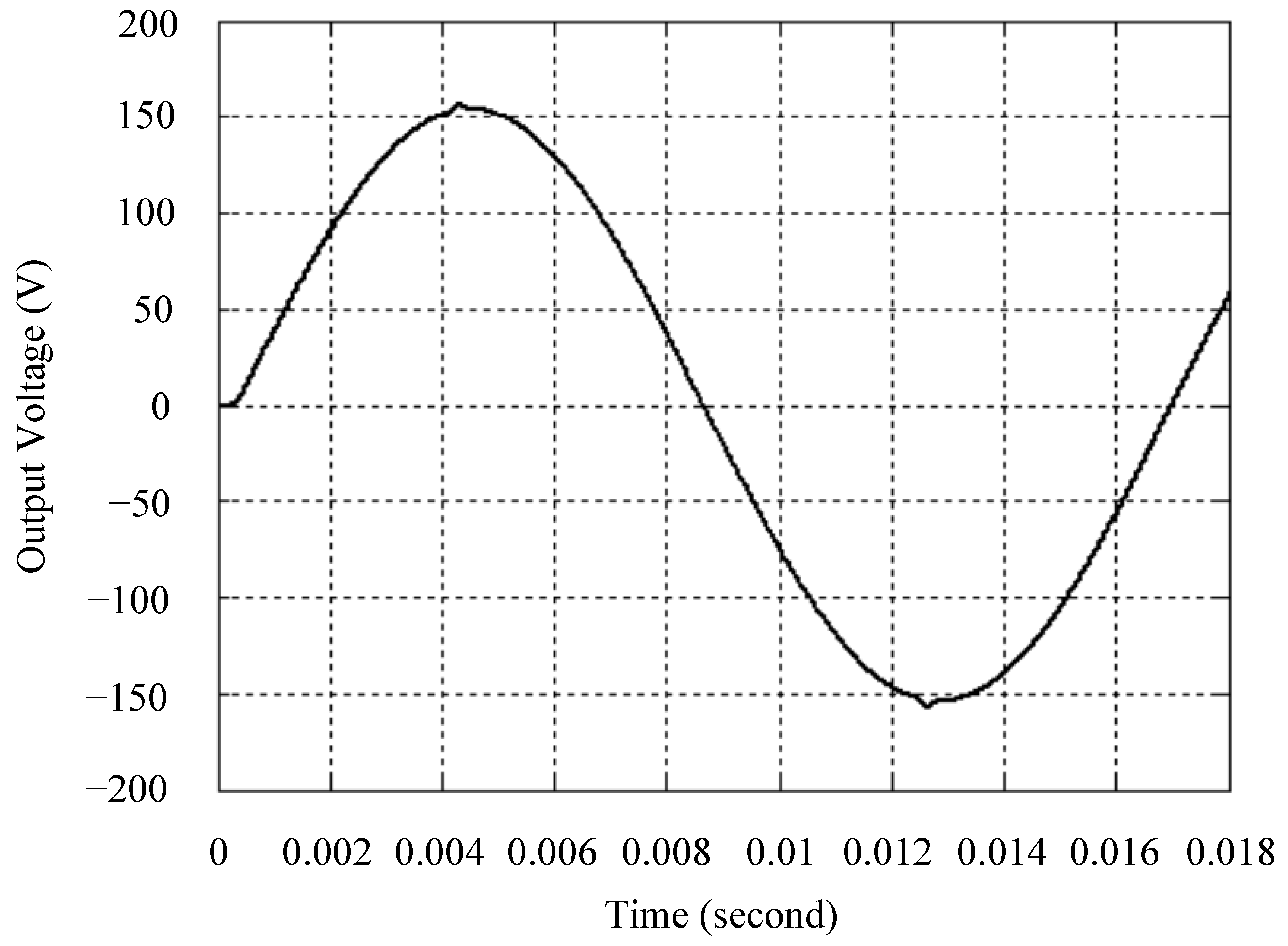
4. Simulation and Experimental Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- King, A.; Knight, W. Uninterruptible Power Supplies; McGraw-Hill Professional Publishing: New York, NY, USA, 2002. [Google Scholar]
- Platts, J.; Aubyn, J.S. Chapter 9: Applications to Telecommunications. In Uninterruptible Power Supplies; Institution of Engineering and Technology: London, UK, 2024. [Google Scholar]
- May, G.J. Standby battery requirements for telecommunications power. J. Power Sources 2006, 158, 1117–1123. [Google Scholar] [CrossRef]
- Ferraro, M.; Brunaccini, G.; Sergi, F.; Aloisio, D.; Randazzo, N.; Antonucci, V. From Uninterruptible Power Supply to resilient smart micro grid: The case of a battery storage at telecommunication station. J. Energy Storage 2020, 28, 101207. [Google Scholar] [CrossRef]
- Chandra, P.S.; Darwin, N.; Ramkumar, R.S.; Nithishkumar, S.; Somasundharam, P.L. IoT-Powered UPS Battery Monitoring: Ensuring High availability and reliability for Critical Systems. E3S Web Conf. 2023, 399, 04007. [Google Scholar]
- Alqinsi, P.; Edward, I.J.M.; Ismail, N.; Darmalaksana, W. IoT-Based UPS Monitoring System Using MQTT Protocols. In Proceedings of the 2018 4th International Conference on Wireless and Telematics (ICWT), Nusa Dua, Bali, Indonesia, 12–13 July 2018; pp. 1–5. [Google Scholar]
- Priya, V.V.; Charan, N.S.S. Industrial Uninterruptible Power Supply using IoT. RVJSTEAM 2022, 3, 34–39. [Google Scholar]
- Roncero-Sánchez, P.L.; Feliu-Batlle, V.; García-Cerrada, A.; García-González, P. Repetitive-Control System for Harmonic Elimination in Three-Phase Voltage-Source Inverters. IFAC Proc. Vol. 2005, 38, 430–435. [Google Scholar] [CrossRef]
- Raju, E.S.N.; Jain, T. Real-time Validation of a Robust LQG based Decentralized Supplementary Control Loop to Mitigate Instability in an Islanded AC Microgrid. Energy Procedia 2017, 117, 535–542. [Google Scholar] [CrossRef]
- Azizi, S.M. Robust Controller Synthesis and Analysis in Inverter-Dominant Droop-Controlled Islanded Microgrids. IEEE/CAA J. Autom. Sin. 2021, 8, 1401–1415. [Google Scholar] [CrossRef]
- Sabanovic, A.; Fridman, L.M.; Spurgeon, S.M. Variable Structure Systems: From Principles to Implementation; Institution of Engineering and Technology: London, UK, 2004. [Google Scholar]
- Utkin, V.I. Variable Structure Systems with Sliding Modes. IEEE Trans. Autom. Control 1977, 22, 212–222. [Google Scholar] [CrossRef]
- Moghaddam, R.K.; Rabbani, M. Methods of Developing Sliding Mode Controllers: Design and Matlab Simulation; Wiley-IEEE Press: Piscataway, NJ, USA, 2025. [Google Scholar]
- Pichan, M.; Rastegar, H. Sliding-Mode Control of Four-Leg Inverter with Fixed Switching Frequency for Uninterruptible Power Supply Applications. IEEE Trans. Ind. Electron. 2017, 64, 6805–6814. [Google Scholar] [CrossRef]
- Chern, T.L.; Chang, J.; Chen, C.H.; Su, H.T. Microprocessor-Based Modified Integral Discrete Variable-Structure Control for UPS. IEEE Trans. Ind. Electron. 1999, 46, 340–347. [Google Scholar] [CrossRef]
- Tai, T.L.; Chen, J.S. UPS inverter Design Using Discrete-Time Sliding Mode Control Scheme. IEEE Trans. Ind. Electron. 2002, 49, 67–75. [Google Scholar]
- Széll, K.; Korondi, P. Mathematical Basis of Sliding Mode Control of an Uninterruptible Power Supply. Acta Polytech. Hung. 2014, 11, 87–106. [Google Scholar]
- Li, S.H.; Yu, X.H.; Fridman, L.; Man, Z.H.; Wang, X.Y. Advances in Variable Structure Systems and Sliding Mode Control—Theory and Applications; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Wu, S.B.; Su, X.Q.; Wang, K.D. Time-Dependent Global Nonsingular Fixed-Time Terminal Sliding Mode Control-Based Speed Tracking of Permanent Magnet Synchronous Motor. IEEE Access 2020, 8, 186408–186420. [Google Scholar] [CrossRef]
- Pichan, M.; Markadeh, G.R.A.; Blaabjerg, F. Continuous finite-time control of four-leg inverter through fast terminal sliding mode control. Int. Trans. Electr. Energy Syst. 2020, 30, e12355. [Google Scholar] [CrossRef]
- Dhar, S.; Dash, P.K. A Finite Time Fast Terminal Sliding Mode I–V Control of Grid-Connected PV Array. J. Control Autom. Electr. Syst. 2015, 26, 314–335. [Google Scholar] [CrossRef]
- Kumar, P.; Bhaskar, D.V.; Behera, R.K.; Muduli, U.R. Continuous Fast Terminal Sliding Surface-Based Sensorless Speed Control of PMBLDCM Drive. IEEE Trans. Ind. Electron. 2023, 70, 9786–9798. [Google Scholar] [CrossRef]
- Wan, Z.S.; Fu, Y.; Liu, C.; Yue, L.W. Sliding Mode Control Based on High Gain Observer for Electro-Hydraulic Servo System. J. Electr. Comput. Eng. 2023, 2023, 7932117. [Google Scholar] [CrossRef]
- Khan, A.M.; Bijalwan, V.; Baek, H. Dynamic high-gain observer approach with sliding mode control for an arc-shaped shape memory alloy compliant actuator. Microsyst. Technol. 2024, 30, 1593–1600. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhu, S.H. Adaptive Sliding Mode Control Based on Uncertainty and Disturbance Estimator. Math. Probl. Eng. 2014, 2014, 982101. [Google Scholar] [CrossRef]
- Deng, J.L. Control problems of grey systems. Syst. Control Lett. 1982, 1, 288–294. [Google Scholar]
- Wu, L.f.; Chen, Y. Fractional Grey System Model and Its Application; Springer: Singapore, 2025. [Google Scholar]
- Zeng, B.; Shi, Z.Z. Grey Prediction Methods and Their Applications; Springer: Singapore, 2024. [Google Scholar]
- Li, C.C.; Chen, Y.J.; Xiang, Y.H. An unbiased non-homogeneous grey forecasting model and its applications. Appl. Math. Model. 2025, 137, 115677. [Google Scholar] [CrossRef]
- Liu, S.H.; Qi, Q.; Hu, Z.M. An Improved Nonhomogeneous Grey Model with Fractional-Order Accumulation and Its Application. J. Math. 2021, 2021, 9962565. [Google Scholar] [CrossRef]
- Cao, L.; Cao, X.; Wang, Q. Fuzzy Grey Model for Forecasting Non-homogeneous Exponential Sequence. Int. J. Fuzzy Syst. 2022, 24, 957–966. [Google Scholar] [CrossRef]
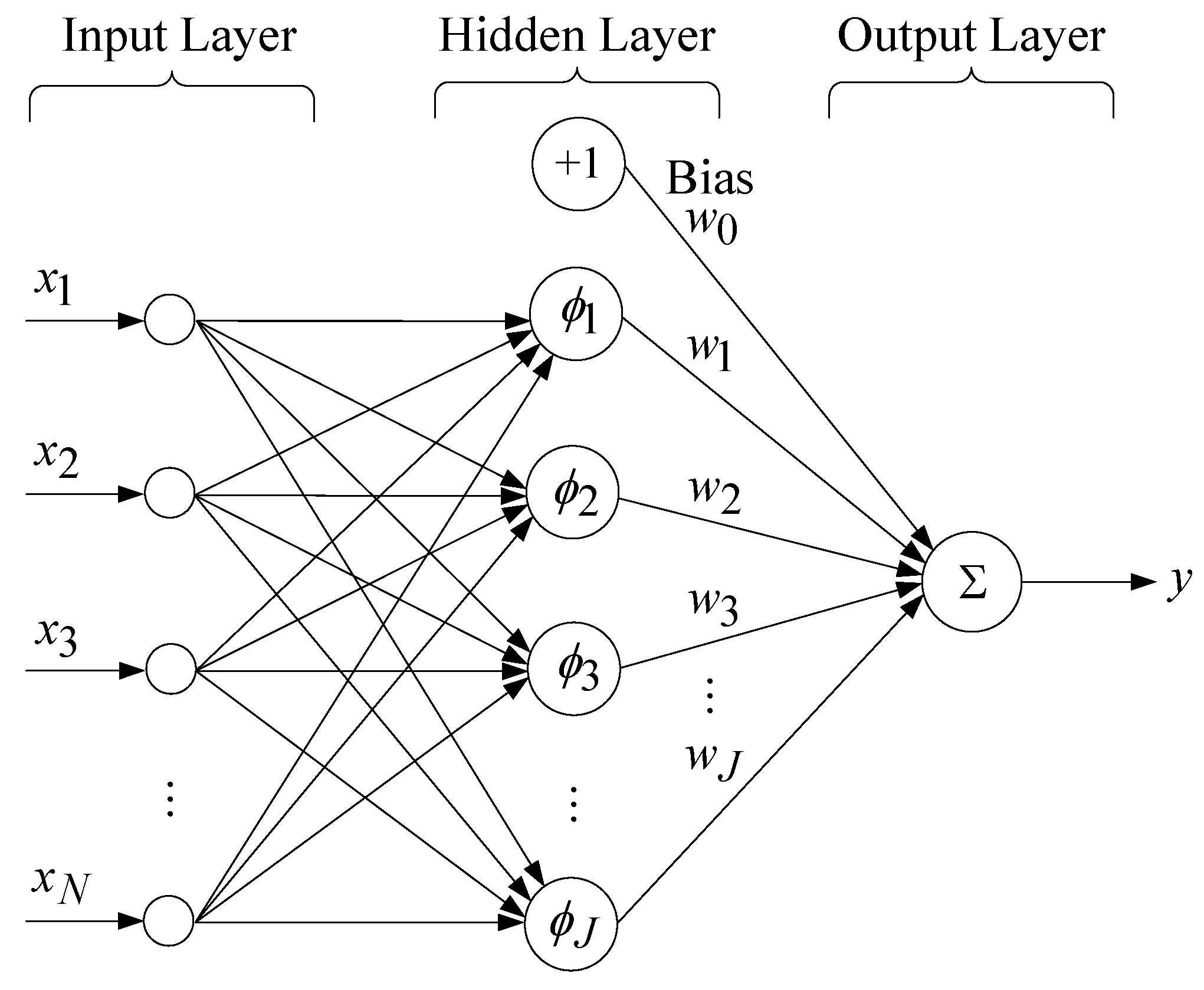
- Liu, J.K. Radial Basis Function (RBF) Neural Network Control for Mechanical Systems: Design, Analysis and Matlab Simulation; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Sundararajan, N.; Saratchandran, P.; Lu, Y.W. Radial Basis Function Neural Networks with Sequential Learning; World Scientific Publishing: Hackensack, NJ, USA, 1999. [Google Scholar]
- Sahni, M.; Sahni, R.; Merigo, J.M. Neural Networks, Machine Learning, and Image Processing: Mathematical Modeling and Applications; CRC Press: Boca Raton, FL, USA, 2024. [Google Scholar]
- Liu, Y.; Liu, M.; Sun, J. Research on Grey Neural Network Optimal Combination in Wind Power Generation Forecasting Technique. J. Phys. Conf. Ser. 2022, 2181, 012028. [Google Scholar] [CrossRef]
- Zhang, L.; Xue, H.; Li, Z.; Wei, Y. Robust stability analysis of switched grey neural network models with distributed delays over C. Grey Syst. Theory Appl. 2022, 12, 879–896. [Google Scholar] [CrossRef]
- Zhang, J.G.; Wan, D. Integrated buffer monitoring and control based on grey neural network. J. Oper. Res. Soc. 2019, 70, 516–529. [Google Scholar] [CrossRef]
- Cui, L.; Zhang, Q.; Yang, L.; Bai, C. A Performance Prediction Method Based on Sliding Window Grey Neural Network for Inertial Platform. Remote Sens. 2021, 13, 4864. [Google Scholar] [CrossRef]
- Karrach, L.; Pivarčiová, E. Using Different Types of Artificial Neural Networks to Classify 2D Matrix Codes and Their Rotations—A Comparative Study. J. Imaging 2023, 9, 188. [Google Scholar] [CrossRef]
- Dash, C.S.K.; Behera, A.K.; Dehuri, S.; Cho, S.B. Radial basis function neural networks: A topical state-of-the-art survey. Open Comput. Sci. 2016, 6, 33–63. [Google Scholar] [CrossRef]
- Saha, A.; Keeler, J.D. Algorithms for Better Representation and Faster Learning in Radial Basis Function Networks. Adv. Neural Inf. Process. Syst. 1989, 2, 482–489. [Google Scholar]
- Benoudjit, N.; Verleysen, M. On the Kernel Widths in Radial-Basis Function Networks. Neural Process. Lett. 2003, 18, 139–154. [Google Scholar] [CrossRef]
- Zhang, S.B.; Hu, J.M.; Bao, Z.H.; Wu, J.R. Prediction of spectrum based on improved RBF neural network in cognitive radio. In Proceedings of the 2013 International Conference on Wireless Information Networks and Systems (WINSYS), Reykjavik, Iceland, 29–31 July 2013; pp. 243–247. [Google Scholar]
- Zhang, S.B.; Hu, J.M.; Bao, Z.H.; Wu, J.R. Distance weighted K-Means algorithm for center selection in training radial basis function networks. IAES Int. J. Artif. Intell. (IJ-AI) 2019, 8, 54–62. [Google Scholar]
- Lacerda, E.G.M.; Carvalho, A.C.P.L.F.; Ludermir, T.B. Evolutionary optimization of RBF networks. In Proceedings of the Sixth Brazilian Symposium on Neural Networks, Rio de Janeiro, Brazil, 22–25 November 2000; pp. 219–224. [Google Scholar]
- Castañeda, G.; Nava, L.M.F.; Ríos, A.A.; Cadenas, J.A.M. Computing Pseudoinverse Matrices with Single-Layer Neural Networks. In Proceedings of the 2023 20th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE), Mexico City, Mexico, 25–27 October 2023; pp. 1–4. [Google Scholar]
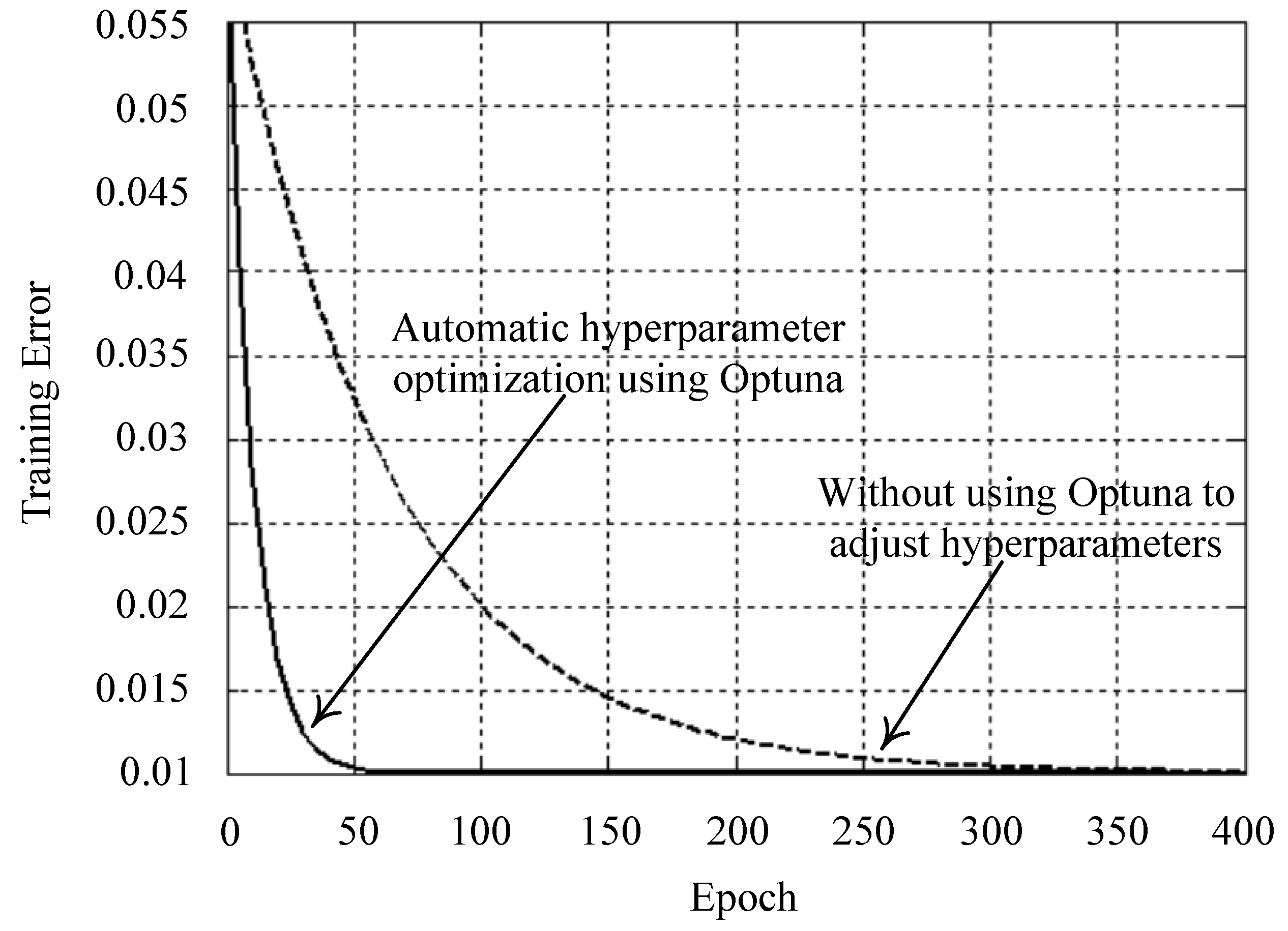
- Hassanali, M.; Soltanaghaei, M.; Gandomani, T.J.; Boroujeni, F.Z. Software development effort estimation using boosting algorithms and automatic tuning of hyperparameters with Optuna. J. Softw. Evol. Process 2024, 36, e2665. [Google Scholar] [CrossRef]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar]
- Kenny, A.; Ray, T.; Limmer, S.; Singh, H.K.; Rodemann, T.; Olhofer, M. Using Bayesian Optimization to Improve Hyperparameter Search in TPOT. In Proceedings of the Genetic and Evolutionary Computation Conference, Melbourne, VIC, Australia, 14–18 July 2024; pp. 340–348. [Google Scholar]
- Rimal, Y.; Sharma, N.; Alsadoon, A. The accuracy of machine learning models relies on hyperparameter tuning: Student result classification using random forest, randomized search, grid search, bayesian, genetic, and optuna algorithms. Multimed. Tools Appl. 2024, 83, 74349–74364. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines, 3rd ed.; Pearson Education Limited: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Arlot, S.; Celisse, A. A survey of cross-validation procedures for model selection. Stat. Surv. 2010, 4, 40–793. [Google Scholar] [CrossRef]
- IEEE Standard 519-2014; IEEE 519 Recommended Practice and Requirements for Harmonic Control in Electric Power Systems. IEEE: New York, NY, USA, 2014.
- European Standard EN50160; Voltage Characteristics of Electricity Supplied by Public Distribution Systems. CENELEC: Brussels, Belgium, 2010.
- IEEE Standard 1159–2019; IEEE Recommended Practice for Monitoring Electric Power Quality. IEEE: New York, NY, USA, 2019.
- Anjum, W.; Husain, A.R.; Abdul, A.J.; Abbas, M.A.; Alqaraghuli, H. Continuous dynamic sliding mode control strategy of PWM based voltage source inverter under load variations. PLoS ONE 2020, 15, e0228636. [Google Scholar] [CrossRef]
- Mohammadhassani, F.; Narm, H.G. Dynamic sliding mode control of single-stage boost inverter with parametric uncertainties and delay. IET Power Electron. 2021, 14, 2127–2138. [Google Scholar] [CrossRef]
- Augusto, L.D.; Lourenço, L.F.N.; Altuna, J.A.T.; Filho, A.J.S. Sliding mode combined with PI controller applied for current control of grid-connected single-phase inverter under distorted voltage conditions. Eletrônica Potência 2025, 30, e202536. [Google Scholar] [CrossRef]
- Kim, H.S.; Sul, S.K. A Novel Filter Design for Output LC Filters of PWM Inverters. J. Power Electron. 2011, 11, 74–81. [Google Scholar] [CrossRef]
- Ahmad, A.A.; Abrishamifar, A.; Farzi, M. A New Design Procedure for Output LC Filter of Single Phase Inverters. In Proceedings of the 2010 Power Electronics and Intelligent Transportation System (PEITS), Shenzhen, China, 13–14 November 2010; pp. 86–91. [Google Scholar]
- Kim, J.; Choi, J.; Hong, H. Output LC Filter Design of Voltage Source Inverter Considering the Performance of Controller. In Proceedings of the 2000 International Conference on Power System Technology, Perth, WA, Australia, 4–7 December 2000; pp. 1659–1664. [Google Scholar]
- Dòria-Cerezo, A.; Olm, J.M.; Repecho, V.; Biel, D. Complex-valued sliding mode control of an induction motor. IFAC-PapersOnLine 2020, 53, 5473–5478. [Google Scholar] [CrossRef]
- Susperregui, A.; Martínez, M.I.; Tapia-Otaegui, G.; Solsona, J.A.; Jorge, S.G.; Busada, C.A. Complex-Valued Sliding-Mode Control for DFIG Synchronization to Non-Ideal Grids. IFAC-PapersOnLine 2023, 56, 2746–2752. [Google Scholar] [CrossRef]
- Dòria-Cerezo, A.; Olm, J.M.; Biel, D.; Fossas, E. Sliding Modes in a Class of Complex-Valued Nonlinear Systems. IEEE Trans. Autom. Control 2021, 66, 3355–3362. [Google Scholar] [CrossRef]
- Hyun, J.H.; Maaz, S.M.; Lee, D.C.; Kim, D.H. Asymmetric and Harmonic Current Suppression of Dual Three-Phase PMSM Based on Double-Integral Sliding Mode Control. IEEE Access 2025, 13, 34038–34050. [Google Scholar] [CrossRef]
- Al-Baidhani, H.; Kazimierczuk, M.K. Simplified Double-Integral Sliding-Mode Control of PWM DC-AC Converter with Constant Switching Frequency. Appl. Sci. 2022, 12, 10312. [Google Scholar] [CrossRef]
- Appikonda, M.; Kaliaperumal, D. Design of double-integral sliding-mode controller for fourth-order double input DC-DC boost converter with a voltage multiplier cell. Int. J. Electron. 2024, 111, 42–63. [Google Scholar] [CrossRef]
- Noniya, R.; Kachhwaha, M.; Krishna, D.V.; Fulwani, D. A New Robust Approach for Synchronization of Single-phase Inverters using Sliding Mode Controlled Harmonic Oscillators. In Proceedings of the 50th Annual Conference of the IEEE Industrial Electronics Society (IECON), Chicago, IL, USA, 3–6 November 2024; pp. 1–5. [Google Scholar]
- Zhang, Q.; Lu, X.Q.; Zhang, C.; Su, S.; Xie, Q.Y. A Novel Sliding Mode Control Strategy for VSG-Based Inverters with Disturbance Estimation. IET Gener. Transm. Distrib. 2025, 19, e70025. [Google Scholar] [CrossRef]
- Xue, J.; Ma, J.; Ma, X.; Zhang, L.; Bai, J. Research on Voltage Prediction Using LSTM Neural Networks and Dynamic Voltage Restorers Based on Novel Sliding Mode Variable Structure Control. Energies 2024, 17, 5528. [Google Scholar] [CrossRef]
- Ye, L.; Fang, L.P.; Dang, Y.G.; Wang, J.J. A novel intervention effect-based quadratic time-varying nonlinear discrete grey model for forecasting carbon emissions intensity. Inf. Sci. 2024, 675, 120711. [Google Scholar] [CrossRef]
- Zuo, H.; Zuo, K. Application of a Fractional Generalized Discrete Grey Model to Forecast COVID-19 in Japan Diamond Princess Cruises. J. Math. 2025, 1, 9029570. [Google Scholar] [CrossRef]
- Tong, Q.J.; Wang, L.W.; Li, L.N.; Zhang, J.K. Network Public Opinion Prediction Based on Conformable Fractional Non-homogeneous Discrete Grey Model. Eng. Lett. 2023, 31, EL_31_1_32. [Google Scholar]
- Shahparasti, M.; Savaghebi, M.; Hosseinpour, M.; Rasekh, N. Enhanced Circular Chain Control for Parallel Operation of Inverters in UPS Systems. Sustainability 2020, 12, 8062. [Google Scholar] [CrossRef]
- Liu, Y.T.; Ye, X.; Peng, J.C. EMI filter design for single-phase grid-connected inverter with noise source impedance consideration. IET Power Electron. 2020, 13, 3963–3974. [Google Scholar] [CrossRef]
- Luna, M.; La Tona, G.; Accetta, A.; Pucci, M.; Di Piazza, M.C. An Evolutionary EMI Filter Design Approach Based on In-Circuit Insertion Loss and Optimization of Power Density. Energies 2020, 13, 1957. [Google Scholar] [CrossRef]
- Saccenti, L.; Bianchi, V.; De Munari, I. Study of a Synchronization System for Distributed Inverters Conceived for FPGA Devices. Appl. Syst. Innov. 2021, 4, 5. [Google Scholar] [CrossRef]




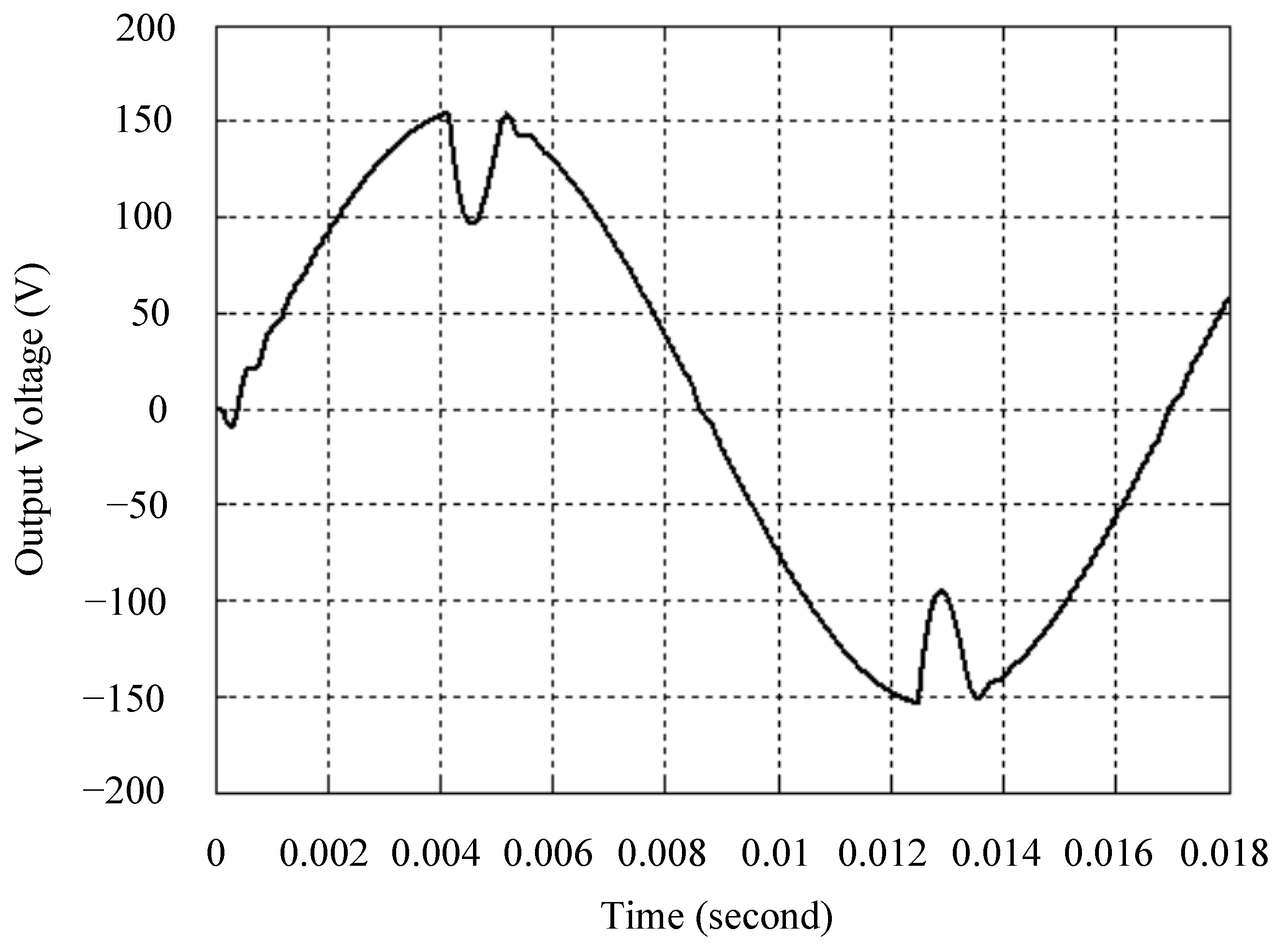
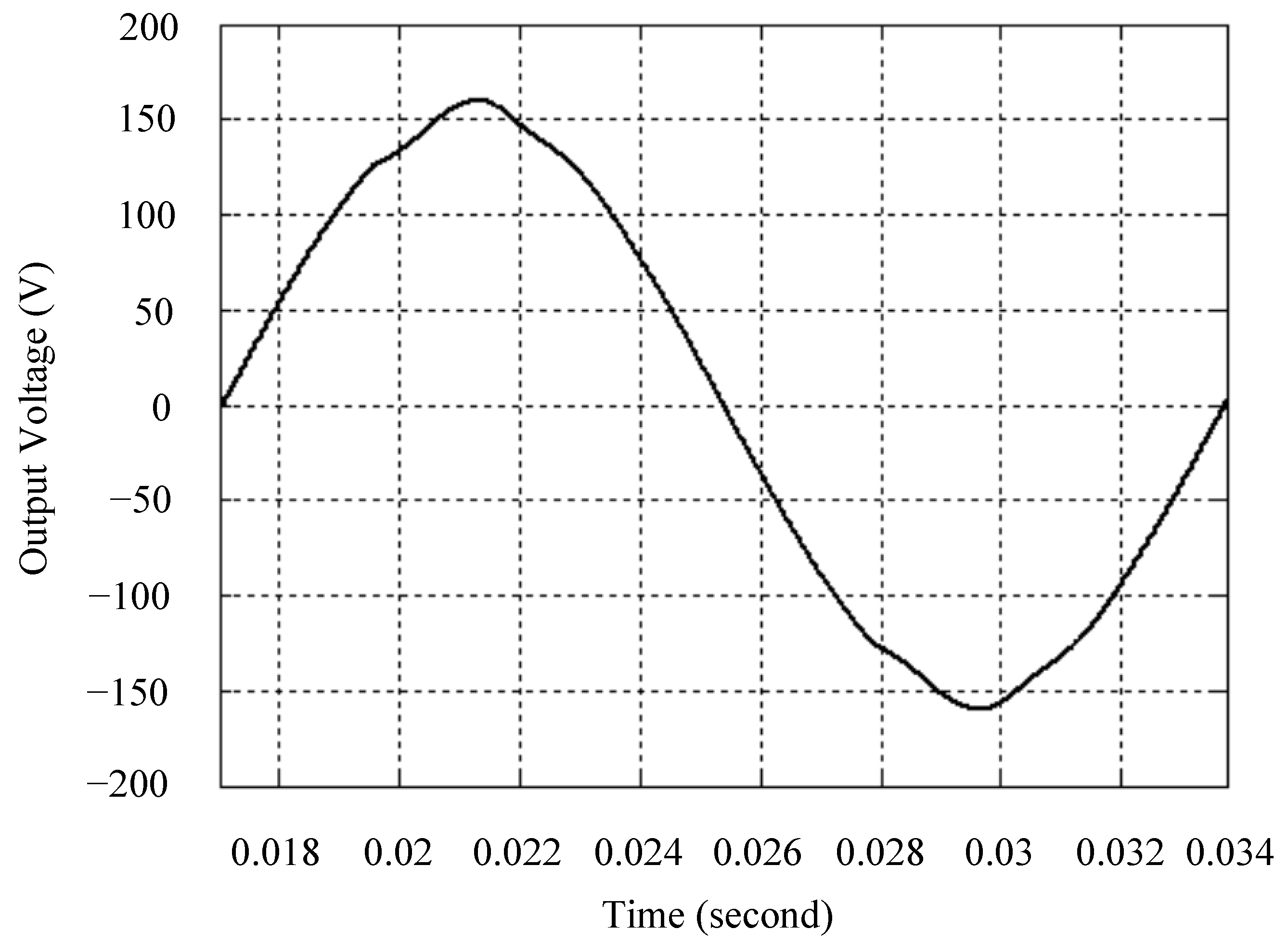
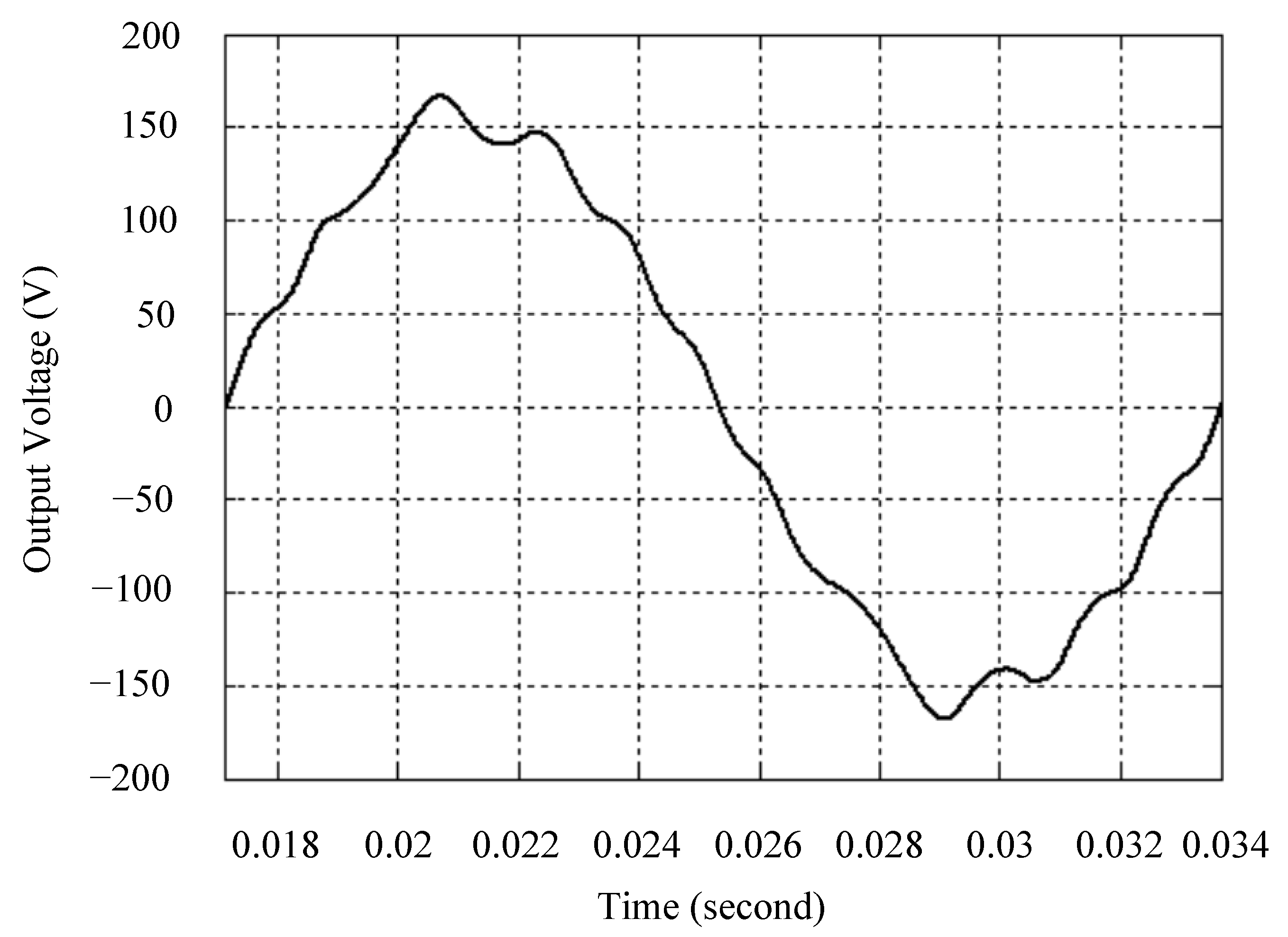
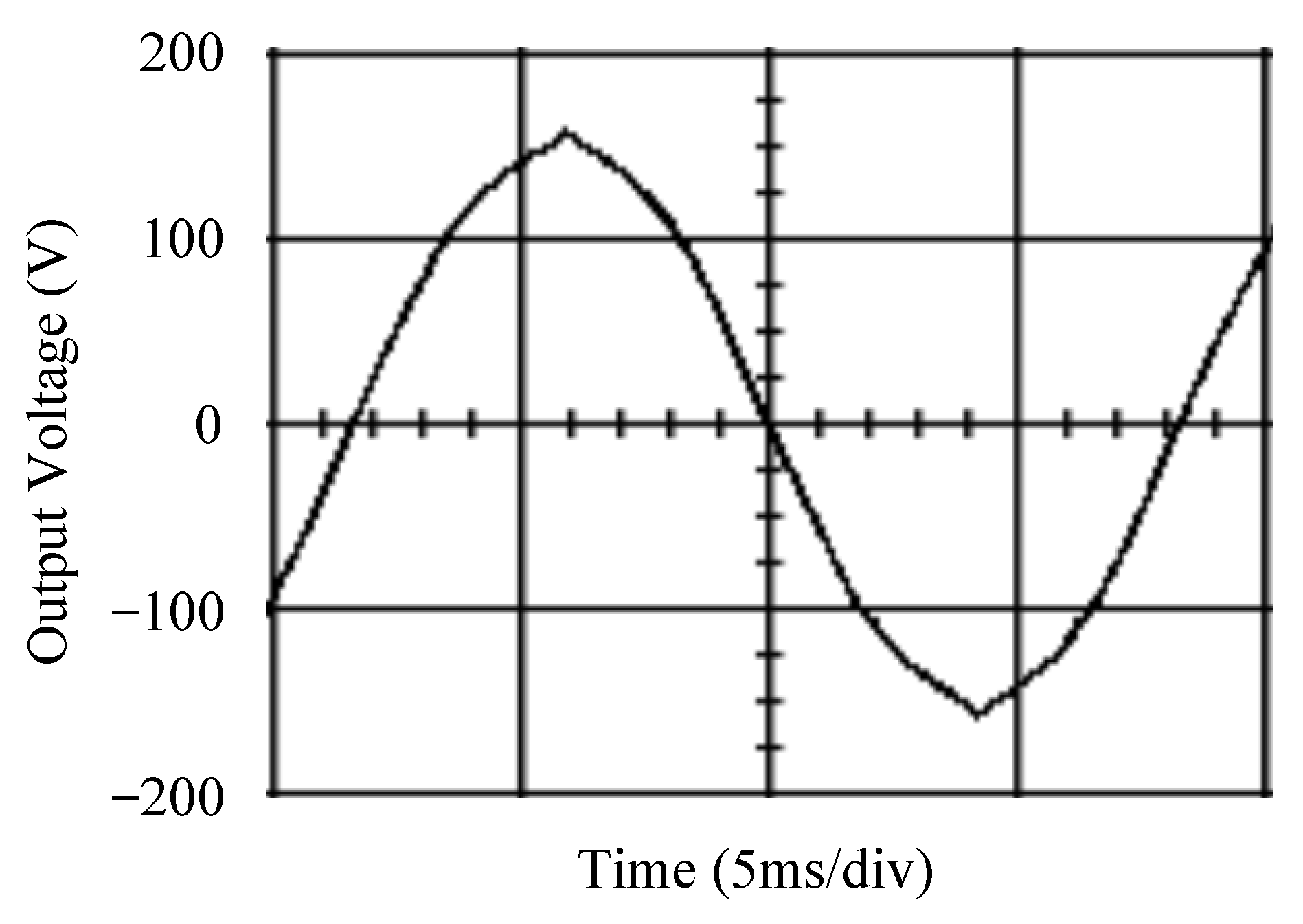



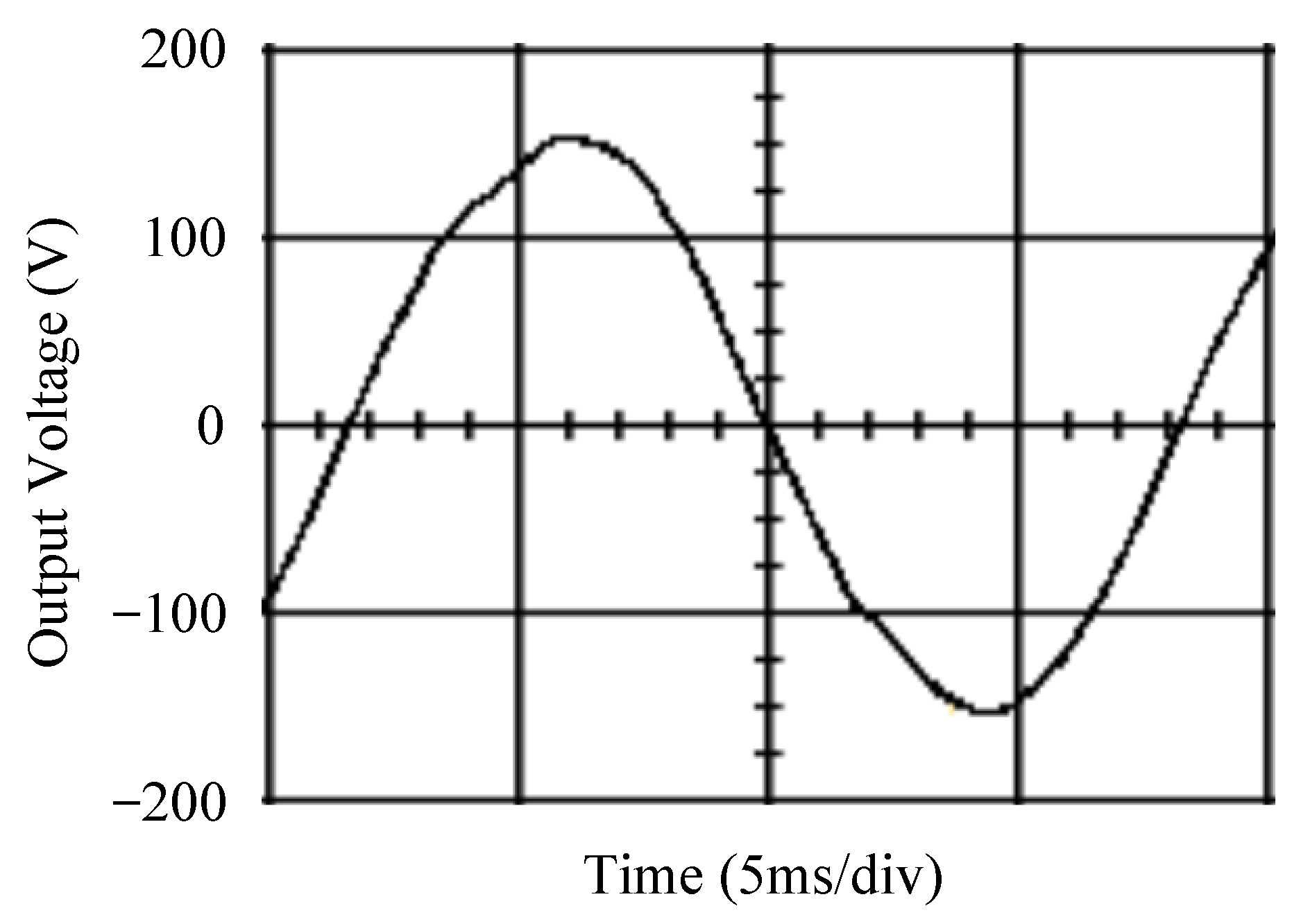
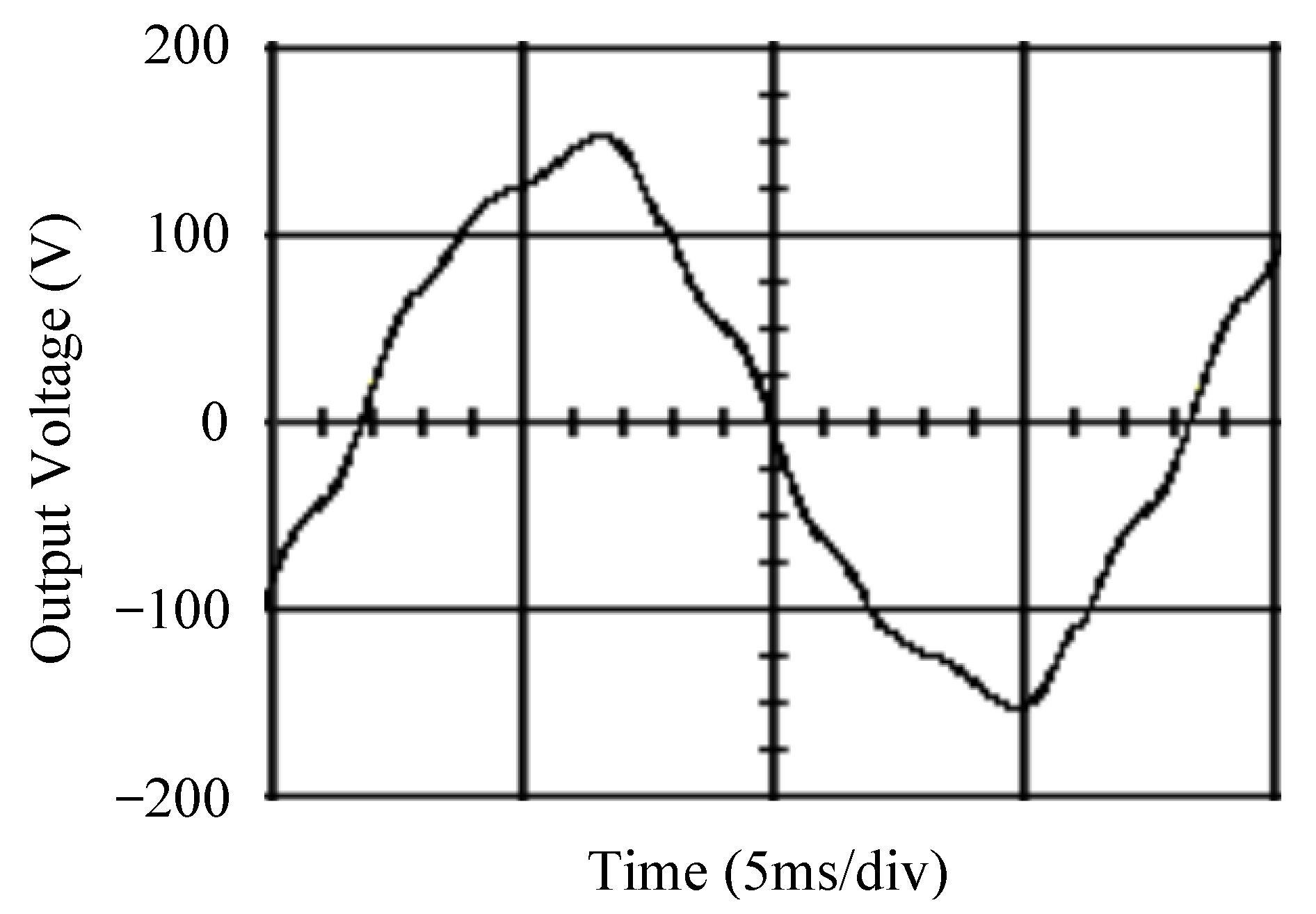
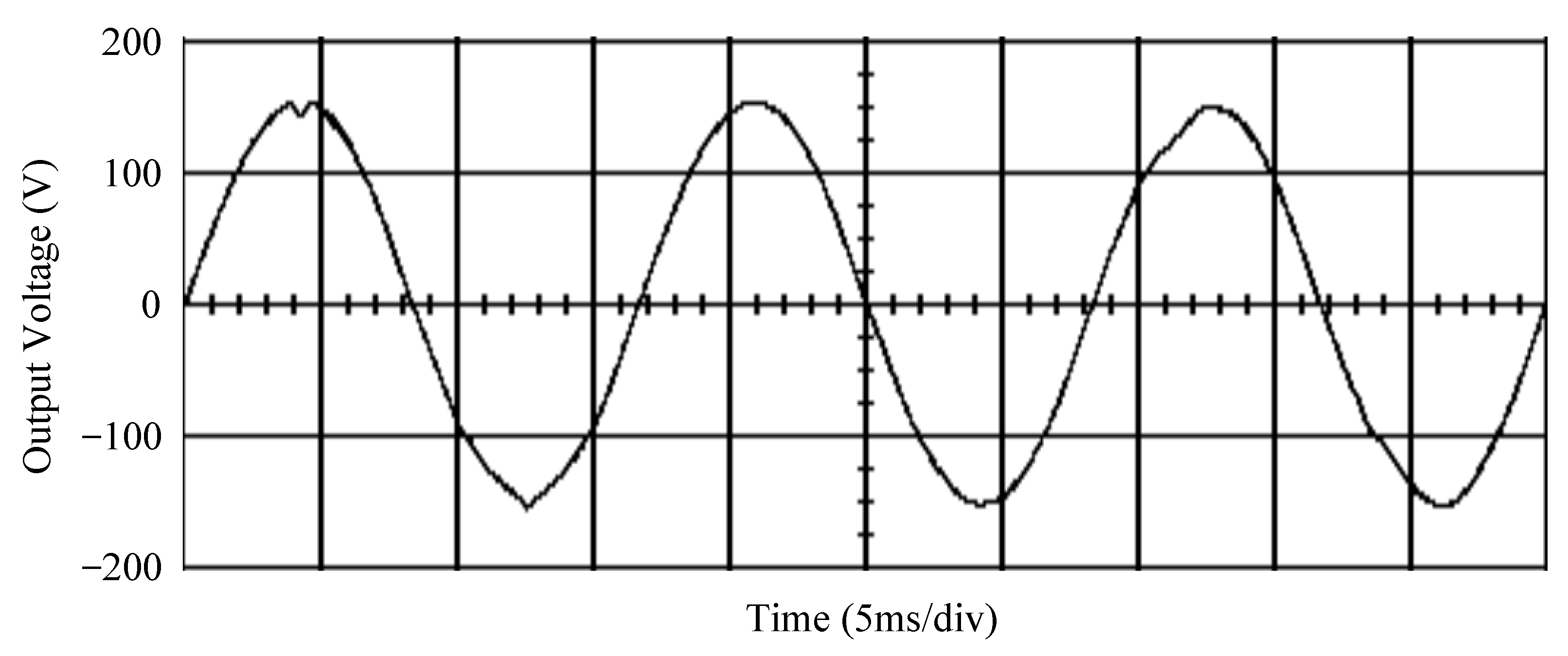
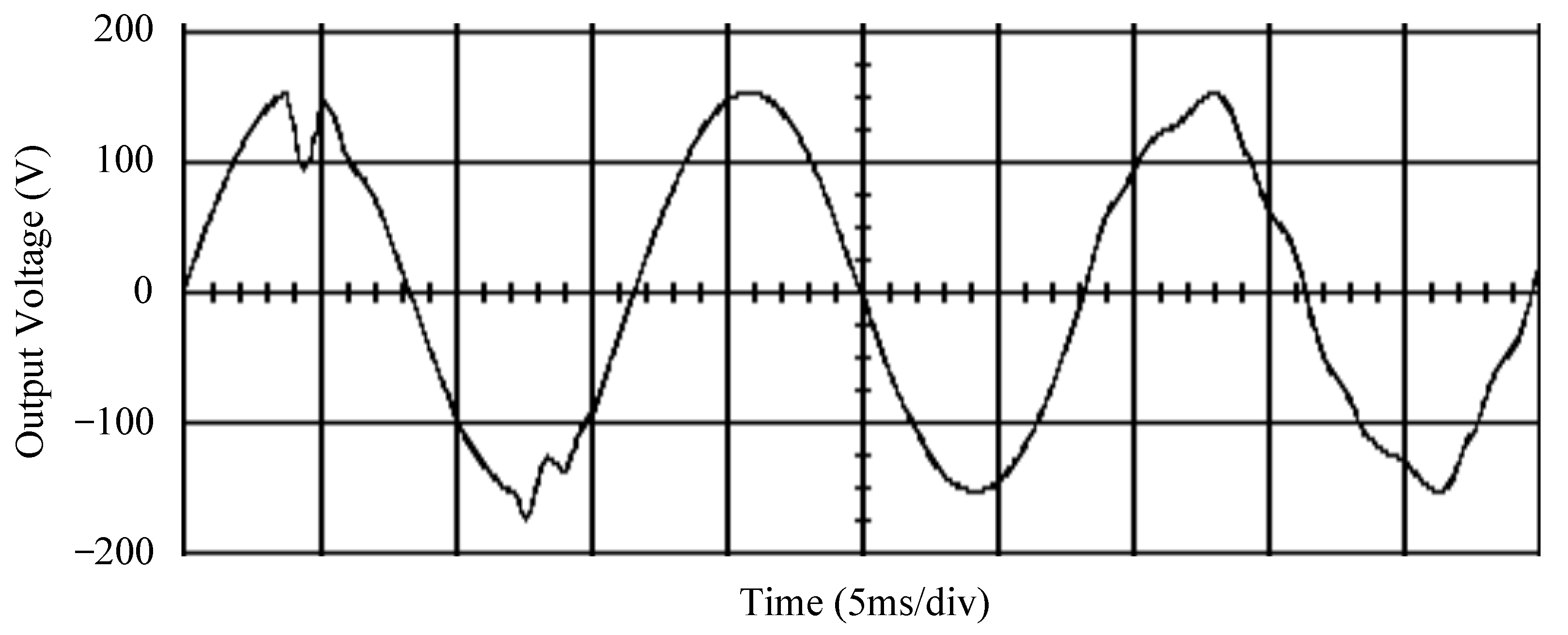
| Parameters | Values |
|---|---|
| DC-link voltage () | 200 V |
| Filter inductor () | 1 mH |
| Filter capacitor () | 20 μF |
| Resistive load () | 12 ohm |
| Switching frequency | 30 kHz |
| AC output voltage () | V |
| Frequency of AC output voltage | 60 Hz |
| Methods | Results | ||
|---|---|---|---|
| Simulations (Suggested control technique) | Abrupt loading removal | Abrupt loading increase | Rectifier-type nonlinear loading |
| Voltage swell | Voltage dip | THD | |
| 1.26 V | 10.78 V | 0.61% | |
| Simulations (Classical SMC) | Abrupt loading removal | Abrupt loading increase | Rectifier-type nonlinear loading |
| Voltage swell | Voltage dip | THD | |
| 15.21 V | 59.42 V | 18.73% | |
| Methods | Results | ||
|---|---|---|---|
| Experiments (Suggested control technique) | Abrupt loading removal | Abrupt loading increase | Rectifier-type nonlinear loading |
| Voltage swell | Voltage dip | THD | |
| 2.47 V | 11.82 V | 0.59% | |
| Experiments (Classical SMC) | Abrupt loading removal | Abrupt loading increase | Rectifier-type nonlinear loading |
| Voltage swell | Voltage dip | THD | |
| 16.32 V | 61.81 V | 19.14% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, E.-C.; Tseng, Y.-W.; Cheng, C.-A. Intelligent Robust Control Design with Closed-Loop Voltage Sensing for UPS Inverters in IoT Devices. Sensors 2025, 25, 3849. https://doi.org/10.3390/s25133849
Chang E-C, Tseng Y-W, Cheng C-A. Intelligent Robust Control Design with Closed-Loop Voltage Sensing for UPS Inverters in IoT Devices. Sensors. 2025; 25(13):3849. https://doi.org/10.3390/s25133849
Chicago/Turabian StyleChang, En-Chih, Yuan-Wei Tseng, and Chun-An Cheng. 2025. "Intelligent Robust Control Design with Closed-Loop Voltage Sensing for UPS Inverters in IoT Devices" Sensors 25, no. 13: 3849. https://doi.org/10.3390/s25133849
APA StyleChang, E.-C., Tseng, Y.-W., & Cheng, C.-A. (2025). Intelligent Robust Control Design with Closed-Loop Voltage Sensing for UPS Inverters in IoT Devices. Sensors, 25(13), 3849. https://doi.org/10.3390/s25133849








