A Fault-Tolerant Localization Method for 5G/INS Based on Variational Bayesian Strong Tracking Fusion Filtering with Multilevel Fault Detection
Abstract
1. Introduction
- (1)
- In this paper, the noise is modeled using a Pearson VII-type distribution, which has a flexible tail control capability and a multi-parameter adjustment mechanism, can adjust the thickness of the tail of the probability density function through the shape parameter, and capture the phenomenon of the frequent occurrence of extreme values in the observed data. The 5G/INS tightly coupled model is localized with high accuracy and continuity by using variational Bayesian strong tracking filtering based on the above model;
- (2)
- In this paper, a hierarchical fault detection structure is proposed, which adopts the rationality detection based on the combination of hierarchical voting mechanism and wavelet analysis to screen the boundary of the observation data output from the inertial components, so as to deal with the abrupt change phenomenon in time, and adopts the consistency of two-channel detection of dynamic fault tolerance management to focus on the temporal correlation, which ensures the continuity and convergence of the evolutionary trajectory of the navigation data in the neighboring cycles and improves the positioning system’s robustness. After fault identification, this paper proposes a robust fault proposal and compensation scheme to reduce the impact of faults on the localization system.
2. 5G/INS Fusion Positioning System Model
2.1. 5G/INS Tightly Coupled Localization Equation of State
2.2. 5G/INS Fusion Positioning Measurement Equation
3. Strong Tracking Fusion Filtering Method Based on Variational Bayesian
3.1. Variational Bayesian Filtering
3.1.1. KL Divergence
3.1.2. Mean Field Theory
3.1.3. Variational Bayesian Solution Process
3.2. Variational Bayesian Anti-Noise Filtering Method Based on 5G/INS Positioning System
3.3. Strong Tracking Correction Method Based on Dynamic Asymptotic Factors
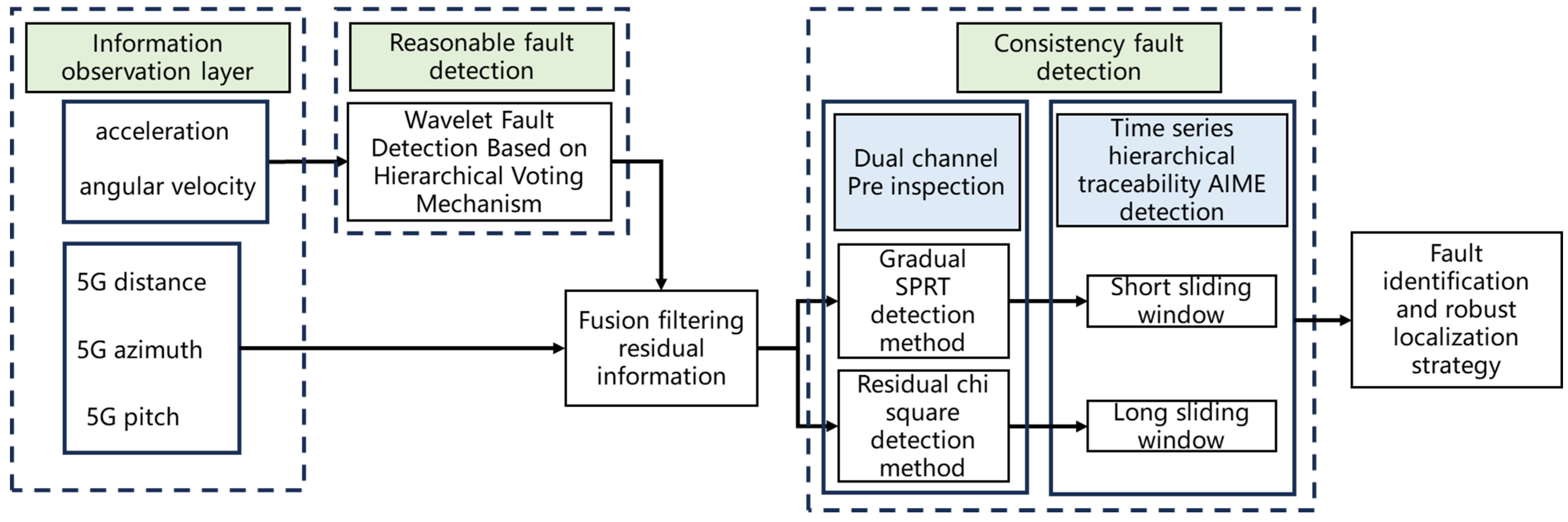
4. Multi-Layer Based Fault Detection Method for 5G/INS
4.1. IMU Observation Information Rationality Fault Detection Method Based on the Combination of Hierarchical Voting Mechanism and Wavelet Analysis
4.2. Coherent Dual-Channel System Cooperative Fault Detection Method Based on Dynamic Fault Tolerance Management
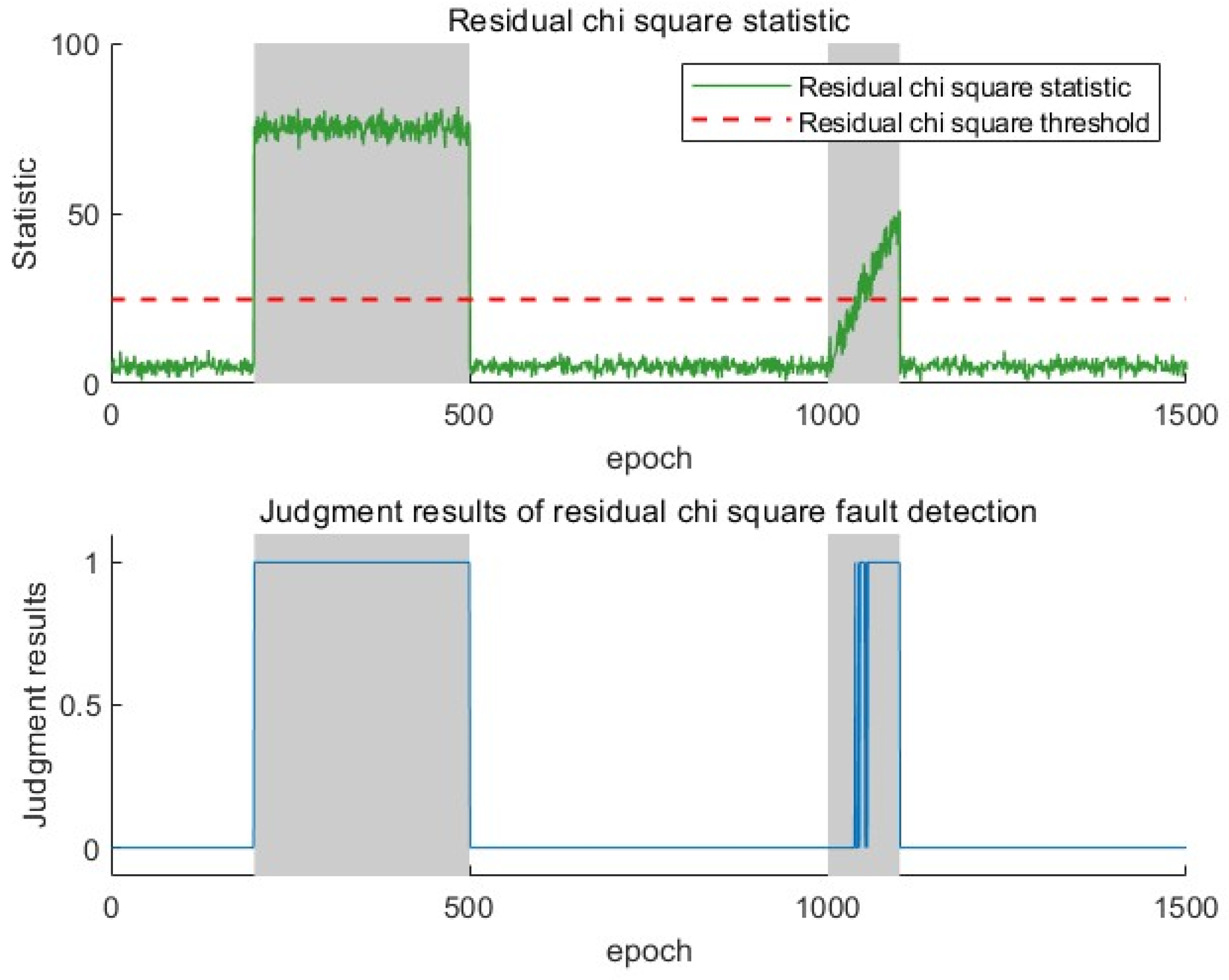
4.2.1. Residual Chi-Square Detection
4.2.2. Gradual SPRT Detection
4.2.3. AIME Detection
4.2.4. Time-Series Hierarchical Traceability Fault Consistency Detection Method Based on Dynamic Fault-Tolerant Management Mechanism
4.2.5. Fault Source Identification Method and Fault Repair Strategy Based on AIME
5. Experiments and Discussions
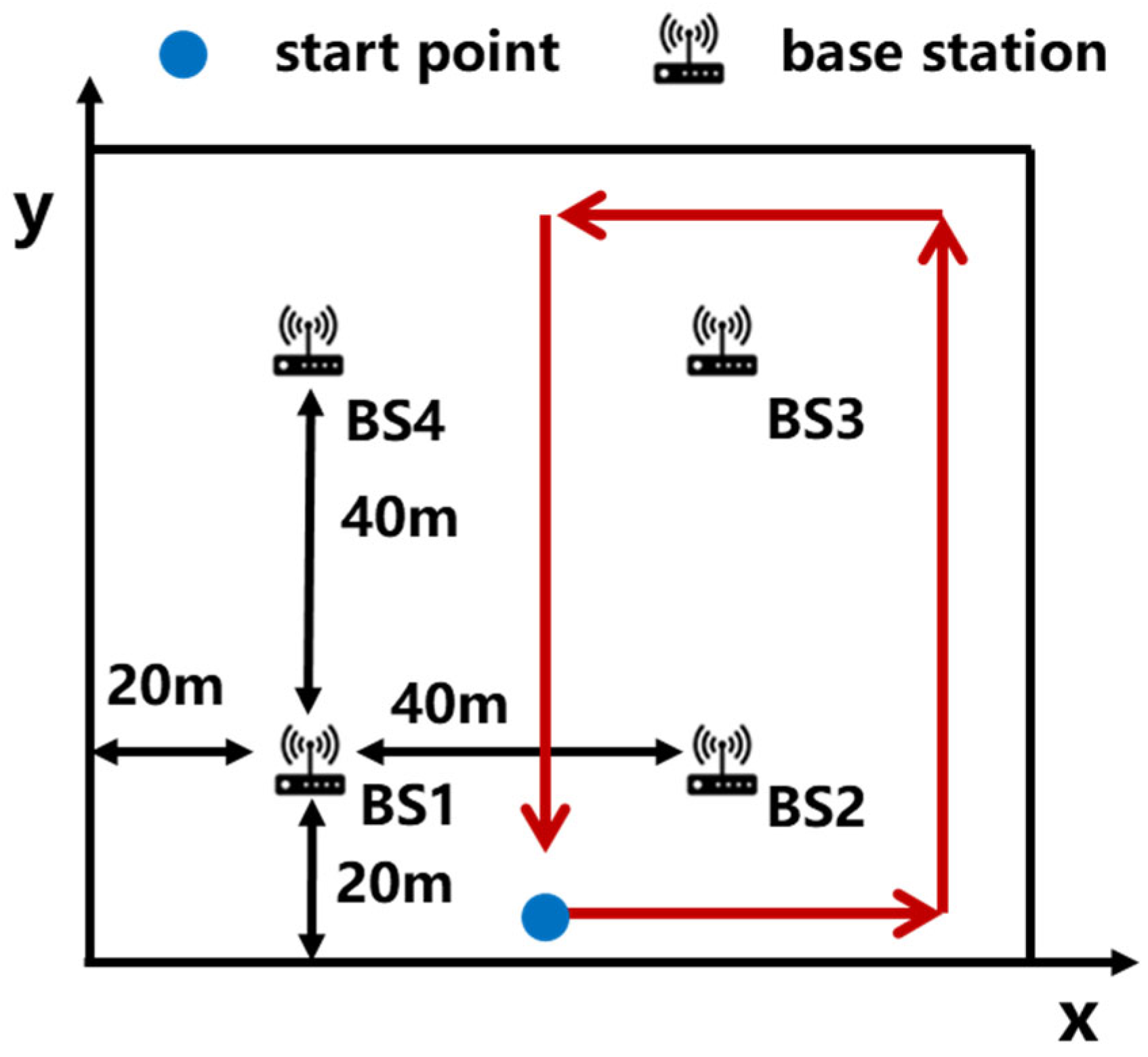
5.1. Experimental Environment and Parameter Settings
5.2. Test Results and Performance Analysis
5.2.1. Validation of Fault Detection Methods for Rationalization of IMU Observation Information
5.2.2. Validation of a Cooperative Fault Detection Method for Coherent Dual-Channel Systems with Dynamic Fault Tolerance Management
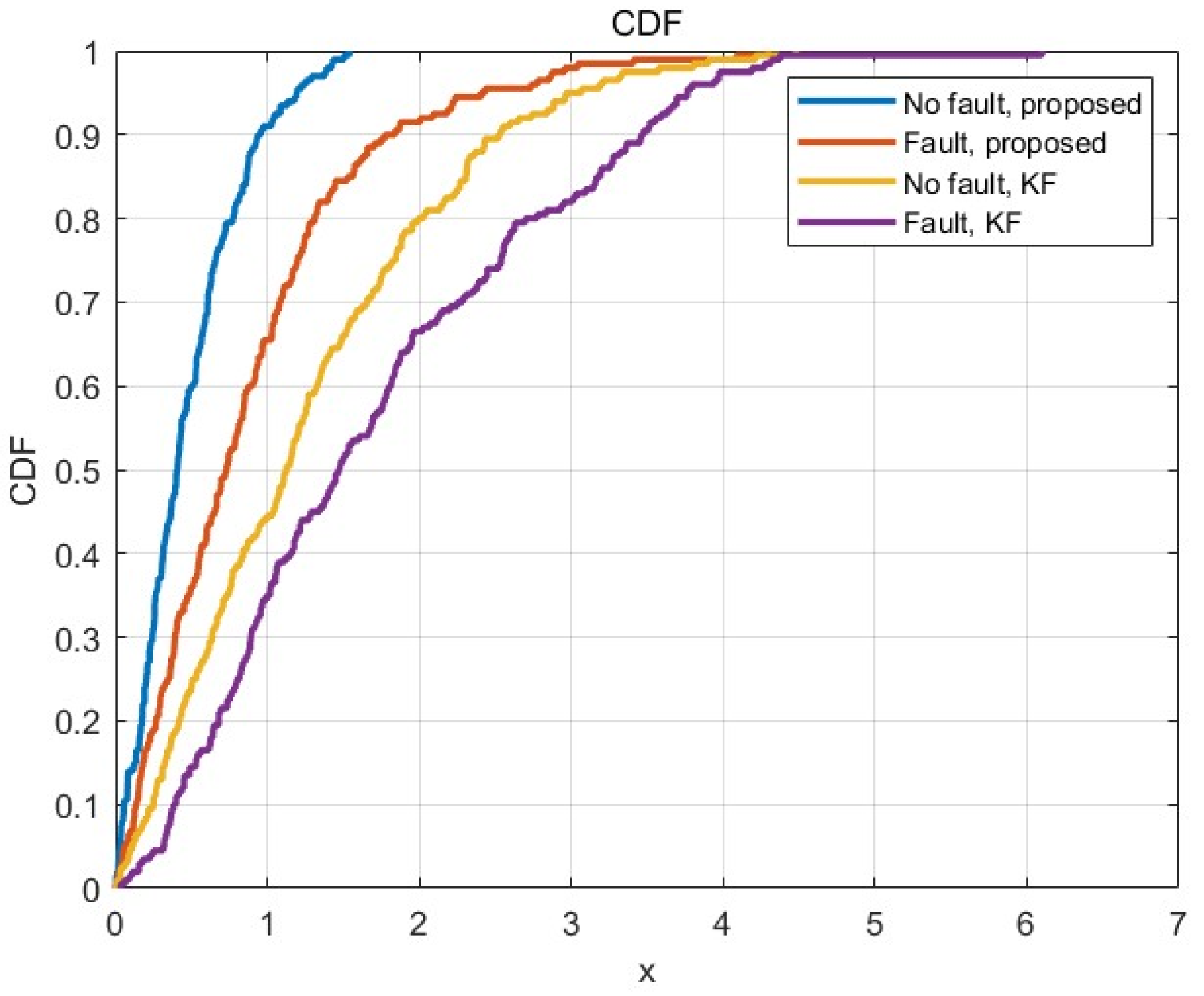
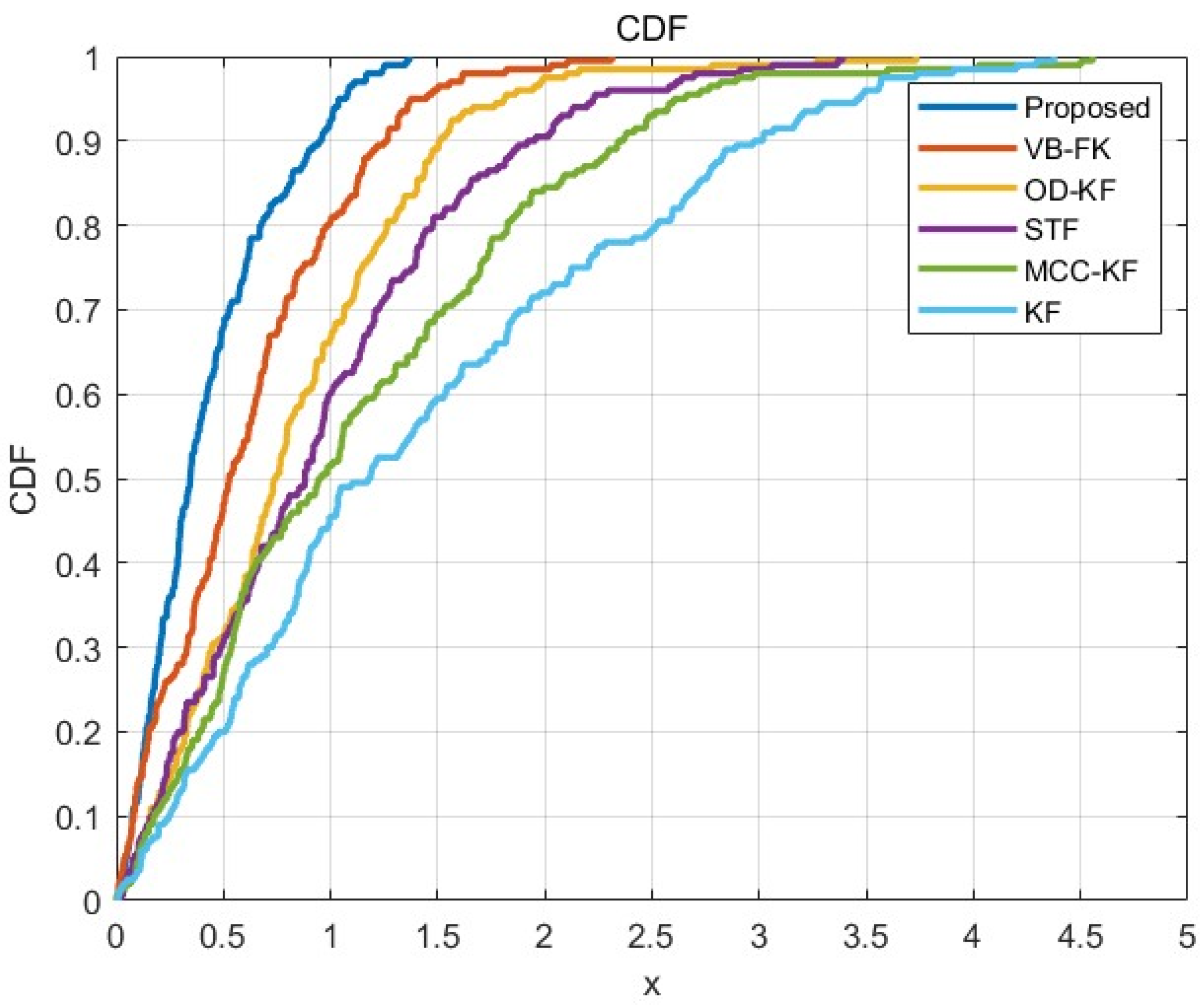
5.2.3. Validation of Strong Tracking Filtering Methods Based on Variational Bayesian
6. Summarize
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- LOS. Navigation for Aviation; Wiley-IEEE Press: Hoboken, NJ, USA, 2021. [Google Scholar]
- Fujii, Y.; Iye, T.; Tsuda, K.; Tanibayashi, A. A 28 GHz Beamforming Technique for 5G Advanced Communication Systems. In Proceedings of the 2022 24th International Conference on Advanced Communication Technology (ICACT), PyeongChang, Republic of Korea, 13–16 February 2022; pp. 96–99. [Google Scholar]
- Sun, B.; Tan, B.; Wang, W.; Lohan, E.S. A Comparative Study of 3D UE Positioning in 5G New Radio with a Single Station. Sensors 2021, 21, 1178–1183. [Google Scholar] [CrossRef] [PubMed]
- 3GPP. Study on NR Positioning, Support (Release 16). Technical Specification ’Ts 38.855, 30, 2019. Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationld=3501 (accessed on 28 March 2019).
- Papp, Z.; Irvine, G.; Smith, R.; Mogyorosi, F.; Revisnyei, P.; Toros, I.; Pasic, A. TDoA based indoor positioning over small cell 5G networks. In Proceedings of the IEEE/IFIP Network Operations and Management Symposium (NOMS), Budapest, Hungary, 25–29 April 2022; IEEE: Piscataway, NJ, USA; IFIP: Laxenburg, Austria, 2022; pp. 1–6. [Google Scholar]
- Menta, E.Y.; Malm, N.; Jäntti, R.; Ruttik, K.; Costa, M.; Leppänen, K. On the Performance of AoA-based Localization in 5G Ultra-dense Networks. IEEE Access 2019, 7, 33870–33880. [Google Scholar] [CrossRef]
- Woodman, O.J. An Introduction to Inertial Navigation; Tech. Rep. UCAM-CLTR-696; Computer Laboratory, University of Cambridge: Cambridge, UK, 2007. [Google Scholar]
- Grewal, M.S.; Weill, L.R.; Andrews, A.P. Global Positioning Systems, Inertial Navigation, and Integration; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Kalman, R.E. A New Approach To Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Wang, Y.; Papageorgiou, M. Real-time Freeway Traffic State Estimation Based on Extended Kalman Filter: A General Approach. Transp. Res. Part B 2007, 39, 11–17. [Google Scholar] [CrossRef]
- Wan, E.A.; van der Merwe, R. The Unscented Kalman Filter; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Xu, T.L. Research on Federated Kalman Filter for Integrated Navigation System. In Proceedings of the 2011 Third Pacific-Aisa Conference on Circuits, Communications and System (PACCS), Wuhan, China, 17–18 July 2011; pp. 77–80. [Google Scholar]
- Arasaratnam, I.; Haykin, S. Cubature kalman filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Sarkka, S.; Nummenmaa, A. Recursive Noise Adaptive Kalman Filtering by Variational Bayesian Approximations. IEEE Trans. Autom. Control 2009, 54, 596–600. [Google Scholar] [CrossRef]
- Li, R.H.; Zhang, R.L.; Lyu, T.C.; Sheng, W.X. ISRJ identification method based on Chi-square test and range equidistant detection. In Proceedings of the International Conference on Microwave and Millimeter Wave Technology, Qingdao, China, 14–17 May 2023; pp. 1–3. [Google Scholar]
- Wang, Q.; Ke, Y.; Miao, Y.Z.; Chen, H.X. Application of the sequential probability ratio test in the detection of a nonlinear Lamb wave. Noise Vib. Control 2021, 41, 98–102. [Google Scholar]
- Ren, X.Y. SINS/GPS/OD Fault-Tolerant Combined Navigation System Study. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2019. [Google Scholar]
- Yang, J. Research on Information Transmission and Fault Detection of Distributed Multi-Source Fusion Autonomous Navigation System. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2014. [Google Scholar]
- Wang, R.; Xiong, Z.; Liu, J.; Xu, J.; Shi, L. Chi-square and SPRT combined fault detection for multisensor navigation. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1352–1365. [Google Scholar] [CrossRef]
- Deng, Z.; Ma, Z. An High Efficiency Angle and Range Estimation Method for Three-Dimensional Near-Field Sources Based on Higher-Order Cumulants. IEEE Wirel. Commun. Lett. 2024, 13, 2857–2861. [Google Scholar] [CrossRef]
- Chen, B.D.; Liu, X.; Zhao, H.Q. Maximum Correntropy Kalman Filter. Automatica 2017, 76, 70–77. [Google Scholar] [CrossRef]
- Roth, M.; Ozkan, E.; Gustafsson, F. A Student’s t Filter for Heavy Tailed Process and Measurement Noise. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013. [Google Scholar]
- Wang, H.W.; Li, H.B.; Fang, J.; Wang, H.P. Robust Gaussian Kalman filter with Outlier Detection. IEEE Signal Process. Lett. 2018, 25, 1236–1240. [Google Scholar] [CrossRef]
- Huang, Y.L.; Zhang, Y.G.; Li, N.; Wu, Z.M. A novel Robust Student’s Based Kalman Filter. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1545–1554. [Google Scholar] [CrossRef]








| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Carrier Frequency | 3.5 GHz | 5G Bandwidth | 100 M |
| Subcarrier spacing | 60 kHz | Goniometric Antenna Array | 4 × 4 |
| Fast Fourier Transform Points | 4096 | Number of resource blocks | 272 |
| 5G Sampling Frequency | 100 Hz | INS Sampling Frequency | 100 Hz |
| Gyro constant drift | Accelerometer Constant Zero Bias | 50 μg | |
| Gyroscope random wander | Accelerometer Random Zero Bias | 5 μg |
| Fault Source | Fault Time | Fault Type | Fault Model |
|---|---|---|---|
| 5G distance | 20–50 s | sudden fault | 10 m |
| 5G pitch | 100–110 s | slow change fault | 0.5 × (t − 100) |
| 5G azimuth | 100–110 s | slow change fault | 0.3 × (t − 100) |
| Fault Detection Method | Sudden Change Fault Begins | Sudden Change Fault Ends | Gradual Change Fault Begins | Gradual Change Fault Ends | Fault Source Identification |
|---|---|---|---|---|---|
| Residual chi-square detection | No delay | No delay | Delay 34 epoch | No delay | Unrecognized |
| SPRT | Delay 8 epoch | Failure to detect the end of the first fault in the sequence and long-term false alarm | Unrecognized | ||
| Gradually eliminating SPRT + Zero setting strategy | Delay 8 epoch | Delay 17 epoch | Delay 7 epoch | Delay 19 epoch | Unrecognized |
| Residual chi-square –gradual SPRT dual channel detection | No delay | No delay | Delay 7 epoch | No delay | Unrecognized |
| Residual chi-square–gradual SPRT dual channel detection + AIME | No delay | No delay | Delay 7 epoch | No delay | The sudden fault is the distance measurement information of the base station 2, and the gradual fault is the direction angle and elevation angle of base station 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Z.; Ma, Z.; Luo, H.; Guo, J.; Tian, Z. A Fault-Tolerant Localization Method for 5G/INS Based on Variational Bayesian Strong Tracking Fusion Filtering with Multilevel Fault Detection. Sensors 2025, 25, 3753. https://doi.org/10.3390/s25123753
Deng Z, Ma Z, Luo H, Guo J, Tian Z. A Fault-Tolerant Localization Method for 5G/INS Based on Variational Bayesian Strong Tracking Fusion Filtering with Multilevel Fault Detection. Sensors. 2025; 25(12):3753. https://doi.org/10.3390/s25123753
Chicago/Turabian StyleDeng, Zhongliang, Ziyao Ma, Haiming Luo, Jilong Guo, and Zidu Tian. 2025. "A Fault-Tolerant Localization Method for 5G/INS Based on Variational Bayesian Strong Tracking Fusion Filtering with Multilevel Fault Detection" Sensors 25, no. 12: 3753. https://doi.org/10.3390/s25123753
APA StyleDeng, Z., Ma, Z., Luo, H., Guo, J., & Tian, Z. (2025). A Fault-Tolerant Localization Method for 5G/INS Based on Variational Bayesian Strong Tracking Fusion Filtering with Multilevel Fault Detection. Sensors, 25(12), 3753. https://doi.org/10.3390/s25123753







